Numerical solution of systems of fractional delay differential equations using a new kind of wavelet basis

Abstract

In the present paper, a new orthonormal wavelet basis, called Chelyshkov wavelet, is constructed from a class of orthonormal polynomials. These wavelet basis and their properties are utilized to obtain their operational matrix of fractional integration in the Riemann–Liouville sense and delay operational matrix. Convergence and error bound of the expansion by this kind of wavelet functions are investigated. Then, these operational matrices along with the Galerkin approach have been implemented to solve systems of fractional delay differential equations (SFDDEs). The main superiority of the proposed technique is that it reduces SFDDEs to a system of algebraic equations. Moreover, accuracy and efficiency of the suggested Chelyshkov wavelet approach are verified through some linear and nonlinear SFDDEs. Finally, the obtained numerical results are compared with those previously reported in the literature.

1 Introduction

It has been found that integer-order calculus is not an appropriate tool for modeling complex systems in science and engineering. The non-integer order differentiation and integration, which is known as fractional calculus, has been recently applied to model many fundamental problems in science and engineering (Oldham and Spanier 1974; Podlubny 1998; Samko et al. 1993). Recently, fractional functional equations have found many applications in various fields of engineering and physics such as colored noise, signal processing, electromagnetism, electrochemistry, continuum and statistical mechanics, solid mechanics and fluid-dynamic traffic and viscoelasticity (Baleanu et al. 2016; Dehghan et al. 2017; Cattani et al. 2017; Srivastava et al. 2017). Therefore, there has been a remarkable attention paid to approximate solution of fractional differential and integral equations (Mohammadi and Ciancio 2017; Jajarmi and Baleanu 2017; Heydari et al. 2017; Mardani et al. 2017).

Recently, delay differential equations (DDEs) have been frequently applied for analysis and predictions in different areas of science and engineering such as economy, control, biology, electrodynamics, medicine and chemistry (Walter et al. 1992; Kuang 1993; Malek-Zavarei and Jamshidi 1987). Contrary to ordinary differential equations (ODEs), DDEs allow the inclusion of former state into mathematical models, thus making it more closer to the real-world phenomenon. Because of these important applications, many researches have been focused on DDEs and their numerical solution. For example, Adams–Bashforth–Moulton method (Wang 2013), Adomian decomposition method (Evans and Raslan 2005), variational iteration method (Yu 2008), hybrid functions (Marzban and Razzaghi 2006), polynomial spectral methods (Hwang and Chen 1986; Ali et al. 2009; Sedaghat et al. 2012; Yang and Huang 2013; Khader and Hendy 2012; Tohidi et al. 2012; Davaeifar and Rashidinia 2017), wavelet methods (Ghasemi and Tavassoli 2011; Sedighi Hafshejani et al. 2011; Saeed and Rehman 2014; Rahimkhani et al. 2017), Laplace transform (Widatalla et al. 2012) and optimal perturbation method (Bildik and Deniz 2017) have been employed to solve DDEs.

Over the last two decades, orthogonal functions and spectral methods have received great attention and became an important tool for solving differential and integral equations. According to structure of orthogonal functions, they are usually classified into main three families: piecewise constant functions (Haar, Walsh, block-pulse, etc.), orthogonal polynomials (Legendre, Chebyshev, Laguerre, etc.) and trigonometric functions (Mohammadi 2016a; Mohammadi and Ciancio 2017; Heydari et al. 2017; Marzban and Razzaghi 2006). In spite of the fact that trigonometric functions and orthogonal polynomials have good convergence behaviour for numerical solution of differential and integral equations, their application to problems with non-analytical solution or coefficients, involves some deficiency. Furthermore, expanding a continuous function with piecewise functions results in a piecewise constant function. Orthogonal wavelet is a special type of orthogonal functions with compact support and ability to represent functions at different levels of resolution. Wavelets have been applied in a wide range of science and engineering fields. For instance, wavelets found many applications in numerical analysis, waveform representation, signal analysis, optimal control and time–frequency analysis (Mohammadi 2016a, b; Rahimkhani et al. 2017).

The main aim of this study is to construct a new kind of orthonormal wavelet basis, called Chelyshkov wavelet, using the Chelyshkov orthogonal polynomials. Some operational matrices for these wavelet functions are introduced and their general formulation will be presented. By using these orthogonal wavelet functions and their operational matrices, an efficient Galerkin method is proposed to approximate solution of SFDDEs. The obtained numerical results illustrate that the presented wavelet method is more efficient and accurate than other existing methods.

The structure of this paper is organized as follows: In Sect. 2, some introductory definitions of fractional derivatives and integrals are presented. Section 3 is devoted to the Chelyshkov wavelet and their properties. Convergence and error bound of the Chelyshkov wavelets expansion are provided in Sect. 4. The operational matrix of fractional integration and delay operational matrix for the Chelyshkov wavelet basis have been derived in Sect. 5. In Sect. 6, an efficient wavelet Galerkin method is proposed to solve SFDDEs. Some illustrative examples are given in Sect. 7. Eventually, some concluding remarks are drawn in Sect. 8.

2 Preliminary remarks on fractional calculus

Fractional order calculus deals with the non-integer order differentiation and integration. Although the fractional order operators enable to model a wider class of problems, there is not a unique definition of fractional derivative. The most customarily used definitions for fractional integral and derivative are the Riemann–Liouville and Caputo definitions, which can be defined as follows (Podlubny 1998):

Definition 1

The Riemann–Liouville fractional integration of order $\nu \ge 0$ may be defined as:

$$\begin{aligned} (I^{\nu }f)(t)=\left\{ \begin{array}{ll} \frac{1}{\Gamma (\nu )}\int _{0}^{t}{(t-\tau )^{\nu -1}{f(\tau )}\,\mathrm{d}\tau },&{}\quad \nu >0,\\ f(t), &{}\quad \nu =0. \end{array} \right. \end{aligned}$$

The following properties of the Riemann–Liouville fractional integral operator $I^\nu$ can be easily verified:

$$\begin{aligned}&I^{\nu _1} ({I}^{\nu _2} f(t)) = I^{\nu _2}( I^{\nu _1} f(t)),\quad \nu _1, \nu _2 \ge 0, \\&I^{\nu _1} (I^{\nu _2} f(t))=I^{\nu _1 + \nu _2} f(t),\quad \nu _1, \nu _2 \ge 0,\\&I^\nu t^\lambda = \frac{\Gamma (\lambda +1)}{\Gamma (\lambda + \nu + 1)}t^{\nu + \lambda },\quad \nu \ge 0,\ \lambda >-1. \end{aligned}$$

Definition 2

For a real number $\nu >0$, the Caputo fractional derivative ${\mathcal {D}}^{\nu }$ is defined as:

$$\begin{aligned} {\mathcal {D}}^{\nu }f(t)=\left\{ \begin{array}{ll} \frac{\mathrm{d}^{n}f(t)}{\mathrm{d}t^{n}}, &{}\quad \nu =n \in {\mathbb {N}},\\ \frac{1}{\Gamma (n-\nu )}\int _{0}^{t}{\frac{f^{(n)}(\tau )}{(t-\tau )^{\nu -n+1}}\,\mathrm{d}\tau },\ t>0,&{}\quad 0 \le n-1<\nu < n. \end{array}\right. \end{aligned}$$

where n is an integer, $t>0$.

Some practical and useful properties of the Caputo fractional operator ${\mathcal {D}}^{\nu }$ can be provided in the following expressions:

$$\begin{aligned}&I^{\nu }D^{\nu } f(t)=f(t)-\sum _{k=0}^{n-1}{f^{(k)}(0^{+})}\frac{t^{k}}{k!},\quad t>0.\\&{\mathcal {D}}^{\nu } I^{\nu } f(t)= f(t).\\&{\mathcal {D}}^{\nu } t^{\lambda }=\left\{ \begin{array}{ll} 0,&{}\quad \hbox {for }\lambda \in {\mathbb {N}}_{0} \hbox { and }\lambda < \nu ,\\ \frac{{\Gamma (\lambda + 1)}}{{\Gamma (\lambda - \nu + 1)}}t^{\lambda - \nu },&{} \quad \hbox {otherwise}. \end{array} \right. \end{aligned}$$

For more details on the fractional derivatives and integrals, the interested reader is referred to Podlubny (1998) and Oldham and Spanier (1974).

3 Chelyshkov wavelets

The main aim of the current section is to construct the Chelyshkov wavelet basis. First, we introduce some useful properties of the Chelyshkov polynomials which are given in Chelyshkov (2006) and Gokmen et al. (2017). Then, the Chelyshkov wavelet will be constructed using the Chelyshkov polynomials and their properties.

3.1 Basic definition of Chelyshkov polynomials

The Chelyshkov polynomials are one of the latest classes of orthogonal polynomials introduced by Chelyshkov (2006) and Gokmen et al. (2017). The Chelyshkov polynomials are explicitly defined by

$$\begin{aligned} \rho _{n,M}(t)=\sum _{j=0}^{M-n}a_{j,n}t^{n+j},\quad n=0,1,\ldots ,M, \end{aligned}$$

(1)

in which

$$\begin{aligned} {a_{j,n}} = {(-1)^{j}}\left( \begin{array}{c} M- n\\ j \end{array} \right) \left( \begin{array}{c} M+n+j+1\\ M-n \end{array} \right) . \end{aligned}$$

(2)

These polynomials are orthogonal over the interval [0, 1] with respect to the weight function $w(t)=1$ and

$$\begin{aligned} \int _{0}^{1}{\rho _{n,M}(t)}{\rho _{m,M}(t)}\,\mathrm{d}t=\frac{\delta _{mn}}{m+n+1}, \end{aligned}$$

where $\delta _{mn}$ is Kronecker delta. Furthermore, these polynomials may be derived with the aid of the Rodrigues’ formula as:

$$\begin{aligned} {\rho _{n,M}(t)} = \frac{1}{{(M- n)!}}\frac{1}{{{t^{M- n}}}}\frac{{{\mathrm{d}^{M- n}}}}{{\mathrm{d}{t^{M- n}}}}({t^{M+ n + 1}}{(1-t)^{M - n}}),\quad n=0,\ldots , M. \end{aligned}$$

According to definition of the Chelyshkov polynomials, it is clear that for a fixed integer number M, the functions ${\rho _{n,M}(t)},n=0,1,\ldots ,M$ are polynomials exactly of degree M. This may be the key difference between the Chelyshkov polynomials and other typical orthogonal polynomials in the interval [0, 1], such as shifted Legendre polynomials (Mohammadi and Hosseini 2011), shifted Chebyshev polynomials (Bhrawy and Alofi 2013) and shifted Chebyshev polynomial of the second kind (Mohammadi 2016c), where the kth polynomial has degree k. The graph of shifted Chebyshev polynomials, shifted Legendre polynomials, shifted Chebyshev polynomial of the second kind and Chelyshkov polynomials for $M=4$ is plotted in Fig. 1. It is worth mentioning that the Chelyshkov polynomials are orthogonal with respect to the weight $w(t)=1$. Therefore, their application to approximate solution of functional equations is more efficient and reliable in comparison to the Chebyshev polynomial of the second kind and shifted Chebyshev polynomials. Any integrable function f(t) on the interval [0, 1) could be expressed by Chelyshkov polynomials as:

$$\begin{aligned} f(t) \simeq \sum \limits _{i = 0}^{M} {c_i {\rho _{i,M}(t)}}=C^{\mathrm{T}}\Phi (t), \end{aligned}$$

(3)

where B and $\Phi (x)$ are $(M+1)$ vectors given by

$$\begin{aligned} C= [c_0, c_1,\ldots , c_M],\quad \Phi (t) = [{{\rho _{0,M}(t)}, {\rho _{1,M}(t)},\ldots , {\rho _{M,M}(t)}}]. \end{aligned}$$

(4)

and

$$\begin{aligned} c_{i}=(2i+1)\int _{0}^{1} {{\rho _{i,M}(t)}f(t)}\,\mathrm{d}t. \end{aligned}$$

(5)

Fig. 1

The graph of orthogonal polynomials in the interval [0, 1]. a The Chelyshkov polynomials, b the shifted Legendre polynomials, c the shifted Chebyshev polynomials, d the shifted Chebyshev polynomial of the second kind

3.2 Construction of Chelyshkov wavelets

Wavelets are a set of functions which can be defined from dilation and translation of a mother wavelet function $\psi$. As the dilation and translation parameters vary continuously, we have a family of continuous wavelets functions (Mohammadi and Ciancio 2017; Rahimkhani et al. 2017). The Chelyshkov wavelets $\psi _{nm} (x)$ are defined on the interval [0, 1) by

$$\begin{aligned} \psi _{nm}(t)=\left\{ \begin{array}{ll} \sqrt{2m+1}2^{\frac{k}{2}}{\rho _{m,M}}(2^{k}t-n) &{} \quad \frac{n}{2^{k}}\le t< \frac{n+1}{2^{k}}\\ 0 &{}\quad \hbox {otherwise}, \end{array}\right. \end{aligned}$$

(6)

where $n=0,1,\ldots ,2^{k}-1$ and $m=0,1,\ldots ,M$ and ${\rho _{m,M}(t)}$ are the Chelyshkov polynomials of degree m defined in (1). The set of Chelyshkov wavelets $\psi _{nm}(t),n=0,1,\ldots ,2^{k}-1, m=0,1,\ldots ,M$ constitutes an orthonormal set on the interval [0, 1]. For $M=3$ and $k=1$, the set of Chelyshkov wavelets $\psi _{nm}(t),n=0,1, m=0,1, 3$ can be derived as:

$$\begin{aligned} \psi _{00}(t)= & {} \left\{ \begin{array}{ll} 4\sqrt{2} ( -70{t}^{3}+60{t}^{2}-15t+1),&{}\quad 0 \le t< \frac{1}{2}, \\ 0&{}\quad \frac{1}{2} \le t<1, \end{array} \right. \\ \psi _{01}(t)= & {} \left\{ \begin{array}{ll} 4\sqrt{6} (42{t}^{3}-30t^{2}+5t ), &{}\quad 0 \le t< \frac{1}{2}, \\ 0&{}\quad \frac{1}{2} \le t<1, \end{array} \right. \\ \psi _{02}(t)= & {} \left\{ \begin{array}{ll} 8\sqrt{10}(-7t^{2}+3t^{2}),&{}\quad 0 \le t< \frac{1}{2}, \\ 0&{} \quad \frac{1}{2} \le t<1, \end{array} \right. \\ \psi _{03}(t)= & {} \left\{ \begin{array}{ll} 8\sqrt{14}{t}^{3},&{}\quad 0 \le t< \frac{1}{2}, \\ 0,&{}\quad \frac{1}{2} \le t<1, \end{array} \right. \\ \psi _{10}(t)= & {} \left\{ \begin{array}{ll} 0,&{}\quad 0 \le t< \frac{1}{2}, \\ \sqrt{2} ( -280{t}^{3}+660{t}^{2}-510t+129),&{}\quad \frac{1}{2} \le t<1, \end{array} \right. \\ \psi _{11}(t)= & {} \left\{ \begin{array}{ll} 0 &{}\quad 0 \le t< \frac{1}{2},\\ \sqrt{6} ( 168\,{t}^{3}-372\,{t}^{2}+266\,t-61 ),&{} \quad \frac{1}{2} \le t<1, \end{array} \right. \\ \psi _{12}(t)= & {} \left\{ \begin{array}{ll} 0&{}\quad 0 \le t< \frac{1}{2}, \\ \sqrt{10} ( -56{t}^{3}+108{t}^{2}-66t+13) &{}\quad \frac{1}{2} \le t<1, \end{array} \right. \\ \psi _{13}(t)= & {} \left\{ \begin{array}{ll} 0 &{}\quad 0 \le t< \frac{1}{2},\\ \sqrt{14} (2t-1)^{3},&{}\quad \frac{1}{2} \le t <1. \end{array} \right. \end{aligned}$$

Based on definition of the Chelyshkov wavelet, it is clear that the wavelet $\psi _{nm}(t)$ is a polynomial of degree M over the interval $[{\frac{n}{{2^k }},\frac{{n + 1}}{{2^k }}})$. Moreover, any square-integrable function f(t) over [0, 1) can be expressed with the aid of Chelyshkov wavelets as:

$$\begin{aligned} f(t) \simeq f_{M,k}(t)= \sum _{n=0}^{2^{k}-1}\sum _{m=0}^{M}{c_{nm}\psi _{nm}(x)=C^{\mathrm{T}}\Psi (t)}, \end{aligned}$$

(7)

where C and $\Psi (t)$ are ${\hat{m}}=2^{k}(M+1)$ vectors given as:

$$\begin{aligned}&C=\left[ c_{00},\ldots , c_{0(M-1)},\ldots , c_{(2^{k}-1)0}, \ldots , c_{(2^{k}-1)(M-1)}\right] ^{\mathrm{T}},\\&\Psi (x)=\left[ \psi _{00}(x),\ldots ,\psi _{0M}, \ldots , \psi _{2^{k}-1)0}(x),\ldots ,\psi _{(2^{k}-1)M}(x)\right] ^{\mathrm{T}}. \end{aligned}$$

and

$$\begin{aligned} c_{nm}= \langle {{\psi _{nm}}(t), f(t)}\rangle =\int _0^1 {\psi _{nm}(t)f(t)}\,\mathrm{d}t. \end{aligned}$$

(8)

The expansion (7) may be rewritten as:

$$\begin{aligned} f_{M,k}(x) = \sum \limits _{i = 1}^{{\hat{m}}} {c_i \psi _{i}(x)}=C^{\mathrm{T}}\Psi (x), \end{aligned}$$

where

$$\begin{aligned} C = [c_1, c_2,\ldots ,c_{{\hat{m}}}],\quad \Psi (x) = [ {\psi _{1}(x),\psi _{2}(x),\ldots ,\psi _{{\hat{m}}}(x)}], \end{aligned}$$

(9)

and

$$\begin{aligned} c_i = c_{nm},\quad \psi _{i}(x) = \psi _{nm}(x),\qquad i = n(M+1) + m +1. \end{aligned}$$

4 Convergence analysis

In this section, some theorems on convergence and error bound of the Chelyshkov polynomials and wavelets expansion have been presented. Hereafter, $\Vert . \Vert _{2}$ denotes the $L^{2}[0, 1]$ norm defined by

$$\begin{aligned} \Vert f\Vert ^{2}_{2} = {\int _0^1 {|{f(t)}|}^2}(t)\,\mathrm{d}t. \end{aligned}$$

Theorem 4.1

Let $f(t) \in C^{m+1}[0, 1]$ is expanded with the aid of the Chelshkov polynomials as : 

$$\begin{aligned} f(t) \simeq f_{M}(t)=\sum \limits _{i = 0}^{M} {c_i \rho _{i} (t)}, \end{aligned}$$

(10)

then

$$\begin{aligned} \Vert {f(t) - f_M (t)}\Vert _2 t \le \frac{L}{{\sqrt{(2M + 3)} (M + 1)!}}, \end{aligned}$$

(11)

where $L = \max _{t \in [0,1]}|{f^{(M + 1)} (t)}|.$

Proof

Let the polynomial q(t) be defined as:

$$\begin{aligned} q(t)=f(0)+f^{\prime }(0)t+\frac{f^{\prime \prime }(0)t^{2}}{2!} +\cdots +\frac{f^{(M)}(0)t^{M}}{M!}, \end{aligned}$$

(12)

using the Taylor expansion, there exists $\xi \in (0,1)$ such that

$$\begin{aligned} |{f(t) - q(t)}|=\left| {\frac{{f^{(M + 1)}(\xi )t^{M+1}}}{{(M + 1)!}}} \right| . \end{aligned}$$

(13)

Now, making use of the best approximation property of $f_{M}(t)$ (Kreyszig 1978), we get

$$\begin{aligned} \Vert {f(t) - f_M (t)}\Vert _2^2 \le \Vert {f(t) - q(t)}\Vert _2^2 = \int _0^1 {\left( {\frac{{f^{(m + 1)} (t)t^{M + 1} }}{{(M + 1)!}}} \right) ^2 }\,\mathrm{d}t \le \frac{{L^2 }}{{(2M + 3)(M + 1)!^2 }}, \end{aligned}$$

so the proof will be completed by taking the square root of both sides of this inequality. $\square$

Theorem 4.2

Assume that $f(t) \in C^{m+1}[0, 1]$ is an arbitrary function approximated by the Chelshkov wavelet series as

$$\begin{aligned} f(t)\simeq f_{{{\hat{m}}}} (t) = \sum \limits _{i = 1}^{{{\hat{m}}}} {c_i \psi _i (t)}, \end{aligned}$$

then we have

$$\begin{aligned} \mathop {\lim }\limits _{{{\hat{m}}} \rightarrow \infty } \Vert {f(t) - f_{{{\hat{m}}}} (t)}\Vert = 0. \end{aligned}$$

Proof

According to the definition of $f_{{{\hat{m}}}} (t)$, we have

$$\begin{aligned} \Vert {f(t) - f_{{{\hat{m}}}} (t)}\Vert _{2}^{2}= & {} \int _{0}^{1} {( {f(t) - f_{{{\hat{m}}}} (t)})^2\,\mathrm{d}t = \int _{0}^{1} {\left( {f(t) - \sum \limits _{n = 0}^{2^{k} - 1} {\sum \limits _{m = 0}^M {c_{nm} \psi _{nm} (t)} } } \right) ^2\,\mathrm{d}t}}\\= & {} \sum \limits _{n = 0}^{2^k - 1} {\int _{\frac{n}{{2^k }}}^{\frac{{n + 1}}{{2^k }}} {\left( {f(t) - \sum \limits _{m = 0}^M {c_{nm} \psi _{nm} (t)} } \right) ^2 } }, \end{aligned}$$

using the change of variable $z=2^{k}t-n$ in $2^{k}$ terms of above relation, we get

$$\begin{aligned}&\quad =\sum \limits _{n = 0}^{2^k - 1} {\int _0^1 {\left( {f\left( {\frac{{z + n}}{{2^k }}} \right) - \sum \limits _{m = 0}^M {c_{nm} \psi _{nm} \left( {\frac{{z + n}}{{2^k }}} \right) } } \right) ^2}}\,\mathrm{d}z\\&\quad =\sum \limits _{n = 0}^{2^k - 1} {\int _0^1 {\left( {g_{k}(z) - \sum \limits _{m = 0}^M {c_{nm} \rho _m (z)} } \right) ^2\,\mathrm{d}z} }\\&\quad =\sum \limits _{n = 0}^{2^k - 1} {\Vert {g_n (z) - g_{n,M} (z)}\Vert _2^2 } \end{aligned}$$

in which $g_{n}(z)=\frac{1}{{\sqrt{2m + 1} }}f( {\frac{{z + n}}{{2^k }}})$ and $g_{n,M}(z)$ is its Chelshkov polynomial approximation. Now, make the use of Theorem 4.1 for the functions $g_{n}(z), n=0,1,\ldots ,2^{k}-1$, we have

$$\begin{aligned} \mathop {\lim }\limits _{{{\hat{m}}} \rightarrow \infty } \Vert {f(t) - f_{{{\hat{m}}}} (t)} \Vert _2^2 = \mathop {\lim }\limits _{k \rightarrow \infty } \left( {\sum \limits _{n = 0}^{2^k - 1} {\mathop {\lim }\limits _{M \rightarrow \infty } \Vert {g_n (z) - g_{nM} (z)}\Vert _2^2 } } \right) = 0. \end{aligned}$$

$\square$

Theorem 4.3

Let the Chelshkov wavelet expansion of an arbitrary continuous function f(t) converges uniformly. Thus,  this expansion converges to f(t).

Proof

Consider the Chelshkov wavelet expansion of f(t) as follows:

$$\begin{aligned} {\tilde{f}}(t)=\sum _{n=0}^{\infty }\sum _{m=0}^{\infty }{c_{nm}}\psi _{nm}(t), \end{aligned}$$

where ${c_{nm}} = {\langle {{\psi _{nm}}(t), f(t)} \rangle }$. For fixed values i and j multiplying both sides of above relation by $\psi _{ij}(t)$ and then integrating on [0, 1], we have

$$\begin{aligned} {\left\langle {{\psi _{ij}}(x),{\tilde{f}}(x)} \right\rangle }= & {} {\left\langle {{\psi _{ij}}(x),\sum \limits _{n = 0}^\infty {\sum \limits _{m = 0}^\infty {{c_{nm}}{\psi _{nm}}(x)} } } \right\rangle }\\= & {} \sum \limits _{n = 0}^\infty {\sum \limits _{m = 0}^\infty {{c_{mn}}{{\left\langle {{\psi _{ij}}(x),{\psi _{nm}}(x)} \right\rangle } } = {c_{ij}}} }, \end{aligned}$$

therefore, the functions f(t) and ${\tilde{f}}(t)$ have equal Chelshkov wavelet expansions and accordingly $f(t)= {\tilde{f}}(t)$ for $t \in [0,1]$. $\square$

5 Transformation and operational matrices

This section is devoted to operational matrices of the Chelyshkov wavelets vector $\Psi (t)$. First, two operational matrices for the Chelyshkov polynomials vector $\Phi (t)$ are derived. Then, transformation matrices for the Chelyshkov polynomial vector $\Phi (t)$ and Chelyshkov wavelet vector $\Psi (t)$ will be obtained. Finally, using these transformation matrices, the operational matrix of fractional integration and delay operational matrix of the Chelyshkov wavelet vector $\Psi (t)$ will be derived.

Theorem 5.1

Let $\Phi (t)$ be the $(M+1)$ Chelyshkov polynomials vector as defined in relation (4). Its fractional integral of order $\alpha$ can be expressed as : 

$$\begin{aligned} I^{\alpha }{\Phi (t)} \simeq \Theta ^{(\alpha )}\Phi (t), \end{aligned}$$

(14)

where $\Theta ^{(\alpha )}$ is an $(M+1)$ matrix and its (i, j)th component may be derived as : 

$$\begin{aligned} \Theta ^{(\alpha )}_{i,j} =\left( {\sum \limits _{r = 0}^{M-i+1} {\sum \limits _{s = 0}^{M-j} {\frac{{{ (2j + 1)}{a_{r,i - 1}}{a_{s,j}}}}{{(\alpha +r +i+j+s)}}} } } \right) , \quad i,j=1,2,\ldots ,M+1. \end{aligned}$$

Proof

The ith element of the Chelyshkov polynomials vector $\Phi (t)$ is $\rho _{i-1}(t)$ and its fractional integral of order $\alpha$ could be derived as:

$$\begin{aligned} I^{\alpha } \Phi _{i}(t)=I^{\alpha }\rho _{i-1}(t)=I^{\alpha } \left( {\sum \limits _{r = 0}^{M-i+1} {a_{r,i - 1} t^{r+i-1} } } \right) = \sum \limits _{r = 0}^{M-i+1} {\frac{{a_{r,i - 1} \Gamma ( {r + i})}}{{\Gamma ({r + i + \alpha })}}t^{\alpha +r +i-1 } },\nonumber \\ \end{aligned}$$

(15)

by expanding the term $t^{\alpha +r +i-1 }$ by the Chelyshkov polynomials, we get

$$\begin{aligned} {t^{\alpha +r +i-1 }} \simeq \sum \limits _{j = 0}^{M} {{\beta _{r, j}}{\rho _{j}(t)}}, \end{aligned}$$

(16)

in which $\beta _{r, j}$ can be obtained as:

$$\begin{aligned} {\beta _{r,j}}= & {} (2j + 1)\int _{0}^{1} {\rho _{j}(t)} {t^{\alpha +r +i-1 }}\,\mathrm{d}t\nonumber \\= & {} (2j + 1)\sum \limits _{s = 0}^{M-j} {{a_{s,j}}} \int _0^1 {{t^{\alpha +r +i+j+s-1}}}\,\mathrm{d}t= (2j + 1)\sum \limits _{s = 0}^{M-j} {\frac{{{a_{s,j}}}}{{\alpha +r +i+j+s}}}.\qquad \quad \end{aligned}$$

(17)

Now, by inserting (16) and (17) in (15), we get

$$\begin{aligned} I^{\alpha } {\Phi _{i}(t)} \simeq \sum \limits _{j = 0}^{M} {\left( {\sum \limits _{r = 0}^{M-i+1} {\sum \limits _{s = 0}^{M-j} {\frac{{{ (2j + 1)}{a_{r,i - 1}}{a_{s,j}}}}{{(\alpha +r +i+j+s)}}} } } \right) } \rho _{j}(t), \end{aligned}$$

and this leads to the desired results. $\square$

Theorem 5.2

Suppose $\Phi (t)$ is the $(M+1)$ Chelshkov polynomial vector defined in (4). The delay operational matrix of this vector will be derived as : 

$$\begin{aligned} {\Phi }(\tau t) \simeq \Omega {(\tau )} \Phi (t), \end{aligned}$$

(18)

where $\Omega {(\tau )}$ is the $(M+1) \times (M+1)$ delay matrix and its (i, j)th element can be obtained as:

$$\begin{aligned} \Omega {(\tau )}_{i,j}= {\left( \sum \limits _{r = 0}^{M-i+1} {\sum \limits _{s = 0}^{M-j} {\frac{{{a_{s, j}}{a_{r,i-1}}(2j + 1)\tau ^{r+i-1}}}{{(r+i+s+j)}}} }\right) },\quad i,j = 1,2,\ldots ,M+1. \end{aligned}$$

(19)

Proof

Consider the ith element of $\Phi (t)$, which is $\rho _{i-1}(t)$. Using the analytic form of $\rho _{i-1}(t)$ as defined in (1), we get

$$\begin{aligned} \Phi _{i}(\tau t)=\rho _{i-1}(\tau t) = \sum \limits _{r = 0}^{M-i+1} {{a_{r,i-1}}}\tau ^{r+i-1} t^{r+i-1},\quad i= 1,2,\ldots ,M+1, \end{aligned}$$

(20)

now, by expanding the term $t^{r+i-1}$ by the Chelyshkov polynomials we have

$$\begin{aligned} {t^{r+i-1}} \simeq \sum \limits _{j = 0}^{M} {\beta _{r, j}}{\rho _{j}( t)}, \end{aligned}$$

(21)

in which $\beta _{r,j}$ can be derived as:

$$\begin{aligned} {\beta _{r, j}}= & {} (2j + 1)\int _0^1 {t^{r+i-1}} {\rho _{j}}(t)\,\mathrm{d}t= (2j + 1)\sum \limits _{s = 0}^{M-j} {{a_{s,j}}} \int _0^1 {{t^{r+i+s+j-1}}}\,\mathrm{d}t\nonumber \\= & {} (2j + 1)\sum \limits _{s = 0}^{M-j} {\frac{{{a_{s,j}}}}{{r+i+s+j}}}. \end{aligned}$$

(22)

Making use of the relations (20)–(22), we get

$$\begin{aligned} \Phi _{i}(\tau t) \simeq \sum \limits _{j = 0}^{M} {\left( \sum \limits _{r = 0}^{M-i+1} {\sum \limits _{s = 0}^{M-j} {\frac{{{a_{s, j}}{a_{r,i-1}}(2j + 1)\tau ^{r+i-1}}}{{(r+i+s+j)}}} } \right) }{\rho _{j}}(t),\quad i= 1,2,\ldots ,M+1, \end{aligned}$$

this relation together with (18) get the desired results. $\square$

In the next theorems, two transformation matrices for the Chelyshkov polynomials and Chelyshkov wavelet vectors $\Phi (t)$ and $\Psi (t)$ will be derived. Using these transformation matrices, these vectors can be expanded into each other which is a critical property for next results.

Theorem 5.3

The ${\hat{m}}$ Chelyshkov wavelet vector $\Psi (x)$ can be expanded into the $(M+1)$ Chelyshkov polynomials vector $\Phi (x)$ as

$$\begin{aligned} \Psi (x)\simeq \Lambda \Phi (x), \end{aligned}$$

(23)

where $\Lambda$ is a ${\hat{m}} \times (M+1)$ matrix and

$$\begin{aligned} \Lambda _{ij}=\left( {2j + 1} \right) \sum \limits _{r = 0}^{M - r} {\sum \limits _{s = 0}^{M - s} {\sum \limits _{k = 0}^{r + j} {\left( {\frac{{a_{rj} a_{sm} 2^{ - k\left( {r + j - \frac{1}{2}} \right) } \sqrt{2m + 1} \left( \begin{array}{l} r + j \\ k \\ \end{array} \right) n^{r + j - k} }}{{s + k + 1}}} \right) } } }. \end{aligned}$$

in which $i=1\ldots {\hat{m}},j=1,\ldots ,M+1$.

Proof

The ith component of the Chelyshkov wavelets vector $\Psi (t)$, namely $\psi _{i}(t)$, can be defined by Chelyshkov polynomials as:

$$\begin{aligned} \psi _{i}(t) =\sum \limits _{j = 0}^{M} {{{\Lambda _{ij}}{\rho _{j}}}(t)}, \end{aligned}$$

in which the coefficient $\Lambda _{ij}$ can be obtained as:

$$\begin{aligned} {\Lambda _{ij}} \simeq (2j+1)\int _0^1 {\psi _{i}(x) } {\rho _{j}}(t)\,\mathrm{d}t,\quad i=1\ldots {\hat{m}}. \end{aligned}$$

Substituting the analytical form of the $\rho _{j}(t)$ from the Eq. (1), the coefficient $\Lambda _{ij}$ can be derived as:

$$\begin{aligned} {\Lambda _{ij}}\simeq & {} (2j+1)\sum \limits _{r = 0}^{M-j} {a_{r, j}\int _0^1 {{\psi _{i}}(x){t^{r+j}}}\,\mathrm{d}t}\\= & {} (2j+1)\sum \limits _{r =0}^{M -j}2^{\frac{k}{2}}{\sqrt{2m+1} a_{r,j} \int _{\frac{{n}}{2^k}}^{\frac{n+1}{2^{k}}} {t^{r+j} \rho _m ( {2^{k}t- n})\,\mathrm{d}t} }, \end{aligned}$$

where $i=n(M+1)+m+1$. Now, by change of variable $z=2^{k}t - n$ we get

$$\begin{aligned} {\Lambda _{ij}}\simeq & {} (2j+1)\sum \limits _{r = 0}^{M -j}2^{-k(r+j+\frac{1}{2})}{\sqrt{2m+1} a_{r,j} \int _0^1 {({z + n } )^{r+j} \rho _m (z)\,\mathrm{d}z}}\\= & {} (2j+1)\sum \limits _{r = 0}^{M-j} {\sum \limits _{s = 0}^{M-m} 2^{-k(r+j+\frac{1}{2})}{\sqrt{2m+1} a_{r,j} a_{s,m} \int _0^1 {({z+n})^{r+j} z^{s+m}\,\mathrm{d}z} } }\\= & {} ({2j + 1})\sum \limits _{r = 0}^{M -j} {\sum \limits _{s = 0}^{M-m} {\sum \limits _{k = 0}^{r + j} {\left( {\frac{{a_{rj} a_{s,m} 2^{ - k\left( {r + j + \frac{1}{2}} \right) } \sqrt{2m + 1} \left( \begin{array}{l} r + j \\ k \\ \end{array} \right) n^{r + j - k} }}{{s+m + k + 1}}} \right) } } } \end{aligned}$$

and this completes the proof. $\square$

Theorem 5.4

Let $\Phi (t)$ be the $(M+1)$ Chelyshkov polynomials vector. It can be expanded by the Chelyshkov wavelets as : 

$$\begin{aligned} \Phi (t) \simeq \Pi {\Psi }(t), \end{aligned}$$

(24)

where $\Pi$ is $(M+1) \times {\hat{m}}$ matrix and

$$\begin{aligned} \Pi _{ij}=({2j + 1})\sum \limits _{r = 0}^{M - i + 1} {\sum \limits _{s = 0}^{M - s} {\sum \limits _{k = 0}^{r + i - 1} {\left( {\frac{{a_{r,i - 1} a_{s,m} 2^{ - k\left( {r + i - \frac{1}{2}} \right) } \sqrt{2m + 1} \left( \begin{array}{l} r + i - 1 \\ k \\ \end{array} \right) n^{r + i - k - 1} }}{{r + i + s}}} \right) }}}. \end{aligned}$$

Proof

Consider the ith component of the vector $\Phi (t)$, which is $\rho _{i-1}(t)$. It can be expanded by the Chelyshkov wavelets as follows:

$$\begin{aligned} \Phi _{i}(t)=\rho _{i-1}(t) \simeq \sum \limits _{j = 1}^{{\hat{m}}} {{\Pi _{ij}}{\psi _{j}}(t)}, \end{aligned}$$

in which

$$\begin{aligned} \Pi _{ij}= & {} \int _0^1 {{\phi _{j}}(t)} {\rho _{i-1}(t)}\,\mathrm{d}t=\sum \limits _{r=0}^{M-i+1} {{a_{r,i-1}}} \int _0^1 {{\phi _{j}(t){t^{r+i-1}}\,\mathrm{d}t}}\\= & {} \sum \limits _{r=0}^{M-i+1} {{a_{r,i-1}}} \int _{\frac{n}{2^{k}}}^{\frac{n+1}{2^{k}}} {2^{\frac{k}{2}} \sqrt{2m + 1} } t^{r+i-1} \rho _m ({2^{k}t-n})\,\mathrm{d}t, \end{aligned}$$

where $j=n(M+1)+m+1$. By change of variable $z={2^{k}t-n}$ in the above relation, we get

$$\begin{aligned} \Pi _{ij}= & {} \sum \limits _{r=0}^{M-i+1} {{a_{r,i-1}}} \int _{0}^{1} {2^{-k(r+i-\frac{1}{2})} \sqrt{2m + 1} } (z+n)^{r+i-1} \rho _m (z)\,\mathrm{d}z\\= & {} \sum \limits _{r = 0}^{M-i+1} {\sum \limits _{s = 0}^{M-m} {a_{r,i-1} a_{s,m} {2^{-k(r+i-\frac{1}{2})} \sqrt{2m + 1} } \int _0^1 {(z+n)^{r+i-1} z^{s+m}\,\mathrm{d}z} } }\\= & {} ({2j + 1})\sum \limits _{r = 0}^{M - i + 1} {\sum \limits _{s = 0}^{M -m} {\sum \limits _{k = 0}^{r + i - 1} {\left( {\frac{{a_{r,i - 1} a_{s,m} 2^{ - k\left( {r + i - \frac{1}{2}} \right) } \sqrt{2m + 1} \left( \begin{array}{l} r + i - 1 \\ k \\ \end{array} \right) n^{r + i - k - 1} }}{{s + m + k+1}}} \right) } } }, \end{aligned}$$

and this completes the proof. $\square$

In the next theorems, the operational matrices $\Omega {(\tau )}$ and $\Theta ^{(\alpha )}$ for the Chelyshkov polynomials vector $\Phi (t)$ together with transformations matrices $\Pi$ and $\Lambda$ are used to derive fractional-order integration matrix and delay operational matrix of the Chelyshkov wavelet vector $\Phi (t)$.

Theorem 5.5

Let $\Psi (x)$ be the Chelyshkov wavelets vector defined as defined in (9). The Riemann–Liouville fractional integral of order $\alpha$ for this $\Psi (x)$ can be obtained as : 

$$\begin{aligned} I^{\alpha }\Psi (t) \simeq P^{(\alpha )} \Psi (t), \end{aligned}$$

(25)

where $P^{(\alpha )}=\Lambda \Theta ^{(\alpha )} \Pi$ is a ${\hat{m}}\times {\hat{m}}$ matrix,  and $\Pi$ and $\Lambda$ are transformation matrices derived in (24) and (14). Moreover,  $\Theta ^{(\alpha )}$ is the fractional operational matrix for the Chelyshkov polynomial vector $\Psi (t)$ defined in (14).

Proof

Consider the Chelyshkov wavelet vector $\Psi (x)$. Using the transformation matrix $\Lambda$, it can be written as:

$$\begin{aligned} \Psi (x) \simeq \Lambda {\Phi }(x), \end{aligned}$$

by applying the fractional integration operator $I^{\alpha }$ and using (14), we get

$$\begin{aligned} I^{\alpha }{\Psi (t)} = \Lambda I^{\alpha }\Phi (t) =\Lambda \Theta ^{(\alpha )} \Phi (t), \end{aligned}$$

now the transformation matrix $\Lambda$ results

$$\begin{aligned} I^{\alpha }{\Psi (t)} \simeq \Lambda \Theta ^{\alpha }\Phi (t) =\Lambda \Theta ^{(\alpha )}\Pi \Psi (t), \end{aligned}$$

which yields (26) and completes the proof. $\square$

Theorem 5.6

Let $\Psi {(t)}$ be the ${\hat{m}} \times 1$ Chelyshkov wavelet vector defined in (9). The delay operational matrix of this wavelet vector may be expressed as : 

$$\begin{aligned} \Psi (t)\,\mathrm{d}t\simeq {\mathcal {D}}(\tau ) \Psi (t), \end{aligned}$$

(26)

where ${\mathcal {D}}(\tau ) =\Lambda \Omega (\tau ) \Pi$ is an ${\hat{m}}$ matrix,  $\Pi$ and $\Lambda$ are the transformation matrices and $\Omega (\tau )$ is the delay operational matrix of the Chelyshkov polynomial vector $\Psi (t)$ defined in (18).

Proof

The proof is the same as the previous theorem. $\square$

6 Problem statement and numerical method

In this section, the Chelshkov wavelet basis and their operational matrices are used to approximate solution of SFDDEs. To this end, consider the following problems:

Problem (a):

$$\begin{aligned} \left\{ \begin{array}{l} D^\alpha y_i (t) = f_i ( t,y_1 (t),y_1 ({t - \tau _{11} }),\ldots ,y_1 ({t - \tau _{1r_1 } }),\ldots ,y_n (t),y_n ({t - \tau _{n1} }),\\ \qquad \qquad \qquad \ldots ,y_n ({t - \tau _{nr_n } })),\\ y_i^{(k)} (t) = \lambda _{ik},\quad k = 0,1,\ldots ,m - 1, \\ y_i (t) = u_i (t),\quad t < 0, \end{array} \right. \end{aligned}$$

(27)

Problem (b):

$$\begin{aligned} \left\{ \begin{array}{l} D^\alpha y_i (t) = f_i ( {t,y_1 (t),y_1 ( {\tau _{11} t} ),\ldots ,y_1 ({\tau _{1r_1 } t} ),\ldots ,y_n (t),y_1 ({\tau _{n1} t}),\ldots ,y_1 ({\tau _{nr_n} t})}), \\ y_i^{(k)} (t) = \lambda _{ik},\quad k = 0,1,\ldots ,m - 1, \end{array} \right. \nonumber \\ \end{aligned}$$

(28)

where $i=1,2,\ldots ,n$, $m-1< \alpha \le m$ and $0< \tau _{is} <1, s=1,2,\ldots ,r_{i}$ are delay parameters, $\lambda _{ik}$ are initial conditions and $u_{i}(t), i=1, 2,\ldots , n$ are given continuous functions in the Problem (a). Furthermore, $D^{\alpha }{y_{i}(t)}$ denote the fractional order derivative in the Caputo sense and $y_{i}(t)$ are solution functions to be determined. To derive approximate solution of SFDDEs (a) and (b), we approximate $D^{\alpha }{y_{i}(t)}$ by the Chelshkov wavelets as follows:

$$\begin{aligned} D^\alpha y_{i}(t) \simeq \sum \limits _{i = 0}^{{\hat{m}}} {c_i \psi _i (t)} = C_{i}^{\mathrm{T}} \Psi (t),\quad i=1,2,\ldots ,n, \end{aligned}$$

(29)

by applying the fractional-order Riemann–Liouville operator $I^{\alpha }$ on both sides of these relations and applying the fractional-order operational matrix of the Chelshkov wavelet derived in (4), we have

$$\begin{aligned} y_{i}(t)\simeq I^{\alpha }(C_{i}^{\mathrm{T}}\Psi (t)) +\sum \limits _{i = 0}^{m - 1} {\frac{{\lambda _{ik} }}{{i!}}t^i} = C_{i}^{\mathrm{T}} P^{(\alpha )} \Psi (t) + d^{\mathrm{T}}_{i} \Psi (t),\quad i=1,2,\ldots ,n, \end{aligned}$$

(30)

where $d_{i}$ is the Chelshkov wavelet coefficient vector of the polynomial $\sum _{i = 0}^{m - 1} {\frac{{\lambda _{ik} }}{{i!}}t^i}$. Hence, for the Problem (a), we get

$$\begin{aligned} y_i ({t - \tau _{ij} }) = \left\{ \begin{array}{ll} u_{i}({t - \tau _{ij} }),&{}\quad 0 \le t \le \tau _{ij} \\ C_{i}^{\mathrm{T}} P^{(\alpha )} \Psi ({t - \tau _{ij}}) + d^{\mathrm{T}}_{i} \Psi ({t - \tau _{ij} }),&{}\quad \tau _{ij} \le t \le 1 \end{array} \right. = C^{(\tau _{ij})T}_{*}\Psi (t),\quad \end{aligned}$$

(31)

where $C^{(\tau _{ij})}_{*}$ is an unknown vector function of the vector $C_{i}$ and delay parameter $\tau _{ij}$. Moreover, for the Problem (b), by employing the delay operational matrix of Chelshkov wavelet $\Psi (t)$ derived in (30), we obtain

$$\begin{aligned} y_i ({\tau _{ij} t}) =C_{i}^{\mathrm{T}} P^{(\alpha )} \Psi (\tau _{ij}t) + d_{i} \Psi (\tau _{ij} t)= C_{i}^{\mathrm{T}} P^{\alpha } {\mathcal {D}}_{\tau _{ij}} \Psi (t)+d^{\mathrm{T}}_{i} {\mathcal {D}}_{\tau _{ij}} \Psi (t). \end{aligned}$$

(32)

Now, by inserting (29)–(32) into the Problems (a) and (b), we obtain a system of residual function as follows:

Problem (a):

$$\begin{aligned} R_{1i} (t)= & {} C_{i}^{\mathrm{T}} \Psi (t) -f\left( t, C_{1}^{\mathrm{T}} P^{(\alpha )} \Psi (t) + d^{\mathrm{T}}_{1} \Psi (t), C_{\tau _{11}}^{*T} P^{\alpha } \Psi (t),\ldots ,C_{\tau _{1r_1 }}^{*T} P^{\alpha } \Psi (t),\ldots , \right. \nonumber \\&\quad \left. {C_{n}^{\mathrm{T}} P^{(\alpha )} \Psi (t) + d^{\mathrm{T}}_{n} \Psi (t), C_{\tau _{n1}}^{*\mathrm{T}} P^{\alpha } \Psi (t), C_{\tau _{nr_n }}^{*\mathrm{T}} P^{\alpha } \Psi (t)}\right) ,\quad i = 1,2,\ldots ,n.\nonumber \\ \end{aligned}$$

(33)

Problem (b):

$$\begin{aligned} R_{2i}(t)= & {} C_i^{\mathrm{T}} \Psi (t) - f_i \left( t,C_{1}^{\mathrm{T}} P^\alpha \Psi (t) + d_{1}^{\mathrm{T}} \Psi (t),C_{1 }^{\mathrm{T}} P^\alpha {\mathcal {D}}_{\tau _{11}} \Psi (t)+ d_1^{\mathrm{T}} {\mathcal {D}}_{\tau _{11}} \Psi (t),\ldots ,\right. \nonumber \\&\quad {C_{1}^{\mathrm{T}} P^\alpha {\mathcal {D}}_{\tau _{1r_{1}}} \Psi (t)+ d_1^{\mathrm{T}} {\mathcal {D}}_{\tau _{1r_{1}}} \Psi (t),\ldots ,C_n^{\mathrm{T}} P^\alpha \Psi (t)+ d_n^{\mathrm{T}} \Psi (t),C_n^{\mathrm{T}} P^\alpha {\mathcal {D}}_{\tau _{n1}} \Psi (t)}\nonumber \\&\quad \left. +\, d_n^{\mathrm{T}} {\mathcal {D}}_{\tau _{n1}} \Psi (t),\ldots ,C_n^{\mathrm{T}} P^\alpha {\mathcal {D}}_{\tau _{1r_{n}}} \Psi (t) + d_n^{\mathrm{T}} {\mathcal {D}}_{\tau _{nr_{n}}} \Psi (t)\right) ,\quad i = 1,2,\ldots ,n.\nonumber \\ \end{aligned}$$

(34)

Then, using the typical classical Galerkin approach we have $n{\hat{m}}$ algebraic equations for n unknown coefficient vectors $C_{i}, i=1,2,\ldots ,n$, as:

Problem (a):

$$\begin{aligned} \int _0^1 {R_{1i} (t)} \psi _j (t)\,\mathrm{d}t = 0,\quad i = 1,2,\ldots ,n,\ j = 1,2,\ldots ,{\hat{m}}. \end{aligned}$$

Problem (b):

$$\begin{aligned} \int _0^1 {R_{2i} (t)} \psi _j (t)\,\mathrm{d}t = 0,\quad i = 1,2,\ldots ,n,\ j = 1,2,\ldots ,{\hat{m}}. \end{aligned}$$

which can be solved using the Newton–Raphson method. By substituting the derived vector $C_{i}, i=1,2,\ldots ,n$, in Eq. (30) the solution $y_{i}(t), i=1,2,\ldots ,n$ can be derived for the Problems (a) and (b).

7 Numerical results

To verify applicability and efficiency of the suggested wavelet approach, some illustrative examples have been presented in this section. Numerical examples are considered in both linear and nonlinear cases. Let $y_{i}(t)$ and $y_{i,{\hat{m}}}(t)$ be the exact and approximate solution of the SFDDEs (27) and (28), respectively. The error function $e_{i,{\hat{m}}}(t)=| {y_{i}(t)-y_{i,{\hat{m}}}(t)}|$ and the maximum absolute error $\Vert e_{i,{\hat{m}}}(t)\Vert _\infty$ were computed to verify the accuracy of the obtained numerical results. In all examples, numerical computations are carried out using MAPLE 17 with 30 digits precision.

Fig. 2

The relative error of approximate solutions for $\alpha =1$ and ${\hat{m}}=32$ (Example 1). a $y_{1}(t)$, b $y_{2}(t)$

Example 1

As first example, we consider the following SFDDEs (Hwang and Chen 1986; Ghasemi and Tavassoli 2011)

$$\begin{aligned} \left[ \begin{array}{l} D^\alpha y_1 (t) \\ D^\alpha y_1 (t) \\ \end{array} \right] = \left[ {\begin{array}{cc} 0 &{} 1 \\ { - 25} &{} { - 5t} \\ \end{array}} \right] \left[ \begin{array}{l} y_1 \left( {t - \frac{1}{4}} \right) \\ y_2 \left( {t - \frac{1}{4}} \right) \\ \end{array} \right] + \left[ \begin{array}{l} 0 \\ 1 \\ \end{array} \right] u(t),\quad 0 < \alpha \le 1, \end{aligned}$$

with

$$\begin{aligned} \left[ \begin{array}{l} y_1 (t) \\ y_2 (t) \\ \end{array} \right] = \left[ \begin{array}{l} 0 \\ 0 \\ \end{array} \right] ,\quad - \frac{1}{4} \le t \le 0. \end{aligned}$$

For $\alpha =1$ and $u(t)=1, t\ge 0$, the exact solutions of this system are

$$\begin{aligned} y_1 (t)= & {} \left\{ \begin{array}{ll} 0, &{}\quad 0 \le t< \frac{1}{4}, \\ \frac{1}{32}-\frac{1}{4}t+\frac{1}{2}{t}^{2}, &{}\quad \frac{1}{4} \le t< \frac{1}{2}, \\ \frac{1}{32}-{\frac{19}{96}}t+\frac{3}{16}{t}^{2}+\frac{5}{8}{t}^{3} -{\frac{5}{12}}\,{t}^{4},&{}\quad \frac{1}{2} \le t< \frac{3}{4}, \\ -{\frac{9641}{32768}}+{\frac{37391}{24576}}\,t-{\frac{3183}{1024}} \,{t}^{2}+{\frac{785}{256}}\,{t}^{3}-{\frac{45}{128}}\,{t}^{4} -{\frac{85}{96}}\,{t}^{5}+{\frac{5}{18}}\,{t}^{6}, &{}\quad \frac{3}{4} \le t \le 1, \end{array} \right. \\ y_2(t)= & {} \left\{ \begin{array}{ll} t, &{}\quad 0 \le t< \frac{1}{4}, \\ -{\frac{5}{384}}+t+\frac{5}{8}{t}^{2}-\frac{5}{3}t^{3},&{}\quad \frac{1}{4} \le t< \frac{1}{2}, \\ {\frac{775}{1536}}-{\frac{17}{8}}\,t+{\frac{1295}{192}} \,{t}^{2}-{\frac{115}{24}}\,{t}^{3}-{\frac{75}{32}} \,{t}^{4}+\frac{5}{3}{t}^{5},&{}\quad \frac{1}{2} \le t < \frac{3}{4}, \\ {\frac{3666575}{5505024}}+{\frac{1051}{1024}}t-{\frac{95755}{49152}} {t}^{2}+{\frac{21515}{1536}}{t}^{3}-{\frac{55325}{3072}}{t}^{4}+ {\frac{335}{96}}{t}^{5}+{\frac{2125}{576}}{t}^{6}-{\frac{25}{21}}{t}^{7}, &{}\quad \frac{3}{4} \le t \le 1. \end{array} \right. \end{aligned}$$

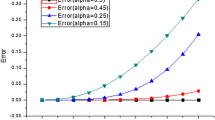
The solution of these SFDDEs has approximated by applying the presented Chelyshkov wavelet method. For $\alpha =1$, by choosing ${\hat{m}}=32 (M=7, k=2)$ the exact solutions are derived up to 22 digits precision and their relative errors $\frac{e_{i,{\hat{m}}}(t)}{\Vert e_{i,{\hat{m}}}(t) \Vert _\infty }$ are shown in Fig. 2. Moreover, the exact and approximate solutions for fractional-orders $\alpha =0.8, 0.85, 0.90, 0.95, 1$ with ${\hat{m}}=32$ are plotted in Fig. 3. Based on the obtained results, it is clear that the proposed wavelet method is accurate for solving such problems and approximate solutions converge to the exact solution as $\alpha$ approaches 1.

Fig. 3

Numerical results for different values of $\alpha$ and ${\hat{m}}=32$ (Example 1). a $y_{1}(t)$, b $y_{2}(t)$

Example 2

Consider the following SFDDEs (Rahimkhani et al. 2017)

$$\begin{aligned} \left[ \begin{array}{l} D^\alpha y_1 (t) \\ D^\alpha y_1 (t) \\ \end{array} \right] = \left[ {\begin{array}{cc} t &{}\quad 1 \\ t &{}\quad 2 \\ \end{array}} \right] \left[ \begin{array}{l} y_1 \left( {t - \frac{1}{3}} \right) \\ y_2 \left( {t - \frac{1}{3}} \right) \\ \end{array} \right] + \left[ {\begin{array}{cc} 2 &{}\quad t \\ {t^2 } &{}\quad 0 \\ \end{array}} \right] \left[ \begin{array}{l} y_1 \left( {t - \frac{2}{3}} \right) \\ y_2 \left( {t - \frac{2}{3}} \right) \\ \end{array} \right] + \left[ \begin{array}{l} 0 \\ 1 \\ \end{array} \right] u(t),\quad 0 < \alpha \le 1, \end{aligned}$$

with

$$\begin{aligned} \left[ \begin{array}{l} y_1 (t) \\ y_2 (t) \\ \end{array} \right] = \left[ \begin{array}{l} 0 \\ 0 \\ \end{array} \right] ,\quad -\frac{2}{3} \le t \le 0. \end{aligned}$$

The exact solutions of this system for $\alpha = 1$ and input function $u(t)=2t+1, t\ge 0$, are

$$\begin{aligned} y_1 (t)= & {} \left\{ \begin{array}{ll} 0,&{}\quad 0 \le t< \frac{1}{3}, \\ \frac{7}{{162}}{{ - }}\frac{2}{9}{{t + }}\frac{1}{6}{{t}}^{{2}} {{ + }}\frac{1}{2}{{t}}^{{3}}&{}\quad \frac{1}{3} \le t< \frac{2}{3},\\ \frac{{11}}{{162}}{{ - }}\frac{{58}}{{243}}{{t + }}\frac{{31}}{{162}}{{t}}^{2} +\frac{1}{9}\mathrm{{t}}^{3} + \frac{7}{{72}}{t}^{4} + \frac{1}{6}{{t}}^{{5}},&{}\quad \frac{2}{3} \le t \le 1. \end{array} \right. \\ y_2 (t)= & {} \left\{ \begin{array}{ll} t+t^{2},&{}\quad 0 \le t< \frac{1}{3}, \\ \frac{4}{486}+t+\frac{7}{9}{t^{2}}+\frac{2}{9}{t^{3}} +\frac{1}{4}t^{4} &{}\quad \frac{1}{3} \le t < \frac{2}{3},\\ \frac{1}{486}+t+\frac{200}{243}t^{2}+\frac{20}{81}t^{3}+ \frac{29}{72}t^{4}-\frac{1}{9}t^{5}+\frac{1}{6}t^{6},&{}\quad \frac{2}{3}\le t \le 1. \end{array} \right. \end{aligned}$$

The proposed technique in Sect. 5 is implemented to solve these SFDDEs for different values of $\alpha$. Figure 4 shows the exact and obtained approximate solutions for $\alpha =0.6, 0.7, 0.8, 0.9, 1$ with ${\hat{m}}=14$. Moreover, comparison of the absolute error of obtained numerical solutions with the presented results in Rahimkhani et al. (2017) is presented in Table 1. From these results, we can realize that the Chelyshkov wavelet method is more efficient in solving these SFDDEs and approximate solutions approach the exact solution as $\alpha$ converges to 1.

Fig. 4

Numerical results for different values of $\alpha$ and ${\hat{m}}=14$ (Example 2). a $y_{1}(t)$, b $y_{2}(t)$

Table 1 The absolute error of obtained numerical solutions with the presented results in Rahimkhani et al. (2017) (Example 2)

Example 3

In this example, we consider a system of nonlinear pantograph delay differential equations as follows (Davaeifar and Rashidinia 2017):

$$\begin{aligned} \left\{ \begin{array}{l} D^\alpha y_1 (t) = 2y_2 \left( {\frac{1}{2}t} \right) + y_3 ( t )+ t\cos \left( {\frac{1}{2}t} \right) , \\ D^\alpha y_2 (t) = - 2y_3^2 \left( {\frac{1}{2}t} \right) - t + 1, \\ D^\alpha y_3 (t) = y_1 (t)+ y_2 (t) -t\cos (t), \\ y_1 (0)=-1,\quad y_2 (0)=0,\quad y_3 (0)=0. \end{array} \right. \quad 0 \le t \le 1\quad 0 < \alpha \le 1. \end{aligned}$$

in which the exact solutions for $\alpha =1$ are $y_{1}(t)=-\cos (t), y_{2}(t)=t\cos (t)$ and $y_{3}(t)=\sin (t)$. Davaeifar and Rashidinia (2017) have been considered and solved this system of pantograph type delay differential equation with integer-order fractional derivative of order $\alpha =1$ by the polynomial collocation method. Here, this problem is also solved by the proposed Chelyshkov wavelet method for different values of M, k and $\alpha$. Figure 5 shows the approximate and exact solutions for ${\hat{m}}=18$ and various fractional order $\alpha$. To confirm accuracy of the presented method, the maximum absolute error of the numerical results for $\alpha =1$ is compared with those derived by collocation method in Davaeifar and Rashidinia (2017) in Table 2. From these results, we can realize that the Chelyshkov wavelet method is efficient for solving these nonlinear SFDDEs and numerical solutions converge to the exact solution as fractional order $\alpha$ tends to 1.

Fig. 5

Numerical results for different values of $\alpha$ and ${\hat{m}}=18$ (Example 3). a $y_{1}(t)$, b $y_{2}(t)$, c $y_{3}(t)$

Table 2 Comparison of the absolute error of Chelyshkov wavelet method with the results presented in Davaeifar and Rashidinia (2017) (Example 3)

Example 4

Now, consider the following nonlinear multi-pantograph SFDDEs (Davaeifar and Rashidinia 2017; Widatalla et al. 2012)

$$\begin{aligned} \left\{ \begin{array}{l} D^{\alpha } y_1 (t) = - y_1 (t) - 2{\mathrm{e}}^{-\frac{3t}{4}} \cos \left( {\frac{1}{2}t} \right) \sin \left( {\frac{1}{4}t} \right) y_1 \left( {\frac{1}{4}t} \right) - \mathrm{e}^{-t} \cos \left( {\frac{1}{2}t} \right) y_2 \left( {\frac{1}{2}t} \right) , \\ D^{\alpha } y_2 (t) =\mathrm{e}^{t} y_{1}^{2} \left( {\frac{1}{2}t} \right) - y_{2}^{2} \left( {\frac{1}{2}t} \right) ,\quad 0 \le t \le 10 < \alpha \le 1,\\ y_1 (0)=1,\quad y_2 (0)=0. \end{array} \right. \end{aligned}$$

For $\alpha =1$, the exact solution of this system is $y_1 (t)=\mathrm{e}^{-t}\cos (t)$ and $y_{2}(t)=\sin (t)$. This fractional system is also solved using the suggested wavelet approach for several values of ${\hat{m}}$ and $\alpha$. The Laplace decomposition and polynomial collocation method have been applied to solve the problem with $\alpha =1$ (Davaeifar and Rashidinia 2017; Widatalla et al. 2012). For the integer-order fractional derivative $\alpha =1$, Tables 3 and 4 present a comparison between the absolute error of the achieved numerical results and those presented in Davaeifar and Rashidinia (2017) and Widatalla et al. (2012). The graphs of the exact and approximate solutions $y_{1}(t)$ and $y_{2}(t)$ for non-integer values of $\alpha$ and ${\hat{m}}=12$ are shown in Fig. 6. In addition, as these results confirm, the presented collocation method is efficient and accurate in solving such nonlinear fractional system. Furthermore, as $\alpha$ approaches 1, the approximate solutions converge to the exact solution.

Table 3 The absolute error of numerical solution for $\alpha =1$ (Example 4)

Table 4 The absolute errors of numerical solution for $\alpha =1$ (Example 4)

Example 5

As last example, we consider the following SFDDEs (Sedaghat et al. 2012; Ali et al. 2009)

$$\begin{aligned} \left\{ \begin{array}{l} D^\alpha y_1 (t) = \sin (t) y_{1} (q t)+\cos (t) y_{2} (qt) +g_{1}(t), \\ D^\alpha y_2 (t) = -\cos (t) y_{1} (q t)+\sin (t) y_{2} (qt) +g_{2}(t), \\ y_{1}(-1)=\lambda _{2},\quad y_{2}(-1)=\lambda _{2}, \end{array} \right. \quad -1 \le t \le 1,\ 0 < \alpha \le 1. \end{aligned}$$

in which, for $\alpha =1$ the functions $g_{1}(t), g_{2}(t)$ and initial conditions $\lambda _{1}, \lambda _{2}$ are compatible with the exact solution $y_{1}(t)=\sin (t)$ and $y_{2}(t)=\cos (t)$. To solve this problem, the interval $[-1, 1]$ was transformed into the interval [0, 1] by applying change of variable $t=2x-1$. Then, the proposed Chelyshkov wavelet method has been employed to approximate its solution. The graphs of exact solution and approximate solutions $y_{1}(t)$ and $y_{2}(t)$ for different values of $\alpha$ and ${\hat{m}}=12$ are shown in Fig. 7. In addition, Table 5 presents the maximum absolute values of the obtained numerical solutions for $\alpha =1$ and different values of ${\hat{m}}$. As these results confirm, the presented wavelet method is efficient and accurate in solving such SFDDEs. Furthermore, as $\alpha$ approaches 1, the approximate solutions converge to the exact solution.

Fig. 6

Numerical results for different values of $\alpha$ and ${\hat{m}}=12$ (Example 4). a $y_{1}(t)$, b $y_{2}(t)$

Fig. 7

Numerical results for different values of $\alpha$ and ${\hat{m}}=12$ (Example 5). a $y_{1}(t)$, b $y_{2}(t)$

Table 5 The absolute errors of numerical solutions $y_1(t)$ and $y_2(t)$ (Example 5)

8 Conclusion

A new kind of orthonormal wavelet basis is constructed from a class of orthonormal polynomials called Chelyshkov polynomials. A comprehensive formulation for the operational matrix of fractional integration and delay operational matrix for this wavelet basis has been given. Then, a numerical Galerkin approach based on these operational matrices is proposed to solve systems of fractional delay differential equations. The main feature of the proposed method is that it reduces system of fractional order delay differential equations into systems of algebraic equations. Some illustrative examples are presented to explain the priority and accuracy of the proposed wavelet method. Moreover, a comparison has been made between our numerical finding and those achieved by other existing methods.