Trigonometric cubic B-spline collocation algorithm for numerical solutions of reaction–diffusion equation systems

Abstract

An algorithm for the reaction–diffusion system including model problems Brusselator, Schnakenberg and Gray–Scott is introduced. The integration of the system is managed by combining the Crank–Nicolson method in time and the cubic trigonometric B-spline collocation method in space. Our aim here is to provide a new code to understand and implement reaction–diffusion-type events. Some problems chosen from the literature to illustrate the efficiency of the algorithm are studied for each model problem.

1 Introduction

Reaction–diffusion systems (RDSs) are mathematical models that reveal several phenomena. Thus, RDS let us give complex behaviors due to the occurrence of both reaction and diffusion terms. Not only do interacting reaction terms lead to interesting behaviors, but also spreading this behavior via diffusion causes to develop pattern formation. Although reaction–diffusion systems are naturally applied in chemistry, physics and phenomena in other fields of science can be defined by various RDSs. Both patterns and some motions of nature are described via RDS to use in fields; for example, wave optics, predator–prey model, spread of infectious diseases, migration of population and spread of forest fires, chemical exchange reaction and transport of ground water in an aquifer.

Many studies have dealt with the solutions of the RDS theoretically and numerically. The numerical studies are of importance because theoretical solutions of the nonlinear RDS exist for the restricted boundary and initial conditions. Some classical numerical methods such as implicit–explicit method (Ruuth 1995), adaptive moving mesh methods (Zegeling and Kok 2004), and partially linearized-implicit $\theta$ methods (Garcia-Lopez and Ramos 1996) have applied to find numerical solutions of the RDS to reveal wide range of behaviors. Polynomial B-splines and exponential B-spline collocation algorithms are constructed to have numerical solutions of RDS in the doctoral work of Sahin (2009) and Ersoy and Dag (2015), respectively. Reaction–diffusion systems are solved via modified cubic B-spline differential quadrature method (Mittal and Rohila 2016).

The collocation method based on the spline functions is preferable for two reasons for numerical solutions of the differential equations. First, it is easy to implement and second, to give us a smoother approximating function, which is continuous in derivatives up to one lower order of spline both within the subintervals and at the interpolating nodes. Fairweather and Meade have made comprehensive survey on numerical solutions of differential equations using spline methods, primarily smoothest spline collocation, modified spline collocation, and orthogonal spline collocation method (Fairweather and Meade 1989). Since then, developments have been substantiated in the formulation and application of the spline collocation method. I. J. Schoenberg came up with both trigonometric spline and trigonometric B-spline in 1964 to interpolate functions (Schoenberg 1964).The trigonometric B-splines are shown to be better for handling the problem of surface approximation in geometric modeling (Wang et al. 2004). Due to application capabilities of the trigonometric B-splines, various forms of the trigonometric B-splines are introduced as an alternative to more usual polynomial B-splines.

Numerical methods constructed through the trigonometric B-splines have started to obtain solutions of the differential equations. Although many polynomial B-spline-based numerical algorithms have been developed for finding solutions of the differential equation, the trigonometric B-spline is not widespread. Numerical solutions of the ordinary differential equation in standard form are given by way of both quadratic and cubic trigonometric B-splines in studies, respectively (Nikolis 2004; Nikolis and Seimenis 2005). The linear two-point boundary value problems of order two and singular two-point boundary value problems are solved by the method of collocation based on trigonometric cubic B-splines (Hamid et al. 2010; Gupta and Kumar 2011). Time-dependent partial differential equation, such as one-dimensional hyperbolic equation (wave equation) with nonlocal conservation condition, nonclassical diffusion problems, Generalized Nonlinear Klien–Gordon equation and advection–diffusion equation, are solved by trigonometric B-spline collocation method (Abbas et al. 2014a, b; Zin et al. 2014a, b; Nazir et al. 2016). Burgers’ equation is dealt with to find solution by way of a trigonometric quadratic B-spline subdomain Galerkin algorithm in the work (Ay et al. 2015). Numerical solution of 1D Hyperbolic Telegraph equation using B-spline and trigonometric B-spline by differential quadrature method is presented in the study (Arora and Joshi 2016)

Since RDSs include the second-order derivatives, the trigonometric B-spline functions enable to opt for the second-order trial function for the collocation method. Our aim is to see the effects of the trigonometric cubic B-spline functions when used with collocation method and give alternative solution algorithm on getting solutions of the RDS. The reaction–diffusion systems are integrated in time and space variables fully to have the algebraic equations. This equation is solved with a variant of Thomas algorithm.

RDSs which we use in this paper are mentioned in Sect. 2. The suggested algorithm is explained in Sect. 3. In Sect. 4 named as numerical results, solutions of the four special RDSs are studied for some test problems. Figures and tables are given to see the suitability as well as the accuracy of the proposed method. In addition, matrix stability analysis is given in Sect. 5.

2 Reaction–diffusion systems

The nonlinear RDS is classified mathematically as the semi-linear parabolic partial differential equations which include Brusselator, Schnakenberg, and Gray–Scott models, and others. General form of the time-dependent one-dimensional nonlinear RDS, including all models studied, is expressed as follows:

$$\begin{aligned} \frac{\partial U}{\partial t}= & {} a_{1}\frac{\partial ^{2}U}{\partial x^{2}} +b_{1}U+c_{1}V+d_{1}U^{2}V+e_{1}UV+m_{1}UV^{2}+n_{1} \nonumber \\ \frac{\partial V}{\partial t}= & {} a_{2}\frac{\partial ^{2}V}{\partial x^{2}} +b_{2}U+c_{2}V+d_{2}U^{2}V+e_{2}UV+m_{2}UV^{2}+n_{2}. \end{aligned}$$

(1)

For computational purpose, spatial domain is confined to be finite interval $[x_{0},x_{N}]$. The initial conditions are

$$\begin{aligned} U(x,0)=U_{0}(x),\qquad V(x,0)=V_{0}(x), \ x\in \varOmega . \end{aligned}$$

(2)

Boundary conditions are going to be defined in every test problem sections. Special cases of the RDSs are specified according to the parameters in Eq. 1 defined in Table 1

Table 1 Models of the RDS

3 Trigonometric cubic B-spline collocation method

The interval [a, b] is divided into equal subelements at the knots $x_{i},i=0,\ldots ,N$ with mesh spacing $h=(b-a)/N$ and $a=x_{0}$, $b=x_{N}.$ Trigonometric cubic B-spline $TCB_{i}(x),i=-1,...N+1$ are defined at these knots over the interval [a, b] together with knots $x_{N-2},x_{N-1},x_{N+1},x_{N+2}$ outside the problem domain as follows:

$$\begin{aligned} \hbox {TCB}_{i}(x)=\frac{1}{\theta } \left\{ \begin{array}{ll} \omega ^{3}(x_{i-2}), &{} x\in \left[ x_{i-2},x_{i-1}\right] \\ \omega (x_{i-2})(\omega (x_{i-2})\phi (x_{i}) \\ +\, \phi (x_{i+1})\omega (x_{i-1}))+\phi (x_{i+2})\omega ^{2}(x_{i-1}), &{} x\in \left[ x_{i-1},x_{i} \right] \\ \omega (x_{i-2})\phi ^{2}(x_{i+1})+\phi (x_{i+2})(\omega (x_{i-1})\phi (x_{i+1})\\ +\, \phi (x_{i+2})\omega (x_{i})), &{} x\in \left[ x_{i},x_{i+1}\right] \\ \phi ^{3}(x_{i+2}), &{} x\in \left[ x_{i+1},x_{i+2}\right] \\ 0, &{} \mathrm{otherwise}, \end{array} \right. \end{aligned}$$

(3)

where $\omega (x_{i})=\sin (\frac{x-x_{i}}{2}), \phi (x_{i})=\sin (\frac{ x_{i}-x}{2}),\theta =\sin (\frac{h}{2})\sin (h)\sin (\frac{3h}{2})$. $\hbox {TCB}_{i}(x)$ are twice continuously differentiable piecewise functions on the interval [a, b]; each of them is nonnegative on subelements $\left[ x_{i-2},x_{i+2}\right]$ and starting with the basis of the TCB-splines of order 1:

$$\begin{aligned} T_{i}^{1}(x)=\left\{ \begin{array}{l} 1,\quad x\in [x_{i},x_{i+1}) \\ 0,\quad \text {otherwise}. \end{array} \right. \end{aligned}$$

(4)

TCB-spline basis of order $k=2,3,...$ can be calculated using the recursive formula:

$$\begin{aligned} T_{i}^{k}(x)=\frac{\sin (\frac{x-x_{i}}{2})}{\sin (\frac{x_{i+k-1}-x_{i}}{2}) }T_{i}^{k-1}(x)+\frac{\sin (\frac{x_{i+k}-x}{2})}{\sin (\frac{x_{i+k}-x_{i+1} }{2})}T_{i+1}^{k-1}(x), k=2,3,4,... \end{aligned}$$

(5)

The values of $\hbox {TCB}_{i}(x),\hbox {TCB}_{i}^{^{\prime }}(x)$ and $\hbox {TCB}_{i}^{^{\prime \prime }}(x)$ at the knots $x_{i}$’s can be computed from Eq. 3 as in Table 2.

Table 2 Values of $\mathrm{TCB}_{i}(x)$ and its principle two derivatives at the knot points

The approximate solutions $U_{N}(x,t)$ and $V_{N}(x,t)$ are sought in terms of trigonometric B-splines as follows:

$$\begin{aligned} U(x,t)\approx U_{N}(x,t)= & {} {\sum \limits _{i=-1}^{N+1}}\hbox {TCB}_{i} (x)\delta _{i}(t),\nonumber \\ V(x,t)\approx V_{N}(x,t)= & {} {\sum \limits _{i=-1}^{N+1}}\hbox {TCB}_{i}(x)\gamma _{i}(t), \end{aligned}$$

(6)

where time-dependent parameters $\delta _{i}$ and $\gamma _{i}$ are to be determined from the collocation method together with using the boundary and initial conditions.

The nodal values of U, V, and its first and second derivatives at the knots are given in terms of parameters by the following relations:

$$\begin{aligned}&\begin{array}{ll} U_{i}=\alpha _{1}\delta _{i-1}+\alpha _{2}\delta _{i}+\alpha _{1}\delta _{i+1}&{}\,\,\,V_{i}=\alpha _{1}\gamma _{i-1}+\alpha _{1}\gamma _{i} +\alpha _{1}\gamma _{i+1} \\ U_{i}^{\prime }=\beta _{1}\delta _{i-1}+\beta _{2}\delta _{i+1} &{}\,\,\,V_{i}^{\prime }=\beta _{1}\gamma _{i-1}+\beta _{2}\gamma _{i+1}\\ U_{i}^{\prime \prime }=\lambda _{1}\delta _{i-1}+\lambda _{2}\delta _{i}+\lambda _{1}\delta _{i+1}&{}\,\,\,V_{i}^{\prime \prime }=\lambda _{1}\gamma _{i-1}+\lambda _{2}\gamma _{i}+\lambda _{1}\gamma _{i+1},\\ \end{array} \end{aligned}$$

(7)

where the coefficients are

$$\begin{aligned} \begin{array}{ll} \alpha _{1}=\sin ^{2}(\frac{h}{2})\csc (h)\csc (\frac{3h}{2}) &{} \alpha _{2}= \frac{2}{1+2\cos (h)} \\ \beta _{1}=-\frac{3}{4}\csc (\frac{3h}{2}) &{} \beta _{2}=\frac{3}{4}\csc ( \frac{3h}{2}) \\ \lambda _{1}=\frac{3((1+3\cos (h))\csc ^{2}(\frac{h}{2}))}{16(2\cos (\frac{h }{2})+\cos (\frac{3h}{2}))} &{} \lambda _{2}=-\frac{3\cot ^{2}(\frac{h}{2})}{ 2+4\cos (h)}. \end{array} \end{aligned}$$

(8)

Using the Crank–Nicolson scheme

$$\begin{aligned} U_{t}= & {} \frac{U^{n+1}-U^{n}}{\varDelta t}, U=\frac{U^{n+1}+U^{n}}{2},\nonumber \\ V_{t}= & {} \frac{V^{n+1}-V^{n}}{\varDelta t}, V=\frac{V^{n+1}+V^{n}}{2} \end{aligned}$$

(9)

leads to the time-integrated RDS equation system:

$$\begin{aligned}&\frac{U^{n+1}-U^{n}}{\varDelta t}-a_{1}\frac{U_{xx}^{n+1}+U_{xx}^{n}}{2} -b_{1}\frac{U^{n+1}+U^{n}}{2}-c_{1}\frac{V^{n+1}+V^{n}}{2}\nonumber \\&\quad -\,d_{1}\frac{ (U^{2}V)^{n+1}+(U^{2}V)^{n}}{2} -e_{1}\frac{(UV)^{n+1}+(UV)^{n}}{2}-m_{1}\frac{(UV^{2})^{n+1}+(UV^{2})^{n} }{2}\nonumber \\&\quad -\,n_{1}=0 \nonumber \\&\frac{V^{n+1}-V^{n}}{\varDelta t}-a_{2}\frac{V_{xx}^{n+1}+V_{xx}^{n}}{2} -b_{2}\frac{U^{n+1}+U^{n}}{2}-c_{2}\frac{V^{n+1}+V^{n}}{2}\nonumber \\&\quad -\,d_{2}\frac{ (U^{2}V)^{n+1}+(U^{2}V)^{n}}{2} -e_{2}\frac{(UV)^{n+1}+(UV)^{n}}{2}-m_{2}\frac{(UV^{2})^{n+1}+(UV^{2})^{n} }{2}\nonumber \\&\quad -\,n_{2}=0, \end{aligned}$$

(10)

where $U^{n+1}=U(x,t^{n+1})$ and $V^{n+1}=V(x,t^{n+1})$ denote the solutions at the $(n+1)$th time level. Here, $t^{n+1}=t^{n}+\varDelta t$, $\varDelta t$ is the time step and nth level is $t^{n}=n\varDelta t$. Linearization of the nonlinear terms $(U^{2}V)^{n+1},$ $(UV^{2})^{n+1}$, and $(UV)^{n+1}$ in Eq. 10 is managed by the following which is given in the study: (Rubin and Graves 1975) as:

$$\begin{aligned} (U^{2}V)^{n+1}= & {} U^{n+1}U^{n}V^{n}+U^{n}U^{n+1}V^{n} +U^{n}U^{n}V^{n+1}-2U^{n}U^{n}V^{n} \nonumber \\ (UV^{2})^{n+1}= & {} U^{n+1}V^{n}V^{n}+U^{n}V^{n+1}V^{n} +U^{n}V^{n}V^{n+1}-2U^{n}V^{n}V^{n} \nonumber \\ (UV)^{n+1}= & {} U^{n+1}V^{n}+U^{n}V^{n+1}-U^{n}V^{n}. \end{aligned}$$

(11)

When we substitute (11) in (10), the linearized general model equation system takes the form as follows:

$$\begin{aligned}&-\frac{a_{1}}{2}U_{xx}^{n+1}+\beta _{m1}U^{n+1}+\beta _{m2}V^{n+1} = \frac{a_{1}}{2}U_{xx}^{n}\nonumber \\&\quad \quad +\beta _{m3}U^{n}+\beta _{m4}V^{n}+n_{1}\nonumber \\&-\frac{a_{2}}{2}V_{xx}^{n+1}+\beta _{m5}U^{n+1}+\beta _{m6}V^{n+1} = \frac{a_{2}}{2}V_{xx}^{n}\nonumber \\&\quad \quad +\beta _{m7}U^{n}+\beta _{m8}V^{n}+n_{2}, \end{aligned}$$

(12)

where

$$\begin{aligned} \beta _{m1}= & {} \frac{1}{\varDelta t}-\frac{b_{1}}{2}-d_{1}U^{n}V^{n}-\frac{ e_{1}}{2}Vn-\frac{m_{1}}{2}(V^{n})^{2}, \nonumber \\ \beta _{m2}= & {} -\frac{c_{1}}{2}-\frac{d_{1}}{2}(U^{n})^{2}-\frac{e_{1}}{2} Un-m_{1}U^{u}V^{n}, \nonumber \\ \beta _{m3}= & {} \frac{1}{\varDelta t}+\frac{b1}{2} -\frac{m1}{2}(V^{n})^{2}, \nonumber \\ \beta _{m4}= & {} \frac{c1}{2}-\frac{d1}{2}(U^{n})^{2}, \nonumber \\ \beta _{m5}= & {} -\frac{b_{2}}{2}-d_{2}U^{n}V^{n} -\frac{e_{2}}{2}Vn-\frac{m_{2}}{2}(V^{n})^{2}, \nonumber \\ \beta _{m6}= & {} \frac{1}{\varDelta t}-\frac{c_{2}}{2}-\frac{d_{2}}{2}(U^{n})^{2}-\frac{e_{2}}{2}Un-m_{2} U^{u}V^{n}, \nonumber \\ \beta _{m7}= & {} \frac{b_{2}}{2}-\frac{m_{2}}{2}(V^{n})^{2},\nonumber \\ \beta _{m8}= & {} \frac{1}{\varDelta t}+\frac{c_{2}}{2}-\frac{d_{2}}{2}(U^{n})^{2}. \end{aligned}$$

(13)

Substitution of the approximate solutions at the knots (7) into (12) yields algebraic equation system:

$$\begin{aligned}&\nu _{m1}\delta _{m-1}^{n+1}+\nu _{m2}\gamma _{m-1}^{n+1}+\nu _{m3}\delta _{m}^{n+1}+\nu _{m4}\gamma _{m}^{n+1}+\nu _{m5}\delta _{m+1}^{n+1}+\nu _{m6}\gamma _{m+1}^{n+1}\nonumber \\&\quad \quad =\nu _{m7}\delta _{m-1}^{n}+\nu _{m8}\gamma _{m-1}^{n}+\nu _{m9}\delta _{m}^{n}+\nu _{m10}\gamma _{m}^{n}+\nu _{m11}\delta _{m+1}^{n}+\nu _{m12}\gamma _{m+1}^{n}+n_{1} \nonumber \\&\nu _{m13}\delta _{m-1}^{n+1}+\nu _{m14}\gamma _{m-1}^{n+1}+\nu _{m15}\delta _{m}^{n+1}+\nu _{m16}\gamma _{m}^{n+1}+\nu _{m17}\delta _{m+1}^{n+1}+\nu _{m18}\gamma _{m+1}^{n+1}\nonumber \\&\quad \quad =\nu _{m19}\delta _{m-1}^{n}+\nu _{m20}\gamma _{m-1}^{n}+\nu _{m21}\delta _{m}^{n}+\nu _{m22}\gamma _{m}^{n}+\nu _{m23}\delta _{m+1}^{n}+\nu _{m24}\gamma _{m+1}^{n}+n_{2}, \end{aligned}$$

(14)

where the coefficients $\nu _{m}$ are obtained by

$$\begin{aligned} \begin{array}{ll} \nu _{m1}=\beta _{m1}\alpha _{1}-\frac{a_{1}}{2}\lambda _{1} &{} \nu _{m13}=\beta _{m5}\alpha _{1} \\ \nu _{m2}=\beta _{m2}\alpha _{1} &{} \nu _{m14}=\beta _{m6}\alpha _{1}- \frac{a_{2}}{2}\lambda _{1} \\ \nu _{m3}=\beta _{m1}\alpha _{2}-\frac{a_{1}}{2}\lambda _{2} &{} \nu _{m15}=\beta _{m5}\alpha _{2} \\ \nu _{m4}=\beta _{m2}\alpha _{2} &{} \nu _{m16}=\beta _{m6}\alpha _{2}- \frac{a_{2}}{2}\lambda _{2} \\ \nu _{m5}=\beta _{m1}\alpha _{1}-\frac{a_{1}}{2}\lambda _{1} &{} \nu _{m17}=\beta _{m5}\alpha _{1} \\ \nu _{m6}=\beta _{m2}\alpha _{1} &{} \nu _{m18}=\beta _{m6}\alpha _{1}- \frac{a_{2}}{2}\lambda _{1} \\ \nu _{m7}=\beta _{m3}\alpha _{1}+\frac{a_{1}}{2}\lambda _{1} &{} \nu _{m19}=\beta _{m7}\alpha _{1} \\ \nu _{m8}=\beta _{m4}\alpha _{1} &{} \nu _{m20}=\beta _{m8}\alpha _{1}+ \frac{a_{2}}{2}\lambda _{1} \\ \nu _{m9}=\beta _{m3}\alpha _{2}+\frac{a_{1}}{2}\lambda _{2} &{} \nu _{m21}=\beta _{m7}\alpha _{2} \\ \nu _{m10}=\beta _{m4}\alpha _{2} &{} \nu _{m22}=\beta _{m8}\alpha _{2}+ \frac{a_{2}}{2}\lambda _{2} \\ \nu _{m11}=\beta _{m3}\alpha _{1}+\frac{a_{1}}{2}\lambda _{1} &{} \nu _{m23}=\beta _{m7}\alpha _{1} \\ \nu _{m12}=\beta _{m4}\alpha _{1} &{} \nu _{m24}=\beta _{m8}\alpha _{1}+ \frac{a_{2}}{2}\lambda _{1}. \end{array} \end{aligned}$$

(15)

The system (14) can be converted into the matrix system:

$$\begin{aligned} A{\mathbf {x}}^{n+1}=B{\mathbf {x}}^{n}+F. \end{aligned}$$

(16)

Boundary conditions are applied to adapt the system (12). The Dirichlet boundary conditions $U(x_{0},t)=\sigma _{0}$, $U(x_{N},t)=\sigma _{N}$, and $V(x_{0},t)=\eta _{0}$, $V(x_{N},t)=\eta _{N}$ become

$$\begin{aligned} m= & {} 0 \quad \delta _{-1}^{n}=\frac{1}{\alpha _{1}}\left( \sigma _{0}-\alpha _{2}\delta _{0}^{n}-\alpha _{1}\delta _{1}^{n}\right) ,\,\,\, \gamma _{_{-1}}^{n}=\frac{1}{\alpha _{1}}(\eta _{0}-\alpha _{2}\gamma _{_{0}}^{n}-a_{1}\gamma _{_{1}}^{n}), \nonumber \\ m= & {} N \quad \delta _{N+1}^{n}=\frac{1}{\alpha _{1}}\left( \sigma _{N}-\alpha _{1}\delta _{N-1}^{n}-\alpha _{2}\delta _{N}^{n}\right) , \,\,\,\gamma _{N+1}^{n}=\frac{1}{\alpha _{1}}(\eta _{N}-\alpha _{1}\gamma _{N-1}^{n}-a_{2}\gamma _{N}^{n}), \end{aligned}$$

(17)

and the Neumann boundary conditions $U_{x}(x_{0},t)=U_{x}(x_{N},t)=0$ and $V_{x}(x_{0},t)=V_{x}(x_{N},t)=0$ give the following equations:

$$\begin{aligned} m= & {} 0\quad \delta _{-1}^{n}=\frac{1}{\beta _{1}}(U_{x}(x_{0},t)-\beta _{2}\delta _{1}^{n}), \ \gamma _{_{-1}}^{n}=\frac{1}{\beta _{1}} (V_{x}(x_{0},t)-\beta _{2}\gamma _{1}^{n}), \nonumber \\ m= & {} N\quad \delta _{N+1}^{n}=\frac{1}{\beta _{2}}(U_{x}(x_{N},t)-\beta _{1}\delta _{N-1}^{n}), \ \gamma _{N+1}^{n}=\frac{1}{\beta _{2}} (V_{x}(x_{N},t)-\beta _{1}\gamma _{N-1}^{n}).\quad \end{aligned}$$

(18)

Thus, using one of the coupled boundary conditions, we can eliminate the parameters $\delta _{-1}^{n},\delta _{N+1}^{n},\gamma _{_{-1}}^{n},\gamma _{N+1}^{n}$ from the system (14). Thus, the modified system contains $2N+2$ linear equation having $2N+2$ unknown parameters. This system can be solved using the Thomas algorithm (Thomas 1975).

Solutions can be found at each step at the knots on the problem domain using the (14) and (17), respectively, once the initial parameters $d^{0}=(\delta _{-1}^{0},\gamma _{-1}^{0},\delta _{0}^{0},\gamma _{0}^{0}...,\delta _{N+1}^{0},\gamma _{N+1}^{0})$ are computed. To do so, the approximate solution at $t=0$ should match up with the initial conditions at the knots and the first derivative of the approximate solutions should also match up with the Neumann boundary conditions at knots $x_{0}$ and $x_{N}$:

$$\begin{aligned} \begin{array}{ll} U(x_{0},0)=U_{N}(x_{0},0)=\beta _{1}\delta _{-1}^{0} +\beta _{2}\delta _{1}^{0} &{}\\ U(x_{i},0)=U_{N}(x_{i},0)=\alpha _{1}\delta _{i-1}^{0} +\alpha _{2}\delta _{i}^{0}+\alpha _{1}\delta _{i+1}^{0}&{} \\ U(x_{N},0)=U_{N}(x_{N},0)=\beta _{1}\delta _{N-1}^{0} +\beta _{2}\delta _{N+1}^{0}&{}\\ &{}i=0,\ldots ,N\\ V(x_{0},0)=V_{N}(x_{0},0)=\beta _{1}\gamma _{-1}^{0} +\beta _{2}\gamma _{1}^{0} &{}\\ V(x_{i},0)=V_{N}(x_{i},0)=\alpha _{1}\gamma _{i-1}^{0} +\alpha _{2}\gamma _{i}^{0}+\alpha _{1}\gamma _{i+1}^{0}&{}\\ V(x_{N},0)=V_{N}(x_{N},0)=\beta _{1}\gamma _{N-1}^{0} +\beta _{2}\gamma _{N+1}^{0}&{}. \end{array} \end{aligned}$$

Solving systems above separately give the initial parameters $d^{0}$.

4 Numerical solutions and test results

In this section, we will compare the efficiency and accuracy of suggested method on the given reaction–diffusion equation system models. The obtained results for each model will be compared with the earlier studies given in the references. The accuracy of the schemes is measured in terms of the following discrete error norms: $L_{\infty }=|U-U_{N}|_{\infty }={\max \limits _{j}^{}}|U_{j}-(U_{N})_{j}^{n}|$, the relative error $=\sqrt{\frac{\sum _{j=0}^{N}|U_{j}^{n+1}-U_{j}^{n}|^{2}}{\sum _{j=0}^{N}|U_{j}^{n+1}|}}$. Order of convergence is computed using the following form:

$$\begin{aligned} \mathrm{order} =\frac{\log \frac{(L_{\infty })_{\varDelta t_{m}}}{(L_{\infty })_{\varDelta t_{m+1}}}}{\log \frac{\varDelta t_{m}}{\varDelta t_{m+1}}}, \end{aligned}$$

(19)

where $(L_{\infty })_{\varDelta t_{m}}$ is the error norm $L_{\infty }$ with time step $\varDelta t_{m}$.

4.1 Linear problem

The linear form of the problem (1) has been solved to calculate error norms for testing the method:

$$\begin{aligned} \frac{\partial U}{\partial t}= & {} d\frac{\partial ^{2}U}{\partial x^{2}}-aU+V \nonumber \\ \frac{\partial V}{\partial t}= & {} d\frac{\partial ^{2}V}{\partial x^{2}}-bV, \end{aligned}$$

(20)

which has analytical solutions given as follows:

$$\begin{aligned} U(x,t)= & {} (e^{-(a+d)t}+e^{-(b+d)t})\cos (x), \nonumber \\ V(x,t)= & {} (a-b)(e^{-(b+d)t})\cos (x). \end{aligned}$$

(21)

Three different cases in terms of dominance of reaction or of diffusion were considered in numerical computation. The initial conditions can be obtained, when $t=0$ in (21) solutions. When solution region is selected as $(0, \frac{\pi }{2})$ interval, the boundary conditions are described as follows:

$$\begin{aligned} U_{x}(0,t)= & {} 0 \qquad U(\pi /2,t)=0,\nonumber \\ V_{x}(0,t)= & {} 0\qquad V(\pi /2,t)=0. \end{aligned}$$

(22)

In numerical calculations, the program is going to run up to time $t=1$ for $N=512$ and $\varDelta t$, and reaction and diffusion mechanism is examined for different selections of constants a, b,  and d. The error value $L_{\infty }$ is presented in the tables.

First, the system (20) is studied for parameters $a=0.1, b=0.01$ and $d=1$ which is diffusion dominated case. The boundary and initial conditions are chosen to coincide with (Sahin 2009). In Table 3, $L_{\infty }$ error norms and pointwise rate of order are recorded for both U and V, for $N=512$ and various $\varDelta t$, and the results of Chou et al. (2007), Sahin (2009) and Ersoy and Dag (2015) are also given in the same table. When Table 3 is examined, it seems that accuracy of the obtained results for function U and V is very close to those found with application of both polynomial cubic B-spline collocation method (PCBCM) (Sahin 2009) and the Crank–Nicolson and multi-grid method (CN-MGM) (Chou et al. 2007). The suggested algorithm produces lower accuracy than the collocation method based on the exponential B-splines including one free parameter (EBCM) (Ersoy and Dag 2015). The free parameter of the exponential B-spline function was found experimentally at every time steps and this increases the cost of the algorithm.

Table 3 Error norms $L_{\infty }$ for diffusion dominant case for $a=0.1,$ $b=0.01,$ $d=1,$ and $N=512$

Second, the parameters of system (20) are selected as $a=2, b=1, d=0.001$ which is reaction-dominated case. The obtained results in terms of $L_{\infty }$ norm are given in Table 4 and similar accuracy is obtained for solutions of the U and V for Eq. 20. The suggested method together with PCBCM, CN-MGM, and implicit integration factor method (IIFM) produces similar results except for the EBCM.

Table 4 Error norms $L_{\infty }$ for reaction-dominated case for $a=2,$ $b=1,d=0.001,$ and $N=512$

Finally, with parameters $a=100,b=1,d=0.001,$ reaction dominated with stiff reaction case solution of the reaction–diffusion equation is obtained. Once more, the suggested method provides the same magnitude of the error with PCBCM, CN-MGM, and IIFM, as shown in Table 5.

Table 5 Error norms $L_{\infty }$ for reaction-dominated case with stiff reaction for $a=100,$ $b=1,d=0.001,$ and $N=512$

4.2 Nonlinear problem (Brusselator model)

One of the special forms of nonlinear RDS is the Brusselator model predicting oscillations in chemical reaction. First, the system was presented by Prigogine and Lefever (Prigogine and Lefever 1968) which describes some chemical reactions with two components:

$$\begin{aligned} \frac{\partial U}{\partial t}= & {} \varepsilon _{1}\frac{\partial ^{2}U}{ \partial x^{2}}+A+U^{2}V-(B+1)U \nonumber \\ \frac{\partial V}{\partial t}= & {} \varepsilon _{2}\frac{\partial ^{2}V}{ \partial x^{2}}+BU-U^{2}V, \end{aligned}$$

(23)

where $\varepsilon _{i},$ $i=1,2$ are diffusion constants, x is the spatial coordinate and U, V are functions of x and t which represent concentrations. The initial conditions are selected similar to those in the reference Zegeling and Kok (2004):

$$\begin{aligned} U(x,0)=0.5,\quad V(x,0)=1+5x, \end{aligned}$$

(24)

and the first derivative initial boundary condition is replaced by the second derivative initial boundary conditions for this test problem as follows:

$$\begin{aligned} \begin{array}{ll} U_{xx}(x_{0},t)=0 &{} U_{xx}(x_{N},t)=0,\\ V_{xx}(x_{0},t)=0 &{} V_{xx}(x_{N},t)=0.\\ \end{array} \end{aligned}$$

(25)

In the system (23), the coefficients are taken as $\ \varepsilon _{1}=\varepsilon _{2}=10^{-4},$ $A=1,$ and $B=3.4$ to coincide with parameters in the paper (Zegeling and Kok 2004). The solutions are obtained in the region $x\in \left[ 0,1\right]$ with use of space step $N=200$, time step $\varDelta t=0.01$ and the program is run by the time $t=15$. The solutions under these selections of boundary and initial conditions are periodically moving wave given in Figs. 1 and 2 in which a period of 7.7 is measured. The smaller $\varepsilon _{1},\varepsilon _{2}$ are chosen; steeper wave is produced. Thus, the algorithm gives a fairly moving waves.

Fig. 1

Repetitive spot pattern of waves of the function U

Fig. 2

Repetitive spot pattern of waves of the function V

The density values for periodical motion are given in Table 6 and these values can be verified with the Table 7, study of Sahin (2009).

Table 6 Density values for periodic motion of TCB

Table 7 Density values for periodic motion of cubic B-spline (Sahin 2009)

Exhibited periodical movement is seen clearly in Figs. 3, 4, 5, 6 which shows the change of the density of functions. When these figures are examined, we can see that the waves display periodical motion.

Fig. 3

Density variation for U for $N=200$ $\varDelta t=0.01$

Fig. 4

Density variation for U for $N=200$ $\varDelta t=0.01$

Fig. 5

Density variation for V for $N=200$ $\varDelta t=0.01$

Fig. 6

Density variation for V for $N=200$ $\varDelta t=0.01$

4.3 Nonlinear problem (Schnakenberg model)

Schnakenberg model is another well-known RDS model. There are many studies in the literature on this model. First, it is proposed by Schnakenberg (1979) and given as follows:

$$\begin{aligned} \frac{\partial U}{\partial t}= & {} \frac{\partial ^{2}U}{\partial x^{2}}+\gamma (a-U+U^{2}V)\nonumber \\ \frac{\partial V}{\partial t}= & {} d\frac{\partial ^{2}V}{\partial x^{2}}+\gamma (b-U^{2}V), \end{aligned}$$

(26)

where U and V denote the concentration of activator and inhibitor, respectively; d is diffusion coefficients; $\gamma$, a, and b are rate constants of the biochemical reactions. The oscillation problem is taken into account for Schnakenberg model. Accordingly, the parameters for system (26) are selected as $a=0.126779$, $b=0.792366,d=10$ and $\gamma =10^{4}$. The problem’s initial conditions are as follows:

$$\begin{aligned} U(x,0)= & {} 0.919145+0.001{\sum \limits _{j=1}^{25}}\frac{\cos (2\pi jx)}{j}\nonumber \\ V(x,0)= & {} 0.937903+0.001{\sum \limits _{j=1}^{25}}\frac{\cos (2\pi jx)}{j} \end{aligned}$$

(27)

which are on the interval $[-1,1]$. Computations are performed until the time $t=2.5$ for space/time combinations given in Table 8. The obtained relative error values are given in Table 8 together with the results of polynomial cubic B-spline collocation method (Sahin 2009).

Table 8 Relative error values for $N=100$ in $t=2.5$

As shown in Table 8, the algorithm produces accurate results even when the time increment is larger. Figure 7 is drawn to show the oscillation movements for values $\varDelta t=5\times 10^{-5}$, $N=100$ and $N=200$. It is shown in Fig. 7 that the functions U and V make nine oscillations when $N=200$ and one of them does not seen in the complete form of oscillations when $N=100$. This result with the references Madzvamuse et al. (2003), Ruuth (1995) shows that the finer mesh is necessary to have accurate solutions.

4.4 Nonlinear problem (Gray–Scott model)

Some patterns existing in nature are performed via the Gray–Scott RDS which was first introduced by Gray and Scott (1984) and the system is given as follows:

$$\begin{aligned} \frac{\partial U}{\partial t}= & {} \varepsilon _{1}\frac{\partial ^{2}U}{\partial x^{2}}-U^{2}V+f(1-U), \nonumber \\ \frac{\partial V}{\partial t}= & {} \varepsilon _{2} \frac{\partial ^{2}V}{\partial x^{2}}+U^{2}V-(f+k)V. \end{aligned}$$

(28)

In this section, the numerical method was run to model repetitive spot patterns on Gray–Scott system. The parameters for the system (28) were chosen from the reference Craster and Sassi (2006) and $\varepsilon _{1}=10^{-4},\varepsilon _{2}=10^{-6},f=0.024$ and $k=0.06$. The initial conditions, both Dirichlet and Neumann boundary conditions of the system (28), were taken as follows:

$$\begin{aligned} U(x,0)= & {} 1-\frac{1}{2}\sin ^{100}(\pi \frac{(x-L)}{2L})\nonumber \\ V(x,0)= & {} \frac{1}{4}\sin ^{100}(\pi \frac{(x-L)}{2L}), \end{aligned}$$

(29)

$U(x_{0},t)=U(x_{N},t)=1,V(x_{0},t)=V(x_{N},t)=0$ and $U_{x}(x_{0},t)=U_{x}(x_{N},t)=0,V_{x}(x_{0},t)=V_{x}(x_{N},t)=0$, respectively. Solutions were obtained over intervals $[-200,200]\times [0,2000)$ for space step $h=1$ and time step $\varDelta t=0.2$. The initial pulses and solutions are depicted in Fig. 8, when times $t=0$ and $t=2000$, so the repetitive patterns can be observed. Figures 8, 9, 10 demonstrate pulse split for U and V as time advance; the initial pulses are split into two pulses and separated from each other, and once more, the same repeats for each pulse.

Fig. 7

Oscillation movement for $N=100$ and $N=200$ at the moment $t=2.5$

Fig. 8

Splitting process of repetitive spot pattern of waves

Fig. 9

Repetitive spot pattern of waves of the function U

Fig. 10

Repetitive spot pattern of waves of the function V

5 Stability analysis

The stability of the recursive system (16) can be written in the matrix form:

$$\begin{aligned} {\mathbf {x}}^{n+1}=M{\mathbf {x}}^{n}+Q, \end{aligned}$$

(30)

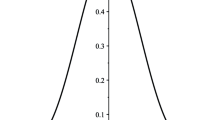
which is studied by finding eigenvalues of the iterative matrix $M=A^{-1} B$ whose eigenvalues $\lambda _{i}$ are expected as $max|\lambda _{i}|<1$. Thus, eigenvalues of M are demonstrated for linear problem and Schnakenberg model in Figs. 11 and 12.

Fig. 11

Eigenvalues of matrix M for linear problem with $N=512$ and $\varDelta t=0.005$, $t=1$, and $\mathrm{max}|\lambda _{i}|=0.9993$

Fig. 12

Eigenvalues of matrix M for Schnakenberg model with $N=100$ and $\varDelta t=5\times 10^{-6}$, $t=2.5$, $\mathrm{max}|\lambda _{i}|=0.9609$

We have demonstrated eigenvalues graphically at a specific time. During the run of the algorithm, we have observed that eigenvalues are almost less then 1 at all the time steps. Similar treatments can be carried out for other test problems and found absolute value of the eigenvalues which are less then 1, as well. Hence, the solution of the recursive formula is unconditionally stable.

6 Conclusion

A collocation algorithm based on trigonometric cubic B-splines is build up for getting solutions of the system of reaction–diffusion equation. Some basic reaction–diffusion equations known as Brusselator model, Schnakenberg model and Gray–Scott model are studied to show efficiency of the algorithm. First, linear reaction–diffusion problem which has the analytical solution is dealt with to make comparison with earlier studies and the suggested algorithm produces similar accuracy with polynomial cubic B-spline algorithm, CN-MG method and IIF2 methods. Exponential cubic B-spline collocation method with free parameters produces least error as shown in Tables 3, 4, 5. Time pointwise rate of order of convergence is calculated as 2 approximately for some parameters as given in Tables 3, 4, 5. Thus, the order of the Crank–Nicolson method is verified for the suggested algorithm. Each reaction–diffusion model is studied with a delicate test problem in terms of numerical computation to express usage of the algorithm. Especially, the method copes with solutions having sharp variations. Eigenvalues of iterative matrix are drawn in Figs. 11 and 12, and found to be less than 1, so that the iterative scheme of the integrated reaction–diffusion equation is stable. Consequently, trigonometric cubic B-spline collocation algorithm is an effective method with simplicity and cheap cost and produce the acceptable results for the solutions of the reaction–diffusion systems. This algorithm can be reliably used to solve some other nonlinear differential equations.