Optimization of collision-free paths in a differential-drive robot by a smoothing piecewise-linear approach

Abstract

This paper presents a methodology for optimizing pre-calculated collision-free paths of differential-drive wheeled robots. The main advantage of this methodology is that optimization is done by considering the kinematics and mechanical constraints of the mobile robot. In accordance to this proposal, the optimized path is achieved by applying recursively a local smoothing on an initial path which is originally modeled as a one-dimensional piecewise linear function. By this recursive smoothing, it can be ensured that the original piecewise linear function can be transformed into a smooth one that fulfill the constraints established by the kinematic equations of the wheeled mobile in terms of a minimum radius of curvature. As a result of this, a trajectory which guarantees lower power consumption and lower mechanical wear, is obtained. To show the better performance of the proposed approach, numerical simulation results are contrasted to those obtained from other reported methods with regards to path length, minimum radius of curvature, cross track error, continuity and resulting acceleration.

1 Introduction

Path optimization is one of the trending topics of research in the area of path planning for mobile robots (Latombe 1991). Generally, the optimization is focused on determining a path that ensures the best use of the mechanical resources of the mobile robot by considering the kinematics restrictions imposed by the trajectory shape. Since there are many types of robots with different capabilities, limitations, and applications, it is difficult to find a general definition of “optimal path”. Basically, optimization focuses on two important aspects: energy and security. Concerning to energy, power consumption of a robot is directly related to its physical structure as well as to its mechanical constrains to move and rotate. In regard to safety, this is related to the planned path which should ensure that the robot and obstacles are free of collision in the presence of some inevitable errors such as imperfections in the obstacles, finite calculations or uncertainty in the workspace (Lavalle 2006). In accordance with published literature so far, there are techniques dealing with the problem of path optimization in mobile robots, being one of them, the so-called path smoothing. As representative examples of this technique it can be mentioned those based on spline interpolation (Kamasamudram 2013; Chang and Huh 2015; Elbanhawi et al. 2015), in recursive forms such as Bézier curves (Ho and Liu 2009; Choi et al. 2010; Yang and Choi 2013) or geometric shapes as arcs (Lepej et al. 2015; Brezak and Petrovic 2011; Li and Meek 2005) or hypocycloids (Ravankar et al. 2016), etc. In all these cases, the methodologies perform a trajectory segmentation near the breakpoints, producing systems of polynomial equations with high computational complexity, or generating a large amount of points (that are stored in memory) that subsequently the robot will assign as speed for each wheel. Alternatively, our proposal is oriented to optimize collision-free paths described as continuous piecewise-linear (PWL) functions by following a smoothing procedure similar to that described in Jimenez-Fernandez et al. (2016a). Its main advantage is that the optimized path takes also into consideration the kinematics of the differential-drive wheeled robot. In contrast to the previously mentioned methods, the benefits associated to this methodology are: easy representation of the trajectory as one-dimensional PWL functions, which can reproduce an infinite number of points in comparison to any pre-calculated table, fast evaluation (a direct function evaluation) and easy modification of the smoothing level in the breakpoints by only changing a parameter. This paper is organized as follows: Sect. 2 presents the smooth piecewise model in which our proposed methodology is based. Section 3 describes the kinematics equations for a differential-drive wheeled robot. Section 4 explain in detail the methodology to determine the best smoothing coefficients which ensure an optimal path in terms of the radius of curvature and the kinematics model equations. Section 5 illustrates how the motion planning for the robot ensures that the optimized path is correctly traversed. In Sect. 6 simulation examples are presented to demonstrate the effectiveness of the proposed methodology. Finally, Sect. 7 exposes the concluding remarks of this work.

2 Smooth piecewise-linear model

Although exists many PWL models reported in literature (Leenaerts and Van-Bookhoven 1998; Guzelis and Goknar 1991; Kahlert and Chua 1990; Julian et al. 1999), the methodology here proposed is based on the canonical description of Chua and Kang (1997), Kang and Chua (1978) and Chua and Deng (1986, 1988). This model is preferred over all others due to its compact and explicit formulation expressed as:

$$\begin{aligned} \displaystyle f(x) = a_{0}+a_{1}x+\sum _{j=1}^{n}b_{j}|x-x_{j}| \end{aligned}$$

(1)

where $a_{0}, a_{1}$ and $b_{j}$ are constants that represent model parameters meanwhile $x_{j}$ denotes the jth breakpoint in a single-valued PWL function constituted by n linear segments.

In accordance with Jimenez-Fernandez et al. (2016a, b), a smooth version of (1) can be achieved by approximating the absolute-value terms $\left| x-x_{j}\right|$ by

$$\begin{aligned} \displaystyle |x-x_{j}| = \frac{\ln (1+e^{-\alpha (x-x_{j})})+\ln (1+e^{\alpha (x-x_{j})})}{\alpha } \end{aligned}$$

(2)

where $\alpha$ is the smoothing parameter which allows different approach levels depending on the assigned value. The effect of varying $\alpha$ in (2) is shown in Fig. 1.

Fig. 1

Smooth approximation of $|x-x_{j}|$ for $x_{j}=1$, $\alpha =20,7,4$

Based in this approximation, the form of (1) can be now expressed in terms of exponential and natural logarithms as:

$$\begin{aligned} \displaystyle f(x) = A_{0}+A_{1}x+\sum _{j=1}^{n}B_{j}\ln \left( 1+e^{-\alpha (x-x_{j})}\right) \end{aligned}$$

(3)

where similarly as (1) $A_{0},A_{1}$ and $B_{j}$ are model parameters.

For further information about (3) reader is referred to Jimenez-Fernandez et al. (2016a, b).

3 Differential robot kinematics

It is well known that a differential-drive wheeled robot is a non-holonomic system because it can not change its direction instantly (Lavalle 2006). This type of robot consists of two main wheels that are independently controlled by a motor and a caster wheel placed in the rear. To build a simple model of the kinematics of a differential robot only two parameters are needed: the distance D between the left and right wheels, and the wheel radius r. According to Lavalle (2006), this kinematic model can be expressed by the following equations system:

$$\begin{aligned} v_{x}= & {} r \frac{(v_{\mathrm{R}}+v_{\mathrm{L}})}{2} \cos (\theta _{\mathrm{R}})\nonumber \\ v_{y}= & {} r \frac{(v_{\mathrm{R}}+v_{\mathrm{L}})}{2}\sin (\theta _{\mathrm{R}}) \nonumber \\ \omega= & {} \frac{r(v_{\mathrm{R}}-v_{\mathrm{L}})}{l} \nonumber \\ v_{\mathrm{T}}= & {} \frac{v_{\mathrm{R}}+v_{\mathrm{L}}}{2} \nonumber \\ v_{\psi }= & {} v_{\mathrm{R}}-v_{\mathrm{L}} \end{aligned}$$

(4)

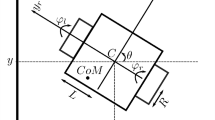
where $v_{x}$ and $v_{y}$ are the translational speed, $v_{\mathrm{T}}$ is a combination of translational speeds as shown in Fig. 2, r is the radius of the robot’s wheels, $\theta _{\mathrm{R}}$ is the angle between the axis of symmetry of the mobil and the axis x of the work space, $\omega$ is the angular velocity, $v_{\mathrm{R}}$ and $v_{\mathrm{L}}$ are the speeds of the left and right wheels, respectively. The two action variables represented by $v_{\mathrm{T}}$ (translation) and $v_{\psi }$ (rotation), are also considered.

Fig. 2

Representation of position and speed of the differential robot

Based on (4), it is possible to deduce the location and orientation of the robot because these parameters change according to differential-drive, this means, decrease or increase the speed of the left or right wheel. If $v_{\mathrm{R}} = v_{\mathrm{L}}$, then this describes a straight path, but if $v_{\mathrm{R}} \ne v_{\mathrm{L}}$, then this rotates clockwise or counter-clockwise depending on the speed of each wheel. The curvature produced by the rotational motion has at its rotation center the so-called ICC (instantaneous center of curvature). The parameters involved in a curved trajectory are shown in Fig. 3.

Fig. 3

Curve path described for a differential robot

Representing each wheel speed ($v_{\mathrm{R}}$ and $v_{\mathrm{L}}$) in terms of angular velocity $\omega$, the following equations system are obtained:

In the case of a left-turn:

$$\begin{aligned} \begin{array}{l} v_{\mathrm{R}} = \omega (R+l/2) \\ v_{\mathrm{L}} = \omega (R-l/2). \end{array} \end{aligned}$$

(5)

In the case of a right-turn:

$$\begin{aligned} \begin{array}{l} v_{\mathrm{R}} = \omega (R-l/2) \\ v_{\mathrm{L}} = \omega (R+l/2) \end{array} \end{aligned}$$

(6)

from (5) it can be stated that

$$\begin{aligned} \frac{v_{\mathrm{R}}}{R+l/2}=\frac{v_{\mathrm{L}}}{R-l/2} \end{aligned}$$

(7)

and respectively, from (6) it follows

$$\begin{aligned} \frac{v_{\mathrm{R}}}{R-l/2}=\frac{v_{\mathrm{L}}}{R+l/2} \end{aligned}$$

(8)

and after solving (7) and (8) for R, results

$$\begin{aligned} R = \pm \frac{l}{2}\frac{v_{\mathrm{R}}+v_{\mathrm{L}}}{v_{\mathrm{R}}-v_{\mathrm{L}}} \end{aligned}$$

(9)

where R is the radius having the curvature described by the path followed by the mobile. In accordance to (9) it must be noted that R is considered as positive in the right-turn case and negative in the left-turn case.

Having knowledge of the physical functioning of the differential-drive wheeled robot, it is possible to deduce a strategy that allows to generate a smooth path which takes into consideration the radius of curvature described by the mobile when it is turning.

4 Control of smoothing by a curvature radius criteria

An optimal trajectory that produces a less wear of a differential-drive wheeled robot, is that which minimizes abrupt changes of direction (smooth trajectory) because it avoids the rotational inversion of the wheels and it also demands the least amount of variations in speed. However, determining a smooth path by approximating the absolute value in a PWL trajectory is only a part of the work. The next step is to link it to the physical dimensions of the mobile robot to obtain suitable values of the smoothing parameters $(\alpha _{j})$. Moreover, it is also imperative to prevent inversion in the rotational direction of the wheels in the presence of a path with sharp curves. In that regard, taking into account Fig. 3, it can be observed that the minimum radius of curvature that should describe the mobile to avoid rotational inversion in the wheels is $R>l/2$ because it ensures that the ICC will always be outside of the robot body. If $R=l/2$, then the ICC will be in the center of one of the wheels giving as result that during rotation only one of these to be in motion and the other in zero speed, this condition is undesirable because the kinetic energy will be completely lost in one of the motors. This situation derives in two problems: an increase of energy consumption because of having to recover the movement of the stopped motor and mechanical wear caused by the vibration during each turning on/off of the motor. To determine in which part of the path the turning radius does not fulfill the above described condition, the radius of curvature for a curve described in Cartesian coordinates (x, y) is defined as follows:

$$\begin{aligned} \displaystyle R_{\mathrm{c}} = \frac{\left[ \left( \frac{\mathrm{d}x}{\mathrm{d}t}\right) ^{2}+\left( \frac{\mathrm{d}y}{\mathrm{d}t}\right) ^{2}\right] ^{\frac{3}{2}}}{\left| \frac{\mathrm{d}x}{\mathrm{d}t}\frac{\mathrm{d}^{2}y}{\mathrm{d}t^{2}}-\frac{\mathrm{d}y}{\mathrm{d}t}\frac{\mathrm{d}^{2}x}{\mathrm{d}t^{2}}\right| } \end{aligned}$$

(10)

where x(t) and y(t) are the smooth PWL parametric equations describing the path to follow by the differential robot.

4.1 Methodology to ensure an appropriate radius of curvature

Consider a collision-free trajectory approximated by n linear segments in a Cartesian space. To ensure that the minimum radius of curvature along the path always be greater than l / 2, first, it is necessary to describe the trajectory as a smooth PWL function and then to adjust its smoothing parameters $\alpha _{j}$, for $j=2,3,\ldots ,(n+1)$, at the breakpoint which requires it. In most cases it corresponds to a decrease in value. The methodology proposed to determine the appropriate coefficient for each breakpoint can be summarized as follows:

• 1. Obtain the pair of smooth PWL parametric equations $\{x(t),y(t)\}$ from a list P of initial breakpoints and smoothing coefficients that describe the path to follow by the robot.

  $$\begin{aligned} P = \left\{ (X_{1},Y_{1}),(X_{2},Y_{2},\alpha _{2})\cdots (X_{i-1},Y_{i-1},\alpha _{j}),(X_{i},Y_{i})\right\} \end{aligned}$$

  for $i=1,2,\ldots ,(n+1)$ being $X_{i}$ and $Y_{i}$ coordinates in the Cartesian space and $\alpha _{j}$ specific constants that must be initially selected (usually a large value) in such a way that they guarantees to hold the collision-free condition. It is important to point out that the first and last points ($P_{1}$ and $P_{n+1}$) do not have assigned any smoothing parameter ($\alpha _{j}$). The reason for this is that three points are necessary to define an arc. Due to this fact, index j runs from 2 to n. It should be noted that due to the trajectory must be followed by the robot during certain period of time, the resulting parametric functions are also time-dependent functions, here denoted as: $\{x(t),y(t)\}$.

• 2. Replace the parametric equations $\{x(t),y(t)\}$ in the radius of curvature formula (10),

  $$\begin{aligned} R_{\mathrm{c}}(t) = \frac{\left[ \left( \frac{\mathrm{d}x(t)}{\mathrm{d}t}\right) ^{2}+\left( \frac{\mathrm{d}y(t)}{\mathrm{d}t}\right) ^{2}\right] ^{\frac{3}{2}}}{\left| \frac{\mathrm{d}x(t)}{\mathrm{d}t}\frac{\mathrm{d}^{2}y(t)}{\mathrm{d}t^{2}}-\frac{\mathrm{d}y(t)}{\mathrm{d}t}\frac{\mathrm{d}^{2}x(t)}{\mathrm{d}t^{2}}\right| } \end{aligned}$$

  where $R_{\mathrm{c}}(t)$ is also a time-dependent function.

  From this function, the minimum radius $\mathrm{min}\{R_{\mathrm{c}}(t)\}$ described in the trajectory is determined. In our proposal, this is done by a discrete evaluation of $R_{\mathrm{c}}(t)$. The precision of this result will depend on the step size, and therefore, on the number of evaluation points. For N samples per linear segment in a PWL trajectory, the $\mathrm{min}\{R_{\mathrm{c}}(t)\}$ is expressed as:

  $$\begin{aligned} \mathrm{min}\{R_{\mathrm{c}}(t)\}=\{R_{\mathrm{c}}(t_{1}),R_{\mathrm{c}}(t_{2}),\ldots ,R_{\mathrm{c}}(t_{k})\} \end{aligned}$$

  where $t_{1}=0$ and $t_{k+1}=(t_{k})+h$ for $k=1,2,\ldots ,(N\times n)-1$; with h denoting the step size given by

  $$\begin{aligned} h=\frac{\lambda }{N\times n} \end{aligned}$$

  where length of $\lambda$ will be defined by the range of the parametric functions: $\{x(t),y(t)\}$, from the starting point $P_{1}$ to the ending point $P_{n+1}$.

• 3. If there is any breakpoint that does not satisfy the condition of a minimum radius of curvature (lower than l/2), it is identified by obtaining the value of t that produces $\mathrm{min}\{R_{\mathrm{c}}(t)\}$. Then, a sweep of N / 2 samples after and before this point is performed (from $t = t_{k-N/2}$ to $t_{k+N/2}$ with respect to the value of t where $R_{\mathrm{c}}(t)<l/2$). After that, if during the search process an integer value is found, then it is assumed this corresponds to the position of the coordinate pair of the array P which is necessary to make an adjustment in its smoothing parameter. Fig. 4 shows graphically the search of the breakpoint with a radius of curvature conflict.

• 4. Once the ith breakpoint has been identified, it proceeds to modify the smoothing parameter associated with the coordinate pair. To gradually increase the radius of curvature, the smoothing parameter is slightly decreased as $\alpha _{i}=\alpha _{i}-\delta$.

• 5. From here, all the previous steps are recursively repeated by considering the updated smoothing parameters. This process will stop until the condition $\mathrm{min}\{R_{\mathrm{c}}(t)\} > l/2$ be satisfied for all the breakpoints.

Fig. 4

Search breakpoint with minimum radius of curvature

This methodology is summarized as an algorithm in Algorithm 1, where smoothPWL() represents the function to obtain the smooth parametric functions.

Similarly, in Algorithm 2 the function smoothPWL() is expressed as an algorithm.

5 Motion planning

After considering the kinematic of the differential robot, the smooth trajectory and the radius of curvature formula, the velocities of each of the wheels can be assigned within a normalized range where 1 corresponds to the maximum speed of the motors ($Vel_{maxMot}=1$) and 0 to the minimum speed ($Vel_{minMot}=0$). Negative speed (reverse rotation of the motor) is not considered because the path has been optimized so that there is no such effect.

When the robot describes a straight path, it is considered that both wheels are rotating at maximum speed, however, when it turns, the speed of the inner wheel must be decreased while the speed of the outer wheel that moves through the arc path must continue at maximum speed. From this, Eq. (9) can be used to obtain the speed of one of the wheels as follows: From this, Eq. (9) can be used to obtain the turn right speed ($v_{\mathrm{R}}$) and the turn left speed ($v_{\mathrm{L}}$) of the wheels as follows:

$$\begin{aligned} \displaystyle v_{\mathrm{R}}=\frac{v_{\mathrm{L}}(2R-l)}{2R+l} \end{aligned}$$

(11)

$$\begin{aligned} \displaystyle v_{\mathrm{L}}=\frac{v_{\mathrm{R}}(2R-l)}{2R+l} \end{aligned}$$

(12)

where $v_{\mathrm{R}}=Vel_{maxMot}$ in (12), $v_{\mathrm{L}}=Vel_{maxMot}$ in (11), l is the distance between the wheels of the mobile robot and R is the time-dependent radius of curvature which is replaced by the discrete evaluation of Eq. (10) for $t=0$ to $t=t_{(N\times n)-1}+h$ with h denoting the step size as defined in the Step 2 in the previous section. The resulting list of speeds corresponds to a set of speeds of both wheels, therefore, it is necessary to classify the speed of the left wheel to the speed of the right wheel. To establish a numerical criteria to determine to which wheel the calculated speed corresponds is necessary to determine the direction of the rotation as shown in Fig. 5. This figure represents three consecutive discrete points: $\left\{ x(t_{k}),y(t_{k})\right\} ,\left\{ x(t_{k+1}),y(t_{k+1})\right\} ,$ and $\left\{ x(t_{k+2}),y(t_{k+2})\right\}$ in a path with an angle $\varphi$ with respect to x axis. It is also considered that a change of direction given by the angle $\varphi _{r}$ or the angle $\varphi _{l}$ occurs between the last two points.

Fig. 5

Method for determining the direction of rotation of the mobile robot

From this, the turn condition can be defined in terms of a signum function $sgn(\cdot )$ in such a way that a positive result will correspond with a turn right and a negative with a turn left. This criteria can be summarized as

$$\begin{aligned}&g=sgn(\varphi -\varphi _{t}) \\&\text {Turn condition} {\left\{ \begin{array}{ll} \text {Right}, &{}\quad \text {if }g=+1, \text {when } \varphi _{t}=\varphi _{r}\\ \text {Left}, &{}\quad \text {if }g=-1, \text {when } \varphi _{t}=\varphi _{l} \end{array}\right. } \end{aligned}$$

Based on this, evaluations of smooth PWL functions $\left\{ x(t),y(t)\right\}$ are performed to determine the current position of the mobile robot, a time after $t_{k+1}$ and two times after $t_{k+2}$.

Taking this into account, the angle $\varphi$ is obtained with respect to the points $\left\{ x(t_{k}),y(t_{k})\right\}$ and $\left\{ x(t_{k+1}),y(t_{k+1})\right\}$ by

$$\begin{aligned} \varphi = \mathrm {atan2}\left( \frac{y(t_{k+1})-y(t_{k})}{x(t_{k+1})-x(t_{k})}\right) \end{aligned}$$

similarly, $\varphi _{r}$ or $\varphi _{l}$ are obtained for the points $\left\{ x(t_{k+1}),y(t_{k+1})\right\}$ and $\left\{ x(t_{k+2}),y(t_{k+2})\right\}$ by

$$\begin{aligned} \varphi _{r,l} = \mathrm {atan2}\left( \frac{y(t_{k+2})-y(t_{k+1})}{x(t_{k+2})-x(t_{k+1})}\right) \end{aligned}$$

If $sgn(\varphi -\varphi _{t})=+1$ then it is turning to the right, therefore, $Vel_{\mathrm{R}}=v_{\mathrm{R}}$ and $Vel_{\mathrm{L}}=Vel_{maxMot}$. On the contrary, if $sgn(\varphi -\varphi _{t})=-1$ it is then turning to the left, therefore, $Vel_{\mathrm{R}}=Vel_{maxMot}$ and $Vel_{\mathrm{L}}=v_{\mathrm{L}}$.

6 Simulation results

In this section, two examples of collision-free PWL trajectories are shown to demonstrate the effectiveness of the proposed methodology. The software Maple Release 18 was used to perform the symbolic and numerical manipulations as well as to plot the graphs of resulting functions. In both examples, it is considered that the distance between the wheels of the differential robot is $l=14$ cm and the trajectory is also in centimeters.

6.1 Example 1

The following smooth PWL path (Fig. 6) whose breakpoints and smoothing coefficients are shown in Table 1 is taken as example.

Fig. 6

Example of a PWL path and smooth PWL path in an area with obstacles (circles)

Based on the function construction strategy of Jimenez-Fernandez et al. (2016b), the parametric equations describing the trajectory are given by

$$\begin{aligned} x(t)= & {} -\frac{1}{\alpha _{2}\alpha _{3}} \bigg ( 5 \Big ( -21t\alpha _{2}\alpha _{3}+19\alpha _{3}\ln \left( 1+e^{-\alpha _{2}(t-1) } \right) \nonumber \\&+ 19 \alpha _{3}\ln \left( 1+e^{\alpha _{2} \left( t-1 \right) } \right) - 18 \alpha _{2} \ln \left( 1+e^{-\alpha _{3} \left( t-2\right) }\right) \nonumber \\&- 18 \alpha _{2} \ln \left( 1+e^{\alpha _{3}\left( t-2\right) }\right) + 17 \alpha _{2}\alpha _{3}\Big )\bigg ) \nonumber \\ y(t)= & {} -\frac{1}{\alpha _{2}\alpha _{3}} \bigg ( 5 \Big ( 2t\alpha _{2}\alpha _{3}+7\alpha _{3}\ln \left( 1+e^{-\alpha _{2}(t-1) } \right) \nonumber \\&+ 7 \alpha _{3}\ln \left( 1+e^{\alpha _{2} \left( t-1 \right) } \right) - 7 \alpha _{2} \ln \left( 1+e^{-\alpha _{3} \left( t-2\right) }\right) \nonumber \\&- 7 \alpha _{2} \ln \left( 1+e^{\alpha _{3}\left( t-2\right) }\right) + 7 \alpha _{2}\alpha _{3}\Big )\bigg ) \end{aligned}$$

(13)

for an arbitrary value of $\alpha _{j}$.

Table 1 Breakpoints and smoothing coefficients for the smooth path depicted in Fig. 6 (coordinates in cm)

After substituting these equations in the radius of curvature formula (10) and subsequently evaluating it, the graph of Fig. 7 is obtained.

Fig. 7

Graph of radius of curvature for the smooth path in Fig. 6 ($R_{\mathrm{c}}$ in cm)

In this figure, it can be observed two concave formations that correspond to the radius of curvature described by the two turns in the smooth trajectory which starts in the point $P_{1}$, and ends in the point $P_{4}$. To get a more detailed look at particular portion of graph $R_{\mathrm{c}}(t)$, a zoom-in view of Fig. 7 is shown in Fig. 8.

Fig. 8

Zoom-in view of Fig. 7

In Fig. 8 it can be clearly seen that the minimum radius described by the trajectory under analysis is 4.32 cm. From this result, it can be noticed that the condition of no inversion in the rotational direction of one of the wheels has been broken because the minimum radius of curvature is 7 cm (distance $l=14$ cm between wheels established in this problem).

Using data of Table 1 and applying the described optimization methodology, the new smoothing parameters which describe a path that avoids the rotational inversion of a wheel in sharp curves of Table 2 are determined.

Table 2 Breakpoints and smoothing parameters after applying the optimization methodology (coordinates in cm)

Figure 9 shows a comparison between the trajectory with initial smoothing parameters and the new one using the coefficients of Table 2.

Fig. 9

Example of a collision-free PWL path, smooth PWL path and smooth PWL path with restrictions in radius of curvature in an area with obstacles (circles)

Performing motion planning of the smooth PWL trajectory with curvature restrictions of Fig. 9 whose smoothing coefficients are shown in Table 2, the speed of each wheel is obtained by Eqs. (11) and (12). These results are shown in Fig. 10a, b, respectively. In this figure the path length corresponds to the normalized length between breakpoints.

Figure 10 shows the decrease in speed when the differential robot is rotating in any of the breakpoints of the trajectory. It can also be seen that the minimum speed that must reach the wheels is very close to zero without reaching it, to avoid the loss of kinetic energy in the robot motors.

Fig. 10

Normalized wheel speed. a Velocity of the right wheel. b Velocity of the left wheel

6.2 Example 2

For this example, the breakpoints and initial smooth parameters shown in Table 3 are considered. Similarly as in the previous example, the distance between the wheels of the differential robot is also considered as $l=14$ cm.

After applying the path optimization methodology, the new smoothing parameters of Table 4 are determined.

Using data of Table 4 the optimal smooth PWL trajectory which overcomes the radius of curvature restriction and avoids the rotational inversion of wheels can be obtained. Figure 11 shows such optimal trajectory (in point line style) contrasted with the other graphs: initial smooth PWL trajectory (dashed line) and PWL (solid line).

Table 3 Breakpoints and smoothing parameters for the path of example 2 (coordinates in cm)

Table 4 Breakpoints and optimized smoothing parameters obtained for example 2 (coordinates in cm)

Fig. 11

PWL path, smooth PWL path and smooth PWL path with restrictions in radius of curvature in an area with obstacles (circles)

As can be seen in Fig. 11, the fifth breakpoint in the trajectory that starts in $P_{1}$, and ends in $P_{7}$, is related to the highest smoothing action (lowest coefficient, being $\alpha _{5}=5.5$). In the other cases, smoothing action was lower than in $P_{5}$ because the angles formed in these breakpoints do not form an angle as closed as in this specific point.

In Fig. 12, the graphs of motion planning for the mobile robot consisting normalized speeds for each wheel are shown.

Fig. 12

Normalized wheels speed. a Velocity of the right wheel. b Velocity of the left wheel

Taking into consideration that the parametric equations x(t) and y(t) represent the position of the robot respect to time, then it is possible to obtain the accelerations that the trajectory describes using the second derivative of the parametric equations. This result is shown in Fig. 13.

Fig. 13

Second derivative of the smooth PWL functions x(t) and y(t) with initial smoothing coefficients and after applying the proposed approach

From Fig. 13, it can be seen that the acceleration peaks caused by the turns along the path are reduced in amplitude because of the smoothing action, mainly the corresponding peak at $t=4$. In this regards, it is important to clarify that although PWL models have the problem of differentiability at breakpoints, in our case, the acceleration curves of Fig. 13 could be computed due to the smooth piecewise trajectories were described in the form of the model reported in Jimenez-Fernandez et al. (2016b) what ensures a complete derivativecontinuity.

7 Results and discussion

In this section, the performance of the proposed optimization methodology is compared with two traditional smoothing approaches: the Bézier (Choi et al. 2008) based and the polynomial-interpolation (Huh and Chang 2014) based methodologies. In this comparative analysis, five performance indicators have been considered: path length, minimum radius of curvature, cross track error, continuity and resulting acceleration. With the aim of illustrating these indicators, two illustrative examples are provided.

7.1 Example 1

Consider a $\mathrm{min}\left\{ R_{\mathrm{c}}\right\} =7.4$ cm in a collision-free PWL path described by the following breakpoints:

$$\begin{aligned} P&=\Big \{(0,0),(10,60),(60,60),(71,80),(70,100), \nonumber \\&\quad \quad (50,121),(70,140),(100,130),(110,60),(90,20), \nonumber \\&\quad \quad (120,20),(180,1),(170,50),(140,90),(180,120)\Big \} \end{aligned}$$

The PWL planned path (P) and the set of smooth trajectories for our proposed methodology, Bézier, and polynomial interpolation approaches are shown in Fig. 14.

Fig. 14

Planned path (PWL), proposed (smooth PWL), Bézier and polynomial-interpolation trajectories (circles denote obstacles)

In Fig. 15, it can be observed the cross track error which is estimated by the deviation of the optimized smooth trajectory (proposed) and the others, here considered, smoothing approaches with respect to the PWL planed path of reference.

Fig. 15

Cross track error of the polynomial-interpolation, Bézier, and the proposed smoothing approaches

Path length, minimum radius of curvature and mean-error of the average cross track (derived from Fig. 15) are listed in Table 5.

From the above Table, it can be seen that our proposal is able to generate not only a smoother but also a shorter trajectory, this with a minimum cross track error (mean-error) compared to the others approaches.

In Fig. 16, in the first column, it can be observed the functions $\left\{ x(t),y(t)\right\}$ of each one of the trajectories generated by the analyzed methodologies. These graphs corresponds with a parametric decomposition of path length. Likewise, in the second and third columns, their respective first derivative (velocity) and second order derivative (acceleration) are shown. These graphs show that the proposed approach generates continuous and smoother trajectories.

7.2 Example 2

Similarly as in the previous example, a $\mathrm{min}\left\{ R_{\mathrm{c}}\right\} =7.4$ cm is considered. Now, the collision-free PWL planed path is described by the following breakpoints:

$$\begin{aligned} P&=\Big \{(0,0),(10,100),(40,100),(90,20),(120,10), \\&\quad \quad (140,20),(150,30),(101,90),(100,110),(125,120), \\&\quad \quad (140,100),(180,20),(220,30)\Big \} \\ \end{aligned}$$

In Fig. 17 the smooth trajectories generated by the proposed smooth PWL, Bézier and polynomial interpolation approaches are shown. This trajectory represents a peculiar study case due to their quick turns and close distance between consecutive breakpoints.

Table 5 Path length, radius of curvature ($\mathrm{min}\left\{ R_{\mathrm{c}}\right\}$) and cross track error results

Fig. 16

Path length (first column), velocity (second column) and acceleration (third column) profiles with the three methodologies

Fig. 17

Planned path (PWL), proposed (smooth PWL), Bézier and polynomial-interpolation trajectories (circles denote obstacles)

From Fig. 17, it can be appreciated high overshoots in the polynomial interpolation approach. This is more evident between segments ${\overline{P2P3}}$, ${\overline{P6P7}}$, ${\overline{P8P9}}$ and ${\overline{P12P13}}$. These sudden deviations of the path are reflected in the more pronounced cross track error peaks shown in Fig. 18.

Fig. 18

Cross track error of the polynomial-interpolation, Bézier, and the proposed smoothing approaches

A comparative performance of the three smoothing approaches under analysis is summarized in Table 6.

From the above Table, it can be seem that both methodologies, polynomial and Bézier do not reach the minimum radius of curvature (7.4 cm). In contrast, our proposal with a $\mathrm{min}\left\{ R_{\mathrm{c}}\right\} =7.4$ cm ensures that there is no turning inversion in any of the wheels of differential-drive robot. The effect of not fulfilling the condition of minimum radius of curvature can be appreciated as the presence of negative velocities in the motion planning graphs depicted in Fig. 19. In Fig. 20 a comparison between acceleration generated by the methodology based on Bézier curves and the proposed methodology is graphically shown. From this figure, the better performance of our proposal is again highlighted. First, the discontinuities at the junctions of Bézier curves lead to sudden acceleration peaks, this in contrast with the proposed methodology where minor perturbations with a smoother behavior are obtained. Second, a lower acceleration is achieved by our proposal. As can be seen in Fig. 20, the acceleration due to Bézier methodology is over zero levels while the proposed smooth PWL approach reach levels close to zero several times along to the path length.

Table 6 Path length, radius of curvature (RC) and cross track error results

Fig. 19

Normalized wheel speed. Velocity of the right wheel (top), velocity of the left wheel (bottom)

Fig. 20

Acceleration for Example 2, comparison between the proposed methodology and the Bézier approach

8 Conclusion

The proposed methodology against other existing approaches like polynomial and Bézier reveals better performance characteristics. For example, from a practical point of view, based on the criteria of minimum radius of curvature, it ensures that there is no turning inversion in any of the wheels of differential-drive robot, a more stability is presented in those cases where the trajectory under study includes close breakpoints and abrupt turns, and it generates trajectories with lower cross track error what avoids collision with obstacles. From a mathematical perspective, the proposed methodology also shows important advantages. For example, compared to polynomial and Bézier, it suffers a minimum deviation along the planed path, it has the capability of controlling independently the smoothness grade at specific breakpoints, and finally, a function continuity is guaranteed in addition to lower overshooting for high order derivatives which translates into lower levels of acceleration.