Analysis of the orbital evolution of exoplanets

Abstract

An exoplanet, or extrasolar planet, is a planet that does not orbit the Sun, but is around a different star, stellar remnant, or brown dwarf. Up to now, about 1900 exoplanets were discovered. To better understand the dynamics of these exoplanets, a study with respect to possible collisions of the planet with the central star is shown here. We present an expanded model in a small parameter that takes into account up to the fifth order to analyze the effect of this potential in the orbital elements of the extrasolar planet. Numerical simulations were also performed using the N-body simulations, using the software Mercury, to compare the results with the ones obtained by the analytical model. The numerical simulations are presented in two stages: one considering the celestial bodies as point masses and the other one taking into account their dimensions. This analysis showed that the planet collided with the central star in the moment of the first inversion for orbits with high inclinations in various situations. The results of the simulations of the equations developed in this study are consistent with the N-body numerical simulations. We analyze also the flip of the inclination taking into account the coupling of the perturbations of the third body, effect due to the precession of periastron and the tide effect. In general, we find that such perturbations combined delay the time of first inversion, but do not keep the planet in a prograde or retrograde orbit.

1 Introduction

The number of exoplanets discovered (planets orbiting around other stars, not the Sun) is officially already near 1900. From this number, 12 could be habitable planets, since the distances of their orbits around their mother stars is suitable for the existence of liquid water on the surface. This point has attracted the attention of researchers from several fields, including celestial mechanics. In particular, to analyze the dynamic characteristics of the exoplanets, which are typically found in retrograde orbits, several theories have been proposed to explain, for example, the behavior of the orbital inclination. This fact may be caused by an inversion of the inclination from prograde to retrograde trajectories. A study with respect to possible collisions of the extrasolar planet with the central star is presented in the present paper.

Several papers (Naoz et al. 2013; Lithwick and Naoz 2011; Beaugé et al. 2012; Laskar and Boué 2010) have analyzed the behavior of the inclination of extrasolar planets, but the case of possible collisions during this evolution is not much studied. In the present work we study the secular dynamics of hierarchical triple systems (when there is a clearly defined binary and a third body, which stays separated from the binary, see Valtonen and Karttunen 2006) composed by a Sun-like central star and a Jupiter-like planet, which are under the gravitational influence of a further perturbing star (brown dwarf).

In the present paper, for the first time, the gravitational potential is developed in closed form up to the fifth order [$R_{2}$ (quadrupole), $R_{3}$ (octupole), $R_{4}$ (hexadecapole) and $R_{5}$ (hexapole)] in a small parameter ($\alpha =a_{1}/a_{2}$), where $a_{1}$ is the semi-major axis of the planet and $a_{2}$ is the semi-major axes of the disturbing body, to analyze the behavior of the inclination and eccentricity of the inner planet. The choice of the small parameter ($\alpha$) is made because, in general, the hierarchical systems have highly eccentric orbits which makes it difficult the expansion of the perturbation in series of the eccentricity. It is more convenient to use the ratio of the semi-major axis of the planet ($a_{1}$) and the disturbing star ($a_{2}$), because exact expressions can be computed for the secular system (see Correia et al. 2013). The orbit of the disturbing star is considered to be elliptical, planar and fixed in space. In order to develop the long-period disturbing potential, the double-averaged method is applied (Szebehely 1989). The average is applied with respect to the eccentric anomaly of the planet and the true anomaly of the perturbing star. In the present research, the longitude of the ascending node ($h_{1}$) of the planet has not been eliminated, as done, for example, in the research presented in Kozai (1962). Note that the perturbation caused by the second-order $R_{2}$ term was extensively analyzed in Kozai (1962) and Lidov (1962), using the restricted three-body problem and by several other authors in diverse applications in celestial mechanics.

As the behavior of the inclination is strongly influenced when by the consideration of the term $R_{3}$ (see Naoz et al. 2011), this paper analyzes the behavior of the inclination for higher orders of the potential to see what happens with the dynamics. Note that the choice of using up to the fifth order is arbitrary, and it is motivated by the fact that the computational of high orders are difficult. When considering in the octupole term in the disturbing potential, the inclination of the inner planet can flip from prograde to retrograde trajectories (Naoz et al. 2011; Carvalho et al. 2013). The results showed that the inclusion of the $R_{4C}$ term gives results that are worst than the ones given by the $R_{3C}$ term, but the inclusion of the $R_{5C}$ term corrects the problem. Correia et al. (2013) shows that the effects of the tides combined with gravitational interactions helped to reduce the initial mutual inclination to small values on time scales. This effect is not a direct consequence of the tides on the orbits, but results from a secular forcing of the inner planet’s flattening.

We call the period of the first inversion of the inclination (prograde–retrograde) by “inversion time”. We calculate the value of the eccentricity of the planet exactly at the inversion time and we show the results in diagrams. The main goal is to analyze the behavior of the inclination of the planet and the possible collision of the planet with the central star. Lidov and Ziglin (1976) found a set of initial conditions such that a collision between the bodies $m_{0}$ and $m_{1}$ occurs. The authors show a region of the parameters of the problem for which the planar retrograde motion is unstable. The collision between the bodies $m_{0}$ and $m_{1}$ occurs when the orbits are almost orthogonal. Correia et al. (2012) considers the tidal effect, due to the non-spherical shape of the planet ($J_{2}$), coupled with the gravitational force due to the disturbing star.

We also performed full numerical integrations using the Burlish–Stoer method from the Mercury package (Chambers 1999), to compare the results with the ones obtained by the analytical model. In this work we adapt the Mercury package to the binary problem.

2 Equations of motion

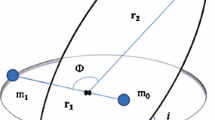
The triple system under study is characterized by a planet $m_{1}$ in an elliptical orbit around the center of mass of the system $m_{0}$–$m_{1}$, where $m_{0}$ is a central star, also moving around the center of mass of the system $m_{0}$–$m_{1}$. There is also a further perturbing star (brown dwarf-$m_{2}$) moving in an outer elliptical orbit around the center of mass of the system. Let us consider that the orbit of the disturbing body is planar and fixed in space. The vector $\mathbf {r_{1}}$ represents the position of $m_{1}$ with respect to the center of mass of the system and the vector $\mathbf {r_{2}}$ is the position of the body $m_{2}$ with respect to the center of mass of the inner orbit. $\Phi$ is the angle between $\mathbf {r_{1}}$ and $\mathbf {r_{2}}$.

The Hamiltonian of the triple system can be written as follows (Harrington 1969; Ford et al. 2000, 2004):

$$\begin{aligned} \begin{array}{l} F=\frac{Gm_{0}m_{1}}{2a_{1}}+\frac{G(m_{0}+m_{1})m_{2}}{2a_{2}}+ \frac{G}{a_{2}}\sum _{j=2}^{\infty }\alpha ^{j} M_{j}\left( \frac{r_{1}}{a_{1}}\right) ^{j}\left( \frac{a_{2}}{r_{2}}\right) ^{j+1}P_{j}(\cos \Phi ), \end{array} \end{aligned}$$

(1)

where G is the gravitational constant, $P_{j}$ are the Legendre polynomials and

$$\begin{aligned} \begin{array}{l} M_{j}=m_{0}m_{1}m_{2}\frac{m_{0}^{j-1}-(-m_{1})^{j-1}}{(m_{0}+m_{1})^{j}} \end{array} \end{aligned}$$

(2)

For the first time, we shall deal with the expansion up to the fifth order in $\alpha$. We developed the disturbing potential taking into account the expression for $\cos \Phi$ written in the following form (Yokoyama et al. 2003):

$$\begin{aligned} \cos (\Phi )= & {} 1/4\,( -1+{ c_{2}})( -1+ {c_{1}}) \cos ( { f_{1}}+{ g_{1}}-{ h_{1}}-{ f_{2}}-{ g_{2}}+{ h_{2}}) \nonumber \\&+\, 1/4\, ( 1+{c_{1}}) ( 1+{c_{2}}) \cos ( {f_{1}}+{g_{1}}+{h_{1}}-{ f_{2}}-{g_{2}}-{ h_{2}})\nonumber \\&-\,1/4\,( 1+{c_{2}})( -1+{ c_{1}}) \cos ( {f_{1}}+{g_{1}}-{ h_{1}}+{ f_{2}}+{ g_{2}}+{ h_{2}})\nonumber \\&-\,1/4\,( -1+{ c_{2}})( 1+{c_{1}}) \cos ( { f_{1}}+{ g_{1}}+{h_{1}}+{ f_{2}}+{ g_{2}}-{ h_{2}})\nonumber \\&+\,1/2\,{ s_{1}}\,{ s_{2}}\,( \cos ( { f_{1}} +{ g_{1}}-{ f_{2}}-{ g_{2}}) -\cos ( {f_{1}}+{ g_{1}}+{f_{2}}+{g_{2}})), \end{aligned}$$

(3)

where we use the shortcut $s_{1}=\sin i_{1}$, $c_{1}=\cos i_{1}$, $s_{2}=\sin i_{2}$, and $c_{2}=\cos i_{2}$. Here $i_{j}$, $g_{j}$, $h_{j}$ and $f_{j}$ (for $j=1, 2$) are the inclination, argument of the periastron, longitude of the ascending node and true anomaly of the inner and outer orbit, respectively. Let us consider the orbit of the disturbing body as planar and fixed in space. Then, the orbital elements of the disturbing star are $i_{2}=0$, $g_{2}=0$ and $h_{2}=0$. Replacing these values in Eq. (3), the following equation is obtained:

$$\begin{aligned} \cos (\Phi )= & {} \frac{1}{2}(1+\cos (i_{1})) \cos (f_{1}+g_{1}+h_{1}-f_{2})\nonumber \\&+ \frac{1}{2}(1-\cos (i_{1})) \cos (f_{1}+g_{1}-h_{1}+f_{2}) \end{aligned}$$

(4)

Those equations are written in a inertial reference system that has the equator of the main body in the x–y plane.

The algebraic manipulation and the average method used to eliminate short-period terms of the potential are presented in Carvalho et al. (2015). The details of the development of the equations presented here can be found in Carvalho et al. (2015). Thus, we obtain the disturbing potential expanded up to the fifth order in a small parameter. The long-period disturbing potential can be written as (see Carvalho et al. 2015)

$$\begin{aligned} \begin{array}{l} R_{2C}=15{\beta _{3}}{{L_{1}}}^{4}\,( {{e_{1}}}^{2}(s_{1}^{2}) \cos ( 2\,{g_{1}}) +3/5\,( {{e_{1}}}^{2}+2/3)(c_{1}^{2}-1/3)){(-{{e_{2}}}^{2}+1)^{-3/2}{{L_{2}}}^{-6}} \end{array} \end{aligned}$$

(5)

$$\begin{aligned} R_{3C}= & {} -{\frac{675}{128}}\,{{L_{1}}}^{6}{e_{2}}\,{\beta _{4}}\,{e_{1}}\,\Big ( {\frac{7}{9}}\,{{e_{1}}}^{2}(c_{1}+1)( c_{1}-1) ^{2} \cos ( -{h_{1}}+3\,{g_{1}})\nonumber \\&-( {c_{1}}^{2}+2/3\,c_{1}-1/15)(c_{1}-1)\,( {{e_{1}}}^{2}+4/3)\cos ( {g_{1}}-{h_{1}})\nonumber \\&+(c_{1}+1) \Big (\Big ( -{\frac{7}{9}}\,{{e_{1}}}^{2}{c_{1}}^{2}+{\frac{7}{9}} \,{{e_{1}}}^{2}\Big ) \cos ( {h_{1}}+3\,{g_{1}})+\,({c_{1}}^{2}-2/3\,c_{1}-1/15)\nonumber \\&\times \, \cos ({g_{1}}+{h_{1}})\times ( {{e_{1}}}^{2}+4/3)\Big )\Big )( -{{e_{2}}}^{2}+1)^{-5/2}{{L_{2}}}^{-8} \end{aligned}$$

(6)

$$\begin{aligned} R_{4C}= & {} {\frac{19845}{1024}}{\beta _{5}}\,{{L_{1}}}^{8}\bigg ( 4/9\,( {{e_{1}}}^{ 2}+2)( {{c_{1}}}^{2}+{c_{1}}+1/7) {{e_{2}}}^{2 }( {c_{1}}-1)^{2}{{e_{1}}}^{2}\nonumber \\&\times \,\cos (2\,{g_{1}}- 2\,{h_{1}})+4/9\,( {{e_{1}}}^{2}+2)({c_{1}}+1)^{2}{{e_{2}}}^{2}( {{c_{1}}}^{2}-{c_{1}}+1/ 7) {{e_{1}}}^{2}\cos ( 2\,{g_{1}}\nonumber \\&+\,2\,{h_{1}})-\,1/3\,{{e_{1}}}^{4}{{e_{2}}}^{2}( {c_{1}}+1) ({c_{1}}-1 ) ^{3}\cos ( 4\,{g_{1}}-2\,{h_{1}})\nonumber \\&-1/3 \,{{e_{1}}}^{4}{{e_{2}}}^{2}( {c_{1}}-1)( {c_{1}}+1)^{3}\cos ( 4\,{g_{1}}+2\,{h_{1}})\nonumber \\&-\,4/3\, ( {{e_{1}}}^{2}+2)( {c_{1}}+1)({{c_{1}}}^{2}-1/7)( {{e_{2}}}^{2}+2/3)( {c_{1}}-1) {{e_{1}}}^{2}\cos ( 2\,{g_{1}}) \nonumber \\&-{ \frac{10}{21}}\,( {c_{1}}+1) {{e_{2}}}^{2} \left( {{ e_{1}}}^{4}+8/3\,{{e_{1}}}^{2}+{\frac{8}{15}}\right) ( {{c_{1}}}^{2}-1/7)( {c_{1}}-1)\cos ( 2\,{h_{1}})\nonumber \\&+\,( {{e_{2}}}^{2}+2/3)( {{e_{1}}} ^{4}( {c_{1}}-1)^{2}( {c_{1}}+1)^{2}\cos ( 4\,{g_{1}})\nonumber \\&+\,5/7\,\left( {{e_{1}}}^{4}+8/3\,{{e_{1} }}^{2}+{\frac{8}{15}}\right) \left( {{c_{1}}}^{4}-6/7\,{{c_{1}}}^{2}+{\frac{3}{35}}\right) \bigg )\bigg )\nonumber \\&\times \,( -{{ e_{2}}}^{2}+1)^{-7/2}{{L_{2}}}^{-10} \end{aligned}$$

(7)

$$\begin{aligned} R_{5C}= & {} {\frac{165375}{4096}}{\beta _{6}}{L_{1}}^{10} e_{1}\bigg ( -{\frac{9}{10}}(c_{1}-1)^{2}{e_{1}}^{2}( { e_{1}}^{2}+8/3)(c_{1}+1)( {e_{2}}^{2}+4/3)\nonumber \\&\times \,({c_{1}}^{2}+2/5c_{1}-1/15) \cos (-h_{1}+3g_{1})+{\frac{3}{20}}(c_{1}-1)^{3}\left( c_{1}+{\frac{13}{15}}\right) {e_{1}}^{2}\nonumber \\&\times \,({e_{1}}^{2}+8/3)(c_{1}+1/3 ){e_{2}}^{2}\cos ( 3g_{1}-3h_{1}) -{\frac{3}{20}}(c_{1}-1/3) {e_{1}}^{2}\nonumber \\&\times \,({ e_{1}}^{2}+8/3)(c_{1}+1)^{3}{e_{2}}^{2} \left( c_{1}-{\frac{13}{15}}\right) \cos ( 3g_{1}+3h_{1}) +{\frac{33}{50}}(c_{1}-1)^{3}{e_{1}}^{4}\nonumber \\&\times \,( c_{1}+1)^{2}({e_{2}}^{2}+4/3 ) \cos ( 5g_{1}-h_{1}) -{\frac{11}{100}}{e_{1}}^{4}{e_{2}}^{2}(c_{1}+1)\nonumber \\&\times \,(c_{1}-1)^{4}\cos (5g_{1}-3h_{1}) +{\frac{ 11}{100}}{e_{1}}^{4}{e_{2}}^{2}(c_{1}-1)(c_{1}+1)^{4}\cos ( 5g_{1}+3h_{1})\nonumber \\&+\, ( c_{1}-1)\left( {c_{1}}^{4}+4/5{c_{1}}^{3}-2/5{c_{1}}^{2}-{\frac{4}{15}}c_{1}+{\frac{1}{ 105}}\right) ( {e_{2}}^{2}+4/3)\nonumber \\&\times \,( {e_{1}}^{4}+4{e_{1}}^{2}+8/5)\cos ( g_{1}-h_{1}) -\bigg ( -{\frac{9}{10}}( c_{1}-1) {e_{1}}^{2} ( {e_{1}}^{2}+8/3)\nonumber \\&\times \,(c_{1}+1)({c_{1}}^{2}-2/5c_{1}-1/15)( {e_{2}}^{2}+4/3 ) \cos ( h_{1}+3g_{1})\nonumber \\&+\,1/6(c_{1}-1)^{2}{e_{2}}^{2}( {e_{1}}^{4}+4{e_{1}}^{ 2}+8/5)( {c_{1}}^{2}+2/5c_{1}-1/15) \cos ( g_{1}-3h_{1})\nonumber \\&-\,1/6( c_{1}-1) ( c_{1}+1)({c_{1}}^{2}-2/5c_{1}-1/15 ) {e_{2}}^{2}( {e_{1}}^{4}+4{e_{1}}^{2}+8/5)\nonumber \\&\times \,\cos (g_{1}+3h_{1}) +\bigg ( {\frac{33}{50}}{e_{1}}^{4}( c_{1}-1)^{2}( c_{1}+1)^{2}\cos ( 5g_{1}+h_{1})\nonumber \\&+\,\cos (g_{1}+h_{1})\left( {c_{1}}^{4}-4/5{c_{1}}^{3}-2/ 5{c_{1}}^{2}+{\frac{4}{15}}c_{1}+{\frac{1}{105}}\right) ( {e_{1}}^{4}+4{e_{1}}^{2}+8/5)\bigg )\nonumber \\&\times \,({e_{2}}^{2}+4/3)\big )( c_{1}+1)\big ) e_{2})( -{e_{2}}^{2}+1)^{-9/2}{L_{2}}^{-12} \end{aligned}$$

(8)

where we use the shortcut $s_{1}=\sin i_{1}$, $c_{1}=\cos i_{1}$.

Where

$$\begin{aligned} \begin{array}{l} L_{1}={\frac{{m_{0}}\,{m_{1}}\,\sqrt{G ( {m_{0}}+{m_{1}} ) {a_{1}}}}{{m_{0}}+{m_{1}}}} \end{array} \end{aligned}$$

(9)

$$\begin{aligned} \begin{array}{l} L_{2}={\frac{{m_{2}}\, \left( {m_{0}}+{m_{1}} \right) \sqrt{G \left( { m_{0}}+{m_{1}}+{m_{2}} \right) {a_{2}}}}{{m_{0}}+{m_{1}}+{m_{2} }}} \end{array} \end{aligned}$$

(10)

$$\begin{aligned} \begin{array}{l} \beta _{3}=\frac{1}{16}\,{\frac{{G}^{2} \left( {m_{0}}+{m_{1}} \right) ^{7}{{m_{2}}}^ {7}}{ \left( {m_{0}}+{m_{1}}+{m_{2}} \right) ^{3}{{m_{0}}}^{3}{{ m_{1}}}^{3}}} \end{array} \end{aligned}$$

(11)

$$\begin{aligned} \begin{array}{l} \beta _{4}=\frac{1}{4}\,{\frac{{G}^{2} \left( {m_{0}}+{m_{1}} \right) ^{9}{{m_{2}}}^{ 9} \left( {m_{0}}-{m_{1}} \right) }{ \left( {m_{0}}+{m_{1}}+{m_{2}} \right) ^{4}{{m_{0}}}^{5}{{m_{1}}}^{5}}} \end{array} \end{aligned}$$

(12)

$$\begin{aligned} \begin{array}{l} \beta _{5}=\frac{1}{8}\,{\frac{{G}^{2} \left( {m_{0}}+{m_{1}} \right) ^{10}{{m_{2}}}^ {11} ( {{m_{0}}}^{3}+{{m_{1}}}^{3} ) }{ \left( {m_{0}}+{ m_{1}}+{m_{2}} \right) ^{5}{{m_{0}}}^{7}{{m_{1}}}^{7}}} \end{array} \end{aligned}$$

(13)

$$\begin{aligned} \begin{array}{l} \beta _{6}=\frac{1}{8}{\frac{{G}^{2} \left( {m_{0}}+{m_{1}} \right) ^{12}{{m_{2}}}^ {13} ( {{m_{0}}}^{4}-{{m_{1}}}^{4} ) }{ \left( {m_{0}}+{ m_{1}}+{m_{2}} \right) ^{6}{{m_{0}}}^{9}{{m_{1}}}^{9}}} \end{array} \end{aligned}$$

(14)

Therefore, the long-period disturbing potential is written as

$$\begin{aligned} \begin{array}{l} \langle F \rangle =R_{0}+R_{2C}+R_{3C}+R_{4C}+R_{5C}, \end{array} \end{aligned}$$

(15)

where

$$\begin{aligned} \begin{array}{l} R_{0}=\frac{Gm_{0}m_{1}}{2a_{1}}+\frac{G(m_{0}+m_{1})m_{2}}{2a_{2}} \end{array} \end{aligned}$$

(16)

It is possible to replace Eq. (15) in the Lagrange planetary equations (Kovalevsky 1967) to analyze the orbital elements of the planet, in particular the inclination and eccentricity. Evolutions of those elements can be obtained from numerical simulations that are performed using the software Maple.

3 Results

Now the results, divided into two parts, is presented. The first part takes into account the disturbing potential up to the fourth order, and it shows maps with respect to the eccentricities of the planet and of the disturbing star. The second part takes into account the disturbing potential up to the fifth order. A comparison of different orders of the disturbing potential is shown. It should be mentioned that the longitude of the ascending node of the planet appears in the equations of motion. Since we are considering the disturbing body in a planar orbit, the orbital elements of the disturbing star are $i_{2}=0$, $g_{2}=0$ and $h_{2}=0$, which are the inclination, argument of the periastron and longitude of the ascending node of the outer orbit, respectively.

3.1 Planet collision analysis with the central star

The methodology consists in replacing Eq. (15) in the Lagrange planetary equations (Kovalevsky 1967) and numerically integrate the set of nonlinear differential equations using the software maple, to obtain the variations of the orbital elements of the planet as a function of time. The initial conditions were obtained from Naoz et al. (2011) and then they were modified to generalize the study, as described in the text in the appropriate location. The numerical integrations of the Lagrange equations were made using software maple. The numerical integration used the routine “dsolve” of the software Maple with the options “numeric” and “method$=$rkf45”. It finds a numerical solution using a Fehlberg fourth–fifth order Runge–Kutta method with degree four. The default values for rkf45 are absolute error of 1e$-$7 and relative error of 1e$-$6. The value for initial step, if not specified, is determined by the method, taking into account the local behavior of the ODE system.

In this section an approach is presented to investigate possible collisions of the planet with the central star. In the results shown in Figs. 1 and 2, the argument of the periastron of the planet is equal to $g_{1}=250^{\circ }$ and in Figs. 3 and 4 it is given by $g_{1}=0^{\circ }$. In all captions in Figs. 1, 2, 3 and 4 the orbital elements are $a_{1}=6\, \mathrm{AU}$, $a_{2}=100\, \mathrm{AU}$, $i_{1}=65^{\circ }$, $h_{1}=180^{\circ }$ (Naoz et al. 2013, 2011). The star has mass $1M_{\bigodot }$, the planet has mass $1M_{J}$ and the perturbing brown dwarf has mass $40M_{J}$. Comparison of these figures are made by looking at different values of the argument of peristron, eccentricity and different orders of the disturbing potential due to the third body (star or another planet). The color scale represents the value of the eccentricity of the planet at the moment of the first inversion of the inclination, i.e., when the inclination changes its value from prograde to retrograde. For the first time, when the terms $R_{2C}+R_{3C}$ (see Fig. 1) are taken into account, the eccentricity of the planet increases to high values at the first inversion, which may cause a collision with the central star. In particular, note that the values for $e_{2}=0.6$ and $e_{2}=0.7$ in the map shown in Fig. 1 present yellow points, indicating that the eccentricity reaches high values, close to unity. This fact characterizes that the planet may collide with the central star. Note also that the highest values of $e_{1}$ are obtained for small values of the initial eccentricity of the body $m_{1}$ ($e_{1}(0)$) and large values of the initial eccentricity of the body $m_{2}$ ($e_{2}(0)$). For values of $e_{2}(0)$ smaller than 0.5 there is no inversion of the inclination of the planet in the simulation period. In Correia et al. (2013), the authors show that, when the dimensions of the bodies (two-planet systems) are taken into account, the planet is most likely to collide with the star.

Fig. 1

Diagram $e_{1}(0)$ $\times$ $e_{2}(0)$ $\times$ $e_{1}(t_{\mathrm{inv}})$. Perturbations: $R_{2C}+R_{3C}$. Initial conditions $g_{1}=250^{\circ }$, $h_{1}=180^{\circ }$. The colors indicate the value of the eccentricity of the planet exactly at the time of the first inversion ($t_{\mathrm{inv}}$ in multiples of $10^{7}$ years), and the gray color indicates that no flip occurred along the integration

Fig. 2

Diagram $e_{1}(0)$ $\times$ $e_{2}(0)$ $\times$ $e_{1}(t_{\mathrm{inv}})$. Perturbations: $R_{2C}+R_{3C}+R_{4C}$. Initial conditions: $g_{1}=250^{\circ }$, $h_{1}=180^{\circ }$. The colors indicate the value of the eccentricity of the planet exactly at the time of the first inversion ($t_{\mathrm{inv}}$ in multiples of $10^{7}$ years), and the gray color indicates that no flip occurred along the integration

Looking at Fig. 2, that considers the disturbing potential with the $R_{2C}+R_{3C}+R_{4C}$ terms, it is possible to see that the highest values of $e_{1}$ at the first inversion occurs when $e_{2}(0)=0.6$. Note that the concentration of yellow points indicates a range of values $e_{1}$ which may result in a possible collision with the central star. Several authors (see Naoz et al. 2011, 2012, 2013; Li et al. 2014) have analyzed the three-body problem considering a triple system where the disturbing star has, in general, high eccentricity ($e_{2}(0)=0.6$, $e_{2}(0)=0.7$). This fact characterizes this orbit as a very important one and it must be analyzed very carefully, because most of the orbits of the planet around this star may collide, as shown in Fig. 2. The difference between Figs. 1 and 2 is basically the concentration of orbits with high eccentricities, caused by the expansion of the potential up to the fourth order.

Now, considering the value of the argument of the periastron equal to 0$^{\circ }$ ($g_{1}=0^{\circ }$), we obtain Figs. 3 and 4. Note that, in this case, both models have similar characteristics but still larger values are noticed of the eccentricity for the model that takes into account the terms $R_{2C}+R_{3C}+R_{4C}$. In various simulations we note that the initial choice of the argument of the periastron of the inner planet is extremely important to characterize the behavior of how the eccentricity is changing. Comparing Figs. 1 and 2 with Figs. 3 and 4 we noticed that, in the simulation where $g_{1}=250^{\circ }$ (Figs. 1, 2), there was no inversion of the inclination for various values of $e_{1}$. Especially for values of $e_{1}$ larger than 0.18 there was no inversion in the simulated period ($3.5\times 10^{7}$ years). In the case where $g_{1}=0^{\circ }$ (Figs. 3, 4) there was inversion of the inclination for values for $e_{1}$ up to 0.25 during the simulated period. This behavior presented by the periastron argument can also be seen in Fig. 5, where orbits in the range $150 \le g \le 300$ take longer to have the first inversion of the inclination.

Fig. 3

Diagram $e_{1}(0)$ $\times$ $e_{2}(0)$ $\times$ $e_{1}(t_{\mathrm{inv}})$. Perturbations: $R_{2C}+R_{3C}$. Initial conditions: $g_{1}=0^{\circ }$, $h_{1}=180^{\circ }$. The colors indicate the value of the eccentricity of the planet exactly at the time of the first inversion ($t_{\mathrm{inv}}$ in multiples of $10^{7}$ years), and the gray color indicates that no flip occurred along the integration

Fig. 4

Diagram $e_{1}(0)$ $\times$ $e_{2}(0)$ $\times$ $e_{1}(t_{\mathrm{inv}})$. Perturbations: $R_{2C}+R_{3C}+R_{4C}$. Initial conditions: $g_{1}=0^{\circ }$, $h_{1}=180^{\circ }$.The colors indicate the value of the eccentricity of the planet exactly at the time of the first inversion ($t_{\mathrm{inv}}$ in multiples of $10^{7}$ years), and the gray color indicates that no flip occurred along the integration

3.2 Analysis of the behavior of the inclination of the planet

In this section a comparison of the effects of different orders of the disturbing potential is presented. Figure 5 shows the inversion time for different values of the argument of the planet periastron. In this figure the inversion time for different orders of the disturbing potential is considered. Note that for orbits in the range $150 \le g_{1} \le 300$ the inversion time diverges when comparing the three models, while for other values of the periastron the inversion time is the same for all three models.

Fig. 5

$g_{1} \times t_{\mathrm{inv}}$, $i_{1}=65^{\circ }$. Initial conditions: $a_{1}=6$ AU, $a_{2}=100$ AU, $e_{1}=0.01$, $e_{2}=0.6$, $h_{1}=180^{\circ }$. The star has mass $1M_{\bigodot }$, the planet has mass $1M_{J}$ and the outer brown dwarf has mass $40M_{J}$

Fig. 6

$t_{\mathrm{inv}} \times i_{1}$, $g_{1}=0^{\circ }$. Initial conditions: $a_{1}=6$ AU, $a_{2}=100$ AU, $e_{1}=0.01$, $e_{2}=0.6$, $h_{1}=180^{\circ }$. The star has mass $1M_{\bigodot }$, the planet has mass $1M_{J}$ and the outer brown dwarf has mass $40M_{J}$

Figure 6 shows the results of a simulation where the inclination of the orbit of the planet starts with 5$^\circ$, varying in steps of 5$^\circ$ up to 85$^\circ$ (time simulation of $3.5 \times 10^7$ years). It is worth noting that only the orbits with inclination $i_{1}\ge 50^{\circ }$ presented inversion, i.e., the inclination flip in its orientation (prograde to retrograde). For higher values of the initial inclination the inversion time is smaller. Note that taking into account the perturbation due to the $R_{2C}+R_{3C}+R_{4C}$ terms, the first inversion time is larger than the other two models to 65$^\circ$. For values of the initial inclination between 65$^\circ$ and 70$^\circ$, the time of the first inversion coincide for all three models. For values of the initial inclination between 70$^\circ$ and 85$^\circ$, the first inversion time is larger for the model taking into account the terms $R_{2C}+R_{3C}$ and the other two models agree. Note that the larger the initial value of the inclination, the smaller the time of the first flip.

Fig. 7

Temporal evolution of the inclination. Initial conditions: $a_{1}=6$ AU, $a_{2}=100$ AU, $i_{1}=65^{\circ }$, $e_{1}=0.01$, $e_{2}=0.6$, $g_{1}=0$, $h_{1}=180^{\circ }$. The star has mass $1M_{\bigodot }$, the planet has mass $1M_{J}$ and the outer brown dwarf has mass $40M_{J}$

Fig. 8

Temporal evolution of the inclination. Initial conditions: $a_{1}=6$ AU, $a_{2}=100$ AU, $e_{1}=0.01$, $e_{2}=0.6$, $g_{1}=0$, $h_{1}=180^{\circ }$. The star has mass $1M_{\bigodot }$, the planet has mass $1M_{J}$ and the outer brown dwarf has mass $40M_{J}$. Direct numerical integration of the problem of three bodies (considering their dimensions), $i_{1}=65^{\circ }$

The graphics of the inclination versus time are shown in Figs. 7, 8, 9 and 10. Figures 7 (except the red line) and Fig. 10 were obtained from numerical simulation (using the software Maple) of equations developed, namely Eqs. (5)–(8), considering different orders of the disturbing potential. Figures 7 (line red), 8, 9a and b were obtained using the N-body numerical simulations with the Mercury code (Chambers 1999). As we can observe in Figs. 1, 2, 3 and 4, the eccentricity of the inner orbit can occasionally reach extremely high values and its inclination can become higher than 90$^\circ$. Looking at Fig. 7 it is clear that, at the first inversion of the inclination, the three models show similar results. But, for the second inversion and the next ones, there are different characteristics for the models $R_{2C}+R_{3C}$ and $R_{2C}+R_{3C}+R_{4C}$ present different results from direct numerical integration of the problem of three bodies, while the model $R_{2C}+R_{3C}+R_{4C}+R_{5C}$ is in agreement with the direct simulation, as shown in Fig. 7.

Fig. 9

Temporal evolution of the inclination. Initial conditions: $a_{1}=6$ AU, $a_{2}=100$ AU, $e_{1}=0.01$, $e_{2}=0.6$, $g_{1}=0$, $h_{1}=180^{\circ }$. The star has mass $1M_{\bigodot }$, the planet has mass $1M_{J}$ and the outer brown dwarf has mass $40M_{J}$. a Direct numerical integration of the problem of three bodies (considering the dimensions of the body), $i_{1}=50^{\circ }$, b direct numerical integration of the problem of three bodies (considering the dimensions of the body), $i_{1}=80^{\circ }$

Fig. 10

Temporal evolution of the inclination. Initial conditions: $a_{1}=6$ AU, $a_{2}=100$ AU, $i_{1}=50^{\circ }$, $e_{1}=0.01$, $e_{2}=0.6$, $g_{1}=0$, $h_{1}=180^{\circ }$. The star has mass $1M_{\bigodot }$, the planet has mass $1M_{J}$ and the outer brown dwarf has mass $40M_{J}$

Looking at Figs. 5 and 6 we get a range of values of the argument of the periastron ($150\le g_{1}\le 300$ $^\circ$) and inclination, where the models can show different inversion times in the first flip. Figures 7 and 8 show the behavior of the inclination of the planet considering the three body problem in two stages, one considering the celestial body as a point mass and the other taking into account a body with physical dimensions. When the existence of the radius of the planet is taken into account, i.e., the celestial body is not considered as a mass point, the orbit may collide for higher values of the inclination, as shown in Figs. 8 (65$^\circ$), 9a (50$^\circ$) and b (80$^\circ$). This result is in agreement with Lidov and Ziglin (1976), where it is found that a set of initial conditions (higher values of the inclination), such that a collision between the bodies $m_{0}$ and $m_{1}$ may occur. Note that for values of the inclination near 90$^\circ$, the inversion time is lower than that for other values of the inclination (see, for example, Fig. 9b). Thus, the orbit migrates from prograde to retrograde in lower inversion times, but considering the radius of the planet the collision may occur at the first inversion. As a result, the growth of the inclination and eccentricity of the planet reached high values, as we can see in Figs. 1, 2, 3, 4, 5, 6 and 7, which may cause the planet to collide with the central star.

Now, analyzing Fig. 10 (initial inclination of 50$^{\circ }$), we find that the model developed up to the third order (octupole) shows the same behavior of the one presented by the model developed up to the fifth order. The model that considers development up to the fourth order already has a time delay in the first inversion. Note that comparing the results with the direct simulation of the three body problem (considering the dimensions of the body), shown in Fig. 9a, the models represented by $R_{2C}+R_{3C}$ and $R_{2C}+R_{3C}+R_{4C}+R_{5C}$ show very well the behavior of the dynamics of the problem. Analyzing other cases we noticed that the main effect related to the inversion of the inclination between prograde and retrograde orbits is caused by the odd terms of the development with respect to the Legendre polynomials, especially due to the $R_{3C}$ and $R_{5C}$ terms.

Figures 11 and 12 show the time of the first inversion of the planet’s inclination for different values of the eccentricity of the planet and disturbing star. Figure 11 is made taking into account the disturbing potential expanded to the fifth order, and Fig. 12 shows the behavior of the inversion of the inclination, considering the direct numerical integration. Note that for the highly eccentric orbits of the disturbing star, the flip occurs in a short period of time. For orbits with small eccentricity of the disturbing star the flip almost does not occur in the simulation time used. When there is an inversion of the inclination, the time to experience this phenomenon is much higher than in the case of highly eccentric orbits. As shown in Figs. 11 and 12, the analytical model (up to the fifth order) is in accordance with the direct numerical integration with minor differences. Figure 13 shows exactly the modulus of the difference between the analytical and numerical models.

Fig. 11

$e_{2} \times e_{1} \times t_{\mathrm{inv}}$. Disturbing potential $R_{2C}+R_{3C}+R_{4C}+R_{5C}$. Initial conditions: $a_{1}=6$ AU, $a_{2}=100$ AU, $i_{1}=65^{\circ }$, $g_{1}=0^{\circ }$, $h_{1}=180^{\circ }$. The star has mass $1M_{\bigodot }$, the planet has mass $1M_{J}$ and the outer brown dwarf has mass $40M_{J}$. The colors indicate the time in multiples of $10^{7}$ years, and the gray color indicates that no flip occurred along the integration

Fig. 12

$e_{2} \times e_{1} \times t_{\mathrm{inv}}$. Direct numerical integration. Initial conditions: $a_{1}=6$ AU, $a_{2}=100$ AU, $i_{1}=65^{\circ }$, $g_{1}=0^{\circ }$, $h_{1}=180^{\circ }$. The star has mass $1M_{\bigodot }$, the planet has mass $1M_{J}$ and the outer brown dwarf has mass $40M_{J}$. The colors indicate the time in multiples of $10^{7}$ years, and the gray color indicates that no flip occurred along the integration

Fig. 13

$e_{2} \times e_{1} \times t_{\mathrm{inv}}$. The difference between direct numerical integration and the disturbing potential expanded to the fifth order. Initial conditions: $a_{1}=6$ AU, $a_{2}=100$ AU, $i_{1}=65^{\circ }$, $g_{1}=0^{\circ }$, $h_{1}=180^{\circ }$. The star has mass $1M_{\bigodot }$, the planet has mass $1M_{J}$ and the outer brown dwarf has mass $40M_{J}$. The colors indicate the time in multiples of $10^{7}$ years, and the gray color indicates that no flip occurred along the integration

3.3 Force due to the effect of general relativity (GR) and tide

In this section an approach is presented with respect to the secular problem in first order in a post-Newtonian expansion of general relativity (GR) and tide effects. It is known that the Kozai–Lidov (1962, 1962) mechanism can produce highly eccentric orbits for a highly inclined perturbed orbit. However, this effect may be reduced or modified if the inner binary separation at pericenter is sufficiently small for additional forces to overcome the tidal torque exerted by the outer binary (see Liu et al. 2014). If the energy associated with these additional forces exceeds the interaction potential given by Eq. (1) (see Liu et al. 2014), the Kozai–Lidov mechanism is said to be arrested. These forces are represented in Eqs. (17) and (18). The post-Newtonian potential associated with periastron advance is (e.g., Liu et al. 2014; Eggleton and Kiseleva-Eggleton 2001).

$$\begin{aligned} \begin{array}{l} \langle R_{\mathrm{GR}} \rangle =-{\frac{3{G}^{2}{m_{0}}{m_{1}}\, \left( {m_{0}}+{m_{1}} \right) }{{{a_{1}}}^{2}{c}^{2}\sqrt{1-{{e_{1}}}^{2}}}}, \end{array} \end{aligned}$$

(17)

where c is the speed of light. The perturbation considered in Eq. (17) gives rise to the precession of the argument of periastron of the inner orbit.

The potential due to the non-dissipative tidal bulge on $m_{1}$ is given by (e.g., Liu et al. 2014; Eggleton and Kiseleva-Eggleton 2001)

$$\begin{aligned} \begin{array}{l} \langle R_{\mathrm{TIDE}} \rangle =-{\frac{G( 1+3{{e_{1}}}^{2}+3/8{{e_{1}}}^{4}){{m_{0}}}^{2}{k_{2,1}}{{R_{J}}}^{5}}{{{a_{1}}}^{6}( 1-{{e_{1}} }^{2})^{9/2}}}, \end{array} \end{aligned}$$

(18)

where $k_{2,1}$, $R_{1}$ are the tidal Love number and the radius of $m_{1}$, respectively. For the other constants, we have $k_{2,1}=0.37$ and $R_{J}=142984/2$ (Liu et al. 2014).

The long-period disturbing potential can be written as

$$\begin{aligned} \begin{array}{l} R=\sum _{j=2}^{5}R_{jC}+R_{\mathrm{GR}}+R_{\mathrm{TIDE}} \end{array} \end{aligned}$$

(19)

This potential is replaced in the Lagrange planetary equations (Kovalevsky 1967) and integrated numerically to compare the different orders of the disturbing potential.

Fig. 14

Temporal evolution of the inclination. Initial conditions: $a_{1}=6$ AU, $a_{2}=100$ AU, $e_{1}=0.01$, $e_{2}=0.6$, $g_{1}=45^{\circ }$, $h_{1}=180^{\circ }$. The star has mass $1M_{\bigodot }$, the planet has mass $1M_{J}$ and the outer brown dwarf has mass $40M_{J}$

Fig. 15

Temporal evolution of the inclination. Initial conditions: $a_{1}=6$ AU, $a_{2}=100$ AU, $e_{1}=0.01$, $e_{2}=0.6$, $g_{1}=45^{\circ }$, $h_{1}=180^{\circ }$. The star has mass $1M_{\bigodot }$, the planet has mass $1M_{J}$ and the outer brown dwarf has mass $40M_{J}$

Figure 14 shows the planet inclination behavior considering different orders of the disturbing potential. For the considered initial conditions ($g_{1}=45$ $^\circ$), the potential considering the terms $R_{2C}+R_{3C}+R_{4C}$ and $R_{2C}+R_{3C}+R_{4C}+R_{5C}$ have similar results. Taking into account the $R_{2C}+R_{3C}$ potential the behavior of the inclination is different. In this case, after the second inversion, the planet remains for a long time in prograde orbits, while in the other two models the planet remains $50~\%$ of the time in prograde and retrograde orbits. Note that, when it is taken into account, the perturbations due to the precession of the periastron (GR) and the tide effect, the flip of the inclination does not occur in the simulated period. The inclination is controlled by the coupling of the forces considered in the dynamics and, therefore, does not present the effect of the flip in the inclination of the inner planet (see Fig. 15). But, increasing the simulation time, we can see that there are still inclination inversions even considering the additional forces in the system, as shown in Fig. 16. Considering the coupling of the perturbations used, that are the perturbations of the third body, effects due to the precession of periastron and the tide effect, in general, we find that such perturbations combined delay the time of first inversion, but not exactly keeps the planet in a prograde or retrograde orbit (see Fig. 16). Note that, when it is taken into account up to the fifth order of the disturbing potential combined with the relativistic effects and the tide effect, we found that the inclination migrates from prograde to retrograde and then remains in a retrograde orbit until the end of the simulation. This inclination behavior is shown in Fig. 17. As shown in Figs. 15 and 17, the relativistic and tide effects completely change the dynamics of the inclination behavior.

Fig. 16

Temporal evolution of the inclination. Initial conditions: $a_{1}=6$ AU, $a_{2}=100$ AU, $e_{1}=0.01$, $e_{2}=0.6$, $g_{1}=45^{\circ }$, $h_{1}=180^{\circ }$. The star has mass $1M_{\bigodot }$, the planet has mass $1M_{J}$ and the outer brown dwarf has mass $40M_{J}$

Fig. 17

Temporal evolution of the inclination. Initial conditions: $a_{1}=6$ AU, $a_{2}=100$ AU, $e_{1}=0.01$, $e_{2}=0.6$, $g_{1}=45^{\circ }$, $h_{1}=180^{\circ }$. The star has mass $1M_{\bigodot }$, the planet has mass $1M_{J}$ and the outer brown dwarf has mass $40M_{J}$

4 Conclusions

The present paper investigated the problem of the inversion of the inclination of the planet disturbed by a distant brown dwarf. The mathematical model considered the $R_{5C}$ term of the potential of the disturbing body, which was not done by previous researches. The results showed that the inclusion of this term changes the times of the inversion of the inclination of the orbit. To develop the equations of motion, the double-averaged method is applied to eliminate the short-period terms of the disturbing potential. The disturbing potential was explicitly presented up to the fifth order considering the disturbing star in a planar orbit. A comparison of different orders of the disturbing potential is presented. The results show that the odd terms of the development of the disturbing function in terms of Legendre polynomials represents better the dynamic behavior of the system when compared with the numerical simulation of the problem of three bodies. In particular, the terms $R_{3C}$ (octupole) and $R_{5C}$ (hexapole). We note that the initial choice of the argument of the periastron of the inner planet is extremely important to describe the behavior of how the eccentricity is changing.

We show maps with respect to the eccentricities of the planet and of the disturbing star. These maps represent the value of the eccentricity of the planet at the moment of the first inversion of the inclination, i.e., when the inclination changes its value from prograde to retrograde. We showed that the eccentricity can reach very high values and their inclination can become higher than 90$^\circ$.

Another point investigated is related to the collision of the planet with the mother star. Including this verification, several results were found. Regions that had oscillations in inclination in fact resulted in possible collisions before the inversion. Some examples are as follows: for $i=50^{\circ }$ (see Fig. 9a) the collision happened after $1 \times 10^7$ years; for $i=80^{\circ }$ (see Fig. 9b) the collision happened after $0.2\times 10^7$ years. We observed that, taking into account the radius of the planet (considering the dimensions of the body) in the direct numerical integrations, the planet may collide with the star for high values of the inclination. Note that the collision occurs exactly at the first inversion.

Here we also presented an approach with respect to the secular problem of first order in a post-Newtonian expansion of the general relativity (GR) and tide effect. We showed the third body perturbation effect in different orders of the disturbing potential and also inserted extra forces in the dynamics to evaluate the characteristic of the inclination due to these forces. In general, we find that such perturbations combined delay the time of first inversion, but do not keep the planet in a prograde or retrograde orbit.

We present a model for the disturbing potential that takes into account the perturbation of the third body expanded up to the fifth-order, the effects of tides and the general relativity, which is a more realistic model. Besides that, this fact generates results, which are in closer agreement with the direct numerical integration. So, in general, the present paper showed a more realistic study of this interesting problem in planetary celestial mechanics.