1 Introduction

Over the last decade, brushless DC (BLDC) motors have grown in popularity thanks to their highly efficient use of permanent magnets (Prabhu et al., 2023). Compared to conventional DC motors or induction motors, BLDC motors offer numerous benefits, including quick dynamic response, a simple structure, and high performance in terms of torque density, power density, power factor, and efficiency (Saiteja et al., 2024). Consequently, these motors have become prevalent in electric transportation systems, predominantly employing field-oriented control (FOC) for regulating speed, making rotor position information very important (Akrami et al., 2024). However, employing position sensors may not be the optimal solution due to potential higher costs, increased weight, and the susceptibility of sensors to failure under environmental conditions of elevated humidity or temperatures (Chi et al., 2023; Sayed et al., 2024).

A control strategy called sensorless control has emerged as an interesting solution that increases robustness and enables FOC of the motor to decouple torque and flux without requiring a physical speed sensor (Rauth & Samanta, 2020). Based on speed working conditions, the methods of sensorless control can be categorized into two strategies: one for low-speed conditions relying on high-frequency injection, and another for medium to high speeds relying on back-electromotive force (back-EMF) (Ning et al., 2023). The back-EMF strategy has become increasingly prevalent in recent studies, owing to its effectiveness in extending operational speed conditions across the entire speed range (Harshit Mohan & Dwivedi, 2020). Typically, it is designed in two steps: firstly, acquiring the estimated back-EMF through an observer, and secondly, extracting position and speed information from the estimated back-EMF.

Observer-based strategies for back-EMF estimation in sensorless control are extremely favored in the literature, with sliding mode observers (SMOs), Kalman filters, model reference adaptive systems, and extended state observers (ESOs) being prominent methods (Zou et al., 2024; Quang et al., 2014; Zhao et al., 2014; Li et al., 2023). Among these, the SMO and ESO are particularly robust due to their simple designs and remarkable insensitivity to motor parameters (Xu et al., 2019; Chen et al., 2023a). However, the SMO faces challenges due to the chattering phenomenon, often requiring multiple additional filters to achieve accurate back-EMF estimation, whereas the ESO operates effectively as a low-pass filter and does not need extra filtering to accurately estimate the back-EMF (Chen et al., 2023a). In Ok et al. (2024), the authors substituted the signum function of the SMO with a sigmoid function featuring a variable acceleration slope to minimize chattering during sensorless speed and position estimation. The study in Du et al. (2016) introduced a strategy based on ESO with high-frequency current injection to cover the entire speed range. This method significantly reduced speed chattering and phase delay in ESO when compared to SMO. Similarly, the research in Qu et al. (2020) showed that employing ESO to estimate back-EMF effectively resolves the phase delay and chattering issues inherent in SMO due to its discontinuous function.

Regardless of the observer employed in the first step to accurately estimate the back-EMF, the second step remains the objective in sensorless control strategies, aiming to extract the estimated position and speed. Traditionally, the direct calculation method using an arc-tangent function is an open-loop method in which the position estimation error is not considered, leading to the appearance of high-frequency noise (Li et al., 2024). To address these position estimation errors in steady state, a closed-loop method known as phase-locked loops (PLLs) is employed. Several advanced types of PLLs exist, including steady-state linear Kalman filter-based PLLs (SSLKF-PLLs) (Golestan et al., 2018), finite-position-set PLLs (FPS-PLLs) (Chen et al., 2023b), and quadrature PLLs (QPLLs). The QPLL, which relies on a proportional-integral (PI) controller, is commonly used (Jiang et al., 2021). However, traditional linear PI controllers used in conventional QPLL strategies are limited by the nonlinearity of the inverter and the presence of harmonics in the estimated back-EMF, which constrain sensorless control performance. There are numerous techniques described in the literature for suppressing harmonics in the estimated back-EMF, including the second-order generalized integrator (Sreejith & Singh, 2021), ADALINE-network-based filter (Zhang et al., 2016), and adaptive notch filter (Ge et al., 2021). To simplify the system and enhance computational efficiency, harmonics can be directly suppressed within the QPLL based on a linear ESO, as described in Jiang et al. (2022), rather than eliminating them in the estimated back-EMF.

This paper aims to enhance the sensorless control performance of a BLDC motor. The conventional QPLL is improved by replacing the PI controller with an ESO embedded with an active harmonic compensator technique. The proposed technique uses the P-Q theory to suppress harmonics induced by the estimated back-EMF. By calculating the active and reactive power of the motor, the compensator determines the appropriate compensation current to be directly injected into the QPLL based on ESO.

The following sections will outline the contents of this paper. In Sect. 2, a field-oriented control approach will be presented, including the dq-frame model of the motor and the design of its controllers. Section 3 will introduce the back-EMF observer design, which is based on ESO. In Sect. 4, the design of the QPLL is covered, including both the conventional QPLL and the proposed QPLL based on ESO. The effectiveness of the enhanced QPLL is validated in Sect. 5, where the results are analyzed. Finally, Sect. 6 highlights the conclusion of this work.

2 FOC of BLDC

Some assumptions are made to simplify the BLDC model and achieve a smooth control design, such as ignoring magnetic saturation, eddy currents, and hysteresis losses. In the dq-frame, the electrical equations of the BLDC can be written as:

$$\begin{aligned} \left\{ \begin{aligned}&v_d = R_s i_d + L_d \frac{\textrm{d}i_d}{\textrm{d}t} + e_d \\&v_q = R_s i_q + L_q \frac{\textrm{d}i_q}{\textrm{d}t} + e_q \\ \end{aligned} \right. \end{aligned}$$
(1)

where \(v_d\), \(v_q\), \(i_d\), and \(i_q\) represent the dq-frame stator voltages and currents, respectively. \(R_s\) is the stator resistance. \(L_d\) and \(L_q\) are the dq-frame inductances. \(e_d\) and \(e_q\) are the back-electromotive force in the dq-frame, which can be expressed as follows:

$$\begin{aligned} \left\{ \begin{aligned}&{{e}_{d}}=-\omega {{L}_{q}}{{i}_{q}} \\&{{e}_{q}}=\omega ({{L}_{d}}{{i}_{d}}+{{\psi }_{f}}) \\&\omega ={{n}_{p}}\Omega \\ \end{aligned} \right. \end{aligned}$$
(2)

where \(\omega \) and \(\Omega \) are the electrical and mechanical rotor speeds, respectively. \(n_p\) is the number of pole pairs. \({\psi }_{f}\) is the permanent magnet flux of the rotor.

The equation of motion for the BLDC mechanical speed is expressed as follows:

$$\begin{aligned} J\frac{\textrm{d}\Omega }{\textrm{d}t}={{T}_{e}}-{{T}_{L}}-f\Omega \end{aligned}$$
(3)

where J and f are the moment of inertia and friction coefficient, respectively. \(T_L\) is the load torque. \(T_e\) is the electromagnetic torque, and in the case of surface-mount permanent magnet BLDC with equal d-axis and q-axis inductances (\(L_d = L_q= L_s\)), it can be expressed as follows:

$$\begin{aligned} {{T}_{e}}=1.5{{n}_{p}}{{\psi }_{f}}{{i}_{q}} \end{aligned}$$
(4)
Fig. 1
figure 1

Control structure

Full size image

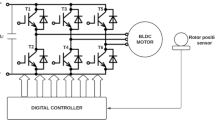
The proposed control approach for the BLDC relies on the structural diagram depicted in Fig. 1. Using cascaded PI controllers, a field-oriented control is implemented as follows:

  • The outer speed controller loop calculates the reference quadratic current using the following equation:

    $$\begin{aligned} i_{q}^\textrm{ref}={{K}_{p\Omega }}({{\Omega }^\textrm{ref}}-\hat{\Omega })+{{K}_{i\Omega }}\int {({{\Omega }^\textrm{ref}}-\hat{\Omega })\textrm{d}t} \end{aligned}$$
    (5)

    where the superscript “\(^\textrm{ref}\)” denotes the reference. \(\hat{\Omega }\) represents the estimated mechanical speed. \({K}_{p\Omega }\) and \({K}_{i\Omega }\) are the proportional and integral parameters of the speed loop, respectively.

  • The inner current controllers loop consists of the direct and quadratic control laws. In order to maximize the torque output, it is necessary to maintain the direct current at zero and control the quadratic current based on the torque reference in order to track the speed reference. Therefore, the direct and quadratic control laws can be expressed using the following equation:

    $$\begin{aligned} \left\{ \begin{aligned}&v_{d}^\textrm{ref}={K_{pi}}(i_{d}^\textrm{ref}-i_{d})+{K_{ii}}\int (i_{d}^\textrm{ref}-i_{d})\textrm{d}t+e_{d} \\&v_{q}^\textrm{ref}={K_{pi}}(i_{q}^\textrm{ref}-i_{q})+{K_{ii}}\int (i_{q}^\textrm{ref}-i_{q})\textrm{d}t+e_{q} \\ \end{aligned} \right. \end{aligned}$$
    (6)

    where \({K}_{pi}\) and \({K}_{ii}\) are the proportional and integral parameters of the dq-frame current loop, respectively.

The pole placement method establishes the control design parameters, which remain selected as follows:

$$\begin{aligned} \left\{ \begin{aligned}&{{K}_{p\Omega }}=\frac{(2\xi J{{\omega }_{\Omega }}-f)}{(1.5{{n}_{p}}{{\psi }_{f}})}\ ;\text { }{{K}_{i\Omega }}=\frac{(J\omega _{\Omega }^{2})}{(1.5{{n}_{p}}{{\psi }_{f}})} \\&{{K}_{pi}}=2\xi {{L}_{s}}{{\omega }_{c}}-{{R}_{s}};\text { }{{K}_{ii}}={{L}_{s}}\omega _{c}^{2} \\ \end{aligned} \right. \end{aligned}$$
(7)

where \(\xi \) represents the damping coefficient. \(\omega _{\Omega }\) and \({\omega }_{c}\) are the natural frequencies of the speed and current loop controllers, respectively.

3 Back-EMF observer based on ESO

To directly obtain the electrical position of the rotor from the back-EMF observer, it is necessary to use the stationary frame model. The current model in the stationary frame can be expressed as:

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\textrm{d}{{i}_{\alpha }}}{\textrm{d}t}=-\frac{{{R}_{s}}}{{{L}_{s}}}{{i}_{\alpha }}+\frac{1}{{{L}_{s}}}{{v}_{\alpha }}+{{E}_{\alpha }} \\&\frac{\textrm{d}{{i}_{\beta }}}{\textrm{d}t}=-\frac{{{R}_{s}}}{{{L}_{s}}}{{i}_{\beta }}+\frac{1}{{{L}_{s}}}{{v}_{\beta }}+{{E}_{\beta }} \\ \end{aligned} \right. \end{aligned}$$
(8)

where \({i}_{\alpha }\) and \({v}_{\alpha }\) denote the current and voltage in the \(\alpha \)-axis, \({i}_{\beta }\) and \({v}_{\beta }\) denote the current and voltage in the \(\beta \)-axis. \({E}_{\alpha }\) and \({E}_{\beta }\) are the unknown signals in the model given by:

$$\begin{aligned} \left\{ \begin{aligned}&{{E}_{\alpha }}=-\frac{1}{{{L}_{s}}}{{e}_{\alpha }} \\&{{E}_{\beta }}=-\frac{1}{{{L}_{s}}}{{e}_{\beta }} \\ \end{aligned} \right. \end{aligned}$$
(9)

where \({e}_{\alpha }\) and \({e}_{\beta }\) represent the back-EMF in the \(\alpha \beta \)-frame, expressed as follows:

$$\begin{aligned} \left\{ \begin{aligned}&{{e}_{\alpha }}=-\omega {{\psi }_{f}}\sin (\theta ) \\&{{e}_{\beta }}=\omega {{\psi }_{f}}\cos (\theta ) \\ \end{aligned} \right. \end{aligned}$$
(10)

where \(\theta \) denotes the electrical position of the rotor. It is evident that the back-EMF in (9) does not depend on the current or voltage, which makes the stationary frame a suitable choice for estimating the back-EMF signals.

By taking the unknown signals (\({E}_{\alpha }\) and \({E}_{\beta }\)) as system states in order to estimate them, the ESO can be designed as follows:

$$\begin{aligned} \left\{ \begin{aligned}&{{\varepsilon }_{\alpha }}={{i}_{\alpha }}-{{{\hat{i}}}_{\alpha }} \\&\frac{\textrm{d}{{{\hat{i}}}_{\alpha }}}{\textrm{d}t}={{f}_{\alpha }}({{i}_{\alpha }},{{v}_{\alpha }},t)+{{{\hat{E}}}_{\alpha }}+{{h}_{1}}{{\varepsilon }_{\alpha }} \\&\frac{\textrm{d}{{{\hat{E}}}_{\alpha }}}{\textrm{d}t}={{h}_{2}}{{\varepsilon }_{\alpha }} \\ \end{aligned} \right. \end{aligned}$$
(11)
$$\begin{aligned} \left\{ \begin{aligned}&{{\varepsilon }_{\beta }}={{i}_{\beta }}-{{{\hat{i}}}_{\beta }} \\&\frac{\textrm{d}{{{\hat{i}}}_{\beta }}}{\textrm{d}t}={{f}_{\beta }}({{i}_{\beta }},{{v}_{\beta }},t)+{{{\hat{E}}}_{\beta }}+{{h}_{1}}{{\varepsilon }_{\beta }} \\&\frac{\textrm{d}{{{\hat{E}}}_{\beta }}}{\textrm{d}t}={{h}_{2}}{{\varepsilon }_{\beta }} \\ \end{aligned} \right. \end{aligned}$$
(12)

where \(\hat{i}_{\alpha }\), \(\hat{i}_{\beta }\), \(\hat{E}_{\alpha }\), and \(\hat{E}_{\beta }\) are the estimates of \({{i}_{\alpha }}\), \({{i}_{\beta }}\), \({{E}_{\alpha }}\), and \({{E}_{\beta }}\), respectively; \({\varepsilon }_{\alpha }\) and \({\varepsilon }_{\beta }\) are the estimation errors. \({{f}_{\alpha }}({{i}_{\alpha }},{{v}_{\alpha }},t)\) and \({{f}_{\beta }}({{i}_{\beta }},{{v}_{\beta }},t)\) are the known terms in (8) that contain the current and voltage in the \(\alpha \beta \)-frame. \({h}_{1}\) and \({h}_{2}\) represent the constant gains of the observer, and their design is the same for both the \(\alpha \)-axis and \(\beta \)-axis due to the symmetrical structure of the back-EMF in the \(\alpha \beta \)-frame.

Taking the Laplace transformation of (8), (11), and (12) yields:

$$\begin{aligned} \left\{ \begin{aligned}&\frac{{{\varepsilon }_{\alpha }}(s)}{{{E}_{\alpha }}(s)}=\frac{{{\varepsilon }_{\beta }}(s)}{{{E}_{\beta }}(s)}=\frac{s}{{{s}^{2}}+{{h}_{1}}s+{{h}_{2}}} \\&{{\varepsilon }_{\alpha }}(s)=\frac{s{{{\hat{E}}}_{\alpha }}(s)}{{{h}_{2}}};\text { }{{\varepsilon }_{\beta }}(s)=\frac{s{{{\hat{E}}}_{\beta }}(s)}{{{h}_{2}}} \\ \end{aligned} \right. \end{aligned}$$
(13)

where s denotes the Laplace operator.

According to (13), the transfer function of the estimated back-EMF can be expressed as:

$$\begin{aligned} {{G}_{\alpha \beta }(s)}=\frac{{{{\hat{E}}}_{\alpha }}(s)}{{{E}_{\alpha }}(s)}=\frac{{{{\hat{E}}}_{\beta }}(s)}{{{E}_{\beta }}(s)}=\frac{{{h}_{2}}}{{{s}^{2}}+{{h}_{1}}s+{{h}_{2}}} \end{aligned}$$
(14)

The transfer function in (14) exhibits insensitivity to motor parameters, highlighting the robustness of the ESO in estimating the back-EMFs even when faced with variations in parameters. By appropriately selecting the observer bandwidth as \(\omega _o\), the gains of the observer can be parameterized as \(h_1 = 2\omega _o\) and \(h_2 = \omega _o^2\). Consequently, the estimation errors \({{\varepsilon }_{\alpha }}\) and \({{\varepsilon }_{\beta }}\) will exponentially converge to zero, enabling us to obtain an accurate estimate of the equivalent back-EMF as follows:

$$\begin{aligned} \left\{ \begin{aligned}&{{{\hat{e}}}_{\alpha }}=-{{L}_{s}}{{{\hat{E}}}_{\alpha }} \\&{{{\hat{e}}}_{\beta }}=-{{L}_{s}}{{{\hat{E}}}_{\beta }} \\ \end{aligned} \right. \end{aligned}$$
(15)

To eliminate the impact of \({{G}_{\alpha \beta }(s)}\) on amplitude and phase lag, the estimated signals should be compensated as follows:

$$\begin{aligned} \left\{ \begin{aligned}&\hat{e}_{\alpha }^{'}={{{\hat{e}}}_{\alpha }}(\omega _{o}^{2}+\omega ^{2} )/\omega _{o}^{2}\ \\&\hat{e}_{\beta }^{'}={{{\hat{e}}}_{\beta }}(\omega _{o}^{2}+\omega ^{2})/\omega _{o}^{2}\ \\&{{{\hat{\theta }}}^{'}}=\hat{\theta }+\arctan (2{{\omega }_{o}}\omega /(\omega _{o}^{2}-{{\omega }^{2}})) \\ \end{aligned} \right. \end{aligned}$$
(16)
Fig. 2
figure 2

Bode diagram of back-EMF observer

Full size image

Figure 2 illustrates the Bode diagram of \({{G}_{\alpha \beta }(s)}\) at various observer bandwidths, exhibiting characteristics similar to those of low-pass filters. The high electrical rotor speed (\(\omega \)) necessitates a higher observer bandwidth (\(\omega _o\)) to maintain the amplitude and phase of the estimated back-EMFs same as the actual values. Consequently, the observer bandwidth should be as large as possible compared to the electrical rotor speed (\(\omega _o \gg \omega \)), ensuring equality between estimated and actual back-EMFs (where \({(\omega _{o}^{2}+\omega ^{2} )}/{\omega _{o}^{2}} \approx 1\) and \(\arctan ({2{{\omega }_{o}}\omega }/{(\omega _{o}^{2}-{{\omega }^{2}})}) \approx 0\)).

4 QPLL Design

The QPLL stands out as a powerful and smooth approach for extracting accurate position and speed information from the estimated back-EMF. In contrast, the direct method may encounter calculation challenges, resulting in high-frequency noise caused by the direct application of an arc-tangent function. This high-harmonic noise has the potential to impact the accuracy of position and speed estimation.

Fig. 3
figure 3

Conventional QPLL

Full size image

4.1 Conventional QPLL

The structural diagram for the conventional QPLL is depicted in Fig. 3. The compensated estimated back-EMFs in (16) are used to approximately detect the electrical phase error, which serves as the input to the PI controller to generate the electrical speed in the output. Meanwhile, the integration of the output yields the estimated electrical position of the rotor. Consequently, the transfer function from the actual electrical position (\(\theta \)) to the estimated electrical position (\(\hat{\theta }\)) can be expressed as follows:

$$\begin{aligned} \frac{\hat{\theta }(s)}{\theta (s)}=\frac{{{K}_{p}}s+{{K}_{i}}}{{{s}^{2}}+{{K}_{p}}s+{{K}_{i}}} \end{aligned}$$
(17)

where \({K}_{p}\) represents the proportional gain, which can be tuned as \(2\sigma \), and \({K}_{i}\) denotes the integral gain, which can be adjusted as \({{\sigma }^{2}}\). The parameter \(\sigma \) corresponds to the QPLL bandwidth and should be carefully selected by taking into account the speed-tracking rate and noise.

4.2 Proposed QPLL Based on ESO

The structural diagram illustrating the proposed QPLL based on ESO is depicted in Fig. 4. The design of this proposed QPLL enhances the conventional version by substituting the PI controller with an improved ESO embedded with a harmonic compensation technique.

Based on (3) and (4), the dynamics of electrical motion can be expressed as follows:

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\textrm{d}\theta }{\textrm{d}t}=\omega \\&\frac{\textrm{d}\omega }{\textrm{d}t}={k_t}{{i}_{q}}-\frac{{{n}_{p}}}{J}{{T}_{L}}-\frac{f}{J}\omega \\ \end{aligned} \right. \end{aligned}$$
(18)

where \({{k}_{t}}={1.5n_{p}^{2}{{\psi }_{f}}}/{J}\).

To facilitate the design of an ESO, the model dynamics in (18) should be reformulated by defining the known and unknown terms as follows:

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\textrm{d}\theta }{\textrm{d}t}=\omega \\&\frac{\textrm{d}\omega }{\textrm{d}t}={{k}_{t}}i_{q}^\textrm{ref}+{{f}_{\theta }}+{{d}_{\theta }} \\&{{f}_{\theta }}={{k}_{t}}({{i}_{q}}-i_{q}^\textrm{ref})-\frac{f}{J}\hat{\omega } \\&{{d}_{\theta }}=-\frac{{{n}_{p}}}{J}{{T}_{L}}-\frac{f}{J}(\omega -\hat{\omega })+{{\delta }_{\theta }}(t) \\ \end{aligned} \right. \end{aligned}$$
(19)

where \(\hat{\omega }\) represents the estimated electrical speed, \({{\delta }_{\theta }}(t)\) denotes the remaining unmodeled dynamics. \({{f}_{\theta }}\) encompasses the known term, while \({{d}_{\theta }}\) represents the unknown term to be estimated by the ESO.

By considering \({{d}_{\theta }}\) as an additional state in system (19), the design of the ESO can be formulated as follows:

$$\begin{aligned} \left\{ \begin{aligned}&{{\varepsilon }_{\theta }}=\theta -\hat{\theta } \\&\frac{\textrm{d}\hat{\theta }}{\textrm{d}t}=\hat{\omega }+{{\beta }_{1}}{{\varepsilon }_{\theta }} \\&\frac{\textrm{d}\hat{\omega }}{\textrm{d}t}={{k}_{T}}i_{q}^\textrm{ref}+{{f}_{\theta }}+{{{\hat{d}}}_{\theta }}+{{\beta }_{2}}fal({{\varepsilon }_{\theta }},\alpha ,\delta ) \\&\frac{\textrm{d}{{{\hat{d}}}_{\theta }}}{\textrm{d}t}={{\beta }_{3}}fal({{\varepsilon }_{\theta }},\alpha ,\delta ) \\ \end{aligned} \right. \end{aligned}$$
(20)

where \({{{\hat{d}}}_{\theta }}\) represents the estimates of \({d}_{\theta }\), \({{\varepsilon }_{\theta }}\) denotes the electrical phase error, and \({{\beta }_{1}}\), \({{\beta }_{2}}\), and \({{\beta }_{3}}\) denote the gains of a third-order ESO. By selecting the ESO bandwidth \(\sigma \), the gains can be tuned as follows: \(3\sigma \) for \({{\beta }_{1}}\), \(3\sigma ^2\) for \({{\beta }_{2}}\), and \(\sigma ^3\) for \({{\beta }_{3}}\). \(fal({{\varepsilon }_{\theta }},\alpha ,\delta )\) represents a nonlinear function defined by the following expression:

$$\begin{aligned} fal({{\varepsilon }_{\theta }},\alpha ,\delta )=\left\{ \begin{array}{ll} \frac{{{\varepsilon }_{\theta }}}{{{\delta }^{(1-\alpha )}}}, &{} \left| {{\varepsilon }_{\theta }} \right| \le \delta \\ \text {sign}({{\varepsilon }_{\theta }}){{\left| {{\varepsilon }_{\theta }} \right| }^{\alpha }}, &{} \left| {{\varepsilon }_{\theta }} \right| >\delta \\ \end{array} \right. \end{aligned}$$
(21)

where \(\alpha \) represents the tracking factor, and \(\delta \) denotes the filtering factor employed to establish the error threshold.

Fig. 4
figure 4

Proposed QPLL Based on ESO

Full size image

Under low-speed conditions, the motor generates small back-EMFs with nonideal components due to the nonlinearity of the inverter. The estimated nonideal back-EMF can be represented as the sum of the fundamental harmonic component (\(\hat{e}_{f\alpha \beta }\)) and the high-order harmonic components (\(\Delta \hat{e}_{h\alpha \beta }\)) (Zhang et al., 2016). This can be expressed as follows:

$$\begin{aligned} \left\{ \begin{aligned}&\hat{e}_{\alpha } = \hat{e}_{f\alpha } + \Delta \hat{e}_{h\alpha } \\&\hat{e}_{\beta } = \hat{e}_{f\beta } + \Delta \hat{e}_{h\beta } \\ \end{aligned} \right. \end{aligned}$$
(22)

The influence of the nonideal back-EMF will be evident not only in the electrical phase error detector but also in the electromagnetic torque, which can be characterized as follows:

$$\begin{aligned}{} & {} {{T}_{e}}={{T}_{ef}}+\Delta {{T}_{eh}} \end{aligned}$$
(23)
$$\begin{aligned}{} & {} {{T}_{ef}}=1.5{{n}_{p}}\left[ \frac{{{{\hat{e}}}_{f\alpha }}{{i}_{\alpha }}+{{{\hat{e}}}_{f\beta }}{{i}_{\beta }}}{{\hat{\omega }}} \right] \end{aligned}$$
(24)
$$\begin{aligned}{} & {} {{T}_{eh}}=1.5{{n}_{p}}\left[ \frac{\Delta {{{\hat{e}}}_{h\alpha }}{{i}_{\alpha }}+\Delta {{{\hat{e}}}_{h\beta }}{{i}_{\beta }}}{{\hat{\omega }}} \right] \end{aligned}$$
(25)

where \({T}_{ef}\) is the main torque produced by the fundamental harmonic and \({T}_{eh}\) is the pulsation torque produced by the high-order harmonics.

According to (4), the q-axis current is responsible for producing the electromagnetic torque. Therefore, directly reconstructing the q-axis current can help suppress high-order harmonics within the enhanced QPLL. To achieve this, the reference for the quadratic current in (20) is modified by adding an additional compensating quadratic current. This compensating current is based on the P-Q theory, which utilizes high-pass and low-pass filters to extract harmonics from reactive and active motor powers. The calculation of this compensating current involves the following two steps:

  • Active and reactive power calculations are performed using the following equation:

    $$\begin{aligned} \left\{ \begin{aligned}&P=v_{d\_f}^\textrm{ref}{{i}_{d}}+v_{q\_f}^\textrm{ref}{{i}_{q}} \\&Q=v_{q\_f}^\textrm{ref}{{i}_{d}}-v_{d\_f}^\textrm{ref}{{i}_{q}} \\ \end{aligned} \right. \end{aligned}$$
    (26)

    where \(v_{d\_f}^\textrm{ref}\) and \(v_{q\_f}^\textrm{ref}\) are the direct and quadratic voltage control laws filtered by low-pass filters (LPF).

  • The calculation for the compensating quadratic current reference is determined through the following equation:

    $$\begin{aligned} i_{q}^{comp}=\frac{{\Delta P}v_{q\_f}^\textrm{ref}-{\Delta Q}v_{d\_f}^\textrm{ref}}{{{(v_{d\_f}^\textrm{ref})}^{2}}+{{(v_{q\_f}^\textrm{ref})}^{2}}} \end{aligned}$$
    (27)

    where \({\Delta P}\) and \({\Delta Q}\) are the oscillating powers extracted by high-pass filters (HPF), and their values are obtained as follows:

    $$\begin{aligned} \left\{ \begin{aligned}&\Delta P=(1-\frac{{{\omega }_{f}}}{s+{{\omega }_{f}}})P \\&\Delta Q=(1-\frac{{{\omega }_{f}}}{s+{{\omega }_{f}}})Q \\ \end{aligned} \right. \end{aligned}$$
    (28)

    where \({\omega }_{f}\) represents the pulsating frequency.

5 Results Analysis

To validate the proposed sensorless control for the BLDC, simulation results were obtained using MATLAB/Simulink based on the control structure diagram depicted in Fig. 1. The parameters of the BLDC are listed in Table 1, and further details about the motor can be found in Mariano et al. (2017). Simulink offers the capability to conduct processor-in-the-loop (PIL) tests, which provide a useful means to assess the control system on hardware, enabling Simulink models to operate in real time. To implement the proposed control on a digital signal processor (DSP) board (TMS320F28069M), it is necessary to configure hardware implementation settings and build the PIL block by generating code from the proposed control model. Pulse width modulation (PWM) signals were generated using space vector pulse width modulation (SVPWM) at a switching frequency of \(50 \, \textrm{kHz}\). These PWM signals controlled the inverter that supplied power to the motor from a DC-link voltage of \(22 \, \textrm{V}\). Although the BLDC and inverter were not physically existing, they were instead modeled and simulated concurrently with the controller operating in real time.

Table 1 Motor parameters
Full size table
Fig. 5
figure 5

Speed performance with varying \(\omega _f\) values

Full size image
Table 2 Comparison of MSE for speed and position estimates at different \( w_f \) values
Full size table

Prior to motor operation, back-EMF is not available. Therefore, in sensorless control methods relying on estimated back-EMF, it is crucial to initially accelerate the motor to a specific speed for accurate back-EMF signal estimation. In the results presented in this paper, motor startup followed the strategy outlined in Wang et al. (2012). By applying a speed ramp-up frequency while maintaining a constant q-axis current and regulating the d-axis current to zero under rated load torque, the proposed sensorless control was subsequently activated at \(8\, \textrm{milliseconds}\). The natural frequencies of the speed and current loop PI controllers are tuned to \(\omega _{\Omega }=625 \, \mathrm {rad/s}\) and \({\omega }_{c}=12500 \, \mathrm {rad/s}\), respectively. The ESO bandwidth for the back-EMF observer is adjusted to \(\omega _o=500000 \, \mathrm {rad/s}\). Both the conventional and enhanced QPLL bandwidths are configured to \(\sigma =650 \, \mathrm {rad/s}\). The \(\alpha \beta \)-frame voltage used in the back-EMF observer was calculated as follows:

$$\begin{aligned} \left\{ \begin{aligned}&{{v}_{\alpha }}=\frac{{{v}_{DC}}}{3}(2{{S}_{1}}-{{S}_{2}}-{{S}_{3}}) \\&{{v}_{\beta }}=\frac{\sqrt{3}{{v}_{DC}}}{3}({{S}_{2}}-{{S}_{3}}) \\ \end{aligned} \right. \end{aligned}$$
(29)

where \({S}_{i}\) (\(i=1,\ldots ,3\)) denote the switching pulses applied across each up-leg of the inverter. \({v}_{DC}\) is the DC-link voltage.

Fig. 6
figure 6

Hodograph of \(\alpha \beta \)-frame back-EMF estimated by ESO and SMO

Full size image
Fig. 7
figure 7

Response to load and speed changes

Full size image

To set the pulsating frequency parameters of the filters, it is important to note that, unlike the power grid system where the fundamental frequency remains constant, the frequency in a motor system varies with the desired speed. Therefore, we performed a series of simulations with a constant pulsating frequency value of \(2\pi 100\) for the low-pass filters and used varying pulsating frequency values for the high-pass filters. These values included both fixed frequencies and frequencies that varied proportionally to the electrical reference speed (\(\omega ^\textrm{ref}=n_p\Omega ^\textrm{ref}\)). Figure  5 illustrates the actual speed performance of the enhanced QPLL with different \(\omega _f\) values (\(2\pi 500\), \(2\pi 300\), \(2\pi 100\), \(\omega ^{\text {ref}}\), \(5\omega ^{\text {ref}}\), and \(10\omega ^{\text {ref}}\)). It is observed that at high speeds (\(\Omega ^{\text {ref}} = 400 \, \, \mathrm {rad/s}\)), the speed pulsation is significantly reduced and remains nearly the same across different \(\omega _f\) values, due to the natural frequency of the speed loop controller filtering out the pulsations. At medium and low speeds (\(\Omega ^{\text {ref}} = 200 \, \, \mathrm {rad/s}\) and \(\Omega ^{\text {ref}} = 20 \, \, \mathrm {rad/s}\)), the pulsation is notably minimized when the pulsating frequency varies proportionally to the electrical reference speed (\(\omega _f = 5\omega ^{\text {ref}}\)), compared to other values. Table 2 shows the comparison of mean square error (MSE) for speed and position estimates with the same cases mentioned above. It is evident that for optimal performance, the intermediate \(\omega _f\) value of \(5\omega ^{\text {ref}}\) is the best choice.

To demonstrate the effectiveness of the ESO in estimating back-EMF, we conducted a comparative analysis with a second-order SMO based on the super-twisting algorithm, which is the most commonly used conventional back-EMF observer. Figure  6 presents a hodograph of the \(\alpha \beta \)  frame back-EMF, with the reference speed set to \(\Omega ^\textrm{ref}=100 \, \mathrm {rad/s}\) and the load torque set to the rated torque. The hodograph illustrates that the ESO provides a more accurate estimation of back-EMF with significantly reduced chattering noise compared to the conventional second-order SMO.

Figure 7 presents a comparative analysis of the conventional and enhanced QPLL performance under varying reference speeds and load torques. The speed reference is set from 200 to \(20 \, \mathrm {rad/s}\) in sudden decreased steps, while the load torque starts with a rated load torque of \(0.1437 \, \textrm{Nm}\). At time \(0.15 \, \textrm{s}\), the load torque is reduced to 5% of the rated torque until it returns to its full rated value at time \(0.25 \, \textrm{s}\). It is clear that the enhanced QPLL significantly minimizes the oscillations in both speed and position estimation errors when compared with the conventional QPLL, especially evident at lower speeds.

Table 3 Conventional and enhanced QPLL comparison
Full size table
Fig. 8
figure 8

Response to J increased by 160%

Full size image
Fig. 9
figure 9

Response to speed changes

Full size image
Fig. 10
figure 10

Stator current waveform of phase “a”

Full size image

Table 3 presents the results obtained from both the conventional and enhanced QPLLs in steady state. In this experiment, the speed reference was set at \({{\Omega }^\textrm{ref}}=2\pi 20\, \mathrm {rad/s}\), and the load torque was set to the full rated load torque (\(0.1437 \, \textrm{Nm}\)). The results indicate that the enhanced QPLL significantly reduced torque ripples and the total harmonic distortion (THD) of the current. The torque ripples were reduced by approximately 35% compared to the conventional QPLL, and the THD was reduced by about 7%.

In order to evaluate the robustness performance of the conventional and enhanced QPLL, we analyzed the effect of varying the moment of inertia (J) illustrated in Fig. 8. The speed reference is set to \({\Omega }^\textrm{ref}=100\, \mathrm {rad/s}\), and the load torque is set to the rated torque. At \(0.1 \, \textrm{s}\), the moment of inertia increases by 160%. It is evident that both methods confirm robustness against parameter mismatches. However, the enhanced QPLL outperforms the conventional technique during the transient time and significantly reduces speed fluctuation and torque ripples.

Figure 9 compares the results obtained from the enhanced QPLL, both with and without the compensator, tested under rated load torque across a range of reference speeds. The speed references vary with sudden decreases in steps, ranging from 200 to \(20 \, \mathrm {rad/s}\). It can be seen that the QPLL without the compensator increased the ripples of speed and torque under low speed. In contrast, the enhanced QPLL effectively reduced the magnitude of these ripples.

Figure 10 illustrates the performance of the phase “a” stator current for the enhanced QPLL both with and without the compensator, under a low-speed reference of \(20 \, \mathrm {rad/s}\) and the rated load torque. The results indicate a noticeable improvement in the quality of the stator current waveform when the compensator becomes active at \(t = 0.2 \, \textrm{s}\). Specifically, the compensator significantly reduces the chattering noise, leading to a smoother current waveform.

6 Conclusion

The paper introduced a sensorless control strategy based on extended state observers that has proven to be an effective method for enhancing the speed-tracking performance of the BLDC motor. Due to its simple design and smooth estimation, an extended state observer was used to estimate the back-EMF without requiring any additional filters. Another extended state observer was incorporated into the QPLL, allowing the QPLL to be embedded with an active harmonic compensator to suppress the noise harmonics induced by the estimated back-EMF. The compensator design utilized the P-Q theory to calculate a compensation signal to be directly injected into the QPLL based on ESO. The results showed that compared to the conventional QPLL, the proposed strategy significantly reduced torque ripples and speed/position estimation errors under reference speed and load torque variation, especially at lower speed references.