1 Introduction

In recent years, with the rapid development of permanent magnet materials and control technology, PMSMs have been widely used in high-end technical fields such as aerospace, subway traction systems, and robots (Brandstetter & Krecek, 2013; Li et al., 2019; Urbanski & Janiszewski, 2019; Yi et al., 2019). PMSMs have many advantages over brushed DC motors. For example, the structure is simple, the weak magnetic ability is strong, and the power density is high. However, PMSM is a nonlinear system with multiple variables and strong coupling. The phenomenon of long response time and large output torque fluctuation will occur during operation (Jiang et al., 2021). Therefore, the continuous improvement and optimization of the motor control method is the key to improve the control performance of PMSM. To achieve high-performance control of PMSM, accurate acquisition of rotational speed and rotor position information is necessary. The traditional method of obtaining rotational speed and rotor position is to use mechanical sensors to obtain them. However, the method of using mechanical sensors increases the cost and size of the device. Moreover, the mechanical sensor is easily affected by the surrounding environment and is easily damaged in the case of a harsh surrounding environment. In order to obtain accurate rotational speed and rotor position information without using mechanical sensors, sensorless control methods are proposed (Zhou & Zhou, 2018). The sensorless control method obtains the back-electromotive force (EMF) signal from the stator current by algorithm and then extracts the rotational speed and rotor position information from the observed back-EMF signal. Compared with the use of mechanical sensors, sensorless control technology has many advantages and is currently a research hotspot in the field of mechanical control.

In recent decades, in order to improve the control performance of PMSM in harsh environments, many sensorless control methods have been developed for the field-oriented control of PMSM. The use of sensorless control technology to estimate the motor speed and rotor position information avoids the high cost problem caused by the use of mechanical sensors and improves the performance of the control system. The sensorless control technology of PMSM is mainly divided into two categories: one is the high-frequency voltage injection method based on salient pole tracking (Xin et al., 2009), and the other is the back-EMF method based on the motor model (Wang et al., 2021). The high-frequency voltage injection method is suitable for the estimation of the rotation speed of the PMSM in the range of zero and low speed. Since this method is based on the salient pole tracking of the motor, it cannot be used for surface mounted PMSM without salient polarity. Moreover, this method will introduce high-frequency noise due to the injection of high-frequency voltage, which in turn affects the control performance of the entire system. The back-EMF method based on the motor model is mainly used for speed estimation in medium- and high-speed situations. The method mainly includes model reference adaptive system (Kumar et al., 2021), extended Kalman filter method (Shi et al., 2012), and SMO (Ilioudis, 2015; Kang & Li, 2017; Regaya et al., 2017). Among them, the SMO method is a special nonlinear control method based on the sliding mode control principle (Yang et al., 2021). The peculiarity of this method lies in the discontinuity of control. It can make the system structure change with time and force the system to run with small amplitude and high-frequency buffeting according to the artificially designed sliding trajectory. The key to the realization of this method lies in the choice of sliding surface and switching function. The SMO algorithm is insensitive to external disturbances and system parameter changes and has strong robustness.

Although the sensorless technology based on SMO is widely used in the industrial field because of its simplicity, robustness to parameter changes and fast response speed. However, due to its discontinuous control characteristics, high-frequency chattering is inevitable. The high-frequency chattering in the back-EMF signal will reduce the signal-to-noise ratio of the SMO, cause larger errors in the estimation results, and seriously affect the performance of the observer. The traditional method to reduce chattering is to use a low-pass filter to filter out high-frequency noise and harmonics in the back-EMF signal. However, this method will cause the amplitude attenuation and phase lag of the rotor position, and a phase compensation module needs to be added to the system, which will increase the complexity of the system and affect the control performance of the system. A flux linkage SMO is proposed in Ye (2018, 2019), and an embedded low-pass filter is constructed to filter out high-order harmonics without using an additional compensation module. In Zhu (2018), the continuous saturation function is used instead of the symbolic function as the switching function, and the buffeting is well suppressed. Based on this design idea, a new quasi-SMO is designed in Kim et al. (2011), which uses the S-function of the variable boundary layer as the switching function to suppress chattering. In Ye (2018); Zhou et al. (2013); Ding et al. (2022), a fuzzy control method is proposed to adjust the gain of the SMO, so that the chattering can be effectively suppressed at low speed and the observation performance of the SMO is improved at low speed. In Ge et al. (2020); Wang and Tsai (2017); Wang et al. (2014), the neural network algorithm is used to obtain the gain of SMO. Although it has the effect of suppressing chattering, the computational complexity of the neural network method will increase the complexity of the system. In order to suppress chattering and improve the performance of observers and controllers, various adaptive methods have been proposed in previous studies (Ben Regaya et al., 2018; Chen et al., 2014, 2017; Deng et al., 2019; Lin & Zhang, 2017; Liu et al., 2019; Nguyen et al., 2022; Xu et al., 2021). An adaptive interconnected observer for sensorless control of PMSM is proposed in Traoré et al. (2012), which is robust to the variation of motor parameters. Two kinds of adaptive observers, including adaptive backstepping observer and adaptive SMO, are proposed in Regaya et al. (2013), which improve the estimation accuracy of motor speed and rotor position.

In this paper, an adaptive STASMO algorithm is proposed for sensorless control of PMSM. This method combines the super-twisting algorithm with the SMO algorithm and uses the sigmoid function as the switching function. By selecting appropriate parameters to adjust the convergence speed of sigmoid function, the performance of the observer is improved. An adaptive algorithm is designed to suppress the chattering of the system by adding a speed-related adaptive coefficient before the high-order integral term of the STASMO. The extraction of speed and rotor position information is realized by normalized PLL, which avoids the use of low-pass filter and phase compensation module, and improves the accuracy of estimation results. In addition, this paper also proposes an online estimation method of motor parameters, which can estimate the values of stator resistance and stator inductance online. The robustness of the system to changes in its own parameters is improved. The control strategy adopts vector control method. The speed loop and current loop are established to realize the double closed-loop control of the motor. Through coordinate transformation, the control of three-phase alternating current is transformed into the control of q-axis current generating torque and d-axis current generating magnetic field, and the independent control of torque and excitation is realized. By using the proposed control method to achieve field weakening operation, the torque and speed can be adjusted to maintain stability during startup and sudden load changes. In order to verify the proposed method, a simulation model was built in Matlab/Simulink for simulation, and a surface-mounted PMSM experimental platform with TMS320F28335 as the main control chip was built for experimental verification. Simulation and experimental results show that the method has high observation performance and strong robustness to its own parameter changes.

2 Mathematical Model of PMSM

In order to simplify the analysis, it is assumed that the three-phase PMSM is an ideal motor and satisfies the following conditions: ignoring the saturation of the motor core; the eddy current and hysteresis losses in the motor are not considered; the current in the motor is a symmetrical three-phase sine wave current.

Figure 1 shows the model of PMSM and the relationship between different coordinate systems. The mathematical model of the surface mount three-phase PMSM in the \(\alpha - \beta\) coordinate system can be expressed as (Wang et al., 2021):

$$ \left\{ {\begin{array}{*{20}c} {u_{\alpha } = R_{s} i_{\alpha } + L_{s} \frac{{\text{d}}}{{{\text{d}}t}}i_{\alpha } + E_{\alpha } } \\ {u_{\beta } = R_{s} i_{\beta } + L_{s} \frac{{\text{d}}}{{{\text{d}}t}}i_{\beta } + E_{\beta } } \\ \end{array} } \right. $$
(1)

where \(R_{s}\) is the stator resistance; \(u_{\alpha } ,u_{\beta }\) are the stator voltage; \(i_{\alpha } ,i_{\beta }\) are the stator current; \(L_{s}\) is the stator inductance; \(E_{\alpha } ,E_{\beta }\) are the back-EMF.

Fig. 1
figure 1

The model of PMSM and the relationship between different coordinate systems

Full size image

The back-EMF can be expressed as (Deng et al., 2019):

$$ \left\{ {\begin{array}{*{20}c} {E_{\alpha } = - \omega_{e} \varphi_{f} \sin \theta_{e} } \\ {E_{\beta } = \omega_{e} \varphi_{f} \cos \theta_{e} \begin{array}{*{20}c} {} \\ \end{array} } \\ \end{array} } \right. $$
(2)

where \(\omega_{e}\) is the electrical angular velocity; \(\varphi_{f}\) is the permanent magnet flux linkage; and \(\theta_{e}\) is the rotor electrical position.

3 Traditional SMO

Rewrite the (1) stator voltage equation into the state equation form of stator current:

$$ \left\{ {\begin{array}{*{20}c} {\frac{{\text{d}}}{{{\text{d}}t}}i_{\alpha } = - \frac{{R_{s} }}{{L_{s} }}i_{\alpha } + \frac{{u_{\alpha } }}{{L_{s} }} - \frac{{E_{\alpha } }}{{L_{s} }}} \\ {\frac{{\text{d}}}{{{\text{d}}t}}i_{\beta } = - \frac{{R_{s} }}{{L_{s} }}i_{\beta } + \frac{{u_{\beta } }}{{L_{s} }} - \frac{{E_{\beta } }}{{L_{s} }}} \\ \end{array} } \right. $$
(3)

The traditional SMO can be expressed as:

$$ \left\{ {\begin{array}{*{20}c} {\frac{{\text{d}}}{{{\text{d}}t}}\widehat{i}_{\alpha } = - \frac{{R_{s} }}{{L_{s} }}\widehat{i}_{\alpha } + \frac{{u_{\alpha } }}{{L_{s} }} - \frac{{\nu_{\alpha } }}{{L_{s} }}} \\ {\frac{{\text{d}}}{{{\text{d}}t}}\widehat{i}_{\beta } = - \frac{{R_{s} }}{{L_{s} }}\widehat{i}_{\beta } + \frac{{u_{\beta } }}{{L_{s} }} - \frac{{\nu_{\beta } }}{{L_{s} }}} \\ \end{array} } \right. $$
(4)

where \(\widehat{i}_{\alpha } ,\widehat{i}_{\beta }\) are the observed value of stator current and \(u_{\alpha } ,u_{\beta }\) are the control input of the observer.

Taking the difference between (3) and (4), the error equation of stator current can be obtained as:

$$ \left\{ {\begin{array}{*{20}c} {\frac{d}{{{\text{d}}t}}\widetilde{i}_{\alpha } = - \frac{{R_{s} }}{{L_{s} }}\widetilde{i}_{\alpha } + \frac{{E_{\alpha } - \nu_{\alpha } }}{{L_{s} }}} \\ {\frac{{\text{d}}}{{{\text{d}}t}}\widetilde{i}_{\beta } = - \frac{{R_{s} }}{{L_{s} }}\widetilde{i}_{\beta } + \frac{{E_{\beta } - \nu_{\beta } }}{{L_{s} }}} \\ \end{array} } \right. $$
(5)

where \(\widetilde{i}_{\alpha } = \widehat{i}_{\alpha } - i_{\alpha }\), \(\widetilde{i}_{\beta } = \widehat{i}_{\beta } - i_{\beta }\) are the observation errors of the stator current. The sliding mode function is:

$$ \left\{ {\begin{array}{*{20}c} {\nu_{\alpha } = k\;{\text{sign}}\left( {\widetilde{i}_{\alpha } } \right)} \\ {\nu_{\beta } = k\;{\text{sign}}\left( {\widetilde{i}_{\beta } } \right)} \\ \end{array} } \right. $$
(6)

When the state variable of the observer reaches the sliding surface (\(\widetilde{i}_{\alpha } = 0,\widetilde{i}_{\beta } = 0\)), the state of the observer will always remain on the sliding surface. According to the equivalent control principle of sliding mode control, the control variable at this time can be regarded as the equivalent control variable. It can be obtained that:

$$ \left\{ {\begin{array}{*{20}c} {E_{\alpha } = \nu_{\alpha } = k\;{\text{sign}}\left( {\widetilde{i}_{\alpha } } \right)_{{{\text{eq}}}} } \\ {E_{\beta } = \nu_{\beta } = k\;{\text{sign}}\left( {\widetilde{i}_{\beta } } \right)_{{{\text{eq}}}} } \\ \end{array} } \right. $$
(7)

4 Improved STASMO

4.1 Super-Twisting Algorithm

The super-twisting sliding mode algorithm is derived from the high-order sliding mode control theory, which can effectively suppress the sliding mode chattering and has strong robustness. Unlike other second-order sliding mode control algorithms, the super-twisting sliding mode algorithm does not require any information about the time derivative of the sliding mode variable, which makes the design of the SMO easier.

A. Levant proposed using super-twisting algorithm to eliminate chattering caused by sign function in Levant (1993). The basic form of super-twisting algorithm is:

$$ \left\{ {\begin{array}{*{20}c} \begin{gathered} \frac{{\text{d}}}{{{\text{d}}t}}x_{1} = - k_{1} \left| {\hat{x}_{1} - x_{1} } \right|^{1/2} sign\left( {\hat{x}_{1} - x_{1} } \right) \hfill \\ \begin{array}{*{20}c} {} & {} & {} \\ \end{array}\qquad + x_{2} + \rho_{1} (x_{1} ,t) \hfill \\ \end{gathered} \\ {\frac{{\text{d}}}{{{\text{d}}t}}x_{2} = - k_{2} \;{\text{sign}}\left( {\hat{x}_{1} - x_{1} } \right) + \rho_{2} (x_{2} ,t)} \\ \end{array} } \right. $$
(8)

where \(x_{1}\) and \(x_{2}\) are actual values of state variables; \(\widehat{x}_{1}\) and \(\widehat{x}_{2}\) are estimated values of state variables; \(k_{1}\) and \(k_{2}\) are sliding mode gains; and \(\rho_{1}\) and \(\rho_{2}\) are disturbance terms.

The stability of super-twisting algorithm has been proved in Moreno and Osorio (2012); Moreno and Osorio (2008). According to Moreno and Osorio (2012); Moreno and Osorio (2008), in order to ensure the stability of the system, the disturbance terms \(\rho_{1}\) and \(\rho_{2}\) should meet the following conditions:

$$ \left\{ {\begin{array}{*{20}l} {\left| {\rho_{1} } \right| \le \delta_{1} \left| {x_{1} } \right|^{1/2} } \\ {\rho_{2} = 0\begin{array}{*{20}c} {} & {} \\ \end{array} \begin{array}{*{20}c} {} \\ \end{array} } \\ \end{array} } \right. $$
(9)

where \(\delta\) is a positive constant. Sliding mode gains \(k_{1}\) and \(k_{2}\) should satisfy the following conditions:

$$ \left\{ {\begin{array}{*{20}l} {k_{1} > 2\delta_{1} \begin{array}{*{20}c} {} & {} & {} & {} \\ \end{array} } \\ {k_{2} > k_{1} \frac{{5\delta_{1} k_{1} + 4\delta_{1}^{2} }}{{2(k_{1} - 2\delta_{1} )}}\begin{array}{*{20}c} {} \\ \end{array} } \\ \end{array} } \right. $$
(10)

4.2 STASMO

The STASMO for sensorless control of PMSM can be expressed as:

$$ \left\{ {\begin{array}{*{20}c} \begin{gathered} \frac{{\text{d}}}{{{\text{d}}t}}\widehat{i}_{\alpha } = - \frac{1}{{L_{s} }}k_{1} \left| {\widetilde{i}_{\alpha } } \right|^{\frac{1}{2}} \;{\text{sign}}\left( {\widetilde{i}_{\alpha } } \right) \hfill \\ \begin{array}{*{20}c} {} & {} & {} \\ \end{array} \qquad - \frac{1}{{L_{s} }}\int {k_{2} \;{\text{sign}}\left( {\widetilde{i}_{\alpha } } \right){\text{d}}t + \rho_{1} \left( {\widehat{i}_{\alpha } ,t} \right)} \hfill \\ \end{gathered} \\ \begin{gathered} \frac{{\text{d}}}{{{\text{d}}t}}\widehat{i}_{\beta } = - \frac{1}{{L_{s} }}k_{1} \left| {\widetilde{i}_{\beta } } \right|^{\frac{1}{2}} \;{\text{sign}}\left( {\widetilde{i}_{\beta } } \right) \hfill \\ \begin{array}{*{20}c} {} & {} & {} \\ \end{array} \qquad - \frac{1}{{L_{s} }}\int {k_{2} \;{\text{sign}}\left( {\widetilde{i}_{\beta } } \right){\text{d}}t + \rho_{1} \left( {\widehat{i}_{\beta } ,t} \right)} \hfill \\ \end{gathered} \\ \end{array} } \right. $$
(11)

The disturbance terms \(\rho_{1} \left( {\widehat{i}_{\alpha } ,\;t} \right)\) and \(\rho_{1} \left( {\widehat{i}_{\beta } ,\;t} \right)\) are:

$$ \left\{ {\begin{array}{*{20}c} {\rho_{1} \left( {\widehat{i}_{\alpha } ,t} \right) = - \frac{{R_{s} }}{{L_{s} }}\widehat{i}_{\alpha } + \frac{1}{{L_{s} }}u_{\alpha } } \\ {\rho_{1} \left( {\widehat{i}_{\beta } ,t} \right) = - \frac{{R_{s} }}{{L_{s} }}\widehat{i}_{\beta } + \frac{1}{{L_{s} }}u_{\beta } } \\ \end{array} } \right. $$
(12)

Therefore, the equation of the STASMO can be restated as:

$$ \left\{ {\begin{array}{*{20}c} \begin{gathered} \frac{{\text{d}}}{{{\text{d}}t}}\widehat{i}_{\alpha } = - \frac{{R_{s} }}{{L_{s} }}\widehat{i}_{\alpha } + \frac{1}{{L_{s} }}u_{\alpha } - \frac{1}{{L_{s} }}k_{1} \left| {\widetilde{i}_{\alpha } } \right|^{\frac{1}{2}} \hfill \\ \begin{array}{*{20}c} {} & {} & {} \\ \end{array} \qquad \cdot {\text{sign}}\left( {\widetilde{i}_{\alpha } } \right) - \frac{1}{{L_{s} }}\int {k_{2} \;{\text{sign}}\left( {\widetilde{i}_{\alpha } } \right){\text{d}}t} \hfill \\ \end{gathered} \\ \begin{gathered} \frac{{\text{d}}}{{{\text{d}}t}}\widehat{i}_{\beta } = - \frac{{R_{s} }}{{L_{s} }}\widehat{i}_{\beta } + \frac{1}{{L_{s} }}u_{\beta } - \frac{1}{{L_{s} }}k_{1} \left| {\widetilde{i}_{\beta } } \right|^{\frac{1}{2}} \hfill \\ \begin{array}{*{20}c} {} & {} & {} \\ \end{array} \qquad \cdot {\text{sign}}\;\left( {\widetilde{i}_{\beta } } \right) - \frac{1}{{L_{s} }}\int {k_{2} \;{\text{sign}}\left( {\widetilde{i}_{\beta } } \right){\text{d}}t} \hfill \\ \end{gathered} \\ \end{array} } \right. $$
(13)

The current error equation can be obtained by subtracting (3) from (13):

$$ \left\{ {\begin{array}{*{20}c} \begin{gathered} \frac{{\text{d}}}{{{\text{d}}t}}\widetilde{i}_{\alpha } = - \frac{{R_{s} }}{{L_{s} }}\widetilde{i}_{\alpha } + \frac{1}{{L_{s} }}\left( { - k_{1} \left| {\widetilde{i}_{\alpha } } \right|^{\frac{1}{2}} {\text{sign}}\;\left( {\widetilde{i}_{\alpha } } \right)} \right. \hfill \\ \left. {\begin{array}{*{20}c} {} & {} & {} \\ \end{array} \qquad - \int {k_{2} sign\left( {\widetilde{i}_{\alpha } } \right){\text{d}}t + E_{\alpha } } } \right) \hfill \\ \end{gathered} \\ \begin{gathered} \frac{{\text{d}}}{{{\text{d}}t}}\widetilde{i}_{\beta } = - \frac{{R_{s} }}{{L_{s} }}\widetilde{i}_{\beta } + \frac{1}{{L_{s} }}\left( { - k_{1} \left| {\widetilde{i}_{\beta } } \right|^{\frac{1}{2}} {\text{sign}}\left( {\widetilde{i}_{\beta } } \right)} \right. \hfill \\ \left. {\begin{array}{*{20}c} {} & {} & {} \\ \end{array} \qquad - \int {k_{2} {\text{sign}}\left( {\widetilde{i}_{\beta } } \right){\text{d}}t + E_{\beta } } } \right) \hfill \\ \end{gathered} \\ \end{array} } \right. $$
(14)

The sliding surface is defined as:

$$ \left\{ {\begin{array}{*{20}c} {s_{\alpha } = \widetilde{i}_{\alpha } = \widehat{i}_{\alpha } - i_{\alpha } } \\ {s_{\beta } = \widetilde{i}_{\beta } = \widehat{i}_{\beta } - i_{\beta } } \\ \end{array} } \right. $$
(15)

According to the definition of SMO, its switching function is a discontinuous term with high-frequency switching characteristics. In this paper, a sigmoid function with smooth continuous properties is used instead of the sign function as the switching function. This function has a good suppression effect on chattering. Its expression is:

$$ {\text{sigmoid}}\;(s) = \frac{2}{{1 + e^{{ - {\text{as}}}} }} - 1 $$
(16)

where \(a\) is a positive constant. Figure 2 is the sigmoid function curve. The sigmoid function is a continuous switching function, which can effectively suppress chattering. The value of parameter \(a\) determines the convergence rate of the function curve. When the value of \(a\) is small, the convergence speed of the curve is slow. Although the chattering of the system is suppressed, the tracking performance of the system to the sliding mode surface will be deteriorated, and the system motion will deviate from the sliding mode surface. This will affect the performance of the control system. When the value of \(a\) is large, although the tracking performance of the system to the sliding surface can be improved, the chattering suppression effect will be worse. Therefore, it is necessary to select the value of \(a\) reasonably to effectively suppress chattering while ensuring the tracking performance of the sliding surface.

Fig. 2
figure 2

The sigmoid function curve when \(a\) takes different values

Full size image

When the state variable of the STASMO reaches the sliding mode surface, the current estimation error is approximately zero (\(\widetilde{i}_{\alpha } = 0,\widetilde{i}_{\beta } = 0\)). According to the equivalent control principle of sliding mode control, the back-EMF information estimated by the STASMO can be obtained:

$$ \left\{ {\begin{array}{*{20}c} \begin{gathered} E_{\alpha } = k_{1} \left| {\widetilde{i}_{\alpha } } \right|^{\frac{1}{2}} {\text{sigmoid}}\;\left( {\widetilde{i}_{\alpha } } \right) \hfill \\ \begin{array}{*{20}c} {} & {} & {} \\ \end{array} \quad + \int {k_{2} {\text{sigmoid}}\left( {\widetilde{i}_{\alpha } } \right){\text{d}}t} \hfill \\ \end{gathered} \\ \begin{gathered} E_{\beta } = k_{1} \left| {\widetilde{i}_{\beta } } \right|^{\frac{1}{2}} {\text{sigmoid}}\left( {\widetilde{i}_{\beta } } \right) \hfill \\ \begin{array}{*{20}c} {} & {} & {} \\ \end{array} \quad + \int {k_{2} {\text{sigmoid}}\left( {\widetilde{i}_{\beta } } \right){\text{d}}t} \hfill \\ \end{gathered} \\ \end{array} } \right. $$
(17)

where the linear term \(k_{1} \left| {\widetilde{i}_{\alpha } } \right|^{\frac{1}{2}} {\text{sigmoid}}\left( {\widetilde{i}_{\alpha } } \right)\) determines the convergence speed of the STASMO. The integral term \(\int {k_{2} {\text{sigmoid}}\left( {\widetilde{i}_{\alpha } } \right){\text{d}}t}\) is related to the suppression of the chattering of the STASMO. Generally, the gain \(k_{2}\) of the integral term is larger in order to suppress the high-frequency chattering introduced by the switching function.

4.3 Adaptive STASMO

The super-twisting algorithm can effectively reduce the chattering of the first order SMO, thereby reducing the use of low-pass filters. In order to further weaken the chattering of the system, observe the back-EMF of the system more accurately, and improve the observation accuracy of the observer, an adaptive STASMO is proposed in this paper. It is known that in the STASMO, the main function of the high-order integral term is to filter out the harmonics and noise in the system, thereby making the curve smoother. In this paper, an online adaptive adjustment coefficient is added in front of the high-order integral term. The online adaptive adjustment coefficient is designed as follows:

$$ \eta = \frac{{\hat{\omega }_{e} }}{{\omega_{{{\text{ref}}}} }} $$
(18)

where \(\hat{\omega }_{e}\) is the estimated speed. \(\omega_{{{\text{ref}}}}\) is the reference speed. The back-EMF of the adaptive STASMO is equivalently expressed as:

$$ \left\{ {\begin{array}{*{20}c} \begin{gathered} E_{\alpha } = k_{1} \left| {\widetilde{i}_{\alpha } } \right|^{\frac{1}{2}} {\text{sigmoid}}\;\left( {\widetilde{i}_{\alpha } } \right) \hfill \\ \begin{array}{*{20}c} {} & {} & {} \\ \end{array} \quad+ \eta \int {k_{2} {\text{sigmoid}}\left( {\widetilde{i}_{\alpha } } \right){\text{d}}t} \hfill \\ \end{gathered} \\ \begin{gathered} E_{\beta } = k_{1} \left| {\widetilde{i}_{\beta } } \right|^{\frac{1}{2}} {\text{sigmoid}}\left( {\widetilde{i}_{\beta } } \right) \hfill \\ \begin{array}{*{20}c} {} & {} & {} \\ \end{array} \quad + \eta \int {k_{2} {\text{sigmoid}}\left( {\widetilde{i}_{\beta } } \right){\text{d}}t} \hfill \\ \end{gathered} \\ \end{array} } \right. $$
(19)

When the motor is in the acceleration phase, the speed of the motor rises rapidly. At this time, the high-frequency noise in the system is less, the value of \(\eta\) is small, and the effect of the higher-order integral term is small. When the motor reaches the rated speed, the high-frequency switching after the system reaches the sliding mode surface will increase the chattering. The value of \(\eta\) increases, and the role of the higher-order integral term becomes larger, thereby reducing the chattering. Therefore, the adaptive STASMO can further suppress the chattering of the system and improve the observation accuracy.

In most cases, the voltage drop across the motor stator resistance is negligible. Therefore, (12) can be simplified to:

$$ \rho_{1} (i) \approx \frac{u}{{L_{s} }} $$
(20)

There is \(u \approx \omega_{e} \varphi_{f}\) when the system is moving on a sliding surface. Therefore, (9) can be rewritten as:

$$ \left| {\rho_{1} (i)} \right| \approx \left| {\frac{u}{{L_{s} }}} \right| \approx \left| {\frac{{\omega_{e} \psi_{f} }}{{L_{s} }}} \right| \le \delta_{1} \left| {\widehat{i}} \right|^{\frac{1}{2}} $$
(21)

Using \(\lambda \omega_{e}\) instead of \(\delta_{1}\), (21) can be rewritten as:

$$ \left| {\rho_{1} (i)} \right| \approx \left| {\frac{u}{{L_{s} }}} \right| \approx \left| {\frac{{\omega_{e} \psi_{f} }}{{L_{s} }}} \right| \le \lambda \omega_{e} \left| {\widehat{i}} \right|^{\frac{1}{2}} $$
(22)

When the system state reaches and moves on the sliding surface, \(\left| {\widehat{i}} \right|^{\frac{1}{2}}\) is within a certain range, and there is \(\omega_{{{\text{ref}}}} \approx \omega_{e}\). Therefore, a large enough \(\lambda\) can be chosen such that (22) is satisfied.

Substituting \(\delta_{1} = \lambda \omega_{e}\) and \(\omega_{{{\text{ref}}}} \approx \omega_{e}\) into (10), (10) can be rewritten as:

$$ \left\{ {\begin{array}{*{20}c} {k_{1} > 2\lambda \omega_{e} \approx 2\lambda \omega_{{{\text{ref}}}} \begin{array}{*{20}c} {} & {} & {} \\ \end{array} } \\ \begin{gathered} k_{2} > k_{1} \frac{{5\lambda \omega_{e} k_{1} + 4\lambda^{2} \omega_{e}^{2} }}{{2(k_{1} - 2\lambda \omega_{e} )}} \hfill \\ \begin{array}{*{20}c} {} & {} \\ \end{array} \approx k_{1} \frac{{5\lambda \omega_{{{\text{ref}}}} k_{1} + 4\lambda^{2} \omega_{{{\text{ref}}}}^{2} }}{{2(k_{1} - 2\lambda \omega_{{{\text{ref}}}} )}} \hfill \\ \end{gathered} \\ \end{array} } \right. $$
(23)

Therefore, (22) and (23) can be satisfied by choosing an appropriate value of \(\lambda\) to ensure the stability of the adaptive STASMO.

4.4 Rotor Position Estimation Based on Normalized PLL

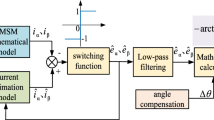
In this paper, a normalized PLL is used to extract the rotor position and speed information from the back-EMF signal. The normalization process is added to the traditional PLL, which makes the parameters of the system more optimized, and improves the speed of tracking the speed and rotor position. The principle diagram of the normalized PLL is shown in Fig. 3.

Fig. 3
figure 3

Schematic diagram of a normalized PLL

Full size image

In the PLL without normalization processing, the position error signal is:

$$ \begin{gathered} \varepsilon = - \hat{E}_{\alpha } \cos \;\hat{\theta }_{e} - \hat{E}_{\beta } \sin \;\hat{\theta }_{e} \hfill \\ = E\sin \;\theta_{e} \cos \;\hat{\theta }_{e} - E\cos \;\theta_{e} \sin \;\hat{\theta }_{e} \hfill \\ = E\sin \left( {\theta_{e} - \hat{\theta }_{e} } \right) \hfill \\ \end{gathered} $$
(24)

The transfer function of the traditional PLL is:

$$ G(s) = \frac{{\hat{\theta }_{e} }}{{\theta_{e} }} = \frac{{Ek_{p} s + Ek_{i} }}{{s^{2} + Ek_{p} s + Ek_{i} }} $$
(25)

When the observer is close to the steady state, \(\theta_{e} - \widehat{\theta }_{e}\) is very small, and \(\sin (\theta_{e} - \widehat{\theta }_{e} )\) and \(\theta_{e} - \widehat{\theta }_{e}\) are approximately equal. At this time, the normalization processing method is adopted in the system, and the signal of the position error can be approximated as:

$$ \varepsilon_{1} \approx \theta_{e} - \widehat{\theta }_{e} $$
(26)

The transfer function of the normalized PLL is:

$$ G(s) = \frac{{\widehat{\theta }_{e} }}{{\theta_{e} }} = \frac{{k_{p} s + k_{i} }}{{s^{2} + k_{p} s + k_{i} }} $$
(27)

Figure 4 is a schematic diagram of an adaptive STASMO.

Fig. 4
figure 4

Schematic diagram of the adaptive STASMO

Full size image

5 Online Estimation of Motor Parameters

Although the SMO has strong robustness, the change of the stator resistance and stator inductance caused by the temperature increase during the long-term operation of the motor will also have a certain impact on the estimation accuracy of the SMO. In order to eliminate the observation error caused by the mismatch between the actual parameters and the set parameters, an online estimation method of stator resistance and stator inductance is proposed in this paper. The stator resistance and stator inductance are estimated online when the motor is running, and the stator resistance and stator inductance are identified and fed back to the system to improve the observation accuracy of the SMO.

5.1 Online Estimation of Stator Resistance

In order to estimate the stator resistance online, ignoring the influence of the change of stator inductance, the error equation of the stator current is rewritten as:

$$ \left\{ {\begin{array}{*{20}c} \begin{gathered} \frac{{\text{d}}}{{{\text{d}}t}}\widetilde{i}_{\alpha } = - \frac{1}{{L_{s} }}\left( {\hat{R}_{s} - R_{s} } \right)\widehat{i}_{\alpha } - \frac{{R_{s} }}{{L_{s} }}\left( {\widehat{i}_{\alpha } - i_{\alpha } } \right) \hfill \\ \begin{array}{*{20}c} {} & {} & {} \\ \end{array} \quad- \frac{{\nu_{\alpha } }}{{L_{s} }} + \frac{{E_{\alpha } }}{{L_{s} }} \hfill \\ \end{gathered} \\ \begin{gathered} \frac{{\text{d}}}{{{\text{d}}t}}\widetilde{i}_{\beta } = - \frac{1}{{L_{s} }}\left( {\hat{R}_{s} - R_{s} } \right)\widehat{i}_{\beta } - \frac{{R_{s} }}{{L_{s} }}\left( {\widehat{i}_{\beta } - i_{\beta } } \right) \hfill \\ \begin{array}{*{20}c} {} & {} & {} \\ \end{array} \quad - \frac{{\nu_{\beta } }}{{L_{s} }} + \frac{{E_{\beta } }}{{L_{s} }} \hfill \\ \end{gathered} \\ \end{array} } \right. $$
(28)

where \(\hat{R}_{s}\) is the estimated value of the stator resistance.

$$ \left\{ {\begin{array}{*{20}c} \begin{gathered} \nu_{\alpha } = k_{1} \left| {\widetilde{i}_{\alpha } } \right|^{\frac{1}{2}} {\text{sigmoid}}\left( {\widetilde{i}_{\alpha } } \right) \hfill \\ \begin{array}{*{20}c} {} & {} & {} \\ \end{array} \quad + \eta \int {k_{2} {\text{sigmoid}}\left( {\widetilde{i}_{\alpha } } \right){\text{d}}t} \hfill \\ \end{gathered} \\ \begin{gathered} \hfill \nu_{\beta } = k_{1} \left| {\widetilde{i}_{\beta } } \right|^{\frac{1}{2}} {\text{sigmoid}}\left( {\widetilde{i}_{\beta } } \right) \\ \hfill \begin{array}{*{20}c} {} & {} & {} \\ \end{array} \quad + \eta \int {k_{2} {\text{sigmoid}}\left( {\widetilde{i}_{\beta } } \right){\text{d}}t} \\ \end{gathered} \\ \end{array} } \right. $$
(29)

The sliding surface is:

$$ S = \left[ {\begin{array}{*{20}c} {s_{\alpha } } \\ {s_{\beta } } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\widetilde{i}_{\alpha } } \\ {\widetilde{i}_{\beta } } \\ \end{array} } \right] $$
(30)

The Lyapunov function is constructed as:

$$ V = \frac{1}{2}S^{T} S + \frac{1}{2}\left( {\hat{R}_{s} - R_{s} } \right)^{2} $$
(31)

The derivative of (31) with respect to time is:

$$ \dot{V} = S^{T} \dot{S} + \left( {\hat{R}_{s} - R_{s} } \right)\dot{\hat{R}}_{s} $$
(32)

The stability condition of the SMO is \(V < 0\), namely:

$$ \begin{gathered} \dot{V} = \left[ {\begin{array}{*{20}c} {\widetilde{i}_{\alpha } } & {\widetilde{i}_{\beta } } \\ \end{array} } \right] \hfill \\ \left[ {\begin{array}{*{20}c} { - \frac{1}{{L_{s} }}\left( {\hat{R}_{s} - R_{s} } \right)\widehat{i}_{\alpha } - \frac{{R_{s} }}{{L_{s} }}\left( {\widehat{i}_{\alpha } - i_{\alpha } } \right) - \frac{{\nu_{\alpha } }}{{L_{s} }} + \frac{{E_{\alpha } }}{{L_{s} }}} \\ { - \frac{1}{{L_{s} }}\left( {\hat{R}_{s} - R_{s} } \right)\widehat{i}_{\beta } - \frac{{R_{s} }}{{L_{s} }}\left( {\widehat{i}_{\beta } - i_{\beta } } \right) - \frac{{\nu_{\beta } }}{{L_{s} }} + \frac{{E_{\beta } }}{{L_{s} }}} \\ \end{array} } \right] \hfill \\ \qquad+ \left( {\hat{R}_{s} - R_{s} } \right)\dot{\hat{R}}_{s} < 0 \hfill \\ \end{gathered} $$
(33)

(33) can be decomposed into the following two equations:

$$ \begin{gathered} \left[ {\begin{array}{*{20}c} {\widetilde{i}_{\alpha } } & {\widetilde{i}_{\beta } } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} { - \frac{1}{{L_{s} }}\left( {\hat{R}_{s} - R_{s} } \right)\widehat{i}_{\alpha } } \\ { - \frac{1}{{L_{s} }}\left( {\hat{R}_{s} - R_{s} } \right)\widehat{i}_{\beta } } \\ \end{array} } \right] \hfill \\ \begin{array}{*{20}c} {} & {} & {} \\ \end{array} + \left( {\hat{R}_{s} - R_{s} } \right)\dot{\hat{R}}_{s} = 0 \hfill \\ \end{gathered} $$
(34)
$$ \left[ {\begin{array}{*{20}c} {\widetilde{i}_{\alpha } } & {\widetilde{i}} \\ \end{array}_{\beta } } \right]\left[ {\begin{array}{*{20}c} { - \frac{{R_{s} }}{{L_{s} }}\widetilde{i}_{\alpha } - \frac{{\nu_{\alpha } }}{{L_{s} }} + \frac{{E_{\alpha } }}{{L_{s} }}} \\ { - \frac{{R_{s} }}{{L_{s} }}\widetilde{i}_{\beta } - \frac{{\nu_{\beta } }}{{L_{s} }} + \frac{{E_{\beta } }}{{L_{s} }}} \\ \end{array} } \right] < 0 $$
(35)

The estimated equation of stator resistance obtained from (34) is:

$$ \hat{R}_{s} = \int {\frac{1}{{L_{s} }}\left( {\widetilde{i}_{\alpha } \widehat{i}_{\alpha } + \widetilde{i}_{\beta } \widehat{i}_{\beta } } \right)} $$
(36)

5.2 Online Estimation of Stator Inductance

In order to estimate the stator inductance online, ignoring the influence of the stator resistance change, the error equation of the stator current is rewritten as:

$$ \left\{ {\begin{array}{*{20}c} \begin{gathered} \frac{{\text{d}}}{{{\text{d}}t}}\widetilde{i}_{\alpha } = - R_{s} \left( {\frac{1}{{\hat{L}_{s} }} - \frac{1}{{L_{s} }}} \right)\widehat{i}_{\alpha } - \frac{{R_{s} }}{{L_{s} }}\widetilde{i}_{\alpha } \hfill \\ \begin{array}{*{20}c} {} & {} & {} \\ \end{array} + \left( {\frac{1}{{\hat{L}_{s} }} - \frac{1}{{L_{s} }}} \right)u_{\alpha } - \frac{{\nu_{\alpha } }}{{\hat{L}_{s} }} + \frac{{E_{\alpha } }}{{L_{s} }} \hfill \\ \end{gathered} \\ \begin{gathered} \frac{{\text{d}}}{{{\text{d}}t}}\widetilde{i}_{\beta } = - R_{s} \left( {\frac{1}{{\hat{L}_{s} }} - \frac{1}{{L_{s} }}} \right)\widehat{i}_{\beta } - \frac{{R_{s} }}{{L_{s} }}\widetilde{i}_{\beta } \hfill \\ \begin{array}{*{20}c} {} & {} & {} \\ \end{array} + \left( {\frac{1}{{\hat{L}_{s} }} - \frac{1}{{L_{s} }}} \right)u_{\beta } - \frac{{\nu_{\beta } }}{{\hat{L}_{s} }} + \frac{{E_{\beta } }}{{L_{s} }} \hfill \\ \end{gathered} \\ \end{array} } \right. $$
(37)

where \(\widehat{L}_{s}\) is the estimated value of the stator inductance.

The Lyapunov function is constructed as:

$$ V = \frac{1}{2}S^{T} S + \frac{1}{2}\left( {\frac{1}{{\hat{L}_{s} }} - \frac{1}{{L_{s} }}} \right)^{2} \hat{L}_{s} $$
(38)

The derivative of (38) with respect to time is:

$$ \dot{V} = S^{T} \dot{S} - \dot{\hat{L}}_{s} \left( {\frac{1}{{\hat{L}_{s} }} - \frac{1}{{L_{s} }}} \right) + \left( {\frac{{L_{s} - \hat{L}_{s} }}{{\hat{L}_{s} L_{s} }}} \right)^{2} \hat{L}_{s} \dot{\hat{L}}_{s} $$
(39)

where \((L_{s} - \widehat{L}_{s} )^{2}\) is a second-order small quantity, which can be ignored, we can get:

$$ \dot{V} = S^{T} \dot{S} - \dot{\hat{L}}_{s} \left( {\frac{1}{{\hat{L}_{s} }} - \frac{1}{{L_{s} }}} \right) $$
(40)

The stability condition of the SMO is \(\dot{V} < 0\), namely:

$$ \begin{gathered} \dot{V} = \left[ {\begin{array}{*{20}c} {\widetilde{i}_{\alpha } } & {\widetilde{i}_{\beta } } \\ \end{array} } \right] \hfill \\ \left[ {\begin{array}{*{20}c} \begin{gathered} - R_{s} \left( {\frac{1}{{\hat{L}_{s} }} - \frac{1}{{L_{s} }}} \right)\widehat{i}_{\alpha } - \frac{{R_{s} }}{{L_{s} }}\widetilde{i}_{\alpha } - \left( {\frac{1}{{\hat{L}_{s} }} - \frac{1}{{L_{s} }}} \right) \hfill \\ \begin{array}{*{20}c} {} & {} & {} & {} \\ \end{array} \begin{array}{*{20}c} {} & {} \\ \end{array} - \frac{{\nu_{\alpha } }}{{L_{s} }} + \frac{{E_{\alpha } }}{{L_{s} }} + \left( {\frac{1}{{\hat{L}_{s} }} - \frac{1}{{L_{s} }}} \right)u_{\alpha } \hfill \\ \end{gathered} \\ \begin{gathered} - R_{s} \left( {\frac{1}{{\hat{L}_{s} }} - \frac{1}{{L_{s} }}} \right)\widehat{i}_{\beta } - \frac{{R_{s} }}{{L_{s} }}\widetilde{i}_{\beta } - \left( {\frac{1}{{\hat{L}_{s} }} - \frac{1}{{L_{s} }}} \right) \hfill \\ \begin{array}{*{20}c} {} & {} & {} & {} \\ \end{array} \begin{array}{*{20}c} {} & {} \\ \end{array} - \frac{{\nu_{\beta } }}{{L_{s} }} + \frac{{E_{\beta } }}{{L_{s} }} + \left( {\frac{1}{{\hat{L}_{s} }} - \frac{1}{{L_{s} }}} \right)u_{\beta } \hfill \\ \end{gathered} \\ \end{array} } \right] \hfill \\ - \dot{\hat{L}}_{s} \left( {\frac{1}{{\hat{L}_{s} }} - \frac{1}{{L_{s} }}} \right) < 0 \hfill \\ \end{gathered} $$
(41)

(41) can be decomposed into the following two equations:

$$ \left[ {\begin{array}{*{20}c} {\widetilde{i}_{\alpha } } & {\widetilde{i}_{\beta } } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} { - \frac{{R_{s} }}{{L_{s} }}\widetilde{i}_{\alpha } - \frac{{\nu_{\alpha } }}{{L_{s} }} + \frac{{E_{\alpha } }}{{L_{s} }}} \\ { - \frac{{R_{s} }}{{L_{s} }}\widetilde{i}_{\beta } - \frac{{\nu_{\beta } }}{{L_{s} }} + \frac{{E_{\beta } }}{{L_{s} }}} \\ \end{array} } \right] < 0 $$
(42)
$$ \begin{gathered} \left[ {\begin{array}{*{20}c} {\widetilde{i}_{\alpha } } & {\widetilde{i}_{\beta } } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} \begin{gathered} - R_{s} \left( {\frac{1}{{\hat{L}_{s} }} - \frac{1}{{L_{s} }}} \right)\widehat{i}_{\alpha } \hfill \\ \begin{array}{*{20}c} {} & {} \\ \end{array} + \left( {\frac{1}{{\hat{L}_{s} }} - \frac{1}{{L_{s} }}} \right)u_{\alpha } - \left( {\frac{1}{{\hat{L}_{s} }} - \frac{1}{{L_{s} }}} \right)\nu_{\alpha } \hfill \\ \end{gathered} \\ \begin{gathered} - R_{s} \left( {\frac{1}{{\hat{L}_{s} }} - \frac{1}{{L_{s} }}} \right)\widehat{i}_{\beta } \hfill \\ \begin{array}{*{20}c} {} & {} \\ \end{array} + \left( {\frac{1}{{\hat{L}_{s} }} - \frac{1}{{L_{s} }}} \right)u_{\beta } - \left( {\frac{1}{{\hat{L}_{s} }} - \frac{1}{{L_{s} }}} \right)\nu_{\beta } \hfill \\ \end{gathered} \\ \end{array} } \right] \hfill \\ \begin{array}{*{20}c} {} & {} & {} & {} \\ \end{array} - \left( {\frac{1}{{\hat{L}_{s} }} - \frac{1}{{L_{s} }}} \right)\dot{\hat{L}}_{s} = 0 \hfill \\ \end{gathered} $$
(43)

The estimation equation of stator inductance obtained from (43) is:

$$ \hat{L}_{s} = \int {\left[ \begin{gathered} \widetilde{i}_{\alpha } \left( {u_{\alpha } - \nu_{\alpha } - R_{s} \widehat{i}_{\alpha } } \right) \hfill \\ \begin{array}{*{20}c} {} & {} & {} & {} \\ \end{array} + \widetilde{i}_{\beta } \left( {u_{\beta } - \nu_{\beta } - R_{s} \widehat{i}_{\beta } } \right) \hfill \\ \end{gathered} \right]} $$
(44)

Figure 5 is a block diagram of an adaptive STASMO with online stator resistance and stator inductance estimation.

Fig. 5
figure 5

Block diagram of an adaptive STASMO with online stator resistance and stator inductance estimation

Full size image

6 Simulations and Experiments

6.1 Analysis of Simulation Results

In order to verify the effectiveness of the sensorless control method of PMSM proposed in this paper, a simulation model is built in Matlab/Simulink for simulation. The overall control block diagram of the system is shown in Fig. 6. Table 1 and Table 2 are the main parameters of the PMSM and the parameters in the adaptive STASMO, respectively. The control system proposed in this paper includes three PI controllers. The speed loop has a PI controller with parameters set to kp = 100 and ki = 20. The current loop has two PI controllers with parameters set to kp = 17 and ki = 5800. The kp and ki in Table 2 are the PI parameters in the normalized PLL. The parameters of the speed loop and current loop PI controllers are first tuned through typical II and I systems of automatic control theory, and then, the appropriate PI parameters are obtained through fine tuning.

Fig. 6
figure 6

The overall control block diagram of the system

Full size image
Table 1 The main parameters of PMSM
Full size table
Table 2 Parameters in the adaptive STASMO
Full size table

In Figures 7, 8, 9, the simulation results of the traditional SMO, the STASMO, and the adaptive STASMO are presented. From the simulation results, it can be seen that the rotation speed error of the traditional SMO is between − 7.2 rpm and 10.5 rpm, and the maximum steady-state error of the rotor position is 0.04 rad. The rotor speed error of the STASMO is between − 2.5 rpm and 1.3 rpm, and the maximum steady-state error of the rotor position is 0.023 rad. The rotor speed error of the adaptive STASMO is between − 0.9 rpm and 1 rpm, and the maximum steady-state error of the rotor position is 0.02 rad. The rotor speed and rotor position error of the STASMO are much smaller than that of the traditional SMO. The addition of the super-twisting algorithm reduces the system chattering and makes the estimated value closer to the actual value. The adaptive STASMO further reduces the error of rotor speed and rotor position, which proves that the adaptive STASMO has obvious weakening effect on chattering and has better observation performance.

Fig. 7
figure 7

The simulation results of the traditional SMO. a Rotor speed. b Rotor speed error. c Rotor position. d Rotor position error

Full size image
Fig. 8
figure 8

The simulation results of the STASMO. a Rotor speed. b Rotor speed error. c Rotor position. d Rotor position error

Full size image
Fig. 9
figure 9

Simulation results of adaptive STASMO. a Rotor speed. b Rotor speed error. c Rotor position. d Rotor position error

Full size image

Figures 10 and 11 show the simulation results of the traditional SMO and the adaptive STASMO when the load changes. The motor is started under no-load conditions, and a load of 6 N·m is suddenly added at 0.5 s. Analyzing the simulation results, it can be obtained that the adaptive STASMO has smaller speed fluctuations when the load is changed than the traditional SMO, and the speed can converge to the actual value faster after the change. Therefore, the adaptive STASMO has stronger ability to resist external interference.

Fig. 10
figure 10

The simulation results of the traditional SMO when the load changes. a Rotor speed. b Rotor speed error

Full size image
Fig. 11
figure 11

Simulation results of the adaptive STASMO when the load changes. a Rotor speed. b Rotor speed error

Full size image

Figure 12 is a comparison of the simulation results of the adaptive STASMO with online stator resistance estimation and the adaptive STASMO without online estimation of stator resistance. The stator resistance of the motor increases by 30% at 0.4 s. From Fig. 12a, it can be seen that the stator resistance online estimation method can effectively track the change of the stator resistance. Therefore, when the stator resistance changes in Fig. 12b, the estimated rotor speed will also change. However, due to the online stator resistance estimation method, the estimated rotor speed can be quickly restored to the desired value. In Fig. 12c, since there is no online stator resistance estimation method, the estimated rotor speed will have a large error after the stator resistance changes.

Fig. 12
figure 12

Simulation results when the stator resistance changes. a Estimation results of stator resistance. b The rotor speed estimation results of the adaptive STASMO with online stator resistance estimation. c The rotor speed estimation results of the adaptive STASMO without online stator resistance estimation

Full size image

Figure 13 is a comparison of the simulation results of the adaptive STASMO with online stator inductance estimation and the adaptive STASMO without online estimation of stator inductance. The stator inductance of the motor increases by 30% at 0.4 s. From Fig. 13a, it can be seen that the stator inductance online estimation method can effectively track the change of the stator inductance. Therefore, when the stator inductance changes in Fig. 13b, the estimated rotor speed will also change. However, due to the online stator inductance estimation method, the estimated rotor speed can be quickly restored to the desired value. In Fig. 13c, since there is no online stator inductance estimation method, the estimated rotor speed will have a large error after the stator inductance changes.

Fig. 13
figure 13

Simulation results when the stator inductance changes. a Estimation results of stator inductance. b The rotor speed estimation results of the adaptive STASMO with online stator inductance estimation. c The rotor speed estimation results of the adaptive STASMO without online stator inductance estimation

Full size image

6.2 Analysis of Experimental Results

In order to verify the effectiveness of the sensorless algorithm for PMSM proposed in this paper, an experimental platform as shown in Fig. 14 was built on the basis of the vector control scheme. The designed algorithm is written into a software program, and the corresponding hardware is designed. Experiments are used to verify the effectiveness of the proposed SMO algorithm. The vector control scheme in this paper adopts \(i_{d} = 0\) control strategy. The space vector pulse width modulation technique is used to make the stator current a sinusoidal signal, and it is assumed that the voltage source inverter has no switching delay and has good linearity. The experiment was carried out on a surface mounted PMSM with a rated power of 2 kW. The parameters of the motor are shown in Table 1. The magnetic powder brake is used to provide the load needed for the experiment. The experimental motor is driven by the TMS320F28335 processor in TI's C2000 series to realize the sensorless control algorithm. A speed torque sensor is connected to the coupling between the motor and the magnetic powder brake. The sensor data is collected to the host computer by the collection card. The current and voltage are measured by a 12-bit A/D converter. The experimental motor control system consists of two parts: a control module and a drive module. The control module selects TMS320F28335 for control. The driver chip selected by the driver module is IR2110. The experiment and simulation are carried out under the same conditions. The switching frequency is 10 kHz. The sampling period is 100 μs.

Fig. 14
figure 14

Experimental platform

Full size image

Figures 15 and 16 are the experimental results of the traditional SMO and the proposed adaptive STASMO for rotor speed and rotor position tracking, respectively. The motor starts without load, and the reference speed is set to 1000 rpm. It can be seen from Fig. 15 that although the traditional SMO can track the rotor speed and rotor position, it will produce larger observation errors. Comparing Figs 15 and 16, it can be clearly seen that the proposed adaptive STASMO greatly reduces the rotor speed and rotor position errors. Therefore, the proposed adaptive STASMO can suppress chattering well and has better observation performance of rotor speed and rotor position. Figures 17 and 18 are the experimental results of the traditional SMO and the proposed adaptive STASMO when the load is changed. The motor starts without load, and a load of 6 N·m is suddenly added at 2.5 s. It can be seen from the figure that the rotor speed change of the adaptive STASMO is smaller when the load changes, and the rotor speed can be restored to the actual value faster. Therefore, the adaptive STASMO has better robustness.

Fig. 15
figure 15

Experimental results of the traditional SMO. a Rotor speed. b Rotor speed error. c Rotor position. d Rotor position error

Full size image
Fig. 16
figure 16

Experimental results of the adaptive STASMO. a Rotor speed. b Rotor speed error. c Rotor position. d Rotor position error

Full size image
Fig. 17
figure 17

Experimental results of the traditional SMO when the load changes. a Rotor speed. b Rotor speed error

Full size image
Fig. 18
figure 18

Experimental results of the adaptive STASMO when the load changes. a Rotor speed. b Rotor speed error

Full size image

Figure 19 shows the experimental results of the traditional SMO and the adaptive STASMO at medium speed. The motor runs smoothly at a speed of 500 rpm. The load of 6 N·m is suddenly added at 2.5 s. It can be seen from Fig. 19 that the adaptive STASMO can effectively suppress chattering at medium speed. When sudden load is applied, its speed fluctuation is small, and the speed curve can restore stability faster. Therefore, the proposed adaptive STASMO still has good observation performance at medium speed.

Fig. 19
figure 19

Experimental results of the traditional SMO and the adaptive STASMO at medium speed. a The traditional SMO. b The adaptive STASMO

Full size image

Long-term operation of the motor can lead to an increase in its temperature, causing changes in stator resistance and stator inductance, which in turn can affect the control of the motor. In order to overcome the impact of changes in motor parameters on the control system, an online estimation method for stator resistance and stator inductance is proposed. The stator resistance and stator inductance are estimated online in real time, and the estimated values are fed back to the control system to improve the performance of the control system. However, in the actual operation of motor, it is difficult to demonstrate the effectiveness of the proposed online estimation method for stator resistance and stator inductance through experiments due to factors such as noise and sampling circuit accuracy. Therefore, in this paper, the effectiveness of the online stator resistance and stator inductance estimation method is verified by simulations, as shown in Figs 12 and 13. In this paper, there is no experiment on the change of motor parameters caused by long-term operation of motor. The experimental part of this paper verifies the observation performance of the proposed adaptive STASMO.

7 Conclusion

In this paper, a sensorless control method for an adaptive STASMO is proposed. Combining the super-twisting algorithm and the SMO algorithm, a STASMO is proposed. An adaptive adjustment coefficient related to the rotational speed is added to the high-order integral term of the STASMO. When the chattering intensifies, the adaptive coefficient increases. When the chattering increases, the adaptive coefficient increases. It will cause the effect of the higher-order integral term to become larger, thereby reducing the chattering. Aiming at the problem that the stator resistance and stator inductance change due to the temperature rise when the motor runs for a long time, an online estimation method of stator resistance and stator inductance is proposed in this paper. Through this method, the values of stator resistance and stator inductance are fed back in real time, which reduces the influence of system parameter error on control performance and improves the overall performance of the system to a large extent. A normalized PLL is used to extract the speed and rotor position information, which avoids the use of a low-pass filter and a phase delay compensation module when obtaining the speed and rotor position with the arctangent function. Simulation and experimental results show that the proposed sensorless control method can weaken the chattering of the system, reduce the observation error, and suppress the adverse effects of motor parameter changes on the observation performance. Compared with the traditional sensorless control method, the method proposed in this paper has better observation performance, is easier to implement in practical systems, and has certain practical value.