Robust Solution for Second-Order Systems Using Displacement–Acceleration Feedback

Abstract

This paper addresses the robust and minimum norm controller design for matrix second-order linear systems by means of combined displacement and acceleration feedback. First, the necessary conditions that ensure solvability are presented. Then, the parametric expressions of gain controller and eigenvector matrix are formulated on the basis of a set of free parameters. The proposed solution simultaneously makes the resulting closed-loop system numerically robust and obtains gain controllers with minimum norms. Also, the solution is general and can be applied when mass matrices are either singular or nonsingular. This is promising for better applicability in many practical applications. Finally, two examples are provided to illustrate the effectiveness of the proposed control strategy.

1 Introduction

This note deals with the following class of second-order linear systems:

$$ \left\{ {\begin{array}{*{20}l} {M\ddot{x}\left( t \right) + D\dot{x}\left( t \right) + Kx\left( t \right) = Cu\left( t \right),} \hfill \\ {x\left( 0 \right) = x_{0} , \dot{x}\left( 0 \right) = \dot{x}_{0} } \hfill \\ \end{array} } \right. $$

(1)

using the displacement–acceleration feedback controller

$$ u\left( t \right) = - F_{d} x\left( t \right) - F_{a} \ddot{x}\left( t \right) $$

(2)

where $M, D, K \in {\mathbb{R}}^{n \times n} \,{\text{and}}\,C \in {\mathbb{R}}^{n \times r}$ are the mass, damping, stiffness and control matrices, respectively. Here, the vectors $x\left( t \right), \dot{x}\left( t \right), \ddot{x}\left( t \right) \in {\mathbb{R}}^{n} \,{\text{and}}\,u\left( t \right) \in {\mathbb{R}}^{r}$ are the displacement, velocity, acceleration and control input vectors, respectively. Furthermore, $F_{a} , F_{d} \in {\mathbb{R}}^{r \times n}$ are, respectively, the acceleration and displacement gain matrices.

Applying controller (2) to system (1), we can obtain the closed-loop dynamics as

$$ \left( {M + CF_{a} } \right)\ddot{x}\left( t \right) + D\dot{x}\left( t \right) + \left( {K + CF_{d} } \right)x\left( t \right) = 0. $$

(3)

Therefore, the proposed controller (2) can modify the mass and stiffness parameters. In order to alter the behavior of the second-order system, displacement–acceleration feedback may be utilized. Accordingly, the regularity of the closed-loop system can be guaranteed.

Matrix second-order systems arise naturally in the study of many types of engineering applications. Common examples are vibration control in structural dynamics, control of mechanical multi-body systems and robotics control. The problem of maintaining the stability of second-order system has been an active area of research. For this model, it is customary to use displacement–velocity feedback in order to achieve a desired behavior, $u\left( t \right) = - F_{d} x\left( t \right) - F_{v} \dot{x}\left( t \right)$. Several parametric expressions for the feedback gains using the eigenstructure assignment (ESA) technique have been reported for second-order systems (Schulz and Inman 1994; Kim et al. 1999; Abdelaziz and Valasek 2005; Ouyang et al. 2012). Furthermore, several algorithms for robust eigenvalue assignment problem have been proposed (Chan et al. 1997; Henrion et al. 2005). The sensitivity measures for the eigenvalues of the quadratic matrix polynomial are derived (Nichols and Kautsky 2001). However, the velocities, especially for large flexible structures, are not as easily and accurately obtainable as accelerations, which have been commonly obtained through the use of accelerometers. From the viewpoint of measurement, accelerometer is a favorable sensor to measure the dynamic structural responses. Acceleration is often easier to measure than displacement or velocity, particularly when the structure is stiff (Preumont 2002). Consequently, the available signals for feedback are displacement and acceleration. Using acceleration feedback control in structural applications has been shown to be a feasible, more accurate and successful method for reducing vibration of engineering structures. This is even more interesting because of the frequent use of accelerometers in practical applications.

Due to the wide use of accelerometers, many types of accelerometers have been developed. The type is based on the measurement technique employed within the accelerometer. The types of accelerometer are piezoelectric, micro-electromechanical system (MEMS), piezoresistive, capacitive, inductive, thermal, strain gauge, and so on. Piezoelectric accelerometers with integral electronics (IEPE) are vibration sensors designed for measurement of dynamic vibration signals over wide frequency range typically from 1 Hz to 10 kHz. The IEPE accelerometers have some good properties, such as low noise, wide dynamic range, wide frequency response, wide temperature range, low output impedance, high sensitivity and the availability of miniature design. Consequently, the IEPE accelerometers are widely used in practice, such as aircraft, automobiles, structure monitoring, medical devices, seismic isolation and stabilization platforms, homeland security, oil and mineral exploration, seismology and earthquake measurements and exotic applications such as active isolators for gravitational wave detectors (Levinzon 2015). The measured acceleration data usually involve unexpected error by the data record, data logger and analysis procedure on the measured data. To cope with these errors, various signal-processing techniques are necessary to eliminate the noise from the data logger.

This work presents the application of displacement–acceleration feedback for matrix second-order linear systems. To the best of my knowledge, there has been little study utilizing this feedback in the literature. The control problem by acceleration, velocity and displacement feedback for second-order system was first considered by Rofooei and Tadjbakhsh (1993). The displacement–acceleration feedback control is implemented on a beam-type tuneable vibration absorber (Alujevic et al. 2012). Moreover, the partial ESA for undamped vibration systems that uses displacement–acceleration feedback is introduced (Zhang et al. 2014). Recently, a direct method for updating finite element models with incomplete modal measured data using displacement–acceleration feedback is developed (Yuan et al. 2016). Additionally, the recent parametric solution for the ESA problem using displacement–acceleration feedback for descriptor second-order system is proposed (Abdelaziz 2016; Gu et al. 2016). The regularization and stabilization conditions for descriptor second-order system are derived.

Descriptor second-order systems arise naturally in mechanical multi-body systems and a variety of other practical applications (Losse and Mehrmann 2008; Kawano et al. 2013; Abdelaziz 2014, 2015). One inherent characteristic of descriptor systems is their impulsive response due to infinite eigenvalues. In fact, impulses may cause degradation in performance, damage components or even destroy the system. Therefore, it is important to study the problem of eliminating the impulsive behavior of a descriptor second-order system via certain feedback controllers. The controllability and observability conditions for descriptor second-order systems are developed (Losse and Mehrmann 2008). A procedure for decoupling the second-order systems with singular mass matrices is studied (Kawano et al. 2013). Recently, the combined velocity and acceleration feedback for matrix second-order system has received significant attention during the last few years, $u\left( t \right) = - F_{v} \dot{x}\left( t \right) - F_{a} \ddot{x}\left( t \right)$; see (Araújo et al. 2016; Abdelaziz 2013, 2014, 2015). The regularization and stabilization conditions for descriptor second-order systems with singular mass matrix are investigated. Moreover, the first-order descriptor systems have been of great interest in the literature because they have comprehensive practical applications in mechanical and electrical fields (Dai 1989).

The main contribution of this research is to present a novel procedure for robust and minimum norm controller design for second-order system using displacement–acceleration variables. First, the parametric expressions for the gain controllers and the right eigenvector matrices are presented. Based on the parametric expressions, the optimum solution is obtained. The proposed solution simultaneously makes the resulting closed-loop system numerically robust and obtains gain controllers with minimum norms. Both the cases of singular and nonsingular mass matrices are discussed. Finally, two examples are provided to illustrate the effectiveness of the proposed control strategy.

2 Statement of the Problem

It is well known that the behavior of closed-loop system (3) is governed by the eigenstructure of its associated polynomial $P_{c} \left( \lambda \right) \in {\mathbb{R}}^{n \times n} \left[ \lambda \right]$

$$ P_{c} \left( \lambda \right) = \lambda^{2} \left( {M + CF_{a} } \right) + \lambda D + K + CF_{d} . $$

(4)

The zeroes of ${ \det }\left( {P_{c} \left( \lambda \right)} \right)$ are known as the characteristic frequencies of the system which can be obtained by solving ${ \det }\left( {P_{c} \left( \lambda \right)} \right) = \mathop \sum \nolimits_{k = 0}^{2n} \alpha_{k} \lambda^{k} = 0$, where $\alpha_{2n} = { \det }\left( {M + CF_{a} } \right)\,{\text{and}}\,\alpha_{0} = { \det }\left( {K + CF_{d} } \right)$. The closed-loop system (3) possesses 2n finite eigenvalues, provided the leading coefficient matrix (M + CF_a) is nonsingular.

Let $\varGamma = \left\{ {\lambda_{i} \in {\mathbb{C}}, i = 1, 2, \ldots , 2n} \right\}$ be a set of pre-specified, self-conjugate eigenvalues. Further, denote the right and left eigenvectors associated with λ_i by $v_{i} \in {\mathbb{C}}^{n} , t_{i} \in {\mathbb{C}}^{n} , i = 1, 2, \ldots , 2n$, and then the following relations hold:

$$\begin{aligned} & \left( {\lambda_{i}^{2} \left( {M + CF_{a} } \right) + \lambda_{i} D + K + CF_{d} } \right)v_{i} = 0,\\ & \qquad v_{i} \ne 0,\quad i = 1, 2, \ldots , 2n,\end{aligned} $$

(5)

and

$$\begin{aligned} & t_{i}^{\text{H}} \left( {\lambda_{i}^{2} \left( {M + CF_{a} } \right) + \lambda_{i} D + K + CF_{d} } \right) = 0, \\ & \qquad t_{i} \ne 0,\quad i = 1, 2, \ldots , 2n.\end{aligned} $$

(6)

where H denotes the conjugate transpose.

Denote

$$ V = \left( {\begin{array}{*{20}c} {v_{1} } & {v_{2} } & \ldots & {v_{2n} } \\ \end{array} } \right) \in {\mathbb{C}}^{n \times 2n} , $$

$$ T = \left( {\begin{array}{*{20}c} {t_{1} } & {t_{2} } & \ldots & {t_{2n} } \\ \end{array} } \right) \in {\mathbb{C}}^{n \times 2n} , $$

$$ \varLambda = {\text{diag}}\left( {\begin{array}{*{20}c} {\lambda_{1} } & {\lambda_{2} } & \ldots & {\lambda_{2n} } \\ \end{array} } \right) \in {\mathbb{C}}^{2n \times 2n} $$

where the columns of V and T comprise the right and left eigenvector matrices of the quadratic polynomial $P_{c} \left( \lambda \right)$ and Λ is in Jordan canonical form with the eigenvalues of $P_{c} \left( \lambda \right)$ on the diagonal. There exist matrices V and T that satisfy

$$ \left\{ {\begin{array}{*{20}l} {\left( {M + CF_{a} } \right)V\varLambda^{2} + DV\varLambda + \left( {K + CF_{d} } \right)V = 0,} \hfill \\ {\varLambda^{2} T^{\text{H}} \left( {M + CF_{a} } \right) + \varLambda T^{\text{H}} D + T^{\text{H}} \left( {K + CF_{d} } \right) = 0.} \hfill \\ \end{array} } \right. $$

(7)

Thus, if the system response needs to be altered by displacement–acceleration feedback, both eigenvalue assignment and eigenvector assignment should be considered. Such design problem is called the ESA.

Recall the controllability conditions for descriptor second-order systems (Losse and Mehrmann 2008).

Lemma 1

A second-order descriptor system (1) is

• (i) R2-controllable if and only if$rank\left( {\begin{array}{*{20}c} {\lambda^{2} M + \lambda D + K} & C \\ \end{array} } \right) = n, \forall \lambda \in {\mathbb{C}}$;

• (ii) strongly C2-controllable if and only if$rank\left( {\begin{array}{*{20}c} M & C \\ \end{array} } \right) = n$.□

It is known that the closed-loop pencil $P_{c} \left( \lambda \right)$ has 2n eigenvalues and the closed-loop system (3) is called regular if det(P_c(λ)) is not identically zero. The polynomial matrix P_c(λ) is said to be stable if det(P_c(λ)) has all roots in ${\mathbb{C}}^{ - }$. If P_c(0) is singular, then det(P_c(0)) is zero, and P_c(λ) has a root at the origin so that P_c(λ) is unstable. On the other hand, if P_c(0) is nonsingular, det(P_c(0)) is nonzero so that det(P_c(λ)) has no roots at the origin. Now, the regularization and stabilization conditions for the closed-loop system (3) are presented (Abdelaziz 2016).

Theorem 1

A second-order descriptor system (1) is regularizable and stabilizable via displacement–acceleration controller (2) if the following conditions are met.

• 1. all eigenvalues are finite and nonzero,

• 2. the system is strongly C2-controllable, or$rank\left( {\begin{array}{*{20}c} M & C \\ \end{array} } \right) = n$, and

• 3. $rank\left( {\begin{array}{*{20}c} K & C \\ \end{array} } \right) = n$.

Proof

See Abdelaziz (2016). □

Throughout the paper, the following assumptions are imposed on matrix second-order descriptor system (1):

Assumption 1

The desired eigenvalues are nonzero and closed under complex conjugation.

Assumption 2

The descriptor second-order system (1) is strongly C2-controllable, or $rank\left( {\begin{array}{*{20}c} M & C \\ \end{array} } \right) = n$.

Assumption 3

$rank\left( {\begin{array}{*{20}c} K & C \\ \end{array} } \right) = n$.

Assumption 4

$rank\left( C \right) = r.$

Remark 1

If the mass matrix M of system (1) is nonsingular, then Assumption 2 is modified to system (1) which is R2-controllable, $rank\left( {\begin{array}{*{20}c} {\lambda^{2} M + \lambda D + K} & C \\ \end{array} } \right) = n, \forall \lambda \in {\mathbb{C}}$. The other assumptions are indeed necessary to guarantee that the closed-loop system is stable and the gain is real.

In many practical applications, system (1) is usually subject to perturbations, and therefore, the eigenvalues of a closed-loop system vary with the system-parameter perturbations. The robust pole assignment problem is finding F_d and F_a such that the eigenvalues of a closed-loop system have minimal sensitivity to the variations in the closed-loop system matrices $\left( {M + CF_{a} } \right), D\, {\text{and}} \left( {K + CF_{d} } \right).$ Therefore, it is desirable that the gains not only assign specified eigenvalues to the closed-loop system but also that the system is robust or insensitive to perturbations. Moreover, the minimization of the norm of controllers F_d and F_a can be considered. Reduction of the norm of controller gains results in the average magnitude of control input being reduced. We now formulate the robust and minimum norm problem for system (1) as follows:

Given second-order system (1) and desired set Γ, compute the controller matrices F_d and F_a such that the norm of feedback gains is minimized and the closed-loop eigenvalues $\lambda_{i} , \forall i,$ are as insensitive as possible to parameter perturbations in the closed-loop system matrices.

3 Parametric Expression for the Gain Controllers

In this section, we will present the parametric expressions for both the gain controllers and the closed-loop eigenvector matrices when the system under consideration is singular or nonsingular.

First, the closed-loop system dynamics (5) can be expressed as

$$ \left( {\lambda_{i}^{2} M + \lambda_{i} D + K} \right)v_{i} + Cw_{i} = 0,\quad i = 1, 2, \ldots , 2n. $$

(8)

where

$$ w_{i} = \left( {F_{d} + \lambda_{i}^{2} F_{a} } \right)v_{i} = \left( {F_{d}\,F_{a} } \right)\left( {\begin{array}{*{20}c} {v_{i} } \\ {\lambda_{i}^{2} v_{i} } \\ \end{array} } \right). $$

Denoting $W = \left( {\begin{array}{*{20}c} {w_{1} } & {w_{2} } & \ldots & {w_{2n} } \\ \end{array} } \right) \in {\mathbb{C}}^{r \times 2n}$, one can obtain that

$$ W = \left( {F_{d}\,F_{a} } \right)\left( {\begin{array}{*{20}c} V \\ {V{{\varLambda }}^{2} } \\ \end{array} } \right). $$

(9)

Pre-multiplying this equation by $\left( {\begin{array}{*{20}c} V \\ {V{{\varLambda }}^{2} } \\ \end{array} } \right)^{ - 1}$, a parametric representation of the displacement–acceleration gain controller is

$$ \left( {F_{d}\,F_{a} } \right) = W\left( {\begin{array}{*{20}c} V \\ {V{{\varLambda }}^{2} } \\ \end{array} } \right)^{ - 1} . $$

(10)

Equation (8) can be rewritten as

$$ \left( {\begin{array}{*{20}c} {\lambda_{i}^{2} M + \lambda_{i} D + K} & C \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {v_{i} } \\ {w_{i} } \\ \end{array} } \right) = 0,\quad i = 1, 2, \ldots , 2n. $$

(11)

The solution to this equation should be in the null space of $\left( {\begin{array}{*{20}c} {\lambda_{i}^{2} M + \lambda_{i} D + K} & C \\ \end{array} } \right).$ Consequently, this equation satisfies $\left( {\begin{array}{*{20}c} {v_{i} } \\ {w_{i} } \\ \end{array} } \right) \in ker\left( {\begin{array}{*{20}c} {\lambda_{i}^{2} M + \lambda_{i} D + K} & C \\ \end{array} } \right), \forall i,$ where ker(.) is the null space.

In the following, we will present the parametric ESA solution to system (1) (Abdelaziz 2016).

Theorem 2

Consider the second-order system (1) and the prescribed, self-conjugate set Γ satisfying Assumptions1–4. The parametric expressions for gain are expressed by

$$ \left( {F_{d}\,F_{a} } \right) = \left( {\begin{array}{*{20}c} {Q_{i2} \theta_{1} } & {Q_{i2} \theta_{2} } & \cdots & {Q_{i2} \theta_{2n} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {Q_{i1} \theta_{1} } & {Q_{i1} \theta_{2} } & \cdots & {Q_{i1} \theta_{2n} } \\ {\lambda_{1}^{2} Q_{i1} \theta_{1} } & {\lambda_{2}^{2} Q_{i1} \theta_{2} } & \cdots & {\lambda_{2n}^{2} Q_{i1} \theta_{2n} } \\ \end{array} } \right)^{ - 1} $$

(12)

where$Q_{i1} \in {\mathbb{C}}^{n \times r} and\,Q_{i2} \in {\mathbb{C}}^{r \times r}$are obtained by

$$\begin{aligned} H_{i} \left( {\begin{array}{*{20}c} {\lambda_{i}^{2} M + \lambda_{i} D + K} & C \\ \end{array} } \right)Q_{i} & = \left( {\begin{array}{*{20}c} {{{\varSigma }}_{i} } & {0_{n,r} } \\ \end{array} } \right),\\ Q_{i} & = \left( {\begin{array}{*{20}c} * & {Q_{i1} } \\ * & {Q_{i2} } \\ \end{array} } \right), \\ i & = 1, 2, \ldots , 2n.\end{aligned} $$

(13)

where$H_{i} \in {\mathbb{C}}^{n \times n} , Q_{i} \in {\mathbb{C}}^{{\left( {n + r} \right) \times \left( {n + r} \right)}} , \,{\text{and}} \,\varSigma_{i} \in {\mathbb{C}}^{n \times n}$. Moreover,$\theta_{i} \in {\mathbb{C}}^{r} , \forall i$, are free parameter vectors satisfying the following two constraints:

$$ \begin{aligned} & Constraint\,1:\theta_{k} = \theta_{i}^{*}\,when\,\lambda_{k} = \lambda_{i}^{*} , i, k; \\ & Constraint\,2:det\left( {\begin{array}{*{20}c} {Q_{i1} \theta_{1} } & {Q_{i1} \theta_{2} } & \ldots & {Q_{i1} \theta_{2n} } \\ {\lambda_{1}^{2} Q_{i1} \theta_{1} } & {\lambda_{2}^{2} Q_{i1} \theta_{2} } & \ldots & {\lambda_{2n}^{2} Q_{i1} \theta_{2n} } \\ \end{array} } \right) \ne 0. \\ \end{aligned} $$

Proof

See Abdelaziz (2016).□

Remark 2

Relation (13) can be obtained using the singular value decomposition (SVD) for $\left( {\begin{array}{*{20}c} {\lambda_{i}^{2} M + \lambda_{i} D + K} & C \\ \end{array} } \right), \forall i,$ where matrices H_i and Q_i are orthogonal, ${{\varSigma }}_{i} = {\text{diag}}\left( {\begin{array}{*{20}c} {\sigma_{i1} } & {\sigma_{i2} } & \cdots & {\sigma_{in} } \\ \end{array} } \right)$ is nonsingular, $\sigma_{i1} \ge \sigma_{i2} \ge \cdots \ge \sigma_{in} > 0$. Further, matrices Q_i1 and Q_i2 are obtained by

$$ Q_{i1} = \left( {\begin{array}{*{20}c} {I_{n} } & {0_{n,r} } \\ \end{array} } \right)Q_{i} \left( {\begin{array}{*{20}c} {0_{n,r} } \\ {I_{r} } \\ \end{array} } \right) \,{\text{and}}\, Q_{i2} = \left( {\begin{array}{*{20}c} {0_{r,n} } & {I_{r} } \\ \end{array} } \right)Q_{i} \left( {\begin{array}{*{20}c} {0_{n,r} } \\ {I_{r} } \\ \end{array} } \right). $$

Remark 3

Note that the parametric solution (12) includes the design vectors $\theta_{i} , \forall i$, which represent the degrees-of-freedom offered by displacement–acceleration feedback. Accordingly, the design vectors $\theta_{i} , \forall i,$ can be utilized as a basic parameter optimization for the closed-loop system (3).

4 Robust and Minimum Norm Controller Design

In this section, an efficient method is proposed to obtain the robust and minimum norm controller design. In many practical cases, there often exist parameter variations or perturbations in the system model. It is well known that the presence of uncertainty in the model greatly influences the control performance and stability of the closed-loop system. Consequently, designing a controller that can tolerate parameter variations or perturbations in the system model is the current research interest. The robust and minimum norm controller design tries to utilize the freedom over the closed-loop eigenvectors to arrange them such that the closed-loop system becomes insensitive to parameter variations.

4.1 Uncertain Second-Order System

For second-order system (1), the perturbations can be defined as $\Delta M, \Delta D, \Delta K \in {\mathbb{R}}^{n \times n} \,{\text{and}}\,\Delta C \in {\mathbb{R}}^{n \times r}$. Accordingly, the system matrices M, D, K and C can be perturbed to $\left( {M + \Delta M} \right), \left( {D + \Delta D} \right), \left( {K + \Delta K} \right)\, {\text{and}}\, \left( {C + \Delta C} \right)$, respectively. Hence, the uncertain second-order linear system associated with (1) can be written as:

$$ \left\{ {\begin{array}{*{20}lll} \left( {M + \Delta M} \right)\ddot{x}_{p} \left( t \right) + \left( {D + \Delta D} \right)\dot{x}_{p} \left( t \right)\\ \quad + \left( {K + \Delta K} \right)x_{p} \left( t \right) = \left( {C + \Delta C} \right)u\left( t \right), \hfill \\ {x_{p} \left( 0 \right) = x_{0} , \dot{x}_{p} \left( 0 \right) = \dot{x}_{0} } \hfill \\ \end{array} } \right. $$

(14)

where $x_{p} \left( t \right), \dot{x}_{p} \left( t \right), \ddot{x}_{p} \left( t \right) \in {\mathbb{R}}^{n}$ are the perturbed displacement, velocity and acceleration vectors.

Now, by applying the displacement–acceleration control input

$$ u\left( t \right) = - F_{d} x_{p} \left( t \right) - F_{a} \ddot{x}_{p} \left( t \right), $$

the uncertain closed-loop system is

$$ \left( {M + \Delta M + \left( {C + \Delta C} \right)F_{a} } \right)\ddot{x}_{p} \left( t \right) + \left( {D + \Delta D} \right)\dot{x}_{p} \left( t \right) + \left( {K + \Delta K + \left( {C + \Delta C} \right)F_{d} } \right)x_{p} \left( t \right) = 0. $$

(15)

Therefore, the uncertain quadratic polynomial pencil can be written as

$$ P_{cp} \left( \lambda \right) = \lambda^{2} \left( {M + \Delta M + \left( {C + \Delta C} \right)F_{a} } \right) + \lambda \left( {D + \Delta D} \right) + K + \Delta K + \left( {C + \Delta C} \right)F_{d} . $$

(16)

The pencil $P_{cp} \left( \lambda \right) \in {\mathbb{R}}^{n \times n} \left[ \lambda \right]$ has 2n eigenvalues, and the uncertain closed-loop system (15) is called regular if the corresponding matrix pencil ${ \det }(P_{cp} \left( \lambda \right))$ is not identically zero.

Now, the necessary conditions presented in Sect. 3 can be further extended to cope with uncertain second-order systems. The following theorem establishes the regularization and stabilization conditions for the uncertain closed-loop system (15).

Theorem 3

Consider the uncertain second-order system (14) satisfying$rank\left( {C + \Delta C} \right) = r.$There exist the real gain matrices$F_{d} \,{\text{and}}\,F_{a}$such that$P_{cp} \left( \lambda \right)$is regular if and only if$rank\left( {\begin{array}{*{20}c} {M + \Delta M} & {C + \Delta C} \\ \end{array} } \right) = n$. Moreover, the uncertain closed-loop system (15) is stable if and only if$rank\left( {\begin{array}{*{20}c} {K + \Delta K} & C \\ \end{array} + \Delta C} \right) = n$.

Proof

The characteristic polynomial of uncertain closed-loop system (15) can be expanded as

$$ { \det }\left( {P_{cp} \left( \lambda \right)} \right) = a_{2n} \lambda^{2n} + \cdots + a_{1} \lambda + a_{0} = 0 $$

(17)

where $a_{2n} = { \det }\left( {M + \Delta M + \left( {C + \Delta C} \right)F_{a} } \right)\,{\text{and}}\,a_{0} = { \det }\left( {K + \Delta K + \left( {C + \Delta C} \right)F_{d} } \right)$. So, the uncertain system (14) possesses 2n finite eigenvalues provided the leading coefficient matrix $\left( {M + \Delta M + \left( {C + \Delta C} \right)F_{a} } \right)$ is nonsingular. Otherwise, if the term $\left( {M + \Delta M + \left( {C + \Delta C} \right)F_{a} } \right)$ is singular, then ${ \deg }\left( {{ \det }\left( {P_{cp} \left( \lambda \right)} \right)} \right) < 2n$ (system has infinite eigenvalues). The pencil $P_{cp} \left( \lambda \right)$ has 2n eigenvalues and the uncertain closed-loop system (15) is called regular if ${ \det }\left( {P_{cp} \left( \lambda \right)} \right)$ is not identically zero. Equation (17) can be rewritten as a finite product as:

$$ det\left( {P_{cp} \left( \lambda \right)} \right) = a_{2n} \left( {\lambda - \lambda_{1} } \right)\left( {\lambda - \lambda_{2} } \right) \cdots \left( {\lambda - \lambda_{2n} } \right) = a_{2n} \lambda^{2n} + \cdots + a_{1} \lambda + a_{2n} \mathop \prod \limits_{i = 1}^{2n} \lambda_{i} $$

(18)

where λ₁, λ₂, …, λ_2n are zeroes of ${ \det }\left( {P_{cp} \left( \lambda \right)} \right)$. Remark that

$$ a_{0} = a_{2n} \mathop \prod \nolimits_{i = 1}^{2n} \lambda_{i} $$

or

$$ { \det }\left( {K + \Delta K + \left( {C + \Delta C} \right)F_{d} } \right) = { \det }\left( {M + \Delta M + \left( {C + \Delta C} \right)F_{a} } \right)\mathop \prod \limits_{i = 1}^{2n} \lambda_{i} . $$

(19)

To guarantee that uncertain closed-loop system (14) is regular, then

$$ { \det }\left( {M + \Delta M + \left( {C + \Delta C} \right)F_{a} } \right) = { \det }\left( {K + \Delta K + \left( {C + \Delta C} \right)F_{d} } \right)\mathop \prod \limits_{i = 1}^{2n} \lambda_{i}^{ - 1} \ne 0. $$

(20)

Finally, from Eq. (20), it can be concluded that $P_{cp} \left( \lambda \right)$ is regular if and only if ${ \det }\left( {K + \Delta K + \left( {C + \Delta C} \right)F_{d} } \right) \ne 0$ and λ_i ≠ 0, ∀i.

If λ = 0, we can verify that

$$\begin{aligned} { \det }\left( {P_{cp} \left( {\lambda = 0} \right)} \right)\\ = \mathop {\lim }\limits_{\lambda \to 0} { \det }\Big( \lambda^{2} \left( {M + \Delta M + \left( {C + \Delta C} \right)F_{a} } \right) + \lambda \left( {D + \Delta D} \right) + K + \Delta K + \left( {C + \Delta C} \right)F_{d} \Big) = { \det }\left( {K + \Delta K + \left( {C + \Delta C} \right)F_{d} } \right)\end{aligned} $$

(21)

Therefore, ${ \det }\left( {P_{cp} \left( 0 \right)} \right) \ne 0$ if and only if the term $\left( {K + \Delta K + \left( {C + \Delta C} \right)F_{d} } \right)$ is nonsingular. Otherwise, $P_{cp} \left( 0 \right)$ is singular if ${ \det }\left( {K + \Delta K + \left( {C + \Delta C} \right)F_{d} } \right) = 0$; then, the system has at least one root at the origin (unstable). This means that all the poles of uncertain system could be shifted to arbitrary finite locations using the displacement–acceleration controller with the exception when $\left( {K + \Delta K + \left( {C + \Delta C} \right)F_{d} } \right)$ is singular. Thus, the necessary condition for stability is ${ \det }\left( {K + \Delta K + \left( {C + \Delta C} \right)F_{d} } \right) \ne 0$.

Without loss of generality, assume that the term $\left( {C + \Delta C} \right)$ is of the form

$$ \left( {C + \Delta C} \right) = \left( {\begin{array}{*{20}c} {0_{n - r,r} } \\ {I_{r} } \\ \end{array} } \right) . $$

(22)

Then, the existence of acceleration controller F_a such that ${ \det }\left( {M + \Delta M + \left( {C + \Delta C} \right)F_{a} } \right) \ne 0$ implies that the first (n − r) rows of $\left( {M + \Delta M} \right)$ are linearly independent which in turn implies that $rank\left( {\begin{array}{*{20}c} {M + \Delta M} & {C + \Delta C} \\ \end{array} } \right) = n$ or the uncertain second-order system (14) is strongly C2-controllable. Similarly, ${ \det }\left( {K + \Delta K + \left( {C + \Delta C} \right)F_{d} } \right) \ne 0$ implies that $rank\left( {\begin{array}{*{20}c} {K + \Delta K} & C \\ \end{array} + \Delta C} \right) = n.$ The proof is then completed. □

Without loss of generality, the uncertainties of uncertain second-order system (14) are restricted as:

Constraint 3: The uncertain second-order system (14) is strongly C2-controllable, or $rank\left( {\begin{array}{*{20}c} {M + \Delta M} & {C + \Delta C} \\ \end{array} } \right) = n$.

Constraint 4:$rank\left( {\begin{array}{*{20}c} {K + \Delta K} & C \\ \end{array} + \Delta C} \right) = n$.

Constraint 5: $rank\left( {C + \Delta C} \right) = r.$

Clearly, Constraints 3–5 ensured the regularization and stabilization for the uncertain closed-loop system (15).

4.2 The Explicit Condition Number

Nichols and Kautsky (2001) derived the sensitivity measures, or condition numbers, for the eigenvalues of the quadratic matrix polynomial and defined a measure of the robustness for the corresponding system. Now, the notion of robustness to the quadratic eigenstructure assignment problem is introduced (Nichols and Kautsky 2001).

Lemma 2

Let $\lambda_{i}$ be a simple eigenvalue of the closed-loop quadratic polynomial P _c (λ) with corresponding right eigenvector v _i and left eigenvector t _i . Then, the explicit condition number $c\left( {\lambda_{i} } \right)$ of the eigenvalues $\lambda_{i}$ is given by

$$\begin{aligned} c\left( {\lambda_{i} } \right) &= \frac{{\sqrt {\left| {\lambda_{i} } \right|^{4} + \left| {\lambda_{i} } \right|^{2} + 1} \left\| {t_{i}^{*} \left( {M + CF_{a} } \right)} \right\|_{2} \left\|v_{i2}\right\| }}{{\left| {t_{i}^{*} \left( {2\lambda_{i} \left( {M + CF_{a} } \right) + D} \right)v_{i} } \right|}},\\ i &= 1, 2, \ldots , 2n.\end{aligned} $$

(23)

Moreover, the condition number $\kappa \left( {\lambda_{i} } \right)$ is defined as

$$ \kappa \left( {\lambda_{i} } \right) = \frac{{c\left( {\lambda_{i} } \right)}}{{\left| {\lambda_{i} } \right|}},\quad \lambda_{i} \ne 0, \quad i = 1, 2, \ldots , 2n. $$

(24)

□

The condition number $c\left( {\lambda_{i} } \right)$ measures the sensitivity of the eigenvalue $\lambda_{i}$ to perturbations in the quadratic polynomial pencil P_c(λ) in an absolute sense. For robust solution, we seek controller matrices F_d and F_a so that the resulting closed-loop eigenvalues are as insensitive as possible to parameter perturbation in the system matrices. On the other hand, the minimization of the norm of displacement and acceleration controllers F_d and F_a can be considered. Reduction of the norm of controller gain matrices results in the average magnitude of control input being reduced. These considerations lead to robust and minimum norm problems.

4.3 Robust and Minimum Norm Solution

The proposed solution to the robust and minimum norm problem can be obtained by solving the constrained optimization problem given as:

$$ {}_{{\begin{array}{*{20}c} {\theta_{i} , \forall i } \\ \end{array} }}^{\text{Minimize}} \varUpsilon = \mathop \sum \limits_{i = 1}^{2n} \left( {\omega_{i}^{2} c\left( {\lambda_{i} } \right)^{2} } \right) + \xi \left\| { \left( {\begin{array}{*{20}c} V \\ {V{{\varLambda }}} \\ \end{array} } \right)} \right\| \left\| {\left( {\begin{array}{*{20}c} V \\ {V{{\varLambda }}} \\ \end{array} } \right)^{ - 1} } \right\| + \psi \left\| {F_{a} } \right\|^{2} + \gamma \left\| {F_{d} } \right\| ^{2} $$

(25)

$$\begin{aligned} {\text{subject}}\,{\text{to:}}\quad \left\{ \begin{array}{*{20}llll} \left( {F_{d}\,F_{a} } \right) = \left( {\begin{array}{*{20}ccc} {Q_{i2} \theta_{1} } & {Q_{i2} \theta_{2} } & \ldots & {Q_{i2} \theta_{2n} } \\ \end{array} } \right)\\ \left( {\begin{array}{*{20}c} {Q_{i1} \theta_{1} } & {Q_{i1} \theta_{2} } & \ldots & {Q_{i1} \theta_{2n} } \\ {\lambda_{1}^{2} Q_{i1} \theta_{1} } & {\lambda_{2}^{2} Q_{i1} \theta_{2} } & \ldots & {\lambda_{2n}^{2} Q_{i1} \theta_{2n} } \\ \end{array} } \right)^{ - 1} ; \hfill \\ { \det }\left( {\begin{array}{*{20}c} {Q_{i1} \theta_{1} } & {Q_{i1} \theta_{2} } & \ldots & {Q_{i1} \theta_{2n} } \\ {\lambda_{1}^{2} Q_{i1} \theta_{1} } & {\lambda_{2}^{2} Q_{i1} \theta_{2} } & \ldots & {\lambda_{2n}^{2} Q_{i1} \theta_{2n} } \\ \end{array} } \right) \ne 0; \hfill \\ {\theta_{k} = \theta_{i}^{*} \,\,{\text{when}}\,\, \lambda_{k} = \lambda_{i}^{*} , i, k;\,{\text{and}}} \hfill \\ {\mathop \sum \limits_{i = 1}^{2n} \omega_{i}^{2} = 1.} \hfill \\ \end{array} \right.\end{aligned}$$

where Υ is the objective function to be minimized, and $\xi , \psi \, {\text{and}}\, \gamma$ are positive scalars representing the weighting factors on $\left\| {\left( {\begin{array}{*{20}c} V \\ {V{{\varLambda }}} \\ \end{array} } \right)} \right\| \left\| {\left( {\begin{array}{*{20}c} V \\ {V{{\varLambda }}} \\ \end{array} } \right)^{ - 1} } \right\|, \left\| {F_{a} } \right\|^{2} \, {\text{and}}\, \left\| {F_{d} } \right\| ^{2}$, respectively. Moreover, the positive weights $\omega_{i} , \forall i$, are satisfying $\mathop \sum \nolimits_{i = 1}^{2n} \omega_{i}^{2} = 1$ (Nichols and Kautsky 2001). Once the optimal solution is obtained, one may compute the robust and minimum norm controllers. Consequently, the proposed technique simultaneously makes the resulting closed-loop system numerically robust and obtains gain controllers with minimum norms.

Remark 4

It should be remarked that minimizing the norms of the displacement and acceleration gain controllers F_d and F_a as small as possible is very important to reduce the signal noises and energy consumption.

4.4 Numerical Algorithm

Finally, we can describe a numerical algorithm to obtain the robust and minimum norm gain controllers for matrix second-order systems.

Input :

Given a second-order system (1) and a nonzero, self-conjugate set Γ satisfying Assumptions 1–4

Step 1 :

Use the SVD to obtain the matrices $Q_{i1} \in {\mathbb{C}}^{n \times r} \,{\text{and}}\, Q_{i2} \in {\mathbb{C}}^{r \times r} , \forall i$, satisfying (13)

Step 2 :

Choose the initial parameter vectors $\theta_{i0} \in {\mathbb{C}}^{r} , \forall i$, satisfying Constraints 1–2 and the positive weights $\omega_{i} , \forall i$, satisfying $\mathop \sum \nolimits_{i = 1}^{2n} \omega_{i}^{2} = 1$

Step 3:

Compute the optimal design parameters $\theta_{i} , \forall i$, which minimize the performance index Υ

Step 4 :

Compute the vectors $v_{i} \,{\text{and}} \,w_{i} , \forall i,$ and construct the matrices $V, W \,{\text{and}}\, {{\varLambda }}$

Step 5 :

Compute the robust and minimum norm controllers using $\left( {F_{d}\,F_{a} } \right) = W\left( {\begin{array}{*{20}c} V \\ {V{{\varLambda }}^{2} } \\ \end{array} } \right)^{ - 1}$

Remark 5

Note that for the constrained optimization problem (25), there are more than one local minimum of the performance index. Thus, by solving the optimization problem repeatedly with different random initial values $\theta_{i0}$, one is able to find the gains in the case when Υ has a very low value. Accordingly, several initial vectors should be considered. For solution to this minimization problem, there are many software packages which can be used. Particularly, the optimization toolbox of MATLAB is very reliable and suitable for solving this problem.

5 Simulation Results

In this section, numerical simulations are conducted to illustrate and verify the proposed control approach.

5.1 Example 1

Consider the analysis of the oscillations of a wing in an air stream (Henrion et al. 2005). The dynamic system equations are given as:

$$ \left( {\begin{array}{*{20}c} {17.600} & {1.280} & {2.890} \\ {1.280} & {0.824} & {0.413} \\ {2.890} & {0.413} & {0.725} \\ \end{array} } \right)\ddot{x}\left( t \right) + \left( {\begin{array}{*{20}c} {7.660} & {2.450} & {2.100} \\ {0.230} & {1.040} & {0.223} \\ {0.600} & {0.656} & {0.658} \\ \end{array} } \right)\dot{x}\left( t \right) + \left( {\begin{array}{*{20}c} {121.000} & {18.900} & {15.900} \\ {0.000} & {2.700} & {0.145} \\ {11.900} & {3.640} & {15.500} \\ \end{array} } \right)x\left( t \right) = \left( {\begin{array}{*{20}c} 1 & 0 \\ 0 & 0 \\ 0 & 1 \\ \end{array} } \right)u\left( t \right). $$

Clearly, the mass matrix M is nonsingular. The system is unstable and its eigenvalues are located at {0.0947 ± 2.5229i, − 0.8848 ± 8.4415i, − 0.9180 ± 1.7606i}. The desired closed-loop eigenvalues are selected as {− 1 ± i, − 2 ± i, − 3 ± i}. The numerical simulations are carried out for two solutions. In this simulation, the MATLAB function ‘svd.m’ is utilized to obtain the matrices $Q_{i1}\,{\text{and}}\,Q_{i2} , \forall i$, satisfying (13).

Non-robust solution:

If the design parameters $\theta_{i} , \forall i,$ are chosen as:

$$ \theta_{1} = \theta_{2} = \left( {\begin{array}{*{20}c} 3 \\ 5 \\ \end{array} } \right), \theta_{3} = \theta_{4} = \left( {\begin{array}{*{20}c} 1 \\ 2 \\ \end{array} } \right), \theta_{5} = \theta_{6} = \left( {\begin{array}{*{20}c} 1 \\ 1 \\ \end{array} } \right), $$

then the displacement and acceleration gain controllers are computed as

$$ \left\{ {\begin{array}{*{20}l} {F_{d} = \left( {\begin{array}{*{20}c} { - 78.3349 - 21.6327 - 12.0036} \\ {5.3295 - 5.6283 - 13.9159} \\ \end{array} } \right), } \hfill \\ {F_{a} = \left( {\begin{array}{*{20}c} { - 22.5565 - 1.8712 - 3.3275} \\ { - 6.3384 - 1.0123 - 1.1335} \\ \end{array} } \right).} \hfill \\ \end{array} } \right. $$

Robust and minimum norm solution:

From a practical point of view, robust and small gains are favorable. Thus, the non-uniqueness of the gains is exploited to obtain robust and minimum gain norm solution. In this simulation, the initial parameter vectors $\theta_{i0}$ and the positive weights $\omega_{i} , \forall i$, are chosen, respectively, as:

$$ \theta_{10} = \theta_{20} = \left( {\begin{array}{*{20}c} 3 \\ 5 \\ \end{array} } \right), \theta_{30} = \theta_{40} = \left( {\begin{array}{*{20}c} 1 \\ 2 \\ \end{array} } \right), \theta_{50} = \theta_{60} = \left( {\begin{array}{*{20}c} 1 \\ 1 \\ \end{array} } \right), $$

$$\begin{aligned} &\omega_{1} = 0.3162,\, \omega_{2} = 0.5000, \,\omega_{3} = 0.3742, \\ &\omega_{4} = 0.3873, \,\omega_{5} = 0.4123,\, \omega_{6} = 0.4359, \end{aligned}$$

satisfying $\mathop \sum \nolimits_{i = 1}^{2n} \omega_{i}^{2} = 1$.

The MATLAB function ‘fmincon.m’ is utilized to solve the constrained optimization problem (25). Then, the optimal design vectors, $\theta_{i}$, are computed as:

$$\begin{aligned} &\theta_{1} = \theta_{2} = \left( {\begin{array}{*{20}c} {13.3898} \\ {1.6876} \\ \end{array} } \right), \theta_{3} = \theta_{4} = \left( {\begin{array}{*{20}c} {10.5277} \\ {1.3257} \\ \end{array} } \right), \\ & \,\theta_{5} = \theta_{6} = \left( {\begin{array}{*{20}c} { - 2.3031} \\ {0.7729} \\ \end{array} }\right).\end{aligned} $$

Thus, the robust displacement and acceleration controller gains are computed as

$$ \left\{ {\begin{array}{*{20}l} {F_{d} = \left( {\begin{array}{*{20}c} { - 115.8018 - 14.3854 - 14.7029} \\ { - 11.6596 - 1.8331 - 14.6968} \\ \end{array} } \right), } \hfill \\ {F_{a} = \left( {\begin{array}{*{20}c} { - 12.0687 1.1882 - 1.2822} \\ { - 1.7965 0.2229 - 0.3167} \\ \end{array} } \right).} \hfill \\ \end{array} } \right. $$

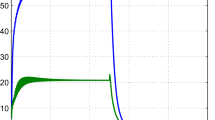
The results of all solutions are presented in Table 1. The following numerical results of the norm of eigenvector matrix $\left\| {V } \right\|$ and the norm of gains F_d and F_a are presented. The simulation results of the closed-loop system for both non-robust and robust solutions are displayed in Fig. 1 using the following initial conditions: $x_{0} = \left[ {{-}\,0.01, {-}\,0.02, 0.01} \right]^{\text{T}} {\text{m}} \,\,{\text{and}} \,\,\dot{x}_{0} = \left[ {{-}\,0.01, 0.01, 0.02} \right]^{\text{T}} \, {\text{m/s}}$. In this figure, the displacements x(t), velocities $\dot{x}\left( t \right)$, accelerations $\ddot{x}\left( t \right)$ and control inputs u(t) of the closed-loop systems are displayed. Additionally, the frequency responses of the open-loop system, the non-robust solution and the robust and minimum norm solution are presented in Fig. 2. One can observe that the robust solution obtains better performance with smaller control inputs compared with the non-robust solution.

Table 1 Simulation results for Example 1

Fig. 1

Transient response for Example 1: a non-robust controller; b robust and minimum norm controller

Fig. 2

Frequency response for Example 1

Perturbed system

To test the robustness of solutions, suppose that the perturbations are defined as: $\Delta M = 0.001M,\, \Delta D = 0.001D,\,{\text{and}}\, \Delta K = 0.001K,$ while matrix C is kept unchanged. It is easy to check that these uncertainties satisfy the regularization and stabilization (Constraints 3–5). In this case, the displacement, velocity and acceleration error trajectories are displayed in Fig. 3 for the non-robust and robust solutions with the computed gain matrices. The displacement, velocity and acceleration error trajectories are denoted, respectively, by

$$ \left\{ {\begin{array}{*{20}c} {e\left( t \right) = x\left( t \right) - x_{p} \left( t \right),} \\ {\dot{e}\left( t \right) = \dot{x}\left( t \right) - \dot{x}_{p} \left( t \right),} \\ {\ddot{e}\left( t \right) = \ddot{x}\left( t \right) - \ddot{x}_{p} \left( t \right).} \\ \end{array} } \right. $$

Fig. 3

Displacement, velocity and acceleration error trajectories for Example 1: a non-robust controller; b robust and minimum norm controller

One can observe that the error trajectories for the robust and minimum norm controller are smaller compared with the non-robust solution. Furthermore, for the non-robust solution and robust and minimum norm solution, the norms of errors in poles due to perturbation are computed, respectively, as 1.2865 and 0.1777. The norm of errors in poles due to perturbations for robust and minimum norm solution is significantly reduced by 624.15% compared with non-robust one.

5.2 Example 2

Consider the four-degree-of-freedom mechanical system shown in Fig. 4. The equation of motion can be written by a descriptor second-order linear system

$$\begin{aligned} &\left( {\begin{array}{*{20}c} {m_{1} } & 0 & 0 & 0 \\ 0 & {m_{2} } & 0 & 0 \\ 0 & 0 & {m_{3} } & 0 \\ 0 & 0 & 0 & 0 \\ \end{array} } \right)\ddot{x}\left( t \right) + \left( {\begin{array}{*{20}c} {b_{1} + b_{2} } & { - b_{2} } & 0 & 0 \\ { - b_{2} } & {b_{2} + b_{3} } & { - b_{3} } & 0 \\ 0 & { - b_{3} } & {b_{3} + b_{4} } & { - b_{4} } \\ 0 & 0 & { - b_{4} } & {b_{4} } \\ \end{array} } \right)\dot{x}\left( t \right)\\ & + \left( {\begin{array}{*{20}c} {k_{1} + k_{2} } & { - k_{2} } & 0 & 0 \\ { - k_{2} } & {k_{2} + k_{3} } & { - k_{3} } & 0 \\ 0 & { - k_{3} } & {k_{3} + k_{4} } & { - k_{4} } \\ 0 & 0 & { - k_{4} } & {k_{4} } \\ \end{array} } \right)x\left( t \right) = \left( {\begin{array}{*{20}c} 1 & 0 \\ 0 & 0 \\ 0 & 0 \\ 0 & 1 \\ \end{array} } \right)u\left( t \right)\end{aligned}$$

where $x\left( t \right) = \left( {\begin{array}{*{20}c} {x_{1} } & {x_{2} } & {x_{3} } & {x_{4} } \\ \end{array} } \right)^{\text{T}}$ and $u\left( t \right) = \left( {\begin{array}{*{20}c} {u_{1} } & {u_{2} } \\ \end{array} } \right)^{\text{T}}$. The system response can be measured directly using the four accelerometers $\ddot{x}\left( t \right) = \left( {\begin{array}{*{20}c} {\ddot{x}_{1} } & {\ddot{x}_{2} } & {\ddot{x}_{3} } & {\ddot{x}_{4} } \\ \end{array} } \right)^{\text{T}}$, and the displacement components can also be obtained as $x\left( t \right) = \left( {\begin{array}{*{20}c} {x_{1} } & {x_{2} } & {x_{3} } & {x_{4} } \\ \end{array} } \right)^{\text{T}}$. The physical system parameters are taken as m₁ = 3 kg, m₂ = 2 kg, m₃ = 2 kg, b₁ = 10 N s/m, b₂ = 15 N s/m, b₃ = 20 N s/m, b₄ = 40 N s/m, k₁ = 5 N/m, k₂ = 10 N/m, k₃ = 15 N/m and k₄ = 20 N/m. The system characteristic frequencies are {∞, − 25.1734, − 8.1208, − 0.5601 ± 0.5461i, − 0.7701, − 0.6488, − 0.5000}. Observe that the first eigenvalue is infinite and may generate undesired dynamical performance. Accordingly, the simulation will be undertaken for the eigenvalues λ_1,2 = − 1 ± i, λ_3,4 = − 2 ± i, λ_5,6 = − 3 ± i, and λ_7,8 = − 4 ± 4i. The numerical simulations are carried out for two solutions.

Fig. 4

Mechanical system

Non-robust solution

If the design parameters $\theta_{i} , \forall i,$ are chosen as:

$$\begin{aligned} &\theta_{1} = \theta_{2} = \left( {\begin{array}{*{20}c} 1 \\ { - 4} \\ \end{array} } \right), \quad \theta_{3} = \theta_{4} = \left( {\begin{array}{*{20}c} 2 \\ 2 \\ \end{array} } \right), \\ &\theta_{5} = \theta_{6} = \left( {\begin{array}{*{20}c} { - 0.5} \\ 2 \\ \end{array} } \right), \quad \theta_{7} = \theta_{8} = \left( {\begin{array}{*{20}c} {0.2} \\ 1 \\ \end{array} } \right),\end{aligned} $$

then the gain controllers are computed as

$$ \left\{ {\begin{array}{*{20}l} {F_{d} = \left( {\begin{array}{*{20}c} { - 99.3083 279.3025 - 304.1245 14.4664} \\ {48.1153 - 134.8441 147.6541 - 9.6541} \\ \end{array} } \right), } \hfill \\ {F_{a} = \left( {\begin{array}{*{20}c} { - 8.4546 39.8169 - 74.7486 44.2007} \\ {2.1727 - 17.5703 29.7346 - 17.7483} \\ \end{array} } \right).} \hfill \\ \end{array} } \right. $$

Robust and minimum norm solution

In this simulation, the initial parameter vectors $\theta_{i0}$ and the positive weights $\omega_{i} , \forall i,$ are taken, respectively, as:

$$ \begin{aligned}&\theta_{10} = \theta_{20} = \left( {\begin{array}{*{20}c} { - 1} \\ 4 \\ \end{array} } \right),\quad \theta_{30} = \theta_{40} = \left( {\begin{array}{*{20}c} {2.5} \\ 2 \\ \end{array} } \right), \\ &\theta_{50} = \theta_{60} = \left( {\begin{array}{*{20}c} {0.2} \\ { - 2} \\ \end{array} } \right), \quad \theta_{70} = \theta_{80} = \left( {\begin{array}{*{20}c} { - 0.3} \\ { - 1.5} \\ \end{array} } \right),\end{aligned} $$

$$ \begin{aligned} \omega_{1} & = 0.3464, \omega_{2} = 0.3000, \omega_{2} = 0.4472, \omega_{4} = 0.3742,\\ \omega_{5} & = 0.3873, \omega_{6} = 0.3317, \omega_{7} = 0.2249, \omega_{8} = 0.3606, \end{aligned} $$

satisfying $\mathop \sum \nolimits_{i = 1}^{2n} \omega_{i}^{2} = 1$.

Then, the optimal design vectors are computed using the proposed algorithm as:

$$ \begin{aligned}&\theta_{1} = \theta_{2} = \left( {\begin{array}{*{20}c} { - 0.3212} \\ {3.4481} \\ \end{array} } \right),\quad \theta_{3} = \theta_{4} = \left( {\begin{array}{*{20}c} {4.4483} \\ {2.7344} \\ \end{array} } \right), \\ &\theta_{5} = \theta_{6} = \left( {\begin{array}{*{20}c} {0.3550} \\ { - 1.7137} \\ \end{array} } \right),\quad \theta_{7} = \theta_{8} = \left( {\begin{array}{*{20}c} { - 1.5693} \\ { - 2.1999} \\ \end{array} } \right)\end{aligned} $$

Consequently, the robust and minimum norm gain controllers are computed as:

$$ \left\{ {\begin{array}{*{20}l} {F_{d} = \left( {\begin{array}{*{20}c} { - 48.1435 237.6409 - 353.0547 127.5210} \\ {23.8031 - 111.3804 162.9032 - 58.3722} \\ \end{array} } \right), } \hfill \\ {F_{a} = \left( {\begin{array}{*{20}c} { - 3.1619 26.9858 - 55.9704 36.8375} \\ { - 0.2100 - 11.2801 20.1939 - 13.6565} \\ \end{array} } \right).} \hfill \\ \end{array} } \right. $$

The results of the two solutions are presented in Table 2. The simulation results for both non-robust solution and robust and minimum norm solution are displayed in Fig. 5 using $x_{0} = \left[ {{-}0.01, {-}0.02, 0.01, {-}0.01} \right]^{\text{T}} {\text{m}}\,\, {\text{and}}\,\, \dot{x}_{0} = \left[ {0.01, 0.02, 0.02, {-}0.03} \right]^{\text{T}} \, {\text{m/s}}.$ It can be deduced that the robust and minimum norm solution obtains better performance with smaller control inputs compared with the non-robust one.

Table 2 Simulation results for Example 2

Fig. 5

Transient response for Example 2: a non-robust controller; b robust and minimum norm controller

Perturbed system

Next, a perturbation study is undertaken to show the behavior of closed-loop system. Suppose that the perturbations are defined as: $\Delta M = 0.001M, \,\Delta D = 0.001D,\,{\text{and}} \,\Delta K = 0.001K$, while C is kept unchanged. Remark that these uncertainties satisfy the regularization and stabilization (Constraints 3–5). Figure 6 illustrates the displacement, velocity and acceleration error trajectories ($e\left( t \right), \dot{e}\left( t \right)\, {\text{and}}\, \ddot{e}\left( t \right)$) for both non-robust solution and robust and minimum norm solution for perturbed closed-loop systems. Observe that the error trajectories for the robust and minimum norm controller are smaller compared with the non-robust solution. Moreover, for the non-robust solution and robust and minimum norm solution, the norms of errors in poles due to perturbation are computed, respectively, as 5.9287 and 1.2263. The norm of errors in poles due to perturbations for robust and minimum norm solution is significantly reduced by 383.47% compared with non-robust solution.

Fig. 6

Displacement, velocity and acceleration error trajectories for Example 2: a non-robust controller; b robust and minimum norm controller

6 Conclusions

This paper has generally formulated and proposed an innovative technique for matrix second-order systems to use direct displacement and acceleration measurements. The availability of accelerometers makes the proposed control methodology favorable to several practical applications where the acceleration signals are easier to obtain than the velocity ones. Explicit necessary conditions that ensure solvability are derived. The parametric expressions for the gain controllers as well as the eigenvector matrices are presented. Furthermore, a reliable algorithm for obtaining the robust and minimum controller gains is proposed. The solution is general and can be applied when the mass matrices are either singular or nonsingular. Two illustrative examples are presented to demonstrate the applicability of proposed control approach.