New Algorithms for Solving the Split Equality Problems in Hilbert Spaces

Abstract

We introduce a new approach by using unconstrained optimization to find a solution to the system of the split equality problems in real Hilbert spaces. Our new algorithms do not depend on the norm of the transfer mappings. We also give the relaxed iterative algorithms corresponding to the proposed algorithms. Finally, we present some numerical experiments to demonstrate the performance of the main results.

1 Introduction

Let $H_1, H_2$ and H be three real Hilbert spaces, let $C\subseteq H_1$ and $Q \subseteq H_2$ be two nonempty, closed and convex sets, let $A: H_1 \rightarrow H$ and $B : H_2 \rightarrow H$ be two bounded linear operators. The split equality problem (SEP, for short) was first introduced and studied by Moudafi et al. in 2013 (see, e.g., [11, 12]). The SEP is stated as follows:

$$\begin{aligned} \text {Find } v\in C,w\in Q\text { such that } A(v)=B(w). \end{aligned}$$

The SEP links closely to many different important problems. For instance, in game theory, in decomposition methods for PDE’s, in decision sciences and inertial Nash equilibration processes (see, e.g., [1, 2]), and the split feasibility problem which was later approached for inversion problems in intensity modulated radiation therapy (see, e.g., [4, 5]).

To find a solution to the SEP, in [11], Moudafi considered the constrained optimization problem:

$$\begin{aligned} \min _{v\in C, w\in Q} \dfrac{1}{2}\Vert Av-Bw\Vert ^2_H. \end{aligned}$$

From observing and writing down the optimal conditions, he obtained the following fixed point formulation:

$$\begin{aligned} {\left\{ \begin{array}{ll} v=P_C(v-\gamma A^*(Av-Bw)),\\ w=P_Q(w+\gamma B^*(Av-Bw)), \end{array}\right. } \end{aligned}$$

where $A^*$ and $B^*$ are the adjoint operators of A and B, respectively. This equation suggests the possibility of iterating, and thus he considered and established the alternating CQ-algorithm for solving the SEP, that is

$$\begin{aligned} {\left\{ \begin{array}{ll} x_{n+1}=P_C(x_n-\gamma A^*(Ax_n-By_n)),\\ y_{n+1}=P_Q(y_n+\gamma B^*(Ax_n-By_n)). \end{array}\right. } \end{aligned}$$

(1.1)

Under some suitable conditions [11, Theorem 2.1], he proved that the iterative sequence generated by (1.1) converges weakly to a solution of the SEP.

Due to their tremendous utility and wide applicability, many algorithms have been set up to solve the SEP or its modified version in different forms. For more details, see, for instance, [6,7,8,9,10, 14,15,16, 19,20,22, 24,25,26] and the references therein.

Very recently, in [23], Tuyen introduced and studied the more general problem, which is said to be the system of split equality problems (SSEP, for short). Namely, suppose that

• (D1) $H_1$, $H_2$ and H are three real Hilbert spaces; $C_i$ and $Q_i$ ($i=1,2,3,\ldots ,N$) are nonempty closed convex subsets of $H_1$ and $H_2$, respectively.

• (D2) $A_i: H_1\rightarrow H$ and $B_i: H_2\rightarrow H$ ($i=1,2,3,\ldots ,N$) are bounded linear operators.

• (D3) $b_i$ ($i=1,2,3,\ldots ,N$) are given elements in H.

• (D4) $\varOmega =\{(v,w) \in \cap _{i=1}^N(C_i\times Q_i): A_i(v)-B_i(w)=b_i, i=1,2,3,\ldots ,N\}\ne \emptyset .$

The SSEP is stated as follows:

$$\begin{aligned} \text {Find an element } p_*\in \varOmega . \end{aligned}$$

Using the Tikhonov regularization method, he proposed implicit and explicit iterative algorithms [23, Theorems 3.1 and 3.5] for solving the Problem SSEP. But, in the first algorithm, we have to solve an implicit equation. For the second algorithm, one of the control parameters requires computing or at least estimating the Lipschitz constant and the norm of the objective operators. In general, they are not easy work to perform in practice.

We also note that if $A_i\equiv A$, $B_i\equiv B$ and $b_i=0$ for all $i=1, 2, 3,\ldots , N$, then the SSEP becomes the multiple-sets split equality problem (MSSEP, for short) which has been studied by Tian et al. in [22]. They also have established a weak convergence algorithm with the split self-adaptive step size for solving the MSSEP.

In this paper, motivated and inspired by the above works, we will focus on and establish several new algorithms for solving the Problem SSEP with another approach. To begin this, for each $x=(v,w)\in \mathbb {H}:=H_1\times H_2$, we define the mapping $U:\mathbb {H}\rightarrow \mathbb {R}$ as follows:

$$\begin{aligned} U(x)=\frac{\sum _{i=1}^N\left[ \Vert A_i(v)-B_i(w)-b_i\Vert ^2_{ H}+\Vert v-P_{C_i}(v)\Vert ^2_{H_1}+\Vert w-P_{Q_i}(w)\Vert ^2_{H_2}\right] }{2}. \end{aligned}$$

We now consider the unconstrained optimization problem:

$$\begin{aligned} \min _{x\in \mathbb {H}} U(x). \end{aligned}$$

(1.2)

It is easy to see that U is a convex function and Problem SSEP is equivalent to Problem (1.2). Thus, $p_*=(v_*,w_*)$ is a solution of Problem SSEP if and only if $\nabla U(p_*)=0$, in which $\nabla U(x)=(U_1(x),U_2(x))$ with

$$\begin{aligned} U_1(x)&=\sum _{i=1}^N\left( \left( I^{H_1}-P_{C_i}^{H_1}\right) (v)+A_i^*\left( A_i(v)-B_i(w)-b_i\right) \right) ,\\ U_2(x)&=\sum _{i=1}^N\left( \left( I^{H_2}-P_{Q_i}^{H_2}\right) (w)-B_i^*\left( A_i(v)-B_i(w)-b_i\right) \right) . \end{aligned}$$

Moreover, we observe that $\nabla U(p_*)=0$ is equivalent to the problem of finding a fixed point $p_*$ of $I-\gamma \nabla U$, that is, $p_*=(I-\gamma \nabla U)(p_*)$ for some $\gamma >0$. Hence, in the present paper, we will introduce and study the convergence of the sequence $\{x_n\}$ defined by

$$x_{n+1}=x_n-\gamma _n\nabla U(x_n),$$

where $\gamma _n>0$ (see more detail in Algorithm 1). We first establish the weak convergence of Algorithm 1. Next, to obtain a strong convergence, we give a modification of Algorithm 1 by using the viscosity approximation method (see Algorithm 2). Some corollaries for solving the system of split feasibility problems are introduced in Section 4. Two relaxed iterative algorithms corresponding to Algorithms 1 and 2 are presented and studied in Section 5. Three numerical examples are discussed in Section 6 to examine the performance of the proposed algorithms.

2 Preliminaries

In this section, we denote by $\langle \cdot ,\cdot \rangle _{\mathcal {H}}$ and $\Vert \cdot \Vert _{\mathcal {H}}$ the inner product and the induced norm in a real Hilbert space $\mathcal H$. The symbols $\rightarrow$ and $\rightharpoonup$ are indicated the strong and weak convergence, respectively.

If $H_1$ and $H_2$ are real Hilbert spaces then $\mathbb {H}:=H_1\times H_2$ is also a Hilbert space (see, e.g., [14, Proposition 2.4] and [17, Proposition 2.2]) with the inner product

$$ \langle (x_1,y_1),(x_2,y_2)\rangle _{\mathbb {H}}=\langle x_1,x_2\rangle _{H_1}+\langle y_1,y_2\rangle _{H_2},\quad \forall (x_1,y_1),(x_2,y_2)\in \mathbb {H}, $$

and the norm on $\mathbb {H}$ is defined by

$$ \Vert (x,y)\Vert _{\mathbb {H}}^2=\Vert x\Vert _{H_1}^2+\Vert y\Vert _{H_2}^2,\quad \forall (x,y)\in \mathbb {H}. $$

The following lemmas are used in the sequel in the proofs of the main results.

Lemma 2.1

Let $P_C^{\mathcal {H}}$ be a metric projection from a real Hilbert space $\mathcal {H}$ into a nonempty, closed and convex subset C of $\mathcal {H}$. Then the following hold:

• (i) ([3, Theorem 3.14]) $\langle x-P_C^{\mathcal {H}}(x),y-P_C^{\mathcal {H}}(x)\rangle _{\mathcal {H}}\le 0,\quad \forall x\in \mathcal {H}, y\in C.$

• (ii) ([23, Lemma 2.1])

  $$\langle x-y,P_C^{\mathcal {H}}(x)-P_C^{\mathcal {H}}(y)\rangle _{\mathcal {H}}\ge \Vert P_C^{\mathcal {H}}(x)-P_C^{\mathcal {H}}(y)\Vert _{\mathcal {H}}^2,\quad \forall x,y\in \mathcal {H}.$$

• (iii) ([23, Lemma 2.1])

  $$\langle x-y,(I^{\mathcal {H}}- P_C^{\mathcal {H}})(x)-(I^{\mathcal {H}}- P_C^{\mathcal {H}})(y)\rangle _{\mathcal {H}}\ge \Vert (I^{\mathcal {H}}- P_C^{\mathcal {H}})(x)-(I^{\mathcal {H}}- P_C^{\mathcal {H}})(y)\Vert _{\mathcal {H}}^2$$

  for all $x,y\in \mathcal {H}$. It also follows that $I^{\mathcal {H}}- P_C^{\mathcal {H}}$ is a nonexpansive mapping.

Lemma 2.2

[13, Lemma 3] Let $\mathcal {H}$ be a real Hilbert space and let $\{x_n\}$ be a sequence in $\mathcal {H}$ such that $x_n\rightharpoonup z$ when $n\rightarrow \infty$. Then we have

$$ \liminf _{n\rightarrow \infty } \Vert x_n-z\Vert _{\mathcal {H}}<\liminf _{n\rightarrow \infty } \Vert x_n-x\Vert _{\mathcal {H}} $$

for all $x\in \mathcal {H}$ and $x\ne z$.

Lemma 2.3

[3, Theorem 4.17] Let C be a nonempty closed convex bounded subset of a Hilbert space $\mathcal {H}$ and $T: C \rightarrow \mathcal {H}$ a nonexpansive mapping. Then the mapping $I^{\mathcal {H}}-T$ is demiclosed, that is, whenever $\{x_n\}$ is a sequence in C which satisfies $x_n\rightharpoonup x \in C$ and $x_n-T(x_n)\rightarrow y\in \mathcal {H}$, it follows that $x-T(x) = y$.

Lemma 2.4

For every $x, y\in \mathcal {H}$, we have

$$\Vert x+y\Vert _{\mathcal {H}}^2\le \Vert x\Vert _{\mathcal {H}}^2+2\langle y,x+y\rangle _{\mathcal {H}}.$$

Lemma 2.5

[18, Lemma 2.6] Let $\{a_n\}$ be a sequence of positive real numbers, $\{b_n\}$ be a sequence of real numbers in (0, 1) such that $\sum _{n=1}^\infty b_n =\infty$ and $\{c_n\}$ be a sequence of real numbers. Assume that

$$a_{n+1}\le (1-b_n)a_n+ b_n c_n,\quad \forall n \ge 1.$$

If

$$\limsup _{k \rightarrow \infty } c_{n_k} \le 0$$

for every subsequence $\{a_{n_k}\}$ of $\{a_n\}$ satisfying

$$ \liminf _{k\rightarrow \infty } (a_{n_k+1}-a_{n_k})\ge 0, $$

then $\lim _{n \rightarrow \infty } a_n =0.$

3 Main Results

In this section, we always suppose all conditions from (D1) to (D4) are held. From now on, we consistently denote $\mathbb {H}:=H_1\times H_2$. To solve Problem SSEP, we first introduce the following algorithm.

Algorithm 1

Step 1. Choose $x_0=(v_0,w_0)\in \mathbb {H}:=H_1\times H_2$ arbitrarily and set $n:=0$.

Step 2. Given $x_{n}=(v_n,w_n)$, compute

$$\begin{aligned} x_{n+1}=x_n-\gamma _n \nabla U(x_n), \end{aligned}$$

(3.1)

with the parameter $\{\gamma _n\}$ is defined by

$$\begin{aligned} \gamma _n=\rho _n\dfrac{D_n}{E_n+F_n+\zeta _n}, \end{aligned}$$

(3.2)

where $\rho _n\in [a,b]\subset (0,2)$, $\{\zeta _n\}$ is a sequence of positive real numbers which is upper bounded by $\zeta$, and

$$\begin{aligned} D_n&:=\sum _{i=1}^N \Vert (I^{H_1}-P_{C_i}^{H_1})(v_n)\Vert ^2_{H_1}+\sum _{i=1}^N \Vert (I^{H_2}-P_{Q_i}^{H_2})(w_n)\Vert ^2_{H_2}\\&\,\,\,\,\,\,+\sum _{i=1}^N \Vert A_i(v_n)-B_i(w_n)-b_i\Vert ^2_{H},\\ E_n&:=\left\| \sum _{i=1}^N\left( (I^{H_1}-P_{C_i}^{H_1})(v_n)+A_i^*(A_i(v_n)-B_i(w_n)-b_i)\right) \right\| ^2_{H_1},\\ F_n&:=\left\| \sum _{i=1}^N\left( (I^{H_2}-P_{Q_i}^{H_2})(w_n)-B_i^*(A_i(v_n)-B_i(w_n)-b_i)\right) \right\| ^2_{H_2}. \end{aligned}$$

Step 3. Set $n\leftarrow n+1$, and go to Step 2.

We have the following theorem.

Theorem 3.1

The sequence $\{x_n\}$ generated by Algorithm 1 converges weakly to a solution of Problem SSEP.

Proof

The proof is split into several steps. We take any point $p=(v,w)\in \varOmega$.

Claim 1

The sequence $\{x_n\}$ is bounded.

It takes from (3.1) that

$$\begin{aligned} \Vert x_{n+1}-p\Vert _{\mathbb {H}}^2&=\Vert x_n-\gamma _n \nabla U(x_n)-p\Vert _{\mathbb {H}}^2\nonumber \\&=\Vert x_n-p\Vert _{\mathbb {H}}^2-2\gamma _n \langle \nabla U(x_n),x_n-p\rangle _{\mathbb {H}}+\gamma _n^2\Vert \nabla U(x_n)\Vert _{\mathbb {H}}^2. \end{aligned}$$

(3.3)

We observe that

$$\begin{aligned} \langle \nabla U(x_n),x_n-p\rangle _{\mathbb {H}}=&\sum _{i=1}^N\left\langle (I^{H_1}-P_{C_i}^{H_1})(v_n),v_n-v\right\rangle _{H_1}\\&+ \sum _{i=1}^N\left\langle (I^{H_2}-P_{Q_i}^{H_2})(w_n),w_n-w\right\rangle _{H_2}\\&+\sum _{i=1}^N\langle A_i^*(A_i(v_n)-B_i(w_n)-b_i),v_n-v\rangle _{H_1}\\&-\sum _{i=1}^N\langle B_i^*(A_i(v_n)-B_i(w_n)-b_i),w_n-w\rangle _{H_2}\\ =&\sum _{i=1}^N\left\langle (I^{H_1}-P_{C_i}^{H_1})(v_n)-(I^{H_1}-P_{C_i}^{H_1})(v),v_n-v\right\rangle _{H_1}\\&+ \sum _{i=1}^N\left\langle (I^{H_2}-P_{Q_i}^{H_2})(w_n)-(I^{H_2}-P_{Q_i}^{H_2})(w),w_n-w\right\rangle _{H_2}\\&+\sum _{i=1}^N\langle A_i(v_n)-B_i(w_n)-b_i,A_i(v_n)-A_i(v)\rangle _{H}\\&-\sum _{i=1}^N\langle A_i(v_n)-B_i(w_n)-b_i,B_i(w_n)-B_i(w)\rangle _{H} \end{aligned}$$

$$\begin{aligned} =&\sum _{i=1}^N\left\langle (I^{H_1}-P_{C_i}^{H_1})(v_n)-(I^{H_1}-P_{C_i}^{H_1})(v),v_n-v\right\rangle _{H_1}\nonumber \\&+ \sum _{i=1}^N\left\langle (I^{H_2}-P_{Q_i}^{H_2})(w_n)-(I^{H_2}-P_{Q_i}^{H_2})(w),w_n-w\right\rangle _{H_2}\nonumber \\&+\sum _{i=1}^N\Vert A_i(v_n)-B_i(w_n)-b_i\Vert ^2_{H}. \end{aligned}$$

(3.4)

In view of Lemma 2.1 (iii) and (3.4), we can find that

$$\begin{aligned} \langle \nabla U(x_n),x_n-p\rangle _{\mathbb {H}}&\ge \sum _{i=1}^N\left\| (I^{H_1}-P_{C_i}^{H_1})(v_n)-(I^{H_1}-P_{C_i}^{H_1})(v)\right\| ^2_{H_1}\\&\,\,\,\,\,\,+ \sum _{i=1}^N\left\| (I^{H_2}-P_{Q_i}^{H_2})(w_n)-(I^{H_2}-P_{Q_i}^{H_2})(w)\right\| ^2_{H_2}\\&\,\,\,\,\,\,+\sum _{i=1}^N\Vert A_i(v_n)-B_i(w_n)-b_i\Vert ^2_{H}\\&=\sum _{i=1}^N\left\| (I^{H_1}-P_{C_i}^{H_1})(v_n)\right\| ^2_{H_1}+\sum _{i=1}^N\left\| (I^{H_2}-P_{Q_i}^{H_2})(w_n)\right\| ^2_{H_2}\\&\,\,\,\,\,\,+\sum _{i=1}^N\Vert A_i(v_n)-B_i(w_n)-b_i\Vert ^2_{H}. \end{aligned}$$

This implies that

$$\begin{aligned} \langle \nabla U(x_n),x_n-p\rangle _{\mathbb {H}}\ge D_n. \end{aligned}$$

(3.5)

Besides, we also note that

$$\begin{aligned} \Vert \nabla U(x_n)\Vert _{\mathbb {H}}^2&=\left\| \sum _{i=1}^N\left( (I^{H_1}-P_{C_i}^{H_1})(v_n)+A_i^*(A_i(v_n)-B_i(w_n)-b_i)\right) \right\| ^2_{H_1}\nonumber \\&\,\,\,\,\,\,+\left\| \sum _{i=1}^N\left( (I^{H_2}-P_{Q_i}^{H_2})(w_n)-B_i^*(A_i(v_n)-B_i(w_n)-b_i)\right) \right\| ^2_{H_2}\nonumber \\&=E_n+F_n. \end{aligned}$$

(3.6)

Thus, it follows from (3.2), (3.3), (3.5) and (3.6) that

$$\begin{aligned} \Vert x_{n+1}-p\Vert _{\mathbb {H}}^2&\le \Vert x_n-p\Vert _{\mathbb {H}}^2-2\gamma _n D_n+\gamma _n^2(E_n+F_n)\nonumber \\&= \Vert x_n-p\Vert _{\mathbb {H}}^2-2\rho _n \dfrac{D_n^2}{E_n+F_n+\zeta _n}+\rho _n^2\dfrac{D_n^2(E_n+F_n)}{(E_n+F_n+\zeta _n)^2}\nonumber \\&\le \Vert x_n-p\Vert _{\mathbb {H}}^2-2\rho _n \dfrac{D_n^2}{E_n+F_n+\zeta _n}+\rho _n^2\dfrac{D_n^2}{E_n+F_n+\zeta _n}\nonumber \\&=\Vert x_n-p\Vert _{\mathbb {H}}^2-\rho _n(2-\rho _n) \dfrac{D_n^2}{E_n+F_n+\zeta _n}. \end{aligned}$$

(3.7)

From the condition $\rho _n\in [a,b]\subset (0,2)$ and (3.7), we obtain

$$\begin{aligned} \Vert x_{n+1}-p\Vert _{\mathbb {H}}^2\le \Vert x_n-p\Vert _{\mathbb {H}}^2. \end{aligned}$$

(3.8)

By employing mathematical induction, we find that the sequence $\{x_n\}$ is bounded.

Claim 2

For every $i=1,2,3,\ldots ,N$, we have

$$\begin{aligned} \left\| (I^{H_1}-P_{C_i}^{H_1})(v_n))\right\| ^2_{H_1}&\rightarrow 0, \end{aligned}$$

(3.9)

$$\begin{aligned} \left\| (I^{H_2}-P_{Q_i}^{H_2})(w_n)\right\| ^2_{H_2}&\rightarrow 0, \end{aligned}$$

(3.10)

$$\begin{aligned} \Vert A_i(v_n)-B_i(w_n)-b_i\Vert ^2_{H}&\rightarrow 0. \end{aligned}$$

(3.11)

From (3.7), we have

$$\begin{aligned} \rho _n(2-\rho _n) \dfrac{D_n^2}{E_n+F_n+\zeta _n}\le \Vert x_n-p\Vert _{\mathbb {H}}^2-\Vert x_{n+1}-p\Vert _{\mathbb {H}}^2. \end{aligned}$$

On the other hand, it takes from (3.8) that the finite limit of the sequence $\{\Vert x_n-p\Vert _{\mathbb {H}}^2\}$ exists. Thus, from the conditions $\rho _n\in [a,b]\subset (0,2)$, $0<\zeta _n\le \zeta$ and the above inequality, we can infer that

$$\begin{aligned} \dfrac{D_n^2}{E_n+F_n+\zeta } \rightarrow 0. \end{aligned}$$

This leads to

$$\begin{aligned} D_n\rightarrow 0. \end{aligned}$$

(3.12)

From the definition of $D_n$ and (3.12), we obtain the limitations (3.9), (3.10) and (3.11), as claimed.

Claim 3

The sequence $\{x_n\}$ converges weakly to $p_*\in \varOmega$.

Since $\{x_n\}$ is a bounded sequence, there exists the subsequence $\{x_{n_k}\}:=\{(v_{n_k},w_{n_k})\}$ of $\{x_n\}$ which converges weakly to some $z=(v_*,w_*)\in \mathbb {H}$, that is,

$$ v_{n_k}\rightharpoonup v_*,\quad w_{n_k}\rightharpoonup w_*. $$

In view of Lemma 2.3, (3.9) and (3.10), we get $(v_*,w_*)\in C_i\times Q_i$ for all $i=1,2,\ldots ,N$. On the other hand, since $A_i$ and $B_i$ are bounded linear operators, we have

$$\begin{aligned} A_i(v_{n_k})-B_i(w_{n_k})-b_i\rightharpoonup A_i(v_*)-B_i(w_*)-b_i,\quad \forall i=1,2,\ldots ,N. \end{aligned}$$

Combining with (3.11), we can infer that

$$ A_i(v_*)-B_i(w_*)-b_i=0,\quad \forall i=1,2,\ldots ,N. $$

Therefore, we have $z\in \varOmega$.

Finally, we shall demonstrate that $x_n\rightharpoonup z$. Suppose that there is another subsequence $\{x_{n_m}\}$ of $\{x_n\}$ such that $x_{n_m}\rightharpoonup \bar{z}$ with $\bar{z}\ne z$. Using an argument similar to the one used above, we again also get that $\bar{z}\in \varOmega$. It follows from Lemma 2.2 and the existence of the finite limit of $\{\Vert x_n-z\Vert _{\mathbb {H}}\}$ that

$$\begin{aligned} \liminf _{k\rightarrow \infty } \Vert x_{n_k}-z\Vert _{\mathbb {H}}&<\liminf _{k\rightarrow \infty } \Vert x_{n_k}-\bar{z}\Vert _{\mathbb {H}}\\&=\liminf _{m\rightarrow \infty } \Vert x_{n_m}-\bar{z}\Vert _{\mathbb {H}}\\&<\liminf _{m\rightarrow \infty } \Vert x_{n_m}-z\Vert _{\mathbb {H}}\\&=\liminf _{k\rightarrow \infty } \Vert x_{n_k}-z\Vert _{\mathbb {H}}. \end{aligned}$$

This is a contradiction. It implies that $x_{n_m}\rightharpoonup z$. Therefore, we obtain that $x_n\rightharpoonup z$.

This completes the proof.$\square$

To obtain the strong convergence theorem, we now combine Algorithm 1 with the viscosity approximation method. The second algorithm is established as follows:

Algorithm 2

Step 1. Choose $x_0=(v_0,w_0)\in \mathbb {H}:=H_1\times H_2$ arbitrarily and set $n:=0$.

Step 2. Given $x_{n}=(v_n,w_n)$, compute

$$\begin{aligned} x_{n+1}=\alpha _n h(x_n)+(1-\alpha _n)(x_n-\gamma _n \nabla U(x_n)), \end{aligned}$$

(3.13)

where $h:\mathbb {H}\rightarrow \mathbb {H}$ is a contraction mapping with constant $\delta \in [0,1)$, $\{\gamma _n\}$ is defined as in (3.2) and $\{\alpha _n\}\subset (0,1)$ satisfies

$$ \lim _{n\rightarrow \infty } \alpha _n=0,\quad \sum _{n=1}^\infty \alpha _n=\infty . $$

Step 3. Set $n\leftarrow n+1$, and go to Step 2.

Theorem 3.2

The sequence $\{x_n\}$ generated by Algorithm 2 converges strongly to $p_*=P_\varOmega (h(p_*))$.

Proof

The proof is divided into several steps. We first put $y_n=x_n-\gamma _n \nabla U(x_n)$ and take any $p\in \varOmega$.

Claim 1

The sequence $\{x_n\}$ is bounded.

It follows from (3.13) that

$$\begin{aligned} \Vert x_{n+1}-p\Vert _{\mathbb {H}}&=\Vert \alpha _n h(x_n)+(1-\alpha _n)(x_n-\gamma _n \nabla U(x_n))-p\Vert _{\mathbb {H}}\\&=\Vert \alpha _n (h(x_n)-p)+(1-\alpha _n)(y_n-p)\Vert _{\mathbb {H}}. \end{aligned}$$

By the convexity of $\Vert \cdot \Vert _{\mathbb {H}}$ and h is a contraction mapping with constant $\delta \in [0,1)$, we can find that

$$\begin{aligned} \Vert x_{n+1}-p\Vert _{\mathbb {H}}&\le \alpha _n\Vert h(x_n)-p\Vert _{\mathbb {H}}+(1-\alpha _n)\Vert y_n-p\Vert _{\mathbb {H}}\nonumber \\&\le \alpha _n[\Vert h(x_n)-h(p)\Vert _{\mathbb {H}}+\Vert h(p)-p\Vert _{\mathbb {H}}]+(1-\alpha _n)\Vert y_n-p\Vert _{\mathbb {H}}\nonumber \\&\le \alpha _n[\delta \Vert x_n-p\Vert _{\mathbb {H}}+\Vert h(p)-p\Vert _{\mathbb {H}}]+(1-\alpha _n)\Vert y_n-p\Vert _{\mathbb {H}}. \end{aligned}$$

(3.14)

By an argument similar as in Claim 1 of Theorem 3.1, we can find that

$$\begin{aligned} \Vert y_n-p\Vert _{\mathbb {H}}^2&=\Vert x_n-\gamma _n \nabla U(x_n)-p\Vert _{\mathbb {H}}^2\nonumber \\&\le \Vert x_n-p\Vert _{\mathbb {H}}^2-\rho _n(2-\rho _n) \dfrac{D_n^2}{E_n+F_n+\zeta _n} \end{aligned}$$

(3.15)

$$\begin{aligned}&\le \Vert x_n-p\Vert _{\mathbb {H}}^2. \end{aligned}$$

(3.16)

From (3.14) and (3.16), we can infer that

$$\begin{aligned} \Vert x_{n+1}-p\Vert _{\mathbb {H}}&\le \alpha _n[\delta \Vert x_n-p\Vert _{\mathbb {H}}+\Vert h(p)-p\Vert _{\mathbb {H}}]+(1-\alpha _n)\Vert x_n-p\Vert _{\mathbb {H}}\\&=(1-\alpha _n(1-\delta ))\Vert x_n-p\Vert _{\mathbb {H}}+\alpha _n \Vert h(p)-p\Vert _{\mathbb {H}}\\&=(1-\alpha _n(1-\delta ))\Vert x_n-p\Vert _{\mathbb {H}}+\alpha _n(1-\delta )\dfrac{\Vert h(p)-p\Vert _{\mathbb {H}}}{1-\delta }\\&\le \max \left\{ \Vert x_n-p\Vert _{\mathbb {H}},\dfrac{\Vert h(p)-p\Vert _{\mathbb {H}}}{1-\delta } \right\} . \end{aligned}$$

By employing mathematical induction, we find that the sequence $\{x_n\}$ is bounded. Hence, the sequences $\{y_n\}$ and $\{h(x_n)\}$ are also bounded.

Claim 2

We have

$$\begin{aligned} \rho _n(2-\rho _n) \dfrac{D_n^2}{E_n+F_n+\zeta _n}\le \Vert x_n-p\Vert _{\mathbb {H}}^2-\Vert x_{n+1}-p\Vert _{\mathbb {H}}^2+\alpha _nM_1, \end{aligned}$$

(3.17)

where $M_1=\sup _{n}\{ \Vert h(x_n)-p\Vert _{\mathbb {H}}^2\}<\infty$.

Indeed, from (3.13), (3.15) and Lemma 2.4, we have

$$\begin{aligned} \Vert x_{n+1}-p\Vert _{\mathbb {H}}^2&= \Vert \alpha _n (h(x_n)-p)+(1-\alpha _n)(y_n-p)\Vert _{\mathbb {H}}^2\\&\le \alpha _n\Vert h(x_n)-p\Vert _{\mathbb {H}}^2+(1-\alpha _n)\Vert y_n-p\Vert _{\mathbb {H}}^2\\&\le M_1\alpha _n+\Vert y_n-p\Vert _{\mathbb {H}}^2\\&\le \Vert x_n-p\Vert _{\mathbb {H}}^2+\alpha _nM_1-\rho _n(2-\rho _n) \dfrac{D_n^2}{E_n+F_n+\zeta _n}. \end{aligned}$$

It is easy to see that the last inequality can be rewritten in the form (3.17), as claimed.

Claim 3

We have the following inequality:

$$\begin{aligned} a_{n+1}\le (1-b_n)a_n+ b_n c_n,\quad \forall n \ge 1, \end{aligned}$$

(3.18)

where

$$\begin{aligned} a_n&:=\Vert x_n-p\Vert _{\mathbb {H}}^2,\\ b_n&:=\alpha _n(1-\delta ),\\ c_n&:=\dfrac{2\langle h(p)-p,x_{n+1}-p\rangle _{\mathbb {H}}}{1-\delta }. \end{aligned}$$

Indeed, one again, from (3.13), (3.16) and Lemma 2.4, we can see that

$$\begin{aligned} \Vert x_{n+1}-p\Vert _{\mathbb {H}}^2=&\Vert \alpha _n (h(x_n)-p)+(1-\alpha _n)(y_n-p)\Vert _{\mathbb {H}}^2\\ =&\Vert \alpha _n (h(x_n)-h(p))+(1-\alpha _n)(y_n-p)+\alpha _n(h(p)-p)\Vert _{\mathbb {H}}^2\\ \le&\Vert \alpha _n (h(x_n)-h(p))+(1-\alpha _n)(y_n-p)\Vert _{\mathbb {H}}^2\\&+2\alpha _n\langle h(p)-p,x_{n+1}-p\rangle _{\mathbb {H}}\\ \le&\alpha _n \Vert h(x_n)-h(p)\Vert _{\mathbb {H}}^2+(1-\alpha _n)\Vert y_n-p\Vert _{\mathbb {H}}^2\\&+2\alpha _n\langle h(p)-p,x_{n+1}-p\rangle _{\mathbb {H}}\\ \le&\alpha _n\delta \Vert x_n-p\Vert _{\mathbb {H}}^2+(1-\alpha _n)\Vert x_n-p\Vert _{\mathbb {H}}^2\\&+2\alpha _n\langle h(p)-p,x_{n+1}-p\rangle _{\mathbb {H}}\\ =&(1-\alpha _n(1-\delta ))\Vert x_n-p\Vert _{\mathbb {H}}^2 +\alpha _n(1-\delta )\dfrac{2\langle h(p)-p,x_{n+1}-p\rangle _{\mathbb {H}}}{1-\delta }. \end{aligned}$$

It is not difficult to see that the above inequality can be rewritten in the form (3.18), as claimed.

Claim 4

The sequence $\{x_n\}$ converges strongly to $p_*=P_\varOmega (h(p_*))$.

Suppose that $\{\Vert x_{n_m}-p_*\Vert ^2\}$ is an arbitrary subsequence of $\{\Vert x_n-p_*\Vert ^2\}$ such that

$$ \liminf _{k\rightarrow \infty }(\Vert x_{n_m+1}-p_*\Vert ^2-\Vert x_{n_m}-p_*\Vert ^2)\ge 0. $$

It follows from Claim 2, $\alpha _{n_m}\rightarrow 0$ and $\rho _{n_m}\in [a,b]\subset (0,2)$ that

$$ \dfrac{D_{n_m}^2}{E_{n_m}+F_{n_m}+\zeta _{n_m}}\rightarrow 0. $$

Since $\zeta _{n_m}\le \zeta$, we have

$$ \dfrac{D_{n_m}^2}{E_{n_m}+F_{n_m}+\zeta }\rightarrow 0, $$

which implies that $D_{n_m}\rightarrow 0$. Hence, we can find that

$$\begin{aligned} \left\| (I^{H_1}-P_{C_i}^{H_1})(v_{n_m})\right\| ^2_{H_1}&\rightarrow 0, \end{aligned}$$

(3.19)

$$\begin{aligned} \left\| (I^{H_2}-P_{Q_i}^{H_2})(w_{n_m})\right\| ^2_{H_2}&\rightarrow 0, \end{aligned}$$

(3.20)

$$\begin{aligned} \Vert A_i(v_{n_m})-B_i(w_{n_m})-b_i\Vert ^2_{H}&\rightarrow 0. \end{aligned}$$

(3.21)

In addition, we also have

$$\begin{aligned} \Vert y_{n_m}-x_{n_m}\Vert _{\mathbb {H}}^2&=\gamma _{n_m}^2(E_{n_m}+F_{n_m})\\&=\rho _{n_m}^2\dfrac{D_{n_m}^2(E_{n_m}+F_{n_m})}{(E_{n_m}+F_{n_m}+\zeta _{n_m})^2}\\&\le b^2\dfrac{D_{n_m}^2}{E_{n_m}+F_{n_m}+\zeta _{n_m}}\rightarrow 0. \end{aligned}$$

This implies that

$$\begin{aligned} \Vert y_{n_m}-x_{n_m}\Vert _{\mathbb {H}}\rightarrow 0. \end{aligned}$$

(3.22)

By the boundedness of $\{x_{n_m}\}$ and $\{h(x_{n_m})\}$, we observe that

$$\begin{aligned} \Vert x_{n_m+1}-x_{n_m}\Vert _{\mathbb {H}}&=\Vert \alpha _{n_m} (h(x_{n_m})-x_{n_m})+(1-\alpha _{n_m})(y_{n_m}-x_{n_m})\Vert _{\mathbb {H}}\nonumber \\&\le \alpha _{n_m} \Vert h(x_{n_m})-x_{n_m}\Vert _{\mathbb {H}}+(1-\alpha _{n_m})\Vert y_{n_m}-x_{n_m}\Vert _{\mathbb {H}}\nonumber \\&\le \alpha _{n_m} M_2+(1-\alpha _{n_m})\Vert y_{n_m}-x_{n_m}\Vert _{\mathbb {H}}, \end{aligned}$$

(3.23)

where $M_2=\sup _{m}\{\Vert h(x_{n_m})-x_{n_m}\Vert _{\mathbb {H}}\}$. Thus, it takes from (3.22) and (3.23) that

$$\begin{aligned} \Vert x_{n_m+1}-x_{n_m}\Vert _{\mathbb {H}}\rightarrow 0. \end{aligned}$$

(3.24)

Finally, to apply Lemma 2.5, from Claim 3, it suffices to prove the following inequality

$$\limsup _{m\rightarrow \infty }c_{n_m}\le 0.$$

It is equivalent to show that $\limsup _{m\rightarrow \infty }\langle h(p_*)-p_*,x_{n_m+1}-p_*\rangle \le 0.$ We first note that

$$\begin{aligned}&\langle h(p_*)-p_*,x_{n_m+1}-p_*\rangle \nonumber \\ =&\langle h(p_*)-p_*,x_{n_m+1}-x_{n_m}\rangle +\langle h(p_*)-p_*,x_{n_m}-p_*\rangle \nonumber \\ \le&\Vert h(p_*)-p_*\Vert \Vert x_{n_m+1}-x_{n_m}\Vert +\langle h(p_*)-p_*,x_{n_m}-p_*\rangle . \end{aligned}$$

(3.25)

Since $\{x_{n_m}\}$ is a bounded sequence (Claim 1), there exists a subsequence $\{x_{n_{m_j}}\}$ of $\{x_{n_m}\}$ which converges weakly to some $z\in \mathbb {H}$, such that

$$\begin{aligned} \limsup _{m\rightarrow \infty }\langle h(p_*)-p_*,x_{n_m}-p_*\rangle _{\mathbb {H}}&=\lim _{j\rightarrow \infty }\langle h(p_*)-p_*,x_{n_{m_j}}-p_*\rangle _{\mathbb {H}}\\&=\langle h(p_*)-p_*,z-p_*\rangle _{\mathbb {H}}. \end{aligned}$$

Furthermore, from (3.19), (3.20), (3.21) and using an argument similar to the proof of Claim 3 in Theorem 3.1, we obtain that $z\in \varOmega$. Besides, from the definition of $p_*$ and Lemma 2.1 (i), we obtain that

$$\begin{aligned} \limsup _{m\rightarrow \infty }\langle h(p_*)-p_*,x_{n_m}-p_*\rangle =\langle h(p_*)-p_*,z-p_*\rangle \le 0. \end{aligned}$$

(3.26)

Using (3.24), (3.25), (3.26), we find that $\limsup _{m\rightarrow \infty }c_{n_m}\le 0$. Hence, it is not difficult to see that all the hypotheses of Lemma 2.5 are satisfied. This guarantees that $\Vert x_n-p_*\Vert \rightarrow 0$.

This completes the proof.$\square$

Remark 3.1

It follows from (3.6) that if $E_n+F_n=0$ then $\nabla U(x_n)=0$. In this case, we have that $x_n=(v_n,w_n)$ is a solution to the SSEP and, thus, we can stop the algorithm. If otherwise, we can select the parameter $\zeta _n=0$ which leads to $\gamma _n=\rho _n\frac{D_n}{E_n+F_n}$. On the other hand, we note that

$$\begin{aligned} E_n+F_n\le&2\left( \sum _{i=1}^N \left\| (I^{H_1}-P_{C_i}^{H_1})(v_n)\right\| ^2_{H_1}+\sum _{i=1}^N \left\| (I^{H_2}-P_{Q_i}^{H_2})(w_n)\right\| ^2_{H_2}\right) \\&+2\sum _{i=1}^N \Vert A_i\Vert ^2 \Vert A_i(v_n)-B_i(w_n)-b_i\Vert ^2_{H}\\&+2\sum _{i=1}^N \Vert B_i\Vert ^2 \Vert A_i(v_n)-B_i(w_n)-b_i\Vert ^2_{H} \le \kappa D_n, \end{aligned}$$

where $\kappa =2\max \{ 1, \max _{1\le i\le N}\{\Vert A_i\Vert ^2\}+\max _{1\le i\le N}\{\Vert B_i\Vert \}^2 \}$. This guarantees that $D_n\rightarrow 0$ whenever $\frac{D_n^2}{E_n+F_n}\rightarrow 0$.

Hence, the conclusions of Theorems 3.1 and 3.2 are still valued by employing an argument similar to the one used in the proof of these.

4 Corollaries

It is easy to see that if $H\equiv H_2$, $B_i$ is the identity mapping on H and $b_i=0$ for all $i=1,2,3,\ldots ,N$, then Problem SSEP becomes the system of split feasibility problems, that is,

$$\begin{aligned} \text {Find an element } p_*\in \widehat{\varOmega }, \end{aligned}$$

(4.1)

where

$$\widehat{\varOmega }=\left\{ (v,w) \in \cap _{i=1}^N(C_i\times Q_i): A_i(v)-w=0,\ i=1,2,3,\ldots ,N\right\} \ne \emptyset .$$

Furthermore, Problem (4.1) reduces to the split feasibility problem in the case that $N=1$.

We now denote $\nabla \widehat{U}(x):=(\widehat{U}_1(x),\widehat{U}_2(x))$ for all $x=(v,w)\in \mathbb {H}$ with

$$\begin{aligned} \widehat{U}_1(x)&:=\sum _{i=1}^N\left( (I^{H_1}-P_{C_i}^{H_1})(v)+A_i^*(A_i(v)-w)\right) ,\\ \widehat{U}_2(x)&:=\sum _{i=1}^N\left( (I^{H_2}-P_{Q_i}^{H_2})(w)-(A_i(v)-w)\right) . \end{aligned}$$

From Algorithm 1, we obtain the following algorithm.

Algorithm 3

Step 1. Choose $x_0=(v_0,w_0)\in \mathbb {H}:=H_1\times H_2$ arbitrarily and set $n:=0$.

Step 2. Given $x_{n}=(v_n,w_n)$, compute

$$\begin{aligned} x_{n+1}=x_n-\widehat{\gamma }_n \nabla \widehat{U}(x_n), \end{aligned}$$

with the parameter $\{\gamma _n\}$ is defined by

$$\begin{aligned} \widehat{\gamma }_n=\rho _n\dfrac{\widehat{D}_n}{\widehat{E}_n+\widehat{F}_n+\zeta _n}, \end{aligned}$$

where $\rho _n\in [a,b]\subset (0,2)$, $\{\zeta _n\}$ is a sequence of positive real numbers which is upper bounded by $\zeta$, and

$$\begin{aligned} \widehat{D}_n&:=\sum _{i=1}^N\left[ \left\| (I^{H_1}-P_{C_i}^{H_1})(v_n)\right\| ^2_{H_1}+\left\| (I^{H_2}-P_{Q_i}^{H_2})(w_n)\right\| ^2_{H_2}+\Vert A_i(v_n)-w_n\Vert ^2_{H_2}\right] ,\\ \widehat{E}_n&:=\Vert \sum _{i=1}^N\left( (I^{H_1}-P_{C_i}^{H_1})(v_n)+A_i^*(A_i(v_n)-w_n)\right) \Vert ^2_{H_1},\\ \widehat{F}_n&:=\Vert \sum _{i=1}^N\left( (I^{H_2}-P_{Q_i}^{H_2})(w_n)-(A_i(v_n)-w_n)\right) \Vert ^2_{H_2}. \end{aligned}$$

Step 3. Set $n\leftarrow n+1$, and go to Step 2.

Theorem 4.1

The sequence $\{x_n\}$ generated by Algorithm 3 converges weakly to a solution $p_*=(v_*,w_*)$ to Problem (4.1).

From Algorithm 2, we obtain Algorithm 4 below.

Algorithm 4

Step 1. Choose $x_0=(v_0,w_0)\in \mathbb {H}:=H_1\times H_2$ arbitrarily and set $n:=0$.

Step 2. Given $x_{n}=(v_n,w_n)$, compute

$$\begin{aligned} x_{n+1}=\alpha _n h(x_n)+(1-\alpha _n)(x_n-\widehat{\gamma }_n \nabla \widehat{U}(x_n)), \end{aligned}$$

where $h:\mathbb {H}\rightarrow \mathbb {H}$ and $\{\alpha _n\}$ are defined as in Step 2 of Algorithm 2 while $\{\widehat{\gamma }_n\}$ is defined as in Step 2 of Algorithm 3.

Step 3. Set $n\leftarrow n+1$, and go to Step 2.

Theorem 4.2

The sequence $\{x_n\}$ generated by Algorithm 4 converges strongly to a unique solution $(v_*,w_*)$ to Problem (4.1) such that $p_*=P_{\widehat{\varOmega }}(h(p_*))$.

5 Relaxed Iterative Algorithms

In this section, we consider Problem SSEP when $C_i$ and $Q_i$ are sublevel sets of the lower semicontinuous convex functions $c_i: H_1 \rightarrow \mathbb {R}$ and $q_i: H_2 \rightarrow \mathbb {R}$ and $i = 1, 2, \ldots , N$, respectively. Namely,

$$\begin{aligned} C_i&=\{v\in H_1: c_i(v)\le 0\},\\ Q_i&=\{w\in H_2: q_i(w)\le 0\}, \end{aligned}$$

where $c_i$ and $q_i$ are respectively subdifferentiable on $H_1$ and $H_2$, and that the subdifferentials $\partial c_i$ and $\partial q_i$ are bounded (on bounded sets).

At points $v_n \in H_1$ and $w_n \in H_2$, we define the subsets $C_{i,n}$ and $Q_{i,n}$ as follows:

$$\begin{aligned} C_{i,n}&=\{v\in H_1: c_i(v_n)\le \langle v_n-v,\mathfrak {c}_{i,n}\rangle _{H_1}\},\\ Q_{i,n}&=\{w\in H_2: q_i(w_n)\le \langle w_n-w,\mathfrak {q}_{i,n}\rangle _{H_2}\}, \end{aligned}$$

where $\mathfrak {c}_{i,n}\in \partial c_i(v_n)$ and $\mathfrak {q}_{i,n}\in \partial q_i(w_n).$ It is not hard to find that $C_{i,n}$ and $Q_{i,n}$ are half-spaces of $H_1$ and $H_2$. They are respectively called the relaxed sets of $C_i$ and $Q_i$. Besides, we also have $C_i\subset C_{i,n}$ and $Q_i\subset Q_{i,n}$.

In general, we are not easy to compute the metric projections $P_{C_i}^{H_1}$ and $P_{Q_i}^{H_2}$. It depends on the construct of the sets $C_i$ and $Q_i$. However, we do have the explicit expression of the metric projections $P_{C_{i,n}}^{H_1}$ and $P_{Q_{i,n}}^{H_2}$, which are

$$\begin{aligned} P_{C_{i,n}}^{H_1}(v)&=v-\max \left\{ 0,\frac{\langle v-v_n,\mathfrak {c}_{i,n}\rangle _{H_1}+c_i(v_n)}{\Vert \mathfrak {c}_{i,n}\Vert ^2_{H_1}}\right\} \mathfrak {c}_{i,n},\\ P_{Q_{i,n}}^{H_1}(w)&=w-\max \left\{ 0,\frac{\langle w-w_n,\mathfrak {q}_{i,n}\rangle _{H_2}+q_i(w_n)}{\Vert \mathfrak {q}_{i,n}\Vert ^2_{H_2}}\right\} \mathfrak {q}_{i,n}. \end{aligned}$$

Therefore, we obtain relaxed iterative algorithms corresponding to Algorithm 1 and Algorithm 2, where $P_{C_i}^{H_1}$ and $P_{Q_i}^{H_2}$ are respectively replaced by $P_{C_{i,n}}^{H_1}$ and $P_{Q_{i,n}}^{H_2}$.

We denote $\nabla \tilde{U}(x):=(\tilde{U}_1(x),\tilde{U}_2(x))$ for all $x=(v,w)\in \mathbb {H}$, where

$$\begin{aligned} \tilde{U}_1(x)&:=\sum _{i=1}^N\left( (I^{H_1}-P_{C_{i,n}}^{H_1})(v)+A_i^*(A_i(v)-B_i(w)-b_i)\right) ,\\ \tilde{U}_2(x)&:=\sum _{i=1}^N\left( (I^{H_2}-P_{Q_{i,n}}^{H_2})(w)-B_i^*(A_i(v)-B_i(w)-b_i)\right) . \end{aligned}$$

From Algorithm 1, we obtain the following algorithm.

Algorithm 5

Step 1. Choose $x_0=(v_0,w_0)\in \mathbb {H}:=H_1\times H_2$ arbitrarily and set $n:=0$.

Step 2. Given $x_{n}=(v_n,w_n)$, compute

$$\begin{aligned} x_{n+1}=x_n-\tilde{\gamma }_n \nabla \tilde{U}(x_n), \end{aligned}$$

with the parameter $\{\tilde{\gamma }_n\}$ is defined by

$$\begin{aligned} \tilde{\gamma }_n=\rho _n\dfrac{\tilde{D}_n}{\tilde{E}_n+\tilde{F}_n+\zeta _n}, \end{aligned}$$

where $\rho _n\in [a,b]\subset (0,2)$, $\{\zeta _n\}$ is a sequence of positive real numbers which is upper bounded by $\zeta$, and

$$\begin{aligned} \tilde{D}_n:=&\sum _{i=1}^N \left\| (I^{H_1}-P_{C_{i,n}}^{H_1})(v_n)\right\| ^2_{H_1}+\sum _{i=1}^N \left\| (I^{H_2}-P_{Q_{i,n}}^{H_2})(w_n)\right\| ^2_{H_2}\\&+\sum _{i=1}^N \Vert A_i(v_n)-B_i(w_n)-b_i\Vert ^2_{H}, \\ \tilde{E}_n:=&\left\| \sum _{i=1}^N\left( (I^{H_1}-P_{C_{i,n}}^{H_1})(v_n)+A_i^*(A_i(v_n)-B_i(w_n)-b_i)\right) \right\| ^2_{H_1}, \\ \tilde{F}_n:=&\left\| \sum _{i=1}^N\left( (I^{H_2}-P_{Q_{i,n}}^{H_2})(w_n)-B_i^*(A_i(v_n)-B_i(w_n)-b_i)\right) \right\| ^2_{H_2}. \end{aligned}$$

Step 3. Set $n\leftarrow n+1$, and go to Step 2.

Theorem 5.1

The sequence $\{x_n\}$ generated by Algorithm 5 converges weakly to a solution of Problem SSEP.

Proof

In view of the proof of Theorem 3.1, we can infer that the sequence $\{x_n\}$ is bounded and

$$\begin{aligned} \left\| (I^{H_1}-P_{C_{i,n}}^{H_1})(v_n))\right\| ^2_{H_1}&\rightarrow 0, \end{aligned}$$

(5.1)

$$\begin{aligned} \left\| (I^{H_2}-P_{Q_{i,n}}^{H_2})(w_n)\right\| ^2_{H_2}&\rightarrow 0, \end{aligned}$$

(5.2)

$$\begin{aligned} \Vert A_i(v_n)-B_i(w_n)-b_i\Vert ^2_{H}&\rightarrow 0. \end{aligned}$$

(5.3)

We will prove that all weak sequential limits of $\{x_n\}$ belong to $\varOmega$. Indeed, since $\{x_n\}$ is a bounded sequence, there exists the subsequence $\{x_{n_k}\}:=\{(v_{n_k},w_{n_k})\}$ of $\{x_n\}$ which converges weakly to some $z=(v_*,w_*)\in \mathbb {H}$. It is equivalent to

$$ v_{n_k}\rightharpoonup v_*,\quad w_{n_k}\rightharpoonup w_*. $$

Since the subdifferential $\partial c_i$ is assumed to be bounded on bounded sets and the sequence $\{x_n\}$ is bounded, there exists a positive real number $M_3$ such that

$$ \Vert \mathfrak {c}_{i,n}\Vert _{H_1}\le M_3 $$

for all $n\in \mathbb {N}$. It follows from $P_{C_{i,n}}^{H_1}({v_n})\in C_{i,n}$ and the definition of $C_{i,n}$ that

$$\begin{aligned} c_i(v_{n_k})&\le \left\langle (I^{H_1}-P_{C_{i,n_k}}^{H_1})(v_{n_k})),\mathfrak {c}_{i,n_k} \right\rangle _{H_1}\nonumber \\&\le \left\| (I^{H_1}-P_{C_{i,n_k}}^{H_1})(v_{n_k})\right\| _{H_1}\Vert \mathfrak {c}_{i,n_k}\Vert _{H_1}\nonumber \\&\le M_3\left\| (I^{H_1}-P_{C_{i,n_k}}^{H_1})(v_{n_k})\right\| _{H_1}. \end{aligned}$$

(5.4)

From (5.1) and (5.4), we can find that

$$ \liminf _{k\rightarrow \infty } c_i(v_{n_k})\le 0. $$

By the lower semicontinuity of the function c, we have

$$ c_i(v_*)\le \liminf _{k\rightarrow \infty } c_i(v_{n_k})\le 0. $$

Therefore, we obtain $v_*\in C_i$. By an argument similar to the one above and using (5.2), we also obtain that $w_*\in Q_i$. Furthermore, using (5.3) and repeating the proof of Theorem 3.1 in Claim 3, we can deduce that

$$ A_i(v_*)-B_i(w_*)-b_i=0. $$

Hence, we have $(v_*,w_*)\in \varOmega$.

Once again, we use a similar argument to the one employed in the last proof of Theorem 3.1 and can conclude that $(v_*, w_*)$ is the unique weak sequential limit of $\{x_n\}$ and that $v_n\rightarrow v_*$ and $w_n\rightarrow w_*$.

This completes the proof.$\square$

From Algorithm 2, we obtain the algorithm below.

Algorithm 6

Step 1. Choose $x_0=(v_0,w_0)\in \mathbb {H}:=H_1\times H_2$ arbitrarily and set $n:=0$.

Step 2. Given $x_{n}=(v_n,w_n)$, compute

$$\begin{aligned} x_{n+1}=\alpha _n h(x_n)+(1-\alpha _n)(x_n-\tilde{\gamma }_n \nabla \tilde{U}(x_n)), \end{aligned}$$

where $h:\mathbb {H}\rightarrow \mathbb {H}$ and $\{\alpha _n\}$ are defined as in Step 2 of Algorithm 2 while $\{\tilde{\gamma }_n\}$ is defined as in Step 2 of Algorithm 5.

Step 3. Set $n\leftarrow n+1$, and go to Step 2.

By using a line of proof similar to the one in the proof of Theorem 3.2 and combining it with Theorem 5.1, we obtain the following theorem.

Theorem 5.2

The sequence $\{x_n\}$ generated by Algorithm 6 converges strongly to $p_*=P_\varOmega (h(p_*))$.

6 Numerical Test

Our algorithms are implemented in MATLAB 14a running on the DESKTOP-8LDGIN0, Intel(R) Core(TM) i5-4210U CPU @ 1.70GHz with 2.40 GHz and 4GB RAM.

Example 6.1

We consider the Problem SSEP under the following hypotheses:

(D1) $H_1=\mathbb {R}^m$, $H_2=\mathbb {R}^k$ and $H=\mathbb {R}^p$ are three finite Euclidean spaces. For each $i=1,2,3$, the sets $C_i$ and $Q_i$ are defined by

$$\begin{aligned} C_i&=\{x\in \mathbb {R}^m:\Vert x-\mathfrak {a}_i\Vert ^2\le \mathfrak {R}_i^2\},\\ Q_i&=\{x\in \mathbb {R}^k:\Vert x-\widehat{\mathfrak {a}}_i\Vert ^2\le \widehat{\mathfrak {R}}_i^2\}, \end{aligned}$$

where the coordinates of the centers $\mathfrak {a}_i$ and $\widehat{\mathfrak {a}}_i$ are randomly generated in the interval $[-2,2]$, the radii $\mathfrak {R}_i$ and $\widehat{\mathfrak {R}}_i$ are also randomly generated in the intervals [10, 20] and [20, 30], respectively.

(D2) $A_i: \mathbb {R}^m\rightarrow \mathbb {R}^p$ and $B_i: \mathbb {R}^k\rightarrow \mathbb {R}^p$ ($i=1,2,3$) are bounded linear operators where the elements of their representing matrices are randomly generated in the closed interval $[-5, 5]$.

(D3) $b_i=0$ for all $i=1,2,3$.

(D4) Since $0=(0,0)\in \varOmega$, we have

$$\varOmega =\{(v,w) \in \cap _{i=1}^3(C_i\times Q_i): A_i(v)-B_i(w)=0, i=1,2,3\}\ne \emptyset .$$

We use Algorithm 2 to $m=100, k=200, p=300$ and $h(x)=0.05x$ for all $x\in \mathbb {R}^m\times \mathbb {R}^k$. It is not difficult to see that $p_*= (0,0)$. We take the initial point $x_0=(v_0,w_0)$ which has the coordinates of $v_0$ and $w_0$ randomly generated in the closed interval [20, 40], and select the control parameters as follows:

$$ \rho _n=1.5,\quad \zeta _n=0.05,\quad \alpha _n=\dfrac{1}{(n+1)^s}\,\, (0<s<1). $$

Table 1 Numerical results of Algorithm 2 with different choices of $\alpha _n$

Fig. 1

The behavior of err with TOL=$10^{-6}$

We use the stopping rule

$$ \text {err}=\Vert x_n\Vert =\sqrt{\Vert v_n\Vert ^2+\Vert w_n\Vert ^2}<\text {TOL}, $$

where TOL is a given tolerant and $x_n=(v_n,w_n)$. The numerical results are presented in Table 1. The behavior of err is shown in Fig. 1.

We also compare our Algorithm 2 with the algorithm defined by [23, Theorem 3.5] (ALGO-T, for short). The parameters for the ALGO-T are chosen as follows:

$$ \alpha _n=\dfrac{1}{(n+1)^{t}}, \quad \varepsilon _n=\dfrac{1.9999}{\alpha _n^{0.495}[(N+\alpha _n)^2+\gamma _{A,B}^4](1+4N^2)}, $$

where $N=3$ and $\gamma _{A,B}=\max _{1\le i\le 3}\{\Vert A_i\Vert , \Vert B_i\Vert \}$. The numerical results are presented in Table 2.

Table 2 Numerical results of ALGO-T with different choices of $\alpha _n$

Example 6.2

We consider Problem (4.1) under the following hypotheses:

(D1) $H_1=H_2=H=L^2[0,1]$ with the inner product

$$\langle x,y \rangle =\int _0^1 x(t)y(t)dt,\quad \forall x=x(t), y=y(t)\in L^2[0,1],$$

and the norm

$$ \Vert x\Vert =\left( \int _0^1 x^2(t)dt\right) ^{\frac{1}{2}},\quad \forall x=x(t)\in L^2[0,1]. $$

The sets $C_i$ and $Q_i$ ($i=1,2,3$) are given by

$$\begin{aligned} C_i&=\{x\in L^2[0,1]: \Vert x\Vert \le r_i\},\\ Q_i&=\{x\in L^2[0,1]:\langle \mathfrak {b}_i, x\rangle =\mathfrak {c}_i\}, \end{aligned}$$

where

$$\begin{aligned} r_i=i+1,\quad \mathfrak {b}_i=\exp (t)+i,\quad \mathfrak {c}_i=\dfrac{i+2}{i^2+1}. \end{aligned}$$

(D2) For each $i=1,2,3$, the operators $A_i: L^2[0,1]\rightarrow L^2[0,1]$ are defined by

$$ A_i(x)(t)=\dfrac{2x(t)}{i^2+1},\quad \forall x=x(t)\in L^2[0,1]. $$

(D3) $b_i=0$ for all $i=1,2,3$.

(D4) It is easy to find that

$$\varOmega =\{(v,w) \in \cap _{i=1}^3(C_i\times Q_i): A_i(v)-w=0, i=1,2,3\}$$

is a nonempty set because $(t,2t/(i^2+1))\in \varOmega$.

We use Algorithm 4 with $h(x)=0.25x$ for all $x\in L^2[0,1]\times L^2[0,1]$, the initial point $x_0=(\exp (t),\log (t+1))$, and select the parameters as follows:

$$\rho _n=0.5,\quad \zeta _n=10i,\quad \alpha _n=\dfrac{1}{(n+1)^{0.025}}.$$

We use the stopping criterion

$$\text {err}=\Vert x_{n+1}-x_n\Vert <\text {TOL},$$

where TOL is a given tolerant. The numerical results are presented in Table 3. The behavior of err is described in Fig. 2.

We also compare our Algorithm 4 with the ALGO-T. The parameters for the ALGO-T are chosen as follows:

$$ \alpha _n=\dfrac{1}{(n+1)^{s}}, \quad \varepsilon _n=\dfrac{1.9999}{\alpha _n^{0.75}[(N+\alpha _n)^2+\gamma _{A,B}^4](1+4N^2)}, $$

where $N=3$ and $\gamma _{A,B}=\max _{1\le i\le 3}\{\Vert A_i\Vert , \Vert B_i\Vert \}$. The numerical results are presented in Table 4.

Table 3 Numerical results of Algorithm 4 with different choices of $\zeta _n$

Fig. 2

The behavior of err with TOL=$10^{-6}$

Table 4 Numerical results of ALGO-T with different choices of $\alpha _n$

Example 6.3

Let $\mathbb {R}^m$ and $\mathbb {R}^k$ be two finite Euclidean spaces. We consider the signal recovery problem through the following LASSO problem:

$$\begin{aligned} \min \left\{ \dfrac{1}{2}\Vert Av-w\Vert ^2:\ v\in \mathbb {R}^k,\ \Vert v\Vert _1\le p\right\} , \end{aligned}$$

where $A \in \mathbb {R}^{m}\times \mathbb {R}^k$, $w\in \mathbb {R}^m$, $p>0$ and $\Vert \cdot \Vert _1$ is $l_1$-norm. A is a perception matrix, which is generated from a standard normal distribution. The true sparse signal $v_*$ is constructed from the uniform distribution in the interval $[-2, 2]$ with random p nonzero elements. In the sample data $w_* = Av_*$ no noise is assumed.

Table 5 Table of numerical results and comparisons among algorithms

Fig. 3

Original signal and recovered signal with $p=128$ and TOL=$10^{-5}$

In relation with the Problem (4.1) and the $N=1$ case, we define

$$\begin{aligned} C=\{v\in \mathbb {R}^k: \Vert v\Vert _1\le p\},\quad Q=\{w_*\}. \end{aligned}$$

Thus, we define a convex function

$$ c(v)=\Vert v\Vert _1-p $$

and denote the relaxed set $C_n$ by

$$ C_n=\{v\in \mathbb {R}^k: c(v_n)\le \langle v_n-v,\mathfrak {c}_n\rangle \}, $$

where $\mathfrak {c}_n\in \partial c(v_n)$. The subdiffrential $\partial c$ at $v_n\in \mathbb {R}^k$ is defined by

$$ [\partial c(v_n)]_j=\text {sign}((v_n)_j),\quad j=1,2,\ldots ,k. $$

We use Algorithm 5 and Algorithm 6 with the initial point $x_0=(v_0,w_0)$, where $v_0$ and $w_0$ are the original points of $\mathbb {R}^k$ and $\mathbb {R}^m$, and select the parameters as follows:

$$\rho _n=1,\quad \zeta _n=1,\quad \alpha _n=\dfrac{1}{10^4n}.$$

In Algorithm 6, the mapping $h:\mathbb {R}^m\times \mathbb {R}^k\rightarrow \mathbb {R}^m\times \mathbb {R}^k$ is given by $h(x)=0.5x$ for all $x\in \mathbb {R}^m\times \mathbb {R}^k$.

The following method of mean square error is used for measuring the recovery accuracy:

$$\text {MSE}=\dfrac{\Vert v_n-v_*\Vert ^2}{k},$$

which is required to be smaller than the given tolerant TOL.

We also compare our Algorithms with some previous algorithms ([24, Algorithm 2-SEF], [25, Algorithm (2.3)] and [10, Algorithm 4.1]). The parameters for each algorithm are chosen as follows:

• Algorithm A ([24, Algorithm 2-SEF]): $\rho _n=3.9.$

• Algorithm B ([25, Algorithm (2.3)]): $\gamma =\dfrac{1}{2\Vert A\Vert ^2}.$

• Algorithm C ([10, Algorithm 4.1]): $\rho _n=3.9.$

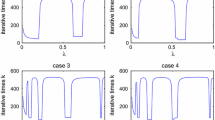
The numerical results that we have obtained are shown in Table 5. In Figs. 3 and 4, we present the illustration of the original signal and recovered signal by using the above algorithms.

Fig. 4

Original signal and recovered signal with $p=256$ and TOL=$10^{-5}$

Remark 6.1

The numerical experiments above show that our new algorithms outperform several previous algorithms proposed in [10, 23,24,25] concerning the number of iterations and the CPU time.