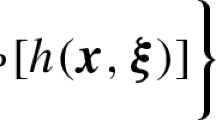Data-driven Stochastic Programming with Distributionally Robust Constraints Under Wasserstein Distance: Asymptotic Properties

Abstract

Distributionally robust optimization is a dominant paradigm for decision-making problems where the distribution of random variables is unknown. We investigate a distributionally robust optimization problem with ambiguities in the objective function and countably infinite constraints. The ambiguity set is defined as a Wasserstein ball centered at the empirical distribution. Based on the concentration inequality of Wasserstein distance, we establish the asymptotic convergence property of the data-driven distributionally robust optimization problem when the sample size goes to infinity. We show that with probability 1, the optimal value and the optimal solution set of the data-driven distributionally robust problem converge to those of the stochastic optimization problem with true distribution. Finally, we provide numerical evidences for the established theoretical results.

1 Introduction

Stochastic programming is a useful decision-making paradigm for dealing with optimization problems under parameter uncertainty [1]. For the modeling or analyzing of stochastic programming problems, it may be essential to take into account multiple criteria [2, 3]. To deal with this issue, the decision model may involve infinitely many constraints. For example, the stochastic optimization model with stochastic dominance constraints proposed in [4, 5] is a semi-infinite constrained stochastic programming problem. One way to handle the semi-infinite constraints is to view them as a robust risk measure constraint and use tractable risk measures to approximate it [6]. [7] utilized the sample average approximation method to solve a stochastic programming problem with second-order stochastic dominance constraints.

Classical stochastic programming is sometimes questioned in reality, because the true distribution of random parameters cannot be precisely known. An alternative modeling scheme is the distributionally robust optimization, where one considers the worst-case expectation instead of the expectation under the true distribution. The worst-case expectation is taken over an ambiguity set, which is a collection of all possible probability distributions characterized by specific known properties. Here, the true distribution is supposed to be in the ambiguity set (at least with a high confidence level). Distributionally robust optimization was first introduced in the seminal works [8, 9] and has developed rapidly in the last decade [10, 11].

Different ambiguity sets have been proposed in the literature. The following two types of ambiguity sets have been widely adopted. Moment-based ambiguity sets contain distributions characterized by certain moment information. [12] considered an ambiguity set with known variance or covariance matrix and known bounds on the mean value. [11] studied an ambiguity set based on support and moment information obtained from samples. [13] developed a unified framework where the ambiguity set is based on known mean and nested cones. [14] studied a robust two-stage stochastic linear programming model with mean-CVaR recourse under the moment ambiguity set. [15] investigated the approximation scheme for distributionally robust stochastic dominance constrained problems under a moment-based ambiguity set, which has infinitely many constraints. An alternative method for specifying the ambiguity set is to contain all the distributions close to a nominal distribution under a prescribed probability metric. [16] considered an ambiguous chance-constrained problem with an ambiguity set determined by the Prohorov metric. Wasserstein distance was adopted in [17, 18] to construct ambiguity sets. The phi-divergence family, such as the Kullback–Leibler divergence, total variation, and $\chi ^2$-divergence, has also been used to define ambiguity sets [10, 19, 20].

The Wasserstein distance-based ambiguity set has attracted much attention among all these ambiguity sets [18, 21, 22]. It has the following three advantages: firstly, Wasserstein distance intuitively describes the minimum cost to move from one mass distribution to another [23]; secondly, there are some probabilistic guarantees on the a priori estimation such that the true distribution belongs to the Wasserstein ambiguity set [24]; thirdly, [22] established the out-of-sample performance guarantee for stochastic optimization problems under the Wasserstein ambiguity set. Therefore, in this paper, we consider the Wasserstein distance-based ambiguity set centered at the empirical distribution, which is constituted by N historical i.i.d. samples. Different from most of the current models, we consider distributionally robust counterparts in both the objective and the countably infinite constraints. We discuss the asymptotic convergence property of the data-driven distributionally robust semi-infinite optimization problem when the sample size goes to infinity.

The main differences between our work and that in [22] lie in three aspects. Firstly, we consider the Wasserstein distance with any order $p \geqslant 1$, while [22] only investigated the case $p=1$. Secondly, the distributionally robust optimization problem we consider involves infinite constraints, which includes a broad class of problems such as the stochastic dominance constrained problem. Infinite constraints naturally increase the difficulties in analyzing asymptotic convergence properties. Finally, the convergence of the optimal solution set is also examined in this paper, which is not considered in [22].

We use the following notations. The m-dimensional random vector $\xi$ is governed by a probability distribution $\text {P}$. Let $\varXi \subset \mathbb {R}^m$ be the support of $\xi$. The N-fold Cartesian product of distribution $\text {P}$ on $\varXi$ is denoted by $\text {P}^N$, which is supported on the Cartesian product space $\varXi ^N$. $\mathcal {P}_p(\varXi )$ denotes the collection of probability distributions ${\textit{Q}}$ supported on $\varXi$ with $\int _{\varXi }\Vert \xi \Vert ^p {\textit{Q}}(d\xi )<\infty$. For a fixed distribution ${\textit{Q}} \in \mathcal {P}_p(\varXi )$, $\mathcal {L}^1({\textit{Q}})$ denotes the space of all ${\textit{Q}}$-integrable functions. The distance between two sets A and B is defined as ${\textit{D}}(A,B):=\sup _{x \in A} \text {dist}(x,B)=\sup _{x \in A}\inf _{y \in B} \Vert x-y\Vert$.

2 Data-driven Distributionally Robust Optimization Under Wasserstein Distance

We consider the following infinitely constrained stochastic optimization model

$$\begin{aligned} \text {(SP)}&\quad \qquad&\min \limits _{z \in Z_0} \quad&f(z):={\text {E}}_{\text {P}}[f(z,\xi )] \\&\quad \qquad&\text {s.t.} \,\quad&{\text {E}}_{\text {P}}[h(\eta ,z,\xi )] \leqslant 0, \quad \forall \eta \in \varGamma , \end{aligned}$$

where $f(z,\xi ): \mathbb {R}^n \times \varXi \rightarrow \mathbb {R}$ is continuous with respect to z for every $\xi$, $h(\eta ,z,\xi ):\varGamma \times \mathbb {R}^n \times \xi \rightarrow \bar{\mathbb {R}}$ is continuous with respect to z for every $(\eta ,\xi )$ and is continuous with respect to $\eta$ for every $(z,\xi )$, $\varGamma$ is a set with infinitely many elements, and $Z_0 \subset \mathbb {R}^n$ is a compact set. Denote the optimal value and the optimal solution set of problem (SP) by $J^*$ and $S^*$, respectively. We assume that $\text {P}$ is unknown, but can be estimated from i.i.d. samples $\{\widetilde{\xi _i}\}_{i=1}^N$. The sample set $\widetilde{\varXi }_N:=\{\widetilde{\xi _i}\}_{i=1}^N (\subset \varXi )$ can be considered as a random collection of samples governed by the distribution $\text {P}^N$. We always use superscript ‘ $\,\widetilde{ }\,$ ’ to emphasize that a variable is treated as random. We first recall the definition of Wasserstein distance.

Definition 1

Let $p \geqslant 1$. The Wasserstein distance $W_p({\textit{Q}}_1,{\textit{Q}}_2)$ between ${\textit{Q}}_1,{\textit{Q}}_2$ $\in \mathcal {P}_p(\varXi )$ is defined via

$$\begin{aligned} \begin{aligned}&W_p({\textit{Q}}_1,{\textit{Q}}_2) \\&\quad :=\Bigg ( \inf \Bigg \{ \int _{\varXi ^2}\Vert \xi _1-\xi _2\Vert ^p\varPi (d\xi _1, d\xi _2) :\begin{array}{ll} \varPi \text { is a joint distribution of }\xi _1\text { and }\xi _2 \\ \text {with marginals }{\textit{Q}}_1 \text { and }{\textit{Q}}_2,\text { respectively} \end{array} \Bigg \} \Bigg )^{\frac{1}{p}}. \end{aligned}\nonumber \\ \end{aligned}$$

(2.1)

Wasserstein distance corresponds to the minimum cost of moving from one mass distribution ${\textit{Q}}_1$ to another ${\textit{Q}}_2$. When ${\textit{Q}}_1$ and ${\textit{Q}}_2$ are both discrete distributions, the optimization problem in Wasserstein distance can be viewed as Monge’s mass transportation problem by treating $\varPi$ as the transportation plan [23]. Wasserstein distance has the following dual representation [17, eq. (7)]

$$\begin{aligned} W_p^p({\textit{Q}}_1,{\textit{Q}}_2)=\sup \limits _{u \in \mathcal {L}^1({\textit{Q}}_1),v \in \mathcal {L}^1({\textit{Q}}_2)} \Bigg \{ \begin{array}{ll} \int _{\varXi }u(\xi _1){\textit{Q}}_1(d\xi _1) + \int _{\varXi }v(\xi _2){\textit{Q}}_2(d\xi _2) :\\ u(\xi _1)+v(\xi _2) \leqslant \Vert \xi _1-\xi _2\Vert ^p, \forall \xi _1,\xi _2 \in \varXi \end{array} \Bigg \}.\nonumber \\ \end{aligned}$$

(2.2)

Due to the representation (2.2), we immediately have the following observation.

Lemma 1

[17] Let $\varPsi :\varXi \rightarrow \mathbb {R}$. Suppose that $\varPsi$ satisfies $| \varPsi (\xi _1)-\varPsi (\xi _2)| \leqslant L_0 \Vert \xi _1-\xi _2\Vert ^p+M_0$ for all $\xi _1,\xi _2 \in \varXi$ and some $L_0,M_0 \geqslant 0$. Then,

$$\begin{aligned} |{\text {E}}_{{\textit{Q}}_1}[\varPsi (\xi )]-{\text {E}}_{{\textit{Q}}_2}[\varPsi (\xi )]|\leqslant L_0 W_p^p({\textit{Q}}_1,{\textit{Q}}_2)+M_0. \end{aligned}$$

We now define

$$\begin{aligned} \widetilde{\mathcal {Q}}_N=\{{\textit{Q}} \in \mathcal {P}_p(\varXi ) : W_p(\,{\textit{Q}},\widetilde{\text {P}}_N)\leqslant \epsilon _N\}, \end{aligned}$$

(2.3)

where $\widetilde{\text {P}}_N:=\frac{1}{N}\sum _{i=1}^N \delta _{\widetilde{\xi _i}}$ is the empirical distribution, and $\epsilon _N$ is a given radius. We consider the following data-driven distributionally robust counterpart of problem (SP)

$$\begin{aligned} \text {(RP)}&\qquad \min \limits _{z \in Z_0} \quad \ \widetilde{f}_N(z):=\sup _{{\textit{Q}} \in \widetilde{\mathcal {Q}}_N}{\text {E}}_{{\textit{Q}}}[f(z,\xi )] \\&\qquad \text {s.t.} \,\quad \sup _{{\textit{Q}} \in \widetilde{\mathcal {Q}}_N}{\text {E}}_{{\textit{Q}}}[h(\eta ,z,\xi )] \leqslant 0, \quad \forall \eta \in \varGamma . \end{aligned}$$

Denote the optimal value and the optimal solution set of problem (RP) by $\widetilde{J}_N^*$ and $\widetilde{S}_N^*$, respectively.

It is worth noting that problem (RP) differs from another kind of distributionally robust model

$$\begin{aligned} \min _{z \in Z_0} \sup _{{\textit{Q}} \in \widetilde{\mathcal {Q}}_N}\{{\text {E}}_{{\textit{Q}}}[f(z,\xi )]:{\text {E}}_{{\textit{Q}}}[h(\eta ,z,\xi )] \leqslant 0, ~\forall \eta \in \varGamma \}. \end{aligned}$$

(2.4)

Problem (RP) aims to define the distributionally robust counterparts in the objective function and in constraints, separately. While, problem (2.4) tries to define the distributionally robust counterpart in terms of the optimal value function. In problem (2.4), all the expectations in the objective function and the constraints are taken under the same worst-case distribution. While, in problem (RP), the worst-case distribution for the objective function ${\textit{Q}}_f^* \in {{\,\mathrm{argmax}\,}}_{{\textit{Q}} \in \widetilde{\mathcal {Q}}_N}$ ${\text {E}}_{{\textit{Q}}}[f(z,\xi )]$ is probably different from the worst-case probability distributions for the constraint functions ${\textit{Q}}_{\eta }^* \in {{\,\mathrm{argmax}\,}}_{{\textit{Q}} \in \widetilde{\mathcal {Q}}_N}$ ${\text {E}}_{{\textit{Q}}}[h(\eta ,z,\xi )],~\eta \in \varGamma$. Problem (RP) derives a more robust solution, which keeps the constraints feasible for all possible distributions in the ambiguity set. While, the optimal solution of problem (2.4) is only feasible for those constraints under the worst-case distribution. In this paper, we focus on the model (RP), and we do not require that ${\textit{Q}}_f^*={\textit{Q}}_{\eta }^*,~\eta \in \varGamma$.

3 Asymptotic Convergence Property

In this section, we will show that with probability 1, the optimal value and the optimal solution set of problem (RP) tend to those of problem (SP) when $N \rightarrow \infty$. For this purpose, we assume that the tail of the distribution $\text {P}$ decays at a fast speed. Concretely, we introduce the following assumption.

Assumption 1

There exist $\alpha > p$, $\gamma >0$ such that

$$\begin{aligned} A:=\int _{\varXi } \exp \{\gamma \Vert \xi \Vert ^{\alpha } \}\text {P}(d\xi )<\infty . \end{aligned}$$

This assumption is mild and has been widely adopted in related researches, such as [18, 22, 25]. If $\varXi$ is compact, Assumption 1 holds trivially.

Based on [24, Theorem 2], Esfahani and Kuhn stated a measure concentration property in [22, Theorem 3.4] for $p=1$. We generalize this result to any integer order $p \geqslant 1$.

Lemma 2

(Concentration Inequality) Given Assumption 1, there exist positive constants $c_1$ and $c_2$ depending only on $\alpha$, $\gamma$, A and m such that

$$\begin{aligned} \text {P}^N\{W_p(\text {P},\widetilde{\text {P}}_N)\geqslant \epsilon _N\} \leqslant \left\{ \begin{array}{ll} c_1\exp \left( -c_2N\epsilon _N^{\max \{m,2p\}}\right) , \quad \text { if } \ \epsilon _N \leqslant 1, \\ c_1\exp \left( -c_2N\epsilon _N^{\alpha }\right) ,\quad \quad \quad \qquad \text {if }\ \epsilon _N > 1, \end{array} \right. \end{aligned}$$

(3.1)

for all $N \geqslant 1,~m \ne 2p$.

This lemma can be easily proved by using [24, Theorem 2]. When $m = 2p$, a similar inequality also holds. The detailed proof is thus omitted here.

Lemma 2 provides a probabilistic estimation that the true distribution $\text {P}$ lies outside the Wasserstein ball $\mathcal {B}(\widetilde{\text {P}}_N,\epsilon _N)$. This probability can be set as some prescribed disaster level $\beta _N$. Solving $\epsilon _N$ in the equation

$$\begin{aligned} \beta _N = \left\{ \begin{array}{c} c_1\exp \left( -c_2N\epsilon _N^{\max \{m,2p\}}\right) , \quad \text { if } \ \epsilon _N \leqslant 1, \\ c_1\exp \left( -c_2N\epsilon _N^{\alpha }\right) ,\quad \quad \quad \qquad \text { if }\ \epsilon _N > 1, \end{array} \right. \end{aligned}$$

(3.2)

we obtain the smallest radius of the Wasserstein ball containing $\text {P}$ with confidence $1-\beta _N$. Namely

$$\begin{aligned} \epsilon _N(\beta _N):= \left\{ \begin{array}{ll} \Big ( \frac{\log (\frac{c_1}{\beta _N})}{c_2N} \Big )^{\frac{1}{\max \{m,2p\}}}, \quad \quad \text {if}\ N \geqslant \frac{\log (\frac{c_1}{\beta _N})}{c_2},\\ \Big ( \frac{\log (\frac{c_1}{\beta _N})}{c_2N} \Big )^{\frac{1}{\alpha }}, \qquad \qquad \quad \text {if}\ N < \frac{\log (\frac{c_1}{\beta _N})}{c_2}, \end{array} \right. \end{aligned}$$

(3.3)

such that

$$\begin{aligned} \text {P}^N\{W_p(\text {P},\widetilde{\text {P}}_N) \leqslant \epsilon _N(\beta _N) \}\geqslant 1-\beta _N. \end{aligned}$$

(3.4)

Note that for a fixed level $\beta _N \equiv \beta > 0$, the radius $\epsilon _N(\beta _N)$ goes to zero as N tends to infinity. We now want to show that, when N tends to infinity, $\widetilde{f}_N$ converges to f with probability 1. To this end, we introduce the following assumptions.

Assumption 2

There exists an $L\geqslant 0$ such that $|f(z,\xi _1)-f(z,\xi _2)| \leqslant L \Vert \xi _1-\xi _2\Vert ^p$ for all $z \in Z_0$.

Assumption 3

$\beta _N \in (0,1)$ satisfies $\sum _{N=1}^{\infty }\beta _N < \infty$ and $\lim _{N \rightarrow \infty }\frac{\log \beta _N}{N}=0$.

The following theorem establishes the pointwise convergence result.

Theorem 1

(Convergence) Given Assumptions 1, 2 and 3, $\text {P}^{\infty }$-almost surely we have that $\widetilde{f}_N$ converges pointwise to f.

Proof

We have from (3.4) that

$$\begin{aligned} \text {P}^N\{\text {P} \in \widetilde{\mathcal {Q}}_N\}\geqslant 1-\beta _N, \end{aligned}$$

which further yields

$$\begin{aligned} \text {P}^N\{\widetilde{f}_N(z) \geqslant f(z),~\forall z \in Z_0\} \geqslant 1-\beta _N. \end{aligned}$$

Applying Borel–Cantelli Lemma (see, e.g., [26, Theorem 2.18]), we obtain

$$\begin{aligned} \text {P}^{\infty }\{\widetilde{f}_N(z)\geqslant f(z),~\forall z \in Z_0, \text { for all sufficiently large }N\}=1. \end{aligned}$$

Hence, it holds that

$$\begin{aligned} \text {P}^{\infty }\left\{ \liminf _{N \rightarrow \infty }\widetilde{f}_N(z) \geqslant f(z),~\forall z \in Z_0\right\} =1. \end{aligned}$$

(3.5)

On the other hand, from the definition of supremum and the fact that $\widetilde{\mathcal {Q}}_N$ is connected, for any $\epsilon >0$, there exists a $\widetilde{{\textit{Q}}}_N \in \widetilde{\mathcal {Q}}_N$ such that

$$\begin{aligned} {\text {E}}_{\widetilde{{\textit{Q}}}_N}[f(z,\xi )]\geqslant \widetilde{f}_N(z)-\epsilon /2. \end{aligned}$$

Then, we have

$$\begin{aligned} \widetilde{f}_N(z)&\leqslant {\text {E}}_{\mathbb {\widetilde{{\textit{Q}}}}_N} [f(z,\xi )]+\epsilon /2\\&= \int _{\varXi }f(z,\xi )\text {P}(d \xi )+\int _{\varXi }f(z,\xi )\widetilde{{\textit{Q}}}_N (d\xi )-\int _{\varXi }f(z,\xi )\text {P}(d \xi )+\epsilon /2 \\&\leqslant {\text {E}}_{\text {P}}[f(z,\xi )]+LW_p^p(\text {P},\widetilde{{\textit{Q}}}_N)+\epsilon /2 \\&\leqslant {\text {E}}_{\text {P}}[f(z,\xi )]+L[W_p(\text {P},\widetilde{\text {P}}_N)+W_p(\widetilde{\text {P}}_N,\widetilde{{\textit{Q}}}_N)]^p+\epsilon /2. \end{aligned}$$

The last but one inequality follows directly from Lemma 1 and Assumption 2. Thus by (3.4), we obtain

$$\begin{aligned} \text {P}^N\Big \{\widetilde{f}_N(z)\leqslant {\text {E}}_{\text {P}}[f(z,\xi )]{+}L(2\epsilon _N(\beta _N))^p{+}\epsilon /2,~\forall z \in Z_0 \Big \} \geqslant \text {P}^N\left\{ \text {P} \in \widetilde{\mathcal {Q}}_N \right\} \geqslant 1{-} \beta _N. \end{aligned}$$

Since $\lim _{N \rightarrow \infty }\epsilon _N(\beta _N)=0$, there exists an $N_1$ such that for all $N \geqslant N_1$, we have $L(2\epsilon _N(\beta _N))^p< \epsilon /2$. This further implies that

$$\begin{aligned} \text {P}^N \left\{ \widetilde{f}_N(z) \leqslant {\text {E}}_{\text {P}}[f(z,\xi )]+\epsilon ,~\forall z \in Z_0 \right\} \geqslant 1-\beta _N. \end{aligned}$$

Again by Borel-Cantelli Lemma, we have

$$\begin{aligned} \text {P}^{\infty }\left\{ \widetilde{f}_N(z)\leqslant f(z)+\epsilon ,~\forall z \in Z_0, \text { for all sufficiently large }N \right\} =1. \end{aligned}$$

Therefore, it holds that

$$\begin{aligned} \text {P}^{\infty }\left\{ \limsup _{N \rightarrow \infty } \widetilde{f}_N(z) \leqslant f(z) + \epsilon ,~\forall z \in Z_0\right\} =1. \end{aligned}$$

Since $\epsilon$ can be chosen arbitrarily, we obtain

$$\begin{aligned} \text {P}^{\infty } \left\{ \limsup _{N \rightarrow \infty } \widetilde{f}_N(z) \leqslant f(z),~\forall z \in Z_0\right\} =1. \end{aligned}$$

(3.6)

The proof follows immediately from (3.5) and (3.6). $\square$

We notice that if moreover, $f(z,\xi )$ is Lipschitz continuous with respect to z, then $\widetilde{f}_N$ converges uniformly to f.

Assumption 4

There exists a $\kappa (\xi )$ such that $|f(z_1,\xi )-f(z_2,\xi )| \leqslant \kappa (\xi )\Vert z_1-z_2\Vert$ for all $z_1,z_2 \in Z_0$ and $K:= \sup _{{\textit{Q}} \in \mathcal {P}_p(\varXi )} {\text {E}}_{{\textit{Q}}}[\kappa (\xi )]< \infty$.

Theorem 2

(Uniform convergence) Suppose that Assumptions 1, 2, 3 and 4 hold, then $\text {P}^{\infty }$-almost surely $\widetilde{f}_N$ converges uniformly to f on $Z_0$.

Proof

According to the Arzel$\grave{\text {a}}$-Ascoli theorem, a sequence in a compact Hausdorff space converges uniformly if and only if it is equicontinuous and converges pointwise. Therefore, what remains to prove is that $\{\widetilde{f}_N(z)\}$ is equicontinuous. By

$$\begin{aligned}&|\widetilde{f}_N(z_1)-\widetilde{f}_N(z_2)| = |\sup _{{\textit{Q}}\in \tilde{\mathcal {Q}}_N}{\text {E}}_{{\textit{Q}}}[f(z_1,\xi )]-\sup _{{\textit{Q}}\in \tilde{\mathcal {Q}}_N}{\text {E}}_{{\textit{Q}}}[f(z_2,\xi )]| \\&\quad \leqslant \sup _{{\textit{Q}}\in \tilde{\mathcal {Q}}_N}|{\text {E}}_{{\textit{Q}}}[f(z_1,\xi )]-{\text {E}}_{{\textit{Q}}}[f(z_2,\xi )]| \leqslant \sup _{{\textit{Q}}\in \tilde{\mathcal {Q}}_N}{\text {E}}_{{\textit{Q}}}|f(z_1,\xi )-f(z_2,\xi )| \\&\quad \leqslant \sup _{{\textit{Q}}\in \tilde{\mathcal {Q}}_N}{\text {E}}_{{\textit{Q}}}[\kappa (\xi )]\Vert z_1-z_2\Vert \leqslant K\Vert z_1-z_2\Vert , \end{aligned}$$

the equicontinuity follows directly.

Equipped with the convergence of the objective function, we can establish the convergence of the optimal value and the optimal solution set. To make a clear statement, we need to consider the following intermediate problem:

$$\begin{aligned} \text {(RCP)}&\quad \min \limits _{z \in Z_0} \quad f(z){:= {\text {E}}_{\text {P}}[f(z,\xi )]} \\&\quad \text {s.t.} \,\quad \sup \limits _{{\textit{Q}} \in \widetilde{\mathcal {Q}}_N}{\text {E}}_{{\textit{Q}}}[h(\eta ,z,\xi )] \leqslant 0, \quad \forall \eta \in \varGamma . \end{aligned}$$

Denote the optimal value and the optimal solution set of problem (RCP) by $\widetilde{{J}}_N$ and $\widetilde{{S}}_N$, respectively.

Firstly, we establish the finite sample guarantee and the asymptotic convergence property between the intermediate problem (RCP) and the true problem (SP).

Theorem 3

(Finite sample guarantee) Given Assumption 1,

$$\begin{aligned} \text {P}^N\left\{ \widetilde{\varXi }_N :J^* \leqslant \widetilde{J}_N \right\} \geqslant 1-\beta _N. \end{aligned}$$

Proof

Let $\widetilde{z}_N \in \widetilde{{S}}_N$. (3.4) implies that

$$\begin{aligned} \text {P}^N\left\{ {\text {E}}_\text {P}\left[ h(\eta ,\widetilde{z}_N,\xi )\right] \leqslant \sup _{{\textit{Q}}\in \widetilde{\mathcal {Q}}_N} {\text {E}}_\text {P}\left[ h(\eta ,\widetilde{z}_N,\xi )\right] ,\,\forall \eta \in \varGamma \right\} \geqslant 1-\beta _N. \end{aligned}$$

Note that problems (RCP) and (SP) have the same objective function. Hence, if $\widetilde{z}_N$ satisfies all the constraints in problem (SP), then it would hold that $J^* \leqslant f(\widetilde{z}_N)$. Therefore, we have

$$\begin{aligned} \begin{aligned}&\text {P}^N\{J^* \leqslant \widetilde{J}_N\} = \text {P}^N \left\{ J^* \leqslant f(\widetilde{z}_N)\right\} \geqslant \text {P}^N\left\{ {\text {E}}_{\text {P}}[h(\eta ,\widetilde{z}_N,\xi )]\leqslant 0,\,\forall \eta \in \varGamma \right\} \\&\quad \geqslant \text {P}^N \left\{ {\text {E}}_\text {P}\left[ h(\eta ,\widetilde{z}_N,\xi )\right] \leqslant \sup _{{\textit{Q}}\in \widetilde{\mathcal {Q}}_N} {\text {E}}_\text {P}\left[ h(\eta ,\widetilde{z}_N,\xi )\right] ,\,\forall \eta \in \varGamma \right\} \geqslant 1-\beta _N.\qquad \quad \quad \end{aligned} \end{aligned}$$

To establish the asymptotic convergence property, we need the following technical assumptions.

Assumption 5

There exists an $\mathcal {L}(\eta )$ such that $|h(\eta ,z,\xi _1)-h(\eta ,z,\xi _2)| \leqslant \mathcal {L}(\eta )\Vert \xi _1-\xi _2\Vert ^p$ for all $z \in Z_0$.

Assumption 6

$\varGamma$ is a countable and compact set.

For simplicity of exposition, let $\vartheta (\eta ,z):={\text {E}}_{\text {P}}[h(\eta ,z,\xi )]$, $\widetilde{\vartheta }_N(\eta ,z):=$ $\sup _{{\textit{Q}} \in \widetilde{\mathcal {Q}}_N}$ ${\text {E}}_{{\textit{Q}}}[h(\eta ,z,\xi )]$, $v(z):=\sup _{\eta \in \varGamma } \vartheta (\eta ,z)$ and $\widetilde{v}_N(z):=\sup _{\eta \in \varGamma }$ $\widetilde{\vartheta }_N(\eta ,z)$. Since h is continuous with respect to z and $\varGamma$ is compact, $\vartheta ,~\widetilde{\vartheta }_N,~v$, and $\widetilde{v}_N$ are all continuous with respect to z. Problems (SP) and (RCP) can be rewritten in the following compact forms, respectively

$$\begin{aligned} \min _{z \in Z_0} f(z) \quad \text {{s.t.} }v(z)\leqslant 0, \end{aligned}$$

and

$$\begin{aligned} \min _{z \in Z_0} f(z)\quad \text {{s.t. } }\widetilde{v}_N(z)\leqslant 0. \end{aligned}$$

Next, we will prove the pointwise convergence result of $\widetilde{v}_N(z)$.

Theorem 4

(Convergence of constraints) Given Assumptions 1, 3, 5, for every $\eta \in \varGamma$, $\text {P}^{\infty }$-almost surely we have that $\widetilde{\vartheta }_N(\eta ,z)$ converges to $\vartheta (\eta ,z)$ pointwise. Moreover, if Assumption 6 also holds, then $\widetilde{v}_N{(z)}$ converges pointwise to v(z).

Proof

Similar to the proof of Theorem 1, the first conclusion can be established immediately.

We know that the intersection set of countable sets with probability 1 also has probability 1. If $\varGamma$ is countable, then $\text {P}^{\infty }$-almost surely it holds that

$$\begin{aligned} \lim _{N \rightarrow \infty } \widetilde{\vartheta }_N(\eta ,z)-\vartheta (\eta ,z)=0, \forall \eta \in \varGamma ,~\forall z \in Z_0. \end{aligned}$$

(3.7)

Since ${h(\eta ,z,\xi )}$ is continuous with respect to $\eta$ and $\varGamma$ is compact, we can easily show that for any $z \in Z_0$, there exists an $\eta ^*$ such that

$$\begin{aligned} \left| \widetilde{v}_N(z)-v(z) \right| \leqslant \sup _{\eta \in \varGamma }\left| \widetilde{\vartheta }_N(\eta ,z)-\vartheta (\eta ,z)\right| =\left| \widetilde{\vartheta }_N(\eta ^*,z)-\vartheta (\eta ^*,z)\right| . \end{aligned}$$

(3.8)

(3.7) and (3.8) together ensure that $\text {P}^{\infty }$-almost surely, we have

$$\begin{aligned} \lim _{N \rightarrow \infty }\widetilde{v}_N(z)=v(z) \end{aligned}$$

for all $z \in Z_0$. This completes the proof.

To establish the asymptotic convergence property of problem (RCP), we need the following assumption like that in [27].

Assumption 7

Assume that there exists an optimal solution $\bar{z}$ of the true problem (SP) such that for any $\epsilon >0$, there is a $z \in Z_0$ with $\Vert z-\bar{z}\Vert \leqslant \epsilon$ and $v(z)<0$.

Theorem 5

(Asymptotic convergence property) Given Assumptions 1, 3, 5, 6 and 7, $\text {P}^{\infty }$-almost surely $\widetilde{J}_N \rightarrow J^*$ and ${\textit{D}}(\widetilde{{S}}_N,{S}^*) \rightarrow 0$ as $N \rightarrow \infty$.

Proof

By Theorem 3 and Borel-Cantelli Lemma, we have

$$\begin{aligned} \text {P}^{\infty }\left\{ J^* \leqslant \liminf _{N \rightarrow \infty } \widetilde{J}_N \right\} =1. \end{aligned}$$

On the other hand, for any $\epsilon >0$, there exists a $z_{\epsilon }\in Z_0$ with $\Vert z_{\epsilon }-\bar{z}\Vert \leqslant \epsilon$ and $v(z_{\epsilon })<0$. Assume that $z_{\epsilon } \rightarrow \bar{z}$ when $\epsilon \rightarrow 0$, by passing to a subsequence if necessary. It is known from Theorem 4 that such $z_{\epsilon }$ satisfies

$$\begin{aligned} \text {P}^{\infty }\left\{ \widetilde{v}_N(z_\epsilon )<0 \text { for all sufficiently large }N \right\} =1, \end{aligned}$$

and consequently,

$$\begin{aligned} \text {P}^{\infty } \left\{ f(z_{\epsilon })\geqslant \widetilde{J}_N \text { for all sufficiently large }N \right\} =1. \end{aligned}$$

We immediately get

$$\begin{aligned} \text {P}^{\infty }\left\{ f(z_{\epsilon })\geqslant \limsup _{N\rightarrow \infty } \widetilde{J}_N \right\} =1. \end{aligned}$$

Since f is continuous, we have that

$$\begin{aligned} \text {P}^{\infty } \left\{ J^*=f(\bar{z})=f(\lim _{\epsilon \rightarrow 0}z_{\epsilon })=\lim _{\epsilon \rightarrow 0}f(z_{\epsilon }) \geqslant \limsup _{N \rightarrow \infty }\widetilde{J}_N \right\} =1. \end{aligned}$$

For the second claim, the following discussions are all understood in the $\text {P}^{\infty }$-almost surely sense. Assume that ${\textit{D}}(\widetilde{{S}}_N,{S}^*) \nrightarrow 0$. Then, there must exist an $\epsilon _0 > 0$ and $\widetilde{z}_N \in \widetilde{{S}}_N$ such that $\text {dist}(\widetilde{z}_N, {S}^*)\geqslant \epsilon _0$ for all sufficiently large N. Since $Z_0$ is compact, we assume by passing to a subsequence if necessary that $\widetilde{z}_N \rightarrow z^*$. Therefore, $z^* \notin {S}^*$. Noticing $\widetilde{z}_N \in \widetilde{{S}}_N$, from the facts that $\widetilde{v}_N$ converges to v pointwise and $\widetilde{v}_N$ is continuous, we know that $v(z^*)=\lim _{N \rightarrow \infty }\widetilde{v}_N(\widetilde{z}_N) \leqslant 0$ and thus $z^*$ is a feasible solution of problem (SP). Hence $f(z^*) > J^*$. By the continuity of f, we have

$$\begin{aligned} \lim _{N \rightarrow \infty }\widetilde{J}_N=\lim _{N \rightarrow \infty }f(\widetilde{z}_N) = f(z^*)>J^*, \end{aligned}$$

which contradicts $\widetilde{J}_N \rightarrow J^*$ .

Next, let us investigate problem (RP). We will discuss how $\widetilde{J}_N^{*}$ approximates $J^*$ and how $\widetilde{{S}}_N^{*}$ approximates ${S}^*$ when $N \rightarrow \infty$.

Theorem 6

Given Assumptions 1-7, $\text {P}^{\infty }$-almost surely $\widetilde{J}_N^* \rightarrow J^*$ and

${\textit{D}}(\widetilde{{S}}_N^*,{S}^* )\rightarrow 0$ as $N \rightarrow \infty$.

Proof

The following discussions are all understood in the $\text {P}^{\infty }$-almost surely sense.

Let $\widetilde{z}_N \in \widetilde{{S}}_N$ and $\widetilde{z}_N^* \in \widetilde{{S}}_N^*$. From Theorem 2, for any $\epsilon > 0$, there exists an $N_1=N_1(\epsilon )$ such that for all $N \geqslant N_1$, it holds that

$$\begin{aligned} \left| \widetilde{f}_N(z)-f(z) \right| \leqslant \epsilon /2,\,\forall z \in Z_0. \end{aligned}$$

Thus we have

$$\begin{aligned} \widetilde{f}_N(\widetilde{z}_N)-f(\widetilde{z}_N) \leqslant \epsilon /2 \end{aligned}$$

(3.9)

and

$$\begin{aligned} f(\widetilde{z}_N^*)-\widetilde{f}_N(\widetilde{z}_N^*) \leqslant \epsilon /2. \end{aligned}$$

(3.10)

Notice that the constraints in problems $\text {(RP)}$ and $\text {(RCP)}$ are the same and it is obvious that

$$\begin{aligned} \widetilde{f}_N(\widetilde{z}_N)\geqslant \widetilde{J}_N^*:=\widetilde{f}_N(\widetilde{z}_N^*) \end{aligned}$$

(3.11)

and

$$\begin{aligned} f(\widetilde{z}_N^*) \geqslant \widetilde{J}_N:=f(\widetilde{z}_N). \end{aligned}$$

(3.12)

Therefore, (3.9) and (3.11) mean that

$$\begin{aligned} \widetilde{J}_N^*-\widetilde{J}_N\leqslant \epsilon /2, \end{aligned}$$

(3.13)

while (3.10) and (3.12) lead to

$$\begin{aligned} \widetilde{J}_N-\widetilde{J}_N^* \leqslant \epsilon /2. \end{aligned}$$

(3.14)

By Theorem 5, for the above $\epsilon$, there must exist an $N_2=N_2(\epsilon )$ such that for all $N \geqslant N_2$, it holds that $|\widetilde{J}_N-J^*|\leqslant \epsilon /2$. Let $N_0=\max \{N_1,N_2\}$. We obtain

$$\begin{aligned} |\widetilde{J}_N^*-J^*|\leqslant |\widetilde{J}_N^*-\widetilde{J}_N|+|\widetilde{J}_N-J^*|\leqslant \epsilon ,\quad \forall N \geqslant N_0. \end{aligned}$$

Hence it holds that $\widetilde{J}_N^* \rightarrow J^*$.

Assume that ${\textit{D}}(\widetilde{S}_N^*,S^*) \nrightarrow 0$. Then, there must exist an $\epsilon _0 > 0$ and $\widetilde{z}_N^* \in \widetilde{S}_N^*$ such that $\text {dist}(\widetilde{z}_N^*, S^*)\geqslant \epsilon _0$ for all sufficiently large N. Since $Z_0$ is compact, we assume by passing to a subsequence if necessary that $\widetilde{z}_N^* \rightarrow z^*$. Therefore, $z^* \notin S^*$. From the facts that $\widetilde{v}_N$ converges to v pointwise and $\widetilde{v}_N$ is continuous, we know that $v(z^*)=\lim _{N \rightarrow \infty }\widetilde{v}_N(\widetilde{z}_N^*) \leqslant 0$ and thus $z^*$ is a feasible solution of problem (SP). Hence $f(z^*) > J^*$. By the uniform convergence of $\widetilde{f}_N$, we have

$$\begin{aligned} \lim _{N \rightarrow \infty }{\widetilde{J}_N^*}=\lim _{N \rightarrow \infty }\widetilde{f}_N(\widetilde{z}_N^*) = f(z^*)>J^*, \end{aligned}$$

which contradicts $\widetilde{J}_N^* \rightarrow J^*$. $\square$

Theorem 6 guarantees that problem $\text {(RP)}$ is a “good” approximation to problem $\text {(SP)}$ in the sense of the optimal value and the optimal solution set. Thus, it is reasonable to consider problem $\text {(RP)}$ instead of problem $\text {(SP)}$ in practical applications.

4 Numerical Experiments

To examine the asymptotic convergence results in Theorem 6, we consider a data-driven distributionally robust portfolio selection problem with second-order stochastic dominance constraints.

4.1 Portfolio Optimization Models

We recall the portfolio optimization model with second-order stochastic dominance constraints proposed in [4]

$$\begin{aligned} \begin{aligned} \min _{z \in \mathbb {R}^n} \quad&{\text {E}}_{\text {P}}[-z^T \xi ] \\ \text {s.t.} \quad&{\text {E}}_{\text {P}}[(\eta _k-z^T \xi )_+ ]\leqslant {\text {E}}_{\text {P}}[(\eta _k - Y(\xi ))_+],~ k=1,\cdots ,J, \\&\sum _{j=1}^{n} z_j = 1, \\&z_j \geqslant 0,~j=1,\cdots ,n. \end{aligned} \end{aligned}$$

(4.1)

Here, we assume that there are n risky assets, z denotes the portfolio vector, and $\xi$ denotes the random return rate vector of the risky assets. We assume that the support set $\varXi$ of the random return rate vectors is finite [17, Corollary 4]. Y represents the benchmark which is a prespecified random variable with finite realizations $\eta _{k}=Y(\xi _{k}),~k=1,\cdots ,J$. $(\cdot )_{+}$ denotes the positive part function, i.e., $(\cdot )_{+} =\max (0,\cdot )$. We further consider the data-driven distributionally robust counterpart of model (4.1)

$$\begin{aligned} \begin{aligned} \min _{z \in \mathbb {R}^n}&\sup _{{\textit{Q}} \in \widetilde{\mathcal {Q}}_N}{\text {E}}_{{\textit{Q}}}[-z^T \xi ] \\ \text {s.t.}&\sup _{{\textit{Q}} \in \widetilde{\mathcal {Q}}_N}{\text {E}}_{{\textit{Q}}}[(\eta _k-z^T \xi )_+ -(\eta _k - Y(\xi ))_+] \leqslant 0,~ k=1,\cdots ,J, \\&\sum _{j=1}^{n} z_j = 1, \\&z_j \geqslant 0,~j=1,\cdots ,n, \end{aligned} \end{aligned}$$

(4.2)

where $\widetilde{\mathcal {Q}}_N$ is the ambiguity set defined in (2.3).

From the strong duality result in [17, Corollary 2], problem (4.2) can be equivalently written as

$$\begin{aligned} \min _{z \in \mathbb {R}_+^n,\lambda _0\geqslant 0,\lambda \in \mathbb {R}_+^{J}}&\lambda _0 \epsilon _N^p +\frac{1}{N}\sum _{i=1}^{N} \sup _{\xi \in \varXi }[-z^T \xi -\lambda _0 \Vert \xi -\widetilde{\xi _i}\Vert ^p] \nonumber \\ \text {s.t.}&\lambda _k \epsilon _N^p +\frac{1}{N}\sum _{i=1}^{N} \sup _{\xi \in \varXi }[(\eta _k-z^T \xi )_+ -(\eta _k - Y(\xi ))_+-\lambda _k \Vert \xi -\widetilde{\xi _i}\Vert ^p] \leqslant 0,\nonumber \\&~k=1,\cdots ,J, \nonumber \\&\sum _{j=1}^{n} z_j = 1. \end{aligned}$$

(4.3)

By introducing auxiliary variables, problem (4.3) can be reformulated as

$$\begin{aligned} \min \limits _{z ,\lambda _0 ,\lambda , \alpha , \beta ,s}&\lambda _0 \epsilon _N^p + \frac{1}{N}\sum _{i=1}^{N}\alpha _i \nonumber \\ \text {s.t.}&\lambda _k \epsilon _N^p+ \frac{1}{N}\sum _{i=1}^{N}\beta _{ik} \leqslant 0, k=1,\cdots ,J, \nonumber \\&\alpha _i \geqslant -z^T{\xi _j} -\lambda _0 \Vert {\xi _j}-\widetilde{\xi }_i\Vert ^p ,~i=1, \cdots , N,~j=1,\cdots ,J,\nonumber \\&\beta _{ik}\geqslant s_{jk}-(\eta _k-Y({\xi _j}))_{+}- \lambda _k \Vert {\xi _j}-\widetilde{\xi }_i\Vert ^p \nonumber \\&~i=1, \cdots , N,~ j=1,\cdots ,J,~ k=1,\cdots ,J,\nonumber \\&s_{jk}\geqslant \eta _k-z^T {\xi _j},~j=1,\cdots ,J,~k=1,\cdots ,J,\nonumber \\&\sum _{j=1}^{n} z_j = 1. \nonumber \\&z \in \mathbb {R}_+^n,\lambda _0 \geqslant 0,\lambda \in \mathbb {R}_+^{J}, \alpha \in \mathbb {R}^N, \beta \in \mathbb {R}^{N \times J},s \in \mathbb {R}_+^{J \times J}. \end{aligned}$$

(4.4)

Therefore, problem (4.2) can be solved through the linear programming reformulation (4.4), which can be efficiently solved by many optimization software. We solve it by Mosek solver in CVX package in MATLAB R2016a on a Dell G7 laptop with Windows 10 operating system, Intel Core i7-8750H processor, and 16 GB RAM.

4.2 Data

We select eight risky assets to constitute the stock pool, which are U.S. three-month treasury bills, U.S. long-term government bonds, S& P 500, Willshire 5000, NASDAQ, Lehmann Brothers corporate bond index, EAFE foreign stock index, and gold. We use the same historical annual return rate data as that in [4], whose statistics and more details can be found in Table 8.1 therein. The benchmark is the return rate of the equally weighted portfolio.

4.3 Numerical Evidences

Firstly, we examine the conservativeness of the data-driven distributionally robust model (4.2). We fix the sample set to be the support set (i.e., $\widetilde{\xi _i}=\xi _i,~i=1,\cdots ,N$ with $N=J$) and solve problem (4.4) for $~\epsilon _N=0.2$, $p=1,2$. We also solve problem (4.1) with the empirical distribution $\widetilde{\text {P}}_N$ as a comparison by using the solution method in [4]. The optimal values and the optimal solutions of the three models are shown in Table 1. We can see that problem (4.4) always gives a more conservative solution than problem (4.1) since $\widetilde{\text {P}}_N$ is contained in the ambiguity set $\widetilde{\mathcal {Q}}_N$. The optimal values of the distributionally robust model are larger than that of the stochastic programming model under the true distribution, which can be viewed as the price of robustness.

Table 1 Comparison of data-driven distributionally robust model and the empirical model

Next, we investigate the trend of the optimal value when the sample size increases. We carry out 5 groups of tests with the sample size being $N=5,10,20,50,100$, respectively. For each group of tests, we randomly generate N independent samples and solve the tested problems. Due to the randomness of sampling, for each group, we repeatedly generate the samples and test the model for 20 times, which provide 20 optimal solutions as well as 20 optimal values. Here, we set $\epsilon _N=5/N$ to satisfy Assumption 3. We summarize in Table 2 the descriptive statistics of the optimal values for each group, which include maximum (max.), minimum (min.), median, mean, and standard deviation (std.). We can see from Table 2 that as the sample size increases, the maximum value, the minimum value, the median value, and the mean value of the optimal values all increase. Then, it is reasonable to infer that the optimal value increases with a high probability when the sample size increases. The standard deviation of the optimal values decreases, which means that model (4.2) becomes more robust with the increase in the sample size.

Table 2 Descriptive statistics of the optimal values under different sample sizes

Then, we adopt a box-plot to characterize the optimal values between mean±std., shown in Fig. 1. From Fig. 1, we can see that the box gets smaller as the sample size increases. This means that the optimal values fluctuate less and thus the model (4.2) becomes more robust with the increase in the sample size. We also observe that the mean value and the median value of the optimal values increase when the sample size increases, but their increase rates are decreasing. These observations verify the asymptotic convergence results in Theorem 6.

Fig. 1

Variation of the optimal value with respect to the sample size

Finally, we briefly show the influence of the order p in the data-driven distributionally robust model (4.2). We carry out 4 groups of tests with $(p,N)=(1,20),(2,20),(1,50),(2,50)$, respectively. For each group, we repeat the tests for 20 times. Let $\epsilon =5/N$. The box-plot showing the max., min., mean, mean±std, and median of the optimal values for the four groups is exhibited in Fig. 2. We can see that for fixed N, the model (4.2) with $p=2$ generates a larger optimal value than that with $p=1$. Additionally, Fig. 2 verifies the asymptotic convergence results for $p=2$ as well.

Fig. 2

Variation of the optimal value with respect to p and N

5 Conclusion

We studied a data-driven distributionally robust stochastic optimization problem with countably infinite constraints. We considered an ambiguity set which contains all probability distributions close to the empirical distribution measured under the Wasserstein distance.

We established the asymptotic convergence property of the distributionally robust optimization problem when the sample size goes to infinity. We proved that with probability 1, the optimal value and the optimal solution set of the data-driven distributionally robust optimization problem tend to those of the stochastic programming problem under the true distribution.

The asymptotic convergence properties lay a foundation for the practical solution and application of distributionally robust optimization problems with infinite constraints. Finally, we solved a data-driven distributionally robust portfolio optimization problem with second-order stochastic dominance constraints to numerically verify the theoretical results.

One of the future research topics would be the relaxation of assumptions in order to generalize the asymptotic convergence properties to non-smooth distributionally robust optimization problems.