1 Introduction

Time-optimal maneuvers are interesting issues in different fields of aerospace engineering. Especially in space missions, time-optimal reorientation is required in many applications, such as antenna pointing in communication satellites, tracking multiple targets on the Earth in imaging satellites, or observing astronomical objects in space telescopes [1]. In addition, a time-optimal 6DOF maneuver in which attitude and position are simultaneously controlled in an overall minimum time, can be considered for time-critical operations, such as space debris removal, on-orbit spacecraft servicing (like repairing or refueling), and supplying oxygen or food to the International Space Station [2,3,4,5,6].

The time-optimal attitude maneuver has been vastly studied in the literature. Bilimoria and Wie [7] considered the time-optimal rest-to-rest reorientation problem for an inertially symmetric rigid body with three orthogonal control axes and cubical constraints on control torques (i.e., all the control torques are less than a specific magnitude). They showed that the eigen-axis rotation maneuver is not time-optimal, and the optimal control has a "bang-bang" structure in all three control axes. In [8], new results for the time-optimal rest-to-rest reorientation problem have been presented. It has been shown that the time-optimal control structure for a specific attitude maneuver is not unique. Furthermore, it has been demonstrated that by considering a spherical constraint for control torques (i.e., 2-norm of control vector to be less than a specific magnitude), the eigen-axis rotation maneuver will be time-optimal. In [9], the time-optimal reorientation problem for an inertially axisymmetric and under-actuated spacecraft has been discussed. Pager and Rao [10] have studied the time-optimal reorientation of a spin-stabilized axisymmetric rigid spacecraft using three control torques. They have analyzed the optimal control structure of various time-optimal maneuvers.

Furthermore, the time-optimal reorientation problem for an inertially asymmetric body has been solved in many works with different considerations. Hu et al. [11] have investigated the time-optimal smooth attitude maneuver for a flexible spacecraft, considering constraints on the control torques and corresponding derivatives and spacecraft angular velocity. In [12], this problem has been solved for a spacecraft with magnetic actuators. Olivares and Staffetti [13] studied the time-optimal reorientation problem for an under-actuated rigid spacecraft equipped with both reaction wheel and thruster, assuming limitations on the control torques and maximum angular momentum of the reaction wheels. In [14], these authors have solved this time-optimal problem for a multi-target maneuver (pointing toward several targets is performed in minimum time), in which constraints on the control torques and maximum angular momentum of the reaction wheels, and maximum angular velocity of the body are taken into account. Furthermore, in some articles, the time-optimal reorientation problem is solved in the presence of attitude constraints [15,16,17,18,19,20].

In addition, the time-optimal rendezvous maneuver between two spacecraft has been studied in some researches. Miele et al. [21] studied the time-optimal rendezvous problem with max-thrust acceleration constraint in fuel-free and fuel-given cases. Zhang and Ye [25] have investigated the time-optimal problem for short-range rendezvous maneuver using on–off constant thrust. They solved this problem for in-plane and out-of-plane motions. In [23] the time-optimal rendezvous maneuver for any number of space agents using only the relative aerodynamic drag has been discussed. Zhang and Parks [22] have studied time-optimal multiphase orbital rendezvous maneuver. They considered the field-of-view requirements in which the target should never appears out of the chaser’s field of view. Jorgensen and Sharf [26] have worked on the time-optimal rendezvous maneuver between a chaser spacecraft and multiple pieces of space debris. In [24] the planar two-body rendezvous problem with the inclusion of atmospheric drag perturbations has been investigated. These articles [21,22,23,24,25,26] have not considered rotational dynamics for the chaser spacecraft. While in the real applications, the position control actuators are fixed to the spacecraft’s body. Therefore, the attitude and position control are coupled. Ma et al. [2] have studied the time-optimal 3DOF planar rendezvous maneuver for approach to a rotating target spacecraft. They have considered that the chaser spacecraft can move in the plane and rotate about the axis perpendicular to the plane. Although, simultaneously attitude and position control have been considered in this article, but the relative dynamic model has been reduced to the simple 3DOF model in which the relative rotational dynamics (about the other two body axes) and translational dynamics (out-of-plane) have been neglected. Furthermore, the orbital dynamics of chaser and target spacecraft have been ignored. Finding the time-optimal maneuver leads to a time-optimal control problem which is often solved by numerical methods. Generally, numerical methods are divided into two categories, namely direct and indirect methods [27,28,29,30,31,32]. In indirect methods, the continuous first-order optimality conditions are derived by applying the calculus of variations and Pontryagin's minimum principle (PMP) [33] to the continuous-time optimal control problem. These optimality conditions lead to a two-point boundary value problem (TPBVP) that include states and costates differential equations and is solved by the shooting method [28]. The shooting method has been frequently used to solve the time-optimal control problem [7,8,9]. In this method, due to no physical sense of costates variables, it is difficult to find a proper initial guess for unknown initial costates and its convergence radius is small. To overcome this problem, some approaches have been provided to solve the TPBVP [34, 35]. Recently, the homotopic approach has been introduced to solve the TPBVP [36,37,38]. The homotopy scheme is used to continuously deform the problem to approximate the original one and find its solutions. In [39,40,41,42] this approach has been adopted to solve the time-optimal control problem. Nevertheless, for the high-order dynamic systems, the computational burden of this approach is very heavy.

In direct methods, the continuous optimal control problem is transcribed into nonlinear programming (NLP) problem by means of discretization methods [28]. Then, the NLP problem is solved with optimization methods such as gradient-based methods or heuristic algorithms [29]. A subset of direct methods are global collocation methods [29, 31, 43]. In these methods, the states and control trajectories are firstly discretized in collocation points and then approximated using global polynomials. A well-developed class of global collocation methods are pseudo-spectral methods such as Gauss pseudo-spectral method (GPM) [44,45,46,47,48], Lobatto pseudo-spectral method [49, 50] and Radau pseudo-spectral method [51,52,53]. The continuous dynamic constraints are discretized and converted into algebraic constraints using pseudo-spectral approaches. The NLP problem consists of dynamic constraints along with other ones such as path and boundary constraints as well as the cost function. In [19, 54, 55] the pseudo-spectral methods have been used to solve the time-optimal control problem.

The indirect methods have a higher accuracy in comparison with the direct method. However, in direct methods, the costates variables are not involved in optimal control problem formulation. Therefore, the problem is less complicated and there is no need to find a proper initial guess for the costates. Also, the dynamic constraints are satisfied only at the collocation points which causes the computational cost to be relatively lower.

Specifically, the GPM uses a set of non-uniform collocation points and guarantees that the polynomial approximation error monotonically decreases as the number of these points are increased [46]. Therefore, the accuracy of this method is improved, when the number of collocation points increases, and the obtained solution converges to the accurate optimal solution, albeit at the expense of increased computation time [46].

Moreover, using the Gauss pseudo-spectral discretization, the first-order optimality conditions of the NLP [Karush–Kuhn–Tucker (KKT) conditions] are equivalent to the discretized form of the continuous first-order optimality conditions of the continuous-time optimal control problem [44, 45]. Hence, there is a mapping between costates values in collocation points and KKT multipliers that are obtained from solving the NLP problem, and a costate estimation can be performed using KKT multipliers. The estimated costates can be utilized for first-order optimality proof of the obtained solution.

As mentioned before, simultaneously time-optimal rotational and translational control of a spacecraft was not considered in previous works. In the current paper, this time-optimal 6DOF maneuver is investigated. As a case study, the problem is formulated for the rendezvous maneuver of a chaser spacecraft with another target spacecraft and is solved using GPM. Considerations like the inertial asymmetry of spacecraft, applying orbital dynamic to rotational and translational dynamics of spacecraft, and coupled attitude and position control, affect the complexity of this problem. This paper assumes that the attitude and position control actuators are independent and fixed in the body frame. Hence, there is a coupling between attitude and position control. The main contributions of this paper are as follows:

  • The time-optimal 6DOF attitude and position control of an inertially asymmetric spacecraft has been developed.

  • Relative orbital dynamics and coupling between attitude and position control have been applied to the problem.

  • The optimal solution for the mentioned problem which satisfies the first-order optimality conditions has been provided.

  • The obtained control forces and moments are “bang-bang” which systemically can be implemented by simple on–off thrusters.

Generally, for the nonlinear and high-order dynamic systems (\(n\ge 3)\), any closed form solution does not exist for time-optimal control problem, and solving this problem using common methods (indirect and direct) leads to open-loop controls and states trajectories [56]. In real applications, it is necessary to design a closed-loop control law for tracking the calculated optimal states trajectories and compensating for the disturbances and uncertainties. Therefore, the whole problem is broken down into two parts: calculating the optimal open-loop controls and states trajectories and designing the closed-loop control law. This paper concentrates on the first sub-problem, and thus, the uncertainties and disturbances are not considered. Development of the closed-loop control law will be provided in future works.

In the following, the relative dynamic model of a spacecraft (chaser) with respect to another one (target) is introduced. Then the continuous time-optimal control problem is defined and transcribed into an NLP problem using GPM. The optimal states and control trajectories are obtained by solving the NLP problem. Similar to most time-optimal control problems, it is shown that the controls are “bang-bang”, which systemically can be implemented by simple on–off thrusters. On–off thrusters are the most popular thrusters in spacecraft control, used especially when high agility of the control system is required [57]. Also, using KKT multipliers, the costate trajectories are estimated. Finally, the first-order optimality proof of the obtained solution is provided.

The rest of the paper is organized as follows: Sect. 2 details the time-optimal 6DOF maneuver problem, GPM implementation, and costate estimation. Section 3 gives the numerical results, and conclusions are drawn in Sect. 4.

2 Time-optimal 6DOF Maneuver Problem

2.1 Relative Dynamic Model

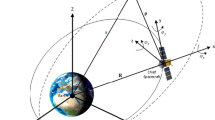
When the distance between two spacecraft is significant, their translational motion is usually described in the Earth-centered inertial (ECI) coordinate system. However, when the distance between two spacecraft is small in comparison to their radial distances from the Earth's center of mass, the relative translational motion is typically described in the target's Local Vertical Local Horizontal (LVLH) coordinate system, in which the z-axis is radially downward to the Earth's center of mass; the y-axis is in the opposite direction of the orbit normal vector, and the x-axis completes the right-hand orthogonal system. The chaser's body, the target's LVLH, and the ECI coordinate systems are presented in Fig. 1. In this paper, the classic and precise notation introduced in [58] is adopted.

Fig. 1
figure 1

Chaser's body, target's LVLH and ECI coordinate systems configuration

Full size image

The Hill's equations are well-known and widely used equations to express relative translational dynamics, when the target is in a circular or near circular orbit. Because of the first order approximation, in the sense of Taylor, used to derive the Hill's equations, and also the lack of inclusion of orbital perturbations, they are mostly appropriate to describe close range relative motions. Whenever their presumptions are fulfilled, the Hill's equations are the best choice due to their simplicity. Accordingly, they have been used in this work as governing equations of relative translational motion. Relative translational dynamic and kinematic equations of the chaser's body with respect to the target's LVLH are described by the Hill’s formulation, as follows [59]:

$$\begin{gathered} \left[ {\begin{array}{*{20}c} {D^{L} \left[ {{\varvec{v}}_{B}^{L} } \right]^{L} } \\ {D^{L} \left[ {{\varvec{s}}_{BL} } \right]^{L} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {{\varvec{A}}_{3 \times 3} } & {{\varvec{B}}_{3 \times 3} } \\ { - {\mathbf{I}}_{3} } & {0_{3} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\left[ {{\varvec{v}}_{B}^{L} } \right]^{L} } \\ {\left[ {{\varvec{s}}_{BL} } \right]^{L} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\frac{1}{{m_{B} }}\left[ {\varvec{f}} \right]^{L} } \\ {0_{3 \times 1} } \\ \end{array} } \right] \hfill \\ {\varvec{A}}_{3 \times 3} = \left[ {\begin{array}{*{20}c} 0 & 0 & { - 2\omega_{n} } \\ 0 & 0 & 0 \\ {2\omega_{n} } & 0 & 0 \\ \end{array} } \right] \hfill \\ {\varvec{B}}_{3 \times 3} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & {\omega_{n}^{2} } & 0 \\ 0 & 0 & { - 3\omega_{n}^{2} } \\ \end{array} } \right] \hfill \\ \end{gathered}$$
(1)

where \({\omega }_{n}\) is the orbital mean angular rate of the target, \({m}_{B}\) is the mass of the chaser. The time derivative of a vector \({\varvec{x}}\) with respect to the frame \(Y\) is indicated by \({D}^{Y}{\varvec{x}}\). Hence, \({D}^{L}\) denotes the time derivative with respect to the target's LVLH (\(L\)). Also, \({\left[{{\varvec{v}}}_{B}^{L}\right]}^{L}{=\left[{v}_{x},{v}_{y},{v}_{z}\right]}^{T}\in {\mathbb{R}}^{3}\) and \({\left[{{\varvec{s}}}_{BL}\right]}^{L}{=\left[{s}_{x},{s}_{y},{s}_{z}\right]}^{T}\in {\mathbb{R}}^{3}\) denote the velocity and position vectors of the chaser's body center of mass with respect to the target's LVLH, respectively, and \({\left[{\varvec{f}}\right]}^{L}\in {\mathbb{R}}^{3}\) denotes the vector of control forces expressed in the target's LVLH.

On the other hand, assuming that the target's body coordinate system is aligned with its LVLH coordinate system, the relative rotational dynamic model is commonly derived between the chaser's body and the target's LVLH coordinate systems.

In order to describe the relative rotational dynamic of the chaser's body with respect to the target's LVLH, which is a non-inertial reference frame, Euler's rotational equation is used as follows [58]:

$${\varvec{I}}_{B} \left[ {D^{B} \left[ {{\varvec{\omega}}^{BL} } \right]^{B} } \right] + \left[ {{\varvec{\omega}}^{BL} } \right]^{B} \times \left( {{\varvec{I}}_{B} \left[ {{\varvec{\omega}}^{BL} } \right]^{B} } \right) + {\varvec{I}}_{B} \left[ {D^{L} \left[ {{\varvec{\omega}}^{LI} } \right]^{B} } \right] + \left[ {{\varvec{\omega}}^{LI} } \right]^{B} \times \left( {{\varvec{I}}_{B} \left[ {{\varvec{\omega}}^{BI} } \right]^{B} } \right) = \left[ {\varvec{m}} \right]^{B}$$
(2)

where \({D}^{B}\) denotes the time derivative with respect to the chaser's body coordinate system (\(B\)), \({{\varvec{I}}}_{B}=diag(\left[{I}_{x},{I}_{y},{I}_{z}\right])\in {\mathbb{R}}^{3\times 3}\) is the inertial matrix of the chaser along its principal axes, and it is assumed that the principal axes coincide with the body coordinate system. Also, \({\left[{{\varvec{\omega}}}^{BL}\right]}^{B}={\left[{\omega }_{x},{\omega }_{y},{\omega }_{z}\right]}^{T}\in {\mathbb{R}}^{3}\),\({\left[{{\varvec{\omega}}}^{LI}\right]}^{B}\in {\mathbb{R}}^{3}\) and \({\left[{{\varvec{\omega}}}^{BI}\right]}^{B}\in {\mathbb{R}}^{3}\) denote the angular velocity vector of the chaser's body coordinate system with respect to the target's LVLH, the angular velocity vector of the target's LVLH with respect to the ECI (\(I\)) and the angular velocity vector of the chaser's body coordinate system with respect to the ECI, respectively. All the angular velocity vectors are expressed in the chaser's body coordinate system. Furthermore, \({\left[{\varvec{m}}\right]}^{B}={\left[{m}_{x},{m}_{y},{m}_{z}\right]}^{T}\in {\mathbb{R}}^{3}\) denotes the vector of control torques, expressed in the chaser's body coordinate system. Assuming the target is in the circular orbit, \({{\varvec{\omega}}}^{LI}\) is constant. Hence, the Euler's equation is stated as follows:

$${\varvec{I}}_{B} \left[ {D^{B} \left[ {{\varvec{\omega}}^{BL} } \right]^{B} } \right] + \left[ {{\varvec{\omega}}^{BL} } \right]^{B} \times \left( {{\varvec{I}}_{B} \left[ {{\varvec{\omega}}^{BL} } \right]^{B} } \right) + \left[ {{\varvec{\omega}}^{LI} } \right]^{B} \times \left( {{\varvec{I}}_{B} \left[ {{\varvec{\omega}}^{BI} } \right]^{B} } \right) = \left[ {\varvec{m}} \right]^{B}$$
(3)

In this paper, the rotational kinematic of the chaser's body coordinate system with respect to the target's LVLH is expressed using the modified Rodrigues parameters (MRP), defined as:

$$\left[ {\varvec{\sigma}} \right]^{BL} = \left[ {\sigma_{x} ,\sigma_{y} ,\sigma_{z} } \right]^{T} = \left[ {\begin{array}{*{20}c} {e_{x} tan\left( {\frac{{\Phi }}{4}} \right)} \\ {e_{y} \tan \left( {\frac{{\Phi }}{4}} \right)} \\ {e_{z} \tan \left( {\frac{{\Phi }}{4}} \right)} \\ \end{array} } \right]$$
(4)

where \({[\sigma ]}^{BL}\) is the MRP vector representing transformation from the target's LVLH to the chaser's body coordinate system. Also, \({e}_{x},{e}_{y}\) and \({e}_{z}\) are the components of Euler axis, and \(\Phi\) is the principal rotation angle. The rotational kinematic equation using MRP is derived as follows [60]:

$$\left[ {\dot{\varvec{\sigma }}} \right]^{BL} = \frac{1}{4}{\varvec{B}}\left( {\left[ {\varvec{\sigma}} \right]^{BL} } \right)\left[ {{\varvec{\omega}}^{BL} } \right]^{B}$$
(5)

where \({\varvec{B}}({[{\varvec{\sigma}}]}^{BL})\) is defined as:

$${\varvec{B}}\left( {\left[ {\varvec{\sigma}} \right]^{BL} } \right) = \left[ {\begin{array}{*{20}c} {1 - \left[ {\varvec{\sigma}} \right]_{2}^{BL2} + 2\sigma_{x}^{2} } & {2\left( {\sigma_{x} \sigma_{y} - \sigma_{z} } \right)} & {2\left( {\sigma_{x} \sigma_{z} + \sigma_{y} } \right)} \\ {2\left( {\sigma_{y} \sigma_{x} + \sigma_{z} } \right)} & {1 - \left[ {\varvec{\sigma}} \right]_{2}^{BL2} + 2\sigma_{y}^{2} } & {2\left( {\sigma_{y} \sigma_{z} - \sigma_{x} } \right)} \\ {2\left( {\sigma_{z} \sigma_{x} - \sigma_{y} } \right)} & {2\left( {\sigma_{z} \sigma_{y} + \sigma_{x} } \right)} & {1 - \left[ {\varvec{\sigma}} \right]_{2}^{BL2} + 2\sigma_{z}^{2} } \\ \end{array} } \right]$$
(6)

in which \({\Vert {{\varvec{\sigma}}}^{BL}\Vert }_{2}^{2}={[\overline{{\varvec{\sigma}} }]}^{LB}{[{\varvec{\sigma}}]}^{BL}\) (\({[\overline{{\varvec{\sigma}} }]}^{LB}\) is the transpose of \({[{\varvec{\sigma}}]}^{BL}\)).

Finally, it should be noted that the control force components are basically defined in the chaser's body coordinate system. Hence, to obtain the control force components in the target's LVLH, as appears in Eq. (1), a transformation has to be applied as follows:

$$\left[ {\varvec{f}} \right]^{L} = \left[ {\varvec{T}} \right]^{LB} \left[ {\varvec{f}} \right]^{B}$$
(7)

where \({\left[{\varvec{f}}\right]}^{B}={\left[{f}_{x},{f}_{y},{f}_{z}\right]}^{T}\in {\mathbb{R}}^{3}\) denotes the vector of control forces and expressed in the chaser's body coordinate system. \({[{\varvec{T}}]}^{LB}\) is the transformation matrix from the chaser's body coordinate system to the target's LVLH and is defined as a function of \({[{\varvec{\sigma}}]}^{BL}\), as follows:

$$\left[ {\varvec{T}} \right]^{LB} = \left[ {\overline{\varvec{T}}} \right]^{BL} = \left[ {{\mathbf{I}}_{3} + \frac{{8\left( {[{{\varvec{\Sigma}}}]^{BL} } \right)^{2} - 4\left( {1 - {\varvec{\sigma}}_{2}^{BL2} } \right)\left[ {{\varvec{\Sigma}}} \right]^{BL} }}{{\left( {1 + {\varvec{\sigma}}_{2}^{BL2} } \right)^{2} }}} \right]^{T}$$
(8)

in which \({\left[\overline{{\varvec{T}} }\right]}^{BL}\) is the transpose of \({[{\varvec{T}}]}^{LB}\), and \({[{\varvec{\Sigma}}]}^{BL}\) is the skew-symmetric matrix corresponding to\({[{\varvec{\sigma}}]}^{BL}\).

2.2 Optimal Control Problem Definition

Consider the following general optimal control problem with the cost function in Bolza form:

$$\min J=\phi \left( x\left( {{t}_{0}} \right),{{t}_{0}},x\left( {{t}_{f}} \right),{{t}_{f}} \right)+\underset{{{t}_{0}}}{\overset{{{t}_{f}}}{\mathop \int }}\,g\left( x\left( t \right),u\left( t \right),t \right)dt$$
(9)

subject to the following dynamic constraints, boundary conditions, and inequality path constraints, respectively:

$$\frac{{d{\varvec{x}}}}{dt} = {\varvec{f}}\left( {{\varvec{x}}\left( t \right),{\varvec{u}}\left( t \right),t} \right)$$
(10)
$$\varvec{\varphi }\left( {{\varvec{x}}\left( {t_{0} } \right),t_{0} ,{\varvec{x}}\left( {t_{f} } \right),t_{f} } \right) = 0 \in {\mathbb{R}}^{q}$$
(11)
$${\varvec{C}}\left( {{\varvec{x}}\left( t \right),{\varvec{u}}\left( t \right),t} \right) \le 0 \in {\mathbb{R}}^{c}$$
(12)

where \({\varvec{x}}(t)\in {\mathbb{R}}^{n}\) and \({\varvec{u}}(t)\in {\mathbb{R}}^{m}\) are the state and control input vectors, respectively. Also \({t}_{0}\) and \({t}_{f}\) are the initial and final times, respectively.

As mentioned earlier, in this paper, the problem is to find the states and control trajectories in a 6DOF maneuver, subject to specific constraints, that minimize the maneuver time denoted as \({t}_{f}\). Therefore the optimal control problem is expressed as:

$$\min J = t_{f}$$
(13)

subject to the dynamic constraints:

$$\begin{gathered} D^{B} \left[ {{\varvec{\omega}}^{BL} } \right]^{B} = {\varvec{I}}_{B}^{ - 1} \left( {\left[ {\varvec{T}} \right]^{B} - \left[ {{\varvec{\omega}}^{BL} } \right]^{B} \times \left( {{\varvec{I}}_{B} \left[ {{\varvec{\omega}}^{BL} } \right]^{B} } \right) - \left[ {{\varvec{\omega}}^{LI} } \right]^{B} \times \left( {{\varvec{I}}_{B} \left[ {{\varvec{\omega}}^{BI} } \right]^{B} } \right)} \right) \hfill \\ \left[ {\dot{\varvec{\sigma }}} \right]^{BL} = \frac{1}{4}{\varvec{B}}\left( {\left[ {\varvec{\sigma}} \right]^{BL} } \right)\left[ {{\varvec{\omega}}^{BL} } \right]^{B} \hfill \\ \left[ {\begin{array}{*{20}c} {D^{L} \left[ {{\varvec{v}}_{B}^{L} } \right]^{L} } \\ {D^{L} \left[ {{\varvec{s}}_{BL} } \right]^{L} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\frac{1}{m}{\varvec{T}}^{LB} \left[ {\varvec{f}} \right]^{B} } \\ {0_{3 \times 1} } \\ \end{array} } \right] - \left[ {\begin{array}{*{20}c} {{\varvec{A}}_{3 \times 3} } & {{\varvec{B}}_{3 \times 3} } \\ { - {\mathbf{I}}_{3} } & {0_{3 \times 3} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\left[ {{\varvec{v}}_{B}^{L} } \right]^{L} } \\ {\left[ {{\varvec{s}}_{BL} } \right]^{L} } \\ \end{array} } \right] \hfill \\ \left[ {\varvec{T}} \right]^{LB} = \left[ {{\mathbf{I}}_{3} + \frac{{8\left( {[{{\varvec{\Sigma}}}]^{BL} } \right)^{2} - 4\left( {1 - {\varvec{\sigma}}_{2}^{BL2} } \right)\left[ {{\varvec{\Sigma}}} \right]^{BL} }}{{\left( {1 + {\varvec{\sigma}}_{2}^{BL2} } \right)^{2} }}} \right]^{T} \hfill \\ \end{gathered}$$
(14)

the boundary conditions:

$$\begin{gathered} {\varvec{x}}_{0} = \left[ {\left[ {{\varvec{\omega}}^{BL} } \right]^{B} ,\left[ {\varvec{\sigma}} \right]^{BL} ,\left[ {{\varvec{v}}_{B}^{L} } \right]^{L} ,\left[ {{\varvec{s}}_{BL} } \right]^{L} } \right]_{{t = t_{0} }}^{T} \hfill \\ {\varvec{x}}_{f} = \left[ {\left[ {{\varvec{\omega}}^{BL} } \right]^{B} , \left[ {\varvec{\sigma}} \right]^{BL} ,\left[ {{\varvec{v}}_{B}^{L} } \right]^{L} ,\left[ {{\varvec{s}}_{BL} } \right]^{L} } \right]_{{t = t_{f} }}^{T} \hfill \\ \end{gathered}$$
(15)

and the constraints on control torques and forces:

$$\begin{gathered} |m_{i} | \le m_{i,\max } ,\quad i = x,y,z \hfill \\ |f_{i} | \le f_{i,\max } ,\quad i = x,y,z \hfill \\ \end{gathered}$$
(16)

In this problem, the state and control input vectors are defined as:

$$\begin{gathered} {\varvec{x}} = \left[ {\left[ {{\varvec{\omega}}^{BL} } \right]^{B} , \left[ {\varvec{\sigma}} \right]^{BL} ,\left[ {{\varvec{v}}_{B}^{L} } \right]^{L} ,\left[ {{\varvec{s}}_{BL} } \right]^{L} } \right]^{T} \hfill \\ {\varvec{u}} = \left[ {\left[ {\varvec{m}} \right]^{B} ,\left[ {\varvec{f}} \right]^{B} } \right]^{T} \hfill \\ \end{gathered}$$
(17)

2.3 Gauss Pseudo-spectral Method

The time-optimal 6DOF maneuver trajectories can be obtained by numerically solving the time-optimal control problem described in the previous section. Pseudo-spectral methods are a class of direct collocation methods that convert the continuous-time optimal control problem to an NLP problem. The basic idea behind these methods is to approximate the states and control trajectories using a basis of global interpolating polynomials, based on a set of discrete points across the interval. This paper uses the GPM to solve the time-optimal control problem. In this method, the states and control trajectories are approximated using the Lagrange polynomials and the base points are the Legendre–Gauss (LG) points. The \(N\) LG points \({\tau }_{1},\dots , {\tau }_{N}\) are defined as the roots of the Nth-degree Legendre polynomial, \({P}_{N}(\tau )\) where [46]

$${P}_{N}\left(\tau \right)=\frac{1}{{2}^{N}N!}\frac{{d}^{N}}{{d\tau }^{N}}[{\left({\tau }^{2}-1\right)}^{N}]$$
(18)

These non-uniform points are located on the interior of the interval [− 1, 1], and are clustered towards the boundaries, as depicted in Fig. 2. In the GPM, the dynamic constraints are forced to be satisfied only at these points (known as the collocation points), which leads to increased computational efficiency.

Fig. 2
figure 2

LG points distribution

Full size image

As mentioned above, the GPM collocation points are located on the interior of the interval [− 1, 1]. Because of this, the optimal control problem of Eqs. (13–16) must be transformed from the time interval \(t\in [{t}_{0},{t}_{f}]\) to \(\tau \in [-\mathrm{1,1}]\) as:

$$\tau = \frac{2t}{{t_{f} - t_{0} }} - \frac{{t_{f} + t_{0} }}{{t_{f} - t_{0} }}$$
(19)

Under this mapping, the optimal control problem of Eqs. (8–11) can be rewritten as:

$$\min J = \phi \left( {{\varvec{x}}\left( { - 1} \right),t_{0} ,{\varvec{x}}\left( 1 \right),t_{f} } \right) + \frac{{t_{f} - t_{0} }}{2}\mathop \smallint \limits_{ - 1}^{1} g\left( {{\varvec{x}}\left( \tau \right),{\varvec{u}}\left( \tau \right),\tau ;t_{0} ,t_{f} } \right)d\tau$$
(20)

subject to the constraints:

$$\frac{{d{\varvec{x}}\left( \tau \right)}}{d\tau } = \frac{{t_{f} - t_{0} }}{2}{\varvec{f}}\left( {{\varvec{x}}\left( \tau \right),{\varvec{u}}\left( \tau \right),\tau ;t_{0} ,t_{f} } \right)$$
(21)
$$\varvec{\varphi }\left( {{\varvec{x}}\left( { - 1} \right),t_{0} ,{\varvec{x}}\left( 1 \right),t_{f} } \right) = 0$$
(22)
$${\varvec{C}}\left( {{\varvec{x}}\left( \tau \right),{\varvec{u}}\left( \tau \right),\tau ;t_{0} ,t_{f} } \right) \le 0$$
(23)

In the GPM, the LG collocation points \(-1<{\tau }_{1}<\dots <{\tau }_{N}<1\) and \({\tau }_{0}=-1\) are considered to approximate the state trajectory using a basis of \(N+1\) Lagrange interpolating polynomials [61],

$${\varvec{x}}\left( \tau \right) \approx {\varvec{X}}\left( \tau \right) = \mathop \sum \limits_{i = 0}^{N} {\varvec{X}}\left( {\tau_{i} } \right)L_{i} \left( \tau \right)$$
(24)

in which \({L}_{i}(\tau )(i=0,\dots ,N)\) are the Lagrange polynomials defined as:

$$L_{i} \left( \tau \right) = \mathop \prod \limits_{j = 0,j \ne i}^{N} \frac{{\tau - \tau_{j} }}{{\tau_{i} - \tau_{j} }}$$
(25)

Additionally, by considering the LG collocation points, the control trajectory is approximated using a basis of \(N\) Lagrange interpolating polynomials \({L}_{i}^{*}(\tau )(i=1,\dots , N)\) as

$${\varvec{u}}\left( \tau \right) = {\varvec{U}}\left( \tau \right) = \mathop \sum \limits_{i = 1}^{N} {\varvec{U}}\left( {\tau_{i} } \right)L_{i}^{*} \left( \tau \right)$$
(26)

where

$$L_{i}^{*} \left( \tau \right) = \mathop \prod \limits_{j = 1,j \ne i}^{N} \frac{{\tau - \tau_{j} }}{{\tau_{i} - \tau_{j} }}$$
(27)

It can be shown that the Lagrange polynomials of Eqs. (25) and (27) satisfy the isolation property as:

$$\begin{gathered} L_{i} \left( {\tau_{j} } \right) = \left\{ {\begin{array}{*{20}c} {1,\quad i = j} \\ {0,\quad i \ne j} \\ \end{array} } \right. \hfill \\ L_{i}^{*} \left( {\tau_{j} } \right) = \left\{ {\begin{array}{*{20}c} {1,\quad i = j} \\ {0,\quad i \ne j} \\ \end{array} } \right. \hfill \\ \end{gathered}$$
(28)

By differentiating the expression provided in Eq. (24), the derivative of \(x(\tau )\) at the LG points, \({\tau }_{k}\), are obtained as follows:

$$\dot{\varvec{x}}\left( {\tau_{k} } \right) \approx \dot{\varvec{X}}\left( {\tau_{k} } \right) = \mathop \sum \limits_{i = 0}^{N} {\varvec{x}}\left( {\tau_{i} } \right)\dot{L}_{i} \left( {\tau_{k} } \right)$$
(29)

The derivative of Lagrange polynomials at the LG points, \({\dot{L}}_{i}({\tau }_{k})(k=1,\dots ,N)\) can be expressed as a differential approximation matrix \({\varvec{D}}\in {\mathbb{R}}^{N\times N+1}\), the elements of which are defined as [46]:

$$D_{ki} = \dot{L}_{i} \left( {\tau_{k} } \right) = \left\{ \begin{gathered} \frac{{\left( {1 + \tau_{k} } \right)\dot{P}_{N} \left( {\tau_{k} } \right) + P_{N} \left( {\tau_{k} } \right)}}{{\left( {\tau_{k} - \tau_{i} } \right)\left[ {\left( {1 + \tau_{i} } \right)\dot{P}_{N} \left( {\tau_{i} } \right) + P_{N} \left( {\tau_{i} } \right)} \right]}},\quad k \ne i \hfill \\ \frac{{\left( {1 + \tau_{i} } \right)\ddot{P}_{N} \left( {\tau_{i} } \right) + 2\dot{P}_{N} \left( {\tau_{i} } \right)}}{{2\left[ {\left( {1 + \tau_{i} } \right)\dot{P}_{N} \left( {\tau_{i} } \right) + P_{N} \left( {\tau_{i} } \right)} \right]}},\quad k = i \hfill \\ \end{gathered} \right.$$
(30)

where \(i=0,\dots ,N\) and \(k=1,\dots ,N\). The continuous dynamic constraints of Eq. (21) are transcribed into the following set of algebraic dynamic constraints using the differential approximation matrix:

$$\mathop \sum \limits_{i = 0}^{N} D_{ki} {\varvec{X}}_{i} - \frac{{t_{f} - t_{0} }}{2}{\varvec{f}}\left( {{\varvec{X}}_{k} ,{\varvec{U}}_{k} ,\tau_{k} ;t_{0} ,t_{f} } \right) = 0,\quad \left( {k = 1, \ldots ,N} \right)$$
(31)

in which \({{\varvec{X}}}_{k}\equiv {\varvec{X}}\left({\tau }_{k}\right)\in {\mathbb{R}}^{n}\) and \({{\varvec{U}}}_{k}\equiv {\varvec{U}}\left({\tau }_{k}\right)\in {\mathbb{R}}^{m }(k=1,\dots , N)\). In the GPM, the dynamic constraints are collocated only at the LG points, and the terminal state is absent in the state approximation. Therefore, \({{\varvec{X}}}_{f}\)(or \({{\varvec{X}}}_{N+1})\) can be constrained via the Gauss quadrature that relates the final state to the initial state as follows [62]:

$${\varvec{X}}_{f} = {\varvec{X}}_{0} + \frac{{t_{f} - t_{0} }}{2}\mathop \sum \limits_{k = 1}^{N} w_{k} {\varvec{f}}\left( {{\varvec{X}}_{k} ,{\varvec{U}}_{k} ,\tau_{k} ;t_{0} ,t_{f} } \right)$$
(32)

where \({w}_{k}\) are the Guass weights. Also, the continuous cost function of Eq. (20) can be approximated with a Gauss quadrature as:

$$J = \phi \left( {{\varvec{X}}_{0} ,t_{0} ,{\varvec{X}}_{f} ,t_{f} } \right) + \frac{{t_{f} - t_{0} }}{2}\mathop \sum \limits_{k = 1}^{N} w_{k} g\left( {{\varvec{X}}_{k} ,{\varvec{U}}_{k} ,\tau_{k} ;t_{0} ,t_{f} } \right)$$
(33)

Finally, the boundary conditions of Eq. (22) and path constraints of Eq. (20) are expressed as:

$$\varvec{\varphi }\left( {{\varvec{X}}_{0} ,t_{0} ,{\varvec{X}}_{f} ,t_{f} } \right) = {\mathbf{0}}$$
(34)
$${\varvec{C}}\left( {{\varvec{X}}_{k} ,{\varvec{U}}_{k} ,\tau_{k} ;t_{0} ,t_{f} } \right) \le {\mathbf{0}},\quad \left( {k = 1, \ldots ,N} \right)$$
(35)

The cost function of Eq. (33) and the algebraic constraints of Eqs. (31), (32), (34) and (35) define an NLP. Solving the NLP gives an approximate solution for the continuous-time optimal control problem defined in the former section.

Some optimal control problems have discontinuities in either the states or control trajectories. In these problems, a common procedure to increase the solution accuracy is dividing the trajectories into \(P\)-phases, which involves repeating the structure for the one-phase formulation \(P\) times. Thus, the algebraic dynamic constraints of Eq. (31) are collocated at the LG points within each phase. In addition, the terminal constraints for the first phase, the initial and terminal constraints for the interior phases, and the initial constraints for the \({P}^{th}\) phase are re-characterized as interior point constraints. These interior point constraints include any continuity conditions in the state or time between adjacent phases [44, 46]. A schematic of how phases can be linked is shown in Fig. 3 for a 4-phases trajectory.

Fig. 3
figure 3

Schematic of linkages for a 4-phases trajectory

Full size image

Accordingly, the boundary constraints of Eq. (34) can be replaced [46]:

$$\begin{gathered} {\mathbf{\mathcal{L}}}^{\left( 1 \right)} \left( {{\varvec{X}}_{0}^{\left( 1 \right)} ,t_{0}^{\left( 1 \right)} } \right) = {\mathbf{0}} \hfill \\ {\mathbf{\mathcal{L}}}_{\left( r \right)}^{{\left( {r + 1} \right)}} \left( {{\varvec{X}}_{f}^{\left( r \right)} ,t_{f}^{\left( r \right)} ,{\varvec{X}}_{0}^{{\left( {r + 1} \right)}} ,t_{0}^{{\left( {r + 1} \right)}} } \right) = {\mathbf{0}} \hfill \\ {\mathbf{\mathcal{L}}}^{\left( P \right)} \left( {{\varvec{X}}_{f}^{\left( P \right)} ,t_{f}^{\left( P \right)} } \right) = {\mathbf{0}} \hfill \\ \end{gathered}$$
(36)

where \(P\) is the number of phases and \(r=1,\dots ,P-1\). \({\mathcal{L}}^{\left(1\right)}\), \({\mathcal{L}}^{\left(P\right)}\) and \({\mathcal{L}}_{(r)}^{(r+1)}\) denote the initial constraints for the first phase, the terminal constraints for the last phase (\(P\)), and the continuity constraints for the interior phases, respectively.

2.4 Costate estimation

The transformed continuous-time optimal control problem of Eqs. (20–23), described in Sect. 2.3, can be solved using the calculus of variations and PMP [33] to obtain a set of first-order optimality conditions [56]. The first-order optimality conditions are found by taking the first-order variation of the augmented Hamiltonian, \(H\), defined as:

$$\begin{aligned} H\left( {{\varvec{x}},{\varvec{\lambda}},{\varvec{\mu}},{\varvec{u}},\tau ;t_{0} ,t_{f} } \right) & = g\left( {{\varvec{x}},{\varvec{u}},\tau ;t_{0} ,t_{f} } \right) + {\varvec{\lambda}}^{T} \left( \tau \right){\varvec{f}}\left( {{\varvec{x}},{\varvec{u}},\tau ;t_{0} ,t_{f} } \right) \\ & \quad - {\varvec{\mu}}^{T} \left( \tau \right){\varvec{C}}\left( {{\varvec{x}},{\varvec{u}},\tau ;t_{0} ,t_{f} } \right) \\ \end{aligned}$$
(37)

in which \({\varvec{\lambda}}\left(\tau \right)\in {\mathbb{R}}^{n}\) is the costate and \({\varvec{\mu}}\left(\tau \right)\in {\mathbb{R}}^{c}\) is the Lagrange multiplier associated with the path constraint. The continuous first-order optimality conditions can be expressed as follows:

$$\begin{gathered} \frac{{d{\varvec{x}}}}{d\tau } = \frac{{t_{f} - t_{0} }}{2}{\varvec{f}}\left( {{\varvec{x}}\left( \tau \right),{\varvec{u}}\left( \tau \right),\tau ;t_{0} ,t_{f} } \right) = \frac{{t_{f} - t_{0} }}{2}\frac{\partial H}{{\partial {\varvec{\lambda}}}} \hfill \\ \frac{{d{\varvec{\lambda}}}}{d\tau } = \frac{{t_{f} - t_{0} }}{2}\left( { - \frac{\partial g}{{\partial {\varvec{x}}}} - {\varvec{\lambda}}^{T} \frac{{\partial {\varvec{f}}}}{{\partial {\varvec{x}}}} + {\varvec{\mu}}^{T} \frac{{\partial {\varvec{C}}}}{{\partial {\varvec{x}}}}} \right) = - \frac{{t_{f} - t_{0} }}{2}\frac{\partial H}{{\partial {\varvec{x}}}} \hfill \\ 0 = \frac{\partial g}{{\partial {\varvec{u}}}} + {\varvec{\lambda}}^{T} \frac{{\partial {\varvec{f}}}}{{\partial {\varvec{u}}}} - {\varvec{\mu}}^{T} \frac{{\partial {\varvec{C}}}}{{\partial {\varvec{u}}}} = \frac{\partial H}{{\partial {\varvec{u}}}} \hfill \\ \varvec{\varphi }\left( {{\varvec{x}}\left( {\tau_{0} } \right),t_{0} ,{\varvec{x}}\left( {\tau_{f} } \right),t_{f} } \right) = {\mathbf{0}} \hfill \\ {\varvec{\lambda}}\left( {\tau_{0} } \right) = - \frac{\partial \phi }{{\partial {\varvec{x}}\left( {\tau_{0} } \right)}} + {\varvec{\nu}}^{T} \frac{{\partial \varvec{\varphi }}}{{\partial {\varvec{x}}\left( {\tau_{0} } \right)}} \hfill \\ {\varvec{\lambda}}\left( {\tau_{f} } \right) = \frac{\partial \phi }{{\partial {\varvec{x}}\left( {\tau_{f} } \right)}} - {\varvec{\nu}}^{T} \frac{{\partial \varvec{\varphi }}}{{\partial {\varvec{x}}\left( {\tau_{f} } \right)}} \hfill \\ H\left( {t_{0} } \right) = \frac{\partial \phi }{{\partial t_{0} }} - {\varvec{\nu}}^{T} \frac{{\partial \varvec{\varphi }}}{{\partial t_{0} }} \hfill \\ H\left( {t_{f} } \right) = - \frac{\partial \phi }{{\partial t_{f} }} + {\varvec{\nu}}^{T} \frac{{\partial \varvec{\varphi }}}{{\partial t_{f} }} \hfill \\ \mu_{j} \left( \tau \right) = 0,\quad when C_{j} \left( {{\varvec{x}},{\varvec{u}},\tau ;t_{0} ,t_{f} } \right) < 0,\quad j = 1, \ldots ,c \hfill \\ \mu_{j} \left( \tau \right) \le 0,\quad when C_{j} \left( {{\varvec{x}},{\varvec{u}},\tau ;t_{0} ,t_{f} } \right) = 0,\quad j = 1, \ldots ,c \hfill \\ \end{gathered}$$
(38)

where \({\varvec{\nu}}\in {\mathbb{R}}^{q}\) is the Lagrange multiplier associated with the boundary condition \(\boldsymbol{\varphi }\).

As mentioned earlier, in the GPM, KKT multipliers obtained from solving the NLP can be used for costate estimation and first-order optimality proof. Using KKT multipliers, a costate estimation for the continuous-time optimal control problem (an estimation for \({\varvec{\lambda}}\left(\tau \right))\), can be obtained at the LG points and the boundary points. Because of brevity, the details are not presented in this paper, and the interested reader is referred to [45]. The Gauss pseudo-spectral costate estimation is stated via the following theorem [45]:

Theorem1 (Gauss pseudo-spectral costate mapping theorem): a costate estimate at the initial time, final time, and the LG points can be found from the KKT multiplier as follows:

$$\begin{gathered} {{\varvec{\Lambda}}}_{k} = \frac{{{\tilde{\mathbf{\Lambda }}}_{k} }}{{w_{k} }} + {\tilde{\mathbf{\Lambda }}}_{f} \hfill \\ {{\varvec{\Lambda}}}_{0} = {\tilde{\mathbf{\Lambda }}}_{0} , {{\varvec{\Lambda}}}_{f} = {\tilde{\mathbf{\Lambda }}}_{f} \hfill \\ \end{gathered}$$
(39)

where \({\widetilde{\Lambda }}_{0}\) is defined as:

$${\tilde{\mathbf{\Lambda }}}_{0}^{T} = - \frac{\partial \phi }{{\partial {\varvec{X}}_{0} }} + \tilde{\varvec{\upsilon }}^{T} \frac{{\partial \varvec{\varphi }}}{{\partial {\varvec{X}}_{0} }}$$
(40)

\({\widetilde{{\varvec{\Lambda}}}}_{k}\), \({\widetilde{{\varvec{\Lambda}}}}_{f}\) and \(\widetilde{\upsilon }\) are the KKT multipliers associated with dynamic constraints of Eq. (31), constraints of Eq. (32) and boundary constraints of Eq. (34), respectively. Also, \({{\varvec{\Lambda}}}_{k}\), \({{\varvec{\Lambda}}}_{0}\) and \({{\varvec{\Lambda}}}_{f}\) are the estimated costates in LG points, initial time and final time, respectively.

3 Numerical Simulation

In this section, the time-optimal control problem described in Sect. 2.2 is solved using GPM. The transformed continuous-time optimal control problem is first converted to the NLP, and then the sequential quadratic programming (SQP) iterative algorithm is utilized to solve the NLP and obtain the approximate controls and states trajectories. The GPM optimization and costate estimation pseudo-code are expressed in Table 1. It should be noted that in the time-optimal control problem, the final time is free. Therefore, the NLP variables include states and controls values in LG points, and \({t}_{f}\).

Table 1 GPM optimization and costate estimation pseudo-code
Full size table

Proximity operations are commonly divided into two stages, namely rendezvous and docking maneuvers. The docking maneuver should be performed at a constant low relative velocity due to safety reasons, and the time-optimality of this maneuver is unnecessary. Therefore, in order to achieve to the target spacecraft in time-critical conditions, the rendezvous maneuver should be designed to be implemented in minimum time. At the end of the rendezvous maneuver, the chaser spacecraft must be in a desired attitude, velocity and position to start the docking maneuver. Without loss of generality, it is assumed that the target's body coordinate system is aligned with its LVLH coordinate system and its docking port is facing up (contrary direction of axis \({{\varvec{z}}}^{L}\)). Also, the chaser spacecraft docking port is in contrary direction of axis \({{\varvec{x}}}^{B}\). Accordingly, in the simulation scenario the chaser spacecraft should be located above the target spacecraft, in the desired attitude, velocity and position, to start the docking maneuver. Assuming that docking will start immediately after rendezvous, the simulation scenario is defined for a rest-to-rest 6DOF rendezvous maneuver.

At the initial time, the chaser spacecraft is located 20 m ahead of the target spacecraft, and the chaser's body coordinate system coincides with the target's LVLH. Also, at the final time, the chaser spacecraft should be located 10 m above the target spacecraft, and the chaser's body coordinate system must have a complete rotation around the \({y}^{B}\) axis. When the chaser spacecraft reaches the final states in the rendezvous maneuver, it starts the docking maneuver and moves toward the target spacecraft at a constant low relative velocity. The docking maneuver is beyond our research and has not be investigated in this section. The schematic of this scenario is shown in Fig. 4. The parameters of the chaser spacecraft are chosen based on the NASA X-ray Timing Explorer (XTE) characteristics [63], as shown in Table 2. Also, the initial and terminal states are given in Table 3. It is assumed that all the chaser's body axes have independent thruster actuators to generate control torques and forces.

Fig. 4
figure 4

Simulation scenario of 6DOF rendezvous maneuver

Full size image
Table 2 Parameters of chaser spacecraft
Full size table
Table 3 Initial and terminal conditions in simulation scenario
Full size table

The number of phases in the GPM discretization and the number of LG points in each phase are considered 20 and 3, respectively. It is assumed that the time interval of the phases is equal. The results of the simulation scenario are shown in Figs. 5, 6, 7, 8, 9, 10, 11, and 12. The rotation sequence for Euler angles trajectories in Fig. 9 is 'YXZ'.

Fig. 5
figure 5

Control torques trajectories

Full size image
Fig. 6
figure 6

Control forces trajectories

Full size image
Fig. 7
figure 7

Angular velocities trajectories

Full size image
Fig. 8
figure 8

MRPs trajectories

Full size image
Fig. 9
figure 9

Euler angles trajectories

Full size image
Fig. 10
figure 10

Relative linear velocities trajectories

Full size image
Fig. 11
figure 11

Relative position trajectories

Full size image
Fig. 12
figure 12

3D schematic of time-optimal 6DOF maneuver

Full size image

Some studies have shown that the control structure for a time-optimal reorientation maneuver, considering cubical constraints on control torques magnitude, is "bang-bang" [7,8,9, 13]. Similarly, the results given in Figs. 5 and 6 show that for a time-optimal 6DOF maneuver, considering the cubical constraint on control torques and forces magnitude, the control structure is "bang-bang". It is the most natural and convenient form of control to be implemented via simple on–off thrusters, which are the most popular and widely used thrusters for spacecraft control due to their simplicity and low cost. The time duration of the time-optimal 6DOF maneuver is \({t}_{f}=25.87 \mathrm{s}\). Furthermore, [7] shows that in the spacecraft time-optimal reorientation maneuver with independent three axes control torques, although the net attitude reorientation is just about one body axis, other control torques (about the other body axes) are also engaged in order to achieve the minimum time. Our results given in Figs. 5 and 6 show that this issue can be generalized for the time-optimal 6DOF maneuver.

As shown in Figs. 7 and 10, the relative angular velocity and relative linear velocity vectors meet the rest condition. Also, results in Figs. 8, 9, and 11 show that the attitude and relative position trajectories meet the desired terminal conditions given in Table 3. The 3D schematic of the time-optimal 6DOF maneuver for the mentioned scenario is shown in Fig. 12.

In order to obtain a first-order optimality proof of the obtained solution, the costate estimation is used. Based on Theorem 1, using KKT multipliers obtained from solving the NLP problem, a costate estimation can be achieved at the LG and boundary points. The results of the costate estimation are shown in Figs. 13, 14, 15, and 16.

Fig. 13
figure 13

Angular velocity costates trajectories

Full size image
Fig. 14
figure 14

MRP costates trajectories

Full size image
Fig. 15
figure 15

Relative velocity costates trajectories

Full size image
Fig. 16
figure 16

Relative position costates trajectories

Full size image

Considering the cost function in Bolza form of Eq. (9), for the assumed time-optimal control problem, the \(\phi \left(x({t}_{0}),{t}_{0},x\left({t}_{f}\right),{t}_{f}\right)\) and \(g\left(x\left(t\right),u\left(t\right),t\right)\) functions are expressed as follows:

$$\begin{gathered} \phi \left( {x\left( {t_{0} } \right),t_{0} ,x\left( {t_{f} } \right),t_{f} } \right) = t_{f} \hfill \\ g\left( {x\left( t \right),u\left( t \right),t} \right) = 0 \hfill \\ \end{gathered}$$
(41)

Also, in this simulation, the boundary conditions \(\boldsymbol{\varphi }\left(x\left({t}_{0}\right),{t}_{0},x\left({t}_{f}\right),{t}_{f}\right)\) are fixed and are not a function of \({t}_{f}\). Hence, according to Hamiltonian and first-order optimality conditions of Eqs. (37) and (38), respectively:

$$H\left( {{\varvec{x}},{\varvec{\lambda}},{\varvec{\mu}},{\varvec{u}},\tau ;t_{0} ,t_{f} } \right) = {\varvec{\lambda}}^{T} {\varvec{f}}\left( {{\varvec{x}},{\varvec{u}},\tau ;t_{0} ,t_{f} } \right)$$
(42)
$$H\left( {t_{f} } \right) = - 1$$
(43)

Regarding the dynamic constraints of Eq. (14), the Hamiltonian, \(H\), does not depend on time:

$$\frac{\partial H}{{\partial t}} = 0$$

Therefore, the Hamiltonian must be constant and equal to -1 along the optimal trajectory.

$$H\left( t \right) = - 1$$

Figure 17 shows that the computed Hamiltonian is approximately equal to -1 and fulfills the first-order optimality conditions.

Fig. 17
figure 17

Hamiltonian trajectory

Full size image

As mentioned earlier, the costates have no physical interpretation, so their variations do not explicitly represent a tangible phenomenon. The main use of the costate variables is to prove the optimality of the obtained solution (according to Eq. 37). The purpose of providing the corresponding graphs (Figs. 13, 14, 15, 16 in the new version) is thus to provide a basis for the reader to verify the Hamiltonian graph (Fig. 17).

4 Conclusion

The time-optimal 6DOF maneuver problem was studied for an inertially asymmetric rigid spacecraft with independent control actuators for attitude and position control. For example, the time-optimal control problem was formulated for a rendezvous maneuver between two spacecraft. In the relative dynamic modeling of spacecraft, the orbital dynamic and coupling between attitude and position control were applied to rotational and translational dynamics. Then, the GPM was used to discretize the time-optimal control problem, and the SQP algorithm was adopted to solve the resulted problem. Finally, the costates were estimated by using the KKT multiplier.

In the simulation, it was observed that the control structure is "bang-bang" for the assumed time-optimal 6DOF maneuver problem. It is the most natural and convenient control structure which can be implemented by simple on–off thrusters. Although the net attitude reorientation was just about one body axis, and the displacement was along two LVLH axes, other control torques and forces (along the other body axes) were also engaged to achieve the minimum time. This observation can also be attributed to the coupling between attitude and position control stated earlier.

As a verification of the obtained solution, the costate estimation results showed that the solution fulfills the first-order optimality conditions.