Trajectory Design Leveraging Low-Thrust, Multi-Body Equilibria and their Manifolds

Abstract

A key challenge in low-thrust trajectory design is generating preliminary solutions that simultaneously specify the spacecraft position and velocity vectors, as well as the thrust history. To mitigate this difficulty, dynamical structures within a combined low-thrust circular restricted 3-body problem (CR3BP) are investigated as candidate solutions to seed initial low-thrust trajectory designs. The addition of a low-thrust force to the CR3BP modifies the locations and stability of the equilibria, offering novel geometries for mission applications. Transfers between these novel equilibria are constructed by leveraging the associated stable and unstable manifolds and insights from the low-thrust CR3BP.

Introduction

A key challenge in low-thrust trajectory design is the construction of a preliminary solution that simultaneously supplies the position, velocity, and thrust vector histories. Although many strategies have emerged to construct spacecraft position and velocity histories in various dynamical models such as the 2-body problem (i.e., Keplerian dynamics) and the circular restricted 3-body problem (CR3BP), fewer methodologies are available to identify a preliminary thrust history. Several strategies to construct a thrust history in the 2-body problem are available [12, 19], but do not accommodate multi-body dynamics. Those methods that do incorporate additional gravitational fields often rely on optimization algorithms to solve boundary value or initial value problems that include the control variables [1, 16, 21]. Some strategies employ machine learning to design an initial guess for thrust histories [6, 17], while others rely on robust collocation schemes to correct rough initial designs [11, 20, 23]. Due to the chaotic nature of the multi-body dynamics, the results obtained from each of these corrections and/or optimization processes are frequently highly dependent on the initial design. Thus, a strategy to construct preliminary low-thrust trajectory designs is useful to improve the convergence and predictability of these algorithms. Additionally, an improved understanding of the low-thrust, multi-body dynamics facilitates the exploration of solutions that are not obvious in simpler models.

In this investigation, dynamical systems techniques are applied to a combined low-thrust, CR3BP (CR3BP+LT) model to gain insights that may be applied to construct preliminary solutions that include low-thrust arcs. Dynamical structures from the CR3BP such as equilibrium solutions, forbidden regions, periodic orbits, and invariant manifolds are already available to inform ballistic designs [13] and have been leveraged in numerous mission scenarios [10, 14, 24]. Several authors combine these ballistic structures with simple low-thrust arcs (e.g., thrust aligned with velocity) to construct low-thrust trajectories in multi-body regimes [18, 23] but, thus far, do not apply dynamical systems techniques to the combined dynamics to gain a fundamental understanding of the flow. A notable exception is the literature detailing investigations into solar sail dynamics in the Earth-Sun and Earth-Moon 3-body systems. These studies offer guidance to select sail parameters that facilitate stable orbits around artificial equilibria [15] and transfers between sequences of artificial equilibria [8]. Subsequent examinations of the combined CR3BP-solar sail dynamics reveal a rich variety of dynamical structures, including invariant manifolds, periodic orbits, and quasi-periodic orbits [7, 9]. Additionally, studies that include the effects of an electrodynamic tether on the spacecraft motion also reveal useful dynamical structures [2]. Similar to the CR3BP-solar sail model or the CR3BP-tether model, the CR3BP+LT supplies structures such as equilibrium points, periodic orbits, invariant manifolds, and forbidden regions to guide the flow [4, 5]. However, in contrast to the solar-sail and tether models, the low-thrust acceleration in the CR3BP+LT may be oriented independently of the spacecraft location (e.g., a sail cannot “thrust” toward the Sun, but a low-thrust engine can deliver such a force). Due to this independence, the CR3BP+LT facilitates a wider range of thrust strategies and may be more readily simplified to gain useful insights. Subsequently, low-thrust paths may be tailored more specifically to a particular mission scenario, expediting convergence in optimization or other numerical algorithms.

Two key properties that are deduced in the CR3BP+LT are leveraged to inform low-thrust trajectory design in this analysis. First, by assuming a constant low-thrust acceleration vector and restricting the motion to the xy-plane, the CR3BP+LT is reduced to a conservative, autonomous, Hamiltonian system. The natural energy (i.e., the Jacobi constant) varies when low-thrust is included, but evolves independently of the spacecraft path and is described by a plane in x-y-energy space. This geometric result supplies intuition that links the evolution of energy along an arc with the low-thrust parameters. Second, the equilibrium solutions in the planar CR3BP+LT occur in unique configurations with manifolds that guide global flow in novel ways. The number and locations of the low-thrust equilibria vary with the magnitude and orientation of the low-thrust acceleration vector, including equilibrium point configurations not available in the natural model [4, 5, 7]. Additionally, the stability properties of the low-thrust equilibria differ from the natural CR3BP equilibria, supplying stable and unstable manifolds that describe new flow patterns throughout the system. Thrust vector parameters are straightforwardly selected to leverage manifolds that facilitate a transfer between regions of the CR3BP+LT separated in both position and energy. This strategy, introduced by Farrés for Sun-Earth solar sail transfers between equilibria [7], is extended to the Earth-Moon low-thrust system and additional insights from the CR3BP+LT are employed to guide the design.

Dynamical Model Development

The first step in computing and leveraging dynamical structures within the CR3BP+LT is the development of the dynamical model. An energy-based approach is first employed to derive the governing equations in the CR3BP and produce an expression for the natural Hamiltonian. By augmenting the CR3BP equations of motion (EOMs) with a low-thrust term, the CR3BP+LT is constructed and the associated low-thrust Hamiltonian is defined. Reasonable assumptions applied to the CR3BP+LT yield a conservative, autonomous system with properties that may be leveraged to facilitate low-thrust trajectory designs.

Circular Restricted 3-Body Problem

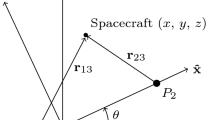
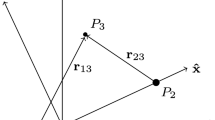
The CR3BP describes the motion of a relatively small body, such as a spacecraft, in the presence of two larger gravitational point masses (P₁ and P₂) with paths that evolve along circular orbits about their mutual barycenter (B). To simplify the governing equations and enable straightforward visualization of periodic solutions, the motion of the spacecraft is described in a right-handed frame ($\hat {\boldsymbol {x}},~\hat {\boldsymbol {y}},~\hat {\boldsymbol {z}}$) that rotates with the two primaries, as seen in Fig. 1, where $\hat {\boldsymbol {x}}$, $\hat {\boldsymbol {y}}$, and $\hat {\boldsymbol {z}}$ are vectors of unit length. The system is parameterized by the mass ratio, μ = M₂/(M₁ + M₂), where M₁ and M₂ are the masses of the primaries and M₁ ≥ M₂. To facilitate numerical integration, the dimensional values are nondimensionalized by characteristic quantities such that the distance between P₁ and P₂ is unity, the mean motion of the two primaries is unity, and the masses of each body range from zero to one [22]. The spacecraft is located relative to the system barycenter in the rotating frame via the vector $\mathbf {r}= \{\begin {array}{lll} x & y & z \end {array}\}^{T}$.

Fig. 1

CR3BP system configuration; two point masses, P₁ and P₂, proceed on circular orbits about their mutual barycenter, B. The behavior of a third, relatively massless particle is described within the rotating coordinate frame, ($\hat {x},~\hat {y},~\hat {z}$)

The equations of motion governing the CR3BP are derived via a Hamiltonian energy approach. Let the kinetic (T) and potential (V ) energies corresponding to the CR3BP system be defined by

$$ \begin{array}{@{}rcl@{}} T &=& \frac{1}{2} \left[ (\dot{x} - y)^{2} + (\dot{y} + x)^{2} + \dot{z}^{2} \right] , \end{array} $$

(1)

$$ \begin{array}{@{}rcl@{}} V &=& \frac{-(1-\mu)}{r_{13}} - \frac{\mu}{r_{23}}, \end{array} $$

(2)

where $\dot {x}$, $\dot {y}$, and $\dot {z}$ are the derivatives of the position states with respect to nondimensional time as observed in the rotating frame, and r₁₃ and r₂₃ are the distances between the spacecraft (P₃) and the first and second primaries, respectively:

$$ r_{13} = \sqrt{(x+\mu)^{2} + y^{2} + z^{2}} , \qquad r_{23} = \sqrt{(x-1+\mu)^{2} + y^{2} + z^{2}}. $$

Next, form the Hamiltonian,

$$ H_{nat} = \frac{1}{2} v^{2} - \frac{1}{2} \left( x^{2} + y^{2} \right) - \frac{1-\mu}{r_{13}} - \frac{\mu}{r_{23}}, $$

(3)

where the squared velocity magnitude is $v^{2}=\dot {x}^{2}+\dot {y}^{2}+\dot {z}^{2}$. By applying Hamilton’s canonical equations of motion, a set of differential equations that govern the motion of P₃ emerges,

$$ \begin{array}{@{}rcl@{}} \ddot{x} &=& 2\dot{y} + {\varOmega}_{x}, \end{array} $$

(4)

$$ \begin{array}{@{}rcl@{}} \ddot{y} &=& -2\dot{x} + {\varOmega}_{y}, \end{array} $$

(5)

$$ \begin{array}{@{}rcl@{}} \ddot{z} &=& {\varOmega}_{z}, \end{array} $$

(6)

where Ω is the CR3BP pseudo-potential function,

$$ {\varOmega} = \frac{1}{2}(x^{2} + y^{2}) + \frac{1-\mu}{r_{13}} + \frac{\mu}{r_{23}}, $$

(7)

and Ω_x, Ω_y, and Ω_z represent the partial derivative of Ω with respect to the subscripted variables x, y, and z, respectively. Because the CR3BP is autonomous and conservative, H_nat is constant and equivalent to the Jacobi integral, i.e., the Jacobi constant. The Jacobi constant, C = − 2H_nat, is commonly leveraged as a measure of the energy associated with arcs in the CR3BP.

CR3BP Incorporating Low-Thrust

To incorporate low-thrust into the CR3BP multi-body model, the low-thrust acceleration vector is first defined. This vector,

$$ \mathbf{a}_{lt} = \frac{f}{m} \hat{\mathbf{a}}_{lt} , $$

(8)

is oriented relative to the rotating frame via the unit vector $\hat {\mathbf {a}}_{lt}$ and scaled by the nondimensional thrust magnitude, f, and nondimensional spacecraft mass, m = M₃/M_3,0, where M₃ is the instantaneous spacecraft mass and M_3,0 is the initial (wet) spacecraft mass. The nondimensionalization of the thrust magnitude leverages the CR3BP characteristic time, t_∗, and characteristic length, l_∗, for consistency with the CR3BP coordinate nondimensionalization, i.e.,

$$ f = \frac{F t_{*}^{2}}{l_{*} M_{3,0}}. $$

(9)

In this expression, F describes the thrust magnitude in kilonewtons, l_∗ represents the distance between P₁ and P₂ in kilometers, t_∗ is the inverted system mean motion, t_∗ = 1/N, in seconds, and M_3,0 is defined in terms of kilograms. A nondimensional thrust magnitude of f ≈ 1e-2 in the Earth-Moon and Sun-Earth CR3BP+LT systems is consistent with current spacecraft capabilities, such as Deep Space 1, Dawn, or Hayabusa [4]. Accordingly, a low-thrust acceleration magnitude of a_lt = f/m = 7e-2 (i.e., ≈ 0.19 mm/s², consistent with the Deep Space 1 capability) is frequently leveraged in this analysis to represent a large but reasonable low-thrust capability in the Earth-Moon system.

To apply an energy-based derivation of the CR3BP+LT EOMs similar to the derivation leveraged for the CR3BP, the CR3BP dynamics are augmented with a low-thrust acceleration term. While the spacecraft kinetic energy expression in Eq. 1 remains unchanged, the potential energy expression incorporates a low-thrust acceleration term, i.e.,

$$ V_{lt} = \frac{-(1-\mu)}{r_{13}} - \frac{\mu}{r_{23}} - \mathbf{r} \cdot \mathbf{a}_{lt}. $$

(10)

This additional term propagates through the derivation to yield the low-thrust Hamiltonian,

$$ H_{lt} = \frac{1}{2} v^{2} - \frac{1}{2} \left( x^{2} + y^{2} \right) - \frac{1-\mu}{r_{13}} - \frac{\mu}{r_{23}} - \mathbf{r} \cdot \mathbf{a}_{lt}, $$

(11)

which may also be written in terms of the natural Hamiltonian, i.e.,

$$ H_{lt} = H_{nat} - \mathbf{r} \cdot \mathbf{a}_{lt} . $$

(12)

Due to the time-varying nature of the spacecraft mass, the governing equations are not available directly from Hamilton’s canonical equations. However, the low-thrust Hamiltonian offers useful insights into the relationship between the total energy and a_lt that may be used to simplify the dynamical model. Newton’s law is applied to yield the EOMs,

$$ \begin{array}{@{}rcl@{}} \ddot{x} &=& 2\dot{y} + {\varOmega}_{x} + \mathbf{a}_{lt} \cdot \hat{\mathbf{x}}, \end{array} $$

(13)

$$ \begin{array}{@{}rcl@{}} \ddot{y} &=& -2\dot{x} + {\varOmega}_{y} + \mathbf{a}_{lt} \cdot \hat{\mathbf{y}}, \end{array} $$

(14)

$$ \begin{array}{@{}rcl@{}} \ddot{z} &=& {\varOmega}_{z} + \mathbf{a}_{lt} \cdot \hat{\mathbf{z}}, \end{array} $$

(15)

$$ \begin{array}{@{}rcl@{}} \dot{m} &=& \frac{-f l_{*}}{I_{sp} g_{0} t_{*}}, \end{array} $$

(16)

where I_sp is the specific impulse associated with the propulsion system, and g₀ = 9.80665e-3 km/s². These low-thrust EOMs are consistent with Eqs. 4, 5 and 6 that govern the natural CR3BP; the low-thrust equations are simply augmented with the a_lt terms.

CR3BP+LT Simplifications for Global Insight

To facilitate analyses in the CR3BP+LT, simplifications are applied to reduce the number of dimensions in the problem. The conservative, natural problem admits one integral of the motion (the Hamiltonian, H_nat), reducing the natural problem dimension by one. However, due to the non-autonomous nature of the CR3BP+LT, the low-thrust Hamiltonian is not constant in general and, thus, does not necessarily offer a similar dimension reduction. Nevertheless, an analysis of the time derivative of the low-thrust Hamiltonian supplies useful insights. First, differentiate the first term in Eq. 12, i.e., the expression for the natural Hamiltonian,

$$ \frac{\partial H_{nat}}{\partial\tau} = \dot{x} \left( \ddot{x} - {\varOmega}_{x} \right) + \dot{y} \left( \ddot{y} - {\varOmega}_{y} \right) + \dot{z} \left( \ddot{z} - {\varOmega}_{z} \right), $$

(17)

where τ is nondimensional time. Substitute the CR3BP+LT equations of motion from Eqs. 13–16 into this derivative expression and simplify:

$$ \frac{\partial H_{nat}}{\partial\tau} = \dot{x} \left( 2\dot{y} + \mathbf{a}_{lt} \cdot \hat{\mathbf{x}} \right) + \dot{y} \left( -2\dot{x} + \mathbf{a}_{lt} \cdot \hat{\mathbf{y}} \right) + \dot{z} \mathbf{a}_{lt} \cdot \hat{\mathbf{z}} = \mathbf{v} \cdot \mathbf{a}_{lt}, $$

(18)

where $\mathbf {v} = \{\begin {array}{lll}\dot {x} & \dot {y} & \dot {z} \end {array}\}^{T}$ is the spacecraft velocity vector in the rotating frame. The derivative of the second term in Eq. 12 is straightforwardly evaluated,

$$ \frac{\partial}{\partial\tau} \left[ \mathbf{r} \cdot \mathbf{a}_{lt} \right] = \mathbf{v} \cdot \mathbf{a}_{lt} + \mathbf{r} \cdot \dot{\mathbf{a}}_{lt}. $$

(19)

Combine (18) and (19) to yield the time derivative of H_lt,

$$ \frac{\partial H_{lt}}{\partial\tau} = -\mathbf{r} \cdot \dot{\mathbf{a}}_{lt}. $$

(20)

If a_lt is constant, both in magnitude and orientation as viewed in the rotating frame, then $\dot {\mathbf {a}}_{lt} = \mathbf {0}$ and H_lt is constant during low-thrust propagations. Essentially, if a_lt is constant, the CR3BP+LT is a conservative system and the low-thrust Hamiltonian may be leveraged as an integral of the motion in the low-thrust problem.

While preserving a fixed orientation, i.e., a fixed $\hat {\mathbf {a}}_{lt}$ vector, is a familiar attitude control strategy, preserving a constant acceleration magnitude, a_lt, is less common. Consider the expression, $\mathbf {a}_{lt} = (f/m) \hat {\mathbf {a}}_{lt}$ with a fixed orientation and a fixed thrust magnitude ($\hat {\mathbf {a}}_{lt}$ = constant, f = constant) but with variable mass. Accordingly, the time derivative of a_lt, evaluated as

$$ \dot{\mathbf{a}}_{lt} = \frac{f\dot{m}}{m^{2}} \hat{\mathbf{a}}_{lt} = -a_{lt}^{2} \frac{l_{*}}{I_{sp} g_{0} t_{*}} \hat{\mathbf{a}}_{lt}, $$

(21)

is non-zero when $\dot {m} \neq 0$. To determine if $\dot {a}_{lt}$, given by the scalar coefficient, $a_{lt}^{2} l_{*}/(I_{sp} g_{0} t_{*})$, is sufficiently small to be ignored, compare $\dot {a}_{lt}$ with the energy range associated with the natural equilibrium solutions, i.e., the H_nat values associated with the CR3BP Lagrange points. For example, let a_lt = 7e-2, a large but reasonable acceleration magnitude, and let I_sp = 1500 seconds, a relatively low efficiency for a low-thrust system. The $\dot {a}_{lt}$ magnitude in the Earth-Moon CR3BP-LT evaluates to approximately 3.4e-4 while the energy range between the Lagrange points with the highest and lowest energies, ΔH_nat = H_nat(L₅) − H_nat(L₁), is approximately 0.1, three orders of magnitude larger than $\dot {a}_{lt}$. Subsequently, the H_lt variations due to the time-varying spacecraft mass are very small compared to the L₅ → L₁ energy range, and H_lt is reasonably approximated as a constant for propagations with a maximum mass consumption of 15%, i.e., m(τ) > 0.85. Note that the magnitude of $\dot {\mathbf {a}}_{lt}$ increases quadratically with a_lt; accordingly, this assumption is valid only for small acceleration magnitudes, i.e., low-thrust capabilities. Additionally, this assumption is not applicable to all systems, particularly those with large l_∗/t_∗ ratios (resulting in a large $\dot {\mathbf {a}}_{lt}$ magnitude) and with very small L₅ → L₁ energy ranges, such as the Sun-Earth system (where $\dot {a}_{lt}/{\varDelta } H_{nat} \approx 22$). As the analyses in this investigation leverage the dynamics of the Earth-Moon system, H_lt and a_lt are reasonably approximated as constants without adjustments to the characteristic quantities. Accordingly, the variable acceleration quantity f/m is replaced by the constant value a_lt, removing the need for the mass time-derivative in Eq. 16. These simplifications – a constant low-thrust Hamiltonian and a constant acceleration magnitude – effectively reduce the problem dimension by two.

The simplifying assumption of a constant low-thrust acceleration vector yields additional insights to guide low-thrust trajectory design. Although H_nat does not represent a dynamically significant quantity in the CR3BP+LT (rather, it is merely a component of the low-thrust Hamiltonian, expressed in Eq. 11), it remains a useful reference to the natural CR3BP. Low-thrust arcs are frequently a means to transition between natural structures with fixed H_nat values; thus, the evolution of H_nat in the CR3BP+LT is relevant. While H_nat is not constant in general when low-thrust is active, H_nat evolves independently of the spacecraft path when a_lt is fixed in the rotating frame. This property is available from the time-derivative of H_nat, expressed in Eq. 18. As the a_lt vector is constant, this expression is integrable, yielding the equation

$$ H_{nat}(\tau_{f}) - H_{nat}(\tau_{0}) = \int\limits_{\tau_{0}}^{\tau_{f}} \mathbf{v} \cdot \mathbf{a}_{lt} \text{d} \tau = (\mathbf{r}(\tau_{f}) - \mathbf{r}(\tau_{0})) \cdot \mathbf{a}_{lt}. $$

(22)

Accordingly, the natural Hamiltonian value along any low-thrust arc is available given the initial H_nat value, the initial and final position, and the fixed low-thrust acceleration vector. This relationship supplies useful insights that link the geometry of low-thrust arcs to the evolution of H_nat, facilitating intuitive design strategies.

Finally, to further reduce the system complexity, only planar motion is explored. Thus, $z(\tau ) = \dot {z}(\tau ) = 0$ for all τ, and the low-thrust pointing vector, $\hat {\mathbf {a}}_{lt}$, is described by the planar vector

$$ \hat{\mathbf{a}}_{lt} = \left\{\begin{array}{ccc}\cos\alpha & \quad \sin\alpha & \quad 0 \end{array}\right\}^{T} . $$

(23)

These simplifications facilitate the analysis of the dynamical structures in the CR3BP+LT while also supplying insights that are useful for spatial (3D) path planning.

Energy Planes

In the planar CR3BP+LT, every low-thrust arc with a_lt fixed in the rotating frame lies entirely within a plane oriented in x-y-H_nat space by the low-thrust orientation angle, α, and the magnitude, a_lt. This energy plane includes the initial position and energy along the low-thrust arc, defined by an initial control point, $\boldsymbol {\rho }_{0} = \{\begin {array}{lll} x_{0} & y_{0} & H_{nat,0} \end {array}\}^{T}$. A low-thrust trajectory may be represented by the control point variation,

$$ {\varDelta} \mathbf{\rho}(\tau) = \mathbf{\rho}(\tau) - \mathbf{\rho}_{0} = {\varDelta} x \hat{\mathbf{x}} + {\varDelta} y \hat{\mathbf{y}} + {\varDelta} H \hat{\mathbf{H}} $$

(24)

where $\boldsymbol {\rho }(\tau )=\{\begin {array}{lll}x(\tau ) & y(\tau ) & H_{nat}(\tau ) \end {array}\}^{T}$ is a control point that reflects the spacecraft position and H_nat value at nondimensional time τ. Accordingly, Δρ(τ) locates the spacecraft relative to the origin of the energy plane, as depicted in Fig. 2a. The plane is oriented via two rotations: a rotation of α about $\hat {\mathbf {H}} = \hat {\mathbf {H}}^{\prime }$ to the intermediate frame, ($\hat {\mathbf {x}}^{\prime }$, $\hat {\mathbf {y}}^{\prime }$, $\hat {\mathbf {H}}^{\prime }$), followed by a rotation of γ about $\hat {\mathbf {y}}^{\prime } = \hat {\mathbf {y}}^{\prime \prime }$ to a frame fixed in the energy plane, ($\hat {\mathbf {x}}^{\prime \prime }$, $\hat {\mathbf {y}}^{\prime \prime }$, $\hat {\mathbf {H}}^{\prime \prime }$), as seen in Fig. 2b. The first angle, α, orients the low-thrust acceleration vector, as noted in Eq. 23. The second rotation angle, γ, is related to the low-thrust acceleration magnitude via the relationship

$$ \tan\gamma = -a_{lt}. $$

(25)

As a short proof that such a plane exists with this orientation, rewrite the general control point variation in Eq. 24 in the energy plane-fixed frame,

$$ \begin{array}{@{}rcl@{}} {\varDelta} \mathbf{\rho} &=& \left[ {\varDelta} x C_{\alpha} C_{\gamma} + {\varDelta} y S_{\alpha} C_{\gamma} - {\varDelta} H S_{\gamma} \right] \hat{\mathbf{x}}^{\prime\prime} + \left[ {\varDelta} y C_{\alpha} - {\varDelta} x S_{\alpha} \right] \hat{\mathbf{y}}^{\prime\prime} \\ &&+\left[ {\varDelta} x C_{\alpha} S_{\gamma} + {\varDelta} y S_{\alpha}S_{\gamma} + {\varDelta} H C_{\gamma} \right] \hat{\mathbf{H}}^{\prime\prime} , \end{array} $$

(26)

where $C_{\alpha } = \cos \limits \alpha$, $S_{\alpha } = \sin \limits \alpha$, $C_{\gamma } = \cos \limits \gamma$, and $S_{\gamma } = \sin \limits \gamma$. A trajectory confined to the plane possesses a zero-valued $\hat {\mathbf {H}}^{\prime \prime }$ component; thus, rearrange the terms in the $\hat {\mathbf {H}}^{\prime \prime }$ component and equate them to zero,

$$ {\varDelta} H + \tan\gamma \left( {\varDelta} x C_{\alpha} + {\varDelta} y S_{\alpha} \right) = 0 . $$

(27)

When Eq. 25 is substituted for the $\tan \gamma$ term, Eq. 27 is identical to the energy path-independence relationship in Eq. 22. Subsequently, Eq. 27 represents the true dynamics; the out-of-plane component of Δρ(τ) is identically zero for all τ and the low-thrust arc is confined to the energy plane while a_lt remains fixed in the CR3BP+LT rotating frame. This plane links a particular energy change to the geometry of a low-thrust transfer arc. If the geometry of such a transfer is relatively unperturbed by variations in the low-thrust acceleration vector, α and a_lt may be selected to orient the energy plane to deliver a desired energy change based on the existing geometry. Additionally, these results supply an analytical basis for previous findings that the energy along low-thrust arcs varies as a function of the angle between the low-thrust acceleration vector and the spacecraft rotating velocity vector, i.e., the angle between $\hat {\mathbf {a}}_{lt}$ and v [4]. When v is aligned with $\hat {\mathbf {a}}_{lt}$, the spacecraft moves “uphill” on the energy plane, increasing the H_nat value. Similarly, a spacecraft with $\hat {\mathbf {a}}_{lt} \perp \mathbf {v}$ follows a path that contours across the energy plane at a constant value of H_nat. While these properties of the H_nat value are straightforwardly derived from the time derivative in Eq. 18, the energy plane supplies a more intuitive representation of the energy variations. Similar to a hiker faced with a steep slope, a low-thrust spacecraft may leverage sequential energy planes as a set of “switchbacks” to rapidly increase energy. In fact, the well-known energy-optimal low-thrust spiral that employs a control law with $\hat {\mathbf {a}}_{lt} = \pm \hat {\boldsymbol {v}}$ is simply a strategy to continuously reorient the energy plane such that the spacecraft is always moving along the steepest energy gradient. Accordingly, α and a_lt are straightforwardly selected to deliver specific energy evolutions during the preliminary design process.

Fig. 2

The energy plane is located and oriented relative to the rotating x-y frame with a third dimension representing H_nat

Gateway Manipulation Using Energy Planes

Bounds on the spacecraft motion in the natural CR3BP, termed forbidden regions, are linked to the instantaneous value of H_nat along a trajectory [22]. Let these bounds be represented by the set of points $\mathbb {F}_{nat} = \mathbb {F}_{nat}\left (H_{nat} \right )$. The H_nat values associated with the natural equilibrium solutions, $L_{1},~\dots ,~L_{5}$, represent critical configurations at which the forbidden regions shrink (or grow) to permit (or restrict) access to regions in the xy-plane. For example, for H_nat values slightly higher than the H_nat(L₁) value, the forbidden regions include a narrow neck near the L₁ point, i.e., a “gateway,” through which trajectories may pass to transit between the P₁ and P₂ regions. Similar gateways form as H_nat increases past the L₂ and L₃ energy levels, and the H_nat value corresponding to the L_4/5 equilibrium points is the highest energy for which planar motion is restricted by the forbidden regions in the CR3BP. Accordingly, to enable transit between regions in the CR3BP, the H_nat value along an arc must be sufficiently high to open the required gateways.

Since the H_nat value changes along low-thrust arcs, the $\mathbb {F}_{nat}$ structures are not static and are, thus, difficult to visualize and employ in the low-thrust trajectory design process. However, recall that when a_lt is fixed in the rotating frame, the low-thrust Hamiltonian, H_lt, remains constant. Accordingly, a set of bounding low-thrust forbidden regions, $\mathbb {F}_{lt} = \mathbb {F}_{lt}(H_{lt})$, are available. These $\mathbb {F}_{lt}$ structures are related to the $\mathbb {F}_{nat}$ structures via the energy plane, as illustrated by the sample configuration in Fig. 3.

Fig. 3

Earth-Moon CR3BP+LT forbidden regions for a_lt = 7e-2, α = 80^∘, and H_lt = − 1.5561

An “energy surface”, shown in blue, is constructed from planar $\mathbb {F}_{nat}$ structures across a range of H_nat values; each horizontal slice through this surface is a natural forbidden region at a specific H_nat value. This structure bounds all planar motion over the full range of H_nat values; thus, low-thrust arcs are bounded by the energy surface even as H_nat varies. Because H_nat varies along an energy plane, the intersection of the energy plane and the forbidden region energy surface bounds the low-thrust motion. This intersection, plotted as white contours in Fig. 3a and as black contours in Fig. 3b, defines the low-thrust forbidden region, $\mathbb {F}_{lt}(H_{lt})$. In this example, the origin of the energy plane (a maroon plane in Fig 3a) is located by the control point, $\boldsymbol {\rho }=\{\begin {array}{lll}0.5 & 0 & -1.55 \end {array}\}^{T}$, plotted as a red point, and oriented by the low-thrust orientation angle, α = 80^∘, and the low-thrust acceleration magnitude, a_lt = 7e-2. Variations in H_nat (the third component of ρ) translate the plane vertically, while changes in a_lt affect the inclination of the plane and adjustments to α rotate the energy plane about the control point. Due to this coupling between the H_nat evolution and the geometry of low-thrust arcs, a preliminary set of control parameters are intuitively available: To ensure a gateway is open when the spacecraft arrives there, select α and a_lt to incline and orient the energy plane such that $\mathbb {F}_{lt}$ permits transit through the gateway. Similar strategies are straightforwardly derived from these relationships to facilitate access to other regions of the CR3BP.

To illustrate the manipulation of the forbidden regions via insights from an energy plane, consider a ballistic path that passes from the system interior (i.e., near P₁) through the L₁ and L₂ gateways to the exterior region, as plotted in black in Fig. 4a. Assume that the path must be modified to prohibit one or both gateway transits; the exact locations along the ballistic arc at which to enable the low-thrust system are available from the geometry of the associated energy plane. For example, to avoid escape to the system exterior, it is sufficient to reduce the H_nat value along the low-thrust arc such that, at the location of the L₂ gateway transit, the spacecraft H_nat value is lower than the H_nat value at L₂, H_nat(L₂). Let the low-thrust magnitude be a_lt = 7e-2 and the low-thrust orientation be α = 180^∘. In this configuration, the change in the H_nat value along the resulting low-thrust propagation is proportional to the change in x position, i.e.,

$$ {\varDelta} H_{nat} = -a_{lt} {\varDelta} x. $$

(28)

This relationship, while simple due to the convenient choice of α, is straightforwardly derived from any energy plane orientation via trigonometric expressions.

Fig. 4

The transit behaviors of low-thrust arcs (colored) in the Earth-Moon CR3BP+LT for a_lt = 7e-2 and α = 180^∘ originating from different locations on a ballistic arc (black) are predicted by a simple trigonometric property of the energy plane geometry

To determine if applying low-thrust with α = 180^∘ will sufficiently decrease H_nat to close the L₂ gateway, the initial H_nat value on the escaping ballistic path as well as the distance from L₂ along the x-axis are considered. As the goal in this low-thrust application is the reduction of H_nat to H_nat(L₂) at $x = x_{L_{2}}$, where $x_{L_{2}}$ is the location of L₂ on the x-axis, rearrange (28) and solve for the right-most x-coordinate at which thrusting may be to sufficient to reduce H_nat,

$$ \begin{array}{@{}rcl@{}} {\varDelta} x &=& \frac{-1}{a_{lt}} {\varDelta} H_{nat}, \\ \max x_{0, lt} &=& x_{L_{2}} + \frac{1}{a_{lt}}\left( H_{nat}(L_{2}) - H_{nat,0} \right), \end{array} $$

(29)

where H_nat,0 is the energy of the ballistic arc. If low-thrust is enabled before the spacecraft reaches this x-coordinate along the ballistic arc, the H_nat value decreases more than enough to close the L₂ gateway by the time the spacecraft reaches $x_{L_{2}}$. Similarly, if thrust is enabled after the spacecraft has passed this x-coordinate, the L₂ gateway will not be closed when the spacecraft reaches $x_{L_{2}}$ and the possibility exists that the spacecraft will escape. This boundary is marked in Fig. 4b by a left-pointing black arrow at the top of the plot. Each colored, dotted line in this plot represents the energy plane associated with a low-thrust propagation that begins at H_nat,0 = − 1.55 and a range of x-coordinates. Accordingly, the transition from blue arcs (arcs that cannot transit the L₂ gateway) to green arcs (arcs that may transit L₂) corresponds with the energy plane that intersects L₂ in this x vs. H_nat space. The configuration space (x vs. y) representation of these arcs, plotted in Fig. 4a, also demonstrate these transit properties; none of the blue trajectories pass through the L₂ gateway while many of the green trajectories do escape to the system exterior. However, note that some of the green trajectories do not escape through the L₂ gateway in the allotted propagation time. The H_nat values on these arcs are too high to prohibit transit, but the higher energy values do not guarantee transit. Finally, note that a similar ${\min \limits } x_{0,lt}$ may be defined to locate the right-most x-coordinate at which the low-thrust must be enabled to transit the L₁ gateway. This value, marked by a right-pointing triangle in Fig. 4b, is collocated with the transition between red and blue arcs, where red represents paths that sufficiently decrease H_nat to close the L₁ gateway by the time the spacecraft reaches $x_{L_{1}}$. Similarly, the blue arcs represent low-thrust arcs that do not decrease H_nat to close the L₁ gateway. Many of these arcs transit through the open L₁ gateway but, like the green arcs, some do not transit despite possessing sufficient energy.

This analysis demonstrates that the energy plane is a useful tool to predict the transit or capture behavior along a low-thrust arc. The geometry of the ballistic transit arc employed in this example (seen in black in Fig. 4b) is only slightly modified by a low-thrust force during the approach to the P₂ vicinity; thus, the energy along the low-thrust arcs is straightforwardly controlled as the path moves predictably along the prescribed energy plane. However, as the arcs traverse the dynamic regions near L₁, P₂, and L₂, the trajectory geometry is significantly affected by the addition of low-thrust and, thus, is more difficult to predict. Regardless of these sensitivities, the energy along each low-thrust arc is confined to the energy plane and transit (or capture) is well-predicted by the sufficient conditions derived from the energy history. This strategy is also applicable to scenarios other than gateway transit behavior; any problem that requires a specific energy value at a specific location (i.e., targeting a control point, $\boldsymbol {\rho } = \{\begin {array}{lll}x & y & H_{nat} \end {array}\}^{T}$) is facilitated by the CR3BP+LT energy planes.

Planar Low-Thrust Equilibrium Solutions

While insights from the energy plane are useful to modify ballistic paths, dynamical structures from the CR3BP+LT supply additional geometries that may be leveraged to facilitate low-thrust trajectory design. One such group of structures is the equilibrium solutions associated with the planar (2D) dynamics in the CR3BP+LT; these solutions supply an initial characterization of the local and global dynamics when low-thrust is included in the model. Linearizations of the nonlinear dynamics relative to the equilibria describe local stable, unstable, and center manifolds. To represent the full nonlinear flow, global invariant manifolds are constructed by transitioning the linear results to the nonlinear model [22]. By manipulating the low-thrust acceleration vector, the number and location of equilibrium solutions in the CR3BP+LT are affected, which subsequently affects the existence and characteristics of various nearby dynamical structures. Accordingly, the equilibrium solutions in the CR3BP+LT are relevant to low-thrust mission applications, particularly as the equilibria locations evolve relative to the familiar CR3BP equilibrium points.

To initiate a fundamental understanding of the flow in the CR3BP+LT consider the simplified planar dynamics with a fixed a_lt vector, consistent with the previous simplifications. The equilibrium solutions solve (13) and (14) when all time derivatives ($\dot {x}$, $\ddot {x}$, $\dot {y}$, $\ddot {y}$) are zero. In the natural CR3BP (a_lt = 0), five such equilibria exist, i.e., the Lagrange points or libration points [22]. As the addition of the perturbing low-thrust acceleration introduces two new variables, the thrust orientation angle, α, and magnitude, a_lt, the locations of the equilibrium solutions are no longer fixed [4, 5, 7]. Given a value of a_lt, the locations of the equilibrium solutions vary with α, as plotted in Fig. 5. The location of each equilibrium solution identifies a point in the xy-plane where the low-thrust acceleration vector offsets the natural acceleration vector to yield a net-zero acceleration in the rotating frame. Accordingly, the closed, colored contours of equilibria depicted in Fig. 5 are termed zero acceleration contours (ZACs) [4]. Each ZAC represents a set of equilibria at a fixed a_lt value for the full range of α values with at least one equilibrium solution on each ZAC for every value of α. To identify these structures independently of the natural equilibrium point solutions, let the ZACs near L₁ and L₂ be notated $\mathbb {E}_{1}$ and $\mathbb {E}_{2}$, and let the C-shaped ZAC that includes points near L₃ be labeled $\mathbb {E}_{3}$. Note that these designations are specific to the a_lt value that yields the ZACs. For instance, when a_lt is small, the ZACs remain near the natural solutions, yielding five ZACs: $\mathbb {E}_{1},~\mathbb {E}_{2},~\dots ,~\mathbb {E}_{5}$. However, as a_lt increases, ZACs merge [4, 5]. In this investigation, a_lt = 7e-2 is employed for consistency; at this low-thrust magnitude, the $\mathbb {E}_{3},~\mathbb {E}_{4}$ and $\mathbb {E}_{5}$ structures are combined into the $\mathbb {E}_{3}$ ZAC. Groups of equilibria at specific α values are denoted via function notation, i.e., $\mathbb {E}_{3}(-60^{\circ })$ specifies the set of low-thrust equilibria within the larger $\mathbb {E}_{3}$ set at α = − 60^∘. Note that the $\mathbb {E}_{3}(-60^{\circ })$ may include multiple equilibrium points on the $\mathbb {E}_{3}$ contour that correspond to an α angle of − 60^∘. To identify specific equilibrium points on a ZAC, the notation ${E_{i}^{j}}(\alpha )$ is employed, where i references the ZAC, $\mathbb {E}_{i}$, and j designates the individual equilibria in order of ascending H_lt value. For example, $\mathbb {E}_{3}(-60^{\circ })$ includes three equilibria; thus, ${E_{3}^{1}}(-60^{\circ })$ corresponds to the equilibria with the lowest H_lt value, ${E_{3}^{2}}(-60^{\circ })$ possesses an intermediate H_lt value, and ${E_{3}^{3}}(-60^{\circ })$ is characterized by the highest H_lt value. In the absence of a superscript, e.g., E₁(− 60^∘), only one equilibrium solution exists on the specified ZAC at the given angle.

Fig. 5

Low-thrust equilibrium solutions (colored by α) in the Earth-Moon CR3BP+LT for a_lt = 7e-2 and α ∈ [− 180^∘, 180^∘]; the natural equilibrium solutions are included as black asterisks

As the locations of the low-thrust equilibrium solutions evolve with variations in a_lt and α, the stability properties of each point also vary. These properties are determined by inspecting the eigenvalues of the Hessian matrix, $\partial \dot {\mathbf {q}}/\partial \mathbf {q}$, evaluated at the equilibrium point location, where $\mathbf {q}=\{\begin {array}{llll}x & y & \dot {x} & \dot {y} \end {array}\}^{T}$ is the state vector and $\dot {\mathbf {q}}$ reflects the time derivatives of the states consistent with Eqs. 13 and 14. Real eigenvalues (in the complex plane) represent stable (negative) and unstable (positive) motion, while eigenvalues on the imaginary axis reflect oscillatory motion. Combinations of the two types are also possible and are characterized by spiral-shaped flow patterns in position space (i.e., the xy-plane). Due to the Hamiltonian nature of the CR3BP+LT with a_lt fixed in the rotating frame, eigenvalues occur in pairs, either as real pairs symmetric across the imaginary axis (i.e., ± λ) or as complex conjugate pairs. The former pair, characterized by stable and unstable motion, is termed a saddle, while a pair of imaginary eigenvalues is denoted a center mode; the combined saddle-center (e.g., spiral) motion is termed a mixed mode.

The linear modes associated with an equilibrium solution identify the local dynamics and may predict nonlinear flow patterns. For example, oscillatory motion (periodic or quasi-periodic) is frequently available near an equilibrium solution with a center mode, i.e., a center subspace. Similarly, trajectories that asymptotically approach an equilibrium point in forward and reverse time are guided by the stable and unstable manifolds of the saddle mode. The four-dimensional phase space near each planar equilibrium point is described by four eigenvalues (two pairs), or two modes. In practice, these modes occur in four different combinations: (i) saddle × center (S×C); (ii) center × center (C×C); (iii) mixed × mixed (M×M); and (iv) saddle × saddle (S×S). The Earth-Moon CR3BP+LT equilibria for a_lt = 7e-2 are characterized by the first three combinations at various locations in the xy-plane, as apparent in Fig. 6. The dynamics near equilibria on $\mathbb {E}_{1}$ and $\mathbb {E}_{2}$ are consistent with the S×C motion associated with natural L₁ and L₂ equilibria, as observed in Fig. 6b. In contrast, $\mathbb {E}_{3}$ includes S×C motion on the “inner ring,” C×C motion on the “outer ring,” and some M×M motion near the tips of the C-shaped contour. Due to the proximity of different linear modes, the low-thrust dynamics in some locations are very sensitive to the value of α employed to orient the low-thrust vector. For instance, both C×C and S×C equilibrium solutions are available near the L₄ and L₅ points at the same a_lt value and the opposite α values (opposite by 180^∘). As a result, the global flow in a single area (e.g., near L_4/5) is controllable via manipulations of the low-thrust acceleration vector and suitable parameters may be identified to yield flow structures for inclusion in low-thrust trajectories.

Fig. 6

Low-thrust equilibrium solutions (colored by stability) in the Earth-Moon CR3BP+LT for a_lt = 7e-2 and α ∈ [−π, π]; the natural equilibrium solutions are included as black asterisks

Stable and Unstable Invariant Manifolds

The linear dynamics in the vicinity of the low-thrust equilibrium points are straightforwardly transitioned to the full nonlinear model to supply insight into global flow patterns in the CR3BP+LT. Whereas the eigenvalues of the Hessian matrix describe the type of motion (e.g., stable, unstable, oscillatory), the eigenvector associated with each eigenvalue defines the direction of the flow in four-dimensional space. For example, the eigenvector associated with the positive, real eigenvalue lies tangent to the unstable manifold near the equilibrium solution. Similarly, the eigenvector associated with the negative, real eigenvalue is tangent to the stable manifold near the equilibrium point. Thus, by perturbing the equilibrium solution along the stable or unstable eigenvector and propagating the resulting trajectory in the nonlinear model, a representation of the global stable or unstable invariant manifold associated with the equilibrium point is constructed, as depicted for the natural L₁, L₂, and L₃ saddle modes in Fig. 7. While these manifolds originate tangent to the eigenvectors near the equilibria, the nonlinear flow diverges from the linear approximation as the distance from the equilibrium solution increases. The natural triangular points, characterized by C×C modes, do not possess stable or unstable manifolds to guide the flow into and out of the L₄ or L₅ regions. Additionally, note that the H_nat value along each manifold arc remains constant, as evident in Fig. 7b, as H_nat is a constant integral of the motion in the natural CR3BP.

Fig. 7

Manifolds associated with the natural Earth-Moon CR3BP equilibria; L₁, L₂, and L₃ possess saddle modes with stable and unstable manifolds while L₄ and L₅ are characterized by center × center modes, represented by circles about these equilibria

By applying the same approach, manifolds are constructed for the Earth-Moon CR3BP+LT equilibrium points. While these manifolds appear similar to the ballistic manifolds, there are several key differences. The Earth-Moon low-thrust equilibria for a_lt = 7e-2 and α = 180^∘, plotted as black diamonds in Fig. 8a, are similar in location and stability to the natural equilibria, although the $\mathbb {E}_{3}(180^{\circ })$ solutions that are not located on the x-axis (i.e., ${E^{2}_{3}}(180^{\circ })$ and ${E^{3}_{3}}(180^{\circ })$) lie noticeably closer to the Moon than the natural triangular points. Furthermore, the geometries of the stable and unstable manifolds corresponding to the E₁(180^∘) and E₂(180^∘) points remain very similar to the natural manifolds plotted in Fig. 7. One key difference between the low-thrust equilibria manifolds and the natural equilibria manifolds is the energy profile for each manifold, plotted in Figs. 8b and 7b, respectively. While H_nat is constant along the ballistic CR3BP arcs, H_nat varies from the originating state along the low-thrust structures. Accordingly, the low-thrust equilibrium point manifold arcs may be employed to transit throughout the xy-plane while simultaneously delivering an energy change prescribed by the associated energy plane.

Fig. 8

Manifolds associated with the Earth-Moon CR3BP+LT equilibria for a_lt = 7e-2 and α = 180^∘ maintain a similar geometry and qualitative stability characteristics as the natural equilibria manifolds, but vary in energy

Transit Design Leveraging Manifold Arcs

To illustrate the use of the energy plane and the manifolds associated with the low-thrust equilibrium points, consider the design of a transfer from the lunar vicinity to a stable orbit near the natural Earth-Moon L₅ point. One option is to construct a transfer from the L₁ and L₂ equilibria manifold arcs that depart the lunar vicinity and move throughout the xy-plane. However, these trajectories, plotted in Fig. 7a, do not approach the L₅ region, even when propagated for longer time intervals than depicted in the plot. Furthermore, these natural manifold paths maintain a fixed H_nat value consistent with the originating equilibrium point and, thus, do not approach the much higher H_nat(L₅) value. An additional complication arises from the fact that L₅ is characterized by C×C motion and, thus, possesses no stable or unstable manifolds to further attract the flow. Farrés mitigates this problem when designing similar transfers in the Sun-Earth-solar sail system by searching a grid of sail orientations and states near the triangular point that, when propagated in reverse time, may be linked to the E₁(0) or E₂(0) unstable manifolds in both position and energy [7]. While this method is effective, insights from the energy planes combined with the novel unstable equilibria near L₅ in the CR3BP+LT may be leveraged to construct a design without reliance on a grid search.

A transfer design that incorporates both the energetic and geometric differences between the L₅ and lunar regions is facilitated by leveraging manifolds associated with the low-thrust equilibria. Motion near the Moon is available from the manifolds associated with points on the $\mathbb {E}_{1}$ and $\mathbb {E}_{2}$ sets. Because the $\mathbb {E}_{1}$ and $\mathbb {E}_{2}$ structures for a_lt = 7e-2 are characterized by S×C motion regardless of α, many manifolds that depart the region are available. A survey of these manifolds over the full range of α values indicates that, while small differences are apparent as α varies, the general flow geometry (as visualized in Fig. 8a) remains consistent. Thus, the energy on these manifold trajectories may be designed relatively independently of the geometry by selecting an α value to supply an appropriate energy plane, i.e., an energy plane sloped in a desirable orientation.

To develop an initial guess for a transfer between the Moon and L₅, the manifolds associated with an Earth-Moon CR3BP+LT $\mathbb {E}_{2}$ solution are explored (alternatively, manifolds corresponding to an $\mathbb {E}_{1}$ point may be leveraged). As illustrated in Fig. 9b, the H_nat value associated with L₅ is significantly larger than the H_nat values at the $\mathbb {E}_{2}$ (or $\mathbb {E}_{1}$) sets. To maximize the H_nat value available at L₅ along a single low-thrust arc originating from one of these low-thrust equilibria, the energy plane is aligned with the Moon-L₅ line, e.g., α = − 120^∘, as plotted in Fig. 9. However, even with the plane oriented to maximize the energy at the L₅ location, the slope of the energy plane is too shallow to reach H_nat(L₅) at the L₅ position, visualized as an “energy gap” between the energy plane and the L₅ point in Fig. 9b. The slope of the plane is a function of the low-thrust acceleration magnitude, a_lt, and is limited by the capabilities of the propulsion system. Accordingly, given the limitation of a_lt = 7e-2, a single manifold arc originating from an $\mathbb {E}_{2}$ point cannot reach the natural L₅ point with the desired energy. Additional energy manipulations are required to construct a set of “energy switchbacks” that reach both the L₅ position and energy level.

Fig. 9

The energy plane associated with the Earth-Moon CR3BP+LT E₂(− 120^∘) point for a_lt = 7e-2 (γ ≈ 4^∘) is too shallow to reach H_nat(L₅) at the L₅ location

To facilitate an energy increase from H_nat(L₂) to H_nat(L₅), low-thrust flow originating near the natural L₅ point is linked to low-thrust flow near the Moon. In contrast to the natural CR3BP, the CR3BP+LT possesses equilibrium points near L₅ on the $\mathbb {E}_{3}$ structure with S×C motion. In the Earth-Moon CR3BP+LT with a_lt = 7e-2, these equilibria, plotted as red points in Fig. 6a, are located near L₅ when α ≈− 60^∘. While the locations and energies of the equilibria on $\mathbb {E}_{1}$ and $\mathbb {E}_{2}$ vary only a small amount with α, the $\mathbb {E}_{3}$ equilibrium point locations shift over large distances throughout the xy-plane as α varies. Accordingly, only the ${E^{1}_{3}}(-60^{\circ })$ solution near L₅ supplies manifolds that evolve sufficiently to attract flow. The energy along these manifold trajectories evolves on the energy plane oriented by α = − 60^∘, as depicted in Fig. 10. A transfer from E₂(− 120^∘) to ${E^{1}_{3}}(-60^{\circ })$ may leverage flow along both energy planes. Such a transfer originates at the E₂(− 120^∘) point and subsequently flows along the corresponding energy plane. Then, at an intersection between the E₂(− 120^∘) energy plane and the ${E^{1}_{3}}(-60^{\circ })$ energy plane, α is switched from − 120^∘ to − 60^∘. The resulting propagation then flows along the ${E^{1}_{3}}(-60^{\circ })$ energy plane, which includes the ${E^{1}_{3}}(-60^{\circ })$ equilibrium solution very near the location and energy of the natural L₅ point, facilitating the required energy change.

Fig. 10

The energy planes corresponding to the low-thrust equilibrium points ${E^{1}_{3}}(-60^{\circ })$ near L₅ and E₂(− 120^∘) contain all trajectories originating from the two equilibria; control adjustments at the intersection of the two planes facilitates transfers between the two points

The intersection of two energy planes defines a line, ${\mathscr{H}}_{1,2}$, in x-y-H_nat space. Let ρ_ref be a reference control point located anywhere on ${\mathscr{H}}_{1,2}$, as depicted in Fig. 11. This reference point may be chosen arbitrarily, but can offer useful insights when located at a convenient geometric location or Hamiltonian value. Additionally, define a vector, H_int, that points along the ${\mathscr{H}}_{1,2}$ intersection line. The set of control points on the intersection line are given by

$$ \mathcal{H}_{1,2}: \boldsymbol{\rho} =\boldsymbol{\rho}_{ref} + l \mathbf{H}_{int}, $$

(30)

where H_int is derived from the cross product of the two energy plane normal vectors, $\hat {\boldsymbol {H}}_{1}^{\prime \prime }$ and $\hat {\boldsymbol {H}}_{2}^{\prime \prime }$,

$$ \mathbf{H}_{int} =\left\{ \begin{array}{ll} \cos\left( [\alpha_{1} + \alpha_{2}]/2 \right) \\ \sin\left( [\alpha_{1} + \alpha_{2}]/2 \right) \\ a_{lt}\cos\left( [\alpha_{2} - \alpha_{1}]/2 \right) \end{array}\right\}, $$

(31)

and both energy planes correspond to the same a_lt value (i.e., the same γ angle) but different α values. Note that H_int is not directly equal to the cross product of the normal vectors but is scaled to satisfy (30). Finally, let ${\varSigma }_{{\mathscr{H}}_{1,2}}$ represent the projection of ${\mathscr{H}}_{1,2}$ into the xy-plane and define a coordinate, l, measured along ${\varSigma }_{{\mathscr{H}}_{1,2}}$ relative to ρ_ref where l > 0 maps to points on ${\mathscr{H}}_{1,2}$ with H_nat values greater than the Hamiltonian at ρ_ref.

Fig. 11

The intersection of two energy planes, ${\mathscr{H}}_{1,2}$ is decomposed into the H_int vector and the l coordinate, measured along the projection of the intersection line, ${\varSigma }_{{\mathscr{H}}_{1,2}}$; the base point, ρ_ref, locates the line in x-y-H_nat space

To identify links between trajectories on these energy planes, the ${\varSigma }_{{\mathscr{H}}_{1,2}}$ hyperplane is employed as a stopping condition for planar trajectories. Because ${\mathscr{H}}_{1,2}$ defines points that lie on both energy planes, proximity between two points (i.e., similar l values) on the projection, ${\varSigma }_{{\mathscr{H}}_{1,2}}$, indicates not only similar positions in the xy-plane, but also similar H_nat values. Furthermore, a switch from α₁ to α₂ at a point on ${\varSigma }_{{\mathscr{H}}_{1,2}}$ ensures that the trajectory transitions from the first energy plane to the second.

While the displacement along ${\varSigma }_{{\mathscr{H}}_{1,2}}$ relative to ρ_ref, represented by l, supplies position and energy information, an additional coordinate is required to represent the full spacecraft state. Given l, the spacecraft position and H_nat value are computed via (30). Additionally, the velocity magnitude at this point is available by solving the H_nat expression in Eq. 3 for the spacecraft speed in the rotating frame, v. Only the velocity direction is undefined; thus, a Poincaré map leveraging the coordinates l and $\theta _{v}=\arctan (\dot {y}/\dot {x})$ supplies the complete spacecraft state; intersections on this map guarantee full state continuity between trajectories. In contrast to traditional Poincaré maps in the CR3BP that include only trajectories at one energy level, this representation incorporates arcs with various H_nat values. Additionally, as the full state of each map crossing is available from the 2D representation, multiple low-thrust paths may be linked together, or low-thrust and natural arcs may be connected. Such a map is leveraged to identify a transfer between the unstable manifold of E₂(− 120^∘), plotted in magenta in Fig. 12, and the stable manifold of ${E^{1}_{3}}(-60^{\circ })$, plotted in blue. Each manifold trajectory crosses the the ${\varSigma }_{{\mathscr{H}}_{1,2}}$ hyperplane (or, equivalently, ${\mathscr{H}}_{1,2}$ in x-y-H_nat space), plotted as a dashed red line in Fig. 12a, at least once. The hyperplane crossing points are transformed to l and 𝜃_v coordinates and plotted in polar form on the Poincaré map in Fig. 12b. Each ${\varSigma }_{{\mathscr{H}}_{1,2}}$ crossing on the ${E^{1}_{3}}(-60^{\circ })$ stable manifold is marked by a black square and labeled with a lowercase roman numeral to link the points between configuration space and the map. The E₂(− 120^∘) unstable manifold crossings are left unlabeled as several occur far from the primaries and are not depicted in Fig. 12a. In this example, ρ_ref is selected such that the reference H_nat value is identical to the natural L₂ energy, H_nat(L₂). Accordingly, l > 0 corresponds to energies greater than H_nat(L₂) and l < 0 indicates lower energy values; the boundary at l = 0 is plotted as a dashed-gray circle in Fig. 12b for reference.

Fig. 12

The stable manifold arcs (blue) of the ${E_{3}^{1}}(-60^{\circ })$ point and the unstable manifold arcs (magenta) of the E₂(− 120^∘) point are propagated in the Earth-Moon CR3BP+LT for a_lt = 7e-2; crossings of the energy plane intersection line are marked and included in a Poincaré map to identify a transfer with minimal discontinuities

By leveraging the information available from the Poincaré map, a transfer from the lunar vicinity to L₅ is constructed. Two points near l = 0 and 𝜃_v = 160^∘, one from a stable manifold and another from an unstable manifold, are selected due to their close proximity to one another on the map. The corresponding trajectories, plotted in blue and magenta in Fig. 13, are discontinuous in position, velocity, and natural Hamiltonian value. Thus, some corrections are required. To preserve the lunar flybys, the initial state on the E₂(− 120^∘) unstable manifold trajectory is constrained in position and energy (H_nat). Additionally, near the destination, a single revolution of a small, natural L₅ short period orbit is included to ensure the spacecraft remains near L₅ after arrival; this orbit is fully constrained to preserve its geometry and energy. Each manifold arc is subdivided into smaller segments, each of which maintains a fixed α value, independent of the other segments, and a thrust magnitude of a_lt = 7e-2 as in a turn-and-hold strategy. A multiple shooting differential corrections algorithm, consistent with the algorithm described by Cox [3], is then applied to eliminate the position and velocity discontinuities between the arcs. The position and velocity vectors and the spacecraft mass at the beginning of each segment are allowed to vary, as is the epoch associated with the beginning of each segment. The only control variable included in the corrections is the α angle; both β and a_lt are held constant. As a result of the corrections, a continuous transfer is constructed and plotted as a solid arc in Fig. 14, with low-thrust segments in orange and ballistic segments in blue. To achieve this result, the initial design is first corrected in the simplified CR3BP+LT with constant a_lt on all low-thrust arcs. Following convergence in the simplified model, the transfer is transitioned to the unrestrained CR3BP+LT with variable mass (i.e., variable a_lt = f/m) where the thrust magnitude is fixed at f = 7e-2 and the engine efficiency is parameterized by I_sp = 3000 seconds. Although the initial design is constructed by leveraging insights from the simplified model with a constant a_lt value, convergence in the unrestrained model is achieved rapidly, i.e., in fewer than 20 iterations. The final spacecraft mass along the converged trajectory in Fig. 14 is 0.9668; thus, the spacecraft requires propellant equivalent to approximately 3.32% of the spacecraft wet mass to complete the transfer. This mass fraction may be reduced further by applying optimization techniques, but represents a feasible scenario even without optimization. For comparison, Deep Space 1, with low-thrust capabilities consistent with this example, was equipped with 82 kg of Xenon propellant for maneuvers, i.e., about 17% of the spacecraft wet mass.¹

Fig. 13

The unstable E₂(− 120^∘) manifold arc (magenta), stable ${E^{1}_{3}}(-60^{\circ })$ manifold arc (blue), and natural L₅ short period orbit (green) are linked together as an initial design for a Moon to L₅ transfer

Fig. 14

Following corrections, the transfer is continuous in position, velocity, mass, and energy; the majority of the transfer leverages low-thrust (orange segments) to reach the natural L₅ SPO (blue)

As the initial design, represented by dashed arcs, includes minimal discontinuities due to the Poincaré map analysis, the converged solution consequently maintains the geometry of the initial guess in x-y-H_nat space. Additionally, the control history, plotted in Fig. 14d, remains similar to the preliminary solution with α ≈− 120^∘ for the first 5.5 time units and reaches α ≈− 60^∘ over the duration of the final thrusting segments. The variations in α between the preliminary design and the converged solution (most notably the final segment with α ≈− 10^∘) are the control response adjusting the preliminary solution to meet the constraints imposed as part of the corrections process. These similarities between the initial and final solutions are not surprising as the differential corrections algorithm employs an update that minimizes the variations from the initial design (i.e., a “minimum-norm” update). While the convergence properties of the algorithm depend on many variables, including the numerical implementation strategy, convergence in any corrections scheme is generally more rapid and more consistent with the initial design when the discontinuities (i.e., constraint violations) are initially small; a very discontinuous initial guess forces the differential corrections algorithm to make more significant changes to the design to meet the specified constraints. Thus, by leveraging insights from the CR3BP+LT, an initial design is straightforwardly constructed with minimal discontinuities in both configuration space and in energy that may be rapidly corrected. In contrast to a transfer construction procedure that employs only arcs from the natural CR3BP, these low-thrust dynamical insights supply a preliminary control profile (i.e., α, β, and a_lt for the low-thrust segments) that subsequently delivers a suitable transfer geometry and a suitable energy profile.

Concluding Remarks

By leveraging reasonable simplifying assumptions, the high-dimensional, non-conservative low-thrust multi-body model is reduced to a simpler, conservative system with properties that supply useful insights for the generation of preliminary low-thrust trajectory designs. One such property is the existence of an energy plane that describes the evolution of the natural Hamiltonian term along any low-thrust arc. The geometry of the plane relates the control variables, i.e., the magnitude and orientation of the low-thrust acceleration vector, to the energy evolution along a trajectory. As a result of this relationship, an initial guess for the control history may be designed to satisfy the energetic constraints on the trajectory. One application of this plane is the analytical prediction of an arc’s transit and capture properties given only the initial position, velocity, and control states. Additionally, a Poincaré map incorporating intersections between two energy planes supplies a useful interface to identify links between low-thrust and natural arcs at various energy levels. By selecting map crossings near one another on this map, initial designs with minimal discontinuities are constructed and may be straightforwardly corrected with a variety of constraints.