The Three-Body Interaction Effect on the Families of 3D Periodic Orbits Associated to Sitnikov Motion in the Circular Restricted Three-Body Problem

Abstract

This paper deals with a modified version of the Circular Restricted Three-Body Problem (CR3BP). In this version, the additional effect of a three-body interaction is taken into account. In particular, we examine numerically the result of this interaction on the evolution of the well-known family of Sitnikov motion of CR3BP as well as that on the families of 3D periodic orbits bifurcating from this family.

Introduction

The Sitnikov problem [35] is a special case of the Restricted Three-Body Problem (R3BP). The considered dynamical system is formed by two point-like primary bodies of equal masses, i.e. when the mass parameter μ equals to 0.5, moving in either circular (circular Sitnikov problem) or elliptic orbits (elliptic Sitnikov problem) around their common center of mass due to their mutual Newtonian attraction, and a third body of negligible mass, oscillating, under the influence of the gravitational forces of the primaries, along a line which is perpendicular to the orbital plane of the primaries and contains their barycentre. This kind of rectilinear oscillations for the third body constitutes a special family of periodic orbits emanating from L₁ and it is called Sitnikov family.

Many other publications deal with Sitnikov or Sitnikov-like motion. For example: [23] derived a mapping which reflects the properties of the Sitnikov motion in the CR3BP. Then, by studying this mapping instead of the differential equations of the problem, they compared the resulting prediction with the conclusions coming of the relative numerical results. They also studied the KS-entropy of the system. Hagel [16] studied the Sitnikov case of the Elliptic R3BP. He introduced an analytic approach to the solution of the Sitnikov Problem. He stated that this approach can be used for bounded small amplitude solutions (i.e. orbits having an initial amplitude $z_{\max \limits }<0.2$ in dimensionless variables) and eccentricities of the primary bodies in the interval (− 0.4,0.4) (according to Hagel, the meaning of negative eccentricities is that the primaries start in their most distant position while in case of e > 0 they start in their closest position). Alfaro and Chiralt [1] also explored the Sitnikov motion in the Elliptic R3BP. They showed that there exist two complementary sequences of intervals of values of the eccentricity parameter e that accumulate to the maximum admissible value of this parameter. Dvorak [14] also worked on the same problem for moderate values of e and examined the complexity of motion as well as the Poincaré surfaces of section. Belbruno et al. [2] studied the period function of the Sitnikov motion as well as the families of periodic orbits that bifurcate from the Sitnikov ones in the case of the CRTBP. Kallrath et al. [21] presented a method to determine the period and a parameterisation of periodic solutions for the Sitnikov configuration in the Elliptic R3BP. Jalali and Pourtakdoust [19] examined the solutions at the 3/2 commensurability for the Sitnikov’s case of Elliptic R3BP. The phase portrait of system was used to reveal the existence of such orbits. Ollé and Pacha [25] used certain isolated symmetric periodic orbits found for some limiting restricted three-body problems, such as Sitnikov problem, to obtain by numerical continuation families of symmetric periodic orbits of the Elliptic R3BP. Corbera and Llibre [10] proved, by means of a Poincaré map, the existence of symmetric periodic orbits of the elliptic Sitnikov problem. Furthermore, using the presence of the Bernoulli shift as a subsystem of that Poincaré map, they proved that not all the periodic orbits of the Sitnikov problem are symmetric ones. Faruque [15] found a new analytic expression for the position of the infinitesimal body in the elliptic Sitnikov problem which is valid for small bounded oscillations in cases of moderate primary eccentricities. Hagel and Llotka [17], working on the elliptic Sitnikov problem, used a high order perturbation approach to the problem in order to obtain precise analytical expressions for the stability of the system. Perdios [27] dealt with the Sitnikov family of the CR3BP. By studying the stability of the family, he determined several new critical orbits at which families of three dimensional periodic orbits of the same or double period bifurcate. Then, he computed a number of such families for equal as well as for nearly equal masses of the primaries. Kovács and Érdi [22] worked on the Sitnikov motion in CR3BP. They explored its extended phase space by using a stroboscopic map and computing escape times in order to find the intrinsic connection between the geometry of the phase space and the dynamical behaviour of the system. Properties of the phase space are analysed both in the central regular region and far from it. A paper of Sidorenko [34] was devoted to the stability of the Sitnikov orbits in the CR3BP. Especially, he was interested in the alternation of stability and instability within the family formed by these orbits, whenever their amplitude is varied in a continuous monotone manner.

Meanwhile, several modifications of the CR3BP or the N-body problem have been used in order to model more accurately real systems in solar or stellar dynamics. For example, a version of the CR3BP which takes into account the oblateness of the primaries, the photogravitational CR3BP that considers the radiation pressure when the primaries are radiation sources, as well as combinations of them have been proposed. A number of the relative publications deals with Sitnikov motions in these variant models. See, for example, [12, 20, 29, 31]. Regarding studies of the Sitnikov motion in systems with more than three primary bodies we may refer to the works of [8, 37] and [38], among others.

Another modification of the CR3BP has been recently proposed by [3, 6] and [4, 5, 7]. As it was argued by those authors, this particular modification can be used in modelling binary star systems with a small companion. For such systems, the masses of the two stars are often approximated from observational data and may vary over time due to mass exchange, producing an uncertainty in the mass ratio. Due to such an uncertainty, the gravitational field may not be accurately modelled by pairwise gravitational interactions only. So, an additional, coupled, three-body interaction can be incorporated to the classical CR3BP. This interaction is expressed by an additional force that depends on a parameter k and the resulting problem is reduced to the CR3BP when k = 0.

The study of periodic orbits is of great importance for both mathematical and practical point of view. Besides of the particular meaning of these orbits, their stability provides information about their evolution as well as reflects the behavior of nearby trajectories. In order to underline the significance of periodic solutions, Poincaré [30] called them “precious”. Due to the continuation property in Hamiltonian systems, families consisting of such orbits can be formed in the space of initial conditions depending on their special characteristics. Bifurcation theory, which describes how small changes in an input parameter may result in dramatic modifications in the system output, is also of considerable usefulness for understanding the behaviour of any dynamical system. The consequence of this theory in the study of families of periodic orbits is that a bifurcation point can cause a change in the stability of the periodic orbits along a family, the formation of a new family, or the termination of the current family [33]. This is a reason for investigating the possible bifurcations of families of periodic orbits.

The most common methods applied for the determination of families of periodic orbits of the R3BP and its modifications, are the use of either the equilibrium points or the bifurcation points of other families of periodic solutions. In the case of families of three-dimensional periodic orbits, an alternative approach is to utilize the Sitnikov family which can be easily computed since its members are solutions of an one-degree of freedom problem. Then, its critical or resonant members may serve as starting orbits for generating families of 3D periodic solutions, i.e. solutions for a problem of three-degrees of freedom. In the sequel, these families can be utilised in order to obtain families that continue to exist for primaries of not equal masses. Therefore, the Sitnikov family can be used as a generator of families of three-dimensional periodic orbits [26].

Based on the previous discussion, in this contribution we study the family of Sitnikov motion in the CR3BP with three-body interaction as well as the families of three-dimensional periodic orbits bifurcating from this family. Our aim is to produce a manifold of periodic solutions in the full phase space and investigate its evolution with respect to the parameters of the problem in order to gain more insight about the dynamics of this special model.

The paper is organized as follows : In “Equations of Motion”, the equations of motion are given. In “Stability and Bifurcation Points of the Sitnikov Family”, the linear stability of the Sitnikov motion is explored in terms of the Floquet theory and a number of critical as well as self-resonant orbits, up to period quadrupling bifurcation points, of the Sitnikov family are determined for k = 1. Also, certain critical orbits are numerically continued by varying the parameter k, in order to determine for which values of this parameter they exist. In “Families Emanating from Bifurcation Points of the Sitnikov Family for k = 1”, we numerically compute, for μ = 0.5, the families of three-dimensional periodic solutions bifurcating from these critical and self-resonant orbits. In “Families of 3D Periodic Orbits Bifurcating from the Sitnikov Family: Numerical Continuation with Respect to μ”, we numerically continue the families bifurcating from the critical orbits of the Sitnikov family for all values of the mass parameter for which they exist. Finally, in “Summary - Conclusions”, we summarise and conclude our work.

Equations of Motion

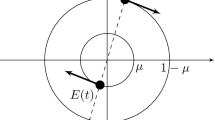
We consider a sidereal frame and let P₁, P₂ be two primary bodies, with masses m₁ and m₂, moving in a circular orbit around their center of mass which is located at the origin of the frame. Let a third body p of negligible mass m moving in the plane of motion of the primaries under their gravitational field without affecting them. We transform the aforementioned frame to a rotating system Oxyz by supposing that the primaries always lie on the Ox −axis of this system. This system can be turned into a dimensionless one by assuming that the distance between the primaries as well as the sum of their masses are equal to one, while the unit of time is chosen so as to make the gravitational constant unity. According to this system, the masses of the primaries are 1 − μ and μ, correspondingly, where $\mu =m_{2}/(m_{1}+m_{2})\leqslant 0.5$ is the mass parameter [36]. Then, the equations of motion of the particle p are [3, 13]:

$$ \begin{array}{@{}rcl@{}} \ddot{x}{\kern-.5pt}-{\kern-.5pt}2\dot{y} &=& x-\frac{1{\kern-.5pt}-{\kern-.5pt}\mu}{{r_{1}^{3}}}(x{\kern-.5pt}+{\kern-.5pt}\mu)-\frac{\mu}{{r_{2}^{3}}}(x{\kern-.5pt}+{\kern-.5pt}\mu{\kern-.5pt}-{\kern-.5pt}1) -k\left[\frac{x+\mu{\kern-.5pt}-{\kern-.5pt}1}{r_{1}{r_{2}^{3}}}+\frac{x+\mu}{{r_{1}^{3}}r_{2}}\right] = \frac{\partial\varOmega}{\partial x},\!\\ \ddot{y}+2\dot{x} &=& y-\frac{(1-\mu)y}{{r_{1}^{3}}}-\frac{\mu y}{{r_{2}^{3}}} -k\left[\frac{y}{r_{1}{r_{2}^{3}}}+\frac{y}{{r_{1}^{3}}r_{2}}\right] = \frac{\partial\varOmega}{\partial y},\\ \ddot{z} &=& -\frac{(1-\mu)z}{{r_{1}^{3}}}-\frac{\mu z}{{r_{2}^{3}}} -k\left[\frac{z}{r_{1}{r_{2}^{3}}}+\frac{z}{{r_{1}^{3}}r_{2}}\right] = \frac{\partial\varOmega}{\partial z}, \end{array} $$

(1)

where $r_{1}=\sqrt {(x+\mu )^{2}+y^{2}+z^{2}}$ and $r_{2}=\sqrt {(x+\mu -1)^{2}+y^{2}+z^{2}}$ are the distances of p from the primaries P₁ and P₂ and

$$ \varOmega=\left( \frac{x^{2}+y^{2}}{2}+\frac{1-\mu}{r_{1}}+\frac{\mu}{r_{2}}\right) + \left( \frac{k}{r_{1}r_{2}}\right) $$

is the corresponding pseudo-potential function. In this function, the terms enclosed by the left pair of parentheses express the effect of the pairwise gravitational attraction applied to p by P₁ and P₂. The quantity in the right pair of parentheses, which depends on the inverse of the product of r₁ and r₂, describes the interaction effect. The values of the parameter k can be positive, negative or zero. In the case where it is zero, the potential of the problem reduces to that of the classical CR3BP. If the value of k is positive, the three-body interaction is attractive, while if it is negative, the interaction is repulsive [3].

Equation 1 admit the following integral :

$$ 2{\varOmega} -(\dot{x}^{2}+\dot{y}^{2}+\dot{z}^{2})=C, $$

(2)

where C is an energy-like integral constant [3].

Consider now the case μ = 0.5 and $x(t)=y(t)=\dot x(t)=\dot y(t)=\ddot x(t)=\ddot y(t)=0$. Then,

$$ r_{1}=r_{2}=\left( \frac{1}{4}+z^{2}\right)^{1/2} $$

and the third equation of Eq. 1 becomes

$$ \ddot z = - z \left[ \frac{1}{\left( \frac{1}{4}+z^{2}\right)^{3/2}}+ \frac{2k}{\left( \frac{1}{4}+z^{2}\right)^{2}} \right], $$

(3)

while the Jacobi integral becomes :

$$ \frac{2}{\left( \frac{1}{4}+z^{2}\right)^{1/2}}+ \frac{2k}{\left( \frac{1}{4}+z^{2}\right)}- \dot z^{2}=C. $$

Equation 3 describes rectilinear oscillations along the Oz axis. We name these oscillations Sitnikov motion since, in the case k = 0, they describe this kind of 3D orbits. In Fig. 1a sample curves of the Sitnikov problem are presented in the phase space $(z,\dot z)$ while in Fig. 1b the evolution of the position and velocity variables with respect to time is shown. For both figures, the parameter value k = 1 has been used.

Fig. 1

The Sitnikov family for k = 1: (a) Variation in the phase space $(z,\dot z)$, (b) Variation of the position z (blue) and velocity $\dot z$ (red) versus time

Stability and Bifurcation Points of the Sitnikov Family

We consider small perturbations x = ξ and y = η of the zero planar components of the rectilinear motion. Then, the linearised equations of the perturbed motion are obtained from Eq. 1:

$$ \begin{array}{ll} & \ddot\xi - 2\dot\eta = [F_{1}(z)+F_{2}(z)+F_{6}^{*}(z)]\xi+F_{3}(z)+F_{5}^{*}(z), \\ [0.2cm] & \ddot\eta + 2\dot\xi = [F_{1}(z)+F_{7}^{*}(z)] \eta , \\ [0.2cm] & \ddot z = [F_{1}(z)-1+F_{7}^{*}(z)]z + [F_{4}(z)+F_{8}^{*}(z)] \xi z, \end{array} $$

(4)

where

$$ \begin{array}{@{}rcl@{}} F_{1}(z)\! & = &\! 1- \left( \frac{1-\mu}{g_{1}^{3/2}} + \frac{\mu}{g_{2}^{3/2}} \right), \qquad\quad F_{2}(z)\! =\! 3\mu (1-\mu) \left( \frac{\mu}{g_{1}^{5/2}} + \frac{1-\mu}{g_{2}^{5/2}} \right), \\ F_{3}(z)\! & = &\! -\mu (1-\mu) \left( \frac{1}{g_{1}^{3/2}} - \frac{1}{g_{2}^{3/2}} \right), {\kern6pt} F_{4}(z)\! =\! 3\mu (1-\mu) \left( \frac{1}{g_{1}^{5/2}} \! -\! \frac{1}{g_{2}^{5/2}} \right), \\ F_{5}^{*}(z)\! & = &\! -k\left( \frac{1}{g_{5}} \! +\! \frac{\mu-1}{g_{3}}\right), \qquad\qquad{\kern4pt} F_{6}^{*}(z)\! =\! -k\!\left( \frac{(\mu\! -\! 1)g_{4}}{g_{3}}\! +\! \frac{1}{g_{3}}\! +\! \frac{\mu g_{6}}{g_{5}}\! +\!\frac{1}{g_{5}} \right), \\ F_{7}^{*}(z)\! & = &\! -k\left( \frac{1}{g_{3}} \! +\! \frac{1}{g_{5}} \right), \qquad\qquad \quad{\kern9pt} F_{8}^{*}(z)\! =\! -k\left( \frac{g_{4}}{g_{3}}+\frac{g_{6}}{g_{5}} \right), \end{array} $$

and g₁ = μ² + z², g₂ = (μ − 1)² + z², $g_{3}=g_{1}^{1/2}g_{2}^{3/2}$, $g_{4}=-\frac {3(\mu -1)}{g_{2}}-\frac {\mu }{g_{1}}$, $g_{5}=g_{1}^{3/2}g_{2}^{1/2}$, $g_{6}=-\frac {\mu -1}{g_{2}}-\frac {3\mu }{g_{1}}$. We remark here that $F_{i}^{*}$, i = 5,…,8 denote the terms which come from the three-body interaction and depend on k.

For μ = 0.5 we have that g₁ = g₂ = 1/4 + z². Then, by setting g₀ = 1/4 + z², we obtain that g₁ = g₂ = g₀, $g_{3}=g_{5}={g_{0}^{2}}$, g₄ = −g₆ = 1/g₀, and the corresponding values of $F_{1},F_{2},F_{3},F_{4},F_{5}^{*},F_{6}^{*},F_{7}^{*},F_{8}^{*}$ become :

$$ \begin{array}{@{}rcl@{}} F_{10}(z) & = & 1-\frac{1}{g_{0}^{3/2}}, \qquad F_{20}(z) = \frac{3}{4g_{0}^{5/2}}, \qquad\quad F_{30}(z)=0, \qquad{\kern5pt} F_{40}(z)=0, \\ F_{50}^{*}(z) & = & 0, \qquad\quad\quad\quad{\kern2pt} F_{60}^{*}(z)=-\frac{k}{{g_{0}^{3}}}-\frac{2k}{{g_{0}^{2}}}, \quad F_{70}^{*}(z)=-\frac{2k}{{g_{0}^{2}}}, \quad F_{80}^{*}(z)=0. \end{array} $$

Now, the first two equations of Eq. 4 can be written in the form :

$$ \dot{\varXi} =A(z(t)){\varXi} , $$

(5)

where $\varXi =(\xi ,\eta ,\dot \xi ,\dot \eta )^{\top }$ and

$$ A(z(t))= \left[ \begin{array}{rrrr} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ F_{10}(z)+F_{20}(z)+F_{60}^{*}(z) & 0 & 0 & 2 \\ 0 & \quad F_{10}(z)+F_{70}^{*}(z) & \quad -2 & 0 \end{array} \right]. $$

Equation 5 describe the evolution of the planar perturbations ξ and η of the Sitnikov motion in the problem under consideration and can be called the variational equations of these rectilinear motions. The characteristic roots for these equations will determine the stability of the Sitnikov motion and can be computed by a numerical technique based on the classical Floquet theory. These roots are the solutions s_n, n = 1,2,3,4, of the characteristic equation $\det (B-Is)=0$. In this equation, I denotes the four-dimensional identity matrix and B = X^− 1(t)X(t + T), where X(t) is a fundamental solution of Eq. 5 and T is the period of a particular solution of Eq. 3. Without any loss of generality, we may set X(0) = I so that B = X(T). In case of distinct characteristic roots, there are four independent solutions x_n satisfying the property:

$$ x_{n}(t+T)=s_{n} x_{n}(t), {\kern0.9cm} n=1,2,3,4. $$

(6)

Thus, a solution is periodic if s_n = 1, while for |s_n| < 1 (|s_n| > 1) the motion is bounded (unbounded). The characteristic equation is quartic and it can be written as the product of two quadratic factors :

$$ (s^{2}+a_{1}s+1) (s^{2}+a_{2}s+1)=0, $$

(7)

with

$$ a_{1}=\frac{1}{2}(p_{1}+\sqrt{\varDelta}), a_{2}=\frac{1}{2}(p_{1}-\sqrt{\varDelta}), {\varDelta} ={p_{1}^{2}}-4(p_{2}-2), $$

(8)

where we have abbreviated :

$$ p_{1}=-\text{Tr} B, {\kern0.7cm} p_{2}=\sum\limits_{j=i+1}^{4} \sum\limits_{i=1}^{4} (b_{ii}b_{jj} - b_{ij}b_{ji}), $$

(9)

and b_ij, i, j = 1,2,3,4 are the elements of B. In order to reduce computing time, B can be determined by integrating numerically the fundamental solution matrix from t = 0 to t = T/4, and applying the transformation :

$$ X(T)=[MX^{-1}(T/4)MX(T/4)]^{2}, $$

(10)

where M is the constant symmetry matrix M = diag{1,− 1,− 1,1}.

The stability of a member of the Sitnikov family can be described in terms of a_i, i = 1,2. This member orbit is stable if it satisfies the conditions :

$$ {\varDelta} >0, {\kern0.5cm} |a_{1}|< 2, {\kern0.5cm} |a_{2}|< 2, $$

(11)

but otherwise, it is unstable. The aforementioned method for the determination of the stability has been proposed by [26] and successfully applied by [2, 27] and [28] in the case of the classical Sitnikov problem.

To compute a member of the Sitnikov family for a certain value of the parameter k, we integrate the equations of motion (3) with initial conditions of the form $(z,\dot z)=(0,\dot z_{0})$, where $\dot z_{0}$ is arbitrary. This integration is continued until the rectilinear oscillation reaches its maximum height, i.e. $(z,\dot z)=(z_{\max \limits },0)$. If T is the period of this member, at this stage of motion, the elapsed time is equal to T/4. In order to obtain the stability, it is also necessary to simultaneously integrate the variational equations (4) and apply the technique discussed previously. Due to the symmetry of this kind of orbits, the integration of the equations of motion together with the variational ones for t = 0 up to T/4 is enough to determine the characteristics and the stability of any particular orbit. In order to obtain the whole Sitnikov family, we repeat the same procedure after modifying the value of $\dot z_{0}$ in a systematic way (for example, starting from $\dot z_{0}=0$ and iteratively increasing its value by a step size).

Fig. 2 depicts the variation of the stability parameters of the Sitnikov families versus ${\dot z}_{0}$ for k = 1 and k = 2 together with the corresponding data for the classical case k = 0. If a member fulfils any of the conditions a_i = ± 2, i = 1,2, then it is a critical orbit of this family. In case where a_i = − 2, a family of 3D periodic solutions of the same period bifurcates from this orbit while at a critical orbit with a_i = 2 a period doubling bifurcation of a family of 3D periodic solutions occurs. Following [28], we call these bifurcation points by the names one-to-one and one-to-two, respectively. A corrector scheme to compute a critical orbit of the above kinds can be obtained as follows. Such an orbit has to fulfil one of the conditions :

$$ a_{i}(\dot z_{0})=\pm 2, {\kern0.5cm} i=1,2. $$

If this is false, a proper modification $\delta \dot z_{0}$ should be applied to $\dot z_{0}$ so that :

$$ a_{i}(\dot z_{0}+\delta\dot z_{0})=\pm 2, i=1,2. $$

By linearising this equation we obtain :

$$ a_{i}+\frac{\partial a_{i}}{\partial \dot z_{0}}\delta\dot z_{0}=\pm 2\Leftrightarrow \delta\dot z_{0}=\frac{\pm 2-a_{i}}{\partial a_{i}/\partial \dot z_{0}} {\kern0.5cm} i=1,2, $$

(12)

where the partial derivatives involved in this equation can be computed by additional integrations, i.e. by approximating these derivatives using numerical integration.

Fig. 2

The variation of the stability parameters (a) a₁ and (b) a₂ of the Sitnikov family for k = 0,1,2. The insets correspond to specific magnifications of each figure

Also, a self-resonant member of the Sitnikov family, i.e. a periodic orbit that satisfies the condition

$$ a_{i}=-2\text{cos}\left( 2\pi\frac{n}{m}\right), $$

(13)

for some relatively prime positive integers n and m≠ 1,2, where i either equals to 1 or 2, is a one-to-m bifurcation point (see, e.g., Douskos et al. [11]). The computation of such points can be accomplished by a scheme similar to the one used for the critical points by replacing ± 2 with the value of the r.h.s. of Eq. 13. A number of one-to-one critical orbits of the Sitnikov family for the case k = 0 have been given by [2, 26] and [27]. In order to explore the influence of the three-body interaction, k≠ 0 has to be considered. In our present study, we choose the value k = 1 which corresponds to an arbitrary case where this interaction is attractive.

Critical orbits of the Sitnikov family for k = 1

Figure 3 indicates that the critical orbits of the Sitnikov family which exist in this case correspond only to a_i = − 2, with i = 1,2. We deal with those critical orbits for which z(T/4) ≤ 7, where T is the period of the member orbit. As shown in Fig. 3a, there are eight such orbits with a₁ = − 2. We name them B1, B2,…, B8. With regard to a₂ = − 2, Fig. 3b shows that there are thirteen orbits of this kind, which are named B9, B10,…, B21. In the aforementioned figures, for simplicity reasons, all these orbits are labelled with their running number. The corresponding data are listed in Table 1.

Fig. 3

Critical points of the Sitnikov family for k = 1 coming from the parameter (a) a₁ and (b) a₂

Table 1 One-to-one critical orbits of the Sitnikov familiy for k = 1. B1,B2..,B8 correspond to the case a₁ = − 2 while B9,..,B21 correlate with a₂ = − 2

In the rest of this paper, we will call these critical points by the name of the B-points. Their evolution along the variation of k can be examined by their numerical continuation w.r.t. this parameter. This continuation may be accomplished as follows. Consider such a point satisfying any of the relations :

$$ a_{i}({\dot z}_{0},k)=\pm 2,\quad i=1,2. $$

(14)

If $\delta {\dot z}_{0}$, δk are small modifications of ${\dot z}_{0}$, k, respectively, then, these relations are linearised as follows :

$$ \frac{\partial a_{i}}{\partial{\dot z}_{0}}\delta{\dot z}_{0}+ \frac{\partial a_{i}}{\partial k}\delta k =\pm 2-a_{i},\quad i=1,2. $$

(15)

The partial derivatives involved in this equation can be computed by additional integrations. Let us suppose that, for some k, a Sitnikov periodic orbit satisfying one of Eq. 14 is known. Then, a proper linear scheme for predicting a solution of the same kind for k + δk can be expressed by solving (15) for $\delta {\dot z}_{0}$ :

$$ \delta{\dot z}_{0}=- \frac{\partial a_{i}/\partial k}{\partial a_{i}/\partial{\dot z}_{0}} \delta k. $$

(16)

Suppose now that, for a specific k, a Sitnikov orbit, close to a critical one but having a_i≠ ± 2, is known. Then, a corrector scheme for finding the latter can be obtained by solving (15) for $\delta {\dot z}_{0}$ :

$$ \delta{\dot z}_{0}= \frac{\pm 2-a_{i}}{\partial a_{i}/\partial{\dot z}_{0}}. $$

(17)

Using the above mentioned procedure, we have studied the evolution of B1, B2,…, B9 w.r.t. the variation of k. This evolution is shown in Fig. 4. It can be seen there that any of these points continues to exist for a range of negative values of this parameter. The lower bound of that range is not the same for all B-points. So, B1 seems to exist for k ≥− 0.1. The corresponding lower bound of k for the existence for B2 and B3 is smaller than that for B1, while B2 and B3 points coincide at this value of k. The pairs of points B4 and B5, B6 and B7, B8 and B9 behave like B2 and B3. For example, the lower bound of the range of existence of B4 and B5 is smaller than that of B2 and B3, while B4 and B5 coincide at this limiting value of k. In the case of B8 and B9, we should note that B8 has a₁ = − 2 while B9 has a₂ = − 2.

Fig. 4

The evolution of the critical points B1,B2,…,B9 w.r.t. the variation of k

Self-resonant orbits of the Sitnikov family for k = 1

In this study we deal with self-resonant orbits of the Sitnikov family having a₁ = 1 or a₁ = 0. These orbits correspond to period-tripling or period-quadrupling bifurcation points, respectively, and here are called one-to-three or one-to-four points, correspondingly, according to the definition based on Eq. 13. From Fig. 2, one may roughly see that there are numerous such points. In order to better understand their evolution and detect them, we have zoomed into appropriate regions of this figure and the resulting magnifications are given in Fig. 5. Here, we deal with the first ten leftmost self-resonant orbits, for each case, and we name them C1, C2,…, C10 and D1, D2,…, D10, correspondingly. For simplicity reasons, these points are labelled with their running number in this figure while their corresponding data are given in Table 2. In the rest of this this paper, we will call these self-resonant orbits by the names C-points and D-points, respectively.

Fig. 5

(a) One-to-three and (b) one-to-four bifurcation points of the Sitnikov family for k = 1

Table 2 One-to-three and one-to-four bifurcation points of the Sitnikov familiy for k = 1

Families Emanating from Bifurcation Points of the Sitnikov Family for k = 1

In this section, we study the families of 3D periodic orbits emanating from the bifurcation points mentioned in the previous part of this paper. Such investigation necessitates the exploration of periodic solutions that evolve in the full three-dimensional space. In the present contribution, we are interested in orbits that are of the following types of symmetry :

• S1 : double symmetry w.r.t. the Ox axis and the Oxz plane and

• S2 : double symmetry w.r.t. the Ox axis and the Oyz plane.

For symmetry type S1, a three-dimensional periodic orbit of period T can be determined by using initial conditions of the form $(x_{0},0,0,0,\dot y_{0},\dot z_{0})$ and either seeking a perpendicular intersection of the orbit with the Ox axis at t = T/2, i.e. a final state vector $(x_{T/2},0,0,0,\dot y_{T/2},\dot z_{T/2})$, or a perpendicular intersection of the orbit with the Oxz plane at t = T/4, i.e. a final state vector $(x_{T/4},0,z_{T/4},0,\dot y_{T/4},0)$. The same procedure can be followed for the detection of a three-dimensional periodic orbit of symmetry type S2, but the Oxz plane has now to be changed to Oyz plane. The aforementioned initial or final state vectors uniquely determine such a 3D periodic orbit.

Families Bifurcating from One-to-One Critical Points of the Sitnikov Family

The families originating from the one-to-one critical points B2, B3, B6, B7, B10, B11, B14, B15, B18 and B19 consist of orbits of symmetry type S1 while the members of the families emanating from B1, B4, B5, B8, B9, B12, B13, B16, B17, B20 and B21 are solutions of symmetry type S2. We name these families as b N, where N denotes the running number of the corresponding B-point.

The behaviour of these families is presented in Fig. 6. More specifically, the evolution of the families of orbits of symmetry type S1 is given in Fig. 6a by using their projection on the (x(T/4), z(T/4)) plane while Fig. 6b depicts the development of those that consist of members of symmetry type S2 by utilizing their characteristic curves in the plane (y₀, z₀). Sample three-dimensional periodic orbits are shown in Fig. 7. In particular, the first two frames visualize the shape of two sample orbits of symmetry type S1 which correspond to families b2 and b19, respectively, while the last two frames present sample orbits of symmetry type S2 which belong to families b1 and b21, accordingly. As it can be seen from both frames of Fig. 6, all these families terminate at planar periodic orbits in the Oxy plane. These orbits are given in Figs. 8 and 9 and we note that all of them are retrograde.

Fig. 6

One-to-one bifurcations consisting of orbits of symmetry type (a) S1 and (b) S2

Fig. 7

(a) and (b) Sample 3D orbits of symmetry type S1 (families b2 and b19). (c) and (d) Sample 3D orbits of symmetry type S2 (families b1 and b21). For these orbits we also give their projections on the planes Oxy, Oxz and Oyz

Fig. 8

Terminations in the plane Oxy of the families emanating from the one-to-one bifurcations points of the Sitnikov family: Families of 3D periodic orbits of symmetry type S1. All orbits are retrograde

Fig. 9

Terminations in the plane Oxy of the families emanating from the one-to-one bifurcations points of the Sitnikov family: Families of 3D periodic orbits of symmetry type S2. All orbits are retrograde

Families Bifurcating from Self-Resonant Points of the Sitnikov Family

Regarding the one-to-three bifurcation points, the families originating from C1, C2, C9 and C10 consist of doubly symmetric 3D orbits while the members of the families emanating from C3, C4, C5, C6, C7 and C8 are symmetric w.r.t. the Oxz plane. We name these families as c N, where N denotes the running number of the corresponding C-point. The behaviour of these one-two-three bifurcations is presented in Fig. 10. Families c1 and c2, as it is depicted by their characteristic curves in the plane (x₀, z₀), they join each other. The same holds for the pairs of families c3 and c4, c5 and c6, c7 and c8, c9 and c10.

Fig. 10

One-to-three bifurcations from the Sitnikov family for k = 1

Fig. 11

One-to-four bifurcations from the Sitnikov family for k = 1: The non-solitary families

Next, we study the evolution of the families bifurcating from the one-two-four bifurcation points D1, D2,…, D10. We name these families with d N, where N denotes the running number of the corresponding D-point. Families d1 and d2 consist of 3D doubly symmetric orbits while the members of the rest of them are symmetric w.r.t. the Oxz plane. Figures 11 and 12 present the evolution of these families. The characteristic curves in the plane (x₀, z₀) show that the families composing the pairs d1 and d2, d3 and d4, d5 and d6 join each other.

Fig. 12

One-to-four bifurcations from the Sitnikov family for k = 1: The solitary families

On the contrary, families d7, d8, d9 and d10 do not join to other families. In the sequel, we name this kind of families as “solitary”. They terminate at planar periodic orbits in the Oxy plane. The corresponding termination orbits are given in Fig. 13 and all of them are retrograde.

Fig. 13

Terminations of the families of 3D periodic orbits d7, d8, d9 and d10. All orbits are retrograde

Families of 3D Periodic Orbits Bifurcating from the Sitnikov Family: Numerical Continuation with Respect to μ

Although the Sitnikov family ceases to exist for μ≠ 0.5, its bifurcations survive for primaries of non-equal masses. In this section, we deal with the families bifurcating from the critical points presented in “Critical orbits of the Sitnikov family for k = 1” for k = 1, i.e. the families b N, N = 1,…,21, and we examine their evolution w.r.t. the variation of μ. This can be accomplished by the following procedure.

Consider (4) for μ = 0.5 + δμ, where δμ is a small modification of μ. By linearising these equations with respect to δμ we obtain :

$$ \begin{array}{l} \ddot\xi - 2\dot\eta = \left[1-{\varPhi}^{3/2}(z)+\frac{3}{4}{\varPhi}^{5/2}(z)+F_{6}^{*}(z)\right]\xi+\frac{3}{4}{\varPhi}^{5/2}(z)\delta\mu+F_{5}^{*}(z), \\ [0.2cm] \ddot\eta + 2\dot\xi = \left[1-{\varPhi}^{3/2}(z)+F_{7}^{*}(z)\right] \eta , \\ [0.2cm] \ddot z = -\left[{\varPhi}^{3/2}(z)+F_{7}^{*}(z)\right]z, \end{array} $$

(18)

where

$$ \begin{array}{@{}rcl@{}} {\varPhi}(z) & = & \left( z^{2}+\frac{1}{4}\right)^{-1},\\ F_{5}^{*}(z) & = & k\left[ \frac{1}{z^{2}}{\varPhi}^{2}(z)-{\varPhi}^{2}(z)+k\left( {\varPhi}^{3}(z)+\frac{1}{2z^{2}}{\varPhi}^{3}(z)-\frac{1}{z^{2}}{\varPhi}^{2}(z)\right)\delta\mu\right],\\ F_{6}^{*}(z) & = & k\left[ \frac{5}{4}{\varPhi}^{3}(z)-\frac{1}{z^{2}}{\varPhi}^{2}(z)+k\left( 4{\varPhi}^{3}(z)-\frac{9}{2}{\varPhi}^{4}(z)-\frac{1}{z^{2}}{\varPhi}^{3}(z)\right)\delta\mu\right],\\ F_{7}^{*}(z) & = & k\left[ -\frac{1}{z^{2}}{\varPhi}^{2}(z)-{\varPhi}^{2}(z)+k\left( -\frac{1}{z^{2}}{\varPhi}^{3}(z)+{\varPhi}^{3}(z)\right)\delta\mu\right]. \end{array} $$

These perturbed equations can be used to compute appropriate initial conditions for periodic orbits of System (1). These conditions will arise from a bifurcation point of the Sitnikov family but for a value of the mass parameter slightly different from μ = 0.5. This will be cleared in the following discussion.

The equation for z does not change, therefore the period of a member of the basic family remains the same in this linear consideration for μ = 0.5 + δμ. As stated by Perdios and Markellos [26], it can be shown numerically that, if the first two of Eq. 18 have a periodic solution (for δμ≠ 0) with the period T of a critical orbit of the Sitnikov family of rectilinear motions (for δμ = 0), then this solution is the continuation of the critical Sitnikov orbit to the case μ = 0.5 + δμ. By applying the substitutions y₁ = ξ, y₂ = η, y₃ = z, $y_{4}=\dot \xi ,$$y_{5}=\dot \eta$ and $y_{6}=\dot z,$ Eq. 18 become:

$$ \begin{array}{@{}rcl@{}} \dot y_{1}\! &=& \! y_{4}=f_{1},\\ \dot y_{2}\! &=& \! y_{5}=f_{2},\\ \dot y_{3}\! &=& \! y_{6}=f_{3},\\ \dot y_{4}\! &=&\! 2y_{5}\! +\! \left[1\! -\! {\varPhi}^{3/2}(y_{3})\! +\! \frac{3}{4}{\varPhi}^{5/2}(y_{3})\! +\! F_{6}^{*}(y_{3})\right]\! y_{1}\! +\! \frac{3}{4}{\varPhi}^{5/2}(y_{3})\delta\mu\! +\! F_{5}^{*}(y_{3})=f_{4},\\ \dot y_{5}\! &=&\! -2y_{4}+\left[1-{\varPhi}^{3/2}(y_{3})+F_{7}^{*}(y_{3})\right]y_{2}=f_{5},\\ \dot y_{6}\! &=&\! -\left[{\varPhi}^{3/2}(y_{3})+F_{7}^{*}(y_{3})\right]y_{3}=f_{6}. \end{array} $$

(19)

To compute a periodic solution of this system we consider a bifurcation point of the Sitnikov family whose initial condition vector is :

$$ y_{0}=(0,0,0,0,0,y_{06}), $$

(20)

where $y_{06}=\dot z_{0}$. Then, this initialisation vector is used to integrate (19) until y₆ becomes equal to 0 for the first time. The periodicity conditions that should be satisfied are :

$$ \begin{array}{l} y_{2}(y_{01},y_{05},y_{06})=0,\\ y_{4}(y_{01},y_{05},y_{06})=0. \end{array} $$

(21)

Linearising these conditions, we obtain that :

$$ \begin{array}{l} y_{2}+v_{21}\delta y_{01}+v_{25}\delta y_{05}+v_{26}\delta y_{06}=0,\\ y_{4}+v_{41}\delta y_{01}+v_{45}\delta y_{05}+v_{46}\delta y_{06}=0, \end{array} $$

(22)

where v_ij = ∂y_i/∂y_0j. By considering that some y_0j remains constant, j = 1,5,6, i.e. δy_0j = 0, Eq. 22 can be solved to get corrections for the rest of the initial conditions. The iterative use of the aforementioned process will finally lead to a periodic solution of System (18). The computation of the involved variations v_ij, i = 2,4, j = 1,5,6, can be accomplished by integrating the first order planar variational equations of this perturbed system :

$$ \frac{d}{dt} {\frac{\partial y_{i}}{\partial y_{0j}}}= \sum\limits_{k=1}^{2} {\frac{\partial f_{i}}{\partial y_{k}}}{\frac{\partial y_{k}}{\partial y_{0j}}}+ \sum\limits_{k=4}^{5} {\frac{\partial f_{i}}{\partial y_{k}}}{\frac{\partial y_{k}}{\partial y_{0j}}}, \quad i,j=1,2,4,5, $$

together with Eq. 18 along with the orbit considered at each iteration. By setting

$$ {\mathcal P}=\left( \begin{array}{llll} \displaystyle\frac{\partial f_{1}}{\partial y_{1}} & \displaystyle\frac{\partial f_{1}}{\partial y_{2}} & \displaystyle\frac{\partial f_{1}}{\partial y_{4}} & \displaystyle\frac{\partial f_{1}}{\partial y_{5}} \\ \displaystyle\frac{\partial f_{2}}{\partial y_{1}} & \displaystyle\frac{\partial f_{2}}{\partial y_{2}} & \displaystyle\frac{\partial f_{2}}{\partial y_{4}} & \displaystyle\frac{\partial f_{2}}{\partial y_{5}} \\ \displaystyle\frac{\partial f_{4}}{\partial y_{1}} & \displaystyle\frac{\partial f_{4}}{\partial y_{2}} & \displaystyle\frac{\partial f_{4}}{\partial y_{4}} & \displaystyle\frac{\partial f_{4}}{\partial y_{5}} \\ \displaystyle\frac{\partial f_{5}}{\partial y_{1}} & \displaystyle\frac{\partial f_{5}}{\partial y_{2}} & \displaystyle\frac{\partial f_{5}}{\partial y_{4}} & \displaystyle\frac{\partial f_{5}}{\partial y_{5}} \end{array} \right), \qquad V=\left( \begin{array}{llll} \displaystyle\frac{\partial y_{1}}{\partial y_{01}} & \displaystyle\frac{\partial y_{1}}{\partial y_{02}} & \displaystyle\frac{\partial y_{1}}{\partial y_{04}} & \displaystyle\frac{\partial y_{1}}{\partial y_{05}} \\ \displaystyle\frac{\partial y_{2}}{\partial y_{01}} & \displaystyle\frac{\partial y_{2}}{\partial y_{02}} & \displaystyle\frac{\partial y_{2}}{\partial y_{04}} & \displaystyle\frac{\partial y_{2}}{\partial y_{05}} \\ \displaystyle\frac{\partial y_{4}}{\partial y_{01}} & \displaystyle\frac{\partial y_{4}}{\partial y_{02}} & \displaystyle\frac{\partial y_{4}}{\partial y_{04}} & \displaystyle\frac{\partial y_{4}}{\partial y_{05}} \\ \displaystyle\frac{\partial y_{5}}{\partial y_{01}} & \displaystyle\frac{\partial y_{5}}{\partial y_{02}} & \displaystyle\frac{\partial y_{5}}{\partial y_{04}} & \displaystyle\frac{\partial y_{5}}{\partial y_{05}} \end{array} \right), $$

this system is written as follows :

$$ \frac{dV}{dt}={\mathcal P}V, $$

(23)

where

$$ \begin{array}{@{}rcl@{}} \frac{\partial f_{1}}{\partial y_{j}} & = & 0,\ j = 1,2,5, \frac{\partial f_{1}}{\partial y_{4}} = 1,\\ [6pt] \frac{\partial f_{2}}{\partial y_{j}} & = & 0,\ j = 1,2,4, \frac{\partial f_{2}}{\partial y_{5}} = 1,\\ [5pt] \frac{\partial f_{4}}{\partial y_{j}} & = & 0,\ j = 2,4, \quad\frac{\partial f_{4}}{\partial y_{1}} = 1-{\varPhi}^{3/2}(y_{3}) +\frac{3}{4}{\varPhi}^{5/2}(y_{3}) + F_{6}^{*}(y_{3}), \frac{\partial f_{4}}{\partial y_{5}} = 2,\\ [5pt] \frac{\partial f_{5}}{\partial y_{j}} & = & 0,\ j = 1,5, \quad\frac{\partial f_{5}}{\partial y_{2}} = 1 - {\varPhi}^{3/2}(y_{3})+F_{7}^{*}(y_{3}), \qquad\qquad\quad{\kern7pt} \frac{\partial f_{5}}{\partial y_{4}} = -2. \end{array} $$

Once a periodic solution of System (18) is obtained, the initial conditions of this solution can serve as a prediction for the initial state of a 3D periodic orbit of Eq. 1 for μ = 0.5 + δμ.

Consider now that a 3D periodic orbit of Eq. 1 has been found for any value of μ and that its initial conditions are $(x_{0},y_{0},z_{0},\dot x_{0},\dot y_{0},\dot z_{0})$. We transform the initial coordinate system so that $x_{1}=x,x_{2}=y,x_{3}=z,x_{4}=\dot x,x_{5}=\dot y,x_{6}=\dot z$. If $\hat {V}=\left (\partial x_{i}/\partial x_{0j} \right )$, where x_0j = x_j(0), i, j = 1,…,6, is the variational matrix of the transformed equations of motion (1), then the stability of this orbit can be examined as follows [9]: Let $P=(\alpha +\sqrt {D})/2$ and $Q=(\alpha -\sqrt {D})/2$, where $\alpha =2-\text {Tr}\hat {V}$, $\beta =(\alpha ^{2}+2-\text {Tr}\hat {V}^{2})/2$ and D = α² − 4(β − 2) > 0. Then, an orbit is stable if |P| < 2 and |Q| < 2, while when |P| = 2 or |Q| = 2 the orbit is considered to be critical (for details on the stability and criticality of 3D orbits see also Markellos [24]). For economy in the computations, according to the type of symmetry of the orbit, the variational matrix can be determined by using the following formulae [32] applicable for orbits of symmetry type S1 :

$$ \begin{array}{lll} \textrm{Case I} & : & \hat{V}(T)=L\hat{V}^{-1}(T/2)L\hat{V}(T/2), {\kern0.828cm} (\mathrm{O}xz\ \textrm{plane symmetry}), \\ \textrm{Case II} & : & \hat{V}(T)=M\hat{V}^{-1}(T/2)M\hat{V}(T/2), {\kern0.61cm} (\mathrm{O}x\ \textrm{axis symmetry}), \\ \textrm{Case III} & : & \hat{V}(T)=[M\hat{V}^{-1}(T/4)L\hat{V}(T/4)]^{2}, \quad (\mathrm{O}x\ \text{axis}-\mathrm{O}xz\ \textrm{plane symmetry}), \\ \textrm{Case IV} & : & \hat{V}(T)=[L\hat{V}^{-1}(T/4)M\hat{V}(T/4)]^{2}, \quad (\mathrm{O}x\ \text{axis}-\mathrm{O}xz\ \textrm{plane symmetry}), \end{array} $$

where L = diag{1,− 1,1,− 1,1,− 1} and M = diag{1,− 1,− 1,− 1,1,1}. The third relation of the above formulae is used in the case of starting the integration from the Ox axis while the fourth is used when the integration is started from the Oxz plane. In the case of orbits of symmetry type S2, the matrix $\hat {V}(T)$ is computed using:

$$ \textrm{Case V} : \hat{V}(T)=NV^{-1}(T/2)NV(T/2), {\kern0.3cm} (\mathrm{O}yz\ \textrm{plane symmetry}), $$

where N = diag{− 1,1,1,1,− 1,− 1}. Since for μ≠ 0.5 the last symmetry (Case V) does not exist, the stability of these orbits has to be computed using Case II.

Equation 18 are no longer helpful if μ deviates enough from the value 0.5. Then, the original equations (1) and a numerical continuation procedure, based on constructing series of critical orbits of the bifurcations under consideration, can be used. In this contribution, the determination of critical orbits of both types of symmetry, S1 and S2, was accomplished by using their symmetry properties w.r.t. the Ox axis. In particular, the initial state vector of such an orbit was considered to be of the form $(x_{0},0,0,0,\dot y_{0},\dot z_{0})$. Then, this orbit should simultaneously satisfy the periodicity and criticality conditions

$$ \begin{array}{@{}rcl@{}} &&\dot x(x_{0},\dot y_{0},\dot z_{0};\mu) = 0,\\ &&\dot z(x_{0},\dot y_{0},\dot z_{0};\mu) = 0,\\ &&a_{i}(x_{0},\dot y_{0},\dot z_{0};\mu) = \pm 2, \quad i=1 \quad\text{or}\quad 2, \end{array} $$

(24)

at the appropriate crossing with the Oxz plane, i.e. the n −th crossing if the orbit crosses 2n times this plane along a whole period. This system was used to obtain proper linear schemes for the procedure mentioned above as follows. The linearisation of Eq. 24 results to

$$ \begin{array}{@{}rcl@{}} &&\dot x+\frac{\partial \dot x}{\partial x_{0}}\delta x_{0}+ \frac{\partial \dot x}{\partial \dot y_{0}}\delta \dot y_{0}+ \frac{\partial \dot x}{\partial \dot z_{0}}\delta \dot z_{0}+ \frac{\partial \dot x}{\partial \mu}\delta\mu = 0,\\ &&\dot z+\frac{\partial \dot z}{\partial x_{0}}\delta x_{0}+ \frac{\partial \dot z}{\partial \dot y_{0}}\delta \dot y_{0}+ \frac{\partial \dot z}{\partial \dot z_{0}}\delta \dot z_{0}+ \frac{\partial \dot z}{\partial \mu}\delta\mu = 0,\\ &&a_{i}+ \frac{\partial a_{i}}{\partial x_{0}}\delta x_{0}+ \frac{\partial a_{i}}{\partial \dot y_{0}}\delta \dot y_{0}+ \frac{\partial a_{i}}{\partial \dot z_{0}}\delta \dot z_{0}+ \frac{\partial a_{i}}{\partial \mu}\delta\mu = \pm 2, \end{array} $$

(25)

where δx₀, $\delta \dot y_{0}$, $\delta \dot z_{0}$, δμ are small modifications of x₀, $\dot y_{0}$, $\dot z_{0}$, μ. The partial derivatives involved in this equation can be computed by additional integrations.

Suppose that a critical orbit, satisfying (24), is known for a specific value of μ. Then, a linear scheme for predicting the initial conditions of a solution of the same kind for μ + δμ can be found by solving

$$ \begin{array}{@{}rcl@{}} &&\frac{\partial \dot x}{\partial x_{0}}\delta x_{0}+ \frac{\partial \dot x}{\partial \dot y_{0}}\delta \dot y_{0}+ \frac{\partial \dot x}{\partial \dot z_{0}}\delta \dot z_{0}+ = -\frac{\partial \dot x}{\partial \mu}\delta\mu,\\ &&\frac{\partial \dot z}{\partial x_{0}}\delta x_{0}+ \frac{\partial \dot z}{\partial \dot y_{0}}\delta \dot y_{0}+ \frac{\partial \dot z}{\partial \dot z_{0}}\delta \dot z_{0}+ = -\frac{\partial \dot z}{\partial \mu}\delta\mu,\\ &&\frac{\partial a_{i}}{\partial x_{0}}\delta x_{0}+ \frac{\partial a_{i}}{\partial \dot y_{0}}\delta \dot y_{0}+ \frac{\partial a_{i}}{\partial \dot z_{0}}\delta \dot z_{0} = -\frac{\partial a_{i}}{\partial \mu}\delta\mu, \end{array} $$

(26)

for $\delta x_{0},\delta \dot y_{0},\delta \dot z_{0}$.

Suppose now that, for some value of μ, an orbit, which is close to a critical periodic orbit, is known. Then, a scheme for correcting its initial conditions comes of by solving the following system

$$ \begin{array}{@{}rcl@{}} &&\frac{\partial \dot x}{\partial x_{0}}\delta x_{0}+ \frac{\partial \dot x}{\partial \dot y_{0}}\delta \dot y_{0}+ \frac{\partial \dot x}{\partial \dot z_{0}}\delta \dot z_{0} = -\dot x,\\ &&\frac{\partial \dot z}{\partial x_{0}}\delta x_{0}+ \frac{\partial \dot z}{\partial \dot y_{0}}\delta \dot y_{0}+ \frac{\partial \dot z}{\partial \dot z_{0}}\delta \dot z_{0}+ = -\dot z,\\ &&\frac{\partial a_{i}}{\partial x_{0}}\delta x_{0}+ \frac{\partial a_{i}}{\partial \dot y_{0}}\delta \dot y_{0}+ \frac{\partial a_{i}}{\partial \dot z_{0}}\delta \dot z_{0}+ = \pm 2-a_{i}, \end{array} $$

(27)

for $\delta x_{0},\delta \dot y_{0},\delta \dot z_{0}$.

In the following, the results of the aforementioned procedure are described.

Initially, we consider the evolution of the families of 3D periodic orbits of symmetry type S1.

A first view of the situation can be given by presenting this evolution for some specific values of the mass parameter. We have seen via Fig. 6a that, for μ = 0.5, these families consist of a single branch each and terminate at planar periodic orbits in the Oxy plane. We will describe their behaviour for μ < 0.5 by means of their characteristic curves in the plane (x(T/4), z(T/4)) which are given in Fig. 14. Figure 14a shows that, for μ = 0.4995, all the families are separated in two branches. For example, the family b2 is divided into the branches b2₁ and b2₂. Branch b2₁ terminates at coplanar orbits, as in the case μ = 0.5. Branch b2₂ joins the branch b3₂ of family b3. Branch b3₁ of b3 merges the branch b6₂ of b6 and and so on. Finally, branch b19₁ of b19 joins the branch b22₂ of b22. According to the enumeration described in Section “Critical orbits of the Sitnikov family for k = 1”, b22 is the family that bifurcates from the 22th critical point of the Sitnikov family, which is not included in this research. As it can be seen from Fig. 14a, all these families, formed by joining branches of b N, N = 2,3,6,7,10,11,14,15,18,19,22, terminate at coplanar periodic orbits in the Oxy plane. Figure 14b depicts that, for μ = 0.4, the families composed by b2₂, b3₂ and b6₁, b7₁ do not exist any more.

Fig. 14

The evolution of the families of 3D periodic orbits of symmetry type S1 w.r.t. the variation of μ. Different colors are used to show which pairs of families join each other

Also, the families formed by the branches b14₁-b15₁, b10₂-b11₁ and b18₂-b19₁ have shrunk. In Fig. 14c, we see that the later are absent when μ = 0.3. Figure 14d shows the families constituted by the the rest of the pairs of branches for μ = 0.1 and μ = 0.005.

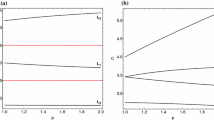
The description of this behaviour can be now completed by means of the results of the numerical continuation of the plane vertically critical orbits at which these branches terminate. For details about vertical stability of planar periodic orbits, we may refer to Hénon [18]. We name these orbits by using the letter P, the running number of the corresponding B-point and the number indicating the specific branch. For example the termination orbit of the branch b2₁ is named P2₁. The vertical stability parameters of P2₁, P2₂, P3₁, P3₂, P6₁, P6₂, P7₁, P7₂, P10₁, P10₂, P11₂, P14₁, P14₂, P15₁, P18₁, P18₂ and P19₂ are a_v = − 1, b_v = 0, c_v≠ 0 while those of P11₁, P15₂ and P19₁ are a_v = − 1, b_v≠ 0, c_v = 0. Figure 15 presents how the half of the period of these critical orbits depends on μ. It is seen there that, for each pair of branches that disappears, the curve (μ, T/2) shows that their bifurcation points come closer to each other, they coincide at a specific value μ and, then, they do not exist any more. On the contrary, the bifurcation points of the rest of the branches still exist when the value of μ approaches 0. So, these branches survive for all values of the mass parameter.

Fig. 15

The evolution of the coplanar bifurcation points of the families of 3D periodic orbits of symmetry type S1 w.r.t. the variation of μ.

Now, we deal with the evolution of the families of 3D periodic orbits of symmetry type S2. As before, we first present this evolution for some specific values of the mass parameter. As it is depicted by Fig. 6b, for μ = 0.5, all the families consist of a single branch each and terminate at planar periodic orbits in the Oxy plane. Their behaviour for μ = 0.4995, μ = 0.4 and μ = 0.3 is described in Figs. 16 and 17 by means of their characteristic curves in the plane $(x_{0},\dot z_{0})$. As it is shown in Fig. 16d, b1 continues to exist when μ approaches 0. On the contrary, it seems that, for some value of μ less than 0.3, the rest of them disappear.

Fig. 16

The evolution of the families of 3D periodic orbits of symmetry type S2 w.r.t. the variation of μ

Fig. 17

The evolution of the families of 3D periodic orbits of symmetry type S2 w.r.t. the variation of μ

We examine this disappearance through the numerical continuation of the plane vertically critical orbits at which these families terminate in the case μ = 0.5. We name these orbits in the same way we used previously. For example, the termination orbit of the family b1₁ is named P1. The vertical stability parameters of P1, P8, P9, P12, P13, P16, P17, P20 and P21 are a_v = 1, b_v = 0, c_v≠ 0 while those of P4 and P5 are a_v = − 1, b_v = 0, c_v≠ 0. Figure 18 presents the evolution of the half of the period of these critical orbits w.r.t. μ. It is seen there that, as the μ decreases, P4 and P5 tend to coincide, and, after a specific value of this parameter, they do not exist any more. In the same way, the members of the pairs P8 −P9, P12 −P13, P16 −P17 and P20 −P21 tend to coincide, finally join each other and, then, they disappear. So, we conclude that the corresponding families behave similarly.

Fig. 18

The evolution of the coplanar bifurcation points of the families of 3D periodic orbits of symmetry type S2 w.r.t. the variation of μ

Summary - Conclusions

This contribution is based on a modified version of the circular Sitnikov problem μ = 0.5, which also takes into account an additional, coupled, three-body interaction force. The aforementioned interaction is expressed by an additional force that depends on a parameter k, which equals to 0 in the classical case. First, the equations determining the motion and the linear stability of the third body are given. Then, the variation of the stability parameters of the Sitnikov family is presented for k = 1,2. Afterwards, 21 critical and 20 self-resonant orbits are chosen in order to study the behaviour of some families of 3D periodic orbits bifurcating from this family when k = 1.

The families emanating from the critical points are one-to-one bifurcations. Ten of them consist of solutions of symmetry type S1 while the rest eleven are composed of members of symmetry type S2. All of them terminate on coplanar orbits. The families emanating from the self-resonant orbits are one-to-three or one-to-four bifurcations. Regarding the families of the first kind, four of them contain double symmetric orbits while the solutions that belong to the rest of them are symmetric w.r.t the Oxz plane. These families form five pairs. The members of every pair join each other. Concerning the families of the second kind, two of them consist of double symmetric orbits while the rest of them contain solutions which are symmetric w.r.t the Oxz plane. Six of these families form three pairs. The members of every pair join each other. The rest of the families remain solitary and terminate on coplanar orbits.

Next, the families bifurcating from the critical orbits are transferred along the variation of the parameter μ. Regarding the families that consist of solutions of symmetry type S1, it is found that, for μ < 0.5, each of them is divided into two branches. All these branches, except one pair of them, were found to compose new families. As μ approaches 0, only six of the resulting families survive. In the case of the families that contain orbits of symmetry type S2, as μ approaches 0, only one of them persists to exist. The rest of them disappear.

In our present study we have chosen to examine a case where the three-body interaction is attractive by selecting a positive value of the parameter k. It would be interesting to also explore the influence of this interaction in a repulsive case, i.e. by considering a negative value of this parameter. We intend to accomplish this in a future work.