Abstract
A novel analytical formula is developed for the second order approximation of the potential function of a pair of charged spacecraft assuming either particle-body or body-body interactions. These approximations use the center of charge (CoCh) as the center of expansions provided that the charge distribution is known. The generated formulas for the potential function are then used to analytically find Coulomb force and corresponding moment about the center of mass (CoM) of the interacting bodies. The resulting expressions are presented in terms of the entire charge and the quadrupole charge tensor (QCT) of each individual body about the corresponding CoCh, as well as the relative distance between the centers of charge of the two charged spacecraft. Because of using expansions about the CoCh, dipole moments of each individual spacecraft do not explicitly appear in the resulting equations. Closed-form approximations of the force and moment are also obtained from the potential function using the CoM expansions. As it is shown, the CoCh expansions are generally more accurate when the distance between the CoCh and the CoM is a significant fraction of the separation distance.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Electrostatic actuation using Coulomb forces is necessary in various spacecraft applications including re-orbiting of GEO debris [7, 16, 22], de-spinning non-cooperative space objects [1, 2], and Coulomb formation flying [4, 9]. In order to design control laws and prescribe needed voltages for these applications, fast and accurate methods are required to calculate the forces and torques on the affected spacecraft using knowledge of the charge distribution of each craft and their relative separations and attitudes. The amount of relative separation between charged spacecraft, as well as their sizes and charge distributions can determine the model needed to achieve satisfactory accuracy within a reasonable time. For example, flat electric fields can be used for large separation distances, the Multi-Sphere Method (MSM) [23] as well as first or second order approximations of radial electric fields can be used for medium separation distances (larger than 5-10 craft radii), while finite element analysis is needed for high accuracy at small separation distances [5, 6]. In some situations the electric field of a spacecraft can be modeled as a point charge so that point-body (particle-body) models may be used to calculate the resulting forces and torques on neighboring spacecraft, while in other situations a point charge model is not appropriate and body-body models must be used.
“Appropriate Fidelity Measure (AFM)” force and torque models are developed in [5] for locally flat and radial electric fields, and the results compared with the MSM method. In particular, the radial electric fields for particle-body interactions are developed to second order using the expansion about the center of mass (CoM) of the spacecraft. This results in expressions in which a charge tensor about the CoM appears in the approximations. Furthermore, the corresponding body-body interaction is generated in [8] with the expansions about the mass centers of the interacting spacecraft resulting in the application of the charge tensors about the CoM. Therefore, in these formulations, the approximations of Coulomb interactions are expressed in terms of the entire charge, dipole moment, and the charge tensor. As in the case of gravity gradient torque approximated to second order using the inertia tensor [11, 21], the particle-body and body-body interaction approximations using the charge tensor about the CoM are more accurate at large separations and less accurate at small separations.
While the separation between the CoM and center of charge (CoCh) is accounted for, the expansions about CoM causes the second order approximation to significantly lose accuracy when this separation is large. This is due to the fact that relying on the charge distribution about the mass center and using the CoM as the center of local expansions does not completely capture all the effects of the charge distribution. Introducing the pseudo-inertia tensor or quadrupole charge tensor (QCT) of a charged pseudo-atom about its CoCh, the approximate resultant force and corresponding moment are generated for pairwise interactions expressed in the form of 1/rs (s > 1 is an integer), and used for Coulomb and Van der Waals interactions in multiscale modeling and simulation of molecular systems [12, 13, 17,18,19,20].
Herein, a closed-form approximation of the force function is developed for a pair of charged spacecraft assuming either particle-body or body-body interactions, from which second order approximations for the forces and torques are obtained. In this scheme, the entire charge, the CoCh, as well as the QCT about the CoCh of each spacecraft are first introduced. Then key operations are presented to obtain the second order approximation of the force function in particle-body and body-body interactions. The resulting formulations are then used to find the resultant Coulomb force as well as the moment about the CoM of each spacecraft. Unlike the previous approximation techniques of Coulomb interactions which use local expansions about the CoM of the body, the method presented in this paper formulates the approximations using expansions about the CoCh of each spacecraft. Therefore, all of the expressions are presented in terms of the total charge of each body, the relative distance between the centers of charge of the interacting spacecraft, as well as the QCT about the CoCh of each one. Because of using expansions about the CoCh, the resulting equations do not explicitly include dipole moments of each spacecraft although these quantities are necessary to obtain the CoCh. Furthermore, we use the new mathematical procedure developed in this paper to find the approximation of the force function using the CoM of each spacecraft as the origin of expansions for both particle-body and body-body interactions, from which forces and moment are obtained. These derivations are independent of the procedure used in [5, 8] since in this paper we develop an approximate force function (opposite of electrostatic potential energy), from which we derive forces and torques, while the final expressions are the same as those in [5, 8]. The results for the particle-body and body-body interactions using CoM and CoCh are compared for a variety of scenarios. It is found that CoCh expansions are generally more accurate when the distance between the CoCh and the CoM is a significant fraction of the separation distance. Finally, it should be noted that the analytical expansions in this article and other works such as [5, 8] are convenient for analytical study of charged spacecraft motions, while various numerical methods such as the Multi-Sphere-Method (MSM) approximations [23] can be used if accuracy and numerical efficiency are critical. Therefore, the contributions in this work do not compete with (and are not compared with) any of these numerical methods, but only with the previously-used CoM-based force and torque approximations.
Physical Properties of Charged Bodies
In the following, we present necessary definitions and properties associated with the electrostatic characteristics of the charged bodies as they will be used in the rest of the paper.
Definition 1
Consider body B (not necessarily a rigid body) shown in Fig. 1 with the charge distribution density function ρq. The dipole moment of this body measured from the center of mass (CoM) i.e. B∗ is defined as
In this equation, p is the position vector of the charge element dq relative to the CoM. Furthermore, depending on the shape of B, τ can represent the length, area, or volume.
Definition 2
For charged body B, the center of charge (CoCh) denoted by Cq is located by
where Q is the entire charge of the body and computed as
It should be noted that Cq exists if the total charge of the body, i.e. Q, is not zero.
Charged body B with center of charge Cq and center of mass B∗
Definition 3
The Quadrupole Charge Tensor (QCT) of body B about the corresponding center of charge Cq is defined as [18, 20]
where \(\mathcal {U}\) denotes the identity tensor, and r is the magnitude of r. We use \({~}^q\mathcal {I}^{B/C_q}\) to represent the QCT since it is similar to the mass moment of inertia tensor notation; however, it is related to the charge distribution and computed about the center of charge. For the Coulomb potential field, this dyadic represents the quadrupole moment tensor [15]. Based on the definition presented in Eq. 4, the trace of this tensor is computed as
Furthermore, as shown in Lemma 2 and proven in [20], the parallel axis theorem [10] can be applied to this tensor.
Lemma 1
The dipole moment mesured from the center of charge is zero. In otherwords, ifris the position vector of the charge element dq measured fromCq,then
Proof
This lemma is proven based on the following relations
□
Lemma 2
Given the QCT of the charged body B aboutCqas\({~}^q\mathcal {I}^{B/C_q}\),one can use the parallel axis theorem to find the QCT of body about anarbitrary point O as
The second term on the right hand side of the above equation is the QCT of the lumped particle with total charge Q located at CoCh of body about O. Defining OCq as the position vector of point Cq relative to O with three components r1, r2, and r3, Eq. 8 can alternatively be expressed as [20]
where
It should be noted that for two interacting spacecraft, the voltage is a known quantity. Furthermore, unlike the gravity gradient problems in which the inertia properties of the bodies do not change, the charge in interacting craft is dynamic [14]. In other words, as two spacecraft move or rotate relative to one another the charge distribution changes, resulting in the change of the dipole moment, the location of the CoCh, and the value of the QCT. In this study, it is assumed that the charge distribution is known through one of the well established methods such as finite element analysis, Methods of Moments [3], or Multi-Sphere Method [23]. Therefore, the location of the CoCh, and the value of the dipole moment and charge tensor relative to the CoM are known up to the accuracy of the method used to find the charge distribution. Finally, since in the following sections the quadrupole charge tensor (QCT) is used, one can apply the parallel axis theorem presented in Lemma 2 to compute QCT from the charge tensor about the CoM.
Particle-Particle Coulomb Force Function
Consider charge element dq on body B and an individual charge \(\bar {q}\) shown in Fig. 1. The Coulomb force function \(V_{\bar {q}dq}\) between these two points is expressed as
where k is Coulomb’s constant, and r′ represents the length of the position vector of dq relative to \(\bar {q}\). The Coulomb force function is the opposite of the electrostatic potential energy. Therefore, the particle-particle Coulomb force vector which is applied to dq from \(\bar {q}\) is expressed as
where \(\mathbf {\nabla }_{\mathbf {r}^{\prime }}(.)\) represents the gradient of a function with respect to r′. This force vector can then be simplified as
Particle-Body Coulomb Approximations Using Expansions About CoCh
Force Function
Consider body B in Fig. 1 (not necessarily a rigid body) with known charge distribution density function ρq and center of charge Cq provided that the entire charge of the body is not zero. The position vector r represents the location of an arbitrary charge element dq in the body measured from Cq. The force function of charged body B due to its interaction with \(\bar {q}\) is then expressed as
Based on the geometry shown in Fig. 1, we can rewrite (14) as
Defining R in terms of its magnitude and unit vector as
we express (15) as
Recalling the binomial series expansion as
we expand (17), resulting in
provided that \(|2 \mathbf {a}_{1} \cdot \frac {\mathbf {r}}{R} + (\frac {{r}}{R})^{2} | < 1\). We now elaborate on the constituent terms of the above expression based on different orders of \(\frac {{r}}{R}\).
-
Zero order terms (ZOT) \(O(\frac {{r}}{R})^{0}\):
$$ \begin{array}{@{}rcl@{}} \text{ZOT} = - \frac{{k \bar{q} }}{R}{\int}_{B} \ \rho_{q} d\tau \overset{(3)}{=} - \frac{{k \bar{q} }}{R}Q \end{array} $$(20) -
First order terms (FOT) \(O(\frac {{r}}{R})\):
$$ \begin{array}{@{}rcl@{}} \text{FOT}= - \frac{{k \bar{q} }}{R}{\int}_{B} \ - \mathbf{a}_{1} \cdot \frac{\mathbf{r}}{R} \rho_{q} d\tau = \frac{{k \bar{q} }}{R^{2}} \mathbf{a}_{1} \cdot {\int}_{B} \ {\mathbf{r}} \rho_{q} d\tau \overset{(6)}{=} {0} \end{array} $$(21) -
Second order terms (SOT) \(O(\frac {{r}}{R})^{2}\):
$$ \begin{array}{@{}rcl@{}} \text{SOT} &=& - \frac{{k \bar{q} }}{R}{\int}_{B} \ {\left[ - \frac{1}{2} (\frac{{r}}{R})^{2} + \frac{3}{2} (\mathbf{a}_{1} \cdot \frac{\mathbf{r}}{R})^{2}\right]} \rho_{q} d\tau \\ &=& \frac{{k \bar{q} }}{2R^{3}}{\int}_{B} \ {\left[ {{r}}^{2} - {3} (\mathbf{a}_{1} \cdot {\mathbf{r}})^{2}\right]} \rho_{q} d\tau \end{array} $$(22)Based on the geometry shown in Fig. 1, we simplify (22) by using (a1 ⋅r)2 = r2 − h2 as
$$ \begin{array}{@{}rcl@{}} \text{SOT} = \frac{{k \bar{q} }}{2R^{3}} ({\int}_{B} \ { {-2{r}}^{2} \rho_{q} d\tau + {{3 }} {\int}_{B} h^{2}} \rho_{q} d\tau) \end{array} $$(23)Referring to Eq. 5, the first integral is related to the trace of \({~}^q\mathcal {I}^{B/C_q}\), while the second integral describes \({~}^q\mathcal {I}^{B/C_q}\) in a1a1 direction. Therefore, the SOT can be simplified as
$$ \begin{array}{@{}rcl@{}} \text{SOT} =\frac{{k \bar{q} }}{2R^{3}}\left[ - \text{tr}({~}^q\mathcal{I}^{B/C_q}) + 3 \mathbf{a}_{1} \cdot {~}^q\mathcal{I}^{B/C_q} \cdot \mathbf{a}_{1}\right] \end{array} $$(24)
In general, we can express the force function as
where \(v^{(i)}_{\bar {q}B}\) is the collection of the terms in \(O(\frac {{r}}{R})^{i}\). Using Eqs. 20, 21, and 24, the approximate Coulomb force function up to the second order terms for particle-body interaction can be expressed as
where
It should be noted that \(\tilde {V}\) indicates a second order approximation of V. The above expression and the associated force and torque which will be derived in the following sections are valid provided that the distance between charge \(\bar {q}\) and the center of charge Cq is much larger than the distance of the farthest charge element on the body from Cq.
Resultant Force from Approximate Force Function
It is proven in the Appendix that the force applied to body B from charge \(\bar {q}\) can be computed by finding the gradient of the force function with respect to R as
The gradient of the approximate force function in Eq. 26 is then computed as
Using the definition of R in terms of its magnitude and unit vector, ∇RR is evaluated as
Now we compute \(\mathbf {\nabla }_{\mathbf {R}} v^{(2)}_{\bar {q}B}\) as
Using the following property
we simplify (31) as
Using the results of Eqs. 30 and 33, we compute \(\tilde {\mathbf {F}}_{\bar {q}B}\) as the second order approximation of the force vector in Eq. 29 as
This equation can alternatively be rewritten as
where \(\mathbf {F}^{(2)}_{\bar {q}B}\) is the collection of the terms in \(O(\frac {{r}}{R})^{2}\) expressed as
Approximation of the Moment about the Mass Center
Since the Coulomb force applied from charge \(\bar {q}\) to B does not necessarily pass through B∗, it creates the following moment about B∗
Based on the geometry shown in Fig. 1, we rewrite this equation as
Since \(\mathbf {F}_{\bar {q}dq}\) and r′ are collinear, the moment about B∗ is simplified as
This moment can alternatively be expressed as
Expressing R in terms of its magnitude and unit vector (see Eq. 16), we rewrite Eq. 39 as
Finally, the second order approximation of moment vector about B∗ denoted as \(\tilde {\mathbf {M}}_{\bar {q}/B^{*}}\) is computed as
It should be noted that \(\mathbf {R}_{C_{q}} \times \tilde {\mathbf {F}}_{\bar {q}B}\) is the moment generated due to the deviation of the CoCh from CoM. If these two points coincide (\(\mathbf {R}_{C_{q}} = \mathbf {0}\)), then \(\tilde {\mathbf {M}}_{\bar {q}/B^{*}}\) is simplified as
We observe that in the particle-body model of charged spacecraft, the approximations using the CoCh are expressed in terms of the charge of the particle, the relative distance between the particle and CoCh of the interacting body, as well as the QCT of the body about its CoCh. Because of using expansions about the CoCh, the resulting equations do not explicitly include the dipole moment of body B, while the computations associated with the dipole moment have already been included in finding the location of the CoCh as shown in Eq. 2.
Body-Body Coulomb Approximations Using Expansions About CoCh
Force Function
Consider bodies B and \(\bar {B}\) in Fig. 2 (not necessarily rigid bodies) with known charge distribution density functions ρq and \(\bar {\rho }_{q}\), respectively. Similar to body B, for body \(\bar {B}\), one can find the entire charge, the dipole moment about the mass center, the location of CoCh, and the QCT about the CoCh, respectively, as
As shown in Fig. 2, \(\bar {\mathbf {r}}\) denotes the position vector of \(d\bar {q}\) from \(\bar {C}_{q}\), while \(\bar {r}\) represents the magnitude of \(\bar {\mathbf {r}}\). Furthermore, depending on the shape of \(\bar {B}\), \(\bar {\tau }\) can represent the length, area, or volume. Finally, based on Eq. 46, \(\bar {C}_{q}\) exists if the entire charge of the body, i.e. \(\bar {Q}\), is not zero.
Body-body interaction
Consider charge elements dq and \(d\bar {q}\) on B and \(\bar {B}\), respectively. Using Eq. 11, the force function between these two bodies is expressed as
Rewriting this equation as
and based on Eq. 14, the term \(-{\int }_{B} \frac {k \ dq d\bar {q}}{r^{\prime }}\) indicates the force function \(V_{d\bar {q}B}\) due to the interaction between charge element \(d\bar {q}\) and body B. Therefore, Eq. 48 is rewritten as
Replacing \(\bar {q}\) with \(d\bar {q}\) in Eq. 25, the above equation is expressed as
Using the second order approximation for the particle-body Coulomb force function in Eq. 26, the approximate body-body force function is written as
Based on the geometry shown in Fig. 2, we rewrite Eq. 52 as
Defining S in terms of its magnitude and unit vector as
we express (53) as
Recalling binomial series expansion, we expand (55) as
provided that \(|-2 \mathbf {e}_{1} \cdot \frac {\bar {\mathbf {r}}}{S} + (\frac {\bar {{r}}}{S})^{2} | < 1\). We now express the above equation using the following auxiliary terms
where
We first elaborate on the constituent terms of \(\mathcal {Z}_{1}\) based on different orders of \(\frac {\bar {{r}}}{S}\).
-
Zero order terms (ZOT) \(O(\frac {\bar {{r}}}{S})^{0}\):
$$ \begin{array}{@{}rcl@{}} \text{ZOT} = - \frac{{k {Q} }}{S}{\int}_{\bar{B}} \ \bar{\rho}_{q} d\bar{\tau} \overset{(44)}{=} - \frac{{k Q \bar{Q} }}{S} \end{array} $$(60) -
First order terms (FOT) \(O(\frac {\bar {{r}}}{S})\):
$$ \begin{array}{@{}rcl@{}} \text{FOT}= - \frac{{k Q}}{S}{\int}_{\bar{B}} \ \mathbf{e}_{1} \cdot \frac{\bar{\mathbf{r}}}{S} \bar{\rho}_{q} d\bar{\tau} = - \frac{{k Q }}{S^{2}} \mathbf{e}_{1} \cdot {\int}_{\bar{B}} \ {\bar{\mathbf{r}}} \bar{\rho}_{q} d\bar{\tau} \overset{(6)}{=} {0} \end{array} $$(61) -
Second order terms (SOT) \(O(\frac {\bar {{r}}}{S})^{2}\):
$$ \begin{array}{@{}rcl@{}} \text{SOT} &=& - \frac{{k Q }}{S}{\int}_{\bar{B}} \ {\left[ - \frac{1}{2} (\frac{\bar{{r}}}{S})^{2} + \frac{3}{2} (\mathbf{e}_{1} \cdot \frac{\bar{\mathbf{r}}}{S})^{2}\right]} \bar{\rho}_{q} d\bar{\tau} \\ &=& \frac{{k Q }}{2S^{3}} {\int}_{\bar{B}} \ {\left[ {\bar{{r}}}^{2} - {3} (\mathbf{e}_{1} \cdot {\bar{\mathbf{r}}})^{2}\right]} \bar{\rho}_{q} d\bar{\tau} \end{array} $$(62)Based on the geometry shown in Fig. 2, we can use \((\mathbf {e}_{1} \cdot \bar {\mathbf {r}})^{2} = \bar {{r}}^{2} - \bar {h}^{2}\) to simplify (62) as
$$ \begin{array}{@{}rcl@{}} \text{SOT} = \frac{{k Q }}{2S^{3}} ({\int}_{\bar{B}} -2{\bar{{r}}^{2} \bar{\rho}_{q} d\bar{\tau} + {{3 }} {\int}_{\bar{B}} \bar{h}^{2}} \bar{\rho}_{q} d\bar{\tau}) \end{array} $$(63)Referring to Eq. 5, the first integral is related to the trace of \({~}^q \bar {\mathcal {I}}^{\bar {B}/\bar {C}_q}\), while the second one describes \({~}^q \bar {\mathcal {I}}^{\bar {B}/\bar {C}_q}\) in e1e1 direction, resulting in
$$ \begin{array}{@{}rcl@{}} \text{SOT} = - \frac{kQ}{2S^{3}} \left[\text{tr}({~}^q \bar{\mathcal{I}}^{\bar{B}/\bar{C}_q}) - 3 \mathbf{e}_{1} \cdot {~}^q \bar{\mathcal{I}}^{\bar{B}/\bar{C}_q} \cdot \mathbf{e}_{1} \right] \end{array} $$(64)Therefore, using Eqs. 60, 61, and 64, we provide the approximation of \(\mathcal {Z}_{1}\) in Eq. 58 as
$$ \begin{array}{@{}rcl@{}} \mathcal{Z}_{1} \approx - \frac{{k Q \bar{Q} }}{S} \left\{1 + \frac{1}{2\bar{Q} S^{2}} \left[\text{tr}({~}^q \bar{\mathcal{I}}^{\bar{B}/\bar{C}_q}) - 3 \mathbf{e}_{1} \cdot {~}^q \bar{\mathcal{I}}^{\bar{B}/\bar{C}_q} \cdot \mathbf{e}_{1} \right] \right\} \end{array} $$(65)
Now, we elaborate on \(\mathcal {Z}_{2}\) in Eq. 59. Replacing \(\bar {q}\) with \(d\bar {q}\) in Eq. 27, we form the expression for \(v^{(2)}_{d\bar {q}B}\), and rewrite \(\mathcal {Z}_{2}\) as
The QCT and its trace produce only terms of second degree in r. Therefore replacing a1 with e1, and R with S does not remove any terms of interest, resulting in
Since \(\frac {{k }}{2S^{2}} \left [\text {tr}({~}^q\mathcal {I}^{B/C_q}) -3 \mathbf {e}_{1} \cdot {~}^q\mathcal {I}^{B/C_q} \cdot \mathbf {e}_{1}\right ]\) contains \(O(\frac {{{r}}}{S})^{2}\) terms, we only keep the \(O(\frac {{{r}}}{S})^{0}\) term in the integral of the above equation, and simplify it as
Finally, using Eqs. 65, and 68, we analytically express \(\tilde {V}_{\bar {B}B}\) as the second order approximation of the force function using local expansions about the CoCh in Eq. 57 as
where
It is noted that the exact force function between B and \(\bar {B}\), i.e. \({V}_{\bar {B}B}\), can be written as
where \(v^{(i)}_{\bar {B}B}\) is the collection of the terms in \(O(\frac {{r}}{S})^{i}\), \(v^{(j)}_{\bar {B}B}\) is the collection of the terms in \(O(\frac {\bar {r}}{S})^{j}\), and \({v}^{(ij)}_{\bar {B}B}\) is the collection of the terms in \(O\!\left ((\frac {{r}}{S})^{i} (\frac {\bar {r}}{S})^{j}\right )\). Therefore, the approximation in Eq. 69 and the corresponding force and torque (developed in the following sections) are valid provided that the distance between Cq and \(\bar {C}_{q}\) is much larger than the distance of the farthest charge element on B from Cq and the distance of the farthest charge element on \(\bar {B}\) from \(\bar {C}_{q}\).
Resultant Force from Approximate Force Function
A similar proof provided in the Appendix can be used to show that the force applied to \(\bar {B}\) from charged body B can be computed by finding the gradient of the associated force function with respect to S as
The gradient of the second order force function approximation in Eq. 69 is then computed as
Using the definition of S based on the associated magnitude and unit vector, ∇SS in the above equation is expressed as
Now we compute \(\mathbf {\nabla }_{\mathbf {S}} v^{(2)}_{\bar {B}B}\) as
Since (76) and (31) are analogous, we compute \(\mathbf {\nabla }_{\mathbf {S}} v^{(2)}_{\bar {B}B}\) by replacing R and a1 with S and e1, respectively, in Eq. 33, resulting in
Similar to the results shown in Eqs. 76 and 77, we can compute \(\mathbf {\nabla }_{\mathbf {S}} \bar {v}^{(2)}_{\bar {B}B}\) as
Finally, based on the results of Eqs. 75, 77, and 78, we express the second order approximation of the force applied to B from \(\bar {B}\) as
where \(\mathbf {F}^{(2)}_{\bar {B}B}\), the collection of the terms in \(O(\frac {{r}}{S})^{2}\), and \(\bar {\mathbf {F}}^{(2)}_{\bar {B}B}\), the collection of the terms in \(O(\frac {\bar {r}}{S})^{2}\), are computed as
Approximation of the Moment About the Mass Center
Replacing \(\bar {q}\) with \(d\bar {q}\) in Eq. 42, we can express the approximate moment generated about B∗ due to the application of Coulomb force from charge element \(d\bar {q}\) to B as
Therefore, the approximate moment generated about B∗ due to the Coulomb force applied from \(\bar {B}\) to B is expressed as
The second integral can produce only terms of second degree in r/R since \({~}^q\mathcal {I}^{B/C_q}\) contains terms of second degree in r. Therefore replacing a1 with e1, and R with S does not remove any terms of interest. Now, we can simplify the second order approximation of the moment about the mass center of \(\bar {B}\) as
The resulting moment can alternatively be expressed in terms of the gradient of the body-body force function as
It should be noted that \(\mathbf {R}_{C_{q}} \times \tilde {\mathbf {F}}_{\bar {B}B}\) is a moment generated due to the deviation of Cq from B∗. If these two points coincide, i.e. \(\mathbf {R}_{C_{q}} = \mathbf {0}\), the approximate moment about B∗ is simplified as
We observe that in the body-body model of charged spacecraft, local expansions about the CoCh of each body result in expressions containing the relative distance between the centers of charge of interacting bodies, the entire charge of each spacecraft, as well as the QCT of each body about its CoCh.
Particle-Body Approximations Using Expansions About CoM
In this section, we derive the approximations using the mass center to compare the results with those previously derived in Section “Particle-Body Coulomb Approximations Using Expansions About CoCh” using the center of charge. In this situation, we denote r as the position vector of the charge element from B∗, while R is a vector directed from \(\bar {q}\) to B∗ as shown in Fig. 3. Using this notation, since the measurements are performed based on the origin of the expansion (CoM), some of the expressions in the new derivations become analogous to those developed before. The only difference is that these terms are now measured from the CoM. For instance, the charge tensor is now computed about the CoM and denoted by \({~}^q\mathcal {I}^{B/B^{*}}\). This tensor can be obtained by applying the parallel axis theorem to \({~}^q\mathcal {I}^{B/C_q}\) as presented in Lemma 2.
Center of mass as the origin of particle-body expansions
Force Function
In order to compute the force function and generate the approximation about the mass center, we follow the procedure presented in Eqs. 14–24. Since r is measured from B∗, the first order term in force function in Eq. 21 is not zero anymore, and must be considered in the force function development. Therefore, the second order approximation of the force function is modified as
where
Since r is measured from the CoM, the integral in Eq. 88 has been replaced by the dipole moment measured from the CoM. Using (1), \(\mathbf {P}^{B/B^{*}} \) can also be expressed as
It should be noted that in the particle-body model of charged spacecraft, local expansions about the CoM of the body result in expressions containing the charge of the particle, the total charge of the interacting body, the relative distance between the charge particle and the CoM of the interacting body, the dipole moment of the spacecraft, as well as the charge tensor about the CoM of the body. Furthermore, the approximation in Eq. 87 and the corresponding force and torque (developed in the following sections) are valid if the distance between B∗ and \(\bar {q}\) is much greater than the distance between the CoM of the body and the corresponding farthest charge element.
Resultant Force from Approximate Force Function
In order to generate the approximate force vector, we compute the gradient of Eq. 87 with respect to R as
All terms in the above equation have already been calculated in Section “Resultant Force from Approximate Force Function” except \(\mathbf {\nabla }_{\mathbf {R}} v^{(1)}_{\bar {q}B}\). This new term is computed as
Using (30) and (32), we simplify the above expression as
As such, the contribution of the first order terms in the gradient of the force function of Eq. 91 is expressed as
Finally, using the CoM as the origin of local expansions, we can analytically express the second order approximate force applied to body B as
where
Moment Vector
According to the geometry shown in Fig. 3, we compute the moment about B∗ as
Expressing R in terms of its unit vector and magnitude, and using the forcing terms in Eq. 95, we modify the second order approximate moment as
We note that the results presented in Sections “Resultant Force from Approximate Force Function” and “Moment Vector” are all in agreement with those in [5].
Body-Body Approximations Using Expansions About CoM
In this section, we derive the approximations using the mass center to compare the results with those previously developed in Section “Body-Body Coulomb Approximations Using Expansions About CoCh” using the center of charge. In this situation, r is measured from B∗, \(\bar {\mathbf {r}}\) is measured from \(\bar {B}^{*}\), R is directed from \(d\bar {q}\) to B∗, and S is directed from \(\bar {B}^{*}\) to B∗ as shown in Fig. 4. Using this notation, since the measurements are performed based on the origin of the expansion (CoM), some of the expressions in the new derivations become analogous to those generated before. The only difference is that these terms are now measured from the CoM. For instance, the charge tensors of B and \(\bar {B}\) are computed about the corresponding CoM and denoted by \({~}^q\mathcal {I}^{B/B^{*}}\), \({~}^q \bar {\mathcal {I}}^{\bar {B}/\bar {B}^{*}}\). They can be calculated by applying the parallel axis theorem presented in Lemma 2 to \({~}^q\mathcal {I}^{B/C_q}\) and \({~}^q \bar {\mathcal {I}}^{\bar {B}/\bar {C}_q}\), respectively.
Derivations of body-body interactions using expansions about CoM
Force Function
In order to compute the force function and generate the approximation about the mass center, we follow the procedure presented in Eqs. 48–68. Since r is measured from B∗, the first order term in force function of Eq. 52 is not zero anymore. Therefore, using (87), we express (52) as
where
We first work on the integral of the first order term which is expressed as
Based on the geometry shown in Fig. 4, we replace \(\frac {\mathbf {a}_{1}}{R^{2}}\) with
Provided that \(| -2 \mathbf {e}_{1} \cdot \frac {\bar {\mathbf {r}}}{S} + (\frac {\bar {{r}}}{S})^{2}|<1\), the binomial expansion of Eq. 104 results in
Now we can express (103) as
Sine \(\mathbf {P}^{B/B^{*}}\) produces only terms of first degree in r, in the above integrals, we only keep terms up to first degree in \(\bar {r}\), resulting in
This equation can be rewritten as
Since \(\bar {\mathbf {r}}\) is measured from the CoM of \(\bar {B}\), according to Eq. 45, the integral \({\int }_{\bar {B}} \bar {\mathbf {r}} \bar {\rho }_{q} d\bar {\tau }\) can be replaced by \(\bar {\mathbf {P}}^{\bar {B}/\bar {B}^{*}}\). Now (108) and therefore (103) are simplified as
In order to compute the remaining terms in Eq. 100, i.e. \((- {\int }_{\bar {B}} \frac {{k Q }}{R} \ (1 +v^{(2)}_{d\bar {q}B} ) \bar {\rho }_{q} d\bar {\tau })\), we can use the result of the integral in Eq. 52 which has already been presented in Eq. 69. However, since the origin of the expansions is not the CoCh, the first order term in Eq. 61 does not vanish anymore, and is expressed as
Therefore, the remaining terms in Eq. 100 are computed as
Finally, using (109) and (111), we simplify the CoM-based second order approximation of force function presented in Eq. 100 as
where \(v^{(1)}_{\bar {B}B}\) is the collection of the terms in \(O(\frac {{r}}{S})\), \(\bar {v}^{(1)}_{\bar {B}B}\) is the collection of the terms in \(O(\frac {\bar {r}}{S})\), \({v}^{(11)}_{\bar {B}B}\) is the collection of the terms of in \(O\left ((\frac {{r}}{S})(\frac {\bar {r}}{S})\right )\), \(v^{(2)}_{\bar {B}B}\) is the collection of the terms in \(O(\frac {{r}}{S})^{2}\), and \(\bar {v}^{(2)}_{\bar {B}B}\) is the collection of the terms in \(O(\frac {\bar {r}}{S})^{2}\). These terms are computed as
It should be noted that in the body-body model of charged spacecraft, local expansions about the CoM of each body result in expressions containing the total charge of each body, the relative distance between the centers of mass of interacting bodies, the dipole moments of the interacting spacecraft, as well as the charge tensor about the mass center of each spacecraft. Furthermore, the approximation in Eq. 112 and the corresponding force and torque (developed in the following sections) are valid if the distance between B∗ and \(\bar {B}^{*}\) is much greater than the distance between the CoM of each body and the corresponding farthest charge element.
Resultant Force from Approximate Force Function
In order to generate the approximate force vector using local expansions about CoM, we compute the gradient of Eq. 112 with respect to S as
Since \(v^{(1)}_{\bar {B}B}\) in the above equation is analogous to \(v^{(1)}_{d\bar {q}B}\) in Eq. 101, following the procedure presented in Eqs. 92 and 93, we can compute the new term \(\mathbf {\nabla }_{\mathbf {S}} v^{(1)}_{\bar {B}B}\) by replacing R with S, and a1 with e1, resulting in
Similarly, we express \(\mathbf {\nabla }_{\mathbf {S}} \bar {v}^{(1)}_{\bar {B}B}\) as
Furthermore, \(\mathbf {\nabla }_{\mathbf {S}} v^{(11)}_{\bar {B}B}\) is computed as
Using (75) and
we simplify \(\mathbf {\nabla }_{\mathbf {S}} v^{(11)}_{\bar {B}B}\) as
Similar to the results presented in Eqs. 77 and 78, we compute \(\mathbf {\nabla }_{\mathbf {S}} v^{(2)}_{\bar {B}B}\) and \(\mathbf {\nabla }_{\mathbf {S}} \bar {v}^{(2)}_{\bar {B}B}\) as
Finally, the analytical expression of the second order approximation of the resultant force applied to B from \(\bar {B}\) in Eq. 118 is presented as
where \(\mathbf {F}^{(1)}_{\bar {B}B}\) is the collection of the terms in \(O(\frac {{r}}{S})\), \(\bar {\mathbf {F}}^{(1)}_{\bar {B}B}\) is the collection of the terms in \(O(\frac {\bar {r}}{S})\), \(\mathbf {F}^{(11)}_{\bar {B}B}\) is the collection of the terms in \(O\left ((\frac {{r}}{S})(\frac {\bar {r}}{S})\right )\), \(\mathbf {F}^{(2)}_{\bar {B}B}\) is the collection of the terms in \(O(\frac {{r}}{S})^{2}\), and \(\bar {\mathbf {F}}^{(2)}_{\bar {B}B}\) is the collection of the terms in \(O(\frac {\bar {r}}{S})^{2}\). These terms are computed as
Moment Vector
Replacing \(\bar {q}\) with \(d\bar {q}\) in Eq. 99, the moment generated by \(d\bar {q}\) about B∗ is computed as
Integrating this equation over \(\bar {B}\) results in
The first integral in the above equation is the similar to the right-hand-side of Eq. 103 in which the dot product is replaced by the cross product. Therefore, it is computed by changing the dot product before \(\mathbf {P}^{B/B^{*}}\) to the cross product in Eq. 109
The second integral in Eq. 133 can produce only terms of second and higher degrees in r/R since \( {~}^{q}\mathcal {I}^{B/B^{*}} \) contains terms of second degree in r. Therefore, replacing a1 with e1, and R with S does not remove any terms of interest. This results in
Using the results of Eqs. 134 and 135, the second order approximation of the moment moment about B∗ in Eq. 133 is computed as
We note that the results presented in Sections “Resultant Force from Approximate Force Function” and “Moment Vector” are all in agreement with those in [8].
Simulation Results
Particle-Body Interaction
Consider bar B with the length of 6 m, (L = 3 m). Mass center B∗ is always located at the geometric center of the bar. This body contains two charged particles, q1 = 4 × 10− 5C located at the distance L0 (−L ≤ L0 ≤ L) from B∗, while q2 = 4 × 10− 5C is at the right end of the bar. This represents a dumbbell model of a spacecraft. Charged particle \(\bar {q} = 4 \times 10^{-5}~C\) is located at the origin of the x − y reference frame. It is assumed that B∗ is always on the y axis.
Schematic for the particle-body example
We denote the distance between \(\bar {q}\) and B∗ as d. Therefore, the configuration of the bar relative to \(\bar {q}\) is determined by d and 𝜃 as shown in Fig. 5. Changing d and 𝜃 respectively in the range 2L ≤ d ≤ 5L and 0 ≤ 𝜃 ≤ π, we compute the force function, net force, and resultant moment about B∗, for each configuration. We use exact calculations to compute the desired quantities. Using the schematic shown in Fig. 5a and b, we then utilize the CoM-based expansions developed in Section “Particle-Body Approximations Using Expansions About CoM” and CoCh-based expansions developed in Section “Particle-Body Coulomb Approximations Using Expansions About CoCh” to compute the desired quantities. The percentage error of the approximate force function, resultant force, moment at each configuration (𝜃i,dj) is calculated as
It should be noted that for this planar system, the moment is a scalar. Also since at some configurations, the moment becomes zero, to avoid any singularity in the evaluation of the relative error in Eq. 139 the absolute value of the exact moment is shifted by a value of one in the denominator.
The percentage error of the force function, resulting force and moment about B∗ using CoM expansion and CoCh expansion for L0 = −L
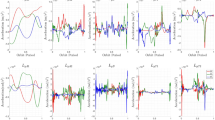
Figures 6, 7 and 8 compare the percentage error in the force function, force, and moment for three different systems with L0 = −L, L0 = 0, and L0 = L. As shown in Fig. 6, when CoM and CoCh coincide, both methods result in the same approximation errors. Figure 7 shows the error when L0 = 0, meaning that the CoCh is deviated from the CoM by 1.5 m. It is observed that using CoCh-based expansion generates a wider region in the configuration space with small errors than using the CoM-based expansion. As shown in Fig. 8, this region increases even more when two particles are located on the right end of the bar, L0 = L, meaning that the CoCh is deviated from the CoM by 3 m. It should be noted that the percentage error for the force function, force, and moment using CoCh-based expansion is on the order of %10− 13. In conclusion, comparing these results indicate that as the CoCh is separated from the CoM, for most of the configurations, the approximations using the CoCh provide more accurate results.
The percentage error of the force function, resulting force and moment about B∗ using CoM expansion and CoCh expansion for L0 = 0
The percentage error of the force function, resulting force and moment about B∗ using CoM expansion and CoCh expansion for L0 = L
We also want to investigate the required minimum distance of the bar from the particle in both methods to reach a desired accuracy as we sweep the location of charge q1 on bar B. In order to do so, we define this problem mathematically as
It should be noted that \((\frac {d}{L})_{min}\) obtained from the above statement guarantees that if we pick a distance d such that d/L ≥ (d/L)min, for all configurations of body B, the error is less than edesired. We find (d/L)min using CoM-based expansion and CoCh-based expansion, and then compare the results. In order to solve this problem numerically, we fix the location of q1 at L0. Then we sweep d/L from 1.1L to 200L with the spatial increments of L/30. For each value of d/L we change the orientation of body by varying 𝜃 from 0 to 2π with the angular increments of π/10. Then for the given d/L we calculate the percentage error at all orientations. If the percentage error for each orientation is less than the desired one, we pick the value of d/L as (d/L)min, otherwise we move to the next value of d/L. Therefore, for the given value of L0 we can solve the stated problem. We then move q1 to another location by changing L0, and repeat the procedure explained previously to find the corresponding (d/L)min.
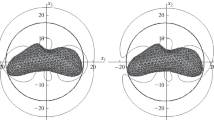
We solve the problem stated in Eq. 140 for the system described previously with the particle-body interaction for the selected error \(e^{V}_{desired}= e^{\mathbf {F}}_{desired}= e^{\mathbf {M}}_{desired} = \%1\) and \(e^{V}_{desired}= e^{\mathbf {F}}_{desired}= e^{\mathbf {M}}_{desired} = \%0.01\). Figure 9 shows (d/L)min versus the distance between CoM and CoCh as we change L0 from − L to L. When q1 is located at − L0, both CoM and CoCh coincide. Therefore, both methods result in the same value for (d/L)min. As we move q1 to the right side of the bar, CoCh separates from the CoM. As this deviation increases, it is observed that (d/L)min increases when we use CoM-based expansion (See curves with 
and 
in Fig. 9) . However, (d/L)min decreases when we use CoCh-based expansion (See curves with 
and 
in Fig. 9). It is also observed that as we decrease the desired error, the deviation between (d/L)min from the CoM- and CoCh-based expansions significantly increases. Therefore, as the CoCh distances from the CoM, the expansion using the CoCh provides acceptable accuracy when the particle is close to the body; however, this is not true for CoM-based expansion. It should be noted that the above problem is a conservative case in which we want to find (d/L)min to reach a desired accuracy for all orientations of the body. However, if it is desired to reach a predefined accuracy for a given orientation, the value of (d/L)min for either of these methods may drop or even become the same.
(d/L)min for different desired errors as a function of the distance between CoM and CoCh. 
: CoCh-expansion with desired error %1, 
: CoM-expansion with desired error %1, 
: CoCh-expansion with desired error %0.01, 
: CoM-expansion with desired error %0.01
Body-Body Interaction
Consider bars B and \(\bar {B}\) with the lengths of 6 m, \((L = \bar {L} = 3~ m)\). Mass centers B∗ and \(\bar {B}^{*}\) are always located at the geometric centers of the bars. Charged particle q1 = 4 × 10− 5C is located at the distance L0 (−L ≤ L0 ≤ L) from B∗, while q2 = 4 × 10− 5C is located at the right end of B. Furthermore, charged particle \(\bar {q}_{1} = q_{1}\) is located at the distance \(\bar {L}_{0}\)\((-\bar {L} \leq \bar {L}_{0} \leq \bar {L})\) from \(\bar {B}^{*}\), while \(\bar {q}_{2} = q_{2}\) is at the right end of \(\bar {B}\). The CoM of \(\bar {B}\) is at the origin of the x − y reference frame while this body always lies on the x axis. We denote the distance between B∗ and \(\bar {B}^{*}\) as d. The configuration of B is determined by \(\bar {\theta }\), d, and 𝜃 as shown in Fig. 10. Changing d and 𝜃 in the range 2L ≤ d ≤ 6L and 0 ≤ 𝜃 ≤ 2π, and considering \(\bar {\theta }\) as a constant quantity, we compute the force field, net force and moment about B∗ for each configuration. We use exact calculation to find these quantities. Then following the schematic shown in Fig. 10a and b, we use the CoM-based expansion developed in Section “Body-Body Approximations Using Expansions About CoM”, and the CoCh-based expansions developed Section “Body-Body Coulomb Approximations Using Expansions About CoCh” to compute the desired quantities. The percentage errors are calculated using the same way explained in the previous section. Figures 11, 12 and 13 compare the percentage errors for three systems described by \((L_{0}=-L,\bar {L}_{0} = - \bar {L}, \bar {\theta } = \pi /3)\), \((L_{0}=0,\bar {L}_{0} = 0, \bar {\theta } = \pi /3)\), and \((L_{0}=L,\bar {L}_{0} = \bar {L}/4, \bar {\theta } = \pi /3)\), respectively. As shown in Fig. 11, when CoM and CoCh coincide, both expansions result in the same approximation errors. Figure 12 shows the error when L0 = 0 and \(\bar {L}_{0} = 0\), meaning that the CoCh of each body is deviated from the corresponding CoM by 1.5 m. It is observed that using CoCh-based expansion generates a wider region in the configuration space with small errors than using the CoM-based expansion. As shown in Fig. 13 this region increases even more when L0 = L and \(\bar {L}=L/4\).
Schematic for the body-body example
The percentage error of the force function, resulting force and moment about B∗ using CoM expansion and CoCh expansion L0 = −L, \(\bar {L}_{0} = - \bar {L}\), and \(\bar {\theta } = \pi /3\)
The percentage error of the force function, resulting force and moment about B∗ using CoM expansion and CoCh expansion L0 = 0, \(\bar {L}_{0} = 0\), and \(\bar {\theta } = \pi /3\)
The percentage error of the force function, resulting force and moment about B∗ using CoM expansion and CoCh expansion for L0 = L, \(\bar {L}_{0} = \bar {L}/4\), and \(\bar {\theta } = \pi /3\)
We also want to investigate the required minimum distance of the bars in both methods to reach a desired accuracy as we sweep the location of charge q1 on bar B. In order to do so, we revise the problem stated in Eq. 140 as
We solve this problem for the system described previously with body-body interaction picking the desired percentage errors as \(e^{V}_{desired}= e^{\mathbf {F}}_{desired}= e^{\mathbf {M}}_{desired} = \%1\), and \(e^{V}_{desired}= e^{\mathbf {F}}_{desired}= e^{\mathbf {M}}_{desired} = \%0.01\). Figures 14 and 15 show the values of (d/L)min versus the distance between CoM and CoCh using both approximation methods for two cases: \((\bar {\theta } = \pi /3,~\bar {L}_{0} = -\bar {L})\) and \((\bar {\theta } = \pi /3,~\bar {L}_{0} = \bar {L}/2)\), respectively. As we move q1 to the right side of the bar, the distance between the CoM and CoCh increases. As these two points separate more, it is observed that (d/L)min increases when we use CoM-based expansion (See curves with 
and 
in Figs. 14 and 15). However, (d/L)min decreases when we use CoCh-based expansion (See curves with 
and 
in Figs. 14 and 15). These figures also indicate that as we decrease the desired error, the deviation between (d/L)min using the CoM expansion and CoCh expansion significantly increases. Therefore, as the CoCh distances from the CoM, the expansion using the CoCh provides acceptable accuracy when the bodies are close to each other; however, this is not true for the CoM-based expansion. Furthermore, as it is shown in Fig. 15 due to the deviation of the CoM and CoCh of \(\bar {B}\), for a given percentage error, CoM and CoCh methods do not have the same (d/L)min when the CoM and CoCh of B coincide. It should be noted that similar to the particle-body system, the above problem is a conservative case in which we find (d/L)min to reach a desired accuracy for all orientations of B. However, if we want to reach a desired accuracy for a given orientation of B, the value of (d/L)min for either of these methods may drop or even become the same.
(d/L)min for different desired percentage errors as a function of the distance between CoM and CoCh for the system with \(\bar {L}_{0}=-\bar {L}\) and \(\bar {\theta } = \pi /3\). 
: CoCh-expansion with desired error %1, 
: CoM-expansion with desired error %1, 
: CoCh-expansion with desired error %0.01, 
: CoM-expansion with desired error %0.01
(d/L)min for desired percentage errors as a function of the distance between CoM and CoCh for the system with \(\bar {L}_{0}=\bar {L}/2\) and \(\bar {\theta } = \pi /3\). 
: CoCh-expansion with desired error %1, 
: CoM-expansion with desired error %1, 
: CoCh-expansion with desired error %0.01, 
: CoM-expansion with desired error %0.01
Conclusion
In this paper, we have derived closed-form approximations to the force function (or electrostatic potential) of a pair of charged spacecraft assuming either particle-body or body-body interactions. This is followed by the derivation of the second order approximation of the resultant force, and the corresponding moment about the center of mass (CoM) of the interacting spacecraft. These formulations can eventually be used in the simulation or analytical analysis of the behavior of two charged spacecraft. Unlike the previous approximations which use expansions about the CoM of each body, the presented method in this paper uses the center of charge (CoCh) to derive the approximations. We have first generated the particle-body and body-body second order approximations for the force function. Then using the gradient, we developed approximate force and the corresponding moment about the CoM of the body. Since CoCh has been used as the origin of the expansion, the resulting approximations have been expressed in terms of the entire charge of each body, the relative location of the centers of charge of the interacting bodies, and the quadrupole charge tensor (QCT) of each body about the corresponding CoCh. Shifting the origin of the expansion from the CoCh to the CoM, we have recovered the CoM-based approximations which have been presented in the literature. We have then used both CoM- and CoCh-based methods to compute the force function, force, and moment in particle-body and body-body examples. As it has been shown, the CoCh expansions are generally more accurate when the distance between the CoCh and the CoM is a significant fraction of the separation distance.
References
Bennett, T., Schaub, H.: Touchless electrostatic three-dimensional detumbling of large axi-symmetric debris. J. Astronaut. Sci. 62(3), 233–253 (2015)
Bennett, T., Stevenson, D., Hogan, E., McManus, L., Schaub, H.: Prospects and challenges of touchless space debris despinning using electrostatics. Adv. Space Res. 56(3), 557–568 (2015)
Gibson, W.C.: The Method of Moments in Electromagnetics. Chapman and Hall/CRC (2007)
Hogan, E.A., Schaub, H.: Collinear invariant shapes for three-spacecraft coulomb formations. Acta Astronaut. 72, 78–89 (2012)
Hughes, J., Schaub, H.: Appropriate fidelity electrostatic force evaluation considering a range of spacecraft separations. In: AAS/AIAA Spaceflight Mechanics Meeting (2016)
Hughes, J., Schaub, H.: Effects of charged dielectrics on electrostatic force and torque. In: Proc. 9th International Workshop on Satellite Constellations and Formation Flying. Boulder (2017)
Hughes, J., Schaub, H.: Rapid charged geosynchronous debris perturbation modeling of electromagnetic disturbances. In: AAS Spaceflight Mechanics Meeting. Napa Valley (2017)
Hughes, J., Schaub, H.: Spacecraft electrostatic force and torque expansions yielding appropriate fidelity measures. In: AAS Spaceflight Mechanics Meeting, pp. 5–9. San Antonio (2017)
Inampudi, R., Schaub, H.: Optimal reconfigurations of two-craft coulomb formation in circular orbits. J. Guid. Control Dyn. 35(6), 1805–1815 (2012)
Kane, T.R., Levinson, D.A.: Dynamics: Theory and Application. Mcgraw-Hill (1985)
Kane, T.R., Likins, P.W., Levinson, D.A.: Spacecraft Dynamics. Mcgraw-Hill (1983)
Laflin, J., Anderson, K.S.: A multibody approach for computing long-range forces between rigid-bodies using multipole expansions. J. Mech. Sci. Technol. 29(7), 2671–2676 (2015). https://doi.org/10.1007/s12206-015-0513-3
Laflin, J.J., Anderson, K.S., Khan, I.M., Poursina, M.: New and extended applications of the divide-and-conquer algorithm for multibody dynamics. J. Comput. Nonlin. Dyn. 9(4), 041004 (2014)
Lai, S.T.: Fundamentals of Spacecraft Charging: Spacecraft Interactions with Space Plasmas. Princeton University Press (2011)
Leach, A.R.: Molecular Modelling Principles and Applications, 2nd edn. Prentice Hall (2001)
Paul, S.N., Frueh, C.: Space debris charging and its effect on orbit evolution. In: AIAA/AAS Astrodynamics Specialist Conference, p. 5254 (2016)
Poursina, M.: Robust framework for the adaptive multiscale modeling of biopolymers. Ph.D. thesis, Rensselaer Polytechnic Institute Troy (2011)
Poursina, M., Anderson, K.S.: Long-range force and moment calculations in multiresolution simulations of molecular systems. J. Comput. Phys. 231(21), 7237–7254 (2012). https://doi.org/10.1016/j.jcp.2012.06.041
Poursina, M., Anderson, K.S.: Efficient coarse-grained molecular simulations in the multibody dynamics scheme. In: Fisette, P., Samin, J.C. (eds.) Multibody Dynamics, Computational Methods in Applied Sciences, vol. 28, pp 147–172. Springer (2013)
Poursina, M., Anderson, K.S.: An improved fast multipole method for electrostatic potential calculations in a class of coarse-grained molecular simulations. J. Comput. Phys. 270, 613–633 (2014)
Schaub, H., Junkins, J.L.: Analytical mechanics of space systems. AIAA (2003)
Schaub, H., Moorer, D.F.: Geosynchronous large debris reorbiter: Challenges and prospects. J. Astronaut. Sci. 59(1–2), 161–176 (2012)
Stevenson, D., Schaub, H.: Multi-sphere method for modeling spacecraft electrostatic forces and torques. Adv. Space Res. 51(1), 10–20 (2013)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix:
Appendix:
In this appendix, we prove that for body B the following resultant force which is computed based on Eq. 13,
can be evaluated by using the gradient of the force function with respect to R.
Using (14), the gradient of the force function of the entire body with respect to R is computed as
Based on the geometry shown in Fig. 1, one can compute ∇Rr′ as
Knowing that \(\mathbf {\nabla }_{\mathbf {R}} \mathbf {R} = \mathcal {U}\), Eq. 144 results in
Using the result of Eq. 145, one can simplify (146) as
which is exactly the same as Eq. 142.
Rights and permissions
About this article
Cite this article
Poursina, M., Butcher, E.A. Electrostatic Force and Moment Approximations of Coulomb Charged Spacecraft Based on Center of Charge. J Astronaut Sci 67, 829–862 (2020). https://doi.org/10.1007/s40295-019-00186-z
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40295-019-00186-z