Solar Sail Transfers and Trajectory Design to Sun-Earth L₄, L₅: Solar Observations and Potential Earth Trojan Exploration

Abstract

The Sun-Earth triangular Lagrange point, L₅, offers an ideal location to monitor the space weather. Furthermore, L₄, L₅ may harbor Earth ‘Trojan’ asteroids and space dust that are of significant interest to the scientific community. No spacecraft has, thus far, entered an orbit in the vicinity of Sun-Earth triangular points in part because of high propellant costs. By incorporating solar sail dynamics in the model representing CR3BP, the concept of a mission to L₄, L₅ can be re-evaluated and the total ΔV can be reconsidered. A solar sail is employed to increase the energy of the spacecraft and deliver the spacecraft to an orbit about an artificial Lagrange point by leveraging solar radiation pressure and, potentially, without any insertion ΔV.

Introduction

Successfully harnessing the solar radiation pressure (SRP) from the Sun can potentially offer unique maneuvering capability to a spacecraft equipped with solar sails. The concept of solar sailing relies on photons from the Sun to propel the spacecraft through the space environment by providing the sail-based spacecraft with continuous acceleration. In 2015, the US-based Planetary Society launched and successfully unfurled its 32 m² LightSail. The sail-craft was able to demonstrate the capability to successfully deploy the sail. Success of JAXA’s IKAROS mission, along with several small to mid-sized solar sail mission concepts, have renewed interest in solar sailing [26, 36].

Scientific Interest

With the launch of the International Sun/Earth Explorer 3 (ISEE-3) in 1978, the near vicinity of the Sun-Earth L₁ libration point has been the preferred location for satellites to monitor space weather. However, as the satellite is positioned along the Sun-Earth line, observations of Coronal Mass Ejections (CMEs) directed towards the Earth are not feasible due to occultation [34]. In addition, the observation of Co-rotating Interaction Regions (CIRs) from the vicinity of L₁ is not advantageous since the time interval between observations and the arrival at Earth is not sufficient to allow preventative measures to minimize the damage. In recent years, the Sun-Earth L₅ region has been investigated for an Earth-Affecting Solar Cause Observatory (EASCO) [10]. The triangular point, L₅, supplies an ideal location for monitoring the space weather away from the Sun-Earth line and aids in efficient detection of CMEs and CIRs [34]. Early detection offers 3-5 days advanced warnings of space weather that can potentially cause severe damage to telecommunications on Earth.

In addition to providing a unique angle to monitor the Sun and assess space weather, the equilateral Lagrange points, L_4,5, may harbor asteroids and space dust that are of significant interest to the scientific community. In 2010, NASA’s Wide-field Infrared Survey Explorer (WISE) spacecraft identified the first Earth Trojan Asteroid (2010 TK₇) in the vicinity of L₄ [5]. A near-Earth Asteroid, 2010 SO₁₆, is currently in the vicinity of Sun-Earth L₅ and is possibly a horseshoe companion of the Earth [4]. The discoveries have opened a window for possible missions and scientific exploration of the bodies themselves as well as the region in the vicinity of the triangular Lagrange points in search of additional Earth Trojans at both L₄ and L₅. The composition of Earth Trojan asteroids can potentially be similar to the rocks that formed the Earth about 4.6 billion years ago. Examination of such bodies - those from the time of the birth of the solar system - can shed new light on the composition of the Earth during its origin and early stages of development.

Objectives

The goal of this investigation is an exploration of the design space for trajectories from a parking orbit about Earth to the vicinity of artificial triangular Lagrange points using a solar sail. Prior to incorporating the sail dynamical model in the Circular Restricted Three-Body Problem (CR3BP), a set of solutions are derived based on the trajectory requirements. Initial solutions are computed that incorporate multiple ΔVs to depart the parking orbit around Earth, shift onto a manifold associated with a periodic orbit near a collinear libration point; the path is directed towards a desired destination and insert into an orbit in the vicinity of the equilateral Lagrange point, L₄ or L₅. Initial investigation aims at a better understanding of the behavior of a sail-based spacecraft and then leveraging the solar radiation pressure to deliver the spacecraft to its destination. The analysis addresses the goal of this investigation through the following objectives:

• 1. Explore the design space by computing a large set of L₁ and L₂ orbits and their associated manifolds.

• 2. Exploit orbits based on their energy and manifolds that reach the desired destination, i.e., vicinity of L₄ or L₅.

• 3. Incorporate solar sails to maneuver the spacecraft and increase the energy level by leveraging SRP.

• 4. Investigate the departure ΔV from an Earth parking orbit.

By investigating the natural dynamics and flow that exists within the context of the CR3BP, a preliminary trajectory is designed to depart the vicinity of the Earth, shift onto a manifold towards the desired target and enter the orbit in the vicinity of L_4,5. The selection of a manifold is based on the target Lagrange point, i.e., L₄ or L₅, energy level of the desired final orbit around the equilateral Lagrange point and the time of flight (TOF) to reach the vicinity of the target along the manifold. An initial departure ΔV is implemented to depart the parking orbit and leverage a stable/unstable manifold. Intermediate ΔV(s) can raise the energy level of the trajectory or serve as a trajectory corrective maneuver. Once the spacecraft reaches the vicinity of the target destination, a final ΔV may be necessary to insert into an orbit about the equilateral Lagrange point. The complete end-to-end trajectory acts as an initial guess for a corrections process that incorporates a solar sail force model into the circular restricted three-body problem (SS-CR3BP).

Incorporating the solar sail in the CR3BP potentially lowers the ΔV requirements by leveraging the solar radiation pressure. As a part of this effort, the solar sail is employed to increase the energy of the spacecraft in lieu of energy raising maneuvers and to deliver the spacecraft to an artificial triangular Lagrange point without any insertion ΔV. Once the corrected final path is achieved, the trajectory is optimized to lower the departure ΔV from the Earth parking orbit.

Previous Contributions

Trajectory and Mission Design to Sun-Earth L ₄, L ₅

In recent years, trajectories to Sun-Earth equilateral Lagrange points have been the focus of a number of applications. With L₅ as an ideal location for early detection and observation of potentially hazardous space weather and the discovery of the first Earth Trojan Asteroid, 2010 TK7, in the vicinity of L₄, the Sun-Earth triangular Lagrange points have gained interest as candidates for future space missions. The STEREO (Solar Terrestrial Relations Observatory) mission, consisting of two nearly identical spacecraft, was launched in 2006. To enable stereoscopic imaging of the Sun, one spacecraft orbits ahead of Earth and the other trails behild. The two spacecraft flew past Sun-Earth L₄ and L₅, respectively, without entering any stable orbit at either Lagrange points. Detailed analysis of an L₅ mission to observe the Sun and assess the space weather was completed by Lo, Llanos and Hintz [20]. In 2011, Llanos, Miller and Hintz continued this work and provided navigational analysis for a mission to L₅ [19]. Gopalswamy et al. [11] proposed the Earth Affecting Solar Cause Observatory (EASCO) mission concept that detailed the scientific issues and instruments necessary to monitor and understand the CMEs and CIRs. Further analysis from EASCO was carried out at the Mission Design Laboratory (MDL), NASA Goddard Space Flight Center and is aimed towards observing the solar maximum in the year 2025 [10]. The results of the MDL study determined that the EASCO mission concept is very achievable as a single observatory carrying 10 science instruments. The authors state that the L₅ point is the next logical location for obtaining solar observation of CMEs that direct solar energetic particles towards the Earth and cause geomagnetic storms. In the following year, Llanos, Miller and Hintz extended their work to incorporate trajectory design to both L₄ and L₅ in the Sun-Earth System [17]. The goal was a strategy to study the Sun’s magnetic field from a vantage point near L₅ and search for Earth Trojan Asteroids in the vicinity of L₄ and L₅.

With the discovery of the Earth Trojan 2010 TK7, the scientific community is intrigued with the idea of additional, smaller asteroids, and space dust in the vicinity of the Sun-Earth triangular Lagrange points. The possibility of investigating the bodies that may be similar in composition to the rocks that formed the Earth is also of interest. Dvorak et al. completed an extensive investigation of the orbit of 2010 TK7 to better understand the motion of bodies in the vicinity of triangular Lagrange points [7]. Based on their analyses, the authors predict the existence of additional ‘interesting objects’ in the vicinity of the L₄ or L₅ equilibrium points. In 2013, Llanos et al. also explored powered heteroclinic and homoclinic connections between the Sun-Earth Lagrange points L₄, L₅ and the quasi-satellite orbit about Earth [18]. Such a transfer trajectory can potentially transfer sample material from the triangular points to the vicinity of the Earth. A team of scientists from NASA Johnson Space Center presented their work on a mission concept at the 46^th Lunar and Planetary Science Conference, 2015 proposing an in-situ science and exploration mission to survey the L₄ and L₅ regions in the Sun-Earth system [16].

Solar Sails

Exploring solar sails to move throughout the solar system is based on a dynamical concept for harnessing the energy carried by photons from the Sun in the form of momentum. Although serious planning to explore the solar system using solar sails has only gained momentum in last few decades, the concept of harnessing solar radiation pressure (SRP) was first studied in 1873 by James Clerk Maxwell [23]. In 2010, the first spacecraft to demonstrate solar radiation pressure as a source of propulsion in flight was launched by the Japanese Space Agency, JAXA. The solar sail spacecraft, Interplanetary Kite-craft Accelerated by Radiation Of the Sun (IKAROS), is a square sail 20 m in diameter and 7.5 μm thick created from polyimide film. The IKAROS sail-craft successfully demonstrated both a propulsive force of 1.12 mN and attitude control capabilities [25]. Thus, IKAROS delivered a pathway for further development in the field of solar sail technology.

On May 20, 2015, the Planetary Society successfully launched LightSail–1 (formerly LightSail–A) as a small technology demonstrator aboard an Atlas V rocket from Cape Canaveral Air Force Station, Florida. The spacecraft successfully deployed its 5.6 m x 5.6 m solar sail on June 7, 2015 and the test flight was declared a success [6]. LightSail–2 is currently scheduled to be launched as a secondary payload aboard the SpaceX Falcon Heavy carrying US Air Force Space Test Program (STP-2) payload no earlier than October 30, 2018. LightSail–2 launch aims at further enhancing and demonstrating the sail-based control strategy. Following deployment, SRP will be leveraged to raise orbit apogee and increase orbital energy of the sail-craft. It is expected that LightSail–3 will follow with a proposed mission that incorporates an insertion into an orbit near the Sun-Earth Lagrangian point, L₁. LightSail–3 will supply early detection and warning of geomagnetic storms capable of damaging power and communications systems on Earth [3]. Thus, the recent success and rejuvenation of interest in harnessing the potential of a solar sail has accelerated the development of the technology. The success of the IKAROS mission and demonstration by LightSail–A are a significant breakthrough and, thus, interest continues in further testing and validating of solar sail technology.

Considerable efforts have focused on solar sail behavior in the vicinity of the artificial collinear Lagrange points, L₁ and L₂. Baoying and McInnes designed new orbits associated with these points by incorporating solar sails in their dynamical model [1]. Their work applied knowledge of accurate approximation of ‘halo’ orbits around the equilibrium points [15]. McInnes and Simmons focused on Sun-centered halo-type trajectories above the ecliptic plane aided by solar sails [24]. In 2012, Sood further explored the solar sail applications to widen the design space in the vicinity of artificially displaced L₁ Lagrange points. Samples of offset, hovering periodic orbits are demonstrated above a displaced L₁ equilibrium point and three-dimensional transfers between halo orbits are constructed to exhibit sailing capabilities [31]. Solar sails have also been proposed for highly non-Keplerian orbits high above the ecliptic plane since solar sails are capable of supplying a continuous propulsive force in the form of SRP from the Sun [35]. Recent work in the Earth-Moon system aims at investigating the behavior in the vicinity of displaced collinear Lagrange points and producing solar sail periodic orbits in the CR3BP [13, 30]. Design of solar sail trajectories with applications to continuous surveillance of the lunar south pole have also been proposed [26, 36]. Research in both the Sun-Earth and Earth Moon system have primarily been focused in the vicinity of the displaced collinear Lagrange points or in the form of hovering orbits close to the primaries.

The capabilities of solar sails to reach the triangular Lagrange points have not yet been exploited for flight. In addition, no spacecraft has reached an orbit about L₄ or L₅ due to high propellant costs associated with transfer and insertion into an orbit about an equilateral Lagrange point [20]. But, solar sails can potentially deliver a viable mission concept by harnessing SRP for transfer trajectories and insertion maneuvers around artificial L₄ or L₅ points. In addition to demonstrating the technology, trajectory design to triangular points can aid in placing the spacecraft at locations from where space weather may be monitored and advance the search for Earth Trojans as well as offer a platform to sample space dust.

Background: Circular Restricted Three-Body Problem

The motion of an infinitesimal mass, P₃, under the gravitational influence of the two larger primaries, P₁ and P₂, is investigated by examining the classical Circular Restricted Three-Body Problem (CR3BP). Casting the problem within the context of the CR3BP offers the essential features of the motion with some mathematical advantages. A rotating frame, R, is defined to be consistent with the orbital motion of the primaries. The dextral, orthogonal set of unit vectors associated with the rotating frame is denoted as $\hat {x}$; $\hat {y}$; $\hat {z}$ where $\hat {x}$ is always directed from P₁ to P₂. The position vectors corresponding to the locations of the three bodies, P₁, P₂ and P₃, relative to the barycenter, are defined as r₁, r₂ and r₃, respectively. The position vector of P₃ relative to P₁ and P₂ can be expressed as r₁₃ = r₃ - r₁ and r₂₃ = r₃ - r₂, respectively, as represented in Fig. 1. Characteristic quantities, i.e., mass, length, and time, are defined to generalize the governing differential equations through nondimensionalization such that

$$\begin{array}{@{}rcl@{}} m^{*} &= & m_{1} + m_{2} \end{array} $$

(1)

$$\begin{array}{@{}rcl@{}} l^{*} &= & r_{1} + r_{2} \end{array} $$

(2)

$$\begin{array}{@{}rcl@{}} t^{*} &= & \sqrt{\frac{l^{*3}}{\tilde{G} m^{*}}} \end{array} $$

(3)

where m₁ and m₂ are the masses of the two primaries, P₁ and P₂, respectively, r_i is the distance between the system barycenter and the two primaries and $\tilde {G}$ is the dimensional universal gravitational constant. Nondimentional time and relative position vectors are then expressed in the form [32]

$$\begin{array}{@{}rcl@{}} \tau &= & \frac{t}{t^{*}} \end{array} $$

(4)

$$\begin{array}{@{}rcl@{}} \boldsymbol{\rho} &= & \frac{\boldsymbol{r}_{3}}{l^{*}} = x\hat{x} + y\hat{y} + z\hat{z} \end{array} $$

(5)

$$\begin{array}{@{}rcl@{}} \boldsymbol{d} &= & \frac{\boldsymbol{r}_{13}}{l^{*}} = (x + \mu)\hat{x} + y\hat{y} + z\hat{z} \end{array} $$

(6)

$$\begin{array}{@{}rcl@{}} \boldsymbol{r} &= & \frac{\boldsymbol{r}_{23}}{l^{*}} = (x -1 + \mu)\hat{x} + y\hat{y} + z\hat{z} \end{array} $$

(7)

$$\begin{array}{@{}rcl@{}} \mu &= & \frac{m_{2}}{m^{*}} \end{array} $$

(8)

where ρ, d, r represent the nondimensional position vectors of P₃ relative to the barycenter, P₁ and P₂, respectively, and μ is the nondimentional mass ratio.

Fig. 1

Geometrical definitions in the circular restricted three-body problem

Within the context of the CR3BP, five particular solutions exist in the rotating frame as depicted in Fig. 2 [8]. These equilibrium solutions, also termed the libration or Lagrangian points, were first recognized by Joseph-Louis Lagrange in 1772 while investigating the three-body problem [32]. In the 3BP, L₁, L₂, and L₃ are the collinear libration points, whereas, L₄ and L₅ are termed as ‘equilateral’ or ‘triangular’ Lagrange points since they form an equilateral triangle with the Sun and the Earth at the other two vertices. In a physical sense, the five particular solutions represent the locations where the combined influence from the two primaries, P₁ and P₂, on the third body, P₃, of negligible mass, are balanced within the context of the rotating frame.

Fig. 2

Lagrangian points in the circular restricted three-body problem

Periodic Orbits, Invariant Manifolds and Jacobi Constant

Several fundamental periodic solutions exist in the vicinity of the equilibrium points that demonstrate their usefulness in trajectory and mission design. Families of planar and three-dimensional orbits have been investigated over the past few decades [2, 12, 15]. The Lyapunov family of planar orbits in the vicinity of L₁ and L₂ Lagrange points appears in Fig. 3a. Although the families comprise of infinite number of periodic orbits, only a finite number of members are illustrated in the figures. In addition to the sets of symmetric periodic orbits, numerous asymmetric periodic orbits are also known to exist in the CR3BP [9, 12, 22]. A corrections algorithm is modified to produce asymmetric periodic orbits in the vicinity of L₄ and L₅ equilateral Lagrange points [12, 27]. A set of short period orbits in the vicinity of L₄ and L₅ appear in Fig. 3b. Note that the families of periodic orbits illustrated in Fig. 3 are in the Sun-Earth rotating frame.

Fig. 3

Sun-Earth L₁, L₂ Lyapunov orbits and L₄, L₅ short-period orbits

In the CR3BP, the periodic orbits in the vicinity of the Lagrange points can either be stable or unstable. The stability characteristics of an orbit are derived from the monodromy matrix, M, that is generated by integrating the state transition matrix, Φ(τ_f, τ₀), for one orbital period, P, i.e.,

$$ M = {\Phi}(P,\tau_{0}) $$

(9)

The monodromy matrix is a real matrix that possesses three reciprocal pairs of eigenvalues, λ_i where i = 1 : 6. The dynamical stability information for the periodic orbit is supplied by the nature of the eigenvalues associated with the monodromy matrix. For any periodic orbit, the monodromy matrix possesses at least one unit eigenvalue and produces a reciprocal of unity to complete the pair, i.e., λ_1,2 = 1. For a complex eigenvalue with magnitude equal to unity, the reciprocal is subsequently equal to the complex conjugate, i.e., λ_3,4 = a ± ib . Lastly, there is a reciprocal pair of real eigenvalues associated with the stable and unstable modes, i.e., $\lambda _{6} = \frac {1}{\lambda _{5}}$ (other than unity). In case of stable periodic orbits, i.e., family of short-period orbits shown in Fig. 3a, stable and unstable modes do not exist. The eigenvalues of the monodromy matrix associated with the stable periodic orbits are either pairs of unity or complex conjugates. The manifold trajectory is generated by exciting a point on the orbit, $\boldsymbol {X}^{*}_{i}$, along the 6-D normalized eigenvector, ν, associated with the stable or unstable mode, i.e.,

$$ \boldsymbol{X} = \boldsymbol{X}^{*}_{i} \pm d\boldsymbol{\nu} $$

(10)

where d is the step size along the selected stable or unstable eigenvector. The step size is system-dependent to avoid violating the linear approximation. In the case of Sun-Earth CR3BP, a typical value of d = 300 km is used as the step size.

A member of the L₁ Lypunov family of orbits is illustrated in Fig. 4a. For visualization purposes, the Earth has been scaled to 20 times its actual size. The stability analysis revealed the stable/unstable eigenvalues of the monodromy matrix associated with the orbit. Leveraging the stable and unstable eigenvectors, invariant manifold structures exist that grant passage into and away from the associated orbit, respectively. Stable and unstable manifolds are computed by perturbing a state along the direction of stable or unstable eigenvector. Such perturbations result in a set of stable and unstable manifolds that exhibit asymptotic flow surface to and from the periodic orbit. A subset of unstable manifolds associated with the Sun-Earth L₁ Lyapunov orbit in Fig. 4a appears in Fig. 4b as depicted in magenta. The unstable manifolds asymptotically depart the Lyapunov orbit and are propagated forward in time for 1800 days (approximately 5 years). The forward propagation demonstrates their flow approaching the two equilateral Lagrange points and the associated subset of short-period family of orbits about L₄ and L₅ are illustrated in purple. To construct low energy transfers, the invariant manifolds form an important tool in the computation and design of complex trajectories. However, it is important to note that the L₄, L₅ short-period orbits lack stable and unstable eigenvalues, thus, inhibiting the existence of manifold trajectories that grant passage into and away from the short-period orbits [29]. Nonetheless, the unstable manifolds associated with the orbit illustrated in Fig. 4a can be leveraged to arrive in the vicinity of the target short-period orbit.

Fig. 4

Periodic orbits and unstable manifolds of the Lyapunov orbit

Within the context of the CR3BP, a unique known integral of motion, i.e., the Jacobi integral, is defined [32]. The Jacobi constant is a scalar and appears as an energy-like quantity for a particular orbit. Analysis employing the Jacobi constant is an effective approach to compute boundaries, orbits, trajectories and transfers [31]. It also forms an important tool in maintaining accuracy in the numerical integration process. However, the addition of other external forces may eliminate the constant, yet it still provides a tool to gauge the changes in the energy-like quantity due to additional forces. The direction in which the Jacobi constant changes can potentially offer an insight into the pros and cons of additional force, thus, making it possible to exploit the force in delivering the spacecraft to its final destination and energy level.

Solar Sail Dynamical Model

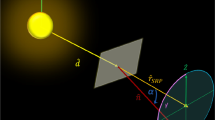
The concept of harnessing the energy carried by photons from the Sun in the form of momentum extends the solar sail model into the CR3BP framework. In the development of a force model, a mathematical description of the direction of force relative to the sail orientation is a key kinematic relationship. The quantity of photons encountered by the solar sail is directly related to the sail orientation with respect to the direction of photon flow. Thus, the orientation of the sail governs the acceleration produced on the solar sail by the incident and reflected photons. A schematic representation appears in Fig. 5. The momentum transfer from the incident and reflected photons acting on a sail results in a net force that continuously accelerates the vehicle. The reference frame of interest is formed from the unit vector, $\hat {z}$, the direction that remains fixed in both the inertial and the rotating frame, as well as the unit vector, $\hat {d}$, along the Sun-sail line. The angle α represents the angle between the Sun-sail unit direction, $\hat {d}$, and the direction vector parallel to the surface normal of the sail, $\hat {n}$. The angle α is also represented in Fig. 5; α is frequently denoted as the cone angle or the nutation angle of the solar sail relative to the Sun-sail line. The second angle in Fig. 5 is represented as the angle γ. The angle γ is defined as the angle between $\hat {k}$ and the projection of $\hat {n}$ onto the plane spanned by $\hat {k}$ and $\frac {\hat {d} \times \hat {z}}{|\hat {d} \times \hat {z}|}$. The unit direction vector $\hat {k}$ is defined as

$$ \hat{k} = \frac{(\hat{d} \times \hat{z}) \times \hat{d}}{|(\hat{d} \times \hat{z}) \times \hat{d}|} $$

(11)

In a sense, γ defines the angle by which the plane spanned by the unit vectors, $\hat {d}$ and $\hat {n}$ has precessed; thus, the angle γ is also the precession angle or the clock angle. Based on the currently available technology, the maximum rate of rotation for attitude control is equal to 0.02 deg/s for a three-axis spacecraft equipped with sails that use sail panel rotations [37]. This attitude control rate is referenced to offer insight into the relative time that is required for a desired attitude maneuver. It is vital to note that if the sail orientation angles, α and γ, remain constant relative to the Sun in the rotating frame, the orientation will change in the inertial frame. Thus, the hardware must continually reorient the sail with respect to the inertial frame. To maintain the orientation of a sail relative to the Sun in the inertial frame, the sail must reorient at approximately one degree per day to maintain the orientation relative to the Sun over a one-year period.

Fig. 5

Solar sail orientation angle definitions

The momentum transfer from the incident and reflected photons acting on a sail result in a net force that continuously accelerates the vehicle. The derivation of the acceleration due to solar radiation pressure is based on three critical assumptions. For the current analysis, it is assumed that the solar sail is ideal and flat with a perfectly reflecting surface, i.e., there is no absorption or refraction but only reflection due to the incident photons. Thus, all the photons experience perfectly elastic collisions and “bounce off” the surface of the solar sail. It is also assumed that the source of photons is the primary, P₁, the Sun. The flow of incident photons is parallel to the Sun-sail line and the resultant force is parallel to the sail surface normal. Considering the assumptions, the solar sail acceleration is expressed as [23],

$$ \boldsymbol{a}_{sail} = \epsilon\frac{2P_{0}}{\sigma}\cos^{2}\alpha \text{ }\hat{n} $$

(12)

where 𝜖 is the efficiency of the sail that typically ranges between 85% - 90% and P₀ is the solar radiation pressure at the distance of 1 AU from the source, i.e., the Sun. In Eq. 12, the load factor, σ, usually expressed in [g/m²], is defined as the ratio of the total mass supported by the sail to the total surface area of the sail. The unit vector in the direction parallel to the surface normal of the sail is represented by vector $\hat {n}$ and is a function of the sail angles, α and γ. A new quantity is also defined as the solar sail characteristic acceleration, a^∗. The characteristic acceleration is the acceleration at 1 AU and, for the particular orientation, such that the sail angle is equal to zero, i.e., α = 0^o [23], or

$$ a^{*} = \epsilon\frac{2 \times P_{0}}{\sigma} = \epsilon\frac{2 \times 4.56}{\sigma} \text{ } [\text{mm/s\(^{2}\)}] $$

(13)

The characteristic acceleration, a^∗, serves as a reference value for comparison with general solar sail accelerations. Consistent with the definition of σ, a characteristic mass-to-area ratio, σ ∗, is defined, such that, equal and opposite force is produced due to solar radiation pressure at 1 AU, i.e.,

$$ \sigma^{*} = \epsilon\frac{2 \times P_{0}\text{ }r_{13}}{\tilde{G}m_{1}} $$

(14)

Recall that $\tilde {G}$ is the dimensional universal gravitational constant; the quantity r₁₃ is the dimensional scalar distance to the third body, i.e., the solar sail spacecraft, from the first primary, P₁, the Sun; and, m₁ is the mass of the first primary, P₁. The introduction of the sail lightness parameter, β, is appropriate as

$$ \beta = \frac{\sigma^{*}}{\sigma} $$

(15)

The sail lightness parameter, also frequently denoted the sail loading parameter, is the ratio of the acceleration due to the solar radiation pressure to the classical solar gravitational acceleration[23]. Thus, the solar sail acceleration expression in Eq. 12, is set equal to one for efficiency, i.e., 𝜖 = 1, and is rewritten as

$$ \boldsymbol{a} = \beta\frac{\tilde{G}m_{1}}{r_{13}^{2}} \cos^{2} \alpha \text{ }\hat{n} $$

(16)

Now, rewriting Eq. 16 in terms of nondimensional quantities

$$ \ddot{\boldsymbol{r}}_{Sail} = \beta\frac{(1 - \mu)}{d^{2}}\cos^{2} \alpha \text{ }\hat{n} $$

(17)

where $\ddot {{r}}_{Sail}$ is the nondimensional vector acceleration of the solar sail due to solar radiation pressure. Recall that d is the nondimensional distance of the solar sail from the Sun. The model for the nondimensional solar sail acceleration in Eq. 17 is now easily included to augment the equations of motion in the classical CR3BP. Thus, a mathematical model that incorporates the solar sail dynamics in the CR3BP can be expressed in a condensed form of the equations of motion for a spacecraft equipped with solar sail and are written as

$$\begin{array}{@{}rcl@{}} \ddot{x} &= & 2\dot{y} + {\Omega}^{*}_{x} + a_{Sail-x} \end{array} $$

(18)

$$\begin{array}{@{}rcl@{}} \ddot{y} &= & -2\dot{x} + {\Omega}^{*}_{y} + a_{Sail-y} \end{array} $$

(19)

$$\begin{array}{@{}rcl@{}} \ddot{z} &= & {\Omega}^{*}_{z} + a_{Sail-z} \end{array} $$

(20)

where ${\Omega }^{*}_{i}$ are the partials of the pseudo-potential, Ω^∗, defined as

$$ {\Omega}^{*} = \frac{1 - \mu}{d} + \frac{\mu}{r} + \frac{1}{2}(x^{2} + y^{2}) $$

(21)

and a_Sail−x, a_Sail−y, and a_Sail−z are the components of the nondimensional solar sail acceleration expressed in the rotating frame [31]. The dynamical model represented in Eqs. 18, 19, and 20 is nonlinear and coupled, thus, no closed-form solution exists.

Solar Sail Trajectory Design

Spacecraft Trajectory Design in the Circular Restricted Three-Body Problem (CR3BP)

Investigating the design space that meets the mission and science requirements constitutes an integral part of the trajectory design process. Prior to incorporating the solar sail in the trajectory design process, a good initial guess is desirable. The process requires exploring the design space, i.e., the solution space that exists in the vicinity of the libration points. Each periodic orbit about the libration point has a Jacobi constant, the only integral of motion known to exist in the CR3BP. The manifolds associated with the libration point orbits provide natural flow to and from the orbit. The design strategy takes into account the following variables: (1) the Jacobi constant of the initial and final orbit, (2) the unstable manifold associated with the initial departure orbit, (3) the departure altitude relative to the Earth, (4) the insertion location along the final arrival orbit, and (5) the number of revolutions of the final orbit. In this section, intuitive search strategy is outlined by exploring the available design space. Flow away from the orbit, along the manifolds, passing the vicinity of the Earth and departing towards the final destination are investigated. A baseline discontinuous trajectory is formulated as an initial guess for differential corrections algorithm.

Selection Criteria – Design Space

The trajectory design process is initiated with the selection of an L₁ periodic orbit based on the Jacobi value of the final desired orbit. However, the orbit selection is not a required step but aids in exploiting possible low cost transfer options that may exist as the two orbits are of similar energy level. Jacobi values corresponding to a subset of L₁, L₂ Lyapunov family and L₅ short period orbits are apparent in Fig. 6. Figure 6 shows that, in general, the L₅ short period orbits (green) are of higher energy (lower Jacobi value) compared to the subset of L₁ and L₂ Lyapunov family of orbits (red and blue, respectively). For preliminary design analysis, a final orbit in the vicinity of L₅ is selected such that the Jacobi constant of the short period orbit is similar to that of the L₁ and L₂ Lyapunov orbits. Thus, orbits corresponding to a Jacobi value of 2.99995 are selected. In Fig. 7a, L₁ and L₂ Lyapunov orbits are depicted relative to the Earth in red and blue, respectively. Though it may visually appear, the two orbits are not mirror images (equal size) of each other. L₅ short period orbit for the same Jacobi value of 2.99995 is illustrated in Fig. 7b. Note that the size of the L₅ short period is two orders of magnitude greater than that of the L₁ and L₂ Lyapunov orbits, though the period of all three orbits is close to 1 year.

Fig. 6

Jacobi values for a subset of L₁ and L₂ Lyapunov family with subset of L₅ short period orbits. The “reference number” is only a place holder for orbits with varying Jacobi values

Fig. 7

L₁, L₂ Lyapunov orbits and L₅ short period orbit for Jacobi value of 2.99995

Trajectory Design Options

Continuing the design process, dynamical properties of manifolds are exploited. The Jacobi value associated with the manifolds remains conserved and possesses the same value as that of the orbit within the rotating frame. Employing manifolds to locate transfer option opens a window to depart from a parking orbit onto a manifold of either L₁ or L₂ Lyapunov orbit and reach the vicinity of L₄ and L₅ to lower the mission cost. For each triangular Lagrange point, four possible transfer options are briefly described that may vary based on the time of flight, ΔV requirements or the overall scientific goal of the mission. Transfer options to L₄

• L₁ unstable manifold to L₄: spacecraft departs from Earth parking orbit along L₁ unstable manifold to arrive in the vicinity of final destination orbit about L₄.

• L₁ stable manifold to L₁ unstable manifold to L₄: spacecraft departs from Earth parking orbit along L₁ stable manifold towards the L₁ Lyapunov orbit. The spacecraft may get into an orbit about L₁ to carry out scientific experiments before departing along the unstable manifold towards its final destination orbit about L₄.

• L₂ unstable manifold to L₄: spacecraft leaves the parking orbit around the Earth along the unstable manifold associated with the L₂ orbit for final destination orbit about L₄.

• L₂ stable manifold to L₂ unstable manifold to L₄: spacecraft departs the Earth parking orbit along L₂ stable manifold towards the L₂ Lyapunov orbit. Similar to option two, the spacecraft may get into an orbit about L₂ to carry out scientific experiments before departing along the unstable manifold towards its final destination orbit about L₄.

Similarly, exploiting the Sun-Earth L₁ and L₂ Lyapunov orbit manifolds, trajectory design options to the vicinity of second triangular Lagrange point, L₅, are listed below. Transfer options to L₅

• L₁ unstable manifold to L₅: spacecraft departs from Earth parking orbit along L₁ unstable manifold to arrive in the vicinity of final destination orbit about L₅.

• L₁ stable manifold to L₁ unstable manifold to L₅: spacecraft departs from Earth parking orbit along L₁ stable manifold towards L₁ Lyapunov orbit. The spacecraft may get into an orbit about L₁ to carry out scientific experiments before departing along the unstable manifold towards its final destination orbit about L₅.

• L₂ unstable manifold to L₅: spacecraft leaves the parking orbit around the Earth along the unstable manifold associated with the L₂ orbit for final destination orbit about L₅.

• L₂ stable manifold to L₂ unstable manifold to L₅: spacecraft departs the Earth parking orbit along L₂ stable manifold towards L₂ Lyapunov orbit. The possibility exists to station the spacecraft in an orbit about L₂ to carry out scientific experiments before departing along the unstable manifold towards its final destination orbit about L₅.

The trajectory design options listed in “Trajectory Design Options” are summarized in Fig. 8. Thus, Sun-Earth Lyapunov manifolds are leveraged to investigate potential trajectory design options to deliver the spacecraft from the vicinity of the Earth to an orbit around triangular Sun-Earth Lagrange points.

Fig. 8

A summary of trajectory design options listed in “Trajectory Design Options”

Differential Corrections and Baseline Trajectory

Exploiting the fundamental solutions (libration point orbits, stable/unstable manifolds) of the CR3BP, a baseline trajectory is constructed that acts as an initial guess in the trajectory design process. The initial guess, a discontinuous trajectory, encompasses the following arcs in the design process: (1) parking orbit about Earth, (2) stable/unstable or a combination of the two manifolds, (3) arrival at the destination orbit, and (4) insertion into final orbit about the equilateral Lagrange point.

As an example of the trajectory design process, consider the L₁ Lyapunov orbit and the L₅ short period orbit depicted in Fig. 7a and b, respectively. Recall, the two orbits are of the same Jacobi value of 2.99995. Thus, the unstable manifold that originates from the L₁ Lyapunov orbit and is propagated until it reaches the vicinity of the destination L₅ short period orbit is of the same energy level as the two orbits. Initially, the spacecraft is stationed in a parking orbit around the Earth. The selection of departure altitude plays an important role in the trajectory design process. As the goal of the work is to incorporate solar sail in the final model, it is desirable to depart from an altitude higher than 800 km. At the altitude of 800 km, the solar radiation pressure and the atmospheric drag are equal. Thus, for the sail to operate efficiently, the recommended altitude is between 800 to 1000 km [38]. In this formulation, a circular Earth parking orbit with an altitude of 1000 km is selected. At the departure location, ΔV is performed to transfer the spacecraft from the parking orbit onto the L₁ orbit’s unstable manifold. The manifold is propagated until it reaches the vicinity of destination short period orbit about L₅. In the example presented with no sail, a final ΔV is permitted to get into the final orbit. Thus, the initial guess to the corrections scheme allows performing two ΔVs to deliver the spacecraft from the Earth parking orbit into an orbit about the L₅ triangular Lagrange point.

Baseline trajectory design is accomplished through the application of a differential corrections scheme to a two-point boundary value problem (2PBVP). Algorithm based on generalized Newton’s Method is employed that involve constraints and free variables. A multiple shooting scheme is applied to reduce the effect of local sensitivities by distributing them among the individual arcs, increasing the accuracy and incorporating relative ease with which constraints can be placed along the trajectory and free variables can be selected. However, integration time is allowed to vary along each segment, thus, resulting in variable-time multiple shooting algorithm [31]. Distribution of sensitivities may also allow the convergence of solutions that may not appear using only one arc. The application of multiple shooting scheme enables placement of constraints at multiple locations along the path rather than just at the end points. As a test case, it is desirable to maintain the sail-based spacecraft in the vicinity of L₅ for a duration of 5 years. To achieve a given number of revolutions, the patch point vector is stacked with 5 orbits about the L₅ Lagrange point. For the initial guess, there are 90 arcs resulting in 90 time segments. In close proximity of the Earth, patch points are added at an interval of 6 days for the first 6 months (30 arcs). Thereafter, additional patch points are introduced once every 30 days for 2.5 years (30 arcs). Once the spacecraft enters an orbit about the L₅ Lagrange point, patch points are added once every 2 months for the next 5 years (30 arcs). Note, these are randomly selected to generate an initial guess.

Mathematical constraints are applied to fix the departure altitude at 1000 km where application of ΔV is allowed in the corrections scheme. Position continuity is enforced along the entire path and velocity continuity is additionally enforced along the path except at the two maneuver locations. Upon arrival in the vicinity of the destination orbit, the second ΔV is performed to deliver the spacecraft from the transfer arc to the final destination about L₅. The resultant corrected trajectory is depicted in Fig. 9. The tolerance for the convergence criteria is set as 10^− 9 which is equivalent to 149.6 m and 0.03 mm/s in dimensional units. Figure 10a and b illustrate close-up views of the two boxes marked I and II, respectively, in Fig. 9. The trajectory appearing in Fig. 10a corresponds to a departure from 1000 km parking orbit around the Earth. The location of departure maneuver, ΔV₁, of 3.041 km/s is marked with a red dot. After the application of the instantaneous maneuver, the spacecraft transfers onto the manifold arc associated with an L₁ Lyapunov orbit towards its final destination in the vicinity of L₅ as depicted in Fig. 10b. Upon arrival, an insertion maneuver of 559 m/s is performed at the location marked by ΔV₂. Thus, the total ΔV required for the transfer trajectory is ΔV_total = 3.6 km/s. The total time of flight (TOF) for the transfer from the Earth parking orbit to arrival in the vicinity of L₅ is 2.879 years (approximately 1036 days).

Fig. 9

Corrected trajectory from the Earth parking orbit to the vicinity of the triangular Lagrange point, L₅, with two ΔV maneuvers

Fig. 10

Departure and arrival trajectories with two ΔVs in CR3BP

Solar Sail Trajectory Design to the Vicinity of L ₄, L ₅

Preliminary design of trajectories in the SS-CR3BP is typically based on a differential corrections scheme. A numerical corrections approach from the CR3BP is extended to incorporate the solar sail angles. The inclusion of the effects of photons on the acceleration of a solar sail based spacecraft increases the complexity associated with the system model. For trajectory design, a two-point boundary value problem can be solved using a differential corrections scheme and implementing solar sail angles as additional design parameters. The corrections scheme is formulated to iteratively modify the initial states based on the linear estimated information available from the state transition matrix (STM).

Sail-Based Differential Correction

The inclusion of sail angles offers additional options for formulation of the shooting scheme. A number of shooting schemes incorporating solar sail angles have been formulated and presented in previous work [31]. In this work, variable-time multiple shooting scheme is developed in which the trajectory is decomposed into a set of arcs, identified in terms of n discrete points, denoted as ‘patch-points’, allowing more flexibility in the corrections process. The overall objective of a multiple shooting differential corrections algorithm is a complete trajectory that is continuous in position and velocity. To achieve such continuity, orientation angles associated with the solar sail are iteratively updated to result in a final converged path. Note that the orientation angles remain fixed relative to the rotating frame over the integration time between two patch points. Allowing the integration time, τ_i, to vary along any segment, further extends the capabilities of using sail angles in the multiple shooting scheme, thus, resulting in the formulation of variable-time multiple shooting algorithm. The updated design variable vector, X now includes additional variables, τ_i. Thus, X is a (9n − 1) × 1 vector since there are n − 1 integration times corresponding to n − 1 arcs between n patch points, i.e.,

$$ \boldsymbol{X} = \left\{ \begin{array}{c} \boldsymbol{X}_{1}(8 \times 1) \\ {\vdots} \\ \boldsymbol{X}_{n}(8 \times 1) \\ \tau_{1} \\ {\vdots} \\ \tau_{n-1} \end{array} \right\} $$

(22)

Note that X_i is an eight-dimensional vector comprised of three position states, three velocity states, and two orientation angles. The constraint vector, F(X) is defined to maintain continuity in both position and velocity states.

$$ \boldsymbol{F}(\boldsymbol{X}) = \left\{ \begin{array}{c} \boldsymbol{X}_{1}(\tau_{f_{1}})[1:6] - \boldsymbol{X}_{2}(\tau_{0_{2}})[1:6] \\ \boldsymbol{X}_{2}(\tau_{f_{2}})[1:6] - \boldsymbol{X}_{3}(\tau_{0_{3}})[1:6]\\ {\vdots} \\ \boldsymbol{X}_{n-1}(\tau_{f_{n-1}})[1:6] - \boldsymbol{X}_{n}(\tau_{0_{n}})[1:6] \\ ||{r}(\tau_{0_{1}})|| - (\frac{R_{E} + 1000 \mathrm{ km}}{l^{*}}) \end{array} \right\} $$

(23)

Continuity is maintained only for the six position and velocity states between each arc as denoted by [1 : 6]. The sail angles are free to differ between two arcs to achieve position and velocity continuity between two segments. Recall, r represent the nondimensional position vectors of P₃ relative to P₂ and R_E is the radius of Earth, approximated as 6,371 km. Final constraint in F(X) involves the altitude of the parking orbit and ensures that the departure altitude of 1000 km above the surface of the Earth is enforced during the corrections process. Thus, the dimensions of the constraint vector are (6(n − 1) + 1) × 1 for n − 1 arcs between n patch points and the additional altitude constraint.

Incorporating sail angles in the multiple shooting algorithm results in modified Jacobian matrix. Many terms within the DF(X) matrix are recognized as the terms of the modified STM the $\phi _{i}(\tau _{f_{i}},\tau _{0_{i}})$. Supplementing the two orientation angles as design variables, the STM, $\phi _{i}(\tau _{f_{i}},\tau _{0_{i}})$ is a 6 × 8 dimensional matrix. Inclusion of integration time along each segment as additional design variables and the altitude as an additional constraints, the DF(X) matrix of dimensions (6(n − 1) + 1) × (9n − 1) is written in the form

$$ D\boldsymbol{F}(\boldsymbol{X}) = \left[\begin{array}{cccccccccc} \!\!\phi_{1}(\tau_{f_{1}},\tau_{0_{1}}) & \!\!-H & 0 & \!0 & \!\!{\ldots} & \!\!0 & \dot{\!\boldsymbol{X}}_{1}[:6,1] & \!\!0 & \!\!0 & \!\!{\ldots} \\ \\ \!\!0 & \!\!\!\phi_{2}(\tau_{f_{2}},\tau_{0_{2}}) & -H & \!0 & \!\!{\ldots} & \!\!0 & \!\!0 & \dot{\boldsymbol{\!\!X}}_{2}[1:6,1] & \!\!0 & \!\!{\ldots} \\ \\ \!\!{\vdots} & {\ddots} & {\ddots} & \!{\ddots} & \!\!{\ddots} & \!\!{\vdots} & \!\!{\vdots} & \!\!{\ddots} & \!\!{\ddots} & \!\!{\vdots} \\ \\ \!\!0 & 0 & {\ldots} & & \!\!\!\phi_{n-1}(\tau_{f_{n-1}},\tau_{0_{n-1}}) & \!\!-H & \!\!0 & \!\!0 & \!\!{\ldots} & \dot{\boldsymbol{X}}_{n-1}[1:6,1] \\ \\ \frac{\partial ||{r}(\tau_{0_{1}})||}{\partial \boldsymbol{\rho}}[1,1:3] & 0 & {\ldots} & & \!\!{\ldots} & & \!\!0 & & \!\!{\ldots} & \!\!0 \end{array}\right] $$

(24)

where H is a 6 × 8 rectangular diagonal matrix with diagonal entries equal to one. $\dot {\boldsymbol {X}}_{i}[1:6,1]$ represents the time derivatives corresponding to the position and velocity states at the end point along the reference segment, X_i[1 : 6,1]. The last row of DF(X) matrix holds the partials for the altitude constraint in the columns corresponding to the initial position state.

Lightness Parameter Selection

The sail lightness parameter, also frequently denoted as the sail loading parameter, is the ratio of the acceleration due to the solar radiation pressure to the classical solar gravitational acceleration used to parameterize the solar sail efficiency. Even though the value for the lightness parameter within the range 0.03 - 0.3 reflects the current technology capabilities, recent IKAROS mission had β value of approximately 0.001 [33]. McDonald and McInnes conducted a recent review of solar sail technology and discussed potential short-, mid-, and long-term solar sail missions with applicable lightness parameter [21]. The lightness number for the short-term, GeoStorm mission is calculated as β ≈ 0.02 and β ≈ 0.1 for the mid-term Solar Polar Orbiter. As for the long-term mission goal, β ≈ 0.3 − 0.6 is calculated for the Interstellar Heliopause Probe. Heiligers and McInnes calculated the β in the range of 0.0388 to 0.0455 for the Sunjammer mission [14]. Therefore, with solar sail technology still in the developmental stages, analyzing the behavior of solar sails with low sail lightness parameters may be more useful in near term mission design and analysis.

Solar Sail Transfer Family to L ₄ and L ₅

Trajectory design incorporating a solar sail begins with the selection of a baseline solution computed in “Differential Corrections and Baseline Trajectory” and plotted in Fig. 10 as an initial guess to the design process. The goal of using a solar sail is to lower the ΔV requirement for the mission by performing a single departure ΔV from Earth parking orbit, accelerating the sail using SRP from the Sun, entering and maintaining the path in the vicinity of destination orbit using the sail itself. Note that, no insertion ΔV is performed to arrive at the final orbit around L₅. Prior to building a family of transfer trajectories, an initial value of sail parameter, β value of 0.042 is arbitrarily selected for preliminary trajectory design. Employing the sail-based differential corrector and continuation in β, a subset of transfer trajectories are constructed for β in the range of 0.005 - 0.06 as depicted in Fig. 11a. The range for β is selected keeping in mind the near-term capabilities in the field of solar sail technology. Two trajectories for β values of 0.005 and 0.06 are marked. The blue arrow indicates the direction of increasing β. During the continuation scheme, steps are taken in β in intervals of 0.001 but for clarity, only a subset of transfer trajectories are plotted in Fig. 11. A zoomed-in view for the transfer trajectories departing Earth parking orbit appears in Fig. 11b. Once again, the departure altitude is constrained to be at 1000 km above the surface of the Earth. The red dots mark the location of ΔV_departure for each trajectory departing from the Earth parking orbit for a specific value of β. Note that only the initial altitude is constrained and not the initial departure position vector relative to Earth, hence, the departure location is allowed to freely change during the corrections process as is evident from Fig. 11b.

Fig. 11

Subset of solar sail corrected trajectory with only departure ΔV maneuver for β = 0.005 - 0.06

Similar to the sail-based trajectories that deliver the spacecraft to the vicinity of Sun-Earth L₅, the strategy is extended to generate a family of transfers to the vicinity of Sun-Earth L₄. The framework leverages the natural dynamics and flow that exists in the CR3BP and the solar radiation pressure acting on the sail. A subset of sail-based transfer trajectories are depicted in Fig. 12 for β in the range of 0.005 - 0.06. Note that the solar sail is leveraged to maintain the trajectories in the vicinity of L₄ without any insertion maneuver, thus demonstrating the capabilities of a solar sail. The two trajectories for β values of 0.005 and 0.06 are marked in Fig. 12a, and the blue arrow indicates the direction of increasing β. A zoomed-in view for the transfer trajectories departing the Earth parking orbit appears in Fig. 12b. Once again, the departure altitude is constrained to be at 1000 km above the surface of the Earth. The red dots mark the location of ΔV_departure for each trajectory departing from the Earth parking orbit for a specific value of β. Note that only the initial altitude is constrained and not the initial departure position vector relative to Earth, hence, the departure location is allowed to freely change during the corrections process as is evident from Fig. 11b.

Fig. 12

Subset of solar sail corrected trajectory to L₄ with only departure ΔV maneuvers for β = 0.005 - 0.06

Transfers to the Vicinity of L ₅

To investigate the properties associated with the family of transfer trajectories, the case of L₅ is further investigated. Recall the definition of sail lightness parameter as the ratio of Solar Radiation pressure (SRP) acceleration to the gravitational acceleration, thus, providing a qualitative measure for the solar sail efficiency. As a result of varying the sail parameter, β for the transfer trajectory, each trajectory is capable of generating variable SRP with a specific upper bound.

Arrival Criterion

The amount of SRP acceleration generated governs the architecture of the trajectory and duration of time it takes for the trajectory to arrive at the vicinity of L₅. In Fig. 13a, arrival for the subset of transfer trajectories appears for the family illustrated in Fig. 11a. The dotted-blue circle marks the location of arrival in the vicinity of the L₅ Lagrangian point. The radius of the circle is ≈ 0.04 AU based on the amplitude of an L₅ short period orbit with Jacobi value equivalent to 2.99995 that was incorporated to find the initial transfer trajectory in the no-sail CR3BP. Three trajectories with their β values are marked to demonstrate how the flow varies as the sail parameter, β changes. Trajectories with lower β values (0.005 and 0.01) form additional ‘cusps’ prior to entering the dotted-blue circle that marks the arrival when compared to relatively higher β values , i.e. 0.06.

Fig. 13

Subset of sail trajectories as they arrive in the vicinity of L₅ and the corresponding SRP over time

Effects of Sail Parameter on SRP Acceleration

The overall behavior of the trajectory, as it arrives in the vicinity of the Lagrangian point, varies with the change in sail parameter. It is evident that, for the subset of transfer trajectories, higher values of β result in trajectories that are closer to the given initial guess. The higher the value of sail parameter β, the more SRP acceleration the sail-craft is capable of generating as apparent from Fig. 13b. As the time increases, the sail-craft with higher β values is able to generate enough acceleration to effectively maintain the spacecraft in the vicinity of L₅ as compared to trajectories with lower β values. As the SRP acceleration varies with the β value, the time of flight (TOF) it takes for each trajectory to enter the blue circle also changes. The magenta dots in Fig. 13b mark the location for a specific transfer trajectory as it reaches the dotted-blue circle. As the β value decreases, the TOF increases relatively slowly as can be seen for the β values ranging from 0.06 - 0.015. Conversely, for sail parameter β = 0.005 and 0.01, the TOF increases by 9-12 months which is also evident from the formation of additional cusps seen in Fig. 13a. Upon arrival, the spacecraft remains in the vicinity of L₅ for at least 4-5 years to carry out assigned scientific mission. Of course, the duration of time spent can be altered based on the mission requirements.

Displacement of Traditional L ₅

Within the context of the CR3BP, Lagrange points are the equilibrium locations where the net gravitational forces of the two primaries completely offset the centripetal force in the rotating frame. Physically, such existing conditions imply that both the velocity and acceleration are zero relative to the rotating frame. With the addition of the solar sail to the force model of the CR3BP, new equilibrium solutions emerge in the form of artificial Lagrange points [24]. Thus, for the transfer trajectories depicted in Fig. 11a, new artificial Lagrange points, L₅’ are evaluated for β ranging from 0.005 - 0.06 and depicted in Fig. 14. With the addition of SRP acceleration the equilibrium points shift towards the Sun as the value of sail parameter, β increases. The artificial Lagrange points depicted are for case corresponding to sail angle, α = 0, i.e., the sail is head-on relative to the Sun-sail direction. For β = 0, the solar sail model generates a special case for the conditions corresponding to the classical CR3BP. Traditional L₅, that is associated with the classical CR3BP, is marked by a black dot. With each transfer trajectory, the value of β is stepped up by 0.005 that results in an equivalent shift of ≈ 200,000 km. For sail parameter, β = 0.06, the total displacement of the artificial equilibrium point relative to traditional L₅ is ≈ 3 million km (0.02 AU). Thus, a spacecraft in the vicinity of displaced Lagrange point, L₅’ can monitor the solar weather from a location relatively closer than a spacecraft around the traditional Lagrange point, L₅.

Fig. 14

Artificial Lagrange points, L₅’ for β = 0.005 – 0.06 relative to traditional Lagrange point L₅

Jacobi Integral Analysis

The single known integral of motion, denoted as the Jacobi constant, exists in the classical CR3BP. In Solar Sail Circular Restricted Three-Body Problem (SS-CR3BP), the Jacobi value is no longer a constant. However, investigating the change in the Jacobi value helps in analyzing the effects of SRP acceleration on the energy level of the spacecraft as apparent in Fig. 15a. In addition to the β values in the range 0.005 - 0.06 being investigated in this section, lower values of β = 0.002 and 0.003 are added to help gain insight into the general trend for the change in Jacobi value over time as the photons continue to bombard the sail-craft. As an example, for β = 0.003 (light-blue), Fig. 15a shows that the sail-craft is able to lower the Jacobi value (increase energy) over the duration of the flight. Quantitative decrease in Jacobi for a specific β value will be discussed in the following section. It is evident from the general trend that for higher values of sail parameter, β, the variation in Jacobi is higher. Hence, with higher β values, the energy of the trajectory can be significantly increased using solar sails.

Fig. 15

Jacobi analysis and non-optimal ΔV_departure

Non-Optimal Parking Orbit Departures

Although the spacecraft builds-up momentum as a result of harnessing SRP from the Sun, an initial boost is provided to insert the spacecraft onto a path (manifold) towards the destination. The initial boost is delivered in the form of an impulsive maneuver, ΔV_departure, that is required to depart from a 1000 km Earth parking orbit as illustrated in Fig. 15b. Note that the ΔV_departure corresponding to a particular value of β, as depicted in this figure, is non-optimal. Recall, each transfer trajectory is constructed employing a continuation in the sail parameter, β. Further analysis in “Local Optimal Departure ΔV” is carried out to optimize the solution, thus, lowering the ΔV_departure requirements.

Solar Sail Trajectory Analysis

To understand the behavior of a sail-based spacecraft and gain both qualitative and quantitative insight, a single transfer trajectory is investigated. Recall that a family was built by continuation in lower values of sail parameter, β, with a step size of δβ = 0.001. Taking into consideration the advancement in the solar sail technology, β = 0.022 is arbitrarily selected for further analysis.

Sail Transfer and Baseline Trajectory

The transfer trajectory for the sail parameter value of 0.022 is extracted and plotted as illustrated in Fig. 16. A baseline trajectory from CR3BP is used as an initial guess for the sail-based dynamical model. The red transfer trajectory is the initial guess derived in the CR3BP, whereas, the sail-based corrected trajectory for β = 0.022 is depicted in light-blue. The departure trajectory from a 1000 km parking orbit around the Earth is illustrated in Fig. 17a. As a result of including a solar sail in the dynamical model, only one ΔV is performed as an initial boost. The ΔV is delivered to insert the sail-craft from the Earth parking orbit onto a trajectory towards the final destination using solar sails. The location of impulsive departure ΔV is marked by ΔV_new and is equal to 3.0341 km/s. The arrival transfer trajectories for both the CR3BP and SS-CR3BP are plotted in Fig. 17b. The velocity discontinuity in the red transfer trajectory (CR3BP) is the location where ΔV₂ was performed to deliver the spacecraft in the vicinity of L₅ for the baseline case (with no sail). As a result of incorporating a solar sail, no insertion ΔV is required, as evident from the light-blue transfer trajectory. Also note the displacement of the artificial Lagrange point, L₅’ relative to the traditional Lagrange point, L₅. The net displacement is ≈ 1.05 million km (0.007 AU) towards the larger primary, P₁, i.e., the Sun as a result of SRP acceleration acting on the sail-craft.

Fig. 16

Sail based (light-blue) and no sail (red) transfer trajectories from the Earth orbit to the vicinity of L₅ in the Sun-Earth system

Fig. 17

Solar sail corrected trajectory with one ΔV maneuver at the departure prior to unfurling the sail with β = 0.022

Jacobi Analysis for β = 0.022 Transfer to L ₅

In the CR3BP, the Jacobi value represents a constant of motion within the rotating frame. The Jacobi value for a trajectory is conserved when no additional forces, i.e., ΔVs, SRP are taken into consideration. ΔV maneuver results in a change in Jacobi constant. Jacobi values for two cases, no sail and sail-based (β = 0.022) trajectories are shown in Fig. 18. The red line represents the case with no sail in the dynamical model. The first jump of 0.0608 in the Jacobi value (at Time = 0 years) is representative of a departure ΔV performed to leave the Earth parking orbit and is equivalent to ΔV₁ = 3.041 km/s. Note the discontinuity added at the top of y − axis for Jacobi value of the departure orbit. The second jump (at Time = 2.9 years) marks the location where ΔV₂ of 559 m/s is performed to further raise the energy (lower Jacobi by 1.896 × 10^− 4) of the trajectory to insert the spacecraft in an orbit about L₅ Lagrange point. Thus, in the no sail case, the required ΔV_total = 3.6 km/s to deliver the spacecraft from a 1000 km parking orbit to the vicinity of L₅. The case exploiting the solar sail technology with β of 0.022 is depicted in light-blue. Only one ΔV is performed that is delivered at the initial time to depart the Earth parking orbit marked as ΔV_new equivalent to 3.034 km/s. Note, no secondary ΔV is performed to insert the spacecraft in an orbit about L₅, instead, the solar sail leverages the SRP to increase the energy of the spacecraft and arrive in a final trajectory about displaced L₅’. The TOF for the sail-based spacecraft is 2.92 years (magenta dot) and exceeds the case with no sail by only ≈ 16 days. In this scenario, incorporating solar sails in the dynamical model (SS-CR3BP) assisted in accomplishing a trajectory solution to an artificial Sun-Earth L₅ by harnessing the SRP. Thus, the use of currently-available solar sail technology significantly reduces the required ΔV to visit the vicinity of Sun-Earth triangular Lagrange points.

Fig. 18

Jacobi analysis of transfer trajectories with no sail (red) and with sail (light-blue) for β = 0.002

Sail Orientation Angles

The magnitude and the direction of the SRP acceleration generated is governed by the orientation of the sail relative to the Sun-sail line. Within the context of the SS-CR3BP, two sail angles are defined as clock angle, α and pitch angle, γ to orient the sail in the rotating frame. For the initial analysis of solar sail, motion in the x − y plane is investigated that is governed by the clock angle α. Recall, the algorithm presented incorporates turn and hold strategy in which the sail maintains a constant orientation along an arc between two successive patch points relative to the Sun-sail line in the rotating frame. However, from a mission perspective, it is important to analyze the sail angles from an inertial observer as the sail is continuously rotating along each arc relative to the Sun. Thus, α is expressed in the inertial frame by angle ψ relative to the inertial $\hat {X}-axis$ as depicted in Fig. 19a undergoing continuous rotation when viewed by an inertial observer. The values for ψ range between ± 180^∘ in the inertial frame relative to the $\hat {X}-axis$. The rate of change in the orientation (slope) of the sail in the inertial frame is ≈ 1^∘/day. The discontinuity in the figure is not physical but an artifact of the definition and bounds of the sail angle, ψ, in the inertial frame. To determine the practicality of the trajectory, it is vital to consider hardware constraints that govern the pointing accuracy of a sail, turn-rate, and gimbal properties, i.e., maximum gimbal torque, maximum gimbal angle, and the maximum gimbal rate. The absolute values for the change in sail orientation angle, |Δψ|, required for the trajectory are illustrated in Fig. 19b for the duration of 8 years. For a 40 × 40 m² sail, Wie established a maximum roll-control torque of ± 1.34 × 10^− 3 N⋅m and the maximum pitch and yaw-control torques of ± 1.45 × 10^− 3 N⋅m that are capable of producing maximum angular accelerations of ± 13.0 × 10^− 6 deg/s² and ± 28.1 × 10^− 6 deg/s², respectively [37]. The maximum turn rate for a three-axis stabilized spacecraft was set at 0.02 deg/s. Thus, the time to reorient the solar sail by a maximum value of |Δψ| = 5.61^∘ is ≈ 4 minutes 40 seconds. In the Sun-Earth system, the reorientation time span is relatively more acceptable as compared to the Earth-Moon system where the time for one complete revolution is much smaller.

Fig. 19

Solar sail orientation angle analysis in the inertial frame

Local Optimal Departure ΔV

By incorporating the solar sail dynamics in the CR3BP, corrections scheme is employed to build a family of transfers from the Earth parking orbit to the vicinity of L₅ for various sail parameter, β. Utilization of design tools, such as periodic orbits, invariant manifolds, the Jacobi value analyses, can potentially deliver low-cost transfer options, but they do not guarantee an optimal solution. However, solutions achieved from studying these inherent properties of the CR3BP regime can assist in formulating a good initial guess for the optimization problem. The objective is to deliver the spacecraft from an Earth parking orbit to the sail-based trajectory towards the final destination, L₅. The initial ΔV maneuver (and the only ΔV) forms the primary performance measure that directly impacts the fuel requirements for the mission. Thus, minimization of the departure ΔV maneuver is the main focus for the optimization process based on the transfer trajectory design requirements.

The general architecture for the optimization process encompasses finding a set of design variables, X, that can minimize or maximize the objective (cost) function, f(X) and is subject to equality constraints, F(X) = 0 or inequality constraints, F(X) ≤ 0. Analysis for a fuel optimal transfer between the Earth parking orbit and the final destination in the vicinity of displaced Lagrange point, L₅’ is formulated as a minimization problem of a constrained nonlinear multivariable function. Identifying the design variables from Eq. 22, with the objective of minimizing ΔV_departure subject to the equality constraint of Eq. 23, F(X) = 0, the optimization problem is stated as

minimize

$$ f(\boldsymbol{X}) = \left|\left|{\Delta} {V}_{departure}\right|\right|^{2} = (V_{x_{1}} - V_{x_{c}})^{2} + (V_{y_{1}} - V_{y_{c}})^{2} + (V_{z_{1}} - V_{z_{c}})^{2} $$

(25)

$$ \text{subject to} \quad \boldsymbol{F}(\boldsymbol{X}) = \left\{ \begin{array}{ccccccccccc} \boldsymbol{X}_{1}(\tau_{f_{1}})[1:6] - \boldsymbol{X}_{2}(\tau_{0_{2}})[1:6] \\ \boldsymbol{X}_{2}(\tau_{f_{2}})[1:6] - \boldsymbol{X}_{3}(\tau_{0_{3}})[1:6]\\ {\vdots} \\ \boldsymbol{X}_{n-1}(\tau_{f_{n-1}})[1:6] - \boldsymbol{X}_{n}(\tau_{0_{n}})[1:6] \\ ||{r}(\tau_{0_{1}})|| - (\frac{R_{E} + 1000 \mathrm{ km}}{l^{*}}) \end{array} \right\} = {0} $$

(26)

where

$$\begin{array}{@{}rcl@{}} \boldsymbol{V}_{1} &= & [\boldsymbol{V}_{x_{1}} \boldsymbol{V}_{y_{1}} \boldsymbol{V}_{z_{1}}]^{T} = \boldsymbol{X}_{1}(\tau_{0_{1}})[4:6] \end{array} $$

(27)

$$\begin{array}{@{}rcl@{}} \boldsymbol{V}_{c} &= & [\boldsymbol{V}_{x_{c}} \boldsymbol{V}_{y_{c}} \boldsymbol{V}_{z_{c}}]^{T} \end{array} $$

(28)

$$\begin{array}{@{}rcl@{}} {\Delta} \boldsymbol{V} &= & \boldsymbol{V}_{1} - \boldsymbol{V}_{c} \end{array} $$

(29)

From the definition, V₁ is the velocity vector of the first patch point at an initial time, $\tau _{0_{1}}$. Whereas, V_c is the velocity vector at the departure location of the spacecraft from the Earth parking orbit. The equality constraints in Eq. 26 are incorporated to maintain the position and velocity continuity along each arc and the last entry in the constraint vector enforces the departure from a 1000 km parking orbit. The design variables consists of three position components, three velocity components, two angles for each patch point, n, and n − 1 integration times between n patch points, thus, resulting in the design variable vector, X of dimensions (9n − 1) × 1.

The optimization problem is solved using Matlab’s fmincon function that attempts to find a constrained minimum subject to nonlinear equalities or inequalities defined in a nonlinear constraint function. Thus, the problem is referred to as constrained nonlinear optimization. The process is initialized by providing the solar sail end-to-end trajectory designed in “Solar Sail Trajectory Analysis” and illustrated in Fig. 16 (light-blue) as an initial guess with tolerance of 10^− 9. Applying the described optimization scheme, the resulting transfer with a local optimal departure maneuver, ΔV_optimal, converged in 9 iterations and appears in Fig. 20 along with the initial guess. The optimization process alters the solar sail trajectory as depicted in magenta and provides ΔV_optimal relative to the non-optimal case in light-blue. As expected with the optimization routine, the overall architecture remains similar to that of a good initial guess. The departure trajectories from a 1000 km altitude Earth parking orbit are illustrated in Fig. 21a. The blue trajectory depicts the sail-based departure from the parking orbit with non-optimal ΔV. The optimal departure maneuver, ΔV_optimal location is marked by a red dot along the parking orbit that delivers the spacecraft onto the magenta sail-based trajectory. The required change in velocity to deliver the spacecraft from the Earth parking orbit onto the sail-based transfer arc is ΔV_optimal = 3.0060 km/s. In this scenario, the optimization scheme lowered the departure ΔV by 28.1 m/s. The arrival in the vicinity of the displaced Lagrange point, L₅’ is illustrated in Fig. 21b for the local optimal and non-optimal departures. As a result of the optimization process, the TOF for the local optimal case increased by ≈ 7 days.

Fig. 20

Sail transfer trajectories with optimal (magenta) and non-optimal (light-blue) departure ΔV from the Earth orbit to the vicinity of L₅

Fig. 21

Sail trajectories for β = 0.022 with optimal (magenta) and non-optimal (light-blue) departure ΔV

As a part of testing and building on the strategy outlined for applying solar sails to the trajectory design process and optimizing the departure ΔV, additional values for β are tested as listed in Table 1.

Table 1 Departure ΔV optimization results for sail parameter, β, values compared to no sail and non-optimal results

The values of β selected are based on current technology capabilities and are within the range of proposed short-term Geostorm and the Sunjammer missions [14, 21]. The first column identifies the case starting with the converged solution in classical CR3BP with no sail. Following the no sail case, three transfer trajectories with different values for the sail parameter, β were converged by a sail-based corrections scheme and supplied to the optimization routine as an initial guess. Column 3 gives the maximum absolute value for the change in sail orientation angle, ψ for the sail-based trajectories. Column 4 is the total time of flight (TOF) for each case to reach the vicinity of the displaced L₅’. Note that the TOF for the no sail case is relatively lower than the non-optimal sail and the three optimized sail-based trajectories. Column 5 gives the maneuver requirements in the form of ΔV_departure from the Earth parking orbit onto the transfer trajectory. From column 6, it is evident that no arrival ΔV is needed in the three sail-based cases as contrary to the no sail case that requires a ΔV_arrival equal to 559 m/s for the spacecraft to insert into an L₅ short period orbit. Thus, by leveraging SRP to maneuver the solar sail, the spacecraft demonstrates the capability to achieve the desired trajectory in the vicinity of displaced Lagrange points. Cost comparison is carried out with previous works in the literature. Lo, Llanos, and Hintz provided preliminary characterization for a typical L₅ mission and gave a case-by-case detailed table for overall performance [20]. The results achieved in this work on solar sail transfer trajectory design are promising in comparison to the data provided by the authors. Comparing the case for the final insertion into an orbit with approximate amplitude of 0.047 AU, previous authors stated the ΔV requirement ranges from 3.74 – 5.01 km/s in the CR3BP.

In the work presented here, incorporating a solar sail in the design scheme enabled harnessing the SRP to explore trajectory design options to Sun-Earth L₄ and L₅. Recall that the departure altitude for this investigation was maintained at an altitude of 1000 km, taking into consideration the effectiveness of the solar sail and avoiding atmospheric drag. However, the transfer trajectories accomplished with the sail reflect the advantages of leveraging the SRP to maneuver the spacecraft. Thus, the overall propulsion requirements in the form of ΔV can potentially be lowered by incorporating solar sail dynamics in the trajectory design process to the vicinity of the triangular Lagrange points, L₄ and L₅. Further cost savings can be achieved by launching SmallSats and CubeSats as secondary payloads, as currently planned for the upcoming Near Earth Asteroid (NEA) Scout mission [28].

Conclusions

To summarize, trajectory design options, incorporating solar sail dynamics, from the Earth parking orbit to the vicinity of triangular Lagrange points are explored. In particular, one transfer strategy is investigated in depth that utilizes the unstable manifold associated with an L₁ Lyapunov orbit to depart from the Earth parking orbit, arrive in the vicinity of the displaced Lagrange point, L₅’ and maintain a trajectory close to the artificial libration point with the help of the solar sail. The change in sail angle |Δψ| in the inertial frame delivered promising results for reorientation of the sail that are within the technological capabilities of today. The optimization scheme further assisted in investigating the ΔV requirement to leave the Earth parking orbit. The trajectory analysis demonstrated that by incorporating solar sail in the dynamical model, solar radiation pressure can be leveraged to maneuver the sail-based spacecraft. Moreover, solar sails provide cost-effective transfers and trajectory design options to the vicinity of triangular Lagrange points, thus, enabling solar observations and exploration of potential Earth Trojans.