Mean Element Propagations Using Numerical Averaging

Abstract

The long-term evolution characteristics and stability of an orbit are well characterized using a mean element propagation of the perturbed two body variational equations of motion. The averaging process eliminates short period terms leaving only secular and long period effects. In this study, a non-traditional approach is taken that averages the variational equations using adaptive numerical techniques and then numerically integrating the resulting equations of motion. Doing this avoids the Fourier series expansions and truncations required by the traditional analytic methods. The resultant numerical techniques can be easily adapted to propagations at most solar system bodies.

Introduction

The mathematical basis of perturbed, two-body mean element orbits is the averaging theory of nonlinear dynamical systems. Via averaging, short period terms (typically less than an orbital period) are eliminated from the variational equations of motion (EOMs) leaving only secular and long period terms. These secular and long-period terms define the key characteristics of an orbit’s long-term evolution, and are known as an orbit’s mean elements. Because mean elements are not obscured by short periodic effects, they are ideal for use in orbit and constellation design. They also reveal the stability characteristics of an orbit (including the possibility of chaotic motions) [1, 2]. As such, mean element trajectories are a necessary component for orbital stability analyses and are essential for lifetime and planetary protection studies. From a practical point of view, mean element propagations are often one or more order(s) of magnitude faster than their osculating element counterparts (i.e., propagations of the full EOMs that include the short period terms), and enable mission designers to explore very large design spaces efficiently.

Averaging the Equations of Motion

The application of averaging theory to obtain mean orbital element propagations has a long history in astrodynamics with roots in the non-linear dynamical systems theory developed by Poincaré in the late 1800’s. More recently, the development of the Draper Semi-Analytic Satellite Theory by Cefola et al. [3, 4] and McClain [5, 7] represents the state of the art as it has been applied to the Earth. A similar development by Kwok [8, 9] applied the theory to Mars and Venus (in addition to the Earth). These theories and tools applied traditional techniques that expand the EOMs in a Fourier series and analytically ‘average out’ the short period terms leaving only the secular and long period terms for a numerical propagation. These ‘semi-analytic’ approaches require detailed expansions for each acceleration type; a difficult task that usually requires some form of truncation (typically in eccentricity) to make the problem tractable, hence limiting their effectiveness for highly eccentric orbits. Furthermore, orbits around non-traditional bodies like asteroids with gravity fields that are better modeled with ellipsoidal or polyhedral formulations currently do not have ready analytic expressions for the averaged gravity field making application of a semi-analytic technique difficult. In this study, the approach taken is to numerically average the variational equations and then numerically integrate the resulting EOMs. Doing this avoids the Fourier series expansion and truncations required by the analytic methods. Numerical approaches have been applied in the past by Uphoff [10], Lutzky and Uphoff [11], and McClain, et al. [7]; however, they limited their investigations to fixed-order numerical averaging (typically a form of Gaussian quadrature). In addition to the fixed-order Gaussian techniques, the present study also examines a readily available robust adaptive numerical cubature routine (CUBPACK) [12, 13]. The result is a complete numerical algorithm that has been developed to work at any solar system body, and is more flexible and accurate than solely fixed-order methods.

1 ^st-Order Averaging and Numerical Techniques

The trajectory of a satellite in two-body perturbed motion can be modeled in a variation of parameter formulation of six 1 ^st-order differential equations of motion. In its simplest form with only one fast angle and no resonances (the case of additional ‘fast’ angles and resonances will be examined later), these EOMs can be represented as

$$ \left[\begin{array}{l} {\dot{{\boldsymbol\alpha}}}\\ {\dot{{\lambda}}} \end{array}\right]=\left[\begin{array}{ll} 0\\ n\left(a\right) \end{array}\right]+\varepsilon \left[\begin{array}{ll} {\mathrm{\textbf{f}}^{\alpha} \left( {\boldsymbol{\boldsymbol{\alpha}} ,\lambda} \right)}\\ {f^{\lambda}\left({\boldsymbol{\alpha}, \lambda} \right)} \end{array}\right] $$

(1)

where the osculating elements have been selected to be an equinoctial set with $\textbf {x} \equiv \left \{{\boldsymbol {\alpha },\lambda }\right \}, \boldsymbol {\alpha } \equiv \left \{{a,h,k,p,q}\right \}$ (see the appendix for a definition of the elements), and $n\left (a\right )=\sqrt {\mu /{a^{3}}}$ is the Keplerian mean motion. For convenience in later developments, $\mathbf {f}\equiv \left \{\textbf {f}^{\boldsymbol {\alpha }}, f^{\lambda }\right \}$ has been defined. The mean longitude λ has been singled out because it is the short periodic (‘fast’) angle in this problem. The parameter ε is a small parameter used to asymptotically order terms. As proven by Sanders et al. [14] in Section 7.8 of their book, there exists a near-identity transformation for a system of the form given by Eq. 1 that eliminates the mean longitude via averaging and approximates the original system to first order $O\left (\varepsilon \right )$ on a time scale of order $O\left ({1/\varepsilon }\right )$ with a set of averaged equations of motion. The averaged equations take the form

$$ \left[\begin{array}{l} {\dot{{\bar{{\boldsymbol{\alpha}}}}}}\\ {\dot{{\bar{{\lambda}}}}} \end{array}\right]=\left[\begin{array}{ll} 0\\ \bar{{n}}\left( {\bar{{a}}} \right) \end{array}\right]+\varepsilon \left[\begin{array}{ll} {\bar{\textbf{f}}}^{\boldsymbol{\alpha}} \left( {\bar{{\boldsymbol{\alpha}}}}\right)\\ \bar{f}^{\lambda}\left(\bar{\boldsymbol{\alpha}}\right) \end{array}\right]+O\left({\varepsilon^{2}} \right) $$

(2)

where the overbar represents the mean elements $\left \{{\bar {{\boldsymbol {\alpha }}},\bar {{\lambda }}}\right \}$ and the mean perturbing functions $\bar {\mathbf {f}}\left ({\bar {{\boldsymbol {\alpha }}}}\right )\text {and}\bar {{n}}\left ({\bar {{a}}} \right )$. These are obtained via

$$ \begin{array}{l} \bar{\textbf{{f}}}^{\boldsymbol{\alpha}} \left({\bar{{\boldsymbol{\alpha}}}} \right)\equiv \frac{1}{2\pi} \int\limits_{-\pi +\lambda_{o}}^{\pi +\lambda_{o}} {\mathrm{\textbf{f}}^{\boldsymbol{\alpha}} \left( {\bar{{\boldsymbol{\alpha}} },\lambda} \right)d\lambda},\\ \bar{{n}}\equiv n\left({\bar{{a}}} \right),\quad \bar{{f}}^{\lambda} \left( {\bar{{\boldsymbol{\alpha}} }} \right)\equiv \frac{1}{2\pi} \int\limits_{-\pi +\lambda_{o}}^{\pi +\lambda_{o}} {f^{\lambda} \left( {\bar{{\boldsymbol{\alpha}} },\lambda} \right)d\lambda} . \end{array} $$

(3)

The system defined by Eq. 1 may also have parameters that it depends on. As long as these parameters are constant or have slow time variations of order $O\left (\varepsilon \right )$, then the averaged equations given in Eq. 2 remain valid on the $O\left ({1/\varepsilon }\right )$ time scale. In Eq. 3 the mean $\bar {{\boldsymbol {\alpha }}}$ elements are treated as constant parameters over the integration, and at any given time t are determined via propagating the EOMs defined in Eq. 2 to that time. The process is initialized via selection of suitable mean element initial conditions at the initial time t _o

$$ \begin{array}{l} \bar{{\boldsymbol{\alpha}} }_{o} \triangleq\bar{{\boldsymbol{\alpha}} }\left( {t_{o}} \right),\\ \bar{{\lambda} }_{o}\triangleq \bar{{\lambda} }\left( {t_{o}} \right). \end{array} $$

(4)

Typically the perturbation functions $\text {\textbf {f}}\left ({\boldsymbol {\alpha } ,\lambda } \right )$ can be expanded in a Fourier series to separate secular, short period, and long period effects. This can be represented formally as

$$ \textbf{f}\left( {\boldsymbol{\alpha} ,\lambda} \right) =\bar{\mathbf{{f}}}\left( \boldsymbol{\alpha} \right)+\sum\limits_{j=-\infty ,j\ne 0}^{\infty} {\textbf{f}}_{j} \left( \boldsymbol{\alpha} \right) e^{ij\lambda} $$

(5)

where $i\equiv \sqrt {-1}$, and performing the averaging operation identified in Eq. 3 on Eq. 5 reveals the averaged equations of motion arise from the first term in the Fourier series. Traditionally, the series is obtained via explicit manipulations of $\mathbf {f}\left ({\boldsymbol {\alpha } ,\lambda } \right )$ to arrive at analytic formulae, which can be easily averaged. In the present study, the numerical average in Eq. 3 will be performed via numerical quadrature (or cubature in the multivariate case).

The motivation for considering a numerical averaging approach stems from several reasons. Foremost, any analytic theory requires some form of truncation typically in the eccentricity functions for the tesseral harmonics and other body perturbations, which limits the range of orbits that can be considered. A numerical averaging approach makes no such truncation. An analytic theory requires that explicit formulation of the Fourier series expansion exist in order to perform the averaging; this is not a requirement in a numerical averaging. Generalized averaging theory requires only that Eq. 1 satisfy some continuity conditions, including a Lipschitz condition, for an averaging operator to exist, and to have an averaged system to be asymptotically near the un-averaged system (c.f. Section 2.8 of Sanders et al. [14]). This result is useful when considering orbital regimes where either an analytic theory hasn’t yet been developed, or a convergent Fourier series might not exist for the perturbation environment. An example of this is the case of small bodies with irregular shape; analytic mean element theories haven’t been developed and may not exist. Another is with low thrust optimal control problems. Finally, since the numerical approach is simpler algorithmically, it represents an approach that can be efficiently implemented and tested in software, and easily extended to new problem domains.

This study examines two specific numerical quadrature (cubature) techniques: a classic fixed-order Gaussian method and a more recent algorithm called CUBPACK developed by Genz and Cools [12] that uses globally adaptive techniques and is readily available on the internet. The generic cubature problem of numerically evaluating an integral can be expressed as

$$ I\left[\textbf{f} \right]=\int\limits_{T} {\textbf{f}}({\mathbf{y}};\boldsymbol{\alpha}) dT $$

(6)

where y is a m-vector, α is a r-vector of parameters, f is a n-vector and T is a collection of m-dimensional hyperrectangles or m-simplices. For the perturbed orbit problems considered here, y is either 1- or 2-dimensional depending on the variables that are to be averaged, $\boldsymbol {\alpha } \equiv \left \{ {a,h,k,p,q} \right \}, \textbf {f}$ is a 6-vector, and T is either a line segment for single variable integration or a square for two variable integration.¹ An overview of various numerical integration techniques is given in Smyth [15] and includes the details for fixed-order Gaussian quadrature. In the current research, the integration order can be specified to be any desired integer. For the CUBPACK algorithm, Genz and Cools [12] describe it as ‘based on a subdivision strategy that chooses for subdivision at each stage the subregion (of the input simplices) with the largest estimated error. This subregion is divided into two, three or four equal volume subregions by cutting selected edges. These edges are selected using information about the smoothness of the integrands in the edge directions. The algorithm allows a choice from several embedded cubature rule sequences for approximate integration and error estimation.’

Two-Body Perturbed Numerical Mean Element Theory and Results

There exist two main variation of parameter approaches used in orbit theory – Lagrange’s equations and Gauss’ equations. The Lagrangian approach requires the system to be derivable from a potential, and hence only applies to conservative force fields. On the other hand, Gauss’ equations work directly with the acceleration expressions and apply to any perturbative force – conservative or non-conservative. The Gaussian approach also allows one to use the osculating accelerations directly when performing the numerical averages, and facilitates use of an existing astrodynamics software system (i.e., GMAT, STK ^TM, FreeFlyer ^TM, etc.) as the basis for developing a mean element propagation capability. This research effort has implemented the mean element propagation algorithms using JPL’s MONTE astrodynamics toolkit for standard calculations such as coordinate transformations, osculating perturbing acceleration calls, and numerical propagations with DIVA [16]. MONTE is the core operational software used to navigate JPL space missions, and has been in use for almost a decade. The DIVA algorithm, the primary propagation routine in MONTE, is a variable-order, variable-step Adams method developed by Krogh and currently available on the web [17–19]. Variants of DIVA have been used extensively for over four decades, and recently Sharp [20] quantitatively compared it to other propagator packages demonstrating DIVA’s ability to accurately propagate solar system trajectories for thousands of years. The mean element tool couples the numerical averaging described in the prior section (i.e., Gaussian quadrature or CUBPACK) with numerical propagations performed by DIVA. Gauss’ variation of parameters and the perturbations of interest are now reviewed. All results in the following examples have been generated using a Linux workstation with two Intel Xeon ^TM×5687 quad-core processors operating at 3.60 GHz, a physical memory of 48 Gb, and a 64 bit RedHat Enterprise 5 operating system.

Gauss’ Variation of Parameters

Gauss’ variation of parameter equations can be represented as

$$ \left[\begin{array}{l} {\dot{{\boldsymbol{\alpha}}}}\\ {\dot{{\lambda}}} \end{array}\right]=\left[\begin{array}{l} 0\\ {n\left( a \right)} \end{array}\right]+\left[\begin{array}{l} \frac{\partial \boldsymbol{\alpha}} {\partial{\dot{\textbf{r}}}}\cdot \sum\limits_{\rho \in \mathrm{P}} {\delta \ddot{\textbf{r}}^{\rho}}\\ \frac{\partial \lambda} {\partial{\dot{\textbf{r}}}}\cdot \sum\limits_{\rho \in \mathrm{P}} {\delta \ddot{\textbf{r}}^{\rho}} \end{array}\right] $$

(7)

where $\dot {\textbf {r}}$ is the velocity vector between the satellite and the central body, $\delta \ddot {\textbf {r}}^{\rho }$are the perturbing accelerations. All quantities are expressed in a common inertial coordinate frame. For this study the set $P=\left \{ {Z,T,O,D,S} \right \}$ of perturbing accelerations that will be considered are:

• 1. Zonal harmonics (Z),

• 2. Tesseral harmonics (T),

• 3. Other body accelerations (O),

• 4. Atmospheric drag on a spherically shaped spacecraft (D),

• 5. Solar radiation pressure on a spherically shaped spacecraft (S).

The first bracket in Eq. 7 is $O\left (1 \right )$ and the second term is $O\left (\varepsilon \right )$ and is equivalent to the perturbing term $\varepsilon \textbf {f}\left ({\boldsymbol {\alpha } ,\lambda } \right )$ in Eq. 1. For orbit applications, the small parameter ε is dependent on the specific perturbation. For instance, the small parameter for the zonal harmonics is often J ₂ while for other body perturbations it is the ratio of the satellite’s semimajor axis to the other body’s apparent semi-major axis around the central body a/a ^O. The derivatives in Eq. 7 have been obtained by many authors for the equinoctial elements (c.f. Danielson et al. [21]), and, for convenience, have been repeated in the appendix. Each of the perturbations in set P is now examined.

Zonal Harmonic Perturbations

It should be noted that second order effects from J ₂ can be significant to specific problems. A numerical second-order averaging method is forthcoming; however, was not available for this research. For the cases examined in this paper, second-order effects did not significantly affect the results or the conclusions.

The non-spherical axial symmetric gravity acceleration perturbations (i.e., the zonal harmonics) from a central body can be expressed as the gradient of the following potential

$$ \delta \ddot{\textbf{r}}^{Z}=-\mathbf{\nabla} \frac{\mu} {r}\sum\limits_{l=2}^{\infty} {\frac{{R_{e}^{l}}} {r^{l}}J_{l} P_{l0} \left( {\sin \phi} \right)} $$

(8)

where $\left \{ {r,\phi ,L} \right \}$ are the planet-centric spherical coordinates of {radial distance, latitude, and East longitude}, R _e is the central body’s equatorial radius, $P_{lm} \left ({\sin \phi } \right )$ are the associated Legendre polynomials (which for the zonals have m≡0), $\left \{ {J_{l}} \right \}$ are the unnormalized zonal harmonic coefficients. A key observation regarding (8) for the numerical averaging is that the acceleration is dependent only on the spacecraft state x and not any other variables, such as the orientation of the central body (as will be the case with the tesseral harmonics). Considering only the zonal harmonics accelerations, Gauss’ equations take the functional form

$$ \left[\begin{array}{l} {\dot{{\boldsymbol{\alpha}}}}\\ {\dot{{\lambda}}} \end{array}\right]=\left[\begin{array}{l} 0\\ {n\left( a \right)} \end{array}\right]+\varepsilon \left[\begin{array}{ll} {\textbf{f}}^{\boldsymbol{\alpha} ,Z}\left( {\boldsymbol{\alpha} ,\lambda} \right)\\ {f^{\lambda ,Z}\left( {\boldsymbol{\alpha} ,\lambda} \right)} \end{array}\right]=\left[\begin{array}{l} 0\\ {n\left( a \right)} \end{array}\right]+\left[\begin{array}{llll} \frac{\partial \boldsymbol{\alpha} \left({\textbf{x}}\right)}{\partial {\dot{\textbf{r}}}}\cdot \delta \ddot{\textbf{{r}}}^{Z}\left({\textbf{x}}\right)\\ \frac{\partial \lambda \left({\textbf{x}}\right)}{\partial {\dot{\textbf{r}}}}\cdot \delta{\ddot{\textbf{{r}}}}^{Z}\left({\textbf{x}}\right) \end{array}\right], $$

(9)

which is an autonomous system that conforms to the basic averaging results identified in Eqs. 2 and 3.

Example 1

Consider a low altitude lunar orbiter with initial osculating and mean orbital elements³ given in Table 1 below.

Table 1 Initial conditions and parameters for frozen low lunar orbiter example

The selected elements are for a low-altitude ‘frozen’ orbit where the argument of periapsis ω and the eccentricity e librate with respect to each other. The only perturbation accelerations present are from the lunar zonal harmonics to the 50 ^th order (a sufficient size based on findings by Lara [23]). The e- ω phase space results are shown in Fig. 1 for a 5-yr propagation of the numerically averaged EOMs (labeled ‘mean’) and the propagation of the direct osculating EOMs (labeled ‘osc’). Note that the osculating EOMs are in standard Cartesian form and integrated using DIVA’s ability to directly integrate second-order equations; they are not in a VOP formulation. The results clearly show the libration oscillation which has a characteristic period of about ∼ 2.5 years. They also demonstrate that the averaged EOMs accurately capture the qualitative motion and have done so in a fraction of the computational cost/time of their osculating counterparts, as presented in Table 2.

Fig. 1

Argument of periapsis and eccentricity phase space of lunar orbiter

Table 2 Comparing 5-yr propagations of the numerically averaged EOMs to the osculating EOMs for the low lunar orbiter

Two different mean element propagations were executed, one with a 130 ^th-order Gaussian numerical quadrature and the other with CUBPACK set to an absolute tolerance of 1.0E-10 and a relative tolerance of 1.0E-7. The numerical integration tolerance for all propagations, mean and osculating, was set to 1.0E-10. The results illustrate the dramatic reduction in required function calls (and speed) needed by the mean element propagations over their osculating counterpart. The CUBPACK-based propagation required 100 times fewer function calls and was 215 times faster than the osculating propagation. The fixed-order Gaussian result is even faster; however, the selection of order 130 was only arrived at after experimenting with several different orders and consideration of the 50 ^th-degree zonal harmonic field. If the selected order is too low (say 100) the quadrature yields errors that cause the numerical integration routine to compensate via selecting progressively smaller step sizes resulting in significantly longer propagation times (of the same order as the osculating propagation). If the selected order is large, the averaging is accurate, but efficiency is lost during the propagation because the numerical integrator can only select step sizes that are consistent with its own error tolerance. That is, it cannot take advantage of the improved averaging accuracy because it is already operating at its limit of required accuracy. In comparison, the adaptive quadrature using CUBPACK worked well without such an investigation. This leads to a preliminary conclusion that the adaptive routines are useful for initial studies and establishing expected results. Then, with careful tuning, the analyst can select an appropriate fix-ordered method to maximize efficiency of parametric trade studies.

Tesseral/Sectorial Harmonic Perturbations

The non-spherical non-symmetric gravity acceleration perturbations (i.e., the tesseral/sectorial harmonics) from a central body can be expressed as the gradient of the following potential

$$ \delta \ddot{\textbf{{r}}}^{T}=\mathbf{\nabla} \frac{\mu} {r}\sum\limits_{l=2}^{\infty} {\sum\limits_{m=1}^{l} {\frac{{R_{e}^{l}}} {r^{l}}}} P_{lm} \left( {\sin \phi} \right)\left( {C_{lm} \cos \left( {mL} \right)+S_{lm} \sin \left( {mL} \right)} \right) $$

(10)

where again $P_{lm} \left ({\sin \phi } \right )$ are the associated Legendre polynomials, now with m≠0 and $\left \{ {C_{lm} ,S_{lm}} \right \}$ are the unnormalized harmonic coefficients (note that J _l =−C _l0). Unlike the zonal harmonic accelerations, accelerations induced by the tesseral harmonics $\left ({m\ne l} \right )$ and sectorial harmonics $\left ({m=l} \right )$ are dependent on the central body’s orientation relative to the spacecraft, in particular via the sidereal angle 𝜃. This too can be a ‘fast’ variable or ‘slow’ one depending on the selected central body. For instance the Earth’s sidereal period is ∼ 1 day while Venus’ sidereal period is 243 days. The relationship between the mean longitude λ and sidereal angle 𝜃 can be made explicit by computing the Fourier expansion of Eq. 10 in equinoctial elements as has been done by several authors including: Cefola [24], McClain [6], and Danielson et al. [21]. The current analysis can benefit by examining the formal Fourier series expansion in a functional form (for generality this also includes the zonal harmonics)

$$ \varepsilon \left[\begin{array}{ll} {\textbf{f}}^{\boldsymbol{\alpha} ,T}\left( {\boldsymbol{\alpha} ,\lambda ,\theta} \right)\\ f^{\lambda ,T}\left( {\boldsymbol{\alpha} ,\lambda ,\theta} \right) \end{array}\right]=\left[\begin{array}{llll} \frac{\partial \boldsymbol{\alpha} \left(\textbf{x}\right)}{\partial{\dot{\textbf{r}}}}\cdot \delta \ddot{\textbf{{r}}}^{T}\left(\textbf{x}\right)\\ \frac{\partial \lambda \left({\textbf{x}}\right)}{\partial\dot{\textbf{r}}}\cdot \delta \ddot{\textbf{{r}}}^{T}\left(\textbf{x}\right) \end{array}\right]=\sum\limits_{j=-\infty}^{\infty} {\sum\limits_{m=0}^{l} \textbf{f}_{jm}^{T} (\boldsymbol{\alpha} )e^{i(j\lambda -m\theta)}} $$

(11)

where $i\equiv \sqrt {-1}$ and $\textbf {f}_{jm}^{T} (\boldsymbol {\alpha } )$ are Fourier coefficients, which are often associated with infinite expansions as well that need to be carefully truncated in any practical analytic averaging theory. In a purely numerical approach to averaging, the ${\textbf {f}}_{jm}^{T} (\boldsymbol {\alpha } )$ coefficients functions do not need to be explicitly determined to perform the averaging. However, the relationships involving the mean longitude λ and the sidereal angle 𝜃 need to be explicitly exposed (as has been done in Eq. 11) to conduct a correct numerical averaging analysis. Examination of Eq. 11 reveals the possibility of three important cases:

• 1. Resonant Case: The mean longitude rate $\dot {{\lambda } }$ (∼ mean motion n) is O(1) and the sidereal rate $\dot {{\theta } }$ is O(1) and initial conditions are such that a deep resonance or shallow resonance exists. Deep resonance exists when the mean longitude and the sidereal rate are commensurate. That is, there exists a rational ratio of two integers that satisfies

  $$ \frac{\dot{{\lambda}}}{\dot{{\theta}}}=\frac{Q}{P}\to Q:P\;\text{resonance for}\, Q\;\text{and}\, P\;\text{integers.}. $$

  (12)

  For instance, at Earth a resonance of Q:P=2:1 is a ∼ 12 hr orbit. A shallow (or near) resonance occurs when $\dot {{\lambda }}/\dot {{\theta }}$ are close to Q/P in some sense. Typically, for the resonance to be significant Q and P should be smaller integers. That is a 2:1 resonance that excites gravity harmonics of order 2 will have much more effect than, say, a 30:1 resonance that excites the typically much smaller order 30 harmonics.

• 2. Non-resonant Case: The mean longitude rate $\dot {{\lambda } }$ (∼ mean motion n) is O(1) and the sidereal rate $\dot {{\theta } }$ is O(1) and the initial conditions are such that no significant resonances exist (i.e., an orbit that is outside of a shallow resonance region). In this case, the integers that satisfy Eq. 12 are too large to be significant. The conditions that need to exist to make this determination are the subject of Kolmogorov-Arnold-Moser (KAM) theory of nonlinear dynamical systems theory [25].

• 3. Adiabatic (or Two Time Scales) Case: The mean longitude rate $\dot {{\lambda } }$ (∼ mean motion n) is O(1) and the sidereal rate $\dot {{\theta } }$ is O(ε). This is another non-resonant case; however, here the sidereal rate is slow enough to be considered a constant during an averaging interval. This applies to Venus, sometimes the Moon, and often other bodies that are tidally locked in a 1:1 spin resonance. Again, the integers that satisfy Eq. 12 are too large to be of importance. Differences with the previous non-resonant case will become apparent in the following development.

Each of these cases will be treated separately.

Case 1- Resonance

In deep resonance or shallow resonance, the commensurability of the mean motion with the planet rotation rate introduces a new slow variable that can be revealed in Eq. 11 by introducing the resonant node ψ. It is defined as

$$ \psi\triangleq P\lambda -Q\theta . $$

(13)

This definition of the node is consistent with the equinoctial elements in that it is non-singular for orbits that are circular or have inclinations below 180 ^∘. However, for missions where repeating ground tracks are relevant, this definition is not as useful as the following that accounts for the fact that the orbital plane and the line of apsides precess when orbiting an oblate central body. This form of the node, called the stroboscopic node ψ _s by Gedeon [26], is defined using

$$ \psi_{s}\triangleq P\left( {\lambda -{\Omega}} \right)-Q\left( {\theta -{\Omega}} \right) $$

(14)

where it should be noted that ψ _s becomes undefined for equatorial orbits (in this event use of the resonant node, given in Eq. 13, should be made). A particular quantity of interest to repeating ground track orbits is the separation between two consecutive equator crossings, called the ground track shift λ _s , and is found using

$$ \lambda_{s} =P_{N} \left({\dot{{\theta}}-\dot{{\Omega}}}\right) $$

(15)

where the nodal period P _N of the orbit is approximately

$$ P_{N} \cong \frac{2\pi} {\dot{{M}}+\dot{{\omega} }}=\frac{2\pi} {\dot{{\lambda} }-\dot{{\Omega}}}. $$

(16)

The condition on λ _s for a ground track to repeat every Q orbits in P days is given by

$$ Q\lambda_{s} =2\pi P, $$

(17)

which is equivalent to the following condition

$$ P\left( {\dot{{\lambda} }-\dot{{\Omega} }} \right)-Q\left( {\dot{{\theta} }-\dot{{\Omega} }} \right)=0\to \dot{{\psi}}_{s} =0. $$

(18)

Hence the stroboscopic node is stationary for an exactly repeating ground track. Reformulating Gauss’ equations with a change of variables using these two definitions is now examined.

First, examine a change of variable to Gauss’ equations in Eq. 7 using the resonant node ψ definition given in Eq. 13. Executing the change of variable leads to a new variation of parameter formulation that takes the form

$$ \left[\begin{array}{c} {\dot{{\boldsymbol{\alpha}}}}\\ {\dot{{\psi}}} \end{array}\right]=\left[\begin{array}{cc} \frac{\partial \boldsymbol{\alpha}} {\partial \dot{\textbf{r}}}\cdot \sum\limits_{\rho \in \mathrm{P}} {\delta \ddot{\textbf{{r}}}}^{\rho}\\ {Pn\left( a \right)-Q\dot{{\theta} }+P\frac{\partial \lambda} {\partial\dot{\textbf{r}}}}\cdot \sum\limits_{\rho \in \mathrm{P}} {\delta {\ddot{\textbf{r}}}}^{\rho} \end{array}\right] $$

(19)

where, in resonance or near resonance, Q and P have been selected to satisfy the following property

$$ \dot{{\psi}}=P\dot{{\lambda}}-Q\dot{{\theta}}=P\left( {n+\dot{{\omega} }+\dot{{\Omega} }} \right)-Q\dot{{\theta} }=O\left( \varepsilon \right). $$

(20)

Note that the change of variables is a generic change to the system; no restriction to only tesseral harmonics being active in Eq. 19 has been made. Hence, if other perturbations (i.e., zonal harmonics, other bodies, drag, and solar pressure) are active they will also participate in the new system of equations as indicated in Eq. 19. This change of variables has eliminated the $O\left (1 \right )$ dependence on the isolated mean motion resonance, and now all of the components of the right hand side of Eq. 19 are $O\left (\varepsilon \right )$ or higher. To affect the change of variable in the acceleration expressions $\delta {\ddot {\textbf {r}}}^{\rho }$ in Eq. 19 the following expressions prove convenient

$$ \begin{array}{l} \theta (t)=-\frac{1}{Q}\psi (t)+\frac{P}{Q}\lambda (t), \\ \lambda (t)=n(t-t_{o} )+\lambda_{o} . \end{array} $$

(21)

For all perturbations other than the tesseral harmonics, this change of variable has no impact on the acceleration because they have no dependence on the sidereal angle; only the tesseral harmonics require a special treatment for this change of variable. Hence, going forward with the analysis in this section the perturbation expressions have been restricted to only the tesseral harmonics. Given that, converting the argument to the exponential in Eq. 11 to a resonant node formulation via substituting Eq. 21 into Eq. 11 yields

$$ j\lambda \left( t \right)-m\theta \left( t \right)=\left( {j-m\frac{P}{Q}} \right)\lambda (t)+\frac{m}{Q}\psi (t)=\left( {jQ-mP} \right)\frac{\lambda (t)}{Q}+\frac{m}{Q}\psi (t) $$

(22)

and produces the following explicit expression for the tesseral harmonics

$$ \varepsilon \left[\begin{array}{ccc} \textbf{f}^{\boldsymbol{\alpha} ,T}\left({\boldsymbol{\alpha} ,\psi ,\lambda} \right)\\ {f^{\psi ,T}\left( {\boldsymbol{\alpha} ,\psi ,\lambda} \right)} \end{array}\right]=\left[\begin{array}{ccc} \frac{\partial \boldsymbol{\alpha}} {\partial \dot{\textbf{r}}}\cdot \delta \ddot{\textbf{r}}^{T}\\ P\frac{\partial \lambda} {\partial \dot{\textbf{r}}}\cdot \delta \ddot{\textbf{r}}^{T} \end{array}\right]=\sum\limits_{j=-\infty}^{\infty} \sum\limits_{m=1}^{l} \textbf{P}\odot \textbf{f}_{jm}^{T} (\boldsymbol{\alpha} )\exp i\left[ {\frac{m}{Q}\psi} \right]\exp i\left[ {\left( {jQ-mP} \right)\frac{\lambda} {Q}} \right] $$

(23)

where $\textbf {P}\equiv \left \{ {1,1,1,1,1,P} \right \}$, and ⊙ is the element-wise product of the two vectors P and $\mathbf {f}_{jm}^{T} (\boldsymbol {\alpha })$. Near a resonance the resonant node is a slowly varying variable by the property in Eq. 20 and the mean longitude continues to be the fast variable.

In a first order formulation of averaging, the node is treated as a constant, and the mean longitude is averaged using

$$\begin{array}{@{}rcl@{}} \varepsilon \left[\begin{array}{cc} {\bar{\textbf{f}}}^{\boldsymbol{\alpha} ,T}\left({\boldsymbol{\alpha} ,\psi} \right)\\ {\bar{{f}}^{\psi ,T}\left( {\boldsymbol{\alpha} ,\psi} \right)} \end{array}\right] &&\equiv \frac{1}{2\pi N}\int\limits_{-N\pi}^{N\pi}\sum\limits_{j=-\infty}^{\infty} \sum\limits_{m=1}^{l} {\textbf{P}}\odot \textbf{f}_{jm}^{T} (\boldsymbol{\alpha})\exp i\left[{\frac{m}{Q}\psi} \right]\exp i\left[{\left( {jQ-mP} \right)\frac{\lambda} {Q}} \right] d\lambda \\ &&=\frac{1}{2\pi N}\sum\limits_{j=-\infty}^{\infty} \sum\limits_{m=1}^{l} {\textbf{P}}\odot \textbf{f}_{jm}^{T} (\boldsymbol{\alpha} )\exp i\left[{\frac{m}{Q}\psi} \right]\int\limits_{-N\pi}^{N\pi} {\exp i\left[ {\left( {jQ-mP} \right)\frac{\lambda} {Q}} \right]}\\ &&=\frac{Q}{\pi N}\sum\limits_{j=-\infty}^{\infty} {\sum\limits_{m=1}^{l} {\textbf{P}}\odot \textbf{f}_{jm}^{T} (\boldsymbol{\alpha} )\exp i\left[{\frac{m}{Q}\psi} \right]}\frac{\sin \left[{\frac{N}{Q}\pi \left({jQ-mP} \right)}\right]}{jQ-mP}. \end{array} $$

(24)

where the integral number N of the averaging operation is indeterminate at this point. If N is assumed to be equal to Q then the following average results

$$\begin{array}{@{}rcl@{}} \begin{array}{ll} \varepsilon \left[\begin{array}{ll} {\bar{\textbf{f}}}^{\boldsymbol{\alpha} ,T}\left({\boldsymbol{\alpha} ,\psi} \right)\\ {\bar{{\!\!f}}^{\psi ,T}\left( {\boldsymbol{\alpha} ,\psi} \right)} \end{array}\right] =\sum\limits_{j=-\infty}^{\infty} \sum\limits_{m=1}^{l} {\textbf{P}}\odot \textbf{f}_{jm}^{T} (\boldsymbol{\alpha} )\exp i\left[ {\frac{m}{Q}\psi} \right],& {N=Q,\;mP=jQ} \\ {} \varepsilon \left[\begin{array}{ll}\\[-12pt] {\bar{\textbf{f}}}^{\boldsymbol{\alpha} ,T}\left({\boldsymbol{\alpha} ,\psi}\right)\\ {\bar{{\!f}}^{\psi ,T}\left( {\boldsymbol{\alpha} ,\psi} \right)} \end{array}\right] =0,& {N=Q,mP\ne jQ} \end{array}.\\ \end{array} $$

(25)

which is consistent with McClain’s [6] findings. Equation 25 illustrates that terms satisfying m P=j Q are resonant long-period terms and survive the averaging, and those terms with m P≠j Q are short periodic and average to zero. Note that for the zonal terms (m= 0) only the j= 0 terms survive the averaging. However, in a numerical averaging approach performing the quadrature over N integral periods can be computationally prohibitive. This motivates further investigation of Eq. 24. Setting N= 1 reveals the following

$$ \varepsilon \left[\begin{array}{cc} {\bar{\textbf{f}}}^{\boldsymbol{\alpha} ,T}\left( {\boldsymbol{\alpha} ,\psi} \right)\\ {\bar{{f}}^{\psi ,T}\left( {\boldsymbol{\alpha} ,\psi} \right)} \end{array}\right]=\begin{array}{cc} {\frac{Q}{\pi} \sum\limits_{j=-\infty}^{\infty} {\sum\limits_{m=1}^{l} {\textbf{P}}\odot \textbf{f}_{jm}^{T} (\boldsymbol{\alpha} )\exp i\left[{\frac{m}{Q}\psi} \right]}} \frac{\sin \left[ {\frac{\pi} {Q}\left( {jQ-mP} \right)}\right]}{jQ-mP}, & {N=1} \end{array}. $$

(26)

Examining this result shows that some terms in the argument for sine will be fractional and survive, hence contributing short periodic terms. However, if the values for m are restricted to those that are integral multiples of Q (i.e., setting m=r Q where s is an integer), then the averaging isolates the long period terms (i.e., those that satisfy j=s P) and still, appropriately, eliminates the short periodic terms (i.e. those that satisfy j≠s P). This is expressed as follows

$$ \begin{array}{ll} \varepsilon \left[\begin{array}{ll} {\bar{\textbf{f}}}^{\boldsymbol{\alpha} ,T}\left({\boldsymbol{\alpha} ,\psi} \right)\\ {\bar{{f}}^{\psi ,T}\left({\boldsymbol{\alpha} ,\psi} \right)} \end{array}\right]=\sum\limits_{s<int(l/Q)} {\textbf{P}\odot \textbf{f}_{\left({sP} \right)\left( {sQ} \right)}^{T} (\boldsymbol{\alpha} )\exp i\left[ {s\psi}\right],}& N=1,\;m=sQ,\,j=sP,s<int(l/Q)\\ \varepsilon \left[\begin{array}{ll} {\bar{\textbf{f}}}^{\boldsymbol{\alpha} ,T}\left({\boldsymbol{\alpha} ,\psi} \right)\\ {\bar{{f}}^{\psi ,T}\left( {\boldsymbol{\alpha} ,\psi} \right)} \end{array}\right]=0, & {N=1,\;m=sQ,\,j\ne sP} \end{array}. $$

(27)

The practical procedure for restricting m=s Q is to explicitly eliminate from consideration those coefficients $\left \{{C_{lm} ,S_{lm}} \right \}$ from the gravity field that do not satisfy the condition before the averaging operation. For example, in a 4 x 4 gravity field and a Q:P=2:1 resonance (i.e., a 12 hr Earth orbiter) the tesseral C _{l m} terms retained in the field would be $\left \{ {C_{22} ,C_{32} ,C_{42} ,C_{44}} \right \}$ while the C _{l m} terms that are set to zero would be $\left \{ {C_{21} ,C_{31} ,C_{33} ,C_{41} ,C_{43}} \right \}$. Similar results apply for the S _{l m} coefficients. This procedure of setting appropriate terms in the field to zero, and averaging over the interval −π<λ<π yields a more efficient numerical averaging procedure.

Now turning to the repeating ground track formulation using the stroboscopic node ψ _s as defined in Eq. 14, an appropriate change of variables to Gauss’ equations yields

$$ \left[\begin{array}{c} {\dot{{\boldsymbol{\alpha}}}}\\ {\dot{{\psi}}_{s}} \end{array}\right]=\left[\begin{array}{c} {\frac{\partial \boldsymbol{\alpha}} {\partial \dot{\textbf{r}}}}\cdot\sum\limits_{j\in \mathrm{P}} {\delta \ddot{\textbf{r}}}^{j}\\ {Pn\left( a \right)-Q\dot{{\theta}}+P\frac{\partial \lambda} {\partial \dot{\textbf{r}}}}\cdot\sum\limits_{j\in \mathrm{P}} {\delta {\ddot{\textbf{r}}}}^{j}+\left( {P-Q} \right)\frac{\partial {\Omega}} {\partial {\dot{\textbf{r}}}}\cdot \sum\limits_{j\in \mathrm{P}} {\delta \ddot{\textbf{r}}^{j}} \end{array}\right]. $$

(28)

The appearance of the longitude of the ascending node in Eq. 28 has not introduced an additional independent variable because it can be related to the equinoctial elements via the following

$$ \begin{array}{l} \sin {\Omega} =\frac{p}{\sqrt {p^{2}+q^{2}}},\\ \cos {\Omega} =\frac{q}{\sqrt {p^{2}+q^{2}}},\\ \dot{{\Omega} }=\frac{q\dot{{p}}-p\dot{{q}}}{p^{2}+q^{2}},\\ \frac{\partial {\Omega}} {\partial \dot{\textbf{r}}}=\frac{q}{p^{2}+q^{2}}\frac{\partial p}{\partial \dot{\textbf{r}}}-\frac{p}{p^{2}+q^{2}}\frac{\partial q}{\partial \dot{\textbf{r}}}. \end{array} $$

(29)

Following a similar process as with the resonant node, it can be shown that the functional form of the equinoctial rates due to the non-spherical gravity harmonics as a function of the stroboscopic node ψ _s and the other equinoctial elements takes the form

$$ \varepsilon \left[\begin{array}{cc} \textbf{f}^{\boldsymbol{\alpha} ,T}\left({\boldsymbol{\alpha} ,\psi_{s} ,\lambda}\right)\\ {f^{\psi ,T}\left( {\boldsymbol{\alpha} ,\psi_{s} ,\lambda} \right)} \end{array}\right] =\sum\limits_{j=-\infty}^{\infty} {\sum\limits_{m=1}^{l} \left\{\begin{array}{l} \left[{\textbf{P}}\odot \textbf{f}_{jm}^{T} (\boldsymbol{\alpha} )+ {\textbf{1}}\odot \left({\frac{(P-Q)q}{p^{2}+q^{2}}f_{jm}^{p,T} (\boldsymbol{\alpha} )-\frac{(P-Q)p}{p^{2}+q^{2}}f_{jm}^{q,T} (\boldsymbol{\alpha} )} \right) \right]\times\\ \exp i\left[{m\left( {\frac{1}{Q}\psi_{s} +\frac{P-Q}{Q}{\Omega}} \right)} \right]\exp i\left[{\left( {jQ-mP} \right)\frac{\lambda} {Q}} \right] \end{array}\right\}} $$

(30)

where $\textbf {1}\triangleq \left \{ {0,0,0,0,0,1} \right \}$. The resulting equation has the same functional dependency on the mean longitude as in Eq. 23. Continuing with the averaging analysis in the same fashion as was done for the resonant node yields a result that is similar in form to Eq. 27, that is

$$ \begin{array}{ll} \varepsilon \left[\begin{array}{l} {\bar{\textbf{f}}}^{\boldsymbol{\alpha},T}\left({\boldsymbol{\alpha} ,\psi_{s}}\right)\\ {\bar{{f}}^{\psi ,T}\left({\boldsymbol{\alpha} ,\psi_{s}} \right)} \end{array}\right]=\sum\limits_{s<int\left( {l/Q} \right)} \begin{array}{l} \left[ {\text{\textbf{P}}\odot \text{\textbf{f}}_{\left( {sP} \right)\left( {sQ} \right)}^{T} (\boldsymbol{\alpha} )+\text{\textbf{1}}\odot \left( {\frac{(P-Q)q}{p^{2}+q^{2}}f_{\left( {sP} \right)\left( {sQ} \right)}^{p,T} (\boldsymbol{\alpha} )-\frac{(P-Q)p}{p^{2}+q^{2}}f_{\left( {sP} \right)\left({sQ}\right)}^{q,T} (\boldsymbol{\alpha} )}\right)}\right] \\ \times \exp i\left[ {r\left( {\psi_{s} +\left( {P-Q} \right){\Omega}} \right)} \right],\quad N=1,\;m=sQ,\,j=sP,s<int(l/ {Q}) \end{array}\\ \varepsilon \left[\begin{array}{ll} \\[-10pt] \bar{\textbf{f}}^{\boldsymbol{\alpha} ,T}\left( {\boldsymbol{\alpha} ,\psi_{s}} \right)\\ {\bar{{f}}^{\psi ,T}\left( {\boldsymbol{\alpha} ,\psi_{s}} \right)} \end{array}\right]=0,\quad N=1,\;m=rQ,\,j\ne sP \end{array} $$

(31)

The same restriction on the included gravity field terms applies, namely restricting to those degree terms that conform to m=s Q.

Case 2 – Non-Resonant: When both the mean longitude and sidereal rate are of the same order and not resonant, Eq. 11 can be examined directly with a focus on the tesserals only (m≠0). Note that terms with j=0 yields terms with frequencies of $m\dot {{\theta } }$ (at Earth these are called the ‘m-dailies’), which for tesserals $\left \{ {C_{l1} ,S_{l1}} \right \}$ produce oscillatory effects at the same frequency as the planet rotation; often a lower frequency than the spacecraft orbit frequency but still ‘fast’ enough to justify averaging. The averaging operator that is appropriate is a double average over the two angles; performing this average yields

$$\begin{array}{@{}rcl@{}} \varepsilon \left[\begin{array}{ll} {\bar{{\bar{\textbf{f}}}}}^{\boldsymbol{\alpha} ,T}\left( \boldsymbol{\alpha} \right)\\ {\bar{{\bar{{f}}}}^{\lambda ,T}\left( \boldsymbol{\alpha} \right)} \end{array}\right] &&\equiv \frac{1}{4\pi^{2}}\int\limits_{-\pi}^{\pi} {\int\limits_{-\pi}^{\pi} {\sum\limits_{j=-\infty}^{\infty} {\sum\limits_{m=1}^{l} {\textbf{f}}_{jm}^{T} (\boldsymbol{\alpha} )\exp i\left[{j\lambda-m\theta} \right]}}} d\lambda d\theta \\ &&=\frac{1}{4\pi^{2}}\sum\limits_{j=-\infty}^{\infty} {\sum\limits_{m=1}^{l} {\textbf{f}}_{jm}^{T} (\boldsymbol{\alpha})\int\limits_{-\pi}^{\pi} {\exp i\left[{j\lambda}\right]} d\lambda \int\limits_{-\pi}^{\pi} {\exp i\left[ {-m\theta} \right]}}d\theta \\ &&=0. \end{array} $$

(32)

Clearly, the non-resonant tesseral harmonics yield no long period or secular effects on the orbit. That is, the tesserals introduce only short period terms that are multiples of the mean longitude and the sidereal rate. The result in Eq. 32 leads to the following conclusion: For satellite orbits that do not have significant mean motion resonances and $\dot {{\theta }}=O\left (1 \right )$ , average over only the zonal harmonic terms and explicitly exclude the tesseral harmonics in the mean element propagation.

Case 3 - Adiabatic (or Two Time Scales): This case is also non-resonant, but now $\dot {{\theta }}\ll \dot {{\lambda }}$ such that $\dot {{\theta }}$ can be considered constant (or adiabatic) over the averaging interval of the mean longitude. As such, no change of variables is required and Eq. 11 can be examined directly (with the zonals included)

$$\begin{array}{@{}rcl@{}} \varepsilon \left[\begin{array}{ll} \bar{\textbf{f}}^{\boldsymbol{\alpha} ,T}\left({\boldsymbol{\alpha} ,\theta} \right)\\ {\bar{{f}}^{\lambda ,T}\left({\boldsymbol{\alpha} ,\theta} \right)} \end{array}\right]&&\equiv \frac{1}{2\pi} \int\limits_{-\pi}^{\pi} {\sum\limits_{j=-\infty}^{\infty} {\sum\limits_{m=0}^{l} {\text{{\textbf f}}_{jm}^{T} (\boldsymbol{\alpha} )\exp i\left[ {j\lambda -m\theta} \right]}}} d\lambda, \\ &&=\frac{1}{2\pi} \sum\limits_{j=-\infty}^{\infty} {\sum\limits_{m=0}^{l} {\textbf{f}}_{jm}^{T} (\boldsymbol{\alpha} )\exp i\left[ {-m\theta} \right]\int\limits_{-\pi}^{\pi} {\exp i\left[ {j\lambda} \right]}} d\lambda, \\ &&=\sum\limits_{m=0}^{l} {\text{\textbf{f}}_{0m}^{T} (\boldsymbol{\alpha} )\exp i\left[ {-m\theta} \right]}. \end{array} $$

(33)

With the mean longitude eliminated the numerical propagator’s step size is determined by the terms with $m\dot {{\theta }}$ (assuming the other angular rate terms perturbing α remain of $O\left (\varepsilon \right ))$, and as m increases the frequencies increase. If the coefficients of these terms $\textbf {f}_{jm}^{T} (\boldsymbol {\alpha })$ do not diminish fast enough, then they could cause the numerical propagator to select small step sizes and diminish the utility of the numerical averaging method. Clearly the presence of these frequencies depends on the order m of the gravity field that an analyst has included in their analysis – the higher the order the more abundant the higher frequency terms. This indicates the need to perform another average over selected terms in Eq. 33; however a more direct method is to simply limit the order of the gravity field to ensure short period terms from the sidereal rotation have been eliminated. Later examples with Venus will illustrate the procedure.

Example of Case 1

Consider a Mars orbiter that is in a deep 2:1 resonance with Mars’ rotation rate. The initial conditions and associated parameters are indicated below in Table 3. The orbit was selected to have a repeating ground track with initial stroboscopic node to induce a libration near a stable fixed point in the semi-major axis stroboscopic node phase space (see Ely [1] for a discussion of this phase space phenomenon). Furthermore, the selected inclination induces a critical inclination-like effect where the line of apsides oscillates, in this case between 269.5 ^∘ and 269.9 ^∘ with a period of ∼ 20 years. A surprising result is the inclination, at 55 ^∘, is much lower than is typical of critically inclined orbits at Earth.

Table 3 Initial conditionsFootnote

The initial mean elements were obtained from the initial osculating elements using a first-order near-identity trans-formation that was derived using the methods described in the companion paper ‘Transforming Mean and Osculating Elements using Numerical Methods,’ also written by the author.

and parameters for Mars resonant orbiter example

For the numerical average computations, the 20 ×20 field is restricted to include only those orders that are multiples of Q=2 (as required in the preceding theory). The numerical averaging results (labeled ‘mean’) and the associated osculating results (labeled ‘osc’) are shown in Fig. 2. The figure contains two subplots, the top plot is the $\left ({a,\psi _{s}} \right )$ phase plane showing the expected libration between the mean semi-major axis and the mean stroboscopic node with period near 200 days, and the bottom plot is the ground track. The mean element solution correctly captures the resonant, long-period motions without the ‘blur’ associated with short periodic oscillations present in the osculating trajectory. Also note that in the ground track plot (bottom), the mean orbit overlays the osculating orbit so that they are indistinguishable at the resolution of the plot. In fact, the repeating ground track of the mean orbit design could be further refined via additional iterations on initial values for $\left ({a,\psi _{s}} \right )$ that approach the fixed-point solution with near zero amplitude oscillations in the phase space. This would be difficult to do with the osculating orbits because even at an exact mean-fixed point the osculating solution oscillates around this point.

Fig. 2

Semimajor axis solution for an elliptical and inclined Mars orbiter in a 2:1 resonance

Tabular results of the propagation performance are presented in Table 4. Two different mean element propagations were executed, one with an 80 ^th-order Gaussian numerical quadrature and the other with CUBPACK set to an absolute tolerance of 1.0E-10 and a relative tolerance of 1.0E-7. The numerical integration tolerance for all propagations, mean and osculating, was set to 1.0E-10. Relative to the zonal-only results given in Table 2 the performance benefit of the averaging is not as pronounced. Nonetheless when doing parametric design, Monte Carlo studies, or any orbit propagation process that involves large number of propagations such a speed up can become significant. As with the zonal-only results, Gaussian averaging retains a relative performance advantage over CUBPACK averaging; hence, a design process combining both techniques would prove to be most effective. In fact, a process of comparing Gaussian averaged results with different quadrature orders with a CUBPACK-based result until the trajectory differences are minimized would lead to a minimally sufficient Gaussian quadrature order. This order would be sufficient to capture the fastest short period terms with the most significant amplitudes, while relegating terms with even faster periods and smaller amplitudes as being insignificant. Finally, for comparison, the orbit specified in Table 3 was also propagated using the semi-analytical propagation tool developed by Kwok [9]. The results (not shown in the figure) were identical to within the single precision output level of the semi-analytic tool. The propagation speed was 2.2 seconds thus; in this case, the two tool’s propagation efficiency was commensurate.

Table 4 Comparison of numerically averaged EOMs 5-yr propagation to osculating EOMs for the Mars resonant orbiter

Example of Case 3 with $\dot {{\theta }} \ll \dot {{\lambda }}$

Consider an orbiter at Venus with initial conditions similar to the Magellan orbiter as given below in Table 5. Two scenarios are examined. In the first scenario the numerical averaging technique will include only the zonal harmonics through degree 10, and in the second scenario the full 10 ×10 field will be included. The osculating propagation will include the 10 ×10 field in both propagations. Recall, that the Venus’ sidereal rate is slow (with a 243-day period), hence can be treated as a slowly varying variable in the EOMs and retained in the mean element propagation. Results of a 10-year propagation for the eccentricity are shown in Fig. 3. The mean and osculating solutions with the full 10 ×10 field overlay each other (their differences shown in the right plot), while the mean solution with only the zonals (10 ×0) exhibits only a secular-like behavior on this time scale. Indeed, 200-year propagations (not shown) yield an eccentricity behavior that is indeed long-period (and not secular). The difference between the results illustrates the tesseral harmonics long-period effects (on scales of hundreds of days) are small relative to the 0.03 eccentricity change induced by the zonals over the 10-year period. Here the zonals are sufficient for capturing the long-term motion of the satellite. The numerical averaging in both mean cases used CUBPACK set to an absolute tolerance of 1.0E-10 and a relative tolerance of 1.0E-7. Both averaging cases were faster than their osculating counterpart with the results shown in Table 6. The numerical integration tolerance for all propagations, mean and osculating, was set to 1.0E-10. In this example, the zonal-only solution provides a sufficient representation of the long period motion and provides an extremely efficient model for orbit design. As has been seen in the prior cases, using a properly selected Gaussian numerical averaging would further improve efficiency. Indeed, a zonal-only case with Gaussian order 48 averaging ran in 0.26 seconds.

Table 5 Initial conditions and parameters for Venus orbiter example

Fig. 3

Eccentricity solutions for a Venus orbiter. Note that the ‘mean with a 10x10 field’ (green) and ‘osc with 10x10 field’ (blue) solutions overlay each other with their differences shown in plot at the right. The ‘mean with 10x0 field’ (red) solution appears secular in this time scale without any apparent long period motion. Differences between the osculating with 10 x 10 field (blue) and mean with 10 x 10 field (green) shown at right

Table 6 Comparison of numerically averaged EOMs 10-yr propagation to osculating EOMs for the Venus orbiter

Other Body Perturbations

Perturbation accelerations from another celestial body can be modeled with the following expression

$$ \delta \ddot{\textbf{r}}^{O}=\mu^{O} \left(\frac{\textbf{r}^{C\to O}-{\textbf{r}}} {\left|{\textbf{r}}^{C\to O}-\textbf{r}\right|^{3}} -\frac{\textbf{r}^{C\to O}}{\left|{\textbf{r}}^{C\to O}\right|^{3}}\right) $$

(34)

where r ^C→O is the vector from the central body to the perturbing body and μ ^O is the gravitational constant of the perturbing body. If there are several perturbing bodies then Eq. 34 applies to each body and the total acceleration is generated via summing the individual contributors. Clearly, Eq. 34 indicates a dependency on both the state of the satellite and the other body. This introduces a time dependency that impacts the averaging process and stems from the orbital motion of the other body. Typically, the associated orbital motion is slow and the other body’s position can be treated as a constant over the satellite’s mean longitude averaging interval. As the period reduces, there is a resultant reduction in the integrator step size to accommodate the increasing frequencies present in the single averaged equations. If the frequencies get too large, a second average over the other bodies mean longitude may be warranted. The choice to do this is dependent on the specific problem being analyzed. As with the tesseral harmonics, an explicit Fourier expansion in the equinoctial elements can be performed with an example of a specific expansion in equinoctial elements developed by Giacaglia [29]. A formal expansion in the satellite’s mean longitude λ and the other body’s mean longitude λ ^O (of its apparent orbit around the central body) takes the form

$$ \varepsilon \left[\begin{array}{ll} {\textbf{f}}^{\boldsymbol{\alpha} ,O}\left( {\boldsymbol{\alpha} ,\lambda ,\lambda^{O}} \right)\\ {f^{\lambda ,O}\left( {\boldsymbol{\alpha} ,\lambda ,\lambda^{O}} \right)} \end{array}\right]\triangleq\left[\begin{array}{llll} {\frac{\partial \boldsymbol{\alpha} \left({\textbf{x}}\right)}{\partial \dot{\textbf{r}}}}\cdot \delta \ddot{\textbf{r}}^{O}\left({\textbf{x}}\right)\\ {\frac{\partial \lambda \left(\textbf{x}\right)}{\partial \dot{\textbf{r}}}}\cdot \delta \ddot{\textbf{r}}^{O}\left(\textbf{x}\right) \end{array}\right]=\sum\limits_{j=-\infty}^{\infty} {\sum\limits_{t=-\infty}^{\infty} {\textbf{f}}_{jt}^{O} (\boldsymbol{\alpha} )e^{i(j\lambda -t\lambda^{O})}}. $$

(35)

Compared to Eq. 11, this result is very similar to the tesseral case with a few subtle differences that will be explored. For most practical situations there are no significant resonances between the two mean longitude rates. Examination of Eq. 35 shows that there exist some combinations of $\left \{ {j,t} \right \}$ that result in a resonance. But as j or t increase, the coefficients $\textbf {f}_{jt}^{O} (\boldsymbol {\alpha })$ diminish in magnitude for a convergent Fourier series. These higher resonances are not significant in most situations on time scales of order $O\left ({1/\varepsilon }\right )$ (again these statements can be made more precise via using the KAM theorem). Hence, resonances with other bodies will not be considered further. With this elimination, there are two distinct cases that need to be examined:

• 1. Adibatic Single Average Case: The other body mean longitude rate is sufficiently slow $\dot {{\lambda } }^{O}\ll \dot {{\lambda } }$ such that $\dot {{\lambda }}^{O}=O\left (\varepsilon \right )$, as will be seen this case involves the typical single average over the satellite’s mean longitude λ.

• 2. Non-Adiabatic Double Average Case: The other body mean longitude rate is still slow $\dot {{\lambda } }^{O}<\lambda$ however the order of the rate is not distinctly between zeroth and first; that is, $O(\varepsilon )<\dot {{\lambda }}^{O}<O(1)$. In this scenario a second average over the other body’s mean longitude λ ^O may be warranted.

Case 1 – Adiabatic Single Averaging

Since the other body’s mean longitude rate is of $O\left (\varepsilon \right )$ this case is equivalent to the adiabatic Case 3 for tesseral harmonics. A single average over the satellite’s mean-longitude λ yields

$$ \varepsilon \left[ \begin{array}{ll} \bar{\textbf{f}}^{\boldsymbol{\alpha} ,O}\left( {\boldsymbol{\alpha}, \lambda^{O}} \right)\\ {\bar{{f}}^{\lambda ,O}\left( {\boldsymbol{\alpha} ,\lambda^{O}} \right)} \end{array}\right]\equiv \frac{1}{2\pi} \int\limits_{-\pi}^{\pi} {\sum\limits_{j=-\infty}^{\infty} {\sum\limits_{t=-\infty}^{\infty} {\text{\textbf{f}}_{jt}^{O} (\boldsymbol{\alpha} )\exp i\left[ {j\lambda -t\lambda^{O}} \right]}} } {\kern 1pt}d\lambda =\sum\limits_{t=-\infty}^{\infty}{\textbf{f}}_{0t}^{O} (\boldsymbol{\alpha})\exp i\left[{-t\lambda^{O}} \right]. $$

(36)

where, noting that $\lambda ^{O}\approx n^{O}(t)t+{\lambda _{o}^{O}}$, shows that the single average still results in a non-autonomous system due to the motion of the other body. The numerical propagator will select a step size that depends on the remaining secular terms, long period terms, and those terms with significant frequencies that are integral multiples of $n^{O}\left (t \right )$. In many situations, this first average over the satellite’s mean longitude is sufficient for an efficient propagation. Indeed, perturbations from the Sun almost never need a double average – the single average suffices.

Case 2 – Non-Adiabatic Double Averaging

In this case, the other body’s mean longitude rate is becoming significant (however still less than spacecraft mean longitude rate). The practical consequence of this is the numerical integration with the single average is beginning to select smaller step sizes to accommodate the higher frequency terms present from the mean motion of the other body. At some point it may become warranted to perform a second average over λ ^O to eliminate the dependence on it. This can be performed formally with the following result

$$ \varepsilon \left[\begin{array}{ll} \bar{\bar{\textbf{f}}}^{\boldsymbol{\alpha} ,O}\left( \boldsymbol{\alpha} \right)\\ \bar{{\bar{{f}}}}^{\lambda ,O}\left( \boldsymbol{\alpha} \right) \end{array}\right]\equiv \frac{1}{2\pi} \int\limits_{-\pi}^{+\pi} {\sum\limits_{t=-\infty}^{\infty} {\textbf{f}}_{0t}^{O} (\boldsymbol{\alpha} )\exp i\left[{-t\lambda^{O}}\right]} d\lambda^{O}=\textbf{f}_{00}^{O} (\boldsymbol{\alpha} ). $$

(37)

This result contains only terms with long period or secular frequencies. Unlike the expression for the central body spherical harmonics that conveniently separates into zonal (i.e., no dependency on the central body’s sidereal angle) and tesseral terms, the expression in Eq. 34 cannot be similarly separated. For the non-resonant tesseral harmonics case (Case 2) this separation allowed the averaging process to operate only on the zonals and eliminated the tesseral harmonics altogether. No such separation exists here so to eliminate the other body mean longitude requires a double average on the system of equations in Eq. 34. The effect of a single average versus double average is now examined for the lunar orbiter case.

Example 2

Consider the same low altitude lunar orbiter as presented earlier in Table 1 except perturbations from the Earth and Sun are included. As an initial investigation, both the Earth and Sun are modeled with two-body orbits with initial elements defined from DE421 at the J2000 epoch [30]. The e- ω phase space results are shown in Fig. 4 for a 5-yr propagation of the numerically single averaged EOMs that include only the zonal perturbations (labeled ‘Zonal Single Avg’ – a repeat of the first example); a single averaged propagation that includes zonals and the Earth/Sun perturbations (labeled ‘Single Avg’) using a 130 ^th-order Gaussian quadrature; a double average propagation (labeled ‘Double Avg’) with zonals and Earth/Sun perturbations where the Earth is double averaged using a 130 ×20 order Gaussian cubature and the Sun is single averaged using a 130 ^th-order Gaussian quadrature; and, finally, a direct propagation of the osculating EOMs (labeled ‘Osculating’). All propagations used a 1.0E-10 integration tolerance.

Fig. 4

Argument of periapsis and eccentricity phase space of lunar orbiter that includes other body perturbations from the Sun and Earth

The libration oscillation is clearly evident, but significantly different than the prior zonal-only case. The interaction of the Earth and Sun perturbations has caused the libration motion to be ‘lower’ in eccentricity space, and not close as with the zonal-only case. Using the ‘Osculating’ result as a reference, both the ‘Single Avg’ and ‘Double Avg’ cases capture the correct qualitative dynamics. Tabular results of the propagation performance are presented in Table 7. The results illustrate the inclusion of the other body perturbations significantly increases the number of required function calls for both the single average and double average cases as compared to the zonals-only. Relative to the osculating results, both averaged solutions are more efficient; however, the double average did not improve sufficiently over the single average to warrant its use. This might seem counterintuitive since the propagator’s average step size has increased, but the additional computational expense of a 2-d averaging required more overall function calls in this problem.

Table 7 Comparison of numerically single/double averaged EOMs 5-yr propagation to osculating EOMs

Solar Radiation Pressure

A simplified form of the perturbation accelerations from solar radiation pressure can be modeled using

$$ \delta \ddot{\textbf{r}}^{S}=-P_{S} C_{R} \frac{A}{m}\frac{\text{A.U.}^{2}} {\left\|\textbf{r}_{S}-\textbf{r}\right\|^{2}} \frac{\textbf{r}_{S} -\textbf{r}} {\left\|{\textbf{r}_{S} -{\textbf{r}}}\right\|} $$

(38)

where

• Radiation pressure on a perfectly absorbing surface at 1 A.U. ≅4.56x10⁻⁶ N m ⁻²,

• Solar radiation pressure coefficient,

• Reflectivity factor: γ =0 full absorption, γ= 1 full specular reflectivity, γ∼ 0.4 diffuse reflectivity,

• Spacecraft area projected in the direction of the Sun,

• Spacecraft mass,

• Astronomical Unit= 149,597,870.7 km,

• Position vector of the spacecraft relative to the central body,

• Position vector of the Sun relative to the central body.

In developing Eq. 38 it has been implicitly assumed that the normal of the cross-sectional area A pointed in the direction of the Sun and the solar radiation pressure coefficient C _R are constant or have slow variations (i.e, $\dot {{A}}\;\text {or}\; \dot {{C}}_{R} =O\left (\varepsilon \right )$ and can be considered adiabatic). For a more detailed high accuracy model development that accounts for complex shapes and orientations the reader is directed to the textbook by Milani, Nobili, and Farinella [31]. However, complex shapes or attitudes can introduce short periodic time dependencies that can negatively impact the efficiency of a mean element propagation. In these cases, it is appropriate to pre-average any parameter in Eq. 38 that might have short periodic time dependent variations and provide the ‘mean valued’ parameters as inputs to the mean element propagation. This is justified, since short periodic effects do not impact mean element propagations on the $O\left ({1/\varepsilon } \right )$ time scale of interest.

Equation 38 conforms to the standard form given in Eq. 1 with averaged results given by Eq. 2. However, the averaging interval is dependent on the period of time that the spacecraft is exposed to the Sun. That is, the entry into shadow by the central body and exit from it are defined by

$$ \left( {L_{\text{entry}} ,L_{\text{exit}}} \right)=\text{True longitudes of entry/exit}, $$

(39)

and dictate a reduced averaging interval for solar radiation pressure as follows

$$ \delta \dot{{\bar{{x}}}}^{S}=\frac{1}{2\pi }\int\limits_{\bar{{L}}-L_{\text{exit}}}^{\bar{{L}}+L_{\text{entry}}} {\frac{\partial{\mathbf{x}}}{\partial \dot{\mathbf{r}}}\cdot \delta{\ddot{\mathbf{r}}}^{S}\frac{d\lambda} {dL}} dL. $$

(40)

The solution to Eq. 40 assumes a cylindrical shadow with the Sun being modeled as a point light source. Higher fidelity models exist for a Sun modeled as a finite size body that yield penumbra regions of partial shadowing and umbra regions of full shadow; however, calculating these regions is computationally expensive and result in mean element propagations that are slower than their osculating counterparts. Given that typical penumbra regions are much smaller relative to the umbra and fairly symmetric (hence averaging to a near-cylindrical shadow result), the cylindrical model is sufficient for predicting mean solar pressure effects. The algorithm used for calculating the limits specified in Eq. 39 is standard and exists in numerous sources. A version that is adapted to the equinoctial elements and implemented in the current study has been documented by Danielson et al. [21].

Atmospheric Drag

Perturbation accelerations from atmospheric drag can be modeled as follows

$$ \delta \ddot{\textbf{r}}^{D}=-\frac{1}{2}C_{D} \frac{A}{m}\rho \left(\textbf{r}_{B};\beta\right) \textbf{v}_{B} \bullet {\textbf{v}}_{B}\frac{\textbf{v}_{B}} {\left\| {\textbf{v}}_{B}\right\|} $$

(41)

where the parameters are defined as,

• Drag coefficient,

• Spacecraft area projected in the direction of the spacecraft body fixed velocity vector v _B ,

• Velocity relative to the fixed frame of the center body,

• Spacecraft mass,

• Atmospheric densityfunction of the body fixed position vector r _B and parameters β.

As with the solar pressure acceleration discussed previously, the drag acceleration in Eq. 41 conforms to the standard form given in Eq. 1 with averaged results given by Eq. 2 provided that the drag coefficient C _D , spacecraft drag normal area A, and the parameters of the density function β are constants, or vary slowly with $O\left (\varepsilon \right )$ time rates of change. As an example, an acceptable time variation in density would be a multi-year dependency due to long term solar flux cycle variations; while an unacceptable one would have a daily density variation (which would result in a significant loss in efficiency for a mean element propagation). Also, as with the solar pressure, it is appropriate to pre-average any parameter in Eq. 41 that might have short periodic time dependent variations and provide the ‘mean valued’ parameters as inputs to a mean element propagation.

For eccentric orbits the spacecraft will enter and exit the atmosphere on each orbit, for efficiency the averaging operation should be limited to the period of the orbit that is in the atmosphere. This condition can be specified as the radial distance r _A to the top of the atmosphere (which is assumed larger than the periapsis radius r _P of the satellite) and then finding the limits in the true longitude that represent the entry/exit points $\left ({L_{EN} ,L_{EX}} \right )$. The first order mean rates for the atmospheric drag then take the form

$$ \delta \dot{\bar{x}}^{D}=\frac{1}{2\pi} \int\limits_{\bar{L}-L_{EN}}^{\bar{{L}}+L_{EX}} \frac{\partial{\textbf{x}}}\partial_{{\mathbf{r}}}\cdot \delta{\ddot{\textbf{r}}}^{D}\frac{d\lambda}{dL}dL $$

(42)

where

$$\begin{array}{@{}rcl@{}} L_{EN}&=&-f_{A} +\omega +{\Omega}, \\ L_{EX}&=&f_{A} +\omega +{\Omega}, \\ f_{A} &=&\arccos \left[ {\frac{a}{r_{A}} \left( {\frac{1-e^{2}}{e}} \right)-\frac{1}{e}} \right]. \end{array} $$

(43)

Of course, if the eccentricity is sufficiently small then the satellite is always in the atmosphere and the limits are restored to $\left ({\bar {{L}}-\pi ,\bar {{L}}+\pi } \right )$.

Lifetime studies of spacecraft in an atmosphere have shown that a correction to the altitude for the density calculation in Eq. 42 must be made. The correction originally found by Izsak [32] and then shown by Green [33] to be a 2 ^nd-order coupling between drag and J ₂ takes the form

$$ {\Delta} h=\frac{J_{2} R_{CB}^{2}} {4a\left( {1-e^{2}} \right)}\left[ {\sin^{2}i\cos 2\left( {f+\omega} \right)+\left( {3\sin^{2}i-2} \right)\left( {1+\frac{e\cos f}{1+\sqrt {1-e^{2}}} +\frac{2\sqrt {1-e^{2}}} {1+e\cos f}} \right)} \right] $$

(44)

where the correction Δh is added to the calculation of height above the central body in evaluating the density $\rho \left (\textbf {r}_{B}; \beta \right )$.

Example 3

This example considers the orbit lifetime prediction of the Mars Odyssey orbiter. The atmospheric model used for the analysis has been developed by Vincent [34] and Vincent et al. [35] for use in lifetime studies of Mars orbiters. It is a simple empirical model that has been fit to the higher fidelity MarsGRAM 2000 density model [36] and retains the essential long-term characteristics due to solar flux variations, but eliminates short periodic dependencies. The atmospheric density is modeled as follows

$$ \rho =\rho_{o} 10^{A_{S} z}10^{A_{11} \sin \left( {2\pi \frac{t-t_{11} }{T_{11}} } \right)}10^{-A_{A} \sin 2\pi \frac{t-t_{A}} {T_{A}} }e^{-\left( {\frac{h-h_{o}} {H}} \right)} $$

(45)

where

$$\begin{array}{@{}rcl@{}} \rho_{o} &=&\text{ Reference density = 1.5E-5 } {\text{kg}}/{\text{km}^{3}} \\ A_{S} &=&\text{Amplitude of the stochastic factor = 0.35,} \\ z&=&\text{ Deviation from the mean of a random variable with a Gaussian normal}\\ &&\text{distribution}, \\ A_{11} &=&\text{ Amplitude of the mean 11-year solar cycle term = 0.35,} \\ t_{11} &=&\text{ Epoch in Julian Days for the solar cycle term = JD 2451057.5, }\\ T_{11} &=&\text{ 11-year solar cycle period = 4014.1 days,} \\ A_{A} &=&\text{Amplitude of the Martian annual term = 0.2,} \\ t_{A} &=&\text{ Epoch in Julian Days for the Martian annual term = JD 2450992.0, } \\ T_{A}&=&\text{ Martian annual period = 686.98 days,} \\ h&=&\text{ Height above the Martian reference ellipsoid,} \\ h_{o} &=&\text{ Reference height = 378.1 km,} \\ H&=&\text{ Scale height = 46.0 km.} \end{array} $$

(46)

For this example a 25 % atmosphere has been selected which corresponds to z=−0.6745, and can be derived by inverting the Gaussian cumulative distribution ${\Phi } \left (z \right )$ given by

$$ {\Phi} \left( z \right)=\frac{1}{2}\left[ {1+\text{erf}\left( {\frac{z}{\sqrt 2} } \right)} \right]. $$

(47)

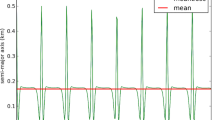
The Mars Odyssey orbit is ‘frozen’ with a small libration in the mean $\left ({e,\omega } \right )$ phase space and is nominally several kilometers above the 25:2 tesseral resonance. Because it is near this resonance, the stroboscopic nodal formulation described previously is needed to capture the correct long-term mean element propagation. In this example all of the perturbations discussed are active, including Mars’ spherical harmonics, the Sun, solar pressure, and atmospheric drag using the density model and parameters given in Eqs. 45 and 46. The specific initial conditions and other associated parameters are delineated in Table 8. Results for the propagated semimajor axis and eccentricity are shown in Fig. 5.

Table 8 Initial conditions and parameters for Mars Odyssey long-term propagation example

Fig. 5

Comparison of numerically single/double averaged EOMs 5-yr propagation to osculating EOMs

Examination of the figure shows that for the first 8000 days both the osculating and mean semimajor axes decay as expected from drag; however, the libration of the eccentricity and associated argument of periapsis (not shown) is increasing in amplitude. After 8000 days, the decay with the semi-major axis is arrested and a long-period oscillation indicative of a deep resonance sets in. The eccentricity and argument of periapsis no longer librate; in fact, the mean argument of periapsis begins to circulate. The orbit has effectively been captured into a 25:2 deep tesseral resonance with Mars at the expense of ‘losing’ its frozen characteristic. This persists for much of the remaining 70 years, but at ∼ 24000 days the orbit exits the 25:2 resonance with the semi-major axis beginning to decay again. The mean element propagation continues, but at a sufficient distance away from the 25:2 resonance the equations of motion should be reformulated to be non-resonant because of the assumption of a quasi-static stroboscopic node. To do this would require monitoring the semi-major axis distance from the deep resonance value while propagating and reconfiguring the equations of motion based on knowledge of the location and size of this and nearby resonances; a topic of future investigation. For the period of propagation shown in these results, the stroboscopic node formulation around the 25:2 resonance is valid and the associated mean element propagation successfully captures the key characteristics of the orbit’s long term evolution. It does so in a fraction of the time of the osculating propagation as indicated in the performance results shown in Table 9.

Table 9 Comparison of numerically averaged EOMs 70-yr propagation to osculating EOMs for the Mars Odyssey orbiter

Conclusions

This study presented algorithms, methods, and results for numerically averaging two-body perturbed equations of motion to perturbations resulting from non-spherical gravity harmonics, other bodies, solar radiation pressure, and drag. The results have shown that the numerically averaged propagations are more efficient than their osculating counterparts in capturing secular and long period motions. The numerical averaging technique correctly models these secular and long period motions, which has been ascertained via comparisons to the associated osculating solutions. Future work will focus on developing higher order corrections using numerical methods as well as an algorithmic method for reconfiguring the EOMs for resonances as an orbit decays.

Appendix: : Direct Equinoctal Elements And Partials

The direct equinoctial elements as functions of the classical elements $\left \{ {a,e,i,{\Omega } ,\omega ,M} \right \}$ can be defined as

$$ \begin{array}{l} a\equiv a, \\ h\equiv e\sin \left( {\omega +{\Omega}} \right), \\ k\equiv e\cos \left( {\omega +{\Omega}} \right), \\ p\equiv \tan \left( {\frac{i}{2}} \right)\sin {\Omega} , \\ q\equiv \tan \left( {\frac{i}{2}} \right)\cos {\Omega} , \\ \lambda \equiv M+\omega +{\Omega} . \end{array} $$

(48)

Some intermediate quantities are now defined. The equinoctial reference frame is composed of three orthogonal unit vectors $\left \{ {\text {\textbf {f}},\text {\textbf {g}},\text {\textbf {w}}} \right \}$ where

• 1. f and g are in the satellite orbit plane,

• 2. w is along the orbit normal,

• 3. The angle between f and the ascending node is equal to the longitude of the ascending node Ω.

Using these properties the unit vectors $\left \{ {\text {\textbf {f}},\text {\textbf {g}},\text {\textbf {w}}} \right \}$are obtained using

$$ \begin{array}{l} \text{\textbf{f}}=\frac{1}{1+p^{2}+q^{2}}\left[ {{\begin{array}{l} {1-p^{2}+q^{2}}\\ {2pq}\\ {-2p} \end{array}} } \right], \\ \text{\textbf{g}}=\frac{1}{1+p^{2}+q^{2}}\left[ {{\begin{array}{l} {2pq} \hfill \\ {1+p^{2}-q^{2}}\\ {2q} \end{array}} } \right], \\ \text{\textbf{w}}=\frac{1}{1+p^{2}+q^{2}}\left[ {{\begin{array}{l} {2p}\\ {-2q}\\ {1-p^{2}-q^{2}} \end{array}} } \right]. \end{array} $$

(49)

From the position r and velocity $\dot {\textbf {r}}$ vectors the following components $\left \{ {X,Y,\dot {{X}},\dot {{Y}}} \right \}$can be computed

$$ \begin{array}{c} \text{\textbf{r}}\equiv X \textbf{f}+Y \textbf{g}\\ \dot{\textbf{r}}\equiv \dot{X}\textbf{f}+\dot{{Y}} \textbf{g} \end{array}\\ \to \begin{array}{c} X=\textbf{r}\cdot \textbf{f}, Y= \textbf{r}\cdot \textbf{g}\\ \dot{{X}}= \textbf{r} \cdot \textbf{f},\dot{Y}= \textbf{r}\cdot \textbf{g} \end{array}. $$

(50)

Finally the partials identified in Gauss’ (7) are

$$\begin{array}{@{}rcl@{}} \frac{\partial a}{\partial{\dot{\textbf{r}}}}&=&\frac{2a^{2} \dot{\textbf{r}}}{\mu} , \\ \frac{\partial h}{\partial{\dot{\textbf{r}}}}&=&\frac{\left({2X\dot{Y}-\dot{X}Y}\right)\textbf{f}-X \dot{X}\textbf{g}}{\mu} +\frac{k\left( {qY-pX} \right)\textbf{w}}{AB}, \\ \frac{\partial k}{\partial{\dot{\textbf{r}}}}&=&\frac{\left({2X\dot{Y}-\dot{X}Y}\right)\textbf{f}-Y\dot{Y}\textbf{g}} {\mu}-\frac{h\left( {qY-pX} \right)\textbf{w}}{AB}, \\ \frac{\partial p}{\partial{\dot{\textbf{r}}}}&=&\frac{CY\textbf{w}}{2AB}, \\ \frac{\partial q}{\partial{\dot{\textbf{r}}}}&=&\frac{CX\textbf{w}}{2AB}, \\ \frac{\partial \lambda} {\partial{\dot{\textbf{r}}}}&=&-\frac{2 \textbf{r}}{A}+\frac{k\frac{\partial h}{\partial \dot{\textbf{r}}}-h\frac{\partial k}{\partial{\dot{\textbf{r}}}}}{1+B} +\frac{\left({qY-pX}\right)\textbf{w}}{A}, \end{array} $$

(51)

Where the following definitions apply

$$\begin{array}{@{}rcl@{}} A=na^{2}=\sqrt {\mu a}, \\ B=\sqrt {1-h^{2}-k^{2}}, \\ C=1+p^{2}+q^{2}. \end{array} $$

(52)