1 Introduction

Residual stress affects fatigue crack and stress corrosion cracking (SCC), and therefore has a severe effect on structural integrity. To ensure structural integrity, the residual stress distribution should be investigated in advance. In steel structures, welding is widely utilized as a production method, and it inevitably causes residual stresses. Thus, various peening techniques using shot, lasers, and water jets have been proposed to reduce or mitigate the tensile residual stress after welding [1–3]. In these methods, an impulsive load is applied to the surface of the target, and compressive residual stresses are introduced. The effect of the peening technique is investigated in various reports [4–6]. However, to investigate its effect on the prevention of SCC or fatigue cracking, it is important to consider the behavior of the stress distribution modified by peening on the operation. This requires a prediction of the stress distribution after peening; thus, numerous impact loads must be considered in the prediction. There are some reports that consider tens of shot collisions in a dynamic elastic-plastic analysis [7, 8] or in which the load distribution is modeled by integrating using the discrete element method (DEM) and the finite element method (FEM) [9]. However, to the authors’ knowledge, there are no reports on analysis that considers numerous shot collisions such as more than thousands of shots.

To predict the effect of modifying the residual stress distribution by peening using FEM, an extremely detailed mesh division that can analyze the behavior of the shot peening process is required. Therefore, the number of computations becomes significant, and it is difficult to perform the analysis using conventional methods such as commercial FE software. In addition, assuming numerous shot collisions, tens of thousands or more collisions should be considered, which leads to a further increase in computational time. Moreover, to discuss the modification of the welding residual stress, the welding residual stress must be investigated in advance, which would make the analysis more difficult.

On the other hand, the authors have proposed idealized explicit FEM (IEFEM) [10], which can predict the welding residual stresses and the deformation of practical structures in realistic computing time. In IEFEM, convergence to a static equilibrium state is considered, although IEFEM is based on dynamic explicit FEM [11]. Thus, it can obtain an accurate solution with shorter computational time. In addition, since IEFEM is based on dynamic explicit FEM, IEFEM is highly suitable for parallelization. By using parallelization with a graphics processing unit (GPU), IEFEM can achieve even faster computation and the residual stress distribution in multi-pass-welded pipe was predicted [12].

In this study, to investigate the effect of the modified stress distribution due to shot peening on operation, an analysis system that can analyze the modification of the residual stress distribution by peening is first proposed based on IEFEM. To analyze the dynamic phenomenon with an impulsive load, IEFEM is extended to consider the dynamic effect. The impulsive load due to the collision of shots is modeled as an equivalent load model, and then, the equivalent load model is introduced into IEFEM considering the dynamic effect. The proposed analysis system is applied to the prediction of the residual stress distribution modification by shot peening in a multi-pass-welded pipe joint. The residual stress distributions obtained by the analysis are compared with those measured by X-ray diffraction (XRD), and the effect of the number of shot collisions on the change in residual stress distribution is discussed.

2 Residual stress analysis of peening process

2.1 Idealized explicit FEM considering dynamic effect

IEFEM was developed to analyze the quasi-static elastic-plastic behavior of welding based on dynamic explicit FEM, and the effects of inertial forces are not considered. On the other hand, an impulsive load acts on the target in the peening process, so the dynamic effect should be taken into account. In this research, the dynamic effect is introduced in the formulation of IEFEM.

In nonlinear FE analyses with dynamic effects, Eq. (1) is utilized as a fundamental equation,

$$ \left[ M\right]{\left\{\;\ddot{U}\right\}}_{t+\Delta t}+\left[ C\right]{\left\{\;\dot{U}\right\}}_{t+\Delta t}+{\left\{ Q\right\}}_{t+\Delta t}={\left\{ F\right\}}_{t+\Delta t} $$
(1)

where [M] and [C] are the mass matrix and damping matrix, and \( {\left\{\;\ddot{U}\right\}}_{t+\Delta t} \), \( {\left\{\;\dot{U}\right\}}_{t+\Delta t} \), {Q} t + Δt , and {F} t + Δt are the acceleration vector, velocity vector, internal force vector, and load vector at time t + Δt, respectively.

Since IEFEM was developed to achieve shorter computing time with the accurate solution by introducing explicit calculation into implicit formulation, IEFEM is introduced to the dynamic analysis based on the implicit formulation. In the case of the implicit formulation, an iterative calculation of the Newton–Raphson method is performed using the following equations, which are obtained by applying the Newmark β method to Eq. (1) and linearizing the internal force vector:

$$ {\left[{K}_{eff}\right]}^{(k)}\left\{\Delta U\right\} =^{(k)}\left\{{F}_{eff}\right\} $$
(2)
$$ \left[{K}_{eff}\right]=\left(\frac{1}{\beta\;\Delta {t}^2}\left[ M\right]+\frac{\gamma}{\beta\;\Delta t}\left[ C\right]+\left[ K\right]\right) $$
(3)
$$ {}^{(k)}\left\{{F}_{eff}\right\}={\left\{ F\right\}}_{t+\Delta t}-{\left[ M\right]}^{\left( k-1\right)}{\left\{\;\ddot{U}\right\}}_{t+\Delta t}-{\left[ C\right]}^{\left( k-1\right)}{\left\{\;\dot{U}\right\}}_{t+\Delta t} -^{\left( k-1\right)}{\left\{ Q\right\}}_{t+\Delta t} $$
(4)
$$ {\left\{\; U\right\}}_{t+\Delta t}={\left\{\; U\right\}}_t+\left\{\Delta U\right\} $$
(5)
$$ {\left\{\;\dot{U}\right\}}_{t+\Delta t}=\frac{\gamma}{\beta\;\Delta t}\left\{\;\Delta U\right\}+\left(1-\frac{\gamma}{2\beta}\right){\left\{\;\dot{U}\right\}}_t+\Delta t\left(1-\frac{\gamma}{2\beta}\right)\;{\left\{\;\ddot{U}\right\}}_{t+\Delta t} $$
(6)
$$ {\left\{\;\ddot{U}\right\}}_{t+\Delta t}=\frac{1}{\beta\;\Delta {t}^2}\left\{\;\Delta U\right\}-\frac{1}{\beta\;\Delta t}{\left\{\;\dot{U}\right\}}_t-\left(\frac{1}{2\beta}-1\right)\;{\left\{\;\ddot{U}\right\}}_t $$
(7)

where [K], [K eff], {ΔU}, and {F eff} are the stiffness matrix, the effective stiffness matrix, displacement increment vector, and effective load vector, respectively. The upper left subscript (k) of each term indicates the iteration count.

To apply the procedures of the idealized explicit method, the following equation is assumed by adding a virtual inertial term and a damping term at the virtual time τ:

$$ \left[{M}_{\mathrm{dum}}\right]{\left\{\;{\ddot{U}}_{\mathrm{dum}}\right\}}_{\tau}+\left[{C}_{\mathrm{dum}}\right]\;{\left\{\;{\dot{U}}_{\mathrm{dum}}\right\}}_{\tau}+\left[{K}_{\mathrm{eff}}\right]\;{\left\{\;{U}_{\mathrm{dum}}\right\}}_{\tau}=\left\{{F}_{\mathrm{eff}}\right\} $$
(8)

where [M dum] and [C dum] are the virtual mass matrix and virtual damping matrix, and \( {\left\{\;{\ddot{U}}_{\mathrm{dum}}\right\}}_{\tau} \), \( {\left\{\;{\dot{U}}_{\mathrm{dum}}\right\}}_{\tau} \), and { U dum} τ are the acceleration vector, velocity vector, and displacement vector at the virtual time τ, respectively.

The application of the central difference to Eq. (8), as with the dynamic explicit method, gives the following equation:

$$ \begin{array}{l}\left(\frac{1}{\Delta {\tau}^2}\left[{M}_{\mathrm{dum}}\right]+\frac{1}{2\Delta \tau}\left[{C}_{\mathrm{dum}}\right]\right){\left\{{U}_{\mathrm{dum}}\right\}}_{\tau +\Delta \tau}={\left\{{F}_{\mathrm{eff}}\right\}}_{\tau}\hfill \\ {}\kern1em +\left[{M}_{\mathrm{dum}}\right]\left(\frac{2}{\Delta {\tau}^2}{\left\{{U}_{\mathrm{dum}}\right\}}_{\tau}-\frac{1}{\Delta {\tau}^2}{\left\{{U}_{\mathrm{dum}}\right\}}_{\tau -\Delta \tau}\right)+\frac{1}{2\Delta \tau}\left[{C}_{\mathrm{dum}}\right]{\left\{{U}_{\mathrm{dum}}\right\}}_{\tau -\Delta \tau}-\left[{K}_{\mathrm{eff}}\right]{\left\{{U}_{\mathrm{dum}}\right\}}_{\tau}\hfill \end{array} $$
(9)

The virtual time step for the virtual time τ is advanced using Eq. (9) until the virtual inertial term and the virtual damping term become negligibly small. Then, by substituting { U dum} into { ΔU}, the same solution as that obtained by the iterative calculation using Eq. (2) can be expected.

In the case where the virtual mass matrix [M dum] and damping matrix [C dum] are derived based on physical laws, i.e., [M dum] = [M] and [C dum] = [C], the virtual time increment Δτ becomes very small, and the number of virtual time steps needed to obtain the converged solution may increase. Here, the advancing of the virtual time step using Eq. (9) is carried out only to obtain the converged solution { U dum}, and it has no effect on the converged solution. In this research, to obtain faster convergence, the virtual mass matrix [M dum] and virtual damping matrix [C dum] are determined by the following equations based on critical damping in one-dimensional oscillation, as described in the literature [13]:

$$ \left[{M}_{\mathrm{dum}}\right]=\left[\begin{array}{ccccc}\hfill {K}_{\mathrm{eff}11}\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill \cdots \hfill \\ {}\hfill 0\hfill & \hfill {K}_{\mathrm{eff}22}\hfill & \hfill \hfill & \hfill 0\hfill & \hfill \hfill \\ {}\hfill \vdots \hfill & \hfill \hfill & \hfill \ddots \hfill & \hfill \vdots \hfill & \hfill \hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill {K}_{\mathrm{eff}\;\mathrm{ii}}\hfill & \hfill \hfill \\ {}\hfill \vdots \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \ddots \hfill \end{array}\right] $$
(10)
$$ \left[{C}_{\mathrm{dum}}\right]=\left[\begin{array}{ccccc}\hfill 2{K}_{\mathrm{eff}11}\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill \cdots \hfill \\ {}\hfill 0\hfill & \hfill 2{K}_{\mathrm{eff}22}\hfill & \hfill \hfill & \hfill 0\hfill & \hfill \hfill \\ {}\hfill \vdots \hfill & \hfill \hfill & \hfill \ddots \hfill & \hfill \vdots \hfill & \hfill \hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 2{K}_{\mathrm{eff}\;\mathrm{ii}}\hfill & \hfill \hfill \\ {}\hfill \vdots \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \ddots \hfill \end{array}\right] $$
(11)

With the use of these matrices, a larger virtual time increment Δτ can be utilized within a solution that does not diverge. In addition, since these matrices are diagonalized, the solution of the simultaneous equations for the calculation of {U dum} τ + Δτ in Eq. (9) is no longer necessary and this can also reduce the computing time.

By using the above formulations, dynamic analyses can be performed according to the procedures of the idealized explicit method. In addition, the parallelization using a GPU to achieve faster computation in this research is considered to be the same method as Ref. [10]. The analysis system is implemented in our in-house code using CUDA environment provided by NVIDIA Corporation [14].

2.2 Equivalent load model

In a shot collision during the shot peening process, the load acts on a very small region over a very short time. In this study, the history of the load distribution from the collision is modeled as an equivalent load model. The load calculated using the equivalent load model is given as a load vector in Eq. (1), and the behavior of the stress distribution in the peening process is analyzed.

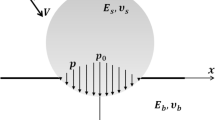
To model the impulsive load from the collision of the shot, the phenomenon shown in Fig. 1 is assumed. In the figure, first, a shot collides with the target surface at an initial velocity of v 1, and a reaction force occurs (Fig. 1a). After that, elastic deformation develops, and the reaction force increases (Fig. 1b). With the progress of the collision, the center of the collision reaches the yield stress, after which plastic deformation occurs (Fig. 1c). After the beginning of plastic deformation, the increase in the reaction force becomes moderate from the center of the collision, where the plastic deformation first began. With the plastic deformation, the reaction force on the surrounding part from the center increases (Fig. 1d). After that, the plastic deformation ends (Fig. 1e), and the collision finishes with a bounced shot at a velocity of v 2 (Fig. 1f). The history of the reaction force distribution is modeled using the function f, which determines the shape of the reaction force distribution, and the function g, which determines the history of the total reaction force, as follows:

$$ P\left(\rho, \tau \right)= f\left(\rho, \kern0.5em t\right)\times g\left(\tau \right) $$
(12)

where ρ, τ, P(ρ, τ), f(ρ, τ), and g(τ) are defined as the normalized distance from the collision center, the normalized time from the beginning of the collision, the load distribution history function, the load distribution function, and the load history function, respectively. Here, ρ and τ are defined as follows:

$$ \rho =\frac{r}{r_0},\kern0.5em \tau =\frac{t}{t_0} $$
(13)

where r and r o are the distance from the collision center and the shot radius, and t and t 0 are the time from the beginning of the collision and the duration of the collision, respectively.

Fig. 1
figure 1

Schematic illustration of reaction force distribution from shot collision (a–f)

Full size image

As an example, the load distribution function is defined as the 6th order polynomial shown in Eqs. (14)–(16) to fit the load distribution to the reaction force obtained by shot collision FE analysis such as ABAQUS. The shape of the distribution function is as shown in Fig. 2, and it can express the tendency of the load distribution assumed in Fig. 1.

$$ f\left(\rho, \tau \right)=\frac{a\left(\rho, \tau \right)}{\int_0^1 a\left(\rho, \tau \right)\;2\pi \rho\;d\rho} $$
(14)
$$ a\;\left(\rho, \tau \right)={a}_6\;\left(\rho, \tau \right){\rho}^6+{a}_4\left(\rho, \tau \right)\;{\rho}^4+{a}_2\left(\rho, \tau \right)\;{\rho}^2+{a}_0 $$
(15)
$$ {a}_0=0.655,{a}_2=4,{a}_4=10000\left(\frac{1}{1+ \exp \left(-5\left(\tau +0.75\right)\right)}-1\right),{a}_6=-10 $$
(16)
Fig. 2
figure 2

Example of load distribution function

Full size image

Assuming Eqs. (17) and (18) as the load history function, the load history is as shown in Fig. 3. The coefficient b in Eq. (17) is determined from the difference in the momentum of the shot m(v 2 − v 1) before and after the collision, i.e., the impulse applied to the target by the shot.

$$ g\left(\tau \right)= b \sin \left(\frac{\tau^7+2\tau}{3}\pi \right) $$
(17)
$$ b=\frac{m\left({v}_2-{v}_1\right)}{t_0{\int}_0^1 \sin \left(\frac{\tau^7+2\tau}{3}\pi \right)\; d\tau} $$
(18)

where, v 1,v 2 and t 0 are the initial velocity, the bounced velocity and the duration of collision, respectively. v 2 and t 0 can be predicted by collision analysis.

Fig. 3
figure 3

Example of load history function

Full size image

In this study, this load distribution history function is defined as an equivalent load model.

In shot peening, numerous shots are blown against the target, and it is necessary to consider the random load distribution in space and time. Here, we construct an analysis system as shown in Fig. 4 to apply the random load distribution over time and space. In this system, before performing dynamic elastic-plastic analysis, the load distribution due to the collision of shots is calculated. To calculate the load, the number of new collisions N c, which newly start from current time step, is determined. This is necessary since temporally and spatially random collision is considered in this analysis system. After that, N c nodes are randomly selected. If the nodes are already selected as collision points, the selection is performed again to avoid duplicated collision. After the selection of new collision points, the selected points are added to the collision node list. Next, the load vector of Eq. (2) is calculated using the nodes in the collision node list as the collision center, and dynamic elastic-plastic analysis is performed as shown in the previous section. After the dynamic elastic-plastic analysis, the collision points that exceed the duration of the collision are removed from the collision point list. By iterating these procedures until the designated time, the behavior of the stress distribution due to the shot peening is analyzed.

Fig. 4
figure 4

Flow of analysis

Full size image

3 Validation of analysis method

3.1 Analysis model and conditions

To investigate the accuracy of the equivalent load model shown in the previous chapter, the proposed analysis system is applied to the prediction of the stress distribution during the collision process for a single shot. The analysis model is shown in Fig. 5. The analysis is also performed using ABAQUS, a commercial nonlinear FE analysis software, and the results for the proposed system and ABAQUS are compared. In the analysis using ABAQUS, a contact model based on the penalty method and the dynamic explicit scheme are employed. The number of nodes and elements in this model are 204,105 and 196,824, respectively. A 2-mm-wide rectangular area with the collision point as its center is meshed with regular hexahedrons 0.04 mm in length, width, and height. In the analysis for the proposed system, Eqs. (12)–(18) are employed as an equivalent load model. The velocity after the collision v 2 and the duration of the collision t 0 are determined from the analysis results for ABAQUS as −10.5 m/s and 2.0 μs, respectively. The target material and shot are assumed to be SUS304 and SUS316, respectively. The bilinear isotropic hardening rule is employed for the work hardening rule. The properties of these materials are shown in Table 1. The initial velocity v 1 of the shot is assumed to be 60 m/s [15].

Fig. 5
figure 5

Analysis model for the collision of a single shot

Full size image
Table 1 Material properties of SUS304 and SUS316
Full size table

3.2 Analysis results

Figure 6 shows the stress distribution in the normal direction σ z along line A-A′, which is equivalent to the contact pressure. In Fig. 6, the squares, triangles and diamonds show the stresses at time 0.2, 0.3, and 1.2 μs from the beginning of the collision, respectively and the red and blue marks show the stresses from the proposed system and ABAQUS, respectively. From Fig. 6, it is found that the similar stress distributions are obtained between the proposed system and ABAQUS. It can also be seen that these stress distributions can reproduce the tendency assumed in Fig. 1.

Fig. 6
figure 6

Distribution of stress in z direction σ z on surface

Full size image

Figure 7 shows the stress distributions in the horizontal direction σ x . Figure 7a, b show the stress distribution from ABAQUS at 1.0 μs at the beginning of the collision and after the collision, respectively. In the same way, Fig. 7c, d show the stress distributions from the proposed system. From Fig. 7c, d, it can be seen that a large compressive stress occurs surrounding the collision point. After the collision, the compressive stress is distributed to 0.5 mm under the collision point, and the tensile stress is distributed in the thin surface layer near the collision point. The mechanism of this stress distribution can be assumed as follows: first, a large compressive load is applied in the z direction to the collision point, and elongating plastic deformation occurs in the horizontal (x and y) directions to keep the volume constant. In this process, compressive stress occurs due to the elastic constraint from the surrounding region (Fig. 7a, c). After the collision, the compressive collision load is completely unloaded. Due to the unloading of the collision load, the elongating elastic strain at the collision point in the horizontal direction is released, and shrinkage occurs in the horizontal directions. On the other hand, the surrounding region of the collision point prevents shrinkage, so tensile stress results on the surface and compressive stress occurs in the surrounding region (Fig. 7b, d).

Fig. 7
figure 7

Comparison of stress distribution in x direction σ x for equivalent force model and ABAQUS (a–d)

Full size image

Figure 8 shows the distribution of stress in the x direction σ x along line A-A′. In Fig. 8, the triangles and squares show the stresses for the proposed system and ABAQUS, respectively. In the same way as in Fig. 8, Fig. 9 shows the distribution of stress in the x direction along line B-B′ in the thickness direction under the collision center. From these figures, it is found that the proposed equivalent load model can reproduce almost the same stress distribution as that for the analysis considering the contact. From Fig. 9, it can also be seen that the stress distribution is not self-equilibrium. This may occur due to the dynamic effect since the stress distribution is extracted just after the shot collision.

Fig. 8
figure 8

Distribution of stress in x direction σ x on surface

Full size image
Fig. 9
figure 9

Distribution of stress in x direction σ x at cross section

Full size image

The computer utilized in this analysis has the following specifications: the CPU is an Intel Core i7 3.5 GHz processor, and the GPU is a NVIDIA GeForce GTX TITAN processor. In the analysis for ABAQUS, six CPU cores were employed, and the computational time was approximately 600 min. The computational time for the proposed system was 10 min.

4 Application to multi-pass-welded pipe joint

4.1 Analysis model and conditions

The effect of the modification of the residual stress distribution in a multi-pass-welded pipe is investigated in this chapter. The analysis model is shown in Fig. 10. A mockup is also prepared to measure and compare the residual stress distribution. A view of the mockup is shown in Fig. 11. The analysis model is meshed using hexahedral elements. The number of nodes and elements are 3,494,600 and 3,004,664, respectively. The procedure of this analysis is as follows: First, the welding residual stress is predicted using the quasi-static thermal elastic-plastic analysis method based on IEFEM [12]. Next, the elements of the inner and outer regions (which are removed by machining) are deactivated, and the redistribution of stress is calculated. Then, the shot peening process is analyzed by the proposed analysis system, and the modification of the stress distribution due to shot peening is investigated.

Fig. 10
figure 10

Analysis model of multi-pass-welded pipe joint (a–b)

Full size image
Fig. 11
figure 11

View of mockup and measurement setup (XRD)

Full size image

Regarding the thermal elastic plastic analysis of welding residual stress, the temperature-dependent material properties of the pipe (SUS316L) and weld metal (Y316L) are assumed as shown in Figs. 12 and 13, respectively. The number of welding layers is 10, and the number of welding passes in each layer is 1. The welding method is tungsten inert gas (TIG) welding. The same welding conditions are used for all of the welding passes. The welding conditions are as follows: current = 180 A, voltage = 10 V, speed = 10 cm/min, and heat efficiency = 0.8. The work hardening rule employed in this analysis is bilinear isotropic hardening. The annealing effect is modeled by setting the equivalent plastic strain of an element to zero at temperatures higher than 850 °C [16].

Fig. 12
figure 12

Temperature-dependent material properties of base metal (SUS316L)

Full size image
Fig. 13
figure 13

Temperature-dependent material properties of weld metal (Y316L)

Full size image

Regarding the analysis of the shot peening process, shot peening is conducted on the outer surface of a pipe after machining, as shown in Fig. 10b. The conditions for shot peening are the same as those in Chapter 3, and Eqs. (12)–(18) are employed as an equivalent load model. The region on which shot peening is performed is assumed to be a range of 70° in the hoop direction from 145° to 215° from the starting point of welding. In addition, the shot peened region is meshed with 0.2 mm cubic hexahedral elements, as shown in Fig. 10b. The ratio of the collision area (on which the load is applied by the equivalent load model) to the area of the shot peened region, which is defined as the collision area ratio R c, is defined by the following equation:

$$ {R}_{\mathrm{c}}=\frac{A\times {N}_{\mathrm{p}}}{S} $$
(19)

where A, N p, and S are the loaded area at the collision, the collision count, and the area of the shot peened region, respectively. In this analysis, shot peening is performed until R c reaches 50.0, which is assumed to be a sufficiently large ratio. The computer employed in this analysis is the same as described in the previous chapter.

4.2 Welding residual stress

Figure 14 shows the welding residual stress distributions on the cross section at 180° from the start of welding. In Fig. 14, panel (a) shows the distribution of residual stress in the axial direction σ z , and panel (b) shows the distribution in the hoop direction σ θ . From this figure, it is found that σ z has a relatively complex distribution that alternates between compression and tension from the outer surface of the pipe toward the inner surface. On the other hand, for the stress in the hoop direction σ θ , it can be seen that a large tensile stress is distributed in the weld metal and its surrounding region except for the inner and outer surfaces of the pipe.

Fig. 14
figure 14

Residual stress distributions at the cross section 180° from the welding starting point (a–b)

Full size image

Figure 15 shows the welding residual stress distribution along line A-A′ defined in Fig. 9a. Line A-A′ is on the outer surface pipe and is 180° from the welding starting point. In Fig. 15, the squares and triangles represent the residual stresses in the axial σ z and hoop σ θ directions measured by XRD, respectively, and the red and blue lines are the residual stresses in the axial σ z and hoopσ θ directions calculated by IEFEM, respectively. From Fig. 15, it is found that the results for IEFEM agree well with those for XRD in both σ z and σ θ . From the results shown in this section, it can be said that the analyzed results reproduce the measured results, and the validity of this analysis can be established.

Fig. 15
figure 15

Comparison of residual stress distribution along line A-A′

Full size image

4.3 Modification of residual stress due to shot peening

Figure 16 shows the distribution of stress in the axial direction σ z at the cross section 180° from the welding starting point for the as-machined surface (Rc = 0.0), Rc = 10.0, Rc = 25.0, and Rc = 50.0. The dynamic effect is considered in this analysis, so the stress distribution obtained by the proposed analysis system contains the dynamic effect, such as the inertial term. Therefore, to remove the dynamic effect from the stress distribution, quasi-static, elastic plastic analysis is performed after each Rc is reached. This is to simulate the shot peening finishes after each Rc is reached. From Fig. 16, it can be seen that the stress at the outer surface is small for the as-machined surface, and larger compressive stresses are found at Rc = 10.0 (b), Rc = 25.0(c), and Rc = 50.0(d).

Fig. 16
figure 16

Change in stress distribution in the axial direction (σ z ) with Rc at the cross section 180° from the welding starting point (a–d)

Full size image

In the same way as in Fig. 16, Fig. 17 shows the distribution of stress in the hoop direction σ θ . From this figure, the same tendency as the stress in the axial direction σ z is found: a larger compressive stress is found with a larger Rc.

Fig. 17
figure 17

Change in stress distribution in the hoop direction (σ θ ) with Rc at the cross section 180° from the welding start point (a–d)

Full size image

Figure 18 shows the distribution of stress in the axial direction σ z along line A-A′. In the figure, the red solid line shows the stress at Rc = 0.0 (as machined). The green dotted line, dashed line, and solid line are the stresses at Rc = 10.0, 25.0, and 50.0, respectively. In addition, the black dotted line is the stress distribution at Rc = 50.0, which considers no welding residual stress. The blue circles are the stresses measured by XRD. From Fig. 18, it is found that the difference between the stress distribution on the as-machined surface and that at Rc = 10.0 is large, and with the increase in Rc, the compressive stress in the peening region becomes larger. Regarding the stress distribution in the peening region, the stress distribution at Rc = 50.0 can reproduce the measured values well. The change in the stress distribution is large in the peened region, and the change is small in the other region. From the comparison of the stress distribution at Rc = 50.0 with and without welding residual stress, it is also shown that the difference in both stress distributions is almost zero on the peened surface. So, it can be assumed that the residual stress after shot peening becomes a strong compression stress regardless of the welding residual stress.

Fig. 18
figure 18

Comparison of stress distribution in the axial direction (σ z ) for each Rc and XRD along line A-A′

Full size image

Figure 19 shows the distribution of stress in the hoop direction σ θ along line A-A′ in the same way as Fig. 18. From the figure, the same tendency as the stress in the axial direction σ z is found: the stress distribution at Rc = 50.0 can reproduce the measured result.

Fig. 19
figure 19

Comparison of stress distribution in the hoop direction (σ θ ) for each Rc and XRD along line A-A′

Full size image

Figures 20 and 21 show the distribution of stress in axial direction σ z and hoop direction σ θ along line B-B′, which is cut-through thickness direction. In these figures, the red solid line, the green dotted line, dashed line, and solid line are the stresses at Rc = 0.0 (as machined), 10.0, 25.0, and 50.0, respectively. In addition, the black dotted line is the stress distribution at Rc = 50.0, which considers no welding residual stress. From these figures, it is found that the difference between the shot peened stress distribution and the as-machined stress distribution is larger with the increase of Rc in both stress in axial direction σ z and hoop direction σ θ . It can also be seen that the shot peened stress distribution gets closer to the as-machined stress distribution in the distant region from the outer surface and the difference between these distributions becomes almost zero at 7 mm from the outer surface. The shot peened stress distributions at Rc = 50 without welding residual stress is almost same as those with welding residual stress in the near region from the outer surface to approximately 0.5 mm in thickness direction.

Fig. 20
figure 20

Comparison of stress distribution in the axial direction (σ z ) for each Rc and XRD along line B-B′

Full size image
Fig. 21
figure 21

Comparison of stress distribution in the hoop direction (σ θ ) for each Rc and XRD along line B-B′

Full size image

As shown in this chapter, a similar stress distribution as the shot peened stress distribution measured by XRD was obtained in the simulation using the proposed system at a collision area ratio of Rc = 50.0. In addition, the analysis finished in 2 days for the welding residual stress analysis and 10 days for the shot peening analysis.

5 Conclusions

In this study, to predict the effect of the modification of the residual stress distribution due to shot peening, the authors proposed an IEFEM-based dynamic analysis method and an equivalent load model that can simulate the load distribution history due to the shot collisions. An analysis system was constructed by integrating the IEFEM-based dynamic analysis method and the equivalent load model to simulate the numerous random shot collisions. The proposed analysis system was applied to the prediction of the modification of the residual stress distribution in a multi-pass-welded pipe joint. As a result, the following results were obtained:

  1. 1.

    An equivalent load model was applied to the analysis of the collision of a single shot. The results were compared with those obtained using ABAQUS considering the contact between the shot and the surface of the target. As a result, it was shown that the results obtained by the equivalent load model agree well with those from ABAQUS.

  2. 2.

    A thermal elastic-plastic analysis method using IEFEM was applied to the prediction of the residual stress distribution of a multi-pass-welded pipe joint. The calculated residual stress distribution was compared with that measured using XRD. As a result, it was found that the residual stress distribution from IEFEM and XRD are in good agreement.

  3. 3.

    The behavior of the stress distribution due to shot peening on the multi-pass-welded pipe joint was analyzed using the proposed analysis system. In the analysis, the welding residual stress calculated using thermal elastic analysis was considered. As a result, a similar stress distribution as that measured by XRD was obtained in case where the collision ratio Rc reached 50.0.