Abstract
We show that for a family of randomly kicked Hamilton–Jacobi equations on the torus, almost surely, the solution of an initial value problem converges exponentially fast to the unique stationary solution. Combined with the earlier results of the authors, this completes the program in the multi-dimensional setting started by E, Khanin, Mazel and Sinai in the one-dimensional case.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
We consider the randomly forced Hamilton–Jacobi equation on the d dimensional torus
where \(b\in \mathbb {R}^d\), \(\nabla \) stands for gradient in x, and \(F^\omega \) is a random potential. By writing \(u(x,t) = \nabla \psi (x,t)\), we obtain the stochastic inviscid Burgers equation
\(f^\omega (y,t) = - \nabla F^\omega (y,t)\) with the condition \(\int u(x,t) dx = b\). Although everywhere below we deal only with the Burgers case, many of our results can be generalized to a much more general case of the Hamilton–Jacobi equation
where H(p) is a strictly convex Hamiltonian which is also assumed to grow sublinearly in p.
We are interested in two types of random potentials. In [11], the authors consider the dimension \(d=1\), with the “white noise potential”
where \(F_i:\mathbb {T}^d \rightarrow \mathbb {R}\) are smooth functions, and \({\dot{W}}_i\) are independent white noises. It is shown that finite time solutions of (1.1) converge exponentially fast to a unique stationary solution. In this paper, we generalize this result to arbitrary dimensions, for a related “kicked” model.
The “kicked force” model was introduced in [5], with
where \(F^\omega _j\) is an i.i.d. sequence of potentials, and \(\delta (\cdot )\) is the delta function. In other words, the system evolves without an external force apart from instant kicks in integer moments of time. The kicks are reflected in adding a random potential which is chosen independently for every integer time. We focus on the “kicked” potential (1.5) as it is simpler, but retains most of the features of the system.
The system (1.3) does not admit classical solutions in general, and the solution is interpreted using the Lax-Oleinik variational principle. There is a semi-group family of operators [see (2.2)]
such that the function \(\psi (x,\tau ) = K_{s,\tau }^{\omega ,b}\varphi (x)\), \(s \le \tau \le t\) is the solution to (1.1) on the interval [s, t] with the initial condition \(\psi (x,s) = \varphi (x)\).
It is shown in [5] that under suitable conditions on the kicked force, almost surely, the system (1.1) admits a unique solution \(\psi ^-_\omega (x,t)\) (up to an additive constant) on the interval \((-\infty , \infty )\). Let us denote
which is the suitable semi-norm for measuring convergence up to an additive constant. Then any solution on [s, t] converges to \(\psi ^-_\omega \) as \(s \rightarrow -\infty \), uniformly over all initial conditions in the semi-norm \(\Vert \cdot \Vert _*\):
Our main result is that, under certain mild conditions on the kicks, the above convergence is exponentially fast.
Main result
Suppose certain conditions are satisfied for the random kicked force (see Theorem 1 for details), there exists a (non-random) \(\lambda >0\) such that, almost surely,
Remark
Exponential convergence is also known to hold in the viscous equation
(see [10]). However, in this case the a priori convergence rate \(\lambda (\nu )\) may vanish in the inviscid limit \(\nu \rightarrow 0\). Since our result provides a non-zero lower bound on convergence rate when \(\nu =0\), it is an interesting question whether there exists a uniform lower bound on \(\lambda (\nu )\).
The a priori convergence rate of the Lax-Oleinik semi-group is only polynomial in time, as evidenced in the case when there is no force, i.e. \(F^\omega = 0\). In the case when the force is non-random, exponential convergence is true when the Aubry set (see for example [4]) consists of finitely many hyperbolic periodic orbits or fixed points ( [6]). According to a famous conjecture of Mañe, this condition holds for a generic force ([8]), however this conjecture is only proven when \(d=2\) for \(C^2\) forces ([2, 3]).
In some sense, [7] proves a random version of Mañe’s conjecture. In the random case, the role of the Aubry set is taken by the the globally minimizing orbit, and it is shown that this orbit is non-uniformly hyperbolic under the random Euler-Lagrange flow. Conceptually, this hyperbolicity is responsible for the exponential convergence of the solutions to (1.1). However, this connection is quite delicate. To illustrate, let us outline the proof in the uniform hyperbolic case:
-
(Step 1) Consider a solution \(K_{-T, 0}^{\omega , b}\varphi \) that is sufficiently close to the stationary solution \(\psi ^-(\cdot , 0)\), this is the case since we know the solution \(K_{-T, 0}^{\omega , b} \varphi \rightarrow \psi ^-(\cdot , 0)\), albeit without any rate estimates.
-
(Step 2) Show that the associated finite time minimizers is close to the Aubry set when \(t \in [-2T/3, -T/3]\). By hyperbolic theory, any orbit that stays in a neighborhood of an hyperbolic orbit for time T / 3 must be exponentially close to it at some point.
-
(Step 3) Finite time minimizer being exponentially close to the Aubry set implies the solution is in fact exponentially close to \(\psi ^-\).
In the non-uniform hyperbolic case, Step 2 fails, because a non-uniform hyperbolic orbit only influence nearby orbits in a random neighborhood whose size changes from iterate to iterate. We are forced to devise a much more involved procedure:
-
(1)
(Step A) Reduce the problem to a local one, where we only study the solution in a small (random) neighborhood of the global minimizer.
-
(2)
(Step B) Consider a solution \(K_{-T, 0}^{\omega , b}\varphi \) is \(\delta \)-close to the stationary solution \(\psi ^-(\cdot , 0)\) locally. Use a combination of variational and non-uniform hyperbolic theory to show that the finite time minimizer is \(\delta ^q\)-close to the global minimizer at some time, where \(q > 1\). This step can only be done up to an exponentially small error.
-
(3)
(Step C) Use step B to show the solution \(K_{-T, 0}^{\omega , b}\varphi \) is \(\delta ^q\)-close to the stationary solution. Feed the new estimates into Step B, and repeatedly upgrade until \(\delta \) is exponentially small.
In this paper, we carry out the above program. One can say that the main theme here is an interplay between dynamics and PDE. On a conceptual level, there are two Lyapunov exponents. One is purely dynamical, it characterizes the hyperbolic properties of the intrinsic dynamical system (the random Lagrangian flow). Another Lyapunov exponent is related to the rate of convergence of the solutions to the PDE (1.1). The positivity of the dynamical exponent is proved in [7]. The main result of the present paper is the positivity of the PDE exponent. Although we don’t prove it here, it should be expected that the two exponents have the same (non-random) value. We plan to address this in the future.
The paper have the following structure. We formulate our assumptions and main result in Sect. 2. Basic properties of the viscosity solutions and stationary solutions are introduced in Sects. 3 and 4. In Sect. 5, we reduce the main result to its local version, as outlined in Step A. This is Proposition 5.1.
In Sect. 6, we describe the upgrade procedure outlined in Step C. Step B is formulated in Proposition 6.1, and the proof is postponed to Sects. 7 and 8.
2 Statement of the main result
Consider the kicked potentials (1.5), where the random potentials \(F^\omega _j\) are chosen independently from a distribution \(P \in \mathcal {P}(C^{2+\alpha }(\mathbb {T}^d))\), with \(0 < \alpha \le 1\).
Given an absolutely continuous curve \(\zeta :[s,t]\rightarrow \mathbb {T}^d\), we define the action of \(\zeta \) to be
In other words, when s, t are integers, we include the kick at time s, but not at time t. For \(0< s < t \in \mathbb {R}\), and \(x, x' \in \mathbb {T}^d\), the action function is
where \(\zeta \) is absolutely continuous. The action function is Lipshitz in both variables.
The backward Lax-Oleinik operator \(K^{\omega ,b}_{s,t} : C(\mathbb {T}^d) \rightarrow C(\mathbb {T}^d)\) is defined as
We take (2.2) as the definition of our solution on [s, t] with initial conditon \(\varphi (x)\). Due to the fact that \(F^\omega (x,t)\) vanishes at non-integer times, \(K_{s,t}^{\omega ,b}\) is completely determined by its value at integer times. In the sequel we consider only \(s=m, t =n \in \mathbb {Z}\). The operators satisfies a semi-group property: for \(s< t < u \),
We now state the conditions on the random potentials. The following assumptions are introduced in [5], which guarantees the uniqueness of the stationary solution.
-
Assumption 1. For any \(y\in \mathbb {T}^d\), there exists \(G_y\in {{\,\mathrm{supp}\,}}P\) s.t. \(G_y\) has a maximum at y and that there exists \(\delta >0\) such that
$$\begin{aligned} G_y(y)-G(x)\ge \delta |y-x|^2. \end{aligned}$$ -
Assumption 2. \(0\in {{\,\mathrm{supp}\,}}P\).
-
Assumption 3. There exists \(G\in {{\,\mathrm{supp}\,}}P\) such that G has a unique maximum.
The following is proved in [5] under the weaker assumption that \(F_j^\omega \in C^1(\mathbb {T}^d)\):
Proposition 2.1
[5]
-
(1)
Assume that assumption 1 or 2 holds. For a.e. \(\omega \in \Omega \), we have the following statements.
-
(a)
There exists a Lipshitz function \(\psi ^-(x,n)\), \(n \in \mathbb {Z}\), such that for any \(m<n\),
$$\begin{aligned} K_{m,n}^{\omega ,b}\psi ^-(x,m)=\psi ^-(x,n). \end{aligned}$$ -
(b)
For any \(n \in \mathbb {Z}\), we have
$$\begin{aligned} \lim _{m\rightarrow -\infty }\sup _{\varphi \in C(\mathbb {T})}\Vert K^{\omega ,b}_{m,n}\varphi (x)-\psi ^-(x,n)\Vert _* =0. \end{aligned}$$
-
(a)
-
(2)
Assume that assumption 3 holds. Then the conclusions for the first case hold for \(b=0\).
It follows from Proposition 2.1 that \(\psi ^-\) is defined uniquely up to an additive constant. For definiteness, we assume \(\psi ^-(0, 0) = 0\). We now restrict to a specific family of kicked potentials. The following assumption is introduced in [5].
-
Assumption 4. Assume that
$$\begin{aligned} F^\omega _j(x)=\sum _{i=1}^M \xi _j^i(\omega )F_i(x), \end{aligned}$$(2.3)where \(F_i:\mathbb {T}^d\rightarrow \mathbb {R}\) are smooth non-random functions, and the vectors \(\xi _j(\omega )=(\xi _j^i(\omega ))_{i=1}^M\) is an i.i.d sequence of vectors in \(\mathbb {R}^M\) with an absolutely continuous distribution.
In [7], a stronger assumption is used to obtain information on the stationary solutions and the global minimizer. These additional structures provides the mechanism for exponential convergence. Let \(\rho : \mathbb {R}^m \rightarrow \mathbb {R}\) be the density of \(\xi _j\).
-
Assumption 5. Suppose assumption 4 holds, and in addition:
-
$$\begin{aligned} \mathbb {E}(|\xi _j|)=\int _{\mathbb {R}^M} |c|\rho (c)dc < \infty . \end{aligned}$$
-
For every \(1\le i \le M\), there exists non-negative functions \(\rho _i \in L^\infty (\mathbb {R})\) and \({\hat{\rho }}_i\in L^1(\mathbb {R}^{M-1})\) such that
$$\begin{aligned} \rho (c)\le \rho _i(c_i) {\hat{\rho }}_i({\hat{c}}), \end{aligned}$$where \(c=(c_1, \ldots , c_M)\), \({\hat{c}}_i =(c_1, \ldots , c_{i-1}, c_{i+1}, \ldots , c_M)\).
-
Assumption 5 is rather mild. We only need to avoid the case that \(\rho \) is degenerate in some directions. In particular, it is satisfied if \(\xi ^1_j, \ldots , \xi ^M_j\) are i.i.d. random variables with bounded densities and finite mean.
We now state the main theorem of this paper.
Theorem 1
-
(1)
Assume that assumption 5 and one of assumption 1 or 2 hold. Assume in addition that the mapping
$$\begin{aligned} (F_1, \ldots , F_M): \mathbb {T}^d \rightarrow \mathbb {R}^M \end{aligned}$$(2.4)is an embedding. For \(b \in \mathbb {R}^d\), let \(\psi ^-_\omega \) be the unique stationary solution in Proposition 2.1. Then there exists a (non-random) \(\lambda >0\) and a random variables \(N(\omega )>0\) such that almost surely, for all \(N > N(\omega )\),
$$\begin{aligned} \sup _{\varphi \in C(\mathbb {T}^d)} \Vert K_{m,n}^{\omega ,b}\varphi - \psi ^-_\omega (\cdot ,n)\Vert _* \le e^{-\lambda N}. \end{aligned}$$ -
(2)
Assume that assumption 3 and 5 hold. Then the same conclusions hold for \(b=0\).
3 Viscosity solutions and the global minimizer
Let \(I \subset \mathbb {R}\) be an interval. An absolutely continuous curve \(\gamma : I \rightarrow \mathbb {T}^d\) is called a minimizer if for each interval \([s,t] \subset I\), we have \(A^{\omega ,b}_{s,t}(\gamma (s), \gamma (t)) = \mathbb {A}^{\omega ,b}(\gamma |_{[s,t]})\). In particular, \(\gamma \) is called a forward minimizer if \(I = (-\infty , t_0]\), a backward minimizer if \(I = [s_0, \infty )\) and a global minimizer if \(I = (-\infty , \infty )\).
Due to the kicked nature of the potential, a minimizer is always linear between integer times. Then any minimizer \(\gamma :[m, n] \rightarrow \infty \) is completely determined by the sequence
The underlying dynamics for the minimizers is given by family of maps \(\Phi _j^\omega :\mathbb {T}^d\times \mathbb {R}^d \rightarrow \mathbb {T}^d \times \mathbb {R}^d\)
The maps belong to the so-called standard family, and are examples of symplectic, exact and monotonically twist diffeomorphisms. For \(m,n\in \mathbb {Z}\), \(m<n\), denote
The (full) orbit of a vector \((x_n,v_n)\) is given by the sequence
If \(\gamma :[m,n]\rightarrow \mathbb {T}^d\) is a minimizer, then \((x_j, v_j)\) defined in (3.1) is an orbit, namely
In this case, we extend the sequence to \((x_m, v_m) = (\Phi _m)^{-1}(x_{m+1}, v_{m+1})\) and call \((x_j, v_j)_{j = m}^n\) a minimizer.
The viscosity solution and the minimizers are linked by the following lemma:
Lemma 3.1
[7, Lemma 3.2]
-
(1)
For \(\varphi \in C(\mathbb {T}^d)\) and \(m < n \in \mathbb {Z}\), for each \(x \in \mathbb {T}^d\) there exists a minimizer \((x_j, v_j)_{j =m}^n\) such that \(x_n =x\), and
$$\begin{aligned} K^{\omega ,b}_{m,n}\varphi (x_n) = \varphi (x_m) + A_{m,n}^{\omega ,b}(x_m, x_n). \end{aligned}$$(3.3)Moreover, the minimizer is unique if \(\psi (x) = K^{\omega ,b}_{m,n}\varphi (\cdot )\) is differentiable at x, and in this case \(v_n = \nabla \psi (x) + b\).
-
(2)
Suppose \(\psi ^-_\omega (x,n)\) is the stationary solution. Then at every \(x\in \mathbb {T}^d\) and \(n \in \mathbb {Z}\), there exists a backward minimizer \((x_j, v_j)_{j = -\infty }^n\) such that \(x_n = x\)
$$\begin{aligned} K^{\omega , b}_{m,n}\psi ^-_\omega (x_n, n) = \psi ^-_\omega (x_m, m) + A_{m,n}^{\omega , b}(x_m, x_n), \quad m < n. \end{aligned}$$Moreover, the minimizer is unique if \(\psi ^-_\omega (\cdot , n)\) is differentiable at x, and in this case \(v_n = \nabla \psi ^-_\omega (x, n) + b\).
In case (1) we call \((x_j, v_j)_{j=m}^n\) a minimizer for \(K_{m,n}^{\omega , b}\varphi (x_0)\), and in case (2) the orbit \((x_j, v_j)_{j=-\infty ^n}\) is called a minimizer for \(\psi ^-(x_n, n)\).
The forward minimizer is linked to the forward operator  , defined as
, defined as

Analog of Proposition 2.1 and Lemma 3.1 hold, which we summarize below.
-
For every \(b \in \mathbb {R}^d\), almost surely, there exists a Lipshitz function \(\psi ^+_\omega (x, m)\), \(m \in \mathbb {Z}\), unique up to an additive constant, such that

We will assume \(\psi ^+(0, 0) = 0\) to fix the additive constant.
-
For each
 there exists a minimizer \((x_j, v_j)_{j=m}^n\) such that \(x_m = x\) and
there exists a minimizer \((x_j, v_j)_{j=m}^n\) such that \(x_m = x\) and 
When
 is differentiable at x we have \(v_m = \nabla \psi (x) + b\).
is differentiable at x we have \(v_m = \nabla \psi (x) + b\). -
For each \(x \in \mathbb {T}^d\), and \(m \in \mathbb {Z}\), there exists a forward minimizer \((x_j, v_j)_{j = m}^\infty \) such that \(x_m = x\),
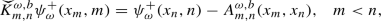
and \(v_m = \nabla \psi ^+_\omega (x, m)\) if \(\psi ^+(\cdot , m)\) is differentiable at x.
The global minimizer is characterized by both \(\psi ^-_\omega \) and \(\psi ^+_\omega \).
Proposition 3.2
Assume that Assumption 4 holds, and one of Assumptions 1 and 2 holds. Assume in addition, the map (2.4) is an embedding. Then for \(b\in \mathbb {R}^d\), almost every \(\omega \), there exists a unique global minimizer \((x_j^\omega , v_j^\omega )_{j \in \mathbb {Z}}\). For each \(j \in \mathbb {Z}\), \(x_j^\omega \) is the unique \(x\in \mathbb {T}^d\) reaching the minimum in
Moreover, \(\psi ^\pm _\omega (\cdot , j)\) are both differentiable at \(x_j\), and \(v_j = \nabla \psi ^-_\omega (x, j) + b = \nabla \psi ^+_\omega (x, j) + b\).
Throughout the paper, the notation \((x_j^\omega , v_j^\omega )_{j \in \mathbb {Z}}\) will be reserved for the global minimizer.
The function
will serve an important purpose for the discussions below.
The random potentials \(F_j^\omega \) are generated by a stationary random process, so there exists a measure preserving transformation \(\theta \) on the probability space \(\Omega \) satisfying
The family of maps \(\Phi ^\omega _j\) then defines a non-random transformation
on the space \(\mathbb {T}^d \times \mathbb {R}^d \times \Omega \). Then from Proposition 3.2,
and the probability measure
is invariant and ergodic under \({\hat{\Phi }}\). The map \(D\Phi _0^\omega : \mathbb {T}^d \times \mathbb {R}^d \times \Omega \rightarrow Sp(d)\), where Sp(d) is the group of all \(2d \times 2d\) symplectic matrices, defines a cocycle over \({\hat{\Phi }}\). Under Assumption 5, its Lyapunov exponents \(\lambda _1(\nu ), \ldots , \lambda _{2d}(\nu )\) are well defined, and due to symplecticity, we have
and \(\lambda _i = -\lambda _{2d-i+1}\).
There is a close relation between the non-degeneracy of the variational problem (3.4), and non-vanishing of the Lyapunov exponents for the associated cocycle.
Proposition 3.3
[7, Proposition 3.10] Assume that assumption 5 and one of assumptions 1 or 2 holds. Assume in addition that the map (2.4) is an embedding. Then for all \(b\in \mathbb {R}^d\), for a.e. \(\omega \), the following hold.
-
(1)
There exist \(C(F,\rho ), R(F,\rho )>0\) depending only on \(F_1, \ldots F_M\) in (2.4) and the density \(\rho \) of \(\xi _j\), and a positive random variable \(a(\omega )>0\), such that for all x satisfying \(\Vert x - x_0^\omega \Vert < R(F, \rho )\), we have
$$\begin{aligned} Q_\omega ^\infty (x, 0) - Q_\omega ^\infty (x_0^\omega , 0) \ge a(\omega )\Vert x-x_0^\omega \Vert ^2, \end{aligned}$$(3.7)and \(a(\omega )\) satisfies
$$\begin{aligned} \mathbb {E}(a(\omega )^{-\frac{1}{2}}) < C(F, \rho ). \end{aligned}$$(3.8) -
(2)
The Lyapunov exponents of \(\nu \) satisfy
$$\begin{aligned} \lambda _d(\nu )<0<\lambda _{d+1}(\nu ). \end{aligned}$$
The second conclusion of Proposition 3.3 implies the orbit \((x_j^\omega , v_j^\omega )\) for the sequence of maps \(\Phi _j^\omega \) is non-uniformly hyperbolic. In particular, it follows that there exists local unstable and stable manifolds. It is shown in [7] that the graph of the gradient of the viscosity solutions locally coincide with the unstable and stable manifolds.
Proposition 3.4
[7, Theorem 6.1] Under the same assumptions as Proposition 3.3, for each \(\epsilon >0\), there exists positive random variables \(r(\omega )>0\), \(C(\omega )>1\), such that the following hold almost surely.
-
(1)
There exists \(C^1\) embedded submanifolds \(W^u(x_0^\omega , v_0^\omega )\) and \(W^s(x_0^\omega , v_0^\omega )\), such that
$$\begin{aligned} (x, \nabla \psi ^-_\omega (x, 0) + b) \in W^u(x_0^\omega , v_0^\omega ), \quad (x, \nabla \psi ^+_\omega (x,0)+ b) \in W^s(x_0^\omega , v_0^\omega ) \end{aligned}$$for all \(\Vert x - x_0^\omega \Vert < r(\omega )\).
-
(2)
For every \(\Vert x - x_0^\omega \Vert < r(\omega )\), let \((x_j^-, v_j^-)_{j \le 0}\) and \((x_j^+, v_j^+)_{j \ge 0}\) be the backward and forward minimizers satisfying \(x_0^\pm = x\). Then
$$\begin{aligned}&\Vert (x_j^\omega , v_j^\omega ) - (x_j^-, v_j^-) \Vert \le C(\omega ) e^{-\lambda '|j|}, \quad j \le 0,\\&\Vert (x_j^\omega , v_j^\omega ) - (x_j^+, v_j^+) \Vert \le C(\omega ) e^{-\lambda '|j|}, \quad j \ge 0, \end{aligned}$$where \(\lambda ' = \lambda _{d+1}(\nu ) - \epsilon \).
4 Properties of the viscosity solutions
4.1 Semi-concavity
Given \(C>0\), we say that a function \(f: \mathbb {R}^d \rightarrow \mathbb {R}\) is C semi-concave if for any \(x\in \mathbb {R}^d\), there exists a linear form \(l_x: \mathbb {R}^d \rightarrow \mathbb {R}\) such that
A function \(\varphi : \mathbb {T}^d \rightarrow \mathbb {R}\) is called C semi-concave if it is C semi-concave as a function lifted to \(\mathbb {R}^d\). The linear form \(l_x\) is called a subdifferential at x. If \(\varphi \) is differentiable at \(x\in \mathbb {T}^d\), then the subdifferential \(l_x\) is unique and is equal to \(d \varphi (x)\). A semi-concave function is Lipshitz.
Lemma 4.1
[4, Proposition 4.7.3]) If \(\varphi \) is continuous and C semi-concave on \(\mathbb {T}^d\), then \(\varphi \) is \(2C\sqrt{d}\)-Lipshitz.
Lemma 4.2
[4] Suppose both \(\varphi _1\) and  is C semi-concave, then over the set
is C semi-concave, then over the set  ,
,  are differentiable, \(\nabla \psi _1(x) = \nabla \psi _2(x)\), and \(\nabla \varphi _1(x)\) is 6C-Lipshitz over the set
are differentiable, \(\nabla \psi _1(x) = \nabla \psi _2(x)\), and \(\nabla \varphi _1(x)\) is 6C-Lipshitz over the set  .
.
Let \(K_0(\omega )=\Vert F_0^\omega \Vert _{C^{2+\alpha }}+1\) and \(K(\omega ) = 2\sqrt{d}(K_0(\omega )+1)\). The action function \(A_{m,n}^{\omega ,b}\) has the following properties.
Lemma 4.3
[7, Lemma 3.2]
-
(1)
The function \(A_{m,n}^{\omega ,b}(x, x')\) is \(1-\)semi-concave in the second component, and is \(K(\theta ^m\omega )-\)semi-concave in the first component. Here \(\theta : \Omega \rightarrow \Omega \) is the time-shift, see (3.6).
-
(2)
For any \(\varphi \in C(\mathbb {T}^d)\), and \(m < n \in \mathbb {Z}\), the function \(K_{m,n}^{\omega , b}\varphi (x)\) is 1 semi-concave, and
 is \(K_0(\theta ^m\omega )\) semi-concave. Either function, as well as the sum of the two functions, are \(K(\theta ^m\omega )\) Lipshitz.
is \(K_0(\theta ^m\omega )\) semi-concave. Either function, as well as the sum of the two functions, are \(K(\theta ^m\omega )\) Lipshitz. -
(3)
For \(n \in \mathbb {Z}\), the functions \(\psi ^-_\omega (\cdot , n)\) is 1 semi-concave, and \(-\psi ^+_\omega (\cdot , n)\) is \(K_0(\theta ^n \omega )\) semi-concave, Either function, as well as the sum of the two functions, are \(K(\theta ^m\omega )\) Lipshitz.
We first state two lemmas concerning the properties of the Lax-Oleinik semigroup, the goal is to obtain Lemma 4.7, which is a version of Mather’s graph theorem ( [9]).
Lemma 4.4
For any \(x \in \mathbb {T}^d\), \(m < n\), \(\varphi \in C(\mathbb {T}^d)\), we have

Proof
For any \(x,y \in \mathbb {T}^d\),
then

\(\square \)
Lemma 4.5
Suppose \(m < n \). Let \((x_j, v_j)_{j=m}^n\) be a minimizer for \(K_{m,n}^{\omega ,b}\varphi \) in the sense of (3.3). Then for each \(m\le j \le n\), we have

and

Proof
By definition \(K_{nn}^{\omega , b}\varphi = \varphi \), so the case \(j = n\) is trivial. For \(m \le j < n\), we have
Then

On the other hand, apply Lemma 4.4 to \(K_{m,j}^{\omega ,b}\varphi \) and \(j < n\) yields

The lemma follows. \(\square \)
Corollary 4.6
Let \((x_j, v_j)_{j=m}^n\) be a minimizer for \(K_{m,n}^{\omega ,b}\varphi \), then it is also a minimizer for  .
.
Proof
Using the calculations in the proof of Lemma 4.5, we get

for all \(m \le j \le n\). The corollary follows. \(\square \)
The following lemma provides a Lipshitz estimate for the velocity of the minimizer in the interior of the time interval.
Lemma 4.7
Suppose \(m < n \) with \(n-m \ge 2\). Let \((x_j, v_j)_{j=m}^n\) and \((y_j, \eta _j)_{j=m}^n\) be two minimizers for \(K_{m,n}^{\omega ,b}\varphi \) in the sense of (3.3). Then for all \(m< j < n\), we have
The same conclusion hold, if \((x_j, v_j)\) and \((y_j, \eta _j)\) are minimizers for  .
.
Proof
We apply Lemma 4.5 to \((x_j, v_j)\) and \((y_j, \eta _j)\). Denote \(\psi _1 = K_{m,j}^{\omega ,j}\varphi \) and  , since \(j-m, n-j \ge 1\), \(\psi _1\) is 1 semi-concave, \(-\psi _2\) is \(K(\theta ^j \omega )\) semi-concave. Since \(x_j, y_j \in {{\,\mathrm{arg\,min}\,}}_x\{\psi _1(x) - \psi _2(x)\}\), Lemma 4.2 and Lemma 3.1 implies
, since \(j-m, n-j \ge 1\), \(\psi _1\) is 1 semi-concave, \(-\psi _2\) is \(K(\theta ^j \omega )\) semi-concave. Since \(x_j, y_j \in {{\,\mathrm{arg\,min}\,}}_x\{\psi _1(x) - \psi _2(x)\}\), Lemma 4.2 and Lemma 3.1 implies
\(\square \)
4.2 Properties of the stationary solutions
Recall that
which takes its minimum at the global minimizer \(x_n^\omega \). To simplify notations, we will drop the subscript \(\omega \) from these functions when there is no confusion.
This function \(Q^\infty \) is very useful, as it can be used to measure the distance to the global minimizer. For all \( \Vert y - x_0^\omega \Vert < r(F)\), we have
Moreover, \(Q^\omega \) is a Lyapunov function for infinite backward minimizers. Namely, if \((y_0, \eta _0) = (y_0, \nabla \psi ^-_\omega (y_0, 0))\) is a backward minimizer, then for any \(j<k\le 0\), we have
(See [7], Lemma 7.2)
Let us also recall, for any \(\lambda ' < \lambda \), there exists functions \(r(\omega )>0\), \(C(\omega )>1\) such that for all backward minimizers \((y_n, \eta _n)_{n \le 0}\) such that
We will also use a process in non-uniform hyperbolicity known as tempering.
Lemma 4.8
([1], Lemma 3.5.7) Let \(g(\omega )>1\) be a random variable satisfying \(\mathbb {E}(\log g(\omega )) < \infty \), then for any \(\epsilon >0\), there exists \(g^\epsilon (\omega )>g(\omega )\) such that
Let’s call a random variable \(g(\omega ) > 0\) tempered if for any \(\epsilon >0\), both \(g, g^{-1}\) admits an upper bound satisfying (4.4). Products and inverses of tempered random variables are still tempered.
The random variables a, K in (4.1) and r, C in (4.3) are tempered.
Lemma 4.9
For any \(\epsilon > 0\), there exists random variables
such that
Proof
Lemma 4.8 applies to \(a(\omega )\) and \(K(\omega )\) since \(\mathbb {E}(\log a^{-1}), \mathbb {E}(\log K) < \infty \). The fact that \(C(\omega )\) and \(r(\omega )\) are tempered can be proven by adapting the proof Theorem 6.1 in [7]. We now explain the adaptations required.
In [7], there exists local linear coordinates (s, u) with the formula \((y, \eta ) = P_j(s, u)\) centered at the global minimizer \((x_j^\omega , v_j^\omega )\), with the estimates \(\Vert DP_j\Vert , \Vert DP_j^{-1}\Vert \le K(\theta ^j \omega )a^{-\frac{1}{2}}(\theta ^j \omega )\) (section 6 of [7]). Then it is shown that there exists a random variable \(r_0(\omega )\) (called r in that paper) such that any orbit \((y, \eta ) \in \{(y, \nabla \psi ^-_\omega (y, 0))\} \cap \{\Vert s\Vert , \Vert u\Vert < r_0\}\) must be contained in the stable manifold. r is tempered because it is the product of tempered random variables. Indeed, the following explicit formula was given in the Proof of Theorem 6.1, section 7 of [7]:
where K, a are the same as in this paper, and the fact that \(\rho , {\tilde{C}}\) are tempered is explained in Lemma 6.5 and Proposition 7.1 of [7]. We now convert to the variable \((y, \eta )\). Since the norm of the coordinate changes are tempered, there exists a tempered random variable \(r_1(\omega )\) such that any orbit contained in
must be contained in the unstable manifold of \((x_0^\omega , v_0^\omega )\).
We now show the same conclusion holds on a neighborhood of the configuration space \(\Vert y - x_0^\omega \Vert < r(\omega )\), with \(r(\omega )\) tempered. Let \((y_0, \eta _0) = (y_0, \nabla \psi ^-(y_0, 0))\) and let \((y_{-1}, \eta _{-1})\) be its backward image. According to Lemma 4.2, \(\Vert \eta _{-1} - v_{-1}^\omega \Vert \le K(\theta ^{-1}\omega )\Vert y_{-1} - x_{-1}^\omega \Vert \), as a result
Finally, using (4.1) and (4.2), we have
We obtain that
implies \((y_1, \eta _1)\) is contained in the unstable manifold of \((x_{-1}^\omega , v_{-1}^\omega )\). r is tempered as it is products of tempered random variables.
The fact that an orbit on the stable manifold of a non-uniformly hyperbolic orbit converge at the rate \(C(\omega ) e^{-\lambda n}\), and that the coefficient \(C(\omega )\) is tempered is a standard result in non-uniform hyperbolicity, see for example [1]. \(\square \)
We now use what we obtained to get an approximation for the stationary solutions.
Lemma 4.10
There exists \(C_1^\epsilon (\omega )>0\), \(e^{-\epsilon } \le C_1^\epsilon (\omega )/C_1^\epsilon (\theta \omega ) \le e^\epsilon \), such that for all \(\Vert y - x_0^\omega \Vert < r(\omega )\), and \(n < 0\), we have
We also have the forward version: for \(n > 0\),
Proof
We only prove the backward version. By definition,
On the other hand, let \((y_n, \eta _n)_{n\le 0}\) be the minimizer for \(\psi ^-_\omega (\psi , 0)\), then
where \(K^\epsilon , C^\epsilon \) are from Lemma 4.9.
We now choose new random variables denoted \(C^{\epsilon /2}\) and \(K^{\epsilon /2}\) by applying Lemma 4.9 again with the new parameter \(\epsilon /2\). Note that
We repeat the proof with the new random variable as upper bounds. The constant in our estimate is replaced with \(K^{\epsilon /2}(\omega ) C^{\epsilon /2}(\omega )\), which we then denote \(C_1^\epsilon (\omega )\). The proof is now complete since \(C_1^\epsilon (\omega )\) satisfies \(e^{-\epsilon } \le C_1^\epsilon (\omega )/C_1^\epsilon (\theta \omega ) \le e^\epsilon \). \(\square \)
Remark
In the last step of the proof, we performed the procedure of “re-choosing” our tempering random variables with a smaller parameter, indicated by the notation \(C^{\epsilon /2}(\omega )\), \(K^{\epsilon /2}(\omega )\) etc. In the future, we will sometimes perform this procedure implicitly by simply changing the superscript \(\epsilon \) into \(\epsilon /2\) in the random variables such as \(C^\epsilon (\omega )\). When the superscript \(\epsilon \) is used in random variables, it always refer to this parameter and not as a power.
5 Reducing to local convergence
In this section we reduce the main theorem to its local version.
Proposition 5.1
Under the same assumptions as Proposition 3.3, there exists \(0< \lambda < \lambda _{d+1}(\nu )\), positive random variables \(0<\tau (\omega )<r(\omega )\), \(D_0(\omega )>0\), and \(N_0(\omega )>0\) such that for all \(N > N_0(\omega )\) and \(\varphi \in C(\mathbb {T})\),
The proof of Proposition 5.1 is given in the next section. Next, we have a localization result, which says any minimizer for \(K_{-N, M}^{\omega ,b}\varphi \) or \(\psi ^-(\cdot , M)\) go through the neighborhood \(\{ \Vert x- x_0^\omega \Vert < \tau (\omega ) \}\) at time \(t =0\), when N, M are large enough.
Proposition 5.2
Under the same assumptions as Proposition 3.3, let \({\tilde{\tau }}(\omega )>0\) be a positive random variable. Then there exists \(M_0 = M_0(\omega )\in \mathbb {N}\) depending on \({\tilde{\tau }}(\omega ), \omega \) such that the following hold.
-
(1)
For any \(N, M \ge M_0(\omega )\), let \((y_n, \eta _n)\), \(-N \le n \le M\) be a (backward) minimizer for \(K_{-N, M}^{\omega , b}\varphi (y_{M})\). Then \(\Vert y_0 - x_0^\omega \Vert < {\tilde{\tau }}(\omega )\).
-
(2)
(The forward version) For any \(N, M \ge M_0(\omega )\), let \((y_n, \eta _n)\), \(-N \le n \le M\) be a (forward) minimizer for
 . Then \(\Vert y_0 - x_0^\omega \Vert < {\tilde{\tau }}(\omega )\).
. Then \(\Vert y_0 - x_0^\omega \Vert < {\tilde{\tau }}(\omega )\).
We prove Proposition 5.2 using the following lemma, stating that the Lax-Oleinik operators are weak contractions.
Lemma 5.3
[5, Lemma 3] For any \(\varphi _1,\varphi _2 \in C(\mathbb {T}^d)\), we have
Proof of Proposition 5.2
We only prove item (1), as the (2) can be proven in the same way. We denote, for \(-N \le m \le M\),
and let \((y_n, \eta _n)\), \(-N \le n \le M\) be a minimizer for \(K_{-N, M}^{\omega ,b}\varphi \). For each \(-N< n < M\), Lemma 4.4 and 4.5 implies

hence

Recall that for \(Q^\infty (x,0) = \psi ^-(x,0) - \psi ^+(x,0)\), we have \(x_0^\omega \) is the unique minimum for \(Q^\infty (\cdot , 0)\). Define
By Proposition 2.1, we can choose \(M_0(\omega )\) large enough such that for \(N, M \ge M_0(\omega )\),

As a result, there exists a constant \(C \in \mathbb {R}\) such that

It follows that the minimum in (5.1) is never reached outside of \(\{\Vert x - x_0^\omega \Vert < {\tilde{\tau }}(\omega )\}\). We obtain \(\Vert y_0 - x_0^\omega \Vert < {\tilde{\tau }}(\omega )\). \(\square \)
We now prove our main theorem assuming Proposition 5.1.
Proof of Theorem 1
It suffices to prove the theorem for \(n =0\).
Let us apply Proposition 5.2 with \({\tilde{\tau }}(\omega ) = \tau (\omega )\) from Proposition 5.1. Let \((y_n, \eta _n)\) be a minimzier of \(K_{-N, M}^{\omega , b}\varphi (y_M)\), and \(({\tilde{y}}_n, {\tilde{\eta }}_n)\) a minimizer for
such that \(y_M = {\tilde{y}}_M\) and \(M = M_0(\omega )\). According to Proposition 5.1, there exists \(C(N, \omega ) \in \mathbb {R}\) such that for all \(\Vert y - x_0^\omega \Vert < \tau (\omega )\),
Then
On the other hand,
Using \(y_M = {\tilde{y}}_M\), combine both estimates, and take supremum over all \(y_M\), we get
To conclude the proof, we need to prove the same estimate on the time interval \([-N, 0]\). Denote \(E_Q = \{ \omega \in \Omega : \quad M_0(\omega ) \le Q\}\) for \(Q \in \mathbb {N}\). Fix some Q such that \(P(E_Q) > 0\), then by ergodicity, almost surely, \(M(\theta ^k \omega ) \le Q\) for infinitely many k. Let us define \(k(\omega )\) as the largest \(k < -Q\) such that \(M_0(\theta ^k \omega ) = Q\), then
provided \(N \ge \max \{Q, N_0(\theta ^k \omega )\} - k\). By reducing \(\lambda \) and taking N larger we can absorb the constant \(D_0(\theta ^k \omega ) e^{\lambda k(\omega )}\). \(\square \)
6 Local convergence: localization and upgrade
In this section we prove Proposition 5.1 (local convergence) using Proposition 6.1 and a consecutive upgrade scheme. It is useful to have the following definition for book keeping.
Recall that the notation \(\{(x_n^\omega , v_n^\omega )\}_{n\in \mathbb {Z}}\) is reserved for the orbit of the global minimizer.
Definition
Given \(\delta >0\), \(N \in \mathbb {N}\), let \((y_n, \eta _n)_{n=-N}^0\) be a minimizer for \(\psi ^N_\omega (\cdot , 0) = K^{\omega ,b}_{-N, 0}\varphi (\cdot )\), we say the orbit satisfies the (backward) \((\varphi , \delta , N)\) approximation property if for every \(-N/3 \le n \le 0\) such that \(\Vert y_n - x_n^\omega \Vert < r(\theta ^n \omega )\), we have
We denote this condition \(\mathbf {AP}^-(\omega , \varphi , \delta , N)\).
The following proposition is our main technical result, which says the approximation property allows us to estimate how close a backward minimizer is to the global minimizer:
Proposition 6.1
Let \(0< \epsilon < \lambda '/6\), there exists random variables \(\rho (\omega ) \in (0, r(\omega ))\) and \(N_1(\omega )>0\) depending on \(\epsilon \), such that if a \(\psi ^N_\omega \) backward minimizer \((y_n, \eta _n)_{n = -N}^0\) satisfies the \(\mathbf {AP}^-(\omega , \varphi , \delta , N)\) condition, withFootnote 1
then there exists an integer k such that \(\max \left\{ \frac{1}{8\epsilon } \log \delta , - \frac{N}{6} \right\} \le k <0\), and
where \(q = (\lambda '-3\epsilon )/(8\epsilon )\).
The proof require a detailed analysis using hyperbolic theory, and is deferred to the next few sections. In this section we prove Proposition 5.1 assuming Proposition 6.1.
We need to use both the forward and backward dynamics.
Definition
Given \(\delta >0\), \(N \in \mathbb {N}\), let \((y_n, \eta _n)_{n=0}^N\) be a minimizer for  , we say the orbit satisfies the (forward) \((\varphi , \delta , N)\) approximation property, if for every \(0 \le k \le N/3\) such that \(\Vert y_k - x_k^\omega \Vert < r(\theta ^k \omega )\), we have
, we say the orbit satisfies the (forward) \((\varphi , \delta , N)\) approximation property, if for every \(0 \le k \le N/3\) such that \(\Vert y_k - x_k^\omega \Vert < r(\theta ^k \omega )\), we have

We denote this condition \(\mathbf {AP}^+(\omega , \varphi , \delta , N)\).
We state a forward version of Proposition 6.1. The proof is the same.
Proposition 6.2
There exists random variables \(0<{\check{\rho }}(\omega )< r(\omega )\) and \({\check{N}}_1(\omega )>0\) such that if a \({\check{\psi }}^N_\omega \) backward minimizer \((y_n, \eta _n)_{n = 0}^N\) satisfies the \(\mathbf {AP}^+(\omega , \varphi , \delta , N)\) condition, and in addition,
then there exists \(0 < k \le \max \left\{ - \frac{1}{8\epsilon } \log \delta , \frac{N}{6} \right\} \) such that
where \(q = (\lambda '-3\epsilon )/(8\epsilon )\).
The main idea for the proof of Proposition 5.1 is to use both the forward and backward dynamics to repeatedly upgrade the estimates. If we have a \(\mathbf {AP}^-\) condition, Proposition 6.1 implies upgraded localization of backward minimizers at a earlier time. This can be applied to get a better approximation of the forward solution for the later time, obtaining an improved \(\mathbf {AP}^+\) condition. We then reverse time and repeat. However, due to technical reasons, we can only apply this process on a sub-interval called a good interval.
Recall that \(K^\epsilon (\omega )\) is the tempered upper bound for the random variable \(K(\epsilon )\), which is an upper bound for the norm of the potential.
Definition
For \(\beta >0\), we say \(j \in [-N, 0]\) is a backward \(\beta \)-good time if for every \(\varphi \in C(\mathbb {T}^d)\) and every \(K_{-N,0}^{\omega , b}\varphi \) minimizer \((y_n, \eta _n)_{n = -N}^0\), we have
where \(\rho (\omega )\) is in Proposition 6.1. Define forward \(\beta \)-good time similarly, by using forward minimizers and \({\check{\rho }}\) from Proposition 6.2. An interval \([n_1, n_2]\) is good if \(n_2\) is backward good and \(n_1\) is forward good.
Write \(\varphi ^N_\omega = K_{-N, 0}^{\omega , b}\varphi \), note that by Corollary 4.6, if \((y_n, \eta _n)\) is a minimizer for \(K_{-N, 0}^{\omega , b}\varphi \), then it is also a minimizer for  . Suppose \([n_1, n_2]\) is a \(\beta \)-good interval in \([-N, 0]\), denote
. Suppose \([n_1, n_2]\) is a \(\beta \)-good interval in \([-N, 0]\), denote

See Fig. 1 for a visualization of the notations.
We now describe the upgrade lemma:
Lemma 6.3
For \(0< \epsilon < \lambda ' /12\) and \(\beta >0\), there exists \(N_2(\omega )>0\) such that if
and if \([-5N/9, -4N/9] \subset [n_1, n_2] \subset [-2N/3, -N/3]\) is a \(\beta \)-good time interval with regards to \([-N,0]\), we have:
-
(1)
For
 defined in (6.5) and \({\bar{N}}= n_2 - n_1\), if $$\begin{aligned} (y_{j+n_2}, \eta _{j +n_2})_{j = - {\bar{N}}}^0 \text { satisfies } \mathbf {AP}^-(\omega _2, \varphi _1, \delta , {\bar{N}}) \text { condition,} \end{aligned}$$
defined in (6.5) and \({\bar{N}}= n_2 - n_1\), if $$\begin{aligned} (y_{j+n_2}, \eta _{j +n_2})_{j = - {\bar{N}}}^0 \text { satisfies } \mathbf {AP}^-(\omega _2, \varphi _1, \delta , {\bar{N}}) \text { condition,} \end{aligned}$$then the orbit

where
$$\begin{aligned} \delta _1 = \max \left\{ \delta ^{q - \frac{1}{4}}, e^{-(\lambda ' - 6\epsilon )N/54} \right\} . \end{aligned}$$(6.6) -
(2)
If

then
$$\begin{aligned} (y_{j+n_2}, \eta _{j +n_2})_{j = - {\bar{N}}}^0 \text { satisfies } \mathbf {AP}^-(\omega _2, \varphi _1, \delta _1, {\bar{N}}) \text { condition,} \end{aligned}$$with \(\delta _1\) given by (6.6).
The reason to require the good time interval to lie in \([-2N/3, -N/3]\) is to apply the following lemma, which says the global minimizer \(x_n^\omega \) is almost a minimizer for finite time solution in the middle of the time interval, for every initial condition \(\varphi \).
Lemma 6.4
There exists \(N_3(\omega )>0\) such that if \(N > N_3(\omega )\), the following holds almost surely, for arbitrary \(\varphi \in C(\mathbb {T}^d)\) and \(-2N/3 \le j < k \le -N/3\):

The proof of the lemma is deferred to Sect. 7.1.
Proof of Lemma 6.3, part (1): Use early localization to estimate forward solutions on the gray interval
Proof of Lemma 6.3
Since \(n_2\) is a backward good time and \(\delta ^{\frac{1}{8}}< \beta < \rho (\theta ^{n_2}\omega ) = \rho (\omega _2)\), condition (6.1) holds for the orbit \((y_{j+n_2}, \eta _{j +n_2})_{j = - {\bar{N}}}^0\) at the shifted time \(\omega _2\), the initial condition \(\varphi _1\), and interval size \({\bar{N}}\).
Therefore by Proposition 6.1, there exists an integer k satisfying \(0 < k - n_2 \le \max \{-\frac{{\bar{N}}}{6}, \frac{1}{8\epsilon } \log \delta \}\), such that
Also, \({\bar{N}}\ge N/9 \ge \beta ^{-1} \ge N_1(\omega _2)\) provided \(N \ge 9 \beta ^{-1}\). Suppose j is an integer satisfying \(n_1 \le n_1 + \bar{N}/3\) and that \(\Vert y_j - x_j^\omega \Vert <r(\theta ^j \omega )\). See Fig. 2 for a relation of different integer times.
By Corollary 4.6,

then

using Lemma 4.7, and the estimates \(e^{\epsilon |k-n_2|} \le \delta ^{-\frac{1}{8}}\), \(e^{\epsilon |k-n_2|} \le e^{\epsilon {\bar{N}}/6}\) and \({\bar{N}}\ge N/9\).
On the other hand, the dual version of Lemma 4.10 implies
Combine the estimates, we get

We now apply Lemma 6.4 to \(\varphi = \varphi ^N_\omega \), to replace the index k with j:

where in the last inequality, we take \(N_2(\omega )\) large enough so that \(C_1(\omega ) e^{-(\lambda ' - \epsilon )N/3} + e^{-(\lambda ' - 3\epsilon ) N/6} < e^{-(\lambda ' - 4\epsilon )N/54}\) and \(2\beta ^{-1} < e^{-\epsilon N/54}\), then we use \(2\beta ^{-1} < \delta ^{-\frac{1}{8}}\).
Observe that by the standard semi-group property,

substitute into (6.8) we obtain  .
.
We now discuss case 2. Starting with the condition  , we obtain \(0 \le k_* - n_1 \le \max \left\{ - \frac{1}{8\epsilon } \log \delta , \frac{N}{6} \right\} \) such that
, we obtain \(0 \le k_* - n_1 \le \max \left\{ - \frac{1}{8\epsilon } \log \delta , \frac{N}{6} \right\} \) such that
Then for all \(k_* < n_2 - {\bar{N}}/3 \le j \le n_2\), if \(\Vert y_j - x_j^\omega \Vert < r(\theta ^j \omega )\), using the fact that \((y_n, \eta _n)\) is a minimizer for \(K_{-N, 0}\varphi \), similar to (6.7) we have
and following the same strategy as before, we get
Since
we obtain \(\mathbf {AP}^-(\omega _2, \varphi _1, \delta _1, {\bar{N}})\). \(\square \)
To carry out the upgrading procedure, we need to show that \(\beta -\)good time intervals exist.
Lemma 6.5
There exists \(\beta _0>0\) such that, for any \(0 < \beta \le \beta _0\), there exists \(N_3(\omega )>0\), and for all \(N> N_3(\omega )\) there exists a \(\beta -\)good time interval \([-5N/9, -4N/9] \subset [n_1, n_2] \subset [-2N/3, -N/3]\).
Proof
Let \(\beta _0>0\) be small enough that
By Proposition 5.2, for any \(0 < \beta \le \beta _0\), there exists \(M_0(\omega )>0\) such that any minimizer \((y_n, \eta _n)_{n=-M}^N\) with \(M, N > M_0(\omega )\) satisfies \(\Vert y_0 - x_0^\omega \Vert < \beta \). We now choose \(\beta _1 >0\) small enough such that
Then, there exists \(N_3(\omega )>0\) such that for all \(N> N_3(\omega )\) the density of \(\beta -\)regular n in \([-N, 0]\) is larger than \(\frac{8}{9}\). In particular, the interval \([-4N/9, -N/3]\) must contain a regular time \(n_2\). We impose \(N_3(\omega ) > 3 \beta _1^{-1}\), then Proposition 5.2 implies for any \(N > N_3(\omega )\), \(\Vert y_{n_2}- x_{n_2}^\omega \Vert < \beta \le \rho (\omega )\), therefore \(n_2\) is a good time.
Apply the same argument, by possibly choosing a different \(N_3(\omega )\), we can find a forward good time \(n_1\) in \([-2N/3, -5N/9]\). \(\square \)
Proof of Proposition 5.1
By Lemma 6.5 there exists a \(\beta -\)good interval. We first show that if for any \(K_{-N, 0}^{\omega , b}\varphi \) backward minimizer \((y_n, \eta _n)_{n = -N}^0\), the condition
holds for an explicitly defined \(\lambda _1\), then Proposition 5.1 follows. Indeed, we only need the estimate
where \(C(n_2, \omega , \varphi ) = \psi ^N_\omega (x_{n_2}^\omega , n_2) - \psi ^-_\omega (x_{n_2}^\omega , n_2)\).
On one hand,
on the other hand, by Lemma 4.10,
if N is large enough. Proposition 5.1 follows by taking \(\lambda = \min \{\lambda _1, (\lambda ' - 2\epsilon )/3\}\).
We now prove (6.9). Choose \(\beta = \beta _0\) as in Lemma 6.5, and \(\delta \) such that
Using Proposition 2.1, there is \(N_0(\omega )\) large enough such that for all \(N_0 > N(\omega )\), all \(\varphi \in C(\mathbb {T}^d)\), we have
In particular, for any minimizer \((y_n, \eta _n)\), we have
Apply Lemma 6.3, obtain

with \(\delta _1 = \max \{\delta ^{q - \frac{1}{4}}, e^{-(\lambda ' - 5\epsilon )N/54} \}\).
Now we are going to apply Lemma 6.3 repeatedly, from \(\mathbf {AP}^-\) to \(\mathbf {AP}^+\) and back until a desired estimate for \(\delta \) is achieved. We shall assume that \(N > N_2(\omega )\). On the first step we get an estimate \(\mathbf {AP}^+(\omega _1, \varphi _2, \delta _1, {\bar{N}})\) for \((y_{j+n_2}, \eta _{j+n_2})_{j = - {\bar{N}}}^0\) where \(\delta _1 = \max \{\delta ^{q - \frac{1}{4}}, e^{-(\lambda ' - 5\epsilon )N/54}\}\). Since \(q - \frac{1}{4} >1\) this estimate is an improvement of \(\delta \) unless \(\delta < e^{-(\lambda ' - 5\epsilon )N/54}\). Notice that if this happens we have already proven our statement with \(\lambda _1 = (\lambda ' - 5\epsilon )/54\). It is easy to see that the level \(\delta < e^{-(\lambda ' - 5\epsilon )N/54}\) will be reached in a finite number of steps depending on N. Notice N is large enough but fixed, this finishes the proof. \(\square \)
7 Properties of the finite time solutions
We have proven all our statements except Proposition 6.1, which we prove in the next two sections.
7.1 The guiding orbit
For \(N \in \mathbb {N}\), denote
We define
which is an analog of \(Q^\infty _\omega \) for finite-time solutions. (Again, the subscript \(\omega \) may be dropped).
The function \(Q^N\) is a Lyapunov function for minimizers, in the following sense:
Lemma 7.1
Let \((y_n, \eta _n)_{n =- N}^0\) be a minimizer for \(K_{-N, 0}^{\omega , b}\varphi (y_0)\) (will use the notation \(\psi ^N(x,0)\) from now on). Then for all \(-N \le j < k \le 0\),
Proof
By definition,

\(\square \)
Let
and define \((z_n^\omega , \zeta _n^\omega )_{n = -N}^\infty \) to be a forward minimizer for \(\psi ^+(\cdot , N)\) starting from \(z_{-N}^\omega \). The orbit \((z_n^\omega , \zeta _n^\omega )\) plays the role of the global minimizer \((x_n^\omega , v_n^\omega )\) in the finite time set up, and is called the guiding orbit. The choice of \(z_N^\omega \) may not be unique, but our analysis will not depend on the choice of \(z_N^\omega \). The orbit \((z_n^\omega , \zeta _n^\omega )\) depends on N but we will not keep N in the notation.
Lemma 7.2
The guiding orbit has the following properties.
-
(1)
$$\begin{aligned} z_n^\omega \in \mathop {{{\,\mathrm{arg\,min}\,}}}\limits _z Q^N(z, n), \quad -N \le n \le 0. \end{aligned}$$
-
(2)
$$\begin{aligned} \zeta _n^\omega = \nabla \psi ^N(z_n^\omega , n) +b = \nabla \psi ^+(z_n^\omega , n) + b, \quad - N \le n \le 0. \end{aligned}$$
where both gradients exists.
-
(3)
$$\begin{aligned} Q^N(z_j^\omega , j) = Q^N(z_k^\omega , k), \quad -N \le j < k \le 0. \end{aligned}$$
-
(4)
\(z_k^\omega \), \(-N \le k \le 0\) is a backward minimizer for \(K_{-N, 0}^{\omega ,b} \varphi \).
Proof
We prove (3) first. Since \((z_j^\omega )_{j \ge -N}\) is a forward minimizer for \(\psi ^+(\cdot , j)\), we have
On other other hand, let \(y_k \in {{\,\mathrm{arg\,min}\,}}Q^N(\cdot , k)\), and let \((y_n)_{n=-N}^k\) be a minimizer for \(\varphi \) ending at \(y_k\). Then by an argument similar to Lemma 7.1, for any \(y \in \mathbb {T}^d\),
In particular, taking \(y = z_k^\omega \), we have \(Q^N(z_k^\omega , k) \ge Q^N(z_{-N}^\omega , -N)\). Using (7.2) for \(j = -N\), we get \(Q^N(z_{-N}^\omega , -N) = Q^N(z_k^\omega , k)\) which implies (3).
This also implies that (7.2) is in fact an equality, therefore \(\psi ^N(z_j^\omega , j) = \psi ^N(z_k^\omega ) - A_{j,k}^{\omega , b}(z_j^\omega , z_k^\omega )\) and (4) follows.
Using again (7.3), we have
which implies (1). Finally, since \(\psi ^N(\cdot , n)\) is a semi-concave function for \(n \ge -N\) and \(\psi ^+\) is semi-convex, (2) follows from Lemma 4.2. \(\square \)
Combine (3) of Lemma 7.2 with Lemma 7.1, we get for all \(-N \le j < k \le 0\),
7.2 Regular time and localization of the guiding orbit
We use a similar concept as the good time, but for a different set of random variables. Let \(0< \beta <1\) be such that
with \(C(\omega ), r(\omega )\) from Proposition 3.4. Let \(M_0(\omega )\) be the random variable given by Proposition 5.2 with \({\tilde{\rho }} = \beta \). Let \(\beta _1 >0\) be such that \(P(M_0(\omega )>\beta _1^{-1})< 1/24\). n is called regular if
using same proof as Lemma 6.5, we get
Lemma 7.3
There exists \(N_1(\omega )>0\) such that for all \(N > N_1(\omega )\), there exists a regular time in each time interval of size at least N / 12 contained in \([-N, 0]\).
Lemma 7.4
There exists \(N_4(\omega )>0\) depending on \(\beta \), \(\epsilon \) such that for all \(N > N_4(\omega )\), and \(- 5N/6 \le k \le 0\), we have
By possibly enlarging \(N_4(\omega )\), we have
Proof
The proof is again very similar to that of Lemma 6.5. Let \(n_*\) be a regular time in \([-5N/6, - 11 N/ 12]\). Then
Apply Proposition 3.3, we get
Since \(n_* \ge -5N/6\), the first estimate follows. For the second estimate, since \(z_k^\omega \) is a minimizer for \(K_{-N, 0}\varphi \), we have
To avoid magnifying the coefficient of \(\epsilon \), let \(K^{\epsilon /2} > K(\omega )\) be the result of applying Lemma 4.9 with parameter \(\epsilon /2\), then
where the last step is achieved by taking \(N_4(\omega )\) large enough. \(\square \)
We are now ready to prove Lemma 6.4.
Proof of Lemma 6.4
We note that Lemma 7.4 proves half of the estimates in Lemma 6.4. The other half is proven using the same argument and reversing time. \(\square \)
For the rest of the paper, we will only deal with time \(n \ge -N/3\). We get a larger exponents in our estimates over the smaller time interval \([-N/3, 0]\). The estimates are summarized in the following statement.
Lemma 7.5
There \(N_4(\omega )>0\) such that for \(N > N_4(\omega )\), the following holds for \(-N/3 \le k \le 0\): let f be any of the following functions: \(\psi ^N(\cdot , k)\), \(\psi ^\pm (\cdot ,k)\), \(A_{m,k}(y, \cdot )\) or \(A_{k,n}(\cdot , y)\). Then
Proof
We note that all choices of f are \(K(\theta ^k\omega )\) Lipshitz functions. Then
for N large enough. \(\square \)
7.3 Stability of the finite time minimizers
We show that if an orbit \((y_n, \eta _n)_{n = -N}^0\) satisfies \(\mathbf {AP}^-(\omega , \varphi , \delta , N)\) condition, then it is stable in the backward time. First, we obtain an analog of (4.1).
Lemma 7.6
Assume the orbit \((y_n, \eta _n)\) satisfies \(\mathbf {AP}^-(\omega , \varphi , \delta , N)\), Then for each \(- N/3 \le k \le 0\) such that \(\Vert y_k - x_k^\omega \Vert < r(\theta ^k \omega )\), we have
Proof
The definition of \(\mathbf {AP}^-\) implies that for all \(\Vert y_k - x_k^\omega \Vert < r(\theta ^k \omega )\),
the lemma follows directly from (4.1). \(\square \)
We combine this with (7.4) to obtain a backward stability for \((y_n, \eta _n)\).
Lemma 7.7
Assume that \((y_n, \eta _n)_{n = -N}^0\) is a minimizer that satisfies the \(\mathbf {AP}^-(\omega , \varphi , \delta , N)\) condition, and such that
There exists \(C_1^\epsilon (\omega ) > 1\) with \(e^{-\epsilon }\le C_1^\epsilon (\omega )/C_1^{\epsilon }(\theta \omega ) \le e^\epsilon \) such that if \(N > N_4(\omega )\), \(- N/3 \le j < k \le 0\), and \(\Vert y_j - x_j^\omega \Vert <r^\epsilon (\theta ^j \omega )\), \( \Vert y_k - x_k^\omega \Vert < r^\epsilon (\theta ^k \omega )\), then
Proof
Apply Lemma 7.5, we have
Combine with Lemma 7.6, we get
Using \(a^\epsilon (\theta ^j \omega ) \ge e^{-\epsilon |j-k|}a^\epsilon (\theta ^k \omega )\), we obtain
therefore
The lemma follows by taking \(C_1^\epsilon = \sqrt{K^\epsilon /a^\epsilon }\). \(\square \)
8 Estimates from non-uniform hyperbolicity
8.1 Hyperbolic properties of the global minimizer
Denote by
the orbit of the global minimizer under the random dynamical system \(\Phi _n^\omega \) (see (3.2)). According to Proposition 3.3, the Lyapunov exponents of the derivative cocycle over this orbit are non-vanishing, which implies this orbit is non-uniformly hyperbolic. It turns out such orbits enjoys much of the same properties as uniformly hyperbolic orbits, using a special Lyapunov norm. The conclusions of Proposition 8.1 below follows from standard theories in smooth dynamics, see for example [1, section 5.1 and 7.2, 7.3].
Proposition 8.1
For any \(\epsilon >0\), the following hold.
-
(1)
(Stable and unstable bundles) For each \(n \in \mathbb {Z}\), there exists the splitting
$$\begin{aligned} \mathbb {R}^{2d} = E^s_n(X_n^\omega ) \oplus E^u_n(X_n^\omega ), \end{aligned}$$where \(\dim E^s_n = \dim E^u_n = d\). The splitting is invariant under the random dynamics, i.e.
$$\begin{aligned} D\Phi _n^\omega \left( E^s_n(X_n^\omega ) \right) = E^s_n(X_{n+1}^\omega ), \quad D\Phi _n^\omega \left( E^u_n(X_n^\omega ) \right) = E^u_n(X_{n+1}^\omega ). \end{aligned}$$We denote by \(\Pi ^s_n, \Pi ^u_n\) the projection onto \(E^s_n, E^u_n\) under this splitting.
-
(2)
(Lyapunov norm) There exist norms \(\Vert \cdot \Vert _n^s\), \(\Vert \cdot \Vert _n^u\) on \(E^s_n, E^u_n\), such that the Lyapunov norm on \(\mathbb {R}^{2d}\) defined by
$$\begin{aligned} (\Vert V\Vert _n')^2 = (\Vert \Pi _n^s V\Vert _n^s)^2 + ( \Vert \Pi _n^u V\Vert _n^u)^2 \end{aligned}$$satisfies the conditions listed below.
-
(3)
(Comparison to Euclidean norm) There exists a function \(M^\epsilon (\omega )>0\) satisfying \(e^{-\epsilon } \le M^\epsilon (\omega )/M^\epsilon (\theta \omega ) \le e^\epsilon \) such that
$$\begin{aligned} \Vert V\Vert \le \Vert V\Vert _n' \le M^\epsilon (\theta ^n \omega ) \Vert V\Vert , \end{aligned}$$where \(\Vert \cdot \Vert \) is the Euclidean norm. We will omit the subscript n from the \(\Vert \cdot \Vert _n'\) and \(\Pi ^{s/u}_n\) when the index is clear from context. s
-
(4)
(Cones)
$$\begin{aligned} \begin{aligned}&\mathcal {C}_n^u = \{ V \in \mathbb {R}^{2d}{:} \quad \Vert \Pi _n^u V\Vert _n^u \le \Vert \Pi _n^s V\Vert _n^s \}, \\&\mathcal {C}_n^s = \{ V \in \mathbb {R}^{2d}{:} \quad \Vert \Pi _n^s V\Vert _n^s \le \Vert \Pi _n^u V\Vert _n^u \}. \end{aligned} \end{aligned}$$The cones \(\mathcal {C}_n^u\) are forward invariant and forward expanding under \(\Phi _n^\omega \), and \(\mathcal {C}_n^s\) are backward invariant and backward expanding. More precisely the following statements hold.
-
(5)
(Hyperbolicity) There exists \(\sigma ^\epsilon (\omega )>0\) with \(e^{-\epsilon } \le \sigma ^{\epsilon }(\omega )/\sigma ^\epsilon (\theta \omega ) \le e^\epsilon \), such that the following hold. Let \(Y_n\) be an orbit of \(\Phi _n^\omega \).
-
(a)
If
$$\begin{aligned} \Vert Y_n - X_n\Vert '< \sigma ^\epsilon (\theta ^n \omega ), \quad \Vert Y_{n-1} - X_{n-1}\Vert ' < \sigma ^\epsilon (\theta ^{n-1}\omega ), \end{aligned}$$then
$$\begin{aligned} \Vert \Pi ^s Y_{n-1} - \Pi ^s X_{n-1}\Vert ' \ge e^{\lambda '} \Vert \Pi ^s Y_n - \Pi ^s X_n\Vert ', \end{aligned}$$where \(\lambda ' = \lambda - \epsilon \). Moreover, if \(Y_n - X_n \in \mathcal {C}_n^s\), then \(Y_{n-1} - X_{n-1} \in C_{n-1}^s\).
-
(b)
If
$$\begin{aligned} \Vert Y_n - X_n\Vert '< \sigma ^\epsilon (\theta ^n \omega ), \quad \Vert Y_{n-1} - X_{n-1}\Vert ' < \sigma ^\epsilon (\theta ^{n-1}\omega ), \end{aligned}$$then
$$\begin{aligned} \Vert \Pi ^u Y_{n-1} - \Pi ^u X_{n-1}\Vert ' \le e^{-\lambda '} \Vert \Pi ^u Y_n - \Pi ^u X_n\Vert '. \end{aligned}$$Moreover, if \(Y_n - X_n \in \mathcal {C}_n^u\), then \(Y_{n-1} - X_{n-1} \in \mathcal {C}_{n-1}^u\).
-
(a)
8.2 Stability of minimizer in the phase space
We improve Lemma 7.7 to its counter part in the phase space, using the Lyapunov norm.
Lemma 8.2
Assume that \((y_n, \eta _n)_{n = -N}^0\) is a minimizer that satisfies the \(\mathbf {AP}^-(\omega , \varphi , \delta , N)\) condition, and such that
There exists \(C_2^\epsilon (\omega )> 1\) and \(e^\epsilon \le C_2^\epsilon (\omega )/C_2^\epsilon (\theta \omega ) \le e^{-\epsilon }\) such that, if \(-N/3< j < k \le 0\) satisfies
then
Proof
Apply Lemma 7.7, we have
Since \(j < -1\), we use Lemma 4.2 to get
and hence
We have
We then replace \(\epsilon \) with \(\epsilon /3\) in the above estimate, and define \(C_2^\epsilon = 6C_1^{\epsilon /3}M^{\epsilon /3}K^{\epsilon /3}\), which satisfies \(e^\epsilon \le C_2^\epsilon (\omega )/C_2^\epsilon (\theta \omega ) \le e^{-\epsilon }\). The lemma follows. \(\square \)
8.3 Exponential localization using hyperbolicity
We show that hyperbolicity, together with Lemma 8.2 lead to a stronger localization. In Lemma 8.3 we show a dichotomy: either \(y_n - x_n^\omega \) contracts for one backward iterate, or \(y_n\) is \(\delta ^q\) close to \(x_n\) to begin with.
Let \(r^\epsilon (\omega )\) and \(K^\epsilon (\omega )\) be the random variable from Lemma 4.9, and note we can always choose \(r^\epsilon (\omega ) < 1\) and \(K^\epsilon (\omega ) > 1\). Define
where \(\sigma ^\epsilon \) is defined in property (5) of Proposition 8.1. We have \(C_3^\epsilon (\omega ) > 1\), \(\rho _0(\omega )< r_1(\omega ) < 1\), and \(e^\epsilon \le \rho _0(\omega )/\rho _0(\theta \omega ), r_1(\omega )/r_1(\theta \omega ) \le e^\epsilon \).
Lemma 8.3
Under the same assumption as in Lemma 8.2, suppose for a given \(-N/6 \le k \le -1\), we have
Then one of the following alternatives hold for \(Y_k\):
-
(1)
$$\begin{aligned} \Vert Y_k - X_k^\omega \Vert ' \le \max \{\delta ^q, e^{-(\lambda ' - 2\delta )N/6}\}, \quad q = (\lambda ' - 3\epsilon )/(8\varepsilon ), \end{aligned}$$(8.3)
in the case \(Y_k - X_k^\omega \in \mathcal {C}_k^s\).
-
(2)
$$\begin{aligned} \Vert \Pi ^u Y_{k-1} - \Pi ^u X_{k-1}\Vert ' \le e^{-\lambda '} \Vert \Pi ^u Y_k- \Pi ^u X_k\Vert ', \end{aligned}$$(8.4)
in the case \(Y_k - X_k^\omega \in \mathcal {C}_k^u\).
Proof
We first describe the idea behind the proof. If \(Y_k - X_k^\omega \in \mathcal {C}_k^u\), and Proposition 8.1 (5)(b) applies, then (8.4) follows directly. Suppose now \(Y_k - X_k^\omega \in \mathcal {C}_k^s\). Since the stable cones are backward invariant, \(Y_j - X_j^\omega \in C_j^s\) for every \(j < k\), then Proposition 8.1 (5)(a) implies that \(\Vert Y_j - X_j^\omega \Vert '\) should grow exponentially with rate \(\lambda '\). Suppose for a moment that Lemma 8.2 holds with \(\delta = 0\), which implies \(\Vert Y_j - X_j^\omega \Vert '\) grows with at most rate \(\epsilon \), this would have been a contradiction. When \(\delta > 0\), the only way for \(Y_k - X_k^\omega \in \mathcal {C}_k^s\) to not contradict Lemma 8.2 is for \(\Vert Y_k - X_k^\omega \Vert '\) to be much smaller than \(\delta \) to begin with.
We now make this argument rigorous. Some of the estimates below are needed to make sure that the conditions of Lemma 8.2 and Proposition 8.1 are met.
Let us denote \(d_k = \Vert Y_k - X_k^\omega \Vert '\). Let \(i_0\) be the unique negative integer that satisfies the condition
Note that \(-N/6 \le i_0 < 0\). Since
and (using \(C_3^\epsilon = \frac{r_1}{3 \sqrt{\rho }_0}\) and (8.2))
We next show that Lemm 8.2 can be applied inductively to the indices j, k for \(j = k-1, \ldots , k + i_0\). Recall that for every \(\epsilon > 0\), the random variable \(K^\epsilon \) is chosen to be an upper bound for \(\Vert \Phi _n^\omega \Vert _{C^2}\), the norm of the random mapping. By (8.1) and (8.2), if \(d_k < r_1(\theta ^k\omega )\), then \(d_{k-1} \le K^{\epsilon /8}(\omega ) d_k< r^{\epsilon /8}(\theta ^k \omega )/2 < r^{\epsilon /8}(\theta ^{k-1}\omega )\), if \(\epsilon \) is small enough. Therefore Lemma 8.2 can be applied to the indices \(k-1, k\) if (8.2) holds.
Suppose that for some \(j \in [i_0 + k, k)\), \(d_{j+1} \le r_1(\theta ^j \omega )\). Then by the same argument as above, \(d_j \le r^{\epsilon /8}(\theta ^j \omega ) < r(\theta ^j \omega )\), Lemma 8.2 applies to j, k. We get
where we applied (8.6) in the second line, and assumed \(\epsilon \) is small enough. (8.8) implies that the inductive procedure can be continued one step further, and we can follow this procedure all the way until \(j = i_0 + k\). For all \(j \in [i_0 + k, k)\), since \(d_j< r_1(\theta ^j \omega ) < \sigma ^{\epsilon /4}(\theta ^j\omega )\), Proposition 8.1 (5) applies .
If \(Y_k - X_k^\omega \in \mathcal {C}_k^u\) (second alternative), (8.4) holds by Proposition 8.1 (5)(b). If \(Y_k - X_k^\omega \in \mathcal {C}^s_k\) (first alternative), then \(Y_j - X_j^\omega \in \mathcal {C}^s_j\) for all \(i_0 + k< j < k\), due to backward invariance of stable cones. As a result, we get from Proposition 8.1 (5)(a) that
Pick \(j = i_0 + k\), and apply Lemma 8.2 again. Then using (8.7), we get
We can choose \(\epsilon \) small enough (and as a result \(|i_0|\) large enough) such that \(e^{-(\lambda '-3\epsilon )|i_0|}< \frac{1}{2}\), then
or
Note that in this case, \(d_k \le \sqrt{\delta }\). Using (8.5) and \(\delta ^{\frac{1}{4}} < \rho _0(\theta ^k\omega )\) from (8.2), we get
We combine with (8.9) to get
where \(q = (\lambda ' - 3\epsilon )/(8\epsilon )\). \(\square \)
We are now ready to prove Proposition 6.1.
Proof of Proposition 6.1
Define
then \(e^{-2\epsilon }\le \rho (\theta \omega )/\rho (\omega ) \le e^{2\epsilon }\). Recall the assumption
and note in particular \(2\delta ^{\frac{1}{2}} < e^{-\lambda '}\) which is needed for Lemma 8.3. We suppose \(N > N_4(\omega )\), so that Lemma 7.7 applies. Let \(j_0\) be the unique integer such that
Then
and
If \(\Vert y_0 - x_0^\omega \Vert <\rho (\omega )\), by Lemma 8.2, we have
Assume \(e^{\epsilon } < 2\), then Lemma 8.3 applies for \(j = -1\). If \(Y_{-1} - X_{-1}^\omega \in \mathcal {C}^s\), then (8.3) hold, we obtain \(\Vert Y_{-1} - X_{-1}^\omega \Vert ' \le \max \{\delta ^q, e^{-(\lambda ' - 3\epsilon )N/6}\}\). We choose \(k = -1\) and the proposition follows. Otherwise, \(Y_{-1} - X_{-1}^\omega \in C^u\), and (8.4) applies. We have
if \(e^\epsilon < \sqrt{2}\). We can apply Lemma 8.3 again.
Let \(j \in [j_0 + 1, -1]\). If \(Y_m - X_m^\omega \in \mathcal {C}^s\) for any of \(m \in [j +1, -1]\), we have \(\Vert Y_{-m} - X_{-m}^\omega \Vert ' \le \max \{\delta ^q, e^{-(\lambda ' - 3\epsilon )N/6}\}\). Choose \(k = m\) and we are done. Otherwise, we have
Therefore this argument can be applied inductively until we reach \(j = j_0\), in which case
We choose \(k = j_0\) and conclude the proof. \(\square \)
References
Barreira, L., Pesin, Y.: Nonuniform Hyperbolicity, Encyclopedia of Mathematics and Its Applications, vol. 115. Cambridge University Press, Cambridge (2007)
Contreras, G., Figalli, A., Rifford, L.: Generic hyperbolicity of Aubry sets on surfaces. Inventiones Mathematicae 200(1), 201–261 (2015)
Contreras, G.: Generic mañé sets. Preprint arXiv:1410.7141
Fathi, A.: Weak KAM Theorem in Lagrangian Dynamics, 10th Preliminary Version. Book preprint (2008)
Iturriaga, R., Khanin, K.: Burgers turbulence and random Lagrangian systems. Commun. Math. Phys. 232(3), 377–428 (2003)
Iturriaga, R., Sánchez-Morgado, H.: Hyperbolicity and exponential convergence of the Lax–Oleinik semigroup. J. Differ. Equ. 246(5), 1744–1753 (2009)
Khanin, K., Zhang, K.: Hyperbolicity of minimizers and regularity of viscosity solutions for a random Hamilton-Jacobi equation. Commun. Math. Phys. 355(2), 803–837 (2017)
Mañé, R.: Lagrangian flows: the dynamics of globally minimizing orbits. Boletim da Sociedade Brasileira de Matemática. Nova Série 28(2), 141–153 (1997)
Mather, J.N.: Variational construction of connecting orbits. Ann. Inst. Fourier (Grenoble) 43(5), 1349–1386 (1993)
Sinai, Y.G.: Two results concerning asymptotic behavior of solutions of the burgers equation with force. J. Stat. Phys. 64(1–2), 1–12 (1991)
Weinan, E., Khanin, K., Mazel, A., Sinai, Y.: Invariant measures for Burgers equation with stochastic forcing. Ann. Math. (2) 151(3), 877–960 (2000)
Acknowledgements
The authors thank the referee for corrections and suggestions that helped improving the paper. The second and the third author acknowledge the support of the NSERC (Grant Nos. 2018-04510 and 2019-07057) Discovery Grant. The first author thanks the University of Toronto for their hospitality during the sabbatical year and his recent visit.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Iturriaga, R., Khanin, K. & Zhang, K. Exponential convergence of solutions for random Hamilton–Jacobi equations. Stoch PDE: Anal Comp 8, 544–579 (2020). https://doi.org/10.1007/s40072-019-00153-7
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40072-019-00153-7




 there exists a minimizer
there exists a minimizer 
 is differentiable at x we have
is differentiable at x we have 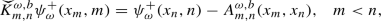
 is
is  . Then
. Then 
 defined in (
defined in (

