Introduction

Process variation is the deviation from designed values for a layout structure or circuit parameter [1]. Aggressive scaling in device dimensions to provide smaller feature sizes and improve speed and functionality in the past decades has received growing attention. However, entering the nanometer regime has resulted in numerous reliability issues due to the high electric field phenomenon [2]. These reliability degradation mechanisms lead to threshold voltage increase and electron mobility decrease. These phenomena cause the MOS transistor parameters to drift from the expected values [3, 4].

Technology development in recent years revolutionized the usage of electronic devices, especially devices with RF and wireless communications applications. Therefore, this vast utilization of electronic devices in everyday life caused abundant new applications ranging from medical to aerospace [5].

Consequently, these broad usage fields show the urgency of new considerations and tradeoffs in designing circuits. Meanwhile, designers focused more on developing high-reliability performance circuits alongside the lowering power budget and the size of the devices. Using wireless electronic devices in biomedical applications and medical devices that have direct contact with human tissues shows the critical role of having reliable devices as well as the priority of this field [6, 7].

As a very first block in the receiver chain of wireless communication systems, LNA is a bottleneck in defining some critical parameters of the receiver front-end specifications [8] especially in ultra-low power receiver topologies [9] in which the main focus is on achieving less hardware to reduce power consumption [10–. Due to tradeoffs between critical design parameters of LNA, like gain, noise figure (NF), and their tradeoffs with application parameters such as power consumption, the consideration in circuit design gets complicated and more sensitive [14, 15].

Many attempts have been devoted to improving the circuit’s immunity to various reliability and variability issues and addressing these issues [16,17,18,19,20,21,22,23]. In the earlier works [18], a body biasing method is used to reduce die-to-die threshold voltage variation. Also, in the investigations [19] and [20], adaptive body bias scheme is employed for power amplifiers and low noise amplifiers to reduce reliability issues and variability. In another work, the effect of hot carriers as one of the reliability degradation mechanisms on LNA performance is investigated [21]. In the literature [22], the variations in LNA, mixer, and voltage-controlled oscillator (VCO) that are implemented with heterojunction bipolar transistors (HBT) are investigated. In the researches [23], the performance drifts for main parameters of LNA under process variation are analyzed, and to partially compensate for these effects; a variable gain scheme is used.

This paper presents a low voltage variable gain LNA and a simple yet effective body biasing technique to mitigate the effect of variations in threshold voltage and mobility. The proposed scheme can work with the low supply voltage. Due to the tunable gain capability, the proposed LNA can operate in a wide range of input power and frequency variations.

Proposed Variable Gain LNA Structure

Proposed LNA with Variable Gain Mechanism

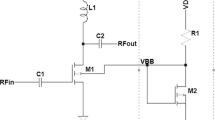
Figure 1 shows the proposed LNA circuit with adaptive body bias. The proposed LNA circuit is capable of providing variable gain through the cascade transistors by the 4-bit controlling signal that provides 15 levels of gain from module1 (0001) to module15 (1111) through disabling or enabling VC1 to VC4. So, there is a wide degree of freedom to change gain from the lowest value of 12.6 dB (mode1) to the highest value of 20.7 dB (mode15). The importance of having a variable gain LNA is due to the different power levels of the received signal in the antenna that forces the receiver gain to be adjustable. In other words, for an input signal with high power, the receiver gain should be small to avoid the receiver chain from saturation; on the other hand, for a small input signal, the gain should be large. All simulation results are given in two high gain and low gain modes.

Fig. 1
figure 1

Variable gain LNA with adaptive body bias circuit

Full size image

Proposed Body Bias Scheme for Reliability and Variability

In general, the main focus in designing this LNA is to reduce the effects of the process variations in the circuit performance. Therefore, the technique followed in this paper is based on a body biasing scheme. The studied adaptive body bias scheme is presented in Fig. 2. The conventional body bias reference is shown in part (a) of Fig. 2. The proposed adaptive body bias reference is pictured in Fig. 2b, and the integration of a body bias circuit with an LNA block is depicted in Fig. 2c. However, the main LNA present in this paper is a variable gain scheme that will be investigated in the following section. The proposed adaptive body bias reference consists of a single transistor and two resistors Fig. 2b. The resistor R1 produces an appropriate voltage drop from VCC, while RB is a current-limiting resistor used to prevent signal leakage and noise coupling between VB and the body terminal of the LNA’s transistor [24]. This combination produces the voltage for biasing the body terminal of the proposed LNA’s input transistors. According to the CMOS regime, there exists a relationship between body terminal voltage and threshold voltage. As will be shown soon in Eq. 5, it seems that if the body voltage can be varied in corresponds to threshold voltage variations, it can create a compensation cycle. As mentioned before, reliability issues in the CMOS transistors indicate threshold voltage increase and electron mobility decrease.

Fig. 2
figure 2

a Conventional body bias [20] b Studied body bias c LNA with adaptive body bias

Full size image

The overall flow of compensation mechanism for both the conventional and proposed body biasing circuits is as follows: Due to reliability issues that are out coming in the shape of Vth increment, the drain current (ID) is decreased; consequently, the resultant VB is increased. Increasing the body voltage of VB, in turn, decreases the threshold voltage of the body-biased input transistor, M1, due to the source body effect. Though, the whole structure configures a feedback scheme that senses the threshold voltage variation and then compensates it through feedback structure. The result is that the threshold voltage variation effects on circuit performance are mitigated [25].

As shown in Fig. 2a, the conventional adaptive body bias circuit [9] needs more voltage headroom compared to the studied circuit in Fig. 2b. Besides, the simulation results show that the circuit in Fig. 2a consumes more power than the circuit in Fig. 2b. Therefore, the studied circuit indicates boosted performance in addressing the reliability issues.

Analytical Support for Proposed Biasing Scheme

  1. (1)

    threshold voltage increment (fluctuation)

In this section, the threshold voltage variation in the circuit is examined, and the effect of using body bias to mitigate this variation is also formulated. As noted earlier, the defects in the reliability mechanism have two apparent effects on the circuit, increasing the threshold voltage and decreasing carrier mobility. From KVL in Fig. 2b, the following expression can be derived:

$$R_{1} I_{D} { + }V_{B} = V_{CC}$$
(1)

Moreover, for an NMOS in the saturation region, the following expression is valid:

$$I_{D} \cong \frac{1}{2}\mu_{n} C_{ox} \left( \frac{W}{L} \right)_{c} \left( {V_{CC} - V_{thc} } \right)^{2} \cong \frac{{\beta_{c} }}{2} \left( {V_{CC} - V_{thc} } \right)^{2}$$
(2)

where VCC is the value of supply voltage, Vthc is the threshold voltage, and \(\beta_{C} = \mu_{n} C_{OX} \left( \frac{W}{L} \right)_{C}\) is the device parameter. Substituting (2) in (1) gives the following equation for VB:

$$V_{B} = V_{CC} - \frac{{\beta_{c} }}{2}R_{1} \left( {V_{CC} - V_{thc} } \right)^{2}$$
(3)

Equation 3 denotes that the value of VB varies by changing Vthc. Using (3), the deviation in VB due to the threshold voltage variations can be expressed as follows:

$${\text{d}}V_{B} = \frac{{{\text{d}}V_{B} }}{{{\text{d}}V_{thc} }} {\text{d}}V_{thc} = \beta_{2} R_{1} \left( {V_{CC} - V_{thc} } \right){\text{d}}V_{thc}$$
(4)

The threshold voltage of the CMOS transistors in terms of body terminal voltage is given by:

$$V_{th LNA} = V_{th0} + \gamma_{b} \left( {\sqrt {2\varphi_{f} - V_{B} } - \sqrt {2\varphi_{f } } } \right)$$
(5)

where Vth0 is threshold voltage with zero VSB, γb is body effect coefficient, and φf is Fermi potential. To examine the relationship between threshold voltage alternation and body voltage, the authors can derivate from (5) to get (6) as follows:

$$dV_{th LNA} = dV_{th0} - \gamma_{b} \frac{{dV_{B} }}{{2\sqrt {2\varphi_{f} - V_{B} } }}$$
(6)

Substitute (5) into (6) gives an equation that demonstrates the relevance of changing the body bias of a transistor and the compensation cycle for threshold voltage:

$$dV_{th LNA} = dV_{th0} - \gamma_{b} \frac{{dV_{thc} }}{{2\sqrt {2\varphi_{f} - V_{B} } }}\beta_{c} R_{1} \left( {V_{CC} - V_{thc} } \right)$$
(7)

Equation 7 indicates that an increase in threshold voltage of M1 (Vth0) is compensated due to Vthc, and using the body biasing scheme improves the circuit robustness against variation.

  • Mobility degradation

Another parameter that changes due to reliability issues is electron mobility. Degradation in mobility denotes with β parameter in the following equations. Using KVL in Fig. 2(b), Eq. 8 is derived:

$$V_{B} = V_{CC} - \frac{{\beta_{c} }}{2}R_{1} \left( {V_{CC} - V_{thc} } \right)^{2}$$
(8)

In order to examine the fluctuation effect, the deviations of (8) are used as follows:

$$dV_{B} = \frac{{dV_{B} }}{{d\beta_{c} }} d\beta_{c}$$
$$dV_{B} = \frac{ - 1}{2}R_{1} \left( {V_{DD} - V_{thc} } \right)^{2} d\beta_{c}$$
(9)

The electron mobility variations also cause the threshold voltage parameter to change, though the following equation can express the variation.

$$dV_{th LNA} = \frac{ - \gamma }{{2\sqrt {2\varphi_{f} - V_{B} } }}dV_{B} = \frac{{\gamma R_{1} }}{{4\sqrt {2\varphi_{f} V_{B} } }}\left( {V_{GS} - V_{thc} } \right)^{2} d\beta_{c}$$
(10)

All of the above equations show how the compensation process is working in order to immune the circuit against process variations. The effect of total variation on the LNA’s current can be expressed as:

$$\begin{gathered} dI_{LNA} = \frac{{dI_{LNA} }}{{dV_{th LNA} }}dV_{th LNA} + \frac{{dI_{LNA} }}{{d\beta_{LNA} }}d\beta_{LNA} \hfill \\ = - \beta_{LNA} \left( {V_{GS} - V_{th LNA} } \right)dV_{th LNA} + \frac{1}{2}\left( {V_{GS} - V_{th LNA} } \right)^{2} d\beta_{LNA} \hfill \\ \end{gathered}$$
(11)
$$dI_{LNA} = \frac{1}{2}\left( {V_{GS} - V_{th LNA} } \right)^{2} d\beta_{LNA} - \beta_{LNA} \left( {V_{CC} - V_{th LNA} } \right)\left( {\frac{{\gamma R_{c} \left( {V_{CC} - V_{thc} } \right)^{2} }}{{4\sqrt {2\varphi_{f} - V_{B} } }}} \right)d\beta_{c}$$
(12)

LNA Parameteric Analysis

In this section, the adaptive body bias circuit's effects on the major parameters of LNAs are calculated.

Noise Figure

Low noise amplifier is the first active block in almost every receiver chain, and the noise performance of this block is a dominant value in determining the noise figure of the whole receiver. This shows the importance of having a stable NF in LNA [26].

The most basic definition of noise figure came into widespread use in the 1940s when Harald Friis defined the noise figure (NF) of a two-port network to be the ratio of the signal-to-noise power ratio at the input to the signal-to-noise power ratio at the output.

$$NF = \frac{{S_{i} /N_{i} }}{{S_{o} /N_{o} }}$$
(13)

Equation 14 expresses the noise factor defined in the two port network with noise sources and a noiseless circuit. The noise factor can be expressed as [20, 27]:

$$F = \frac{{\overline{{i_{s}^{2} }} + \overline{{\left| {i_{n} + \left( {Y_{c} + Y_{s} } \right)\left. {e_{n} } \right|^{2} } \right.}} }}{{\overline{{i_{s}^{2} }} }} = 1 + \frac{{\overline{{i_{n}^{2} }} { + }\left| {Y_{c} + \left. {Y_{s} } \right|^{2} \overline{{e_{n}^{2} }} } \right.}}{{\overline{{i_{s}^{2} }} }}$$
(14)

where \({i}_{s}\) is the noise current from the source, \({Y}_{s}\) is the source admittance, \({i}_{n}\) is the device noise current, \({e}_{n}\) is the device noise voltage, and \({Y}_{c}\) is the correlation admittance. The noise figure is the noise factor that reported the decibel.

Figure 3 shows the small-signal model of an NMOS transistor with noise sources for the studied adaptive body bias circuit at high frequency. Note that the flicker noise at high frequency is ignored. Two primary noise sources in NMOS are the thermal noise currents of drain and gate, which are formulated by the following equations.

$$\overline{{i_{nd1}^{2} }} = 4kT\gamma g_{m1} \Delta f$$
(15)
$$\overline{{i_{ng1}^{2} }} = 4kT\theta \frac{{\omega^{2} C_{gs1}^{2} }}{{5g_{m1} }}\Delta f$$
(16)

where “k” is Boltzmann’s constant, “T” is the absolute temperature, \(\omega\) is the angular frequency, \({g}_{m1}\) is the transconductance of \({M}_{1}\), \({C}_{gs1}\) is the gate-source capacitance of \({M}_{1}\), \(\Delta f\) is the offset frequency, and \(\theta\) is the gate noise coefficient. For long-channel MOSFETs γ is equal to 2/3 in saturation and is equal to a unit in the triode region, yet for short-channel devices, its value can be larger. To calculate the noise factor and its behavior in process variations, first, the parameter in (14) is calculated. For the proposed body biasing circuit, there are two main sources of noise in the output (neglecting flicker noise). The drain noise current of \({M}_{B}\) and the noise current of drain resistor, \({R}_{1}\), as shown in Fig. 3, can be formalized as follows:

$$\overline{{i_{{ndM_{c} }}^{2} }} = 4KT\gamma_{2} g_{mc} \Delta f$$
(17)
$$\overline{{i_{{nR_{1} }}^{2} }} = 4KT\frac{1}{{R_{1} }}\Delta f$$
(18)
Fig. 3
figure 3

body biasing circuit with noise sources

Full size image

The total noise voltage in the output can be written as:

$$\overline{{V_{n,out}^{2} }} = 4KT\left( {\frac{1}{{R_{1} }} + \gamma_{c} g_{mc} } \right)\left( {\frac{{R_{1} r_{o} }}{{R_{1} + r_{o} }}} \right)^{2} \Delta f$$
(19)

The reflected drain current noise in the body terminal of the input transistor is expressed by multiplying (19) in \({g}_{mb1}\) as follows:

$$\overline{{i_{{nB_{1} }}^{2} }} = 4KT\left( {\frac{1}{{R_{1} }} + \gamma_{c} g_{mc} } \right)\left( {\frac{{R_{1} r_{o} }}{{R_{1} + r_{o} }}} \right)^{2} g_{mb1}^{2} \Delta f$$
(20)

Therefore, the total noise current in the drain of the input transistor (\({M}_{1}\)) consists of the noise in the body terminal and the noise in the drain. Though it can be written:

$$\begin{gathered} \overline{{i_{n1}^{2} }} = \overline{{i_{{nB_{1} }}^{2} }} + \overline{{i_{{nd_{1} }}^{2} }} = 4KT\left( {\frac{1}{{R_{1} }} + \gamma_{{M_{B} }} g_{mc} } \right)\left( {\frac{{R_{1} r_{o} }}{{R_{1} + r_{o} }}} \right)^{2} g_{mb1}^{2} \Delta f + 4KT\gamma_{1} g_{m1} \Delta f \hfill \\ = 4KT[(1/R_{1} + \gamma_{c} g_{(mc)} )((R_{1} r_{o} )/(R_{1} { + }r_{o} ))^{2} g_{mb1}^{2} + \gamma_{1} g_{m1} ]\Delta f \hfill \\ \end{gathered}$$
(21)

The input-referred-noise in the gate of the input transistor ( \({M}_{1}\)) can be expressed as:

$$\overline{{V_{n1,in}^{2} }} = \frac{{\overline{{i_{n1}^{2} }} }}{{g_{m1}^{2} }} = 4KT\left[ {\left( {\frac{1}{{R_{1} }} + \gamma_{c} g_{mc} } \right)\left( {\frac{{R_{1} r_{o} }}{{R_{1} r_{o} }}} \right)^{2} \frac{{g_{mb1}^{2} }}{{g_{m}^{2} }} + \frac{{\gamma_{1} g_{m1} }}{{g_{m1}^{2} }}} \right]\Delta f$$
(22)

The equivalent noise resistor is as (23):

$$R_{n1} = \frac{{\overline{{e_{n1}^{2} }} }}{4KT\Delta f} = \frac{{\left( {1 + R_{1} \gamma_{c} g_{mc} } \right)r_{o}^{2} R_{1} }}{{\left( {R_{1} + r_{o} } \right)^{2} }} \frac{{g_{mb1}^{2} }}{{g_{m1}^{2} }} + \frac{{\gamma_{1} g_{m1} }}{{g_{m1}^{2} }}$$
(23)

The drain noise current does not solely indicate the drain noise; meanwhile, when there is no source in the circuit (open circuit condition) a noisy drain current also flows. Multiplication of equivalent input noise voltage by the input admittance gives the value of equivalent input noise current in open circuit condition [27].

$$\overline{{i_{{\mathop {n1}\limits }}^{2} }} = \overline{{V_{n1,in}^{2} }} \left( {j\omega C_{gs} } \right)^{2}$$
(24)

The correlation between gate and drain noise is expressed by \({C}_{1}\) as follows [16]:

$$C_{1} = \frac{{\overline{{i_{ng1.} i_{n1}^{*} }} }}{{\sqrt {\overline{{i_{ng1}^{2} .i_{n1}^{2} }} } }}$$
(25)

The total equivalent input noise current is the sum of the reflected drain noise and the induced gate noise current. The induced gate noise current itself consists of two main sections. \({i}_{ngc1}\) represents the correlated part of gate noise current with the drain noise current of M1, while the other section \({i}_{ngu1}\) is uncorrelated with the drain noise current. The correlation admittance is expressed as follows:

$$Y_{c} = \frac{{i_{n1} + i_{ngc1} }}{{e_{n1} }} = j\omega C_{gs} + \frac{{i_{ngc1} }}{{e_{n1} }} = j\omega C_{gs1} + g_{m1} \frac{{i_{ngc1} }}{{i_{n1} }}$$
(26)

The gate-induced noise is again due to the thermal noise of channel but here the thermal noise is coupled capacitively to the gate and creates noise at the gate. This noise source is correlated with the channel thermal noise [28]

$$g_{m1} \frac{{i_{ngc1} }}{{i_{n1} }} = g_{m1} \frac{{\overline{{i_{ngc1} .i_{n1}^{*} }} }}{{\overline{{i_{n1} .i_{n1}^{*} }} }} = g_{m1} \frac{{\overline{{i_{ng1} .i_{n1}^{*} }} }}{{\overline{{i_{n1}^{2} }} }}$$
(27)

The correlation admittance can be rewritten as:

$$Y_{c} = j\omega C_{gs1} + g_{m1} \frac{{\overline{{i_{ng1} .i_{n1}^{*} }} }}{{\overline{{i_{n1}^{2} }} }} = j\omega c_{gs1} + g_{m1} \frac{{\overline{{i_{ng1} .i_{n1}^{*} }} }}{{\sqrt {\overline{{i_{ng}^{2} }} } \sqrt {\overline{{i_{n1}^{2} }} } }}\sqrt {\frac{{\overline{{i_{ng1}^{2} }} }}{{\overline{{i_{n1}^{2} }} }}} = j\omega C_{gs1} + g_{m1} c_{1} \sqrt {\frac{{\overline{{i_{ng1}^{2} }} }}{{\overline{{i_{n1}^{2} }} }}}$$
(28)

Using the definition of the correlation coefficient may express the induced gate noise as follows:

$$\overline{{i_{ng1}^{2} }} = \overline{{\left( {i_{ngc1} + i_{ngu1} } \right)^{2} }} = 4KT\Delta f(\frac{{\theta \omega^{2} C_{gs1}^{2} \left| c \right|^{2} }}{{5g_{m1} }} + \frac{{\theta \omega^{2} C_{gs1}^{2} \left( {1 - \left| c \right|^{2} } \right)}}{{5g_{m1} }}$$
(29)

The uncorrelated portion of the gate noise is [27]:

$$G_{u1} = \frac{{\overline{{i_{u1}^{2} }} }}{4KT\Delta f} = \frac{{\theta \omega^{2} C_{gs1}^{2} \left( {1 - \left| c \right|^{2} } \right)}}{{5g_{m1} }}$$
(30)

The minimum noise factor can express as:

$$\begin{gathered} F_{min} = 1 + 2R_{n1} \left[ {G_{opt} + G_{c} } \right] \approx 1 + 2R_{n1} \sqrt {\frac{{G_{u1} }}{{R_{n1} }}} \hfill \\ = 1 + \frac{2}{\sqrt 5 }\frac{{\omega C_{gs1} }}{{g_{m1} }}\sqrt {\theta \left( {1 - \left| c \right|^{2} } \right)\left( {\gamma_{1} + \frac{{\left( {1 + R_{1} \gamma_{c} g_{mc} } \right)R_{1} r_{oc}^{2} }}{{\left( {R_{1} + r_{oc} } \right)^{2} }}\frac{{g_{mb1}^{2} }}{{g_{m1} }}} \right)} \hfill \\ \end{gathered}$$
(31)

And:

$$\Delta {F}_{min}= -\frac{\omega {C}_{gs1}}{\sqrt{5}{{g}_{m1}}^{3}} \frac{\theta \left(1-{\left|c\right|}^{2}\right)\left[2{g}_{m1}{\gamma }_{1}+\frac{3{\left({R}_{1}+{r}_{oc}\right)}^{2}\left(1+{R}_{1}{\gamma }_{c}{g}_{mc}\right){{g}_{mb1}}^{2}{{r}_{oc}}^{2}{R}_{1}}{{\left({R}_{1}+{r}_{oc}\right)}^{4}}\right]}{\sqrt{\theta \left(1-{\left|c\right|}^{2}\right)[{\gamma }_{1}+\frac{\left(1+{R}_{1}{\gamma }_{c}{g}_{mc}\right){R}_{1}{{r}_{oc}}^{2}}{{\left({R}_{1}+{r}_{oc}\right)}^{2}}\frac{{{g}_{mb}}^{2}}{{g}_{m1}}}]}\Delta {g}_{m1}+\frac{1}{\sqrt{5}} \frac{\omega {C}_{gs}}{{g}_{m1}}\frac{\theta \left(1-{\left|c\right|}^{2}\right)\left[\frac{2{g}_{mb1}}{{g}_{m}}\frac{\left(1+{R}_{1}{\gamma }_{c}{g}_{mc}\right){{r}_{oc}}^{2}{R}_{1}}{{\left({R}_{1}+{r}_{oc}\right)}^{2}}\right]}{\sqrt{\theta \left(1-{\left|c\right|}^{2}\right)[{\gamma }_{1}+\frac{\left(1+{R}_{1}{\gamma }_{c}{g}_{mc}\right){R}_{1}{{r}_{oc}}^{2}}{{\left({R}_{1}+{r}_{oc}\right)}^{2}}\frac{{{g}_{mb}}^{2}}{{g}_{m1}}}]}\Delta {g}_{mb1}+\frac{1}{\sqrt{5}}\frac{\omega {C}_{gs1}}{{g}_{m1}}\frac{\theta \left(1-{\left|c\right|}^{2}\right)\frac{{{g}_{mb1}}^{2}}{{g}_{m1}}\frac{{{r}_{oc}}^{2}{R}_{1}}{{\left({R}_{1}+{r}_{oc}\right)}^{2}}{{r}_{oc}}^{2}{R}_{1}}{\sqrt{\theta \left(1-{\left|c\right|}^{2}\right)[{\gamma }_{1}+\frac{\left(1+{R}_{1}{\gamma }_{c}{g}_{mc}\right){R}_{1}{{r}_{oc}}^{2}}{{\left({R}_{1}+{r}_{oc}\right)}^{2}}\frac{{{g}_{mb}}^{2}}{{g}_{m1}}}]}\Delta {g}_{mc}$$
(32)

In (32), the second and third terms cause a reduction in total noise factor sensitivity and compensate the effect of the variations.

Small Signal Gain

In RF circuits, S parameters are mostly used to examine the performance of the circuit. S21 is used to define the gain of two-port networks. According to equations in [20]

$$S_{21} = \frac{{ - 2Y_{21} \sqrt {Z_{01} Z_{02} } }}{{\Delta_{1} }}$$
(33)
$$\Delta_{1} = \left( {1 + Y_{11} Z_{01} } \right)\left( {1 + Y_{22} Z_{02} } \right) - Y_{21} Z_{01} Y_{21} Z_{02}$$
(34)

We examine the relevance between \({Y}_{21}\) and the transconductance alternation. For simplicity, the authors first calculated this accordance in an NMOS with no body bias, Fig. 4a.To calculate \({Y}_{21}\), the output node of the model should be tied to the ground as Fig. 4b.

Fig.4
figure 4

a Small signal model of NMOS b Equivalent circuit for the Y21 derivation

Full size image

Doing so, it was obtained Y21 as:

$$Y_{21} \left( f \right) = \left. {\frac{{i_{2} \left( f \right)}}{{V_{1} \left( f \right)}}} \right|_{{V_{2} = 0}} = - j\omega C_{gd} + g_{m}$$
(35)

where \({V}_{1}\) refers to \({V}_{gs}\) in the input terminal (between G and S), and \({V}_{2}\) refers to \({V}_{gd}\) in the out terminal (between drain and source). To show the trans-conductance alternation effect on the \({Y}_{21}\) the following equation expressed:

$$\Delta Y_{21} (f) = \Delta g_{m}$$
(36)

Now, using the small signal model of NMOS with body terminal, Fig. 5a,

$$i_{2} = g_{m1} V_{1} + g_{mb} V_{2} - SC_{gd} V_{1}$$
(37)
Fig. 5
figure 5

(a) small-signal model of the NMOS with body terminal b Small-signal model for the Y21 derivation including the body terminal bias circuit

Full size image

Writing KCL in body node gives:

$$\frac{{V_{2} }}{{r_{o2} R_{1} }} + SV_{2} \left( {C_{db2} + C_{gd2} + C_{ds2} } \right) + SV_{2} \left( {C_{sb1} + C_{db1} } \right) + S\left( {V_{2} - V_{1} } \right)C_{gb1} = 0$$
(38)
$$Y_{21} \left( f \right) = \left. {\frac{{i_{2} \left( f \right)}}{{V_{1} \left( f \right)}}} \right|_{{V_{2} = 0}} = \frac{{Sg_{mb} C_{gb1} }}{{\frac{1}{{r_{o2} R_{1} }} + S\left( {C_{db1} + C_{sb1} + C_{gb1} + C_{db2} + C_{gd2} + C_{ds2} } \right)}} + g_{m1} - SC_{gd1}$$
(39)

From the above equation, the variation of \({Y}_{21}\) is a function of variation in \({g}_{m1}\) and \({g}_{mb}\) is as follows:

$$\Delta Y_{21} = \Delta g_{m1} + \frac{{SC_{gb1} }}{{\frac{1}{{r_{o2} R_{1} }} + SC_{total} }}\Delta g_{mb1}$$
(40)

where

$$C_{total} = C_{db1} + C_{sb1} + C_{gb1} + C_{db2} + C_{gd2} + C_{ds2}$$
(41)

Simulation Results

The layout view of the proposed LNA structure is presented in Fig. 6. The circuit device values are summarized in Table 1. This section presents post-layout simulation results, and their agreement with mathematical analysis is confirmed. The proposed variable gain LNA is designed in TSMC 180 nm CMOS technology. The circuit operates with 0.9 V supply voltage and has a center frequency of 922 MHz. The proposed circuit consumes only 0.8 mW in its high gain mode. The effective transistors aspect ratio is tuned in a 4-bit system via enabling or disabling vc1 to vc4. Through this configuration, 15 levels of gain are available that can be varied from mode1 (0001) to mode15 (1111). So, there exist a wide variety of choices for tuning the LNA’s gain, from the lowest value of 12.6 dB (mode1) to the highest value of 20.7 dB (mode15).

Fig. 6
figure 6

Layout of the designed variable gain LNA with adaptive body bias circuits (a), the enlarged core circuit (b)

Full size image
Table 1 LNA design parameter
Full size table

In order to have a fair comparison and develop the limitations to a higher level between LNA with and without an adaptive body bias circuit, a constant DC bias is applied to the body terminal of the LNA circuit. The value of this DC bias is equal to the output voltage of the circuit shown in Fig. 2b. The bias voltage value is 103.4 Mv (Fig. 6).

Figure 7 shows the NF variations versus threshold voltage variation of the LNA in its high gain (Fig. 7a) and low gain (Fig. 7b) modes. For 16% normalized threshold voltage fluctuation, Fig. 7a illustrates that the normalized NF delicacy of the LNA for proposed, conventional, and DC constant bias circuits is 14.846%, 22.767%, and 72.2836%, respectively. Therefore, the sensitivity of the normalized NF of the proposed LNA decreases about 1.53 and 4.86 times compared to the conventional and DC-constant biased circuits, respectively. Similarly, for the lowest gain level of 12.6 dB, Fig. 7b shows that the normalized NF variation for the proposed circuit decreases about 1.75 and 4.55 times compared to the conventional and constant DC biased circuits, respectively.

Fig. 7
figure 7

Normalized NF variation versus normalized Vth variation of LNA a Highest gain mode b Lowest gain mode

Full size image

The normalized NFmin variation versus threshold voltage variation is examined for the lowest gain and highest gain modes in Fig. 8a and b, respectively. These figures depict that the proposed LNA with adaptive body bias presents a lower NFmin variation compared to the conventional and DC-constant biased circuits. Another crucial parameter of LNAs is S21. Figure 9a shows the normalized S21 variation versus threshold voltage variation at the highest gain mode of the LNA, which is 23.26% for DC body-biased circuit, 8.2410% for the conventional and around 5.1% for the proposed circuit. In other words, the reduction rate compared to the DC scheme is 4.59 times compared to the conventional scheme is 1.62 times. The same analysis is conducted for S21 in the lowest gain mode. The results are shown in Fig. 9b. This figure demonstrates that the sensitivity of the normalized S21 variation for the proposed circuit is reduced 4.82 times compared to the DC body biased and 1.53 times compared to the conventional circuit.

Fig. 8
figure 8

Normalized NFmin versus normalized Vth shift of LNA a Highest gain mode b Lowest gain mode

Full size image
Fig. 9
figure 9

Normalized S21 versus normalized Vth fluctuation of LNA a Highest gain mode b Lowest gain mode

Full size image

Figures 10, 11, and 12 are pictured the NF, NFmin, and S21 parameters variations versus mobility fluctuation, respectively. As it can be noticed from these figures, the proposed circuit performance is better in all cases.

Fig. 10
figure 10

Normalized NF versus normalized mobility variation of LNA a Highest gain mode b Lowest gain mode

Full size image
Fig. 11
figure 11

Normalized NFmin versus normalized mobility shift of LNA a Highest gain mode b Lowest gain mode

Full size image
Fig. 12
figure 12

Normalized small signal gain (S21) versus normalized mobility variation of LNA a a Highest gain mode b Lowest gain mode

Full size image

The net values of these three parameters (NF, S21, and S11) at frequency range of 700 to 1000 Mega Hertz are given in Figs. 13, 14 and 15, showing NF of 2.98 dB, the small-signal gain of 20.6 dB, and the S11 parameter better than -15 dB.respectively.

Fig. 13
figure 13

NF of proposed variable gain LNA in high gain mode

Full size image
Fig.14
figure 14

\({S}_{21}\) of the proposed variable gain LNA in high gain mode

Full size image
Fig. 15
figure 15

\({S}_{11}\) of the proposed variable gain LNA

Full size image

To give a better vision of the LNA performance, the variation rate reduction of NF, NFmin, and S21 for 16% variations is summarized in Table 2, for the whole studied cases. The comparative results with some other similar works are presented in Table 3.

Table 2 The variation rate of NF, NFmin, and S21
Full size table
Table 3 the comparative results with other similar works
Full size table

In order to confirm the versatility improvement of the proposed adaptive body-biased LNA, the performance of three LNA circuits is investigated through Monte-Carlo analysis of their highest gain settings. The number of runs was 20. The results are shown in Fig. 16. It can be seen that the NF of the proposed structure has lower variation compared to the two other structures.

Fig. 16
figure 16

Monte Carlo simulation of the LNA with a DC constant b Conventional adaptive c Studied adaptive body bias technique

Full size image

Conclusion

A low power variable gain LNA with low supply voltage and a simple body biasing circuit is presented, and its performance against process variations and aging effects is investigated. The simulation results show improved performance and robustness of the circuit. Utilizing body biasing in this architecture led to achieving high gain and low NF simultaneously while relaxed process variation and enhancing reliability. The performance of the proposed adaptive body-biased LNA with respect to reliability, threshold voltage, and electron mobility variations up to 16% is evaluated. The results are also compared with those of conventional body-biased structure and DC constant body-biased scheme, and compared to both situations; the proposed circuit indicates an improved performance. The post-layout simulation results in 180 nm CMOS indicate that for a 16% variation in threshold voltage and carrier mobility, the value of variations in both the highest gain mode and lowest gain mode is decreased considerably compared to the two other invested structures. By employing this technique and under 16% threshold voltage and mobility fluctuation, normalized NF is decreased by a factor close to 4.87 and 2.27 times compared to the structure with constant DC body bias, respectively, for high gain and low gain. The analytical equations of the proposed LNA are derived and verified by the post-layout and Monte-Carlo simulations.