Introduction

Vibration-based techniques are extensively been used for developing structural health monitoring (SHM) techniques for bridges [1]. Modal parameter identification is one of the most popular steps among the majority of vibration-based SHM techniques developed so far. In the earlier literature, modal parameter estimation of bridges is carried out popularly using operational modal analysis or experimental modal analysis by instrumenting the entire bridge and measuring the time history responses. Instrumenting the entire bridge is in fact laborious, expensive, and also very tedious to operate. As a cost-effective alternative, Yang et al.[2] have proposed modal frequency parameter estimation using indirect measurements from an instrumented vehicle moving over the bridge. Modal parameter estimation using these indirect measurements has many advantages over the more conventional direct approach with a fully instrumented bridge. The indirect approach is cost-effective, we can do away with tedious and expensive instrumentation, and it is more convenient and also portable. Apart from this it also helps in scanning more bridges in a short time using the instrumented vehicle for modal identification. Even though only a single sensor is used to collect the time history data in the indirect approach, the mode shapes evaluated offer much higher resolution than the traditional direct approach. The reason behind this is that in the indirect approach, the instrumented moving vehicle can act as a moving sensor and therefore can measure the responses at each point on the bridge while traversing. On the other hand, in the traditional approach, limited sensors are spatially distributed along the bridge and the resolution is relatively low [3, 4].

However, it is difficult to estimate modal parameters using the indirect approach. The frequencies associated with the structure (bridge), the vehicle passing over it and the driving frequency make up the measured acceleration response of sensors mounted on an instrumented vehicle’s axle or body during its transit over the deck. Earlier research efforts related to modal parameter estimation of bridges using the responses from an instrumented moving vehicle are reported in the literature [3,4,5,6,7,8,9,10,11,12,13,14]. Zhang et al. [5] used a shaker mounted on a moving vehicle and recorded the applied forces to estimate the frequencies as well as mode shapes of a bridge. Oshima et al. [6] use a multi-axle truck-trailer system for modal parameter estimation through indirect measurements. In his experiments, the vehicle simultaneously carries out two tasks namely exciting the bridge and measuring the resulting vibration responses at three or more moving places on the structure. Vibration responses are measured at various spatial locations on the bridge simultaneously by using N trailers for N different segments of the bridge. Each mode shape vector that contains N components corresponding to N different parts of the bridge is constructed by employing Singular Value Decomposition (SVD) on the measured vibration responses. Bridge stiffness parameters as well as the fundamental frequency are identified successfully using a generalized pattern search algorithm from the responses of the moving vehicle [7]. Bridge modal identification from measured moving vehicle responses on the bridge is attempted by Yang and Chen, [8] employing a modified stochastic subspace identification technique. Kong et al. [9, 10] have employed a customized vehicle consisting of a tractor and two trailers for bridge modal identification. It is reported that the customized vehicle employed in their work has eliminated the influence related to road surface roughness as well as the driving frequencies from the measured moving vehicle responses. Modal parameter estimation of bridges using the moving vehicle vibration responses is carried out by Malekjafarian and Obrien [11, 12]. They have employed a short-time frequency domain decomposition-based algorithm for modal identification. Similarly, Hilbert Transform (HT) is employed by Tan et al. [13] for bridge modal parameter estimation by using responses obtained from a moving vehicle, with a Vehicle Bridge Interaction (VBI) model. Modal parameter identification with indirect measurements has been carried out recently using hybrid methods [14,15,16]. Chen et al. [17] have proposed a classification framework for bridge structural health monitoring using indirect measurements.

A blind modal identification method is employed in a separate investigation by Li et al. [18] to determine bridge modal frequencies. Sitton et al. [19] have evaluated the usefulness of crowdsourcing for bridge monitoring through numerical simulations and lab-level experiments. It is demonstrated through analytical and experimental studies that the multi-vehicle technique can successfully determine the bridge frequency. The crowdsourcing approach demonstrated that indirect SHM may be carried out without the knowledge of the vehicle’s mass and stiffness. Eshkevari et al. [20] employed a network of moving vehicles to determine bridge system parameters. The noise caused by the suspension system of the car is eliminated from the measured vehicle response through deconvolution in the frequency domain. Ensemble EMD, as well as vehicle transfer functions, are utilized in this work. The confounding effects associated with bridge surface roughness are eliminated by employing the second-order blind identification method.

Mei et al. [21] proposed a novel two-step method for bridge modal identification using the measurements from moving vehicles. In the first step, a sparse matrix is formed by mapping the data collected from moving measurement points to virtual fixed locations. The sparse matrix is subsequently filled using a soft computing tool. In the second step, SVD is employed to extract the bridge mode shapes. Using the dynamic response of a vehicle moving even at higher speeds, Jin et al. [22] employed a Short-Time Stochastic Subspace Identification (ST-SSI) technique to identify the natural frequencies of the bridge with a rough road profile. A novel three-step approach is proposed by Li et al. [23] for modal parameter identification from the dynamic responses of a moving vehicle by combining singular spectrum analysis and a dual Kalman filter. A subtraction technique is applied to the derived contact point (CP) responses of the two instrumented vehicles to minimize the influence of the road surface roughness.

Singh and Sandhu [24] proposed a hybrid time–frequency method combining wavelet packet transformation (WPT) with synchro-extracting transform (SET) for modal identification of 220 m long box-girder bridge under various operational challenges. Yang and Wang [25] proposed efficient modal identification procedures using an improved vehicle scanning method. Peng et al. [26] proposed a mode shape identification method using sparse drive-by measurements from a mobile crowdsensing framework. Demirlioglu et al. [27] assess the efficacy of three new vehicle scanning methods for the modal identification of bridges supported by elastic supports. The first two methods use the signal decomposition technique to extract mode shapes from the derived CP response. The third one uses operational modal analysis to predict the mode shapes on each segmented signal by accordingly partitioning the measured signals along the bridge deck. To enhance the quality of the extracted modal parameters, He et al. [28] have derived two residual CP responses from the dynamic measurements of three connected vehicles moving on the bridge. Fast Fourier transform spectrum analysis is used to identify the bridge frequencies from the residual contact responses. Free decay components are extracted from the decomposed modal responses using the random decrement technique. The damping ratios are identified from these free decay components through curve fitting. Yang et al. [29], have used the dynamic responses from a single-axle scanning vehicle equipped with several sensors to accurately identify the modal characteristics of bridges, including the closely spaced modes. They have used a hybrid time–frequency method that combines wavelet transform and singular value decomposition for modal identification. Additional literature on modal parameter estimation using indirect measurements can be found in recent review papers by Wang et al. [30] and Singh et al. [31].

In this paper, efforts are made to extract the bridge’s natural frequencies and mode shapes using the vibration measurements of an instrumented moving vehicle passing over a bridge, using an advanced signal processing technique called variational mode decomposition (VMD). Even though empirical mode decomposition (EMD) or ensemble empirical mode decomposition (EEMD) and their variants are being popularly employed for modal identification as well as structural health monitoring applications in the literature, it is preferred to employ VMD for generating intrinsic mode functions (IMFs) from the measured vibration signal. Solid theoretical foundations of VMD, lesser mode mixing during signal decomposition, and immunity to measurement noise are some of the main reasons for the selection of VMD as a signal decomposition tool in this paper. Teager–Kaiser energy operator (TKEO) along with the discrete energy separation algorithm (DESA), is employed for evaluating the instantaneous amplitude from the IMFS generated using VMD to estimate the mode shapes. Numerical simulation studies have been carried out by a VBI model where the bridge is idealized with an Euler–Bernoulli beam and the vehicle passes over the bridge as a quarter-car model. Parametric investigations are carried out to understand the influence of vehicle speed, the roughness of the road surface, and measurement noise on the extracted modal parameters.

The rest of the paper is organized as follows: The numerical model for VBI using the quarter-car model is presented in the next section. Later the VMD and the TKEO algorithms are briefly discussed. Numerical simulation studies carried out in this paper for modal parameter estimation are presented in the next section. Finally, conclusions are drawn based on the investigations carried out and presented in this paper.

Formulation Details

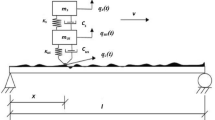
In the VBI model employed in this paper, the bridge is idealized as Euler–Bernoulli beam elements with two degrees of freedom (DOF) at each node (vertical translation and rotation). The vehicle is idealized as a quarter-car with two DOFs. Figure 1 gives the details of the present model. The vehicle is at a constant speed while passing over the bridge. Both vehicle as well as bridge vibrates as the vehicle passes over the bridge and there will be a dynamic interaction between them. As a consequence, bridge vibration responses are influenced by vehicle vibrations.

Fig. 1
figure 1

Quarter car model expressed in spring-mass system

Full size image

The dynamic equilibrium equation of the structure is given in Eq. (1)

$$[{M}_{b}] \{{\ddot{y}}_{b}\} + [{C}_{b}] \{{\dot{y}}_{b}\} + [{K}_{b}] \{{y}_{b}\}=[{N}_{b}]\{{f}_{b}\}$$
(1)

where \([M_{b} ]\), \([C_{b} ]\), and \([K_{b} ]\) are the mass, damping, and stiffness matrices of the bridge (of size n × n) respectively.\({\ddot{y}}_{b}\),\({\dot{y}}_{b}\) and \(y_{b}\) are respectively the acceleration, velocity, and displacement vectors. The vector \(f_{b}\) is the interaction forces of the vehicle and bridge at each CP. These interaction forces are evaluated using the bridge displacement under each vehicle axle and the road surface profile.\([N_{b} ]\) is the location matrix. Similarly, the dynamic equilibrium equation of the quarter car model shown in Fig. 1, is given in Eqs. (2) and (3)

$$M_{v} \ddot{y}_{v} + C_{v} \dot{y}_{v} { + }K_{v} y_{v} = f_{v} {\text{ ; where }}\left\{ {y_{v} } \right\} = \left\{ {\begin{array}{*{20}c} {y_{u} } \\ {y_{s} } \\ \end{array} } \right\};\left\{ {f_{v} } \right\} = \left\{ {\begin{array}{*{20}l} {c_{us} \dot{y}_{c} + k_{us} y_{c} } \hfill \\ 0 \hfill \\ \end{array} } \right\}$$
(2)
$$\left[ {M_{v} } \right] = \left[ {\begin{array}{*{20}l} {m_{us} } \hfill & 0 \hfill \\ 0 \hfill & {m_{s} } \hfill \\ \end{array} } \right]; \, \left[ {C_{v} } \right] = \left[ {\begin{array}{*{20}c} {c_{s} + c_{us} } & { - c_{s} } \\ { - c_{s} } & {c_{s} } \\ \end{array} } \right]; \, \left[ {K_{v} } \right] = \left[ {\begin{array}{*{20}c} {k_{s} + k_{us} } & { - k_{s} } \\ { - k_{s} } & {k_{s} } \\ \end{array} } \right]$$
(3)

The quarter-car model has two degrees of freedom i.e., vehicle axle displacement \(y_{u}\) and vehicle body displacement, \(y_{s}\). The ‘.’ and ‘..’ over \(y_{u}\), \(y_{s}\) represent velocity and acceleration terms respectively.\([{M}_{v}]\),\([{C}_{v}],\) and \([{K}_{v}]\) represent the vehicle mass, damping, and stiffness matrices respectively. The vector \(f_{v}\) represents the dynamic interaction force on the vehicle due to the rough profile of the road surface and the bridge displacements. While \(m_{s}\) and \(m_{us}\) represent the vehicle sprung mass (vehicle body) and the unsprung mass (vehicle axle) respectively. Similarly, \(k_{s}\) and \(k_{us}\) are the suspension and tyre stiffness terms and the corresponding damping terms are \(c_{s}\) and \(c_{us}\). The displacement response at the point of contact between the bridge surface and the wheel of the vehicle is defined in Eq. (4)

$$y_{c} (t) = \, y_{b} (x_{c} ,t) + r(x_{c} ,t)$$
(4)

where \(x_{c}\) represent the spatial location of the bridge and it varies with time as the CP varies with respect to the vehicle position on the bridge. \(y_{b}\) and r are the displacement and surface profile of the bridge respectively.

The coupled system of dynamic equilibrium equations defined in Eq. (5) is obtained by combining Eqs. (1) and (2).

$$[{M}^{c}] \{{\ddot{y}}^{c}\}+ [{C}^{c}] \{{\dot{y}}^{c}\}+ [{K}^{c}] \{{y}^{c}\}= \{F\}$$
(5)

where \([{M}^{c}],\) \([{C}^{c}],\) and \([{K}^{c}]\) represent the mass, damping, and stiffness matrices of the coupled system and are of size (n + 2 × n + 2). Equation (5) can be solved using the Newmark constant average acceleration technique to evaluate the time history responses.

To make the VBI simulations more realistic, the roughness of the road surface must be considered. As per the ISO 8608(1995), there are eight classes of road profiles available. Accordingly, the smoothest road profile is class A, and the worst road profile is class H. For the specified class of roughness profile and spatial frequency \(n_{i}\), the power spectral density (PSD), \({\text{G}}_{d} \left( {n_{i} } \right)\) can be evaluated using Eq. (6), as

$${\text{G}}_{d} \left( {n_{i} } \right) = G_{d} \left( {n_{0} } \right)\left( {\frac{{n_{i} }}{{n_{0} }}} \right)^{ - 2}$$
(6)

where \(n_{0}\) = 0.1 cycle/m. The ISO 8608(1995) Standard provides the values of \(G_{d} (n_{0} )\) for all the eight classes of road profiles Accordingly, the \(G_{d} (n_{0} )\) values for the first three classes i.e., class A, class B, and class C road profiles are given as 16e−06 m3/cycle, 64e−06 m3/cycle, and 256e−06 m3/cycle, respectively. Knowing \(G_{d} (n_{0} )\) values, the surface roughness profile of the bridge [32] can be constructed using Eq. (7).

$$r\left( x \right) = \sum\limits_{i = 1}^{M} {d_{i} } \cos \left( { 2\pi n_{i} x + \Theta_{i} } \right)\quad where\quad d_{i} = \sqrt {2G_{d} \left( {n_{i} } \right)\Delta n}$$
(7)

where M is the number of harmonic waves, used to determine the surface profile of the bridge and varies between 100 and 10,000. \(\Theta_{i}\) is the random phase angle uniformly distributed between 0 and \(2\pi\), \(d_{i}\) is the amplitude, and \(n_{i} = i\Delta n\) is the spatial frequency (cycles/m). \(\Delta n = (n_{U} - n_{L} )/M\), where \(n_{L}\) and \(n_{U}\) are the lower and upper bounds of the spatial frequencies used to define the surface profile. The subscript, i refers to the harmonic wave number.

Determination of CP Response from the Measured Vehicle Response

In field investigations, it is only possible to measure the acceleration time history responses by mounting accelerometers on the body of a moving vehicle during indirect SHM. It is however challenging to identify the natural frequencies of the bridge, in particular the higher modes, from the measured vibration responses. All bridge modal frequencies above the fundamental frequency of the vehicle are suppressed by the low-pass filter applied to the bridge dynamics by the vehicle suspension system. This practical challenge can be overcome by deriving the CP response, (i.e., the time history response at the vehicle’s point of contact with the bridge surface) from the measured vehicle vibration response and using it for bridge modal parameter extraction.

The vehicle equation of motion is used by Yang et al. [33] to offer a closed-form solution for calculating the CP acceleration time history response from the vehicle body vibration measurements. It is outlined below.

Considering the vehicle as a simple mass \((m_{v} )\) supported by a stiffness spring \((k_{v} )\), and neglecting the damping effect, the equation of motion for the vehicle can be expressed using Eq. (8) as

$${m}_{v} \, {\ddot{\text{y}}}_{v}+ \, {k}_{v} ({y}_{v}-{y}_{c})=\text{ 0}$$
(8)

It should be mentioned here that the vehicle damping effects are less pronounced at low speeds when compared to higher speeds. Therefore, the contribution of vehicle damping to the overall response may be minimal, and neglecting it may have negligible effects. Using Eq. (8) \(y_{c}\) can be expressed in the form of Eq. (9) as

$${y}_{c}={y}_{v}+\frac{{m}_{v}{\ddot{y}}_{v}}{{k}_{v}}={y}_{v}+\frac{{\ddot{y}}_{v}}{{\omega }_{v}^{2}} \, where \, {\omega }_{v}^{2}= \frac{{k}_{v}}{{m}_{v}}$$
(9)

where \(\omega_{v}^{{}}\) is the vehicle frequency. The contact point acceleration response can be obtained by twice differentiating Eq. (9) with respect to t. Accordingly, Eq. (10) can be written as

$${\ddot{y}}_{c}={\ddot{y}}_{v}+\frac{{d}^{2}{\ddot{y}}_{v}}{{\omega }_{v}^{2}d{t}^{2}}$$
(10)

where \(\ddot{y}\) is the acceleration. The subscripts c and v refer to the CP and vehicle respectively. Since the vehicle vibration measurements will be in the discrete form, the central difference method can be used to evaluate \(\frac{{d}^{2}{\ddot{y}}_{v}}{d{t}^{2}}.\) Accordingly, the CP acceleration response can be expressed in the form of Eq. (11) as

$$\ddot{y}_{c} = \ddot{y}_{v} + \frac{{\left( {\ddot{y}_{v}^{t + 1} - 2 \ddot{y}_{v}^{t} + \ddot{y}_{v}^{t - 1} } \right)}}{{(\omega_{v} \Delta t)^{2} }}$$
(11)

where \(\Delta t\) is the time step length and the vehicle body acceleration response. \({\ddot{y}}_{v}\) is taken as \({\ddot{y}}_{s}\) in the 2-DOF quarter car vehicle model described in Sect. “Formulation Details”. Superscripts (t + 1), (t), and (t − 1) refer to the values of vehicle body accelerations at time (t + 1), (t), and (t − 1) respectively. The vehicle frequency \(\omega_{v}\) can be evaluated by considering vehicle stiffness, \(k_{v} = k_{s} .k_{us} /(k_{s} + k_{us} )\) and vehicle mass, \(m_{v} = (m_{s} + m_{us} )\) from the 2-DOF quarter-car vehicle model.

However, it is still to be ensured that the ratio of the bridge and vehicle frequency should meet the requirement \(\omega_{bi} /\omega_{v} < \sqrt 2\), to construct the desired number of bridge mode shapes. Here \(\omega_{bi}\) refers to the ith bridge frequency and \(\omega_{v}\) is the vehicle frequency.

Variational Mode Decomposition (VMD)

VMD [34, 35] can be employed to decompose any nonlinear nonstationary signal s(t) into a discrete collection of intrinsic mode functions (IMFs). This decomposition algorithm is non-recursive and has an optimal ability to deal with noise in the signal. The step-by-step VMD signal decomposition procedure is presented below. Here, \(u_{k}\) represents the mode with its respective central frequency \(\omega_{k}\), where k = 1, 2, 3, …K.

  1. 1.

    Initialize \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u}_{k}^{1}\),\(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega }_{k}^{1}\), \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda }^{1}\), and set iteration counter n to 0.

  2. 2.

    Update the previous mode \(u_{k}\) and its associated center frequency \(\omega_{k}\) using Eqs. (12) and (13), respectively.

    $$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u}_{k}^{n + 1} \left( \omega \right) = \frac{{s - \mathop \sum \nolimits_{i < k } \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u}_{i}^{n + 1} \left( \omega \right) - \mathop \sum \nolimits_{i > k} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u}_{i}^{n} \left( \omega \right) + \left( {\frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } \left( \omega \right)}}{2}} \right)}}{{1 + 2\alpha (\omega - \omega_{k}^{n} )^{2} }}$$
    (12)
    $$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega }_{k}^{n + 1} = \frac{{\mathop \smallint \nolimits_{0}^{\infty } \omega \left| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u}_{k}^{n + 1} \left( \omega \right)} \right|^{2} d\omega }}{{\mathop \smallint \nolimits_{0}^{\infty } \omega \left| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u}_{k}^{n + 1} \left( \omega \right)} \right|^{2} d\omega }}$$
    (13)
  3. 3.

    Update Lagrange multiplier λ using Eq. (14), then set n = n + 1

    $$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda }^{{^{n + 1} }} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda }^{n} + \left( {s - \mathop {\sum \hat{u}_{k}^{n + 1} }\limits_{k} } \right)$$
    (14)
  4. 4.

    Repeat Steps (2) and (3) till the convergence criterion given in Eq. (15) is satisfied

    $$\mathop \sum \limits_{k} \frac{{\left\| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u}_{k}^{n + 1} - u_{k}^{n} } \right\|_{2}^{2} }}{{\left\| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u}_{k}^{n} } \right\|_{2}^{2} }} < \varepsilon ,\quad where\varepsilon >$$
    (15)

The VMD procedure requires the setting up of control parameters; i.e., fidelity factor (α) and mode number (K). Since, the number of peaks in the Fourier spectra associated with the signal (i.e., the time history vibration response) can be identified, it is assigned to K in the present work. Since we are interested in extracting low frequencies, the fidelity factor (α) is set to a greater value. Accordingly, α is taken as 9000 in the present work, based on parametric studies carried out by varying fidelity factor from 7000 to 10,000.

Teager Kaiser Energy Operator (TKEO)

TKEO [36,37,38,39]is a more contemporary alternative method to HT, for amplitude-frequency separation of a signal and estimating the instantaneous characteristics of frequency, amplitude, and phase. The instantaneous energy,\({E}_{TK}^{d}(t)\), of a discrete-time signal, u(t), is evaluated using Eq. (16).

$${E}_{TK}^{d}(t)={\psi }_{d}(u(t))={u}^{2}[t]-u[t-1]u[t+1]$$
(16)

The discrete TKEO energy operator \(\psi_{d} (u(t))\) has good adaptation to the instantaneous changes in u(t) and provides exceptional time resolution as it only needs three samples (u(t − 1), u(t), and u(t + 1)) to compute the energy at any time instant t. The instantaneous amplitude, \(A\left(t\right),\) and frequency, \(\Omega (t),\) are estimated by DESA-2 [40] using Eq. (17) and Eq. (18) respectively.

$$\left|A(t)\right|\approx \frac{2{\psi }_{d}(u(t))}{\sqrt{{\psi }_{d}(u(t+1)-u(t-1))}}$$
(17)
$${\Omega }_{i}(t)\approx \frac{1}{2}\mathit{arccos}(1-\frac{{\psi }_{d}(u(t+1)-u(t-1))}{2{\psi }_{d}(u(t))}$$
(18)

To improve the obtained estimation results, the Teager–Kaiser weighted instantaneous frequency \(\omega_{i}\) is analyzed using Eq. (19).

$${\Omega }_{i}={\omega }_{i}T$$
(19)

The modal identification technique with VBI responses by combining VMD with TKEO is detailed in the form of a flow chart in Fig. 2.

Fig. 2
figure 2

Modal identification algorithm combining VMD with TKEO using indirect measurements

Full size image

Numerical Studies

The effectiveness of the proposed VBI and TKEO-based modal identification algorithm is examined through numerical simulations. The proposed method uses the measured vibration data from the passing vehicle to identify the mode shapes and natural frequencies of the bridge. A 20 m span bridge is considered and it is idealized with Euler beam elements by discretizing into 100 elements. The mass density of the structure is 2400 kg/m3, Flexural Rigidity, EI is 54.015E08 Nm2, and the damping ratio is assumed as 0.01. The natural frequencies are worked out to be 3.84 Hz, 15.35 Hz, 34.55 Hz, 61.43 Hz, 95.98 Hz, and 138.21 Hz.

The quarter-car model discussed in the earlier sections is employed to idealize the moving vehicle. The properties of the moving, as well as sensing vehicle, are: body mass mb = 545.5 kg, axle mass ms = 200 kg, body spring (suspension) stiffness ks = 2.0E05 N/m; body spring stiffness kb = 2.0E05 N/m. The natural frequency of the vehicle is 6.99 Hz. In the numerical simulations, the sampling frequency is taken as 1000 Hz, and 2.0 m/s is the vehicle speed. The roughness of the road surface is not considered in this set of simulations.

The parameters of the sensing vehicle are known. Further, the vehicle’s frequencies do not coincide with the natural frequencies of the structure. Therefore, it is possible to recover the dynamic modal responses of the structure from the measured vehicle response for the modal parameter estimation. The measured vehicle vibration response and the CP response evaluated using Eqs. (2) and (8) are shown in Fig. 3a, b respectively. The Fourier spectrum associated with the CP response is presented in Fig. 4a.

Fig. 3
figure 3

Vehicle time history response: a body response b CP response

Full size image
Fig. 4
figure 4

CP response: a FFT spectrum b Zoomed plot around the first frequency of bridge c Zoomed plot around the second frequency of the bridge

Full size image

The first peak value at 0.122 Hz in the Fourier spectrum plot shown in Fig. 4a and marked with a red colored dot, indicates the driving frequency \(2n\pi v/L\), where v is the vehicle speed. The zoomed portions of the first and second bridge frequencies are shown in Fig. 4b, c respectively. The green dots in Fig. 4b, c indicate the shifting frequencies of \({\omega }_{bn}-n\pi v/L\) and \({\omega }_{bn}+n\pi v/L\). The bridge frequencies can be worked out by averaging shifting frequencies. Similarly, all the other frequency values are indicated by the vertical red lines in Fig. 4a. The natural frequencies extracted from the Fourier spectrum plot of CP responses are presented in Table 1. The percentage of variation from the theoretically evaluated natural frequencies is also indicated in Table 1. The term "theoretical evaluated natural frequencies" here refers to the natural frequencies evaluated using the finite element analysis of the structure. Since vibration frequencies related to the vehicle are not present in the CP response and also the frequency resolution of the structure is found to be good, it is proposed to use the CP responses to extract the modal responses using VMD.

Table 1 Natural frequencies of the structure obtained from the CP response
Full size table

It can be observed from Table 1 that the average values of frequencies of the beam obtained from CP responses are compared well with the theoretically evaluated natural frequencies. The variation is found to be significantly higher as we go beyond the 5th natural frequency. Accordingly, in the present work, it is proposed to identify the first five mode shapes using the proposed algorithm.

The VMD discussed in the earlier sections is used to decompose the bridge CP time history response into intrinsic mode functions (IMF). Even though it has been reported that VMD works better than the widely used EMD in terms of overcoming mode mixing and boosting noise suppression, it is extremely sensitive to the settings of the initial control parameters. Especially the control parameters; i.e., the modal component number K and the penalty factor α must be appropriately specified beforehand to obtain the sought-after decomposition of the signal. Improper configurations of these two parameters are likely to result in inconsistent decomposition performances of VMD. As a result, research on optimizing the VMD control settings has drawn a lot of interest. Recently, attempts have been made to optimize these control parameters using metaheuristic algorithms [41, 42]. Therefore, a proper computationally efficient IMF selection strategy is desirable for identifying the dominant frequency modes. Keeping this in view, in this paper, a correlation coefficient-based approach for the selection of IMFs with dominant frequency modes is considered. According to this procedure, first, the correlation coefficient indicating correlation strength between the generated IMF and the time history response is determined using Eq. (20).

$$\gamma \left( {r_{j} ,y} \right) = \frac{{\mathop \sum \limits_{j = 1}^{M} \left( {y\left( t \right) - \overline{y}} \right)\left( {r_{j} \left( t \right) - \overline{r}_{j} } \right)}}{{\sigma_{{r_{i} }} \sigma_{y} }}$$
(20)

where \(y(t)\) is the time history signal to be decomposed, \({r}_{j}(t)\) is the j-th IMF generated using the VMD. While \(\overline{y}\) and \(\overline{r}_{j}\) are the mean values of the original time history signal and j-th IMF signal respectively, \({\sigma }_{y}\) and \({\sigma }_{{r}_{i}}\) are the standard deviation values of the respective signals. Once the correlation coefficients of all the IMFs generated by VMD are evaluated, the relative correlation weight, W of each one is calculated as given in Eq. (21).

$$W(j) = \frac{{\gamma (r_{j} ,y)}}{{\sum\limits_{{j = 1}}^{M} {\gamma (r_{j} ,y)} }}$$
(21)

These weights are sorted in descending order and the top desired number of IMFs with the highest weight are selected.

The first five IMFs generated using the above procedure and their corresponding frequency plots are shown in Fig. 5. It can be observed from the responses shown in Fig. 5, that the VMD technique with appropriate parameter settings can decompose the signal into high-quality modal responses (IMFs) without any mode mixing.

Fig. 5
figure 5

Decomposition of time history measurements using VMD: a IMFs of the signal b FFT spectra of IMFs

Full size image

The TKEO is employed on each of the IMFs to estimate the instantaneous energy of the signal. DESA-2 is then employed to evaluate the instantaneous frequency and amplitude. DESA-2 is employed in the present work, as it is reported to be more computationally efficient and robust with the least errors. Accordingly, the instantaneous amplitude plot of each IMF (i.e., modal response) can be obtained. The mode shape corresponding to the modal response (IMF) being analyzed can be obtained by connecting all the peaks of the instantaneous amplitude plot. Engineering judgment and expertise need to be used to determine the sign of the mode shape [43]. Finally, the normalized mode shapes obtained using the procedure combining VMD and TKEO are presented in Fig. 6. The theoretical mode shapes are also plotted in Fig. 6 for easy appreciation of the quality of the mode shapes generated using the proposed algorithm. The theoretical mode shapes and natural frequencies that are used for comparison in this research come from the structure’s finite element analysis.

Fig. 6
figure 6

First five mode shapes of the structure with CP response using the proposed algorithm: a First mode shape b Second mode shape c Third mode shape d Fourth mode shape e Fifth mode shape

Full size image

Sensitivity of the Proposed Algorithm to the Vehicle Speed

In the numerical studies presented so far, the vehicle speed is 2 m/s. In this section, investigations are carried out, with higher vehicle speeds, i.e. 4 m/s, 6 m/s, 8 m/s, and 10 m/s, to explore the sensitivity of vehicle speed on the VMD decomposition and subsequent mode shape construction. For a typical vehicle speed of 10 m/s Fourier spectrum of CP response is shown in Fig. 7a and a comparison of the Fourier spectrum responses for different vehicle speeds considered in this paper is shown in Fig. 7b. The shifted frequencies with varying speeds of the vehicle are shown in Table 2. The percentage variation of the extracted frequencies from the theoretically evaluated natural frequencies is indicated in parenthesis for each vehicle speed in Table 2. It can be observed from Fig. 7 as well as Table 2 that the first five frequencies are marginally shifted with increased vehicle speeds. The mode shapes constructed using the proposed algorithm with the CP responses with varying vehicle speeds are shown in Fig. 8. The plots shown in Fig. 8, indicate that the modal parameter identification can be carried out with reasonable accuracy even with higher vehicle speeds using the proposed method.

Fig. 7
figure 7

Fourier spectra of the CP response of the vehicle moving on the bridge with varying speeds: a vehicle speed 10 m/s b comparison of Fourier spectra with varying vehicle speeds

Full size image
Table 2 Natural Frequencies of the structure from the CP response with varying vehicle speeds
Full size table
Fig. 8
figure 8

First five Mode shapes of the structure constructed using the proposed algorithm from the CP responses with varying vehicle speeds: a First mode shape b Second Mode shape c Third mode shape d Fourth Mode shape e Fifth mode shape

Full size image

However, it should be pointed out here that the roughness is neglected in all the studies carried out so far using varying vehicle speeds. The dynamic response of the structure is likely to be heavily polluted at higher vehicle speeds due to the impact caused by the rough road surfaces. At the same time, the dynamic components of the vehicle are likely to be enhanced. In view of the dominance of the vehicle-related dynamic components in the measured response, the structure-related components become less obvious. On the other hand, a lower test vehicle speed will result in a longer measurement duration and it helps in identifying a larger number of modes with good accuracy. Hence, it is suggested that a sensing vehicle traveling at a modest speed is advantageous for drive-by bridge health monitoring and modal parameter estimation.

Sensitivity to the Measurement Noise

Investigations are carried out using the CP responses corrupted with varying noise levels. Three different noise levels in the form of SNR 50, 60, and 70 are considered. VMD is employed on the time history data corrupted with noise. The IMF components and their spectra for a typical noise level of SNR-50 are shown in Fig. 9a, b, respectively. Similarly, the mode shapes constructed using the TEKO and DESA-2 algorithms are presented in Fig. 10. It can be observed from Fig. 9 that VMD decomposition performance is satisfactory even with noise-polluted time history signal without mode mixing. Similarly, we can observe from Fig. 10 that the first four mode shapes generated are compared well with the mode shapes obtained using the finite element method (FEM). However, the fifth mode shape is slightly distorted. The investigations carried out on the combined effects of noise and roughness, on the constructed mode shapes are discussed in Sect. “Effect of Surface Roughness”.

Fig. 9
figure 9

Decomposition of noise corrupted time history measurements using VMD—SNR 50. a IMFs of the noise signal b FFT spectra of IMFs

Full size image
Fig. 10
figure 10

First five Mode shapes generated using the proposed algorithm from the noise-corrupted responses—SNR 50: a First mode shape b Second Mode shape c Third mode shape d Fourth Mode shape e Fifth mode shape

Full size image

Effect of Surface Roughness

Investigations are carried out, considering the road surface roughness as Class-C according to the ISO standard specification discussed earlier, and accordingly, the road roughness is evaluated using Eqs. (6) and (7).

Figure 11 shows the decomposition details i.e., the IMFS and their associated Fourier spectrum of the vehicle acceleration time history signal with roughness using VMD. It can be observed from the IMFs generated that only three IMFs are generated with reasonably good accuracy. The corresponding mode shapes constructed using TKEO and DESA-2 algorithms are shown in Fig. 12. It can be observed that while the first two mode shapes generated are comparing well with the FEM mode shapes, the 3rd mode shape constructed is rather distorted.

Fig. 11
figure 11

Decomposition of time history measurements with road surface roughness (Class-C) using VMD a IMFs of the noise signal b FFT spectra of IMFs

Full size image
Fig. 12
figure 12

First three constructed mode shapes using the proposed algorithm considering the road surface roughness—Class-C: a First mode shape b Second Mode shape c Third mode shape

Full size image

Combined Effect of Noise and Road Surface Roughness

Studies are carried out to evaluate the sensitivity of the proposed algorithm with road surface roughness and noise-corrupted measurements. Modal assurance criterion (MAC) is employed to assess the quality of the generated mode shapes and is defined in Eq. (22).

$${\text{Model}}\;\;{\text{Assurance}}\;\;{\text{Criterion}}\;MAC\left( {r,q} \right) = \frac{{\left| {\left\{ {\Phi_{A} } \right\}_{r}^{T} \left\{ {\Phi_{R} } \right\}_{q} } \right|^{2} }}{{\left( {\left\{ {\Phi_{A} } \right\}_{r}^{T} \left\{ {\Phi_{A} } \right\}_{r} } \right)\left( {\left\{ {\Phi_{R}^{T} } \right\}_{q}^{T} \left\{ {\Phi_{R} } \right\}_{q} } \right)}}$$
(22)

Where \({\Phi }_{A}\) and \({\Phi }_{R}\) refers to theoretical (FEM) and reconstructed mode shapes respectively. Subscripts r and q refer to the mode shape numbers. MAC value will be one, if the theoretical as well as reconstructed mode shape using the proposed algorithm are exact. MAC value will be close to zero if they are very poorly correlated. The vehicle speed is considered as 2 m/sec. The MAC values are furnished in Table 3. It can be observed from the results presented in Table 3 that the quality of mode shapes is sensitive to higher road surface roughness. However, they are less sensitive to measurement noise.

Table 3 Performance of the proposed modal identification algorithm under varying road surface roughness and measurement noise
Full size table

Conclusion

A new bridge modal identification algorithm from the responses captured from an instrumented moving vehicle traveling over a bridge is proposed. The proposed algorithm is developed by combining a non-recursive signal decomposition method called VMD with TKEO. The VBI problem is formulated by idealizing the bridge as a simply supported beam with Euler beam elements and the moving vehicle as a quarter-car model. The sensitivity of the proposed modal identification algorithm with varying vehicle speeds, measurement noise, and roughness of the road surface profile is investigated. The following conclusions are drawn based on the investigations carried out and presented in this paper.

  1. 1.

    The extracted CP acceleration response is found to possess the participation of many number of bridge frequencies and not the vehicle dynamics.

  2. 2.

    The IMFs generated from the CP responses using VMD are free from mode mixing. VMD is also found to be less sensitive to measurement noise. However, setting the proper control parameters of VMD is crucial in obtaining the desired quality of decomposition of the signal.

  3. 3.

    The selection of IMFs based on correlation weights is found to be effective in choosing the dominant modal responses from the time history signal.

  4. 4.

    TKEO along with the DESA-2 is found to be accurate and effective in constructing the low-frequency mode shapes of the structure even with measurement noise.

  5. 5.

    A vehicle moving on the bridge at a lower speed (i.e., 2 m/sec) is effective in capturing all the lower dominant modes of the structure. At greater vehicle speeds, the bridge frequencies are often muted by the dominance of the vehicle suspension dynamics. Apart from this, a slow-moving vehicle results in the collection of vibration measurements for a longer duration. A large number of samples helps in identifying the larger number of modes with much higher resolution.

  6. 6.

    Road surface roughness certainly influences the accuracy of the identified modes.