1 Introduction

Satellite communication has gained enormous popularity in the era of fifth-generation (5G) communications owing to its advantages in various applications such as defence, disaster relief, and navigation [1]. Recently, satellite communication systems have shown a great interest of research in the wireless society due to their capability of providing seamless connectivity and high data rate transmission over a wide coverage area [2]. However, masking effect may result due to severe shadowing and heavy obstacles between the satellite and terrestrial users which causes unavailability of the line-of-sight (LOS) communication [3]. To overcome this problem, researchers have conceived the cooperation of terrestrial relay into satellite communication systems to form a new architecture defined as hybrid satellite-terrestrial relay network (HSTRN) [3, 4]. Such systems mainly exploits cooperative relaying technique in an integrated manner to enhance the reliability and coverage performance, especially in subterranean and indoor environment. A new generation standard known as DVB-SH [5] incorporates the framework of HSTRN to provide Satellite services to Handheld devices (SH).

In recent years, many research efforts have been devoted towards improvement of the performance of HSTRN [6,7,8,9,10,11,12]. However, the transmission security aspects are hardly examined for the HSTRN. The information security is one of the major problems in the wireless communication. In the beginning, cryptography techniques were used at upper layers to ensure the security in satellite communication systems [13]. On the contrary, Wyner in [14] has proposed an information-theoretic approach to achieve physical layer security that exploits the characteristics of fading channels. In the context of physical layer security, very limited works have investigated the secrecy performance of the HSTRN [15,16,17,18]. In [15], authors have studied maximum ratio combining and transmit zero-forcing beamforming based schemes to ensure the secrecy of a multiple eavesdropper HSTRN. Secrecy performance analysis of a multi-relay HSTRN configuration has been examined in [16] and [17], where optimal relay section scheme was studied to select the best relay and to enhance security of the considered system. Moreover, physical layer security of a cognitive HSTRN by considering underlay spectrum sharing technique has been examined in [18]. As far as authors are aware, the secrecy performance analysis of a multi-user HSTRN configuration has not been addressed so far. The main purpose of this paper is to analyse a multi-user HSTRN and to highlight the impact of key parameters on the secrecy performance and achievable diversity order of such system. In fact, the deployment of multiple users makes the proposed configuration more favorable for practical applications.

In light of the above discussion, we conduct a comprehensive secrecy performance analysis of a downlink multi-user amplify-and-forward (AF) based HSTRN by employing opportunistic scheduling of terrestrial users. By adopting Shadowed-Rician fading for satellite link and Nakagami-m fading for terrestrial links, we derive an accurate and asymptotic secrecy outage probability (SOP) expressions which are applicable for arbitrary number of users and arbitrary integer values of the fading severity parameters over the two hops. The asymptotic SOP expression helps us in examining the achievable diversity order of the considered HSTRN. We found that the achievable diversity order of the considered system depends on the fading severity parameter of the relay-destinations links and number of terrestrial users while it remains unaffected by the fading severity parameter of satellite link. We also evaluate the expression for probability of non-zero secrecy capacity of the considered system. We validate our analysis with the help of Monte-Carlo simulation results.

The remainder of this paper is organized as follows. In Sect. 2, we first introduce the system model and then describe the heterogeneous channel models. Further, we perform secrecy performance analysis in Sect. 3. Section 4 presents the numerical and simulation results, and finally, the conclusions are given in Sect. 5.

2 HSTRN description

2.1 System model

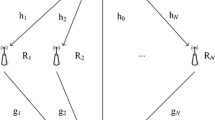
As shown in Fig. 1, we consider a downlink HSTRN consisting of a satellite source S, an AF relay R, N destinations \(\{D_{n}\}_{n=1}^{N}\), and an eavesdropper E. All nodes are equipped with a single antenna. The LOS links between S and \(\{D_{n}\}_{n=1}^{N}\) as well as between S and E are not available owing to the masking effect. Therefore, S communicates with \(\{D_{n}\}_{n=1}^{N}\) via a terrestrial AF relay R in the presence of eavesdropper E. The satellite link (i.e., \(S\rightarrow R\) link) is assumed to undergo Shadowed-Rician fading while terrestrial links (i.e., \(R \rightarrow D_{n}\) and \(R \rightarrow E\) links) experience Nakagami-m fading. All the receiving nodes are inflicted by additive white Gaussian noise (AWGN) with zero mean and variance \(\sigma ^{2}\). Herein, the \(S\rightarrow R \rightarrow D_{n}\) and \(S\rightarrow R \rightarrow E\) links are referred to as the main and the wiretap links, respectively.

Fig. 1
figure 1

System model: HSTRN

Full size image

The overall communication takes place in two time phases by employing an opportunistic user scheduling scheme. In first phase, the satellite source S transmits its signal \(x_{s}\) (with unit energy) to the relay R. Thus, the received signal at R can be given by

$$y_{sr}=\sqrt{P_{s}}h_{sr}x_{s}+n_{r},$$
(1)

where \(P_{s}\) is the transmit power at S, \(h_{sr}\) is the channel coefficient between S and R, and \(n_{r}\) is the AWGN at R.

In the second phase, the relay R first amplifies the received signal \(y_{sr}\) using a gain factor G and then forwards it to the selected destination \(D_{n}\). Meanwhile, the eavesdropper tries to overhear the signal transmitted from relay. Therefore, the signals received at destination \(D_{n}\) and eavesdropper E can be given, respectively, as

$$y_{rd_{n}}=\sqrt{P}_{r}h_{rd_{n}}G\,y_{sr}+n_{d_{n}}$$
(2)

and

$$y_{re}=\sqrt{P}_{r}h_{re}G\,y_{sr}+n_{e},$$
(3)

where \(P_{r}\) is the transmit power at relay R, \(h_{rd_{n}}\) and \(h_{re}\) denote the respective channel coefficients for \(R \rightarrow D_{n}\) and \(R \rightarrow E\) links, while \(n_{d_{n}}\) and \(n_{e}\) represent the AWGN variables at the respective nodes.

Based on (2) and (3), the instantaneous received signal-to-noise ratios (SNRs) at \(D_{n}\) and E can be obtained, respectively, as

$$\gamma _{D_{n}}=\frac{\gamma _{sr}\gamma _{rd_{n}}}{\gamma _{rd_{n}}+\frac{1}{G^{2}\sigma ^{2}}}$$
(4)

and

$$\gamma _{E}= \frac{\gamma _{sr}\gamma _{re}}{\gamma _{re}+\frac{1}{G^{2}\sigma ^{2}}},$$
(5)

where \(\gamma _{sr}=\eta _{s}|h_{sr}|^{2}\), \(\gamma _{rd_{n}}=\eta _{r}|h_{rd_{n}}|^{2}\), and \(\gamma _{re}=\eta _{r}|h_{re}|^{2}\) with \(\eta _{s}=\frac{P_{s}}{\sigma ^{2}}\) and \(\eta _{r}=\frac{P_{r}}{\sigma ^{2}}\). For variable gain relaying, the gain factor G in (4) and (5) can be determined as

$$G=\sqrt{\frac{1}{P_{s}|h_{sr}|^2+\sigma ^{2}}},$$
(6)

and thus, the instantaneous end-to-end SNRs at \(D_{n}\) and E can be given, respectively, as

$$\gamma _{D_{n}}= \frac{\gamma _{sr}\gamma _{rd_{n}}}{\gamma _{sr}+\gamma _{rd_{n}}+1},$$
(7)

and

$$\gamma _{E}= \frac{\gamma _{sr}\gamma _{re}}{\gamma _{sr}+ \gamma _{re}+1}.$$
(8)

To harness the multiuser diversity in the considered network, we utilize the opportunistic scheduling scheme, where the relay select the best user based on the highest instantaneous SNR of \(R \rightarrow D_{n}\) links as

$$\gamma _{rd}= \max _{1\le n\le N} \gamma _{rd_{n}}.$$
(9)

Hence, the actual SNR with the scheduled user can be written as

$$\gamma _{D}= \frac{\gamma _{sr}\gamma _{rd}}{\gamma _{sr}+\gamma _{rd}+1}.$$
(10)

As such, we can define instantaneous capacity of the main link and of the wiretap link by \(C_{D}=\frac{1}{2}\log _{2}(1+\gamma _{D})\) and \(C_{E}=\frac{1}{2}\log _{2}(1+\gamma _{E})\), respectively. Thereby, the achievable secrecy capacity of the considered HSTRN is given by the positive difference between the capacity of the main link and capacity of the wiretap link [19] as

$$\begin{aligned} C_{S}&=[C_{D}-C_{E}]^{+}\\&=\left[ \frac{1}{2}\log _{2}(1+\gamma _{D})-\frac{1}{2}\log _{2}(1+\gamma _{E})\right] ^{+}, \end{aligned}$$
(11)

where \([a]^{+}\triangleq \max (a,0)\).

2.2 Channel model

In this subsection, we illustrate the statistical characterization for fading channels of each hop. As the satellite link (i.e., \(S\rightarrow R\)) follows independent Shadowed-Rician fading distribution, the probability density function (PDF) of \(|h_{sr}|^2\) between satellite S and relay R is given by [6, 20]

$$f_{|h_{sr}|^{2}}(x)=\alpha _{s} \,\text {e}^{-\beta _{s} x} \,_{1\!}F_{1}\left( m_{s};1;\delta _{s} x\right) , \,\,x\ge 0,$$
(12)

where \(\alpha _{s}=(2b_{s} m_{s}/(2b_{s} m_{s}+\varOmega _{s}))^{m_{s}}/2b_{s}\), \(\beta _{s}=1/2b_{s}\), and \(\delta _{s}=\varOmega _{s}/(2b_{s}(2b_{s} m_{s}+\varOmega _{s}))\) with \(\varOmega _{s}\) and \(2b_{s}\) be the average power of LOS and multipath components, respectively, \(m_{s}\) is the fading severity parameter, and \(_{1\!}F_{1}(\cdot ;\cdot ;\cdot )\) is the confluent hypergeometric function of the first kind [25, eq. 9.210.1]. We consider only the integer values of the fading severity parameter of the satellite link [16, 21]. Thus, the hypergeometric function can be represented via Kummer’s transform [22] as

$${}_{1\!}F_{1}(a;b;x)= \text {e}^{x}\sum _{n=0}^{a-b}\frac{(a-b)!x^{n}}{(a-b-n)!n!(b)_{n}},$$
(13)

where \((\cdot )_{n}\) is the Pochhammer symbol [25, p. xliii]. Thereby, for integer \(m_{s}\), we can simplify \(_{1\!}F_{1}\left( m_{s};1;\delta _{s} x\right)\) in (12) using (13) to represent the PDF \(f_{|h_{sr}|^{2}}(x)\) as

$$f_{|h_{sr}|^{2}}(x)=\alpha _{s} \sum _{\kappa =0}^{m_{s}-1}\psi _(\kappa )x^{\kappa }\text {e}^{-(\beta _{s}-\delta _{s})x},$$
(14)

where \(\psi (\kappa )=(-1)^{\kappa }(1-m_{s})_{\kappa }\delta _{s}^{\kappa }/(\kappa !)^{2}\).

The PDF of \(\gamma _{sr}\) can be thus derived by applying the transformation of variable as

$$f_{\gamma _{sr}}(x)=\alpha _{s} \sum _{\kappa =0}^{m_{s}-1}\frac{\psi (\kappa )}{(\eta _{s})^{\kappa +1}}x^{\kappa } \text {e}^{-\left( \frac{\beta _{s}-\delta _{s}}{\eta _{s}}\right) x}.$$
(15)

By integrating the PDF in (15) with the aid of [25, eq. 3.351.2], we can obtain the cumulative distribution function (CDF) of \(\gamma _{sr}\) as

$$\begin{aligned} F_{\gamma _{sr}}(x)&=1-\alpha _{s} \sum _{\kappa =0}^{m_{s}-1}\frac{\psi (\kappa )}{(\eta _{s})^{\kappa +1}}\sum _{p=0}^{\kappa } \frac{\kappa !}{p!} \left( \frac{\beta _{s}-\delta _{s}}{\eta _{s}}\right) ^{-(\kappa +1-p)} \\&\quad \times x^{p}\text {e}^{-\left( \frac{\beta _{s}-\delta _{s}}{\eta _{s}}\right) x}. \end{aligned}$$
(16)

For terrestrial links, the channel coefficients \(h_{rd_{n}}\) and \(h_{re}\) undergo Nakagami-m distribution with fading severity \(m_{d}\) and \(m_{e}\), and average power \(\varOmega _{d}\) and \(\varOmega _{e}\), respectively. As such, the PDF and CDF of channel gain \(\gamma _{rd_{n}}\) are given, respectively, by

$$f_{\gamma _{rd_{n}}}(x)=\left( \frac{m_{d}}{\varrho _{d}}\right) ^{m_{d}}\frac{x^{m_{d}-1}}{\varGamma (m_{d})} \text {e}^{-\frac{m_{d}}{\varrho _{d}}x}$$
(17)

and

$$F_{\gamma _{rd_{n}}}(x)=\frac{1}{\varGamma (m_{d})}\varUpsilon \left( m_{d}, \frac{m_{d}}{\varrho _{d}} x\right) ,$$
(18)

where \(\varrho _{d}=\eta _{r}\varOmega _{d}\), \(\varUpsilon (\cdot ,\cdot )\) and \(\varGamma (\cdot )\) represent, respectively, the lower incomplete and the complete gamma functions [25, eq. 8.350]. Similarly, the PDF and CDF of channel gain \(\gamma _{re}\) are given, respectively, as

$$f_{\gamma _{re}}(x)=\left( \frac{m_{e}}{\varrho _{e}}\right) ^{m_{e}}\frac{x^{m_{e}-1}}{\varGamma (m_{e})} \text {e}^{-\frac{m_{e}}{\varrho _{e}}x}$$
(19)

and

$$F_{\gamma _{re}}(x)=\frac{1}{\varGamma (m_{e})}\varUpsilon \left( m_{e}, \frac{m_{e}}{\varrho _{e}} x\right) ,$$
(20)

where \(\varrho _{e}=\eta _{r}\varOmega _{e}\).

3 Secrecy performance analysis

Here, we first derive the SOP expression of the considered HSTRN and then analyze the asymptotic behavior of the SOP expression. Subsequently, we also calculate the probability of non-zero secrecy capacity.

3.1 SOP

The secrecy outage event is said to occur when the transmitter sends data at a rate \(\mathcal {R}_{S}\) higher than the secrecy capacity \(C_{S}\). Hence, the SOP for considered HSTRN is formulated as

$$\mathcal {P}_{\text {sec}}=\text {Pr}\left[ C_{S}<\mathcal {R}_{S}\right] ,$$
(21)

which can be expressed using (11) as

$$\mathcal {P}_{\text {sec}}=\text {Pr}\left[ \frac{1+\gamma _{D}}{1+\gamma _{E}}<\gamma _{0}\right] ,$$
(22)

where \(\gamma _{0}=2^{2\mathcal {R}_{S}}\). On performing some appropriate approximation, (22) can be given as

$$\mathcal {P}_{\text {sec}}\approx \text {Pr}\left[ \frac{\gamma _{D}}{\gamma _{E}}<\gamma _{0}\right] ,$$
(23)

where we have used the approximation \(\frac{1+x}{1+y}\approx \frac{x}{y}\), which is widely adopted in literature [23, 24] and shown to have negligible effect in broad SNR region. Further, on invoking the SNR expressions from (8) and (10) into (23) and doing some manipulations for large transmit power, we obtain

$$\begin{aligned} \mathcal {P}_{\text {sec}}&\approx \text {Pr}\left[ \frac{\gamma _{sr}\gamma _{rd}}{\gamma _{0}\gamma _{sr}+(\gamma _{0}-1)\gamma _{rd}}<\gamma _{re}\right] \\&=\int _{0}^{\infty }F_{Z}(z)f_{\gamma _{re}}(z)dz, \end{aligned}$$
(24)

where the last expression results after defining \(Z\triangleq \frac{\gamma _{sr}\gamma _{rd}}{\gamma _{0}\gamma _{sr}+(\gamma _{0}-1)\gamma _{rd}}\). To proceed further, we require the CDF \(F_{Z}(z)\) which can be derived as

$$\begin{aligned} F_{Z}(z)&=1-\int _{0}^{\infty }\left( 1-F_{\gamma _{sr}} \left( \frac{z(\gamma _{0}-1)(x+z\gamma _{0})}{x}\right) \right) \\&\quad \times f_{\gamma _{rd}}(x+z\gamma _{0})dx. \end{aligned}$$
(25)

To solve (25), we require the PDF of \(\gamma _{rd}\). After applying order statistics, \(f_{\gamma _{rd}}(x)\) can be given as

$$f_{\gamma _{rd}}(x)= N\left( F_{\gamma _{rd_{n}}}(x)\right) ^{N-1}f_{\gamma _{rd_{n}}}(x).$$
(26)

On invoking (18) with series exploration of \(\varUpsilon (\cdot ,\cdot )\) [25, eq. 8.352.1], the corresponding PDF from (17) into (26), and then applying binomial [25, eq. 1.111] and multinomial [25, eq. 0.314] expansions, we obtain \(f_{\gamma _{rd}}(x)\) as

$$\begin{aligned} f_{\gamma _{rd}}(x)&= N\sum _{\jmath =0}^{N-1}\left( {\begin{array}{c}N-1\\ \jmath \end{array}}\right) \sum _{l=0}^{\jmath (m_{d}-1)}\frac{\omega _{l}^{\jmath }}{\varGamma {(m_{d})}} (-1)^{\jmath } \\&\quad \times \left( \frac{m_{d}}{\varrho _{d}}\right) ^{m_{d}+l} x^{m_{d}+l-1}e^{-\left( \frac{m_{d}}{\varrho _{d}}\right) (\jmath +1)x}, \end{aligned}$$
(27)

where the coefficients \(\omega _{l}^{\jmath }\), for \(0 \le l \le \jmath (m_{d}-1)\), can be calculated recursively \((\text {with }\varepsilon _{l}=\frac{1}{l!})\) as \(\omega _{0}^{\jmath }= (\varepsilon _{0})^{\jmath }\), \(\omega _{1}^{\jmath } = \jmath (\varepsilon _{1})\), \(\omega _{\jmath (m_{d}-1)}^{\jmath } = (\varepsilon _{m_{d}-1})^{\jmath }\), \(\omega _{l}^{\jmath }= \frac{1}{l\varepsilon _{0}}\sum _{q=1}^{l}[q\jmath -l+q]\varepsilon _{q}\omega _{l-q}^{\jmath }\) for \(2\le l \le m_{d}-1\), and \(\omega _{l}^{\jmath } = \frac{1}{l\varepsilon _{0}}\sum _{q=1}^{m_{d}-1}\![q\jmath -l+q]\varepsilon _{q}\omega _{l-q}^{\jmath }\) for \(m_{d}\le l < \jmath (m_{d}\!-1)\).

Now, using (16) and (27) into (25), we can obtain \(F_{Z}(z)\) with the help of [25, eq. 3.471.9], and then substituting the resultant of (25) along with (19) into (24), and then solving the integration with the use of [25, eq. 7.813.1], we obtain SOP as given in (28), shown at the top of the next page,

$$\begin{aligned} \mathcal {P}_{\text {sec}}&= 1-N\sum _{\kappa =0}^{m_{s}-1}\sum _{p=0}^{\kappa }\sum _{\jmath =0}^{N-1}\sum _{l=0}^{\jmath (m_{d}-1)}\sum _{q=0}^{t+l}\left( {\begin{array}{c}N-1\\ \jmath \end{array}}\right) \left( {\begin{array}{c}t+l\\ q\end{array}}\right) \frac{\alpha (\gamma _{0}-1)^{p}\kappa !\psi (\kappa )}{p!(\eta _{s})^{\kappa +1}} \left( \frac{\beta -\delta }{\eta _{s}}\right) ^{-(\kappa +1-p)} \omega _{l}^{\jmath }\frac{(-1)^{\jmath }}{\varGamma (m_{d})}\left( \frac{m_{d}}{\varrho _{d}}\right) ^{m_{d}+l} \\&\quad \times \left( \gamma _{0}\right) ^{t+l-q}\frac{2\sqrt{\pi }}{\varGamma (m_{e})}\left( \frac{m_{e}}{\varrho _{e}}\right) ^{m_{e}}\left( \varPhi +2\sqrt{\frac{\beta -\delta }{\eta _{s}}\gamma _{0}(\gamma _{0}-1)\frac{m_{d}}{\varrho _{d}}(\jmath +1)} \right) ^{-(\mu +l+v)} \left( 4\frac{\beta -\delta }{\eta _{s}}\gamma _{0}(\gamma _{0}-1)\right) ^{v} \\&\quad \times \frac{\varGamma (\mu +l+v)\varGamma (\mu +l-v) }{\varGamma (\mu +l+\frac{1}{2})}{}_{2}F_{1}\left( \mu +l+v;v+\frac{1}{2};\mu +l+\frac{1}{2}; \frac{\varPhi -2\sqrt{\frac{\beta -\delta }{\eta _{s}}\gamma _{0}(\gamma _{0}-1)\frac{m_{d}}{\varrho _{d}}(\jmath +1)}}{\varPhi +2\sqrt{\frac{\beta -\delta }{\eta _{s}}\gamma _{0}(\gamma _{0}-1)\frac{m_{d}}{\varrho _{d}}(\jmath +1)}} \right) . \end{aligned}$$
(28)

where \(t=p+m_{d}-1\), \(v=q-p+1\), \(\mu =t+m_{e}+1\), \(\varPhi =\frac{\beta -\delta }{\eta _{s}}(\gamma _{0}-1)+\frac{m_{d}}{\varrho _{d}}(\jmath +1)\gamma _{0}+\frac{m_{e}}{\varrho _{e}}\), and \(_{2}F_{1}(\cdot ,\cdot ;\cdot ;\cdot )\) is the hypergeometric function of second kind [25, eq. 9.111].

3.2 Asymptotic analysis

To shed more light onto the considered HSTRN secrecy performance, we analyze the asymptotic behaviour of the SOP expression in the high SNR regime. For this, Z can be simplified as \(Z\simeq \min (\gamma _{0} \gamma _{sr} ,(\gamma _{0}-1)\gamma _{rd})\) and the CDF \(F_{Z}(x)\) can be approximated by neglecting the higher order term as

$$F_{Z}(x)\simeq F_{\gamma _{sr}}\left( (\gamma _{0}-1)x\right) +F_{\gamma _{rd}}(\gamma _{0} x).$$
(29)

To proceed, we require asymptotic expressions for \(F_{\gamma _{sr}}(x)\) and \(F_{\gamma _{rd}}(x)\). At high SNR regime, we assume \(\eta _{s} \rightarrow \infty\) and apply the Maclaurin series expansion of the exponential function in (15) to approximate the PDF \(f_{\gamma _{sr}}(x)\) as

$$f_{\gamma _{sr}}(x)\simeq \frac{\alpha _{s}}{\eta _{s}},$$
(30)

and hence, by integrating (30), the asymptotic behaviour of \(F_{\gamma _{sr}}(x)\) can be given as

$$F_{\gamma _{sr}}(x)\simeq \frac{\alpha _{s}}{\eta _{s}} x.$$
(31)

Likewise, one can derive

$$F_{\gamma _{rd}}(x)\simeq \frac{x^{m_{d}N}}{[\varGamma (m_{d}+1)]^{N}}\left( \frac{m_{d}}{\varrho _{d}}\right) ^{m_{d}N}.$$
(32)

Now, invoking (31) and (32) into (29), and substituting the obtained result into (24) along with (19), and then solving the involved integral using [25, eq. 3.351.3], we can obtain the asymptotic SOP expression as

$$\begin{aligned} \mathcal {P}_{\text {sec}}^{\infty }&\simeq \frac{\alpha (\gamma _{0}-1)\varrho _{e}}{\eta _{s}}+\frac{(m_{d}N+m_{e}-1)!}{\left[ \varGamma (m_{d}+1)\right] ^{N}\varGamma (m_{e})} \left( \frac{m_{d}}{\varrho _{d}}\right) ^{m_{d}N} \\&\quad \times \gamma _{0}^{m_{d}N}\left( \frac{m_{e}}{\varrho _{e}}\right) ^{-m_{d}N}. \end{aligned}$$
(33)

which clearly reflects the achievable diversity order of \(\min (1,m_{d}N)\).

Remarks: Our asymptotic analysis of SOP reveals that the considered HSTRN attains a diversity order of \(\min (1,m_{d}N)\). Importantly, the diversity order is mainly bottlenecked by the satellite link, whereby it remains unaffected by the fading severity parameter of satellite link.

3.3 Probability of non-zero secrecy capacity

In this subsection, we calculate the probability for existence of non-zero secrecy capacity. The event of non-zero secrecy occurs when the main link is better than the eavesdropper link, which is given by

$$\mathcal {P}(C_{S}>0)=\text {Pr}\left[ \gamma _{D}>\gamma _{E}\right] .$$
(34)

After invoking (8) and (10) into (34) and performing simplification, (34) can be presented as

$$\begin{aligned} \mathcal {P}(C_{S}>0)&=\text {Pr}\left[ \gamma _{rd}>\gamma _{re}\right] , \\&=\int _{0}^{\infty }F_{\gamma _{re}}(x)f_{\gamma _{rd}}(x)dx. \end{aligned}$$
(35)

After substituting (20) and (27) into (35), the probability for existence of non-zero secrecy capacity can be computed and given as

$$\begin{aligned} \mathcal {P}(C_{S}>0)&=1- N\sum _{\jmath =0}^{N-1}\left( {\begin{array}{c}N-1\\ \jmath \end{array}}\right) \sum _{l=0}^{\jmath (m_{d}-1)}\sum _{n=0}^{m_{e}-1} \\&\quad \times \left( \frac{m_{e}}{\varrho _{e}}\right) ^{n}\frac{\omega _{l}^{\jmath }(-1)^{\jmath }\varGamma (n+m_{d}+l)}{\varGamma (m_{d})n!}\left( \frac{m_{d}}{\varrho _{d}}\right) ^{m_{d}+l}\\&\quad \times \left( \frac{m_{d}}{\varrho _{d}}(\jmath +1)+\frac{m_{e}}{\varrho _{e}}\right) ^{-(n+m_{d}+l)}. \end{aligned}$$
(36)

In deriving (36), we have used [25, eq. 3.351.3].

4 Numerical and simulation results

In this section, we present the numerical and simulation results to confirm the validity of the proposed theoretical studies and examine the impact of various system/channel parameters on the secrecy performance of the considered system. In particular, we examine the SOP and existence of non-zero secrecy capacity performance measures under various system/channel parameters. For this, we set \(\eta _{s}=\eta _{r}\) as transmit SNR. The Shadowing-Rician fading parameters for \(S \rightarrow R\) link are adopted as (\(m_{s},b,\varOmega _{s}=1,0.063,0.0007\)) under heavy shadowing and (\(m_{s},b,\varOmega _{s}=5,0.251,0.279\)) under average shadowing scenarios [21]. For validation of theoretical analysis, we carried out Monte-Carlo simulations.

Figure 2 depicts the SOP performance of the considered HSTRN versus \(\eta _{s}\) for various number of terrestrial users under average and heavy shadowing scenarios of Shadowed-Rician fading channel. By fixing \(\mathcal {R}_{S}=0.5\), \(m_{d}=1\), \(m_{e}=1\), and \(\varrho _{e}=2\) dB, SOP curves are drawn using (28). In addition, we also drawn the asymptotic SOP curves using (33) (for the same configuration), which agree very well with the exact ones in the high SNR region. We can see from this figure that secrecy performance of the system improves with an increase in the number of terrestrial users. However, owing to the bottleneck effect of the satellite link, this performance improvement becomes limited when N increases to a certain extent, as reflected by comparing the curves for \(N=2\) and \(N=10\). It is important to note that the system attains the diversity order of \(\min (1, m_{d} N)\) i.e., unity, which can be seen by the slope of the curves. Moreover, it can be realized that the system performs better under average Shadowed-Rician fading as compared to heavy Shadowed-Rician fading scenario.

Fig. 2
figure 2

SOP versus \(\eta _{s}\) for different number of terrestrial users

Full size image
Fig. 3
figure 3

SOP versus \(\eta _{s}\) with different \(\mathcal {R}_{S}\)

Full size image
Fig. 4
figure 4

SOP versus \(\eta _{s}\) with different \(\varrho _{e}\)

Full size image
Fig. 5
figure 5

Probability of non-zero secrecy capacity versus \(\eta _{s}\) for different N

Full size image

In Fig. 3, we illustrate the SOP performance versus \(\eta _{s}\) with different values of secrecy rate \(\mathcal {R}_{S}\) by assuming \(m_{d}=1\), \(m_{e}=2\), \(\varrho _{e}=2\) dB, and \(N=1\). The curves are plotted under average and heavy shadowed scenarios of \(S \rightarrow R\) link. As can be expected, the SOP of the considered HSTRN degrades with an increase in the secrecy rate \(\mathcal {R}_{S}\). Importantly, this increase in the \(\mathcal {R}_{S}\) does not affect the achievable diversity order of the system.

Figure 4 illustrates the SOP of the system for different values of \(\varrho _{e}\). As shown in the figure, curves are drawn for two different values of \(\varrho _{e}\) (i.e., 2 and 8 dB) under average and heavy shadowing scenarios of Shadowed-Rician fading channels by keeping \(N=2\), \(m_{d}=2\), \(m_{e}=1\), and \(\mathcal {R}_S=0.5\). One can clearly observe that the SOP of the considered HSTRN increases as the \(\varrho _{e}\) increases which indicates the detrimental impact of a more powerful eavesdropper.

Figure 5 depicts the probability of non-zero secrecy capacity versus \(\eta _{s}\) of the considered HSTRN for different number of terrestrial users, where the \(S \rightarrow R\) link is subjected to heavy shadowing scenario. For this, we have fixed \(m_{d}=1\), \(m_{e}=3\), \(\varrho _{e}=2\) dB, and \(\mathcal {R}_S=0.5\). The curves for probability of non-zero secrecy capacity are plotted using (36). As shown in the figure, with an increase of the number of terrestrial users, the achievable non-zero secrecy capacity increases significantly, which enlightens the advantage of deploying multiple terrestrial users.

5 Conclusion

In this paper, we have investigated the secrecy performance of a downlink multi-user HSTRN using AF relaying and opportunistic user scheduling. By following Shadowed-Rician fading for satellite link and Nakagami-m fading for terrestrial links, we derived accurate and asymptotic SOP expressions for the considered system. We obtained the system achievable diversity order and revealed that it remains unaffected by the fading severity parameter of satellite link. Furthermore, we derived the expression for probability of non-zero secrecy capacity. We highlighted the impact of various key system/channel parameters on the secrecy performance of the considered system. Our results revealed that the increase of the number of terrestrial users plays an important role in improving the secrecy performance of the considered HSTRN. Moreover, deployment of multiple antennas at satellite could be a crucial study for future investigation.