Keywords

1 Introduction

Radio access networks (RAN) grant permission to the user to access particular resources of the radio spectrum for the purpose of data transmission [1]. With the evolution of communication networks from 1G to 5G, the performing capability of the network has also elevated in terms of connectivity, latency and user data rates. Numerous Internet of Things (IoT) applications have come into existence like smart homes, automated cars, virtual and augmented reality, etc. These services have demanded the requirements of high reliability, low latency, huge connectivity and high data speed [2,3,4]. Energy limitations are the most significant problem of IoT networks; however, energy harvesting techniques have also been proposed that have contributed to solving this obstacle [20, 21]. Key technologies such as millimeter wave (mmWave) communications, Multiple Input Multiple Output (MIMO), beamforming, and non-orthogonal Multiple Access (NOMA) technique were proposed by the International Telecommunication Union (ITU) to support the development of 5G and 6G communication networks. Integrating the NOMA technique with satellite communication networks is said to be a key development for 5G [5,6,7,8].

Comparing the performance metrics of NOMA and Orthogonal Multiple Access (OMA) technique, the NOMA has proved to be more efficient than the older technique. NOMA utilizes the same resource block to transmit the data of multiple users [9,10,11,12]. All user signals are superimposed, and these signals are differentiated by allocating different power level coefficients to the different users. The allocation of power levels is based on the channel gain of the user. Users with high channel gain will be allotted less power and low channel gain will be allotted with more power. At the receiver, these signals are separated by performing the successive interference cancellation (SIC) technique. The ability of NOMA to perform massive connectivity, acquire less latency and high reliability has made it a novel approach in many other technologies. Very little research has been done on integrating NOMA with terrestrial networks [13, 14]. In [13], the authors conducted a comprehensive study on Cloud RAN technology employed by NOMA networks. In [14], the authors have considered integrating NOMA assisted MIMO technology and NOMA assisted cooperative relay (CR) technology into the terrestrial network applications.

Research works in [15, 16] have mentioned that the problem of security in satellite terrestrial relay networks (STRN) can be approached using Physical Layer Security (PLS). The general concept of PLS is to provide access to the legitimate users while blocking the malicious users and their interception. In [17] and [18], the authors have investigated the secrecy problems in the cognitive SRTN system. In [22], the authors have proposed the cooperative multi-hop transmission protocol (CMT) in the underlay cognitive radio networks and analyze secrecy outage probability (SOP) with the existence of a secondary eavesdropper. Several studies were performed to understand and neutralize the secrecy issues in NOMA networks [19] and [23]. In [19], the authors have studied the application of PLS in NOMA and derived the full analysis of SOP. In [23], a similar system was studied, but in the presence of perfect SIC and imperfect SIC in both the power domain NOMA and code domain NOMA was studied. Asymptotic mathematical expressions were derived to analyze the performance of the system.

To the best of our knowledge, a few paper has considered secure performance of STRN, this motivates us to study secure STRN relying on multiple antennas.

2 System Model

Fig. 1.
figure 1

System model of secure STRN relying on cooperative NOMA.

Full size image

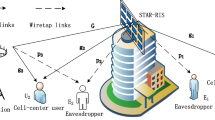
In this paper, we assume a NOMA cooperative satellite network. We assume a satellite (S), two destinations \(D_{i} ({\text{i}} \in \{ 1,2\} )\), and an eavesdropper (E) as shown in Fig. 1. Moreover, (S) is equipped with \(M\) antennas. In addition, we denote \({\mathbf{h}}_{i}\) as the \(M \times 1\) Shadowed-Rician channel vector form of S to \(D_{i}\) and \({\mathbf{h}}_{E}\) is the \(M \times 1\) Shadowed-Rician channel vector form of (S) to \(E\).

Moreover, (S) sends the signal \(s = \sqrt {(a_{1} )} x_{1} + \sqrt {(a_{2} )} x_{2}\), where \(a_{1}\), \(a_{2}\) are the power allocation coefficient and \(x_{1}\), \(x_{2}\) are the message of \(D_{1}\), \(D_{2}\). Therefore, the received signal from S to \(D_{i}\) is given by

$$y_{{D_{i} }} = {\mathbf{h}}_{i}^{\dag } {\mathbf{w}}_{i} \left( {\sqrt {P_{S} } \left( {\sqrt {a_{1} } x_{1} + \sqrt {a_{2} } x_{2} } \right)} \right) + \nu_{i}$$
(1)

where \(P_{S}\) denotes the power transmit at S, \(a_{1}\) and \(a_{2}\) are the power allocation coefficient, \((.)^{\dag }\) is the conjugate transpose, \(\nu_{i} \sim CN(0,\sigma_{i}^{2})\) denotes the additive white Gaussian noise (AWGN), \({\mathbf{w}}_{i}\) is the \(M \times 1\) transmit weight vector and \({\mathbf{w}}_{i} = \frac{{{\mathbf{h}}_{i} }}{{||{\mathbf{h}}_{i} ||_{F} }}\) as [28], in which \(\left\| \cdot \right\| _{F}\) is Frobenius norm.

Next, \(D_{2}\) is decoded with the signal \(x_{2}\) and the signal-to-interference-plus-noise-ratio (SINR) is given by

$$\gamma_{{D_{2} ,x_{2} }} = \frac{{P_{S} a_{2} \left\| {{\mathbf{h}}_{2} } \right\|_{F}^{2} }}{{P_{S} a_{1} \left\| {{\mathbf{h}}_{2} } \right\|_{F}^{2} + \sigma_{2}^{2} }} = \frac{{\eta_{2} a_{2} }}{{\eta_{2} a_{1} + 1}}$$
(2)

where \(\eta_{S} = \frac{{P_{S} }}{{\sigma_{i}^{2} }}\) is the transmitted signal-to-noise ratio (SNR), \(\eta_{i} = \eta_{S} \left\| {{\mathbf{h}}_{i} } \right\|_{F}^{2}\). Then, \(D_{1}\) is decoded with the signal \(x_{1}\) and the SINR is given by.

$$\gamma_{{D_{1} ,x_{1} }} = \frac{{P_{S} a_{2} \left\| {{\mathbf{h}}_{1} } \right\|_{F}^{2} }}{{P_{S} a_{1} \left\| {{\mathbf{h}}_{1} } \right\|_{F}^{2} + \sigma_{1}^{2} }} = \frac{{\eta_{1} a_{2} }}{{\eta_{1} a_{1} + 1}}$$
(3)

with NOMA protocol in [24], by applying SIC to decode its own signal \(x_{1}\) at \(D_{1}\), the SNR is given by

$$\gamma_{{D_{1} ,x_{1} }} = \eta_{1} a_{1}$$
(4)

Meanwhile, the received signal at \(E\) is given by

$$y_{E} = {\mathbf{h}}_{E} {\mathbf{w}}_{E}^{H} \left( {\sqrt {P_{S} } \left( {\sqrt {a_{1} } x_{1} + \sqrt {a_{2} } x_{2} } \right)} \right) + \nu_{E}$$
(5)

where \(\nu_{E} \sim(CN,\sigma_{E}^{2} )\) Then the SINR of E to detect the signal \(x_{2}\) of \(D_{2}\) is given by [25]

$$\gamma_{{E,x_{2} }} = \frac{{P_{S} a_{2} \left\| {{\mathbf{h}}_{E} } \right\|_{F}^{2} }}{{P_{S} a_{1} \left\| {{\mathbf{h}}_{E} } \right\|_{F}^{2} + \sigma_{E}^{2} }} = \frac{{\eta_{E} a_{2} }}{{\eta_{E} a_{1} + 1}}$$
(6)

where \(\eta_{S} = \frac{{P_{S} }}{{\sigma_{E}^{2} }},\eta_{E} = \eta_{S} \left\| {{\mathbf{h}}_{E} } \right\|_{F}^{2}\). Similar to \(D_{1}\), the SINR of \(E\) to detect the signal \(x_{1}\) of \(D_{1}\) is given by

$$\gamma_{{E,x_{1} }} = \eta_{E} a_{1}$$
(7)

In the next section, we intend to examine two performance metrics to highlight advances of Non-Orthogonal Multiple Access (NOMA) and multiple antennas scheme to the considered system.

3 Performance Analysis

In this section, we analyze the connection outage probability (COP) and secrecy outage probability (SOP) of \(D_{i}\). First, the probability density function (PDF) of the channel coefficient \(h_{z}^{j}\) with \(z \in \{ 1,2,E\}\) is given by [26]

$$f_{{\left| {h_{z}^{j} } \right|^{2} }} \left( \gamma \right) = \alpha_{z} e^{{ - \beta_{z} \gamma }}_{1} F_{1} \left( {m_{z} ;1;\delta_{z} \gamma } \right),\begin{array}{*{20}c} {} & {\gamma > 0,} \\ \end{array}$$
(8)

where \(\alpha_{z} = \frac{1}{{2b_{z} }}\left( {\frac{{2b_{z} m_{z} }}{{2b_{z} m_{z} + \Omega_{z} }}} \right)^{{m_{z} }}\), \(\delta_{z} = \frac{{\Omega_{z} }}{{2b_{z} \left( {2b_{z} m_{z} + \Omega_{z} } \right)}}\), \(m_{z}\) is the fading severity parameter, \(\Omega_{z}\) and \(2b_{z}\) are the average power of LOS and multipath components, respectively, and \(_{1} F_{1} (.,.,.)\) denotes the confluent hypergeometric function of the first kind [29, 9 .201.1]. Based on [27], we can simplify (8) as

$$f_{{\left| {h_{z}^{j} } \right|^{2} }} \left( \gamma \right) = \alpha_{z} e^{{ - \left( {\beta_{z} - \delta_{z} } \right)\gamma }} \sum\limits_{b = 0}^{{m_{z} - 1}} {\zeta_{z} \left( b \right)} \gamma^{b} ,$$
(9)

where \(\zeta_{z} \left( b \right) = \left( { - 1} \right)^{b} \left( {1 - m_{z} } \right)_{b} \delta^{b} /\left( {b!} \right)^{2}\) and \((.)_{b}\) is the Pochhammer symbol [29]. Thus, with i.i.d. Shadowed-Rician fading, the PDF of \(\eta_{z}\) can be expressed by

$$f_{{\eta_{z} }} \left( \gamma \right) = \sum\limits_{{b_{1} = 0}}^{{m_{z} - 1}} { \ldots \sum\limits_{{b_{N} = 0}}^{{m_{z} - 1}} {\frac{\Xi \left( z \right)}{{\left( {\eta_{S} } \right)^{\Lambda } }}\gamma^{\Lambda - 1} e^{{ - \frac{{\left( {\beta_{z} - \delta_{z} } \right)}}{{\eta_{S} }}\gamma }} ,} }$$
(10)

3.1 COP of \(D_{2}\)

The COP of \(D_{2}\) is given by [25]

$$P_{2}^{COP} = \Pr \left( {\gamma_{{D_{2} ,x_{2} }} < \varepsilon_{2} } \right)$$
(11)

where \(\varepsilon_{i} = 2^{{R_{i} }} - 1\) and \(R_{i}\) denotes the target rate.

Proposition 1:

The COP of \(D_{2}\) can be obtained as

$$P_{2}^{COP} = \sum\limits_{{b_{1} = 0}}^{{m_{2} - 1}} { \ldots \sum\limits_{{b_{N} = 0}}^{{m_{2} - 1}} {\frac{\Xi \left( 2 \right)}{{\left( {\beta_{2} - \delta_{2} } \right)^{\Lambda } }}} } \gamma \left( {\Lambda ,\frac{{\left( {\beta_{2} - \delta_{2} } \right)\varepsilon_{2} }}{{\eta_{S} \left( {a_{2} - \varepsilon_{2} a_{1} } \right)}}} \right)$$
(12)

Proof:

With help (2), COP of \(D_{2}\) can be rewritten as

$$P_{2}^{COP} = \Pr \left( {\eta_{2} < \frac{{\varepsilon_{2} }}{{\left( {a_{2} - \varepsilon_{2} a_{1} } \right)}}} \right) = \int\limits_{0}^{{\frac{{\varepsilon_{2} }}{{\left( {a_{2} - \varepsilon_{2} a_{1} } \right)}}}} {f_{{\eta_{2} }} \left( x \right)} dx \,$$
(13)

Substituting the PDF in (10) into (13), we obtain the following.

$$P_{2}^{COP} = \sum\limits_{{b_{1} = 0}}^{{m_{2} - 1}} { \ldots \sum\limits_{{b_{N} = 0}}^{{m_{2} - 1}} {\frac{\Xi \left( 2 \right)}{{\left( {\eta_{S} } \right)^{\Lambda } }}} } \int\limits_{0}^{{\frac{{\varepsilon_{2} }}{{a_{2} - \varepsilon_{2} a_{1} }}}} {x^{\Lambda - 1} e^{{ - \frac{{\left( {\beta_{2} - \delta_{2} } \right)}}{{\eta_{S} }}x}} } dx$$
(14)

Based on [29, 3.351.1], the closed-form of \(D_{2}\) is given by

$$P_{2}^{COP} = \sum\limits_{{b_{1} = 0}}^{{m_{2} - 1}} { \ldots \sum\limits_{{b_{N} = 0}}^{{m_{2} - 1}} {\frac{\Xi \left( 2 \right)}{{\left( {\beta_{2} - \delta_{2} } \right)^{\Lambda } }}} } \gamma \left( {\Lambda ,\frac{{\left( {\beta_{2} - \delta_{2} } \right)\varepsilon_{2} }}{{\eta_{S} \left( {a_{2} - \varepsilon_{2} a_{1} } \right)}}} \right)$$
(15)

where \(\gamma (a,b)\) is the upper incomplete gamma functions.

The proof is completed.

3.2 COP of \(D_{1}\)

The COP of \(D_{1}\) is written as [25]

$$P_{1}^{COP} = \Pr \left( {\gamma_{{D_{1} ,x_{1} }} < \varepsilon_{1} } \right)$$
(16)

Substituting (4) into (16), (16) can be rewritten as

$$P_{1}^{COP} = \Pr \left( {\eta_{1} < \frac{{\varepsilon_{1} }}{{a_{1} }}} \right) = \int\limits_{0}^{{\frac{{\varepsilon_{1} }}{{a_{1} }}}} {f_{{\eta_{1} }} \left( x \right)} dx$$
(17)

Similar in Proposition 1, the closed-form of COP for \(D_{1}\) is given by

$$P_{1}^{COP} = \sum\limits_{{b_{1} = 0}}^{{m_{1} - 1}} { \ldots \sum\limits_{{b_{N} = 0}}^{{m_{1} - 1}} {\frac{\Xi \left( 1 \right)}{{\left( {\beta_{1} - \delta_{1} } \right)^{\Lambda } }}} } \gamma \left( {\Lambda ,\frac{{\left( {\beta_{1} - \delta_{1} } \right)\varepsilon_{1} }}{{\eta_{S} a_{1} }}} \right)$$
(18)

3.3 SOP of \(D_{2}\)

As the main result is reported in [25], the SOP of \(D_{2}\) is expressed as

$$P_{2}^{SOP} = \Pr \left( {\gamma_{{E \to x_{2} }} > \varepsilon_{2}^{S} } \right)$$
(19)

where \(\varepsilon_{i}^{S} = 2^{{R_{i} - R_{i}^{S} }} - 1\) is the secrecy rate of \(D_{i}\).

Proposition 2:

The exact closed-form SOP of \(D_{2}\) is given by.

$$P_{2}^{SOP} = \sum\limits_{{b_{1} = 0}}^{{m_{E} - 1}} { \ldots \sum\limits_{{b_{N} = 0}}^{{m_{E} - 1}} {\frac{\Xi \left( 2 \right)}{{\left( {\beta_{E} - \delta_{E} } \right)^{\Lambda } }}} } \gamma \left( {\Lambda ,\frac{{\left( {\beta_{E} - \delta_{E} } \right)\varepsilon_{2}^{S} }}{{\eta_{S} \left( {a_{2} - \varepsilon_{2}^{S} a_{1} } \right)}}} \right)$$
(20)

Proof:

By (6), the SOP of \(D_{2}\) can be rewritten as.

$$P_{2}^{SOP} = \Pr \left( {\eta_{E} > \frac{{\varepsilon_{2}^{S} }}{{a_{2} - \varepsilon_{2}^{S} a_{1} }}} \right) = \int\limits_{{\frac{{\varepsilon_{2}^{S} }}{{a_{2} - \varepsilon_{2}^{S} a_{1} }}}}^{\infty } {f_{{\eta_{E} }} \left( x \right)} dx$$
(21)

With the help of the CDF of \(\eta_{E}\) (10), we can write (21) as

$$P_{2}^{SOP} = \sum\limits_{{b_{1} = 0}}^{{m_{E} - 1}} { \ldots \sum\limits_{{b_{N} = 0}}^{{m_{E} - 1}} {\frac{\Xi \left( E \right)}{{\left( {\eta_{S} } \right)^{\Lambda } }}} } \int\limits_{0}^{{\frac{{\varepsilon_{2}^{S} }}{{a_{2} - \varepsilon_{2}^{S} a_{1} }}}} {x^{\Lambda - 1} e^{{ - \frac{{\left( {\beta_{E} - \delta_{E} } \right)}}{{\eta_{S} }}x}} } dx$$
(22)

Using [29, 3.351.2], the closed-form SOP of \(D_{2}\) is given by

$$P_{2}^{SOP} = \sum\limits_{{b_{1} = 0}}^{{m_{E} - 1}} { \ldots \sum\limits_{{b_{N} = 0}}^{{m_{E} - 1}} {\frac{\Xi \left( 2 \right)}{{\left( {\beta_{E} - \delta_{E} } \right)^{\Lambda } }}} } \Gamma \left( {\Lambda ,\frac{{\left( {\beta_{E} - \delta_{E} } \right)\varepsilon_{2}^{S} }}{{\eta_{S} \left( {a_{2} - \varepsilon_{2}^{S} a_{1} } \right)}}} \right)$$
(23)

where \(\Gamma (a,b)\) denotes the lower incomplete gamma function.

The proof is completed.

3.4 SOP of \(D_{1}\)

As [25], the SOP of \(D_{1}\) can be expressed as.

$$P_{1}^{SOP} = \Pr \left( {\gamma_{{E \to x_{1} }} < 2^{{R_{1} - R_{1}^{S} }} - 1} \right)$$
(24)

In similar to Proposition 2, the exact closed-form of \(D_{1}\) is formulated by

$$\begin{aligned} P_{1}^{SOP} = & \Pr \left( {\eta_{E} > \frac{{\varepsilon_{1}^{S} }}{{a_{1} }}} \right) = \int\limits_{{\frac{{\varepsilon_{1}^{S} }}{{a_{1} }}}}^{\infty } {f_{{\eta_{E} }} \left( x \right)} dx \\ & = \sum\limits_{{b_{1} = 0}}^{{m_{E} - 1}} { \ldots \sum\limits_{{b_{N} = 0}}^{{m_{E} - 1}} {\frac{\Xi \left( E \right)}{{\left( {\beta_{E} - \delta_{E} } \right)^{\Lambda } }}} } \Gamma \left( {\Lambda ,\frac{{\varepsilon_{1}^{S} }}{{\eta_{S} a_{1} }}} \right) \\ \end{aligned}$$
(25)

4 Numerical Result And Discussions

In this section, we set \(a_{2} = 0.8\), \(a_{1} = 0.2\), \(R_{2} = 0.5\) \(R_{1} = 1\), \(R_{1}^{S} = 0.5\) and \(R_{2}^{S} = 0.1\). Moreover, we consider the Shadowed-Rician fading parameters for the satellite links is the heavy shadowing with \(m_{1} = m_{2} = m_{E} = 1\), \(b_{1} = b_{2} = b_{E} = 0.063\) and \(\Omega_{1} = \Omega_{2} = \Omega_{E} = 0.0007\).

In Fig. 2, the simulations were performed to COP versus transmit SNR to analyze the connection outage performance of the system by varying the number of antennas at the satellite. As we can observe, the performance of the system has comparatively increased when the number of antennas were increased from 1 to 2.

Fig. 2.
figure 2

The connection outage performance vs \(\eta_{S} (dB)\) varying the antenna of S \(M\).

Full size image

In Fig. 3, the simulations were performed to SOP versus transmit SNR to analyze the secrecy performance of the system. We can observe that, with the rise in the number of antennas, the SOP of the system shows better performance. We can also observe that increasing a single antenna shows a huge performance gap between the lines. Therefore, we can understand that the number of antennas plays a major role in the efficiency of the system.

Fig. 3.
figure 3

The secrecy outage performance vs \(\eta_{S} (dB)\) varying the antenna of S \(M\).

Full size image

5 Conclusion

In this paper, we considered a NOMA network assisting a cooperative satellite with antennas equipped at the satellite, in the presence of two legitimate users and an eavesdropper. We aimed to investigate the connection performance and the secrecy performance of the system by varying main parameters such as the number of antennas. We have derived the closed-form expressions for COP and SOP and analysed the system behaviour by changing the number of antennas and keeping the remaining parameters constant for fair comparison. We understood that the increase in the number of antennas at the satellite will help the communication links for efficient data transmission.