Common solution to generalized mixed equilibrium problem and fixed point problems in Hilbert space

Abstract

In this paper, we deal with an extra-gradient iterative method for finding a common solution to a generalized mixed equilibrium problem and fixed point problems for a nonexpansive mapping and for a finite family of k-strict pseudo-contraction mappings in Hilbert space. We prove a strong convergence theorem for the extra-gradient iterative method under some mild conditions. Further, we give a numerical example to illustrate the main result.

1 Introduction

Let C be a nonempty, closed and convex subset of a real Hilbert space H. Let $G:C\times C\rightarrow {\mathbb {R}}$ and $\phi :C\times C\rightarrow {\mathbb {R}}$ be nonlinear bifunctions, where ${\mathbb {R}}$ is the set of all real numbers and let $A:C\rightarrow H$ be a nonlinear mapping. In 1994, Blum and Oettli [2] introduced and studied the following equilibrium problem (in short, EP): Find $x\in C$ such that

$$\begin{aligned} G(x,y) \ge 0, \quad \forall y\in C. \end{aligned}$$

(1.1)

The solution set of EP(1.1) is denoted by Sol(EP(1.1)). An important generalization of EP(1.1) is the mixed equilibrium problem (in short, MEP) introduced and studied by Moudafi and Thera [15] which is of finding $x\in C$ such that

$$\begin{aligned} G(x,y) + \langle Ax, y-x\rangle \ge 0, \quad \forall y\in C. \end{aligned}$$

(1.2)

For application of MEP(1.2), see Moudafi and Thera [15].

It is well known that the equilibrium problems have a great impact and influence in the development of several topics of science and engineering. It turned out that many well known problems could be fitted into the equilibrium problems. It has been shown that the theory of equilibrium problems provides a natural, novel and unified framework for several problems arising in nonlinear analysis, optimization, economics, finance, game theory and engineering. The equilibrium problem includes many mathematical problems as particular cases, for example, mathematical programming problem, variational inclusion problem, variational inequality problem, complementary problem, saddle point problem, Nash equilibrium problem in noncooperative games, minimax inequality problem, minimization problem and fixed point problem, see [2, 5, 14].

Now we consider the following generalized mixed equilibrium problem (in short, GMEP): Find $x\in C$ such that

$$\begin{aligned} G(x,y) + \langle Ax, y-x\rangle + \phi (y,x)-\phi (x,x)\ge 0, \quad \forall y\in C. \end{aligned}$$

(1.3)

The solution set of GMEP(1.3) is denoted by Sol(GMEP(1.3)).

If we set $G(x,y)=0, ~\forall x,y\in C$, GMEP(1.3) reduces to the following important class of variational inequalities which represents the boundary value problem arising in the formulation of Signorini problem: Find $x \in C$ such that

$$\begin{aligned} \langle Ax, y-x\rangle + \phi (y,x)-\phi (x,x)\ge 0, \quad \forall y\in C. \end{aligned}$$

(1.4)

Problem (1.4) was discussed in Duvaut and Lions [8] and Kikuchi and Oden [11]. For physical and mathematical formulation of the inequality (1.4), see for example Oden and Pires [19]. For related work, see also Baiocchi and Capelo [1].

If we set $G(x,y)=0 ~\mathrm{and}~\phi (x,y)=0, ~\forall x,y\in C$, GMEP(1.3) reduces to the classical variational inequality problem (in short, VIP): Find $x\in C$ such that

$$\begin{aligned} \langle Ax, y-x \rangle \ge 0,~~\forall y \in C, \end{aligned}$$

(1.5)

which was introduced and studied by Hartmann and Stampacchia [9]. The solution set of VIP(1.5) is denoted by Sol(VIP(1.5)).

Let S be a nonlinear mapping defined on C, the fixed point problem (in short, FPP) for the mapping S is to find $x\in C$ such that

$$\begin{aligned} x=Sx. \end{aligned}$$

(1.6)

F(S) denote the fixed point set of S and is given by $\{x\in C | x=Sx\}.$

In 1976, Korpelevich [12] introduced the following iterative algorithm which is known as extra-gradient iterative method for VIP(1.5):

$$\begin{aligned} \left. \begin{array}{lll} x_0\in C, \\ y_{n}=P_{C}(x_n-\lambda Ax_{n}),\\ x_{n+1}=P_{C}(x_n-\lambda Ay_{n}), \end{array}\right\} \end{aligned}$$

(1.7)

where $\lambda >0$ and $n\ge 0$, A is a monotone and Lipschitz continuous mapping and $P_C$ is the metric projection of H onto C.

In 2006, Nadezkhina and Takahashi [16] proved that the sequences $\{x_{n}\}$ and $\{y_{n}\}$ generated by the following modified version of extra-gradient iterative method (1.7):

$$\begin{aligned} \left. \begin{array}{lll} x_0\in C, \\ y_{n}=P_{C}(x_n-\lambda _n Ax_{n}),\\ x_{n+1}=\alpha _nx_n+(1-\alpha _n)SP_{C}(x_n-\lambda _n Ay_{n}), \end{array}\right\} \end{aligned}$$

(1.8)

where $\lambda _{n}, \alpha _{n}\in (0,1)$ for $n\ge 0$, converge weakly to a common solution to VIP(1.5) and FPP(1.6) for a nonexpansive mapping S.

In 2006, by combining a hybrid iterative method [18] with an extra-gradient iterative method (1.8), Nadezhkina and Takahashi [17] introduced the following hybrid extra-gradient iterative method for approximating a common solution of FPP(1.6) for a nonexpansive mapping S and VIP(1.5) for a monotone and Lipschitz continuous mapping A:

$$\begin{aligned} \left. \begin{array}{ll} x_0\in C, &{}\\ y_n =P_{C}(x_n-\lambda _n Ax_n), &{}\\ z_n=\beta _n x_n +(1-\beta _n)SP_{C}(x_n-\lambda _n Ay_n), &{}\\ C_n=\{z\in C:\Vert z_n-z\Vert ^2\le \Vert x_n-z\Vert ^2\}, &{}\\ Q_n =\{z\in C:\langle x_n-z,x-x_n\rangle \ge 0\}, &{}\\ x_{n+1}=P_{C_n\bigcap Q_n}x_{0},\\ \end{array} \right\} \end{aligned}$$

(1.9)

for $n\ge 0$, and proved a strong convergence theorem.

In 2013, Djafari-Rouhani et al. [6] initiated the study of the following system of unrelated mixed equilibrium problems (in short, SUMEP); more precisely, for each $i=1,2, \ldots ,N$, let $C_i$ be a nonempty, closed and convex subset of a real Hilbert space H with $\bigcap \nolimits _{i=1}^{N}C_i\ne \emptyset$; let $G_i:C_i\times C_i\rightarrow {\mathbb {R}}$ be a bifunction such that $G_i(x_i,x_i)=0,~~\forall x_i \in C_i$ and let $A_i:H\rightarrow H$ be a monotone and Lipschitz continuous mapping, then SUMEP is to find $x\in \bigcap \nolimits _{i=1}^{N}C_i$ such that

$$\begin{aligned} G_i(x,y_i)+\langle A_ix,y_i-x\rangle \ge 0,~~\forall y_i \in C_i,~~~i=1,2,\ldots ,N. \end{aligned}$$

(1.10)

We note that for each $i=1,2,\ldots .,N,$ the mixed equilibrium problem (MEP) is to find $x_i\in C_i$ such that

$$\begin{aligned} G_i(x_i,y_i)+\langle A_ix_i,y_i-x_i\rangle \ge 0,~~\forall y_i \in C_i,~~~i=1,2,\ldots ,N. \end{aligned}$$

(1.11)

We denote by $\mathrm{Sol(MEP}$(1.11)), the solution set of MEP(1.11) corresponding to the mappings $G_i,A_i$ and the set $C_i$. Then the solution set of SUMEP(1.10) is given by $\bigcap \nolimits _{i=1}^{N}\mathrm{Sol(MEP}$(1.11)). If $N=1$ then SUMEP(1.10) is the mixed equilibrium problem MEP(1.2). They proved a strong convergence theorem for the following new hybrid extra-gradient iterative method which can be seen as an important extension of iterative method (1.9) given by Nadezhkina and Takahashi [17], for solving SUMEP(1.10) under some mild conditions: The iterative sequences $\{x^{n}\}$, $\{y_{i}^n\}$ and $\{z_{i}^n\}$ be generated by the iterative schemes

$$\begin{aligned} \left\{ \begin{array}{ll} x^0\in H, &{}\\ y_{i}^{n} =T_{r_{i}^n}(x^n-r_{i}^n A_ix^n), &{}\\ z_{i}^{n} =\alpha _{i}^{n}x^n+(1-\alpha _{i}^{n})S_{i}T_{r_{i}^n}(x^n-r_{i}^n A_iy_{i}^{n}), &{}\\ C_{i}^{n}=\{z\in H:\Vert z_{i}^{n}-z\Vert ^2\le \Vert x^n-z\Vert ^2\}, &{}\\ C^n=\bigcap _{i=1}^N C_{i}^{n}, &{}\\ Q^{n} =\{z\in H:\langle x^n-z,x_{0}-x^n\rangle \ge 0\}, &{}\\ x^{n+1}=P_{C^n\bigcap Q^n}x_{0}, \end{array} \right. \end{aligned}$$

(1.12)

for $n\ge 0$ and for each $i=1,2,\ldots ,N$, where $\{r_{i}^{n}\},~\{\alpha _{i}^{n}\}$ are control sequences. For the further related work, see [10].

It is worth to mention that none of the strong convergence theorems established for the extra-gradient iterative methods presented so far, other than hybrid extra-gradient iterative method (1.12), for approximating a common solution to MEP (1.2), where A is monotone and Lipschitz continuous mapping, and fixed point problem for nonlinear mappings. Therefore, our main focus is to propose an extra-gradient iterative method which is not hybrid type, for solving MEP (1.2), where A is monotone and Lipschitz continuous mapping, and fixed point problems for nonlinear mappings and to establish a strong convergence theorem.

Recall that a nonself mapping $T:C\rightarrow H$ is called k-strict pseudo-contraction if there exists a constant $k\in [0,1)$ such that

$$\begin{aligned} \Vert Tx-Ty\Vert ^{2} \le \Vert x-y\Vert ^{2} + k\Vert (I-T)x - (I-T)y\Vert ^{2},~~\forall x,y\in C. \end{aligned}$$

(1.13)

Set $k=0$ in (1.13), T is said to be nonexpansive and if we set $k=1$ in (1.13), T is said to be pseudo-contractive. T is said to be strongly pseudo-contractive if there exists a constant $\lambda \in (0,1)$ such that $T-\lambda I$ is pseudo-contractive. Clearly, the class of k-strict pseudo-contractions falls into the one between classes of nonexpansive mappings and pseudo-contraction mappings. We note that the class of strongly pseudo-contractive mappings is independent of the class of k-strict pseudo-contraction mappings (see, e.g. [3, 4]). In a real Hilbert space H, (1.13) is equivalent to

$$\begin{aligned} \langle Tx-Ty, x-y\rangle \le \Vert x-y\Vert ^2-\frac{1-k}{2}\Vert (x-Tx)-(y-Ty)\Vert ^2,~~\forall x,y\in C.\nonumber \\ \end{aligned}$$

(1.14)

T is pseudo-contractive if and only if

$$\begin{aligned} \langle Tx-Ty, x-y\rangle \le \Vert x-y\Vert ^2,~~\forall x,y \in C. \end{aligned}$$

(1.15)

T is strongly pseudo-contractive if and only if there exists a positive constant $\lambda \in (0,1)$ such that

$$\begin{aligned} \langle Tx-Ty, x-y\rangle \le (1-\lambda )\Vert x-y\Vert ^2,~~\forall x,y \in C. \end{aligned}$$

(1.16)

Further, we note that the iterative methods for strict pseudo-contractions are far less developed than those for nonexpansive mappings though Browder and Petryshyn [4] initiated their work in 1967; the reason is probably that the second term appearing in the right-hand side of (1.13) impedes the convergence analysis for iterative algorithms used to find a fixed point of the strict pseudo-contraction T. However, on the other hand, strict pseudo-contractions have more powerful applications than nonexpansive mappings do in solving inverse problems (see, Scherzer [21]). Therefore it is interesting to develop the iterative methods for finding a common solution to GMEP(1.3) and fixed point problems for a nonexpansive mapping and for a finite family of k-strict pseudo-contraction mappings. For further work, see for example [13, 22, 25] and the references therein.

Motivated by the recent work [6, 10, 24], in this paper, we propose an extra-gradient iterative method for approximating a common solution to GMEP(1.3) and fixed point problems for a nonexpansive mapping and for a finite family of k-strict pseudo-contraction mappings in Hilbert space. Further, we prove that the sequences generated by the proposed iterative method converge strongly to the common solution to GMEP(1.3) and fixed point problems for a nonexpansive mapping and for a finite family of k-strict pseudo-contraction mappings. Further, we give a theoretical numerical example to illustrate the strong convergence theorem.

2 Preliminaries

We recall some concepts and results which are required for the presentation of the work. Let symbols $\rightarrow$ and $\rightharpoonup$ denote strong and weak convergence, respectively. It is well known that every Hilbert space satisfies the Opial condition, i.e., for any sequence $\{x_n\}$ with $x_{n}\rightharpoonup x$, the inequality

$$\begin{aligned} \liminf \limits _{n\rightarrow \infty } \Vert x_n-x \Vert < \liminf \limits _{n\rightarrow \infty } \Vert x_n-y \Vert , \end{aligned}$$

(2.1)

holds for every $y \in H$ with $y \not = x.$

For every point $x \in H$, there exists a unique nearest point in C denoted by $P_ {C} x$ such that

$$\begin{aligned} \Vert x-P_{C}x\Vert \le \Vert x-y\Vert , ~~ \forall y \in C. \end{aligned}$$

The mapping $P_{C}$ is called the metric projection of H onto C. It is well known that $P_{C}$ is nonexpansive and satisfies

$$\begin{aligned} \langle x-y ,P_{C}x-P_{C}y \rangle \ge \Vert P_{C}x-P_{C}y\Vert ^2, ~~\forall x \in H. \end{aligned}$$

(2.2)

Moreover, $P_{C}x$ is characterized by the fact $P_{C}x\in C$ and

$$\begin{aligned} \langle x-P_{C}x,y-P_{C}x \rangle \le 0,~\forall y\in C \end{aligned}$$

(2.3)

which implies

$$\begin{aligned} \Vert x-y\Vert ^2\ge \Vert x-P_{C}x\Vert ^2 +\Vert y-P_{C}x\Vert ^2,~~\forall x\in H,~y\in C. \end{aligned}$$

(2.4)

Definition 2.1

A mapping $A:H\rightarrow H$ is said to be:

• (i) Monotone if

  $$\begin{aligned} \langle Ax-Ay,x-y\rangle \ge 0, ~~~\forall x,y\in H; \end{aligned}$$

• (ii) $\lambda$-Lipschitz continuous if there exists a constant $\lambda >0$ such that

  $$\begin{aligned} \Vert Ax-Ay\Vert \le \lambda \Vert x-y\Vert , ~~~\forall x,y\in H. \end{aligned}$$

Lemma 2.1

[25] If $T:C\rightarrow H$ is a k strict pseudo-contraction, then T is Lipschitz continuous with Lipschitz constant $\frac{3-k}{1-k}.$

Lemma 2.2

[25] If $T:C\rightarrow H$ is a k-strict pseudo-contraction, then the fixed point set F(T) is closed convex so that the projection $P_{F(T)}$ is well defined.

Lemma 2.3

[25] If $T:C\rightarrow H$ is a k-strict pseudo-contraction with $F(T)\ne \emptyset .$ Then $F(P_{C}T)= F(T).$

Lemma 2.4

[25] If $T:C\rightarrow H$ is a k-strict pseudo-contraction and let for $\lambda \in [k,1)$, define a mapping $S:C\rightarrow H$ by $Sx = \lambda x+ (1-\lambda )Tx$ for all $x\in C.$ Then S is nonexpansive mapping such that $F(S)=F(T).$

Lemma 2.5

[23] Given an integer $N\ge 1$,  for each $i=1,2,\ldots ,N$, let $T_{i}:C\rightarrow H$ be a $k_{i}$-strictly pseudo-contraction for some $0 \le k_{i}< 1$ and $\max \nolimits _{1\le i \le N}k_{i}<1$ such that $\bigcap \nolimits _{i=1}^{N}F(T_{i})\ne \emptyset$. Assume that $\{\eta _{i}\}_{i=1}^{N}$ is a positive sequence such that $\sum \nolimits _{i=1}^{N}\eta _{i}^{n}=1$. Then $\sum \nolimits _{i=1}^{N}\eta _{i}T_{i}:C\rightarrow H$ is a k-strictly pseudo-contraction with coefficient $k=\max \nolimits _{1\le i \le N}k_{i}$ and $F(\sum \nolimits _{i=1}^{N}\eta _{i}T_{i})=\bigcap \nolimits _{i=1}^{N}F(T_{i}).$

Lemma 2.6

[20] For any $x,y,z\in H$ and $\alpha ,\beta ,\gamma \in [0,1]$ with $\alpha +\beta +\gamma =1$, we have

$$\begin{aligned} \Vert \alpha x+\beta y+\gamma z\Vert ^{2}= \alpha \Vert x\Vert ^{2}+\beta \Vert y\Vert ^{2}+\gamma \Vert z\Vert ^{2}-\alpha \beta \Vert x-y\Vert ^{2}-\alpha \gamma \Vert x-z\Vert ^{2}-\beta \gamma \Vert y-z\Vert ^{2}. \end{aligned}$$

Lemma 2.7

[24] Let $\{s_{n}\}$ be a sequence of non-negative real numbers satisfying

$$\begin{aligned} s_{n+1}\le (1-a_{n})s_{n} + a_{n}b_{n} + c_{n},~~ n\ge 0, \end{aligned}$$

where the sequences $\{a_n\}, \{b_n\}, \{c_n\}$ satisfy the conditions: (i) $\{a_n\}\subset [0,1]$ with $\sum \nolimits _{n=0}^{\infty }a_{n}=\infty ,$ (ii) $c_{n}\ge 0$ for all $n\ge 0$ with $\sum \nolimits _{n=0}^{\infty }c_{n} < \infty ,$ and (iii) $\limsup \nolimits _{n\rightarrow \infty }b_{n}\le 0$. Then $\lim \nolimits _{n\rightarrow \infty }s_{n}=0.$

Lemma 2.8

[24] Let $\{s_{k}\}$ be a sequence of real numbers that does not decrease at infinity in the sense that there exists a subsequence $\{s_{k_{j}}\}$ of $\{s_{k}\}$ such that $s_{k_{j}}< s_{k_{j+1}}$ for all $j \ge 0$. Define an integer sequence $\{m_{k}\}_{k\ge k_{0}}$ as

$$\begin{aligned} m_{k}= \max \{k_{0}\le l\le k: s_{l}< s_{l+1}\}, \end{aligned}$$

then $m_{k}\rightarrow \infty$ as $k\rightarrow \infty$ and for all $k\ge k_{0}$ we have $\max \{s_{m_{k}},s_{k}\}\le s_{m_{k+1}}.$

Assumption 2.1

The bifunctions $G: C\times C\longrightarrow {\mathbb {R}}$ and $\phi :C\times C\rightarrow {\mathbb {R}}$ satisfy the following assumptions:

• (i) $G(x,x)=0,~~\forall x \in C;$

• (ii) G is monotone, i.e., $G(x,y)+G(y,x)\le 0,~~\forall x,y \in C;$

• (iii) For each $y \in C$, $x\rightarrow G(x,y)$ is weakly upper-semicontinuous;

• (iv) For each $x \in C$, $y\rightarrow G(x,y)$ is convex and lower semicontinuous.

• (v) $\phi (.,.)$ is weakly continuous and $\phi (.,y)$ is convex;

• (vi) $\phi$ is skew symmetric, i.e.,

  $\phi (x,x)-\phi (x,y)+\phi (y,y)-\phi (y,x)\ge 0,~~\forall x,y\in C;$

• (vii) for each $z\in H$ and for each $x\in C$, there exists a bounded subset $D_{x}\subseteq C$ and $z_{x}\in C$ such that for any $y\in C\setminus D_{x}$,

  $G(y, z_{x})+ \phi (z_{x}, y)- \phi (y,y) + \frac{1}{r}\langle z_{x}-y, y-z\rangle < 0.$

Assumption 2.2

The bifunction $G: C\times C\longrightarrow {\mathbb {R}}$ is 2-monotone, i.e.,

$$\begin{aligned} G(x,y)+ G(y,z)+ G(z,x)\le 0,~~\forall x,y,z\in C. \end{aligned}$$

(2.5)

By taking $y=z$, it is clear that 2-monotone bifunction is a monotone bifunction. For example, if $G(x,y)= x(y-x)$, then G is a 2-monotone bifunction.

Now, we give the concept of 2-skew-symmetric bifunction.

Definition 2.2

The bifunction $\phi :C\times C\rightarrow {\mathbb {R}}$ is said to be 2-skew-symmetric if

$$\begin{aligned} \phi (x,x)-\phi (x,y)+\phi (y,y)-\phi (y,z)+\phi (z,z)-\phi (z,x)\ge 0,~~\forall x,y,z\in C. \end{aligned}$$

(2.6)

We remark that if set $z=x$ or $x=y$ or $y=z$ in (2.6) then 2-skew-symmetric bifunction becomes skew-symmetric bifunction.

Theorem 2.1

[7] Let C be a nonempty closed convex subset of a real Hilbert space H. Let the bifunctions $G: C\times C\longrightarrow {\mathbb {R}}$ and $\phi :C\times C\rightarrow {\mathbb {R}}$ satisfying Assumption 2.1. For $r>0$ and $z\in H$, define a mapping $T_{r}: H\rightarrow C$ as follows:

$$\begin{aligned} T_{r}(z)= \{x\in C: G(x,y)+ \phi (y,x)-\phi (x,x) + \frac{1}{r}\langle y-x,x-z\rangle \ge 0,~ \forall y\in C\}, \end{aligned}$$

for all $z\in H$. Then the following conclusions hold:

• (a) $T_{r}(z)$ is nonempty for each $z\in H;$

• (b) $T_{r}$ is single valued;

• (c) $T_{r}$ is firmly nonexpansive mapping, i.e., for all $z_{1},z_{2}\in H,$

  $$\begin{aligned} \Vert T_{r}z_{1}- T_{r}z_{2}\Vert ^{2}\le \langle T_{r}z_{1}- T_{r}z_{2},z_{1}-z_{2}\rangle ; \end{aligned}$$

• (d) $G( T_{r})=\mathrm{Sol(GMEP}$(1.3));

• (e) $\mathrm{Sol(GMEP}$(1.3)) is closed and convex.

Remark 2.1

It follows from Theorem 2.1(a)–(b) that

$$\begin{aligned}&rG(T_r x,y)+ r\phi (y, T_{r}(x))- r\phi (T_{r}(x), T_{r}(x))+ \langle T_{r}(x)-x,y-T_{r}(x) \rangle \nonumber \\&\quad \ge 0,~~\forall y\in C,~x\in H. \end{aligned}$$

(2.7)

Further Theorem 2.1(c) implies the nonexpansivity of $T_r$, i.e.,

$$\begin{aligned} \Vert T_{r}(x)-T_{r}(y)\le \Vert x-y\Vert ,~~\forall x,y\in H. \end{aligned}$$

(2.8)

Furthermore (2.7) implies the following inequality

$$\begin{aligned} \Vert T_{r}(x)-y\Vert ^2\le & {} \Vert x-y\Vert ^2-\Vert T_{r}(x)-x\Vert ^2+2rG(T_{r}(x),y)\nonumber \\&+2r[\phi (y, T_{r}(x))- \phi (T_{r}(x), T_{r}(x))],~~\forall y\in C, x\in H. \end{aligned}$$

(2.9)

3 Main result

We prove a strong convergence theorem for finding a common solution to GMEP(1.3) and fixed point problems for a nonexpansive mapping and for a finite family of k-strict pseudo-contraction mappings.

Theorem 3.1

Let C be a nonempty closed convex subset of a real Hilbert space H. Let the bifunction $G: C\times C\longrightarrow {\mathbb {R}}$ satisfy Assumption 2.1(i), (iii), (v), (vii) and Assumption 2.2; let the bifunction $\phi :C\times C\rightarrow {\mathbb {R}}$ be 2-skew-symmetric and satisfy Assumption 2.1 (v), (vii) and let $f :C\rightarrow C$ be a $\rho$-contraction mapping. Let $S: C\rightarrow H$ be a nonexpansive mapping and let $A: C\rightarrow H$ be a monotone and Lipschitz continuous mapping with Lipschitz constant $\lambda$. For each $i=1,2\ldots ,N$, let $T_{i}:C\rightarrow H$ be a $k_{i}$-strict pseudo-contraction mapping and let $\{\eta _{i}^{n}\}_{i=1}^{N}$ be a finite sequence of positive numbers such that $\sum \nolimits _{i=1}^{N}\eta _{i}^{n}=1$  for all $n\ge 0$. Assume that $\Gamma =\mathrm{Sol(GMEP}$(1.3))$\bigcap F(S)\bigcap (\bigcap \nolimits _{i=1}^{N}F(T_{i}))\ne \emptyset .$ Let the sequence $\{x_n\}$ be generated by the iterative scheme:

$$\begin{aligned} \left. \begin{array}{lll} x_{0}\in C,\\ y_{n}= T_{r_{n}}(x_{n}-r_{n}Ax_{n}),\\ x_{n+1}=\sigma _{n}f(x_{n}) + (1-\sigma _{n})P_{C}\left[ \alpha _{n}x_{n} +\beta _{n}ST_{r_{n}}(x_{n}-r_{n}Ay_{n})+ \gamma _{n}\sum \nolimits _{i=1}^{N}\eta _{i}^{n}T_{i}x_{n}\right] , \end{array}\right\} \nonumber \\ \end{aligned}$$

(3.1)

for $n\ge 0$, where $\{r_n\} \subset [a,b] \subset (0,\lambda ^{-1})$ and $\{\sigma _n\},\{\alpha _n\},\{\beta _n\},\{\gamma _n\}$ are the sequences in (0, 1) satisfying the following conditions:

• (i) $\alpha _{n} +\beta _{n} +\gamma _{n}=1$, $\liminf \nolimits _{n\rightarrow \infty }\beta _{n}> 0$ and $\liminf \nolimits _{n\rightarrow \infty }\gamma _{n}> 0$;

• (ii) $0\le k_{i}\le \alpha _{n}\le l< 1$, $\lim \nolimits _{n\rightarrow \infty }\alpha _{n}=l;$

• (iii) $\lim \nolimits _{n\rightarrow \infty }\sigma _{n}=0$ and $\sum \nolimits _{n=0}^{\infty }\sigma _{n}=\infty ;$

• (iv) $\sum \nolimits _{n=1}^{\infty }\sum \nolimits _{i=1}^{N}|\eta _{i}^{n}-\eta _{i}^{n-1}| < \infty .$

Then $\{x_{n}\}$ converges strongly to a point ${\hat{x}}\in \Gamma ,$ where ${\hat{x}}= P_{\Gamma }f({\hat{x}}).$

Proof

Setting $u_{n} := T_{r_{n}}(x_{n}-r_{n}Ay_{n})$ and $z_{n}: =\alpha _{n}x_{n} +\beta _{n}ST_{r_{n}}(x_{n}-r_{n}Ay_{n})+ \gamma _{n}\sum _{i=1}^{N}\eta _{i}^{n}T_{i}x_{n}$, then we have $z_{n} :=\alpha _{n}x_{n} +\beta _{n}Su_{n}+ \gamma _{n}\sum _{i=1}^{N}\eta _{i}^{n}T_{i}x_{n}$. Let $p\in \Gamma$, we have

$$\begin{aligned} \Vert Su_{n}-p\Vert ^{2}\le & {} \Vert u_{n}-p\Vert ^{2}. \end{aligned}$$

(3.2)

Further, using Remark 2.1, we have

$$\begin{aligned} \Vert u_{n}-p\Vert ^{2}= & {} \Vert T_{r_{n}}(x_{n}-r_{n}Ay_{n})-p\Vert ^{2}\nonumber \\\le & {} \Vert x_{n}-r_{n}Ay_{n}-p\Vert ^{2}- \Vert x_{n}-r_{n}Ay_{n}-u_{n}\Vert ^{2}\nonumber \\&+\,2r_{n}G(u_{n},p)+ 2r_{n}[\phi (p,u_{n})-\phi (u_{n},u_{n})]\nonumber \\\le & {} \Vert x_{n}-p\Vert ^{2}-\Vert x_{n}-u_{n}\Vert ^{2}+ 2r_{n}\langle Ay_{n},p-u_{n}\rangle +2r_{n}G(u_{n},p)\nonumber \\&+\,2r_{n}[\phi (p,u_{n})-\phi (u_{n},u_{n})]\nonumber \\\le & {} \Vert x_{n}-p\Vert ^{2}-\Vert x_{n}-u_{n}\Vert ^{2}+ 2r_{n}\langle Ay_{n}-Ap,p-y_{n}\rangle +2r_{n}\langle Ap,p-y_{n}\rangle \nonumber \\&+\,2r_{n}\langle Ay_{n},y_{n}-u_{n}\rangle +2r_{n}G(u_{n},p)+ 2r_{n}[\phi (p,u_{n})-\phi (u_{n},u_{n})]. \end{aligned}$$

(3.3)

Since A is monotone and Lipschitz continuous. Since $p\in \mathrm{Sol}$(GMEP(1.3)) and $y_{n}\in C$, we have

$$\begin{aligned} G(p,y_{n})+ \langle Ap, y_{n}-p\rangle + \phi (y_{n},p) - \phi (p,p)\ge 0, ~~ \forall y_{n}\in C, \end{aligned}$$

and hence by using above inequality and monotonicity of A in (3.3), we obtain

$$\begin{aligned} \Vert u_{n}-p\Vert ^{2}\le & {} \Vert x_{n}-p\Vert ^{2}-\Vert x_{n}-u_{n}\Vert ^{2}+ 2r_{n}\langle Ay_{n},y_{n}-u_{n}\rangle +2r_{n}[G(p,y_{n})+ G(u_{n},p)]\nonumber \\&+\, 2r_{n}[\phi (p,u_{n})-\phi (u_{n},u_{n})+\phi (y_{n},p)-\phi (p,p)]\nonumber \\\le & {} \Vert x_{n}-p\Vert ^{2}-\Vert x_{n}-y_{n}\Vert ^{2}-\Vert y_{n}-u_{n}\Vert ^{2}- 2\langle x_{n}-y_{n},y_{n}-u_{n}\rangle \nonumber \\&+\, 2r_{n}\langle Ay_{n},y_{n}-u_{n}\rangle \nonumber \\&+ \,2r_{n}[G(p,y_{n})+ G(u_{n},p)]+ 2r_{n}[\phi (p,u_{n})-\phi (u_{n},u_{n})\nonumber \\&+\,\phi (y_{n},p)-\phi (p,p)]\nonumber \\\le & {} \Vert x_{n}-p\Vert ^{2}-\Vert x_{n}-y_{n}\Vert ^{2}-\Vert y_{n}-u_{n}\Vert ^{2}- 2\langle y_{n}-(x_{n}-r_{n}Ax_{n}),u_{n}-y_{n}\rangle \nonumber \\&+ \,2r_{n}\langle Ax_{n}-Ay_{n},u_{n}-y_{n}\rangle \nonumber \\&+\, 2r_{n}[G(p,y_{n})+ G(u_{n},p)]+ 2r_{n}[\phi (p,u_{n})-\phi (u_{n},u_{n})+\phi (y_{n},p)-\phi (p,p)]\nonumber \\\le & {} \Vert x_{n}-p\Vert ^{2}-\Vert x_{n}-y_{n}\Vert ^{2}-\Vert y_{n}-u_{n}\Vert ^{2}+ 2r_{n}[G(y_{n},u_{n})+ \phi (u_{n},y_{n})- \phi (y_{n},y_{n})]\nonumber \\&+\, 2r_{n}\langle Ax_{n}-Ay_{n},u_{n}-y_{n}\rangle + 2r_{n}[G(p,y_{n})+ G(u_{n},p)]\nonumber \\&+\, 2r_{n}[\phi (p,u_{n})-\phi (u_{n},u_{n})+\phi (y_{n},p)-\phi (p,p)]\nonumber \\\le & {} \Vert x_{n}-p\Vert ^{2}-\Vert x_{n}-y_{n}\Vert ^{2}-\Vert y_{n}-u_{n}\Vert ^{2}+ 2r_{n}\langle Ax_{n}-Ay_{n},u_{n}-y_{n}\rangle \nonumber \\&+\, 2r_{n}[G(p,y_{n})+ G(y_{n},y_{n})+ G(u_{n},p)]+ 2r_{n}[\phi (p,u_{n})-\phi (u_{n},u_{n})\nonumber \\&+\, \phi (y_{n},p)-\phi (p,p)+ \phi (u_{n},y_{n})- \phi (y_{n},y_{n})]. \end{aligned}$$

(3.4)

Since G is 2-monotone and $\phi$ is 2-skew-symmetric then (3.4) implies that

$$\begin{aligned} \Vert u_{n}-p\Vert ^{2}\le & {} \Vert x_{n}-p\Vert ^{2}-\Vert x_{n}-y_{n}\Vert ^{2}-\Vert y_{n}-u_{n}\Vert ^{2}+ 2r_{n}\langle Ax_{n}-Ay_{n},u_{n}-y_{n}\rangle \nonumber \\\le & {} \Vert x_{n}-p\Vert ^{2}-\Vert x_{n}-y_{n}\Vert ^{2}-\Vert y_{n}-u_{n}\Vert ^{2}+ 2r_{n}\Vert Ax_{n}- Ay_{n}\Vert \Vert u_{n}- y_{n}\Vert \nonumber \\\le & {} \Vert x_{n}-p\Vert ^{2}-\Vert x_{n}-y_{n}\Vert ^{2}-\Vert y_{n}-u_{n}\Vert ^{2}+ 2r_{n}\lambda \Vert x_{n}-y_{n}\Vert \Vert u_{n}- y_{n}\Vert \nonumber \\\le & {} \Vert x_{n}-p\Vert ^{2}- (1-r_{n}\lambda )\Vert x_{n}-y_{n}\Vert ^{2}- (1-r_{n}\lambda )\Vert y_{n}-u_{n}\Vert ^{2}. \end{aligned}$$

(3.5)

Next by using Lemma 2.6, we estimate

$$\begin{aligned} \Vert x_{n+1}-p\Vert= & {} \Vert \sigma _{n}f(x_{n}) + (1-\sigma _{n})P_{C}z_{n}-p\Vert \nonumber \\= & {} \Vert \sigma _{n}(f(x_{n})-p)+ (1-\sigma _{n})(P_{C}z_{n}-p)\Vert \nonumber \\\le & {} \sigma _{n}\Vert f(x_{n})-p\Vert + (1-\sigma _{n})\Vert P_{C}z_{n}-p\Vert \nonumber \\\le & {} \sigma _{n}\Vert f(x_{n})-p\Vert + (1-\sigma _{n})\Vert z_{n}-p\Vert . \end{aligned}$$

(3.6)

Now,

$$\begin{aligned} \Vert f(x_{n})-p\Vert= & {} \Vert f(x_{n})- f(p)+ f(p) -p\Vert \nonumber \\\le & {} \Vert f(x_{n})-f(p)\Vert + \Vert f(p)-p\Vert \nonumber \\\le & {} \rho \Vert x_{n}-p\Vert + \Vert f(p)-p\Vert . \end{aligned}$$

(3.7)

Denote $W_{n}= \sum \nolimits _{i=1}^{N}\eta _{i}^{n}T_{i}$, it follows from Lemma 2.5 that the mapping $W_{n}: C\rightarrow H$ is k-strict pseudo-contraction with $k=\max \nolimits _{1\le i \le N}k_{i}$ and $F(W_{n}) = \bigcap \nolimits _{i=1}^{N}F(T_{i})$ and hence using Lemma 2.6 and (3.5), we have

$$\begin{aligned} \Vert z_{n}-p\Vert ^{2}= & {} \Vert \alpha _{n}x_{n}+ \beta _{n}Su_{n}+ \gamma _{n}W_{n}x_{n}- p\Vert ^{2}\nonumber \\= & {} \Vert \alpha _{n}(x_{n}-p)+ \beta _{n}(Su_{n}-p)+ \gamma _{n}(W_{n}x_{n}- p)\Vert ^{2}\nonumber \\= & {} \alpha _{n}\Vert x_{n}-p\Vert ^{2}+ \beta _{n}\Vert Su_{n}-p\Vert ^{2}+ \gamma _{n}\Vert W_{n}x_{n}-p\Vert ^{2}-\alpha _{n}\beta _{n}\Vert x_{n}- Su_{n}\Vert ^{2}\nonumber \\&-\, \alpha _{n}\gamma _{n}\Vert x_{n}- W_{n}x_{n}\Vert ^{2}- \beta _{n}\gamma _{n}\Vert Su_{n}- W_{n}x_{n}\Vert ^{2}\nonumber \\= & {} \alpha _{n}\Vert x_{n}-p\Vert ^{2}+ \beta _{n}\Vert u_{n}-p\Vert ^{2}+ \gamma _{n}(\Vert x_{n}-p\Vert ^{2}+ k \Vert x_{n}-W_{n}x_{n}\Vert ^{2})\nonumber \\&-\, \alpha _{n}\beta _{n}\Vert x_{n}- Su_{n}\Vert ^{2} - \alpha _{n}\gamma _{n}\Vert x_{n}- W_{n}x_{n}\Vert ^{2}- \beta _{n}\gamma _{n}\Vert Su_{n}- W_{n}x_{n}\Vert ^{2}\nonumber \\\le & {} (\alpha _{n}+\beta _{n}+\gamma _{n})\Vert x_{n}-p\Vert ^{2}- (1-r_{n}\lambda )\beta _{n}\Vert x_{n}-y_{n}\Vert ^{2}\nonumber \\&-\, (1-r_{n}\lambda )\beta _{n}\Vert y_{n}-u_{n}\Vert ^{2}+ \gamma _{n}k\Vert x_{n}-W_{n}x_{n}\Vert ^{2} - \alpha _{n}\beta _{n}\Vert x_{n}- Su_{n}\Vert ^{2}\nonumber \\&- \alpha _{n}\gamma _{n}\Vert x_{n}- W_{n}x_{n}\Vert ^{2}- \beta _{n}\gamma _{n}\Vert Su_{n}- W_{n}x_{n}\Vert ^{2}\nonumber \\\le & {} \Vert x_{n}-p\Vert ^{2} -\, \gamma _{n}(\alpha _n-k)\Vert x_{n}-W_{n}x_{n}\Vert ^{2} - (1-r_{n}\lambda )\beta _{n}\Vert x_{n}-y_{n}\Vert ^{2}\nonumber \\&-\, (1-r_{n}\lambda )\beta _{n}\Vert y_{n}-u_{n}\Vert ^{2}\nonumber \\&- \, \alpha _{n}\beta _{n}\Vert x_{n}- Su_{n}\Vert ^{2}- \beta _{n}\gamma _{n}\Vert Su_{n}- W_{n}x_{n}\Vert ^{2}, \end{aligned}$$

(3.8)

which implies

$$\begin{aligned} \Vert z_{n}-p\Vert\le & {} \Vert x_{n}-p\Vert . \end{aligned}$$

(3.9)

Hence, it follows from (3.6), (3.7) and (3.9) that

$$\begin{aligned} \Vert x_{n+1}-p\Vert\le & {} \sigma _{n}[\rho \Vert x_{n}-p\Vert + \Vert f(p)-p\Vert ]+ (1-\sigma _{n})\Vert x_{n}-p\Vert \nonumber \\\le & {} [1-\sigma _{n}(1-\rho )]\Vert x_{n}-p\Vert + \sigma _{n}\Vert f(p)-p\Vert . \end{aligned}$$

(3.10)

Since $1-\rho >0$ for $\rho \in (0,1)$, it follows from mathematical induction that

$$\begin{aligned} \Vert x_{n+1}-p\Vert\le & {} \max \left\{ \Vert x_{0}-p\Vert , \frac{1}{(1-\rho )}\Vert f(p)-p\Vert \right\} , \end{aligned}$$

(3.11)

for all $n\ge 0$. Further, it follows from (3.11), (3.9) and (3.5) that the sequences $\{x_{n}\}$, $\{z_{n}\}$ and $\{u_{n}\}$ are bounded. Again, we estimate $\Vert x_{n+1}-{\hat{x}}\Vert ^{2}$ with ${\hat{x}}= {P_{\Gamma }}f({\hat{x}}).$ Since ${\hat{x}}\in \Gamma \subset C$, we have

$$\begin{aligned} \Vert x_{n+1}- {\hat{x}}\Vert ^{2}= & {} \Vert \sigma _{n}(f(x_{n})-{\hat{x}})+ (1-\sigma _{n})(P_{C}z_{n}-{\hat{x}})\Vert ^{2}\nonumber \\\le & {} (1-\sigma _{n})\Vert P_{C}z_{n}-{\hat{x}}\Vert ^{2}+ 2\langle \sigma _{n}(f(x_{n})-{\hat{x}}), x_{n+1}-{\hat{x}}\rangle \nonumber \\\le & {} (1-\sigma _{n})\Vert z_{n}-{\hat{x}}\Vert ^{2}+ 2\sigma _{n}\langle f(x_{n})-{\hat{x}}, x_{n+1}-{\hat{x}}\rangle . \end{aligned}$$

(3.12)

Now,

$$\begin{aligned} \langle f(x_{n})-{\hat{x}}, x_{n+1}-{\hat{x}}\rangle= & {} \langle f(x_{n})-{\hat{x}}, x_{n}-{\hat{x}}\rangle + \langle f(x_{n})-{\hat{x}}, x_{n+1}-x_{n}\rangle \nonumber \\\le & {} \Vert f(x_{n})-f({\hat{x}})\Vert \Vert x_{n}-{\hat{x}}\Vert + \frac{K}{2}\Vert x_{n+1}-x_{n}\Vert + \langle f({\hat{x}})-{\hat{x}}, x_{n}-{\hat{x}}\rangle \nonumber \\\le & {} \rho \Vert x_{n}-{\hat{x}}\Vert ^{2} + \frac{K}{2}\Vert x_{n+1}-x_{n}\Vert + \langle f({\hat{x}})-{\hat{x}}, x_{n}-{\hat{x}}\rangle , \end{aligned}$$

(3.13)

where $K = \sup \limits _{n}{2\Vert f(x_{n})-{\hat{x}}}\Vert .$ It follows from (3.12), (3.13) and (3.8) with ${\hat{x}}$ in the place of p, that

$$\begin{aligned} \Vert x_{n+1}-{\hat{x}}\Vert ^{2}\le & {} (1-\sigma _{n}(1-2\rho ))\Vert x_{n}-{\hat{x}}\Vert ^{2}+ \sigma _{n}K\Vert x_{n+1}-x_{n}\Vert + 2\sigma _{n}\langle f({\hat{x}})-{\hat{x}}, x_{n}-{\hat{x}}\rangle \nonumber \\&-\, (1-\sigma _{n})\beta _{n}[(1-r_{n}\lambda )[\Vert x_{n}-y_{n}\Vert ^{2} +\Vert y_{n}-u_{n}\Vert ^{2}]+\alpha _{n}\Vert x_{n}-Su_{n}\Vert ^{2}]\nonumber \\&-\, (1-\sigma _{n})\gamma _{n}[(\alpha _{n}-k)\Vert x_{n}-W_{n}x_{n}\Vert ^{2}+ \beta _{n}\Vert Su_{n}-W_{n}x_{n}\Vert ^{2}], \end{aligned}$$

(3.14)

$$\begin{aligned} \Vert x_{n+1}-{\hat{x}}\Vert ^{2}\le & {} (1-\sigma _{n}(1-2\rho ))\Vert x_{n}-{\hat{x}}\Vert ^{2}+ \sigma _{n}K\Vert x_{n+1}-x_{n}\Vert \nonumber \\&+\, 2\sigma _{n}\langle f({\hat{x}})-{\hat{x}}, x_{n}-{\hat{x}}\rangle . \end{aligned}$$

(3.15)

Now, we consider two cases on $s_{n} := \Vert x_{n}-{\hat{x}}\Vert ^{2}$.

Case 1. Let the sequence $\{s_{n}\}$ be decreasing for all $n\ge n_{0} ~(n_{0}\in {\mathbb {N}})$, then it is convergent. Since $\{r_n\} \subset [a,b] \subset (0,\lambda ^{-1})$, $\lim \nolimits _{n\rightarrow \infty }\sigma _{n}=0$, $\{\alpha _n\},\{\beta _n\},\{\gamma _n\}$ are the sequences in (0, 1) such that $\liminf \nolimits _{n\rightarrow \infty }\beta _{n}> 0$ and $\liminf \nolimits _{n\rightarrow \infty }\gamma _{n}> 0$ and $k\le \alpha _{n}~\forall n$, then (3.14) implies

$$\begin{aligned} 0=\lim _{n\rightarrow \infty } \Vert Su_{n}-W_{n}x_{n}\Vert = \lim _{n\rightarrow \infty } \Vert x_{n}-y_{n}\Vert = \lim _{n\rightarrow \infty } \Vert y_{n}-u_{n}\Vert = \lim _{n\rightarrow \infty } \Vert x_{n}-Su_{n}\Vert .\nonumber \\ \end{aligned}$$

(3.16)

This implies that

$$\begin{aligned} \lim _{n\rightarrow \infty } \Vert x_{n}-u_{n}\Vert \le \lim _{n\rightarrow \infty } \Vert x_{n}-y_{n}\Vert + \lim _{n\rightarrow \infty } \Vert y_{n}-u_{n}\Vert =0. \end{aligned}$$

(3.17)

It follows from (3.16), (3.17), inequality

$$\begin{aligned} \Vert x_{n}-W_{n}x_{n}\Vert \le \Vert x_{n}-Su_{n}\Vert + \Vert Su_{n}-W_{n}x_{n}\Vert \end{aligned}$$

and

$$\begin{aligned} \Vert x_{n}-S_{n}x_{n}\Vert \le \Vert u_{n}-x_{n}\Vert + \Vert x_{n}-Su_{n}\Vert \end{aligned}$$

that

$$\begin{aligned} \lim _{n\rightarrow \infty } \Vert x_{n}-W_{n}x_{n}\Vert =0 \end{aligned}$$

(3.18)

and

$$\begin{aligned} \lim _{n\rightarrow \infty } \Vert u_{n}-Su_{n}\Vert =0. \end{aligned}$$

(3.19)

Since $\{x_{n}\} \subset C$ is bounded, there is a subsequence $\{x_{n_{k}}\}$ of $\{x_{n}\}$ such that $x_{n_{k}}\rightharpoonup q$ in C and satisfying

$$\begin{aligned} \limsup _{n\rightarrow \infty }\langle f({\hat{x}})-{\hat{x}},x_{n}-{\hat{x}}\rangle = \lim _{k\rightarrow \infty } \langle f({\hat{x}})-{\hat{x}},x_{n_{k}}-{\hat{x}}\rangle . \end{aligned}$$

(3.20)

Now, for each n, define a mapping $V_{n}x= \alpha _{n}x + (1-\alpha _{n})W_{n}x,$   $\forall x\in C$ and $\alpha _{n}\in [k,1)$. Then by Lemma 2.4, $V_{n}:C \rightarrow H$ is nonexpansive. Further, we have

$$\begin{aligned} \Vert x_{n}-V_{n}x_{n}\Vert= & {} \Vert x_{n}- (\alpha _{n}x_{n}+ (1-\alpha _{n})W_{n}x_{n})\Vert \nonumber \\= & {} \Vert (\alpha _{n}+(1-\alpha _{n})x_{n})-(\alpha _{n}x_{n}+(1-\alpha _{n})W_{n}x_{n})\Vert \nonumber \\= & {} (1-\alpha _{n})\Vert x_{n}-W_{n}x_{n}\Vert . \end{aligned}$$

(3.21)

Taking limit $n\rightarrow \infty$ and using (3.18), we get

$$\begin{aligned} \lim _{n\rightarrow \infty } \Vert x_{n}-V_{n}x_{n}\Vert =0. \end{aligned}$$

(3.22)

Now, by Condition (iv), we may assume that $\eta _{i}^{n}\rightarrow \eta _{i}$ as $n\rightarrow \infty$ for every $1\le i\le N$. It is easy to observe that each $\eta _{i}>0$ and $\sum \nolimits _{i=1}^{N}\eta _{i}=1.$ It follows from Lemma 2.5 that the mapping $W:C\rightarrow H$ defined by $Wx=(\sum \nolimits _{i=1}^{N}\eta _{i}T_{i})x$,  $\forall x\in C$ is a k-strict pseudo-contraction and $F(W)=\bigcap \nolimits _{i=1}^{N}F(T_{i})$. Since $\{x_{n}\}$ is bounded, it follows from Lemma 2.2, condition (iv) and

$$\begin{aligned} \Vert x_{n}-Wx_{n}\Vert\le & {} \Vert x_{n}-W_{n}x_{n}\Vert + \Vert W_{n}x_{n}-Wx_{n}\Vert \nonumber \\\le & {} \Vert x_{n}-W_{n}x_{n}\Vert +\sum _{i=1}^{N}|\eta _{i}^{n}-\eta _{i}|\Vert T_{i}x_{n}\Vert \end{aligned}$$

(3.23)

that

$$\begin{aligned} \lim _{n\rightarrow \infty } \Vert x_{n}-Wx_{n}\Vert =0. \end{aligned}$$

(3.24)

Since

$$\begin{aligned} \Vert W_{n}x_{n}-Wx_{n}\Vert\le & {} \Vert W_{n}x_{n}-x_{n}\Vert +\Vert x_{n}- Wx_{n}\Vert , \end{aligned}$$

(3.25)

it follows from (3.18) and (3.24) that

$$\begin{aligned} \lim _{n\rightarrow \infty } \Vert W_{n}x_{n}-Wx_{n}\Vert =0. \end{aligned}$$

(3.26)

Again, we observe that the mapping $V: C \rightarrow H$ defined by $Vx= lx+ (1-l)Wx$,  for all $x\in C$ and $\alpha _{n}\in [k,1)$, is nonexpansive and $F(V)=F(W).$ Hence, we have

$$\begin{aligned} \Vert x_{n}-Vx_{n}\Vert\le & {} \Vert x_{n}-V_{n}x_{n}\Vert + \Vert V_{n}x_{n}-Vx_{n}\Vert \nonumber \\\le & {} \Vert x_{n}-V_{n}x_{n}\Vert + \Vert \alpha _{n}x_{n} + (1-\alpha _{n})W_{n}x_{n}- l x_{n}- (1-l)Wx_{n}\Vert \nonumber \\\le & {} \Vert x_{n}-V_{n}x_{n}\Vert + |\alpha _{n}-l| \Vert x_{n}- Wx_{n}\Vert + (1-\alpha _{n}) \Vert W_{n}x_{n} - Wx_{n}\Vert .\nonumber \\ \end{aligned}$$

(3.27)

It follows from (3.22), (3.24) and (3.26) that

$$\begin{aligned} \lim _{n\rightarrow \infty } \Vert x_{n}-Vx_{n}\Vert =0. \end{aligned}$$

(3.28)

Now, we prove $q\in F(V)= F(W) = F(W_{n}) = \bigcap \nolimits _{i=1}^{N}F(T_{i})$. Assume that $q\not \in F(V)$. Since $x_{n_{k}}\rightharpoonup q$ and $q\ne Vq$, from Opial condition, we have

$$\begin{aligned} \liminf _{k\rightarrow \infty } \Vert x_{n_{k}}-q\Vert< & {} \liminf _{k\rightarrow \infty } \Vert x_{n_{k}}-Vq\Vert \nonumber \\\le & {} \liminf _{k\rightarrow \infty }{\Vert x_{n_{k}}-Vx_{n_{k}}\Vert + \Vert Vx_{n_{k}}-Vq\Vert }\nonumber \\\le & {} \liminf _{k\rightarrow \infty }\Vert x_{n_{k}}- q\Vert , \end{aligned}$$

(3.29)

which is a contradiction. Thus, we get $q\in F(V) = F(W) = F(W_{n}) = \bigcap \nolimits _{i=1}^{N}F(T_{i}).$ It follows from (3.17) that the sequences $\{x_{n}\}$ and $\{u_{n}\}$ both have the same asymptotic behaviour and hence there is a subsequence $\{u_{n_{k}}\}$ of $\{u_{n}\}$ such that $u_{n_{k}}\rightharpoonup q.$ Further, it follows from (3.17) and opial condition that $q\in F(S)$. Next, we show that $q\in \mathrm{Sol}$(GMEP(1.3)).

It follows from (3.16) that sequences $\{x_{n}\}$ and $\{y_{n}\}$ both have the same asymptotic behaviour. Therefore, there exists a subsequence $\{y_{n_{k}}\}$ of $\{y_{n}\}$ such that $y_{n_{k}}\rightharpoonup q.$ Now, the relation $y_{n}= T_{r_{n}}(x_{n}-r_{n}Ax_{n})$ implies

$$\begin{aligned}&G(y_{n},y)+ \langle Ax_{n_{k}},y_{n_{k}}-y\rangle +\phi (y,y_{n})-\phi (y_{n},y_{n})\\&\quad +\frac{1}{r_{n}}\langle y-y_{n}, y_{n}- (x_{n}-r_{n}Ax_{n})\rangle \ge 0, ~\forall y\in C \end{aligned}$$

which implies that

$$\begin{aligned} \phi (y,y_{n})-\phi (y_{n},y_{n})+\frac{1}{r_{n}}\langle y-y_{n}, y_{n}- (x_{n}-r_{n}Ax_{n})\rangle \ge G(y,y_{n})+ \langle Ax_{n_{k}},y_{n_{k}}-y\rangle . \end{aligned}$$

Hence,

$$\begin{aligned} \phi (y,y_{n_{k}})-\phi (y_{n_{k}},y_{n_{k}})+ \left\langle y-y_{n_{k}},\dfrac{y_{n_{k}}-x_{n_{k}}}{r_{n_{k}}}\right\rangle \ge G(y,y_{n_{k}})+ \langle Ax_{n_{k}},y_{n_{k}}-y\rangle , ~\forall y\in C. \end{aligned}$$

For t, with $0\le t\le 1$, let $y_{t}:= ty+ (1-t)q\in C$ and $r_{n}\ge a,~ \forall n$, then we have

$$\begin{aligned} 0\ge & {} -\phi (y_{t},y_{n_{k}})+ \phi (y_{n_{k}},y_{n_{k}})-\left\langle y-y_{n_{k}},\dfrac{y_{n_{k}}-x_{n_{k}}}{r_{n_{k}}}\right\rangle \nonumber \\&+ \, G(y_{t},y_{n_{k}})+ \langle Ax_{n_{k}},y_{n_{k}}-y_{t}\rangle \nonumber \\= & {} -\langle y-y_{n_{k}},\dfrac{y_{n_{k}}-x_{n_{k}}}{r_{n_{k}}}\rangle -\phi (y_{t},y_{n_{k}})+ \phi (y_{n_{k}},y_{n_{k}})\nonumber \\&+\, G(y_{t},y_{n_{k}})+ \langle Ax_{n_{k}},y_{n_{k}}-y_{t}\rangle \nonumber \\= & {} -\phi (y_{t},q) + \phi (q,q)+ G(y_{t},q)+ \langle Aq,q-y_{t}\rangle , \end{aligned}$$

(3.30)

which implies, on taking limit $k\rightarrow \infty$, that

$$\begin{aligned} \phi (y_{t},q)-\phi (q,q)\ge G(y_{t},q) + \langle Aq,q-y_{t}\rangle . \end{aligned}$$

Now,

$$\begin{aligned} 0= & {} G(y_{t},y_{t})\\\le & {} tG(y_{t},y)+ (1-t)G(y_{t},q)\\\le & {} tG(y_{t},y)+ (1-t)\phi (y_{t},q)-(1-t)\phi (q,q)+(1-t)\langle Aq,y_{t}-q\rangle \\\le & {} tG(y_{t},y)+ (1-t)[\phi (y_{t},q)- \phi (q,q)+\langle Aq,y_{t}-q\rangle ]\\\le & {} tG(y_{t},y)+ (1-t)t[\phi (y,q)- \phi (q,q)]+(1-t)t\langle Aq,y-q\rangle \\\le & {} G(y_{t},y)+ (1-t)[\phi (y,q)- \phi (q,q)]+ (1-t)\langle Aq,y-q\rangle . \end{aligned}$$

Letting $t\rightarrow 0^{+}$ and for each $y\in C$, we have

$$\begin{aligned} G(q,y)+\phi (y,q)-\phi (q,q)+ \langle Aq,y-q\rangle \ge 0, \end{aligned}$$

which implies $q\in \mathrm{Sol}$(GMEP(1.3)). Thus $q\in \Gamma .$ Now, it follows from (2.8) and (3.20) that

$$\begin{aligned} \limsup _{n\rightarrow \infty }\langle f({\hat{x}})-{\hat{x}},x_{n}-{\hat{x}}\rangle = \langle f({\hat{x}})-{\hat{x}},q-{\hat{x}}\rangle \le 0. \end{aligned}$$

(3.31)

Since $x_{n}\in C$, we have

$$\begin{aligned} \Vert x_{n+1}-x_{n}\Vert \le \sigma _{n}\Vert f(x_{n})-x_{n}\Vert +(1-\sigma _{n})[\beta _{n}\Vert Su_{n}-x_{n}\Vert +\gamma _{n}\Vert x_{n}-W_{n}x_{n}\Vert ], \end{aligned}$$

and hence using $\lim \nolimits _{n\rightarrow \infty }\sigma _{n}=0$, (3.16), (3.18), we have

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert x_{n+1}-x_{n}\Vert = 0. \end{aligned}$$

(3.32)

Now, it follows from $\sum \nolimits _{n=0}^{\infty }\sigma _{n}=\infty$, (3.15), (3.31), (3.32) and Lemma 2.7 that $\lim \nolimits _{n\rightarrow \infty }s_{n}=0$. Thus $\{x_{n}\}$ converges strongly to ${\hat{x}}= P_{\Gamma }f({\hat{x}}).$

Case 2. Let there be a subsequence $\{s_{k_{i}}\}$ of $\{s_{k}\}$ such that $s_{k_{i}}< s_{k_{i+1}} ~ \forall i \ge 0$. Then according to Lemma 2.8, we can define a nondecreasing sequence $\{m_{k}\} \subset {\mathbb {N}}$ such that $m_{k}\rightarrow \infty$ as $k\rightarrow \infty$ and $\max \{s_{m_{k}},s_{k}\}\le s_{m_{k+1}}~~\forall k$. Since $\{r_{k}\}\in [a,b]\subset (0,\lambda ^{-1})$,  $\forall k\ge 0$ and $\{\alpha _k\},\{\beta _k\},\{\gamma _k\}$ are the sequences in (0, 1) with conditions (i)–(ii), it follows from (3.14) that

$$\begin{aligned} \lim _{k\rightarrow \infty } \Vert Su_{m_{k}}-W_{m_{k}}x_{m_{k}}\Vert= & {} \lim _{k\rightarrow \infty } \Vert x_{m_{k}}-y_{m_{k}}\Vert = \lim _{k\rightarrow \infty } \Vert y_{m_{k}}-u_{m_{k}}\Vert \nonumber \\= & {} \lim _{k\rightarrow \infty } \Vert x_{m_{k}}-Su_{m_{k}}\Vert =0 . \end{aligned}$$

(3.33)

Further, following similar steps as in Case 1, we obtain

$$\begin{aligned} \limsup _{k\rightarrow \infty }\langle f({\hat{x}})-{\hat{x}},x_{m_{k}}-{\hat{x}}\rangle \le 0. \end{aligned}$$

Since $\{x_{k}\}$ is bounded and $\lim \nolimits _{k\rightarrow \infty }\sigma _{k}=0$, it follows from (3.17), (3.18) and inequality

$$\begin{aligned} \Vert x_{m_{k+1}}-x_{m_{k}}\Vert \le \sigma _{m_{k}}\Vert f(x_{m_{k}})-x_{m_{k}}\Vert + \beta _{m_{k}}\Vert u_{m_{k}}-x_{m_{k}}\Vert +\gamma _{m_{k}}\Vert x_{m_{k}}-W_{m_{k}}x_{m_{k}}\Vert , \end{aligned}$$

that

$$\begin{aligned} \lim _{k\rightarrow \infty }\Vert x_{m_{k+1}}-x_{m_{k}}\Vert = 0. \end{aligned}$$

(3.34)

Since $s_{m_{k}}\le s_{m_{k+1}} ~ \forall k$, it follows from (3.15) that

$$\begin{aligned} (1-2\rho )s_{m_{k+1}}\le K\Vert x_{m_{k+1}}-x_{m_{k}}\Vert + 2\langle f({\hat{x}})-{\hat{x}},x_{m_{k}}-{\hat{x}}\rangle . \end{aligned}$$

Now taking limits as $k\rightarrow \infty$, we obtain $s_{m_{k+1}}\rightarrow 0$ as $k\rightarrow \infty$. Since $s_{k}\le s_{k+1} ~\forall k$, it follows that $s_{k}\rightarrow 0$ as $k\rightarrow \infty .$ Hence $x_{k}\rightarrow {\hat{x}}$ as $k\rightarrow \infty .$ Thus, we have shown that the sequence $\{x_{n}\}$ generated by iterative algorithm (3.1) converges strongly to ${\hat{x}}= P_{\Gamma }f({\hat{x}}).$$\square$

We give the following corollary which is an immediate consequence of Theorem 3.1.

Corollary 3.1

Let C be a nonempty closed convex subset of a real Hilbert space H. Let the bifunction $G: C\times C\longrightarrow {\mathbb {R}}$ satisfy Assumption 2.1 (i), (iii), (v), (vii) and Assumption 2.2; let the bifunction $\phi :C\times C\rightarrow {\mathbb {R}}$ be 2-skew-symmetric and satisfy Assumption 2.1 (v), (vii) and let $f :C\rightarrow C$ be a $\rho$-contraction mapping. Let $A: C\rightarrow H$ be a monotone and Lipschitz continuous mapping with Lipschitz constant $\lambda$. For each $i=1,2\ldots ,N$, let $T_{i}:C\rightarrow H$ be a finite family of nonexpansive mappings and let $\{\eta _{i}^{n}\}_{i=1}^{N}$ be a finite sequence of positive numbers such that $\sum \nolimits _{i=1}^{N}\eta _{i}^{n}=1$  for all $n\ge 0$. Assume that $\Gamma _{1}=\mathrm{Sol}(\mathrm{GMEP}$(1.3))$\bigcap (\bigcap \nolimits _{i=1}^{N}F(T_{i}))\ne \emptyset .$ Let the sequence $\{x_n\}$ be generated by the iterative scheme:

$$\begin{aligned} \left. \begin{array}{lll} x_{0}\in C,\\ y_{n}= T_{r_{n}}(x_{n}-r_{n}Ax_{n}),\\ x_{n+1}=\sigma _{n}f(x_{n}) + (1-\sigma _{n})P_{C}[\alpha _{n}x_{n} +\beta _{n}T_{r_{n}}(x_{n}-r_{n}Ay_{n})\\ \qquad \qquad +\, \gamma _{n}\sum \nolimits _{i=1}^{N}\eta _{i}^{n}T_{i}x_{n}], \end{array}\right\} \end{aligned}$$

(3.35)

for $n\ge 0$ where $\{r_n\} \subset [a,b] \subset (0,\lambda ^{-1})$ and $\{\sigma _n\},\{\alpha _n\},\{\beta _n\},\{\gamma _n\}$ are the sequences in (0, 1) satisfying the following conditions:

• (i) $\alpha _{n} +\beta _{n} +\gamma _{n}=1$, $\liminf \nolimits _{n\rightarrow \infty }\beta _{n}> 0$ and $\liminf \nolimits _{n\rightarrow \infty }\gamma _{n}> 0;$

• (ii) $\lim \nolimits _{n\rightarrow \infty }\sigma _{n}=0$ and $\sum \nolimits _{n=0}^{\infty }\sigma _{n}=\infty ;$

• (iii) $\sum \nolimits _{n=1}^{\infty }\sum \nolimits _{i=1}^{N}|\eta _{i}^{n}-\eta _{i}^{n-1}| < \infty .$

Then $\{x_{n}\}$ converges strongly to a point ${\hat{x}}\in \Gamma _{1},$ where ${\hat{x}}= P_{\Gamma _{1}}f({\hat{x}}).$

Proof

Set $S=I$, the identity mapping on C, and $k_{i}=0$ for $i=1,2,\ldots ,N$ in Theorem 3.1, we get the desired result. $\square$

4 Numerical example

We give a theoretical numerical example which justifies Theorem 3.1.

Example 4.1

Let $H={\mathbb {R}}$, $C= [-1,1]$ and $i=1,2,3.$ Define $G: C\times C\longrightarrow {\mathbb {R}}$ and $\phi :C\times C\rightarrow {\mathbb {R}}$ by $G(x,y)= x(y-x)$ and $\phi (x,y)= y-x$; let the mapping $f:C\rightarrow C$ be defined by $f(x)=\frac{x}{5}, \forall x \in C$; let the mapping $A:C\rightarrow H$ be defined by $A(x)=3x+ 1, \forall x\in C$; let the mapping $T_{i}: C\rightarrow H$ be defined by $T_{i}x=-(1+i)x$ for each $i= 1,2,3$, and let the mapping $S: C\rightarrow H$ be defined by $Sx=\frac{x}{4}, \forall x \in C$. Setting $\alpha _n=\frac{1}{10n}$ and $r_{n}=\frac{1}{5},~\forall n\ge 0$, and $\eta _{1}=\eta _{2}=\eta _{3}=\frac{1}{3}$. Then the sequence $\{x_n\}$ in C generated by the iterative schemes:

$$\begin{aligned} \left. \begin{array}{lll} y_{n}= T_{r_{n}}\left( x_{n}-\frac{1}{5}(3x+1)x_n\right) ;\\ u_{n}= T_{r_{n}}(x_{n}-r_{n}Ay_{n})=\frac{5x_{n}-3y_{n}}{6};\\ z_{n}= \alpha _{n}x_{n}+ \beta _{n}\left( \frac{u_{n}}{4}\right) +\gamma _{n}[\eta _{1}T_{1}x_{n}+\eta _{2}T_{2}x_{n}+\eta _{3}T_{3}x_{n}];\\ x_{n+1}= \frac{x_{n}}{50n}+ \left( 1-\frac{1}{10n}\right) z_{n}, n\ge 0,\\ \end{array}\right\} \end{aligned}$$

(4.1)

converges to a point ${\hat{x}}=\{0\}\in \Gamma .$

Proof

It is easy to prove that the bifunctions G and $\phi$ satisfy Assumption 2.1 (i), (iii), (v), (vii) and Assumption 2.2, and Assumption 2.1 (v), (vii) respectively. Choose $\alpha _{n}=0.7+\frac{0.1}{n^2}$, $\beta _{n}= 0.2-\frac{0.2}{n^2}$ and $\gamma _{n}=0.1+\frac{0.1}{n^2}$ for all $n\ge 0$, then it is easy to observe that the sequences $\{\alpha _n\},\{\beta _n\},\{\gamma _n\}$ are in (0, 1) such that $\alpha _{n} +\beta _{n} +\gamma _{n}=1$ and satisfy the conditions $\liminf _{n\rightarrow \infty }\beta _{n}> 0$ and $\liminf _{n\rightarrow \infty }\gamma _{n}> 0$. Further, for each i, it is easy to prove that $T_{i}$ are $k_{i}$ strict pseudo-contraction mappings with $k_{1}=\frac{1}{3}$, $k_{2}=\frac{1}{2}$ and $k_{3}=\frac{3}{5}$ and $F(T_{i})=\{0\}$. Therefore $k=\max \{k_{1},k_{2},k_{3}\}=\frac{3}{5}$. Also S is nonexpansive mapping with $F(S)=\{0\}$. Hence Sol(GMEP(1.1))$=\{0\}$. Thus $\Gamma =$ Sol(GMEP(1.3))$\bigcap F(S)\bigcap (\bigcap \nolimits _{i=1}^{N}F(T_{i}))=\{0\} \ne \emptyset .$ After simplification, iterative schemes (4.1) are reduced to the following:

$$\begin{aligned} \left. \begin{array}{lll} y_{n}=\frac{1}{3}x_n;\\ u_{n}= \frac{5x_{n}-3y_{n}}{6};\\ z_{n}= \left( 0.7+\frac{0.1}{n^2}\right) x_{n}+ \left( 0.2-\frac{0.2}{n^2}\right) \frac{u_{n}}{4}-3\left( 0.1+\frac{0.1}{n^2}\right) x_{n};\\ x_{n+1}= \frac{x_{n}}{50n}+ (1-\frac{1}{10n})z_{n}, ~n\ge 0.\\ \end{array}\right\} \end{aligned}$$

(4.2)

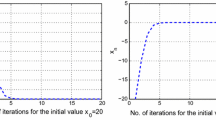
Next, using the software Matlab 7.8, we have following figure and table which show that $\{x_n\}$ converges to ${\hat{x}}=\{0\}$.

Convergence of $\{x_n\}$

No. of iterations	$x_n$ $x_1=-1$	No. of iterations	$x_n$ $x_1=-1$	No. of iterations	$x_n$ $x_1=1$	No. of iterations	$x_n$ $x_1=1$
1	− 0.600000	14	− 0.000784	1	0.600000	14	0.000784
2	− 0.360000	15	− 0.000470	2	0.360000	15	0.000470
3	− 0.216000	16	− 0.000282	3	0.216000	16	0.000282
4	− 0.129600	17	− 0.000169	4	0.129600	17	0.000169
5	− 0.077760	18	− 0.000102	5	0.077760	18	0.000102
6	− 0.046656	19	− 0.000061	6	0.046656	19	0.000061
7	− 0.027994	20	− 0.000037	7	0.027994	20	0.000037
8	− 0.016796	21	− 0.000022	8	0.016796	21	0.000022
9	− 0.010078	22	− 0.000013	9	0.010078	22	0.000013
10	− 0.006047	23	− 0.000008	10	0.006047	23	0.000008
11	− 0.003628	24	− 0.000005	11	0.003628	24	0.000005
12	− 0.002177	25	− 0.000003	12	0.002177	25	0.000003
13	− 0.001306	26	− 0.000002	13	0.001306	26	0.000002

This completes the proof. $\square$

5 Conclusion

We introduced an extra-gradient iterative method for finding a common solution to a generalized mixed equilibrium problem and fixed point problems for a nonexpansive mapping and for a finite family of k-strict pseudo-contraction mappings in Hilbert space and proved the strong convergence of the sequences generated by iterative method. A theoretical numerical example is given to illustrate the Theorem 3.1. It is of further research effort to extend the iterative method presented in this paper for solving these problems in Banach spaces, and for the case when A is multi-valued mapping.