1 Introduction

MHD free convection flow is highly important because of its presence in nature as well as in fluid engineering problems. In nature, convection is found in the rising plume of hot air from fire, oceanic currents and sea wind formation. In fluid engineering convection is commonly visualized in the formation of micro structures during the cooling of metals, MHD generators, MHD pumps, accelerators and flow meters, plasma studies, nuclear reactors, boundary layer flow control, geothermal energy extraction etc. Keeping in view these facts, free convection flow past a vertical plate in the presence of a transverse magnetic field is investigated by several researchers considering different aspects of the problem. Mention may be made of the research studies of Gupta [16, 17], Cramer [9], Pop [33], Kuiken [26], Graham [15], Hossain [20], Aldoss et al. [2], Helmy [19], Kim [25], Takhar et al. [41] and Ahmed et al. [1]. In all these studies effect of heat absorption by the fluid is not taken into account. However, in industrial applications, such as underground disposal of radioactive waste materials, storage of food stuffs, exothermic and/or endothermic chemical reactions, heat removal from nuclear fuel debris and dissociating fluids in packed-bed reactors etc the heat generation or absorption effects are of much significance. Taking into account these facts, Chamkha [5] considered steady hydromagnetic boundary layer flow over an accelerating permeable surface in the presence of thermal radiation, thermal buoyancy force and heat generation or absorption. Sahoo et al. [37] investigated unsteady MHD free convection flow of a viscous incompressible and electrically conducting fluid past an infinite vertical porous plate in the presence of constant suction and heat absorption. It was found that the magnetic field tends to retard fluid velocity and also it has tendency to reduce mean skin friction and mean rate of heat transfer of the conducting fluid. Chamkha [6] studied unsteady hydromagnetic boundary layer flow of a viscous incompressible electrically conducting and heat absorbing fluid along a semi-infinite vertical permeable moving plate embedded in a uniform porous medium. It was found that heat absorption coefficient reduces fluid temperature which resulted in decrease in the fluid velocity. The rate of heat transfer decreases as the heat absorption coefficient increases. Also heat absorption coefficient has tendency to reduce the rate of heat transfer. Rahman and Sattar [35] investigated magnetohydrodynamic convective flow of a micropolar fluid past a continuously moving vertical porous plate in the presence of heat generation or absorption. Ibrahim et al. [21] discussed the effects of chemical reaction and radiation absorption on the unsteady MHD free convection flow past a semi-infinite vertical permeable moving plate with heat source and suction. Khedr et al. [24] studied MHD flow of a micropolar fluid past a stretched permeable surface with heat generation or absorption. Makinde and Aziz [29] studied mixed convection flow from a convectively heated vertical plate to a fluid with internal heat generation.

Flow of a viscous fluid embedded with dust particles is encountered in a wide variety of engineering problems concerned with atmospheric fall out, dust collection, nuclear reactor cooling, rain erosion, guided missiles and paint spraying, petroleum transport, waste water treatment, combustion, power plant piping, corrosive particles in engine oil flow, geothermal systems etc. The possible presence of solid particles such as ash or soot in combustion energy generators and their effect on performance of such devices led to the study of particulate suspension in electrically conducting fluids in the presence of magnetic field. Initially, Saffman [36] discussed the stability of laminar flow of a dusty gas in which the dust particles were uniformly distributed. Liu [28] studied the fluid flow induced by an oscillating infinite plate in a dusty gas. Michael and Miller [32] investigated the motion of a dusty gas with uniform distribution of dust particles occupied in a semi-infinite space above a rigid plane boundary. Radhakrishnamacharya [34] studied pulsatile flow of a dusty fluid through a constricted channel. Ghosh and Debnath [11] discussed hydromagnetic Stokes’ flow of a rotating fluid with suspended small particles. Ghosh and Debnath [12] studied hydromagnetic rotating flow of a two phase fluid particle system in a channel bounded by two parallel plates when one of the plates is set in accelerated motion impulsively from rest. Ghosh and Ghosh [13] solved hydromagnetic flow of two phase fluid near a pulsating plate with a view to its application in the analysis of suspension boundary layers. Attia [4] considered Hall effect on Couette flow with heat transfer of a dusty electrically conducting fluid in the presence of uniform suction/injection. Ghosh and Ghosh [14] investigated hydromagnetic rotating flow of a dusty fluid near a pulsating plate when the flow is generated in the fluid particle system due to velocity tooth pulses subjected on the plate in the presence of a transverse magnetic field. Attia [3] studied unsteady hydromagnetic Couette flow of a dusty fluid with temperature dependent viscosity and thermal conductivity under exponential decaying pressure gradient. Makinde and Chinyoka [30] studied unsteady MHD flow and heat transfer of a dusty fluid between two parallel plates with variable viscosity and thermal conductivity when the fluid is driven by a constant pressure gradient and subjected to a uniform external magnetic field applied perpendicular to the plates with Navier slip condition. In all the aforementioned studies the analytical or numerical solution is obtained assuming conditions for velocity and temperature at the interface of the plate as continuous and well defined. However, there exist several problems of physical interest which may require non uniform or arbritrary wall conditions. Taking into consideration this fact, several researchers [18, 22, 23, 27] investigated the problems of free convection from a vertical plate with step discontinuities in the surface temperature. Chandran et al. [7] considered unsteady natural convection flow of a viscous incompressible fluid near a vertical plate with ramped wall temperature. Seth and Ansari [38] considered hydromagnetic natural convection flow past an impulsively moving vertical plate embedded in a porous medium with ramped wall temperature in the presence of thermal diffusion with heat absorption. Later, Seth et al. [40] extended the work of Seth and Ansari [38] to include the effects of rotation. Recently, Seth et al. [39] studied unsteady natural convection flow of a viscous incompressible electrically conducting fluid past an impulsively moving vertical plate in a porous medium with ramped wall temperature taking into account the effects of thermal radiation.

The aim of the present study is to investigate unsteady MHD free convection flow of a viscous, incompressible, electrically conducting and heat absorbing dusty fluid past an impulsively moving infinite vertical flat plate with a view to highlight the effects of temporary rampedness in wall temperature. Such a flow is likely to be of relevance in many engineering applications, especially where the initial temperature profile assume importance in designing of MHD devices and several natural phenomena occurring due to convection.

2 Formulation of the problem

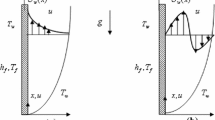
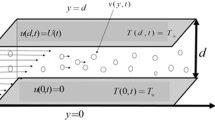
Consider the unsteady MHD free convection flow of a viscous, incompressible, electrically conducting and heat absorbing dusty fluid past an impulsively moving infinite vertical flat plate. Choose the co-ordinate system in such a way that \(x\)-axis is taken along the plate in the upward direction, \(y\)-axis is normal to the plate and \(z\)-axis is perpendicular to \(xy\)-plane. The fluid is permeated by a uniform transverse magnetic field \(B_0\) applied parallel to \(y\)-axis. The physical model of the problem is presented in Fig. 1. Initially, at time \(t^{\prime }\le 0\), the fluid, dust particles and plate are at rest and at a uniform temperature \(T^{\prime }_{\infty }\). At time \(t^{\prime }>0\) the plate starts with uniform velocity \(U_0\) and temperature of the plate is raised or lowered to \(T^{\prime }_{\infty }+(T^{\prime }_{w}-T^{\prime }_{\infty })t^{\prime }/t_0\) when \(t^{\prime }\le t_0\) and thereafter, for \(t^{\prime }>t_0\), is maintained at the uniform temperature \(T^{\prime }_w\). Since the plate is of infinite extent in \(x\), \(z\) directions and is electrically non-conducting all physical quantities, except pressure, are functions of \(y\) and \(t^{\prime }\) only.

Fig. 1
figure 1

Physical model of the problem

Full size image

The fluid under consideration is taken as a metallic liquid, viz. mercury, whose magnetic Reynold number is very small and hence the induced magnetic field produced by the fluid motion is negligible in comparison to the applied one (Cramer and Pai [8]) so that the magnetic field \(\mathbf B \equiv (0,B_0,0)\). Also, no external electric field is applied so the effect of polarization of magnetic field is negligible (Meyer [31]), i.e. \(\mathbf E \equiv (0,0,0)\).

Taking the above assumptions into account, the governing equations for a laminar MHD free convection flow of a viscous incompressible electrically conducting and heat absorbing dusty fluid are given by

$$\begin{aligned} \frac{\partial {u^{\prime }}}{\partial {t^{\prime }}}&= \nu \frac{\partial ^2{u^{\prime }}}{\partial {y^2}}-\frac{\sigma B^2_0}{\rho }u^{\prime }+\frac{k_1 N_0}{\rho }(u^{\prime }_p-u^{\prime })+g\beta ^{\prime }(T^{\prime }-T^{\prime }_\infty ),\end{aligned}$$
(1)
$$\begin{aligned} \frac{\partial {u^{\prime }_p}}{\partial {t^{\prime }}}&= \frac{k_1}{m}(u^{\prime }-u^{\prime }_p),\end{aligned}$$
(2)
$$\begin{aligned} \frac{\partial {T^{\prime }}}{\partial {t^{\prime }}}&= \frac{k}{\rho c_p}\frac{\partial ^2{T^{\prime }}}{\partial {y^2}}+\frac{\rho _p c_s}{\rho c_p \gamma _T}(T^{\prime }_p-T^{\prime })-\frac{Q_0}{\rho c_p}T^{\prime },\end{aligned}$$
(3)
$$\begin{aligned} \frac{\partial {T^{\prime }_p}}{\partial {t^{\prime }}}&= \frac{1}{\gamma _T}(T^{\prime }-T^{\prime }_p), \end{aligned}$$
(4)

where \(u^{\prime }, u^{\prime }_p, T^{\prime }, T^{\prime }_p, g, \beta ^{\prime }, \nu , \sigma , \rho , \rho _p, k, k_1, N_0, Q_0, m, c_p, c_s\) and \(\gamma _T\) are respectively, the component of fluid velocity in \(x\)-direction, component of particle velocity in \(x\)-direction, temperature of the fluid, temperature of the particle, acceleration due to gravity, volumetric coefficient of thermal expansion, co-efficient of viscosity, electrical conductivity, fluid density, particle density, thermal conductivity, Stokes’ resistance coefficient, number density of dust particle which is assumed to be constant, heat absorption coefficient, average mass of the dust particle, specific heat at constant pressure of the fluid, specific heat capacity of the particle and temperature relaxation time.

The initial and boundary conditions are

$$\begin{aligned} u^{\prime }&= u^{\prime }_p=0,\quad T^{\prime }=T^{\prime }_p=T^{\prime }_\infty \qquad \text{ for }\;y\ge 0\;\text{ and }\; t^{\prime }\le 0 ,\end{aligned}$$
(5a)
$$\begin{aligned} u^{\prime }&= U_0\quad \text{ at }\;y=0 \quad \text{ for }\; t^{\prime }>0,\end{aligned}$$
(5b)
$$\begin{aligned} T^{\prime }&= T^{\prime }_\infty +(T^{\prime }_w-T^{\prime }_\infty )t^{\prime }/t_0 \quad \text{ at }\;y=0\quad \text{ for }\;0<t^{\prime }\le t_{0},\end{aligned}$$
(5c)
$$\begin{aligned} T^{\prime }&= T^{\prime }_w\quad \text{ at }\;y=0\quad \text{ for }\;t^{\prime }>t_0,\end{aligned}$$
(5d)
$$\begin{aligned} u^{\prime }&\rightarrow 0, \quad T^{\prime }\rightarrow T^{\prime }_\infty \qquad \text{ as }\;y\rightarrow \infty \quad \text{ for }\;t^{\prime }>0. \end{aligned}$$
(5e)

To reduce the above governing equations into non-dimensional form, the following dimensionless variables and parameters have been introduced

$$\begin{aligned} \left. \begin{array}{ll} \eta &{}={y}/{U_0 t_0},\quad u=u^{\prime }/U_0,\quad t=t^{\prime }/t_0,\quad T=(T^{\prime }-T^{\prime }_\infty )/(T^{\prime }_w-T^{\prime }_\infty ),\\ u_p &{}=\frac{u^{\prime }_p}{U_0},\quad T_p=(T^{\prime }_p-T^{\prime }_\infty )/(T^{\prime }_w-T^{\prime }_\infty ),\quad M=\sigma B^2_0\nu /\rho U^2_0,\\ Gr &{}= g\beta ^{\prime }\nu (T^{\prime }_w-T^{\prime }_\infty )/U^3_0,\quad Pr=\rho \nu c_p/k,\quad R=\frac{k_1 N_0 \nu }{\rho U_0^2},\\ \sigma _1 &{}=\frac{M U_0^2}{\nu k_1},\quad \gamma =\frac{\nu }{\gamma _T U_0^2}, \quad \text{ and }\;\phi =\frac{\nu Q_0}{\rho c_p U_0^2}, \end{array} \right\} \end{aligned}$$
(6)

where, \(\phi , M, R, Gr, \sigma _1, Pr\) and \(\gamma \) are respectively, heat absorption coefficient, magnetic parameter, particle concentration parameter, Grashof number, particle relaxation time parameter, Prandtl number and temperature relaxation time parameter. According to the above non-dimensionalization process, the characteristic time \(t_0\) can be defined as

$$\begin{aligned} t_0=\frac{\nu }{U^2_0}. \end{aligned}$$
(7)

Making use of Eqs. (6) and (7) in Eqs. (1)–(4), the governing equations in no-dimensional form reduce to

$$\begin{aligned} \frac{\partial {u}}{\partial {t}}&= \frac{\partial ^2{u}}{\partial {\eta ^2}}-M u+R(u_p-u)+Gr T,\end{aligned}$$
(8)
$$\begin{aligned} \frac{\partial {u_p}}{\partial {t}}&= \frac{u-u_p}{\sigma _1},\end{aligned}$$
(9)
$$\begin{aligned} \frac{\partial {T}}{\partial {t}}&= \frac{1}{Pr}\frac{\partial ^2{T}}{\partial {\eta ^2}}+\frac{2R}{3Pr}(T_p-T)-\phi T,\end{aligned}$$
(10)
$$\begin{aligned} \frac{\partial {T_p}}{\partial {t}}&= \gamma (T-T_p), \end{aligned}$$
(11)

and the initial and boundary conditions (5), in non-dimensional form, reduce to

$$\begin{aligned} u&= u_p=0,\quad T=T_p=0 \qquad \text{ for }\;\eta \ge 0 \text{ and } t\le 0,\end{aligned}$$
(12a)
$$\begin{aligned} u&= 1 \quad \text{ at }\;\eta =0 \quad \text{ for }\; t>0,\end{aligned}$$
(12b)
$$\begin{aligned} T&= t \quad \text{ at }\; \eta =0 \quad \text{ for }\;0<t\le 1,\end{aligned}$$
(12c)
$$\begin{aligned} T&= 1 \quad \text{ at }\; \eta =0 \quad \text{ for }\;t>1,\end{aligned}$$
(12d)
$$\begin{aligned} u&\rightarrow 0, \quad T\rightarrow 0,\qquad \text{ as }\;\eta \rightarrow \infty ,\;\text{ for }\; t>0. \end{aligned}$$
(12e)

3 Solution of the problem

The governing Eqs. (8)–(11) are solved analytically using Laplace transform technique [10] under the initial and boundary conditions (12) and the expressions for fluid temperature \(T(\eta ,t)\), particle temperature \(T_p(\eta ,t)\), fluid velocity \(u(\eta ,t)\) and particle velocity \(u_p(\eta ,t)\) are expressed in the closed form as

$$\begin{aligned} T(\eta ,t)&= P_1(\eta ,t)-H(t-1)P_1(\eta ,t-1),\end{aligned}$$
(13)
$$\begin{aligned} T_p(\eta ,t)&= P_2(\eta ,t)-H(t-1)P_2(\eta ,t-1),\end{aligned}$$
(14)
$$\begin{aligned} u(\eta ,t)&= P_3(\eta ,t)+\frac{Gr}{b_2\beta }[P_4(\eta ,t)-H(t-1)P_4(\eta ,t-1)\nonumber \\&-P_5(\eta ,t)+H(t-1)P_5(\eta ,t-1)],\end{aligned}$$
(15)
$$\begin{aligned} u_p(\eta ,t)&= P_6(\eta ,t)+\frac{Gr\alpha }{b_2}[P_7(\eta ,t)-H(t-1)P_7(\eta ,t-1)\nonumber \\&-P_8(\eta ,t)+H(t-1)P_8(\eta ,t-1)], \end{aligned}$$
(16)

where,

$$\begin{aligned} P_1(\eta ,t)&= \left( \frac{t}{2}+\frac{c\eta }{4\sqrt{d}}\right) e^{\eta \sqrt{d}}\ \text{ erfc }(t_1)+\left( \frac{t}{2}-\frac{c\eta }{4\sqrt{d}}\right) e^{-\eta \sqrt{d}}\text{ erfc }(t_2),\\ P_2(\eta ,t)&= \left( \frac{\gamma t-1}{2\gamma }+\frac{c\eta }{4\sqrt{d}}\right) e^{\eta \sqrt{d}}\ \text{ erfc }(t_1)+\left( \frac{\gamma t-1}{2\gamma }-\frac{c\eta }{4\sqrt{d}}\right) e^{-\eta \sqrt{d}}\ \text{ erfc }(t_2)\nonumber \\&+\frac{e^{-\gamma t}}{2\gamma }\left( e^{\eta \sqrt{d-\gamma c}}\ \text{ erfc }(t_3)+e^{-\eta \sqrt{d-\gamma c}}\ \text{ erfc }(t_4)\right) ,\\ P_3(\eta ,t)&= \frac{1}{2}\left[ e^{\eta \sqrt{M}}\ \text{ erfc }(t_5)+e^{-\eta \sqrt{M}}\ \text{ erfc }(t_6)\right] ,\\ P_4(\eta ,t)&= \left( \frac{\beta t-1}{2\beta }+\frac{a\eta }{4\sqrt{M}}\right) e^{\eta \sqrt{M}}\ \text{ erfc }(t_5)\\&+\left( \frac{\beta t-1}{2\beta }-\frac{a\eta }{4\sqrt{M}}\right) e^{-\eta \sqrt{M}}\ \text{ erfc }(t_6)\nonumber \\&+\frac{e^{-\beta t}}{2\beta }\left[ e^{\eta \sqrt{M-\beta a}}\ \text{ erfc }(t_7)+e^{-\eta \sqrt{M-\beta a}}\ \text{ erfc }(t_8)\right] ,\\ P_5(\eta ,t)&= \left( \frac{\beta t-1}{2\beta }+\frac{c\eta }{4\sqrt{d}}\right) \ e^{\eta \sqrt{d}}\ \text{ erfc }(t_1)+\left( \frac{\beta t-1}{2\beta }-\frac{c\eta }{4\sqrt{d}}\right) \ e^{-\eta \sqrt{d}}\ \text{ erfc }(t_2)\nonumber \\&+\frac{e^{-\beta t}}{2\beta }\left[ e^{\eta \sqrt{d-\beta c}}\ \text{ erfc }(t_9)+e^{-\eta \sqrt{d-\beta c}}\ \text{ erfc }(t_{10})\right] \\ P_6(\eta ,t)&= \frac{1}{2}\left[ e^{\eta \sqrt{M}}\ \text{ erfc }(t_5)+e^{-\eta \sqrt{M}}\ \text{ erfc }(t_6)\right] \nonumber \\&-\frac{e^{-\alpha t}}{2}\left[ e^{\eta \sqrt{M-\alpha a}}\ \text{ erfc }(t_{11})+e^{-\eta \sqrt{M-\alpha a}}\ \text{ erfc }(t_{12})\right] ,\\ P_7(\eta ,t)&= \left[ \frac{\alpha \beta t-(\alpha +\beta )}{2\alpha ^2\beta ^2}+\frac{a \eta }{4\alpha \beta \sqrt{M}}\right] e^{\eta \sqrt{M}}\ \text{ erfc }(t_5)\nonumber \\&+\left[ \frac{\alpha \beta t-(\alpha +\beta )}{2\alpha ^2\beta ^2}-\frac{a \eta }{4\alpha \beta \sqrt{M}}\right] e^{-\eta \sqrt{M}}\ \text{ erfc }(t_6)\nonumber \\&+\frac{e^{-\alpha t}}{2\alpha ^2(\beta -\alpha )}\left[ e^{\eta \sqrt{M-\alpha a}}\ \text{ erfc }(t_{11})+e^{-\eta \sqrt{M-\alpha a}}\ \text{ erfc }(t_{12})\right] \nonumber \\&-\frac{e^{-\beta t}}{2\beta ^2(\beta -\alpha )}\left[ e^{\eta \sqrt{M-\beta a}}\ \text{ erfc }(t_7)+e^{-\eta \sqrt{M-\beta a}}\ \text{ erfc }(t_8)\right] ,\\ \end{aligned}$$
$$\begin{aligned} P_8(\eta ,t)&= \left[ \frac{\alpha \beta t-(\alpha +\beta )}{2\alpha ^2\beta ^2}+\frac{c \eta }{4\alpha \beta \sqrt{d}}\right] e^{\eta \sqrt{d}}\ \text{ erfc }(t_1)\nonumber \\&+\left[ \frac{\alpha \beta t-(\alpha +\beta )}{2\alpha ^2\beta ^2}-\frac{c \eta }{4\alpha \beta \sqrt{d}}\right] e^{-\eta \sqrt{d}}\ \text{ erfc }(t_2)\nonumber \\&+\frac{e^{-\alpha t}}{2\alpha ^2(\beta -\alpha )}\left[ e^{\eta \sqrt{d-\alpha c}}\ \text{ erfc }(t_{13})+e^{-\eta \sqrt{d-\alpha c}}\ \text{ erfc }(t_{14})\right] \nonumber \\&-\frac{e^{-\beta t}}{2\beta ^2(\beta -\alpha )}\left[ e^{\eta \sqrt{d-\beta c}}\ \text{ erfc }(t_{9})+e^{-\eta \sqrt{d-\beta c}}\ \text{ erfc }(t_{10})\right] , \end{aligned}$$

and

$$\begin{aligned}&\left. \begin{array}{ll} &{}t_1,t_2=\pm \sqrt{\frac{d t}{c}}+\frac{\eta }{2}\sqrt{\frac{c}{t}};\quad t_3,t_4=\pm \sqrt{\left( \frac{d-\gamma c}{c}\right) t}+\frac{\eta }{2}\sqrt{\frac{c}{t}};\\ &{}t_5,t_6=\pm \sqrt{\frac{M t}{a}}+\frac{\eta }{2}\sqrt{\frac{a}{t}};\quad t_7,t_8=\pm \sqrt{\left( \frac{M-\beta a}{a}\right) t}+\frac{\eta }{2}\sqrt{\frac{a}{t}};\\ &{}t_{9},t_{10}=\pm \sqrt{\left( \frac{d-\beta c}{c}\right) t}+\frac{\eta }{2}\sqrt{\frac{c}{t}};\quad t_{11},t_{12}=\pm \sqrt{\left( \frac{M-\alpha a}{a}\right) t}+\frac{\eta }{2}\sqrt{\frac{a}{t}};\\ &{}t_{13},t_{14}=\pm \sqrt{\left( \frac{d-\alpha c}{c}\right) t}+\frac{\eta }{2}\sqrt{\frac{c}{t}}; \end{array}\right\} \\&a=1\!+\!R\sigma _1,\quad \!\! c=\frac{2 R}{3\gamma }+Pr,\quad \!\! d=\phi Pr,\quad \!\! b_1=d\!-\!M,\quad \!\! b_2=c\!-\!a,\quad \!\!\alpha =\frac{1}{\sigma _1}\quad \text{ and }\;\beta =\frac{b_1}{b_2}. \end{aligned}$$

Here \(\text{ erfc(x) }\) and \(H(t-1)\)are respectively, complimentary error function and Heaviside unit step function.

4 Solution of the problem in the case of isothermal plate

Equations (13)–(16) represent analytical solutions for the fluid temperature \(T(\eta ,t)\), particle temperature \(T_p(\eta ,t)\), the fluid velocity \(u(\eta ,t)\) and the particle velocity \(u_p(\eta ,t)\) for the flow of a viscous, incompressible, electrically conducting and heat absorbing dusty fluid past a vertical flat plate with ramped wall temperature. In order to highlight the effects of ramped temperature of the plate on the fluid flow, it is worth while to compare such a flow with a flow near a moving plate with constant temperature. Taking into consideration the assumptions made in Sect. 2, the solutions for the fluid temperature, particle temperature, fluid velocity and particle velocity for free convection flow near an isothermal plate are presented in the following form

$$\begin{aligned} T(\eta ,t)&= P_9(\eta ,t),\end{aligned}$$
(17)
$$\begin{aligned} T_p(\eta ,t)&= P_{10}(\eta ,t),\end{aligned}$$
(18)
$$\begin{aligned} u(\eta ,t)&= P_3(\eta ,t)+\frac{Gr}{b_2}\left[ P_{11}(\eta ,t)-P_{12}(\eta ,t)\right] ,\end{aligned}$$
(19)
$$\begin{aligned} u_p(\eta ,t)&= P_6(\eta ,t)+\frac{Gr \alpha }{b_2}\left[ P_{13}(\eta ,t)-P_{14}(\eta ,t)\right] , \end{aligned}$$
(20)

where,

$$\begin{aligned} P_9(\eta ,t)&= \frac{1}{2}\left[ e^{\eta \sqrt{d}}\ \text{ erfc }(t_1)+e^{-\eta \sqrt{d}}\ \text{ erfc }(t_2)\right] ,\\ P_{10}(\eta ,t)&= \frac{1}{2}\left[ e^{\eta \sqrt{d}}\ \text{ erfc }(t_1)+e^{-\eta \sqrt{d}}\ \text{ erfc }(t_2)\right] \\&-\frac{e^{-\gamma t}}{2}\left[ e^{\eta \sqrt{d-\gamma c}}\ \text{ erfc }(t_3)+e^{-\eta \sqrt{d-\gamma c}}\ \text{ erfc }(t_4)\right] ,\\ P_{11}(\eta ,t)&= \frac{1}{2\beta }\left[ e^{\eta \sqrt{M}}\ \text{ erfc }(t_5)+e^{-\eta \sqrt{M}}\ \text{ erfc }(t_6)\right] \\&-\frac{e^{-\beta t}}{2\beta }\left[ e^{\eta \sqrt{M-\beta a}}\ \text{ erfc }(t_7)+e^{-\eta \sqrt{M-\beta a}}\ \text{ erfc }(t_8)\right] ,\\ P_{12}(\eta ,t)&= \frac{1}{2\beta }\left[ e^{\eta \sqrt{d}}\ \text{ erfc }(t_1)+e^{-\eta \sqrt{d}}\ \text{ erfc }(t_2)\right] \\&-\frac{e^{-\beta t}}{2\beta }\left[ e^{\eta \sqrt{d-\beta c}}\ \text{ erfc }(t_{9})+e^{-\eta \sqrt{d-\beta c}}\ \text{ erfc }(t_{10})\right] ,\\ P_{13}(\eta ,t)&= \frac{1}{2\alpha \beta }\left[ e^{\eta \sqrt{M}}\ \text{ erfc }(t_5)+e^{-\eta \sqrt{M}}\ \text{ erfc }(t_6)\right] \nonumber \\&+\frac{e^{-\beta t}}{2\beta (\beta -\alpha )}\left[ e^{\eta \sqrt{M-\beta a}}\ \text{ erfc }(t_7)+e^{-\eta \sqrt{M-\beta a}}\ \text{ erfc }(t_8)\right] \nonumber \\&-\frac{e^{-\alpha t}}{2\alpha (\beta -\alpha )}\left[ e^{\eta \sqrt{M-\alpha a}}\ \text{ erfc }(t_{11})+e^{-\eta \sqrt{M-\alpha a}}\ \text{ erfc }(t_{12})\right] ,\\ P_{14}(\eta ,t)&= \frac{1}{2\alpha \beta }\left[ e^{\eta \sqrt{d}}\ \text{ erfc }(t_1)+e^{-\eta \sqrt{d}}\ \text{ erfc }(t_2)\right] \nonumber \\&+\frac{e^{-\beta t}}{2\beta (\beta -\alpha )}\left[ e^{\eta \sqrt{d-\beta c}}\ \text{ erfc }(t_{9})+e^{-\eta \sqrt{d-\beta c}}\ \text{ erfc }(t_{10})\right] \nonumber \\&-\frac{e^{-\alpha t}}{2\alpha (\beta -\alpha )}\left[ e^{\eta \sqrt{d-\alpha c}}\ \text{ erfc }(t_{13})+e^{-\eta \sqrt{d-\alpha c}}\ \text{ erfc }(t_{14})\right] . \end{aligned}$$

5 Nusselt number and skin friction

The expressions for Nusselt number \((Nu)\) and skin friction \((\tau )\), which are measures of rate of heat transfer and shear stress at the plate respectively, are presented in the following form for the ramped temperature plate

$$\begin{aligned} Nu&= -\left( \frac{\partial T}{\partial \eta }\right) _{\eta =0}\nonumber \\&= -[F_1(t)-H(t-1)F_1{(t-1)}],\end{aligned}$$
(21)
$$\begin{aligned} \tau \!&= \!\left( \frac{\partial {u}}{\partial {\eta }}\right) _{\eta \!=\!0}\nonumber \\ \!&= \!F_2(t)\!+\!\frac{Gr}{b_2\beta }\left[ F_3(t)\!-\!H(t\!-\!1)F_3(t\!-\!1)\!-\!F_4(t)\!+\!H(t\!-\!1)F_4(t\!-\!1)\right] . \end{aligned}$$
(22)

Nusselt number \((Nu_i)\) and skin friction \((\tau _i)\) for isothermal plate are given by

$$\begin{aligned} Nu_i&= \sqrt{d} \text{ erf }\left( \sqrt{\frac{d t}{c}}\right) +\sqrt{\frac{c}{\pi t}}\ e^{-\frac{d t}{c}},\end{aligned}$$
(23)
$$\begin{aligned} \tau _i&= F_2(t)+\frac{Gr}{b_2}\left[ F_5(t)-F_6(t)\right] , \end{aligned}$$
(24)

where,

$$\begin{aligned} F_1(t)&= -\left( \frac{c+2 d t}{2\sqrt{d}}\right) \ \text{ erf }\left( \sqrt{\frac{d t}{c}}\right) -\sqrt{\frac{c t}{\pi }}\ e^{-\frac{d t}{c}},\\ F_2(t)&= -\sqrt{M}\ \text{ erf }\left( \sqrt{\frac{M t}{a}}\right) -\sqrt{\frac{a}{\pi t}}\ e^{-\frac{M t}{a}},\\ F_3(t)&= -\left[ \frac{a}{2\sqrt{M}}+\left( \frac{\beta t-1}{\beta }\right) \sqrt{M}\right] \text{ erf }\left( \sqrt{\frac{M t}{a}}\right) -\sqrt{\frac{a t}{\pi }}\ e^{-\frac{M t}{a}}\nonumber \\&-\left[ \frac{\sqrt{M-\beta a}}{\beta }\ \text{ erf }\left( \sqrt{\left( \frac{M-\beta a}{a}\right) t}\right) \right] \ e^{-\beta t},\\ F_4(t)&= -\left[ \frac{c}{2\sqrt{d}}+\left( \frac{\beta t-1}{\beta }\right) \sqrt{d}\right] \ \text{ erf }\left( \sqrt{\frac{d t}{c}}\right) -\sqrt{\frac{c t}{\pi }}\ e^{-\frac{d t}{c}}\nonumber \\&-\left[ \frac{\sqrt{d-\beta c}}{\beta }\ \text{ erf }\left( \sqrt{\left( \frac{d-\beta c}{c}t\right) }\right) \right] \ e^{-\beta t},\\ F_5(t)&= -\frac{\sqrt{M}}{\beta }\ \text{ erf }\left( \sqrt{\frac{M t}{a}}\right) +\frac{\sqrt{M-\beta a}}{\beta }\ \text{ erf }\left( \sqrt{\left( \frac{M-\beta a}{a}\right) t}\right) \ e^{-\beta t},\\ \text{ and }\; F_6(t)&= -\frac{\sqrt{d}}{\beta }\ \text{ erf }\left( \sqrt{\frac{d t}{c}}\right) +\frac{\sqrt{d-\beta c}}{\beta }\ \text{ erf }\left( \sqrt{\left( \frac{d-\beta c}{c}\right) t}\right) \ e^{-\beta t}. \end{aligned}$$

6 Numerical results and discussion

To study the effects of heat absorption, magnetic field, thermal buoyancy force, particle concentration and time on the two phase flow, the fluid and particle velocities are displayed graphically versus boundary layer coordinate \(\eta \) for different values of \(\phi , M, Gr, R\) and \(t\) taking \(Pr=0.71, \gamma =1\), and \(\sigma _1=0.1\) whereas, to study the effects of heat absorption, particle concentration, thermal diffusion and time on the fluid and particle temperatures, the temperature profiles for fluid and particle phase are depicted in graphs taking \(\gamma =1\). Nusselt number which is a measure of rate of heat transfer at the plate, and, skin friction which is a measure of shear stress at the plate, are presented in a table to study the effects of various flow parameters affecting these physical quantities.

It is observed from Figs. 2 and 3 that, the fluid and particles velocities for both ramped temperature and isothermal plates decrease with an increase in \(\phi \). This implies that the heat absorption has a decreasing effect on fluid and particle velocities for both ramped temperature and isothermal plates. It is evident from Figs. 4, 5, 6, 7, 8, 9, 10 and 11, that the fluid and particle velocities decrease with an increase in \(M\) or \(R\) whereas, the fluid and particle velocities increase with an increase in \(Gr\) or \(t\) for both ramped temperature and isothermal plates. This implies that an increase in the applied magnetic field has a decelerating effect on the fluid and particle velocities for both ramped and isothermal plates. This is in agreement with the property of the magnetic field that the flow of an electrically conducting fluid in the presence of magnetic field gives rise to a resistive force, known as Lorentz force which tends to retard the fluid velocity in the boundary layer region. The particle concentration has a retarding influence on both the fluid and particle velocities. It also follows that the thermal buoyancy force and time has an accelerating effect on the fluid and particle velocities for both ramped temperature and isothermal plates.

Fig. 2
figure 2

Velocity profile of the fluid when \(t=0.7, R=0.1, Gr=2\) and \(M=3\)

Full size image
Fig. 3
figure 3

Velocity profile of the particle when \(t=1.2, R=0.1, Gr=2\) and \(M=3\)

Full size image
Fig. 4
figure 4

Velocity profile of the fluid when \(t=0.7, R=0.1, Gr=2\) and \(\phi =1\)

Full size image
Fig. 5
figure 5

Velocity profile of the particle when \(t=1.2, R=0.1, Gr=2\) and \(\phi =1\)

Full size image
Fig. 6
figure 6

Velocity profile of the fluid when \(t=0.7, R=0.1, M=3\) and \(\phi =1\)

Full size image
Fig. 7
figure 7

Velocity profile of the particle when \(t=1.2, R=0.1, M=3\) and \(\phi =1\)

Full size image
Fig. 8
figure 8

Velocity profile of the fluid when \(t=0.7, Gr=2, M=3\) and \(\phi =1\)

Full size image
Fig. 9
figure 9

Velocity profile of the particle when \(t=1.2, Gr=2, M=3\) and \(\phi =1\)

Full size image
Fig. 10
figure 10

Velocity profile of the fluid when \(R=0.1, Gr=2, M=3\) and \(\phi =1\)

Full size image
Fig. 11
figure 11

Velocity profile of the particle when \(R=0.1, Gr=2, M=3\) and \(\phi =1\)

Full size image

Figures 12 and 13 show that the fluid temperature, for both ramped temperature and isothermal plates, decreases with an increase in \(\phi \) while the particle temperature, in case of ramped temperature plate, increases and, in case of isothermal plate, it decreases within the thermal boundary layer region with an increase in \(\phi \). Thus it follows that the heat absorption has a decreasing effect on the fluid temperature for both ramped temperature and isothermal plates. Heat absorption tend to increase the particle temperature in case of ramped temperature plate whereas the particle temperature in case of isothermal plate is oppositely affected with heat absorption within the thermal boundary layer. It is noticed from Figs. 14, 15, 16, 17, 18 and 19 that the fluid and particle temperatures, within the thermal boundary layer region, decrease with an increase in \(R\) and \(Pr\) where as, the fluid and particle temperatures increase with an increase in \(t\) for both ramped temperature and isothermal plates. Since \(Pr\) is the ratio of viscosity to the thermal diffusivity, an increase in \(Pr\) implies a decrease in thermal diffusivity. Thus it follows that the fluid and particle temperatures decrease with an increase in particle concentration and increase with an increase in thermal diffusion and time.

Fig. 12
figure 12

Temperature profile of the fluid when \(R=0.1, t=0.7\) and \(Pr=0.71\)

Full size image
Fig. 13
figure 13

Temperature profile of the particle when \(R=0.1, t=1.2\) and \(Pr=0.71\)

Full size image
Fig. 14
figure 14

Temperature profile of the fluid when \(\phi =1, t=0.7\) and \(Pr=0.71\)

Full size image
Fig. 15
figure 15

Temperature profile of the particle when \(\phi =1, t=1.2\) and \(Pr=0.71\)

Full size image
Fig. 16
figure 16

Temperature profile of the fluid when \(\phi =1, t=0.7\) and \(R=0.1\)

Full size image
Fig. 17
figure 17

Temperature profile of the particle when \(\phi =1, t=1.2\) and \(R=0.1\)

Full size image
Fig. 18
figure 18

Temperature profile of the fluid when \(\phi =1, Pr=0.71\) and \(R=0.1\)

Full size image
Fig. 19
figure 19

Temperature profile of the particle when \(\phi =1 Pr=0.71\), and \(R=0.1\)

Full size image

It is observed from Table 1 that the skin friction in both the cases increases with an increase in \(\phi \), \(M\) or \(Pr\), where as, the skin friction for ramped temperature plate decreases, and for isothermal plate it increases with an increase in \(Gr\). This implies that the magnetic field and heat absorption increase the skin friction whereas, the thermal diffusion has a reducing effect on it. The thermal buoyancy force reduces the skin friction for ramped temperature plate whereas, it increases the skin friction in case of isothermal plate. It is evident from Table 1 that the skin friction for ramped temperature plate, has an oscillatory nature with respect to \(t\) and \(R\) whereas, for isothermal plate, it increases with \(t\) and decreases with an increase in \(R\). Thus, it follows that the skin friction, in case of isothermal plate, increases with an increase in time whereas, it decreases with the increase in particle concentration. Also, in case of ramped temperature plate, the skin friction has an oscillatory nature with the increase in time and particle concentration. It is also observed from Table 1 that the Nusselt number for both the cases increases with an increase in \(\phi \), \(R\), or \(Pr\) whereas, the Nusselt number, in case of ramped temperature plate increases and for isothermal plate, it decreases with an increase in \(t\). Thus it may be concluded that the heat absorption and particle concentration increases the rate of heat transfer at the plate whereas, thermal diffusion tends to decrease it for both ramped temperature and isothermal plates. The rate of heat transfer at the plate decreases with an increase in time for isothermal plate while, it increases and attains a maximum and then decreases with an increase in time for ramped temperature plate.

Table 1 Skin friction and Nusselt number
Full size table

7 Conclusion

Unsteady MHD free convection flow of a viscous, incompressible, electrically conducting and heat absorbing dusty fluid past an impulsively moving infinite vertical flat plate with ramped wall temperature is studied. The main objective of the present study is to investigate the combined effects of heat absorption and rampedness in wall temperature on the fluid flow and heat transfer. The important findings of the present work are summarized as below

  • heat absorption has a decreasing effect on fluid and particle velocities for both ramped temperature and isothermal plates.

  • fluid temperature decreases with an increase in heat absorption for both ramped temperature and isothermal plates. The particle temperature, in case of ramped temperature plate, increases and for isothermal plate, it decreases within the thermal boundary layer region with an increase in heat absorption.

  • heat absorption has a tendency to increase the skin friction for both ramped temperature and isothermal plates.

  • heat absorption increase the rate of heat transfer at the plate for both ramped temperature and isothermal plates.

It is also observed that the fluid and particle velocities as well as the fluid and particle temperatures are lower in case of a flow past a flat plate with ramped wall temperature as compared to a flow past an isothermal plate.