1 Introduction

The enhancement of thermal properties of commercial oils is of paramount importance, given the significance of heat transfer in various industries such as power cycles, automotive, and refrigeration systems [1]. Extensive research has been conducted to improve the thermal properties of conventional fluids, with a particular focus on the use of nanomaterials (with an average particle size of 1 to 100 nm) to intensify heat transfer when uniformly dispersed in base fluids like oil, water, or ethylene glycol (EG) [2,3,4,5].

The remarkable properties of nanofluids are high stability, high thermal conductivity, and small size [6, 7]. The viscosity of nanofluids is improved by increasing the concentration and size of nanoparticles. Moreover, the thermal conductivity of nanofluids, which directly influences heat transfer, is improved by increasing temperature and concentration. These unique properties make nanofluids suitable for many applications, including thermal systems, fuel cells, heat exchangers, and car radiators [8,9,10,11,12].

Carbon nanotubes (CNTs) have been the subject of increased study due to their unique structural, mechanical, and electrical properties [13, 14]. Recent research has highlighted the significant potential of carbon nanotubes (CNTs) in enhancing the thermophysical properties of nanofluids, particularly in applications such as solar technologies and heat transfer. CNTs possess exceptional thermal conductivity, mechanical strength, and chemical stability, making them promising candidates for improving the thermal and optical properties of nanofluids [15]. In the context of solar technologies, nanofluids containing CNTs have been shown to enhance the efficiency of solar energy systems by improving heat transfer and optical properties, thereby contributing to the overall performance of these systems [16]. Although CNTs are expensive, they can enhance the thermal properties of fluids when used in combination with nanoparticles, resulting in a powerful and effective fluid. The most well-known cases are single-wall carbon nanotubes (SWCNTs), graphene oxide, double-wall carbon nanotubes (DWCNTs) and multi-wall carbon nanotubes (MWCNTs) [17,18,19,20,21].

The use of nanofluids, particularly hybrid nanofluids, has gained significant attention due to their potential to enhance heat transfer properties. Hybrid nanofluids have been the focus of recent research aimed at accurately predicting their thermophysical properties. For instance, a study by Bhanuteja et al. [1] developed machine learning algorithms to predict the thermophysical properties of hybrid nanofluids, demonstrating the potential for accurate estimation of these properties. Rashidi et al. [22] provided an updated and comprehensive review of the thermophysical properties of hybrid nanofluids, shedding light on the factors influencing these properties and proposing models for their accurate prediction. Rostami et al. [23] focused on the thermal conductivity modeling of nanofluids with ZnO particles, highlighting the use of artificial neural network approaches for accurate prediction of thermal conductivity. These recent studies underscore the growing interest in accurately predicting the thermophysical properties of hybrid nanofluids, particularly through the use of artificial intelligence methods. The development of accurate prediction models for hybrid nanofluids is essential for their effective utilization in various industrial applications, where improved heat transfer properties are of critical importance.

A computing method like artificial neural network (ANN) is an apt way for estimating the thermo-physical properties of nanofluids at less time and lower cost in comparison with the experiments [24] at low and high temperature conditions [25, 26]. For example, Alfaleh et al. [27] focused on the prediction of thermal conductivity and dynamic viscosity of nanofluids using support vector machines (SVMs). The study reviewed various research works on the forecasting and modeling of these properties of nanofluids with SVMs and their outcomes.

Onyiriuka [28] proposed a unique method for modeling the thermal conductivity of nanofluids. He utilized experimental data, modeling correlations from previous studies, and theoretical data streams to estimate the thermal conductivity of nanofluids. The study demonstrated the efficiency and effectiveness of this approach in predicting the enhancement in thermal conductivity, with the robust linear model emerging as the most efficient algorithm, exhibiting high accuracy on validation and test data. A statistical method named principal components analysis and back propagation network (BPN) model were employed by Yousefi et al. [29] to calculate the effective thermal conductivity of various nanofluids contains different nanoparticles, such as ZnO, CuO, Fe3O4, TiO2, and Al2O3 nanoparticles. The thermal conductivity of the aforementioned fluids was dependent on the thermal conductivity of nanoparticle, temperature, the volume fraction of nanoparticle, the thermal conductivity of base fluids, and the diameter of the nanoparticle. The net with one hidden layer whose performance was assessed by mean square error leads the best result. Absolute average deviation and correlation coefficient, which were used to compare the results with experiments and other models, were 1.47% and 0.9942, respectively.

The thermal conductivity of ZnO-MWCNT/EG-water nanofluid as a function of temperature and solid volume fraction was assessed by Hemmat Esfe et al. [30]. They presented a new correlation and a neural network model. The ANN model with two hidden layers and four neurons predicted experimental data accurately. They could validate their results with data published in the literature [31, 32]. Rostamian et al. [18] experimentally studied the thermal conductivity of CuO-SWCNTs-EG water nanofluid in terms of temperature and concentration. A precise correlation based on the experiments was developed by nonlinear regression to estimate the thermal conductivity. In addition, a feed-forward multilayer perceptron neural network was used to calculate the thermal conductivity and it was identified that based on the margin of deviation, ANN modeling can potentially have a high accuracy in predicting the physical properties of the nanofluids, especially for high-temperature applications and microfluidics and passive systems [33].

Shahsavar and Bahiraei [34] and other investigators [19, 26, 35] evaluated the thermal performance of single and two-phase systems, including the measurement of thermal conductivity and viscosity of the working fluid. For example, Shahsavar and Bahiraei [36] measured the thermal properties of a non-Newtonian hybrid nanofluid consisting of Fe3O4 and CNTs in terms of temperature and concentration. Moreover, multilayer perceptron ANN models with backpropagation rule were applied to predict the viscosity and thermal conductivity. Three approaches referred to as “resilient backpropagation,” “Quasi-Newton,” and “Bayesian regularization-based Levenberg–Marquardt” were used to obtain a suitable ANN model. Mean squared error, maximum absolute error, and coefficient of determination were utilized to estimate the accuracy of the model.

In this paper, MLP, RBF, and LSSVM methods are used to calculate the thermal conductivity of ZnO-MWCNT/EG-water nanofluid. To choose an appropriate network, root mean square error, correlation coefficient, and average absolute relative deviation are utilized. The results of modeling are compared with the experimental data and empirical correlation. It is worth saying that the novelty of this work is to develop a new ANN model for predicting the physical properties of a hybrid nanofluid. This adds to the economic viability of the projects and saves the ages of time. This is because one can estimate the physical properties of the nanofluid to ensure that it can have a plausible effect based on the target application. The developed model prevents additional experiments that are expensive and time-consuming though.

2 Details of the Intelligent Models

2.1 Multilayer Perceptron Neural Network (MLP)

Multilayer perceptron (MLP) is a type of artificial neural network that consists of neurons with massively parallel interconnections, arranged in layers and receiving weights [37]. MLP has more than two layers, including an input layer, an output layer, and one or more hidden layers in between. Information always flows in one direction, from inputs to outputs, in a feed-forward manner. Each neuron (except input layer neurons) receives values from adjacent neurons through weighted connections. At each neuron, the weighted inputs are combined with bias values and used as the input argument of an activation function. [38]. In MLP, the number of neurons in the input and output layers depends on the dimension of inputs and outputs of the main problem. The number of hidden layers and their neurons are determined by the trial and error method to minimize the error values [39]. In this work, the MLP was trained using the back-propagation algorithm, the most widely used ANN method. The number of neurons in the input and output layers is obtained based on the conditions of the problem, as mentioned in Sect. 2.1. In contrast, determining the number of hidden layers and hidden neurons is debatable. It was mathematically proved by Cybenko [40] that the MLP using back-propagation could predict every nonlinear function accurately with only one hidden layer. Thus, in our designed neural network structure, there is only one hidden layer. The number of hidden neurons is typically determined by the trial and error method [41]. The structure and topology of the MLP model is presented in Fig. 1.

Fig. 1
figure 1

The structure and topology of the MLP model used in the present research

Full size image

2.2 Radial Basis Function Neural Networks

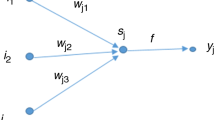
Radial basis function (RBF) neural networks were proposed by many researchers [19, 42,43,44] and can be used for a wide range of applications such as function approximation, classification patterns, spline interpolations, clustering, and mixed methods [45,46,47]. An RBF neural network consists of three layers: input, output, and a hidden layer. The nodes within each layer are connected to the previous layer, as shown in Fig. 2. In this figure, n is the dimension of the input layer.

Fig. 2
figure 2

The structure and topology of the RBF model used in the present research

Full size image

The hidden layer consists of k neurons and one bias neuron. This network is implemented according to Eq. (1) [48]:

$$F\left( x \right) = w_{0} + \mathop \sum \limits_{i = 1}^{k} \left( {w_{i} Q\left( {\left\| {x - c_{i} } \right\|} \right)} \right)$$
(1)

where x is the input vector, \({c}_{i}\) is the center of the ith neuron in the hidden layer,\(\Vert x-{c}_{\text{i}}\Vert\) denotes the Euclidean distance, Q is the Gaussian function, \({\text{w}}_{i}\) is a weight from ith hidden unit to the output node and k is the number of hidden nodes. The Gaussian function Q with the spread \(\sigma\) is defined as follows [49]:

$$Q_{i} \left( r \right) = \exp \left( { - \frac{{r^{2} }}{{2\sigma_{i}^{2} }}} \right)$$
(2)

The parameters of the RBF model, such as the maximum number of neurons (MNN) and the spread of Gaussian function, are determined using the genetic algorithm (GA). Although the trial and error approach also can be used to determine these parameters, it is not recommended due to its time consuming nature. GA is one of the best optimization algorithms inspired by Darwinian evolutionary models. In this algorithm, a population of potential solutions is refined iteratively by the natural selection strategy. In this paper, a primary population size of 50 is considered to start the algorithm. The main principle of GA is "survival of the fittest," so the fitness function should be defined and calculated for each member. In this paper, RMSE is used as a fitness function to calculate the error between the model predictions and the target data. Following this process, the members who represent better solutions have more chances for reproduction than those representing poorer solutions. These better solutions are selected as parents. After that, some genetic operators, including crossover and mutation operators, are applied to parents for producing new offspring. Then, the fitness function is reused to evaluate and rank this new generation. These iterative operations are applied until the termination criteria are met (maximum iteration number of 30). Further details about this algorithm are available in published works [50]. The optimum values of spread and MNN were 1.2 and 17, respectively.

2.3 Least Square Support Vector Machine (LSSVM)

Support vector machine (SVM) has been introduced by Vapnik [51] and has been used for many classification and function estimation problems [52]. Using the concept of SVM, Suykens proposed least squared SVM (LSSVM) [53]. LSSVM is a powerful machine learning technique that has demonstrated its ability to learn complex nonlinear problems [54]. The most crucial difference between LSSVM and SVM is that SVM uses a quadratic optimization problem for training, while LSSVM utilizes linear equations [55]. Considering a given training set of N data points, where \({x}_{k}\in {R}^{M}\) is the multi-dimensional input data and \({y}_{k}\) is the dimensional output data, LSSVM can be obtained by formulating the problem as the following equation:

$$f\left( x \right) = w^{T} \varphi \left( x \right) + b$$
(3)

where \(\varphi \left(x\right)\) and \({w}^{T}\) are kernel function and the transposed output layer vector, respectively. b is the bias value [56].

In LSSVM, for calculation of w and b, Eq. (4) is minimized as cost function [56]:

$${\text{Cost Function}} = \frac{1}{2}w^{T} w + c\mathop \sum \limits_{k = 1}^{N} \left( {\xi_{k} - \xi_{k}^{*} } \right)$$
(4)

Eventually, the resulting LSSVM model for the function prediction can be obtained by solving the following optimization problem (Eq. 5) [56]:

$$s = y\left( x \right) = \mathop \sum \limits_{k = 1}^{N} a_{k} K\left( {x,x_{k} } \right) + b$$
(5)

where K(x,xk) is a kernel function, and αk is the Lagrange multiplier. There are many kernel functions such as linear, polynomial, spline, and Gaussian. In this paper, Gaussian function has been used:

$$K\left( {x,x_{k} } \right) = \exp \left( { - \left\| {x_{k} - x} \right\|^{2} /\sigma^{2} } \right)$$
(6)

where σ is the width of the Gaussian function.

In the LSSVM method, two parameters, including γ and \({\upsigma }^{2}\), used in the mentioned equations, affect the accuracy of the method. These parameters should be specified by users. To determine the optimum values of the model’s parameters, the coupled simulated annealing (CSA) method is applied [57]. The values of γ and \({\sigma }^{2}\) were determined, respectively, to be 3,155,127.70 and 54.76.

3 Material and Methods

3.1 Data Gathering

One of the steps that should be taken to present a reliable model is to utilize valid data with wide ranges [58, 59]. Data used in this study are derived from references [18]. This study computes the thermal conductivity ratio considering the following factors as the input variables: Volume concentration (φ (%)) and Temperature (°C). The statistical values of the mentioned parameters are listed in Table 1.

Table 1 Details of data bank used in the present work
Full size table

3.2 Model Development

In order to develop the model, the following formula is used for normalization, which produces a value between  − 1 and 1. It has the same range of values for each input to the intelligent models. This can guarantee a stable convergence of weight and biases.

$$x_{{{\text{Normal}}}} = 2 \times \frac{{x - x_{{{\text{Min}}}} }}{{x_{{{\text{Max}}}} - x_{{{\text{Min}}}} }} - 1$$
(7)

After normalizing the data, the data set is grouped into two sub-sets of testing and training data. This process is repeated several times for two following reasons:

  • find a homogeneous distribution in each sub-set, and

  • prevent local aggregation of data points.

In this paper, 80% of the data points belongs to the subset of the training, and the rest 20% are members of the subset of the testing.

To evaluate the precision of the proposed models, several statistical parameters such as average absolute relative deviation (AARD%), R-squared (R2), standard deviation (SD), and root mean squared error (RMSE) are utilized (Eqs. 8–11) [60, 61]. In these formulas \(\lambda\) denotes the thermal conductivity ratio.

$$R^{2} = 1 - \frac{{\sum\nolimits_{i = 1}^{N} {\left( {\lambda_{{{\text{Pred}}}} (i) - \lambda_{{{\text{Exp}}}} (i))^{2} } \right)} }}{{\sum\nolimits_{i = 1}^{N} {\left( {\lambda_{{{\text{Pred}}}} (i) - \overline{\lambda }_{{{\text{Exp}}}} )^{2} } \right)} }}$$
(8)
$$\% {\text{AARD}} = \frac{100}{N}\sum\limits_{i = 1}^{N} {\frac{{\left( {\lambda_{{{\text{Pred}}}} (i) - \lambda_{{{\text{Exp}}}} \left( i \right)} \right)}}{{\lambda_{{{\text{Exp}}}} \left( i \right)}}}$$
(9)
$${\text{RMSE}} = \left( {\frac{{\sum\nolimits_{i = 1}^{N} {\left( {\lambda_{{{\text{Pred}}}} (i) - \lambda_{{{\text{Exp}}}} \left( i \right)} \right)^{2} } }}{N}} \right)$$
(10)
$${\text{SD}} = \sum\limits_{i = 1}^{N} {\left( {\frac{{(\lambda_{{{\text{Pred}}}} (i) - \overline{\lambda }_{{{\text{Exp}}}} (i))^{2} }}{N}} \right)^{0.5} }$$
(11)

4 Results and Discussion

Figure 3 compares the RMSE of the networks with a different number of hidden neurons. As can be seen in Fig. 3, the MLP with four hidden neurons has the least cost, so it has the best performance. Also, Fig. 4 shows the convergence process of GA during the optimization process.

Fig. 3
figure 3

Performance of the MLP networks with different numbers of neurons of hidden layer for thermal conductivity ratio

Full size image
Fig. 4
figure 4

Convergence of GA to optimize MNN and spread values to predict the thermal conductivity ratio

Full size image

Table 2 shows the results of the aforementioned statistical parameters for all the developed models. As it is shown in this table, the RBF model is better than the other two methods as the value of the R2 is the highest, and the values of AARD%, RMSE, and SD are the lowest.

Table 2 The performance of the different developed intelligent models
Full size table

Figure 5 shows the schematic representation of these evaluation parameters. As it is evident in Fig. 5a, the R2 value for the RBF model is higher than those for the other two methods. In addition, the lowest value of RMSE for the RBF method shown in Fig. 5b indicates the superiority of this method to other ones. It should be noted that the mentioned comparison includes the total dataset.

Fig. 5
figure 5

The statistical parameters for the MLP, RBF and LSSVM models: a R2, and b RMSE

Full size image

Figure 6 represents the error distribution for these methods. In the analysis of the error distribution diagrams, two factors are essential: the distribution spread (σ) and the location of the distribution’s peak (µ). According to Fig. 6b, the amount of σ in the RBF method is the lowest, which indicates that the standard deviation in the error values is the lowest. Moreover, the location of the distribution’s peak (µ) is sufficiently close to zero.

Fig. 6
figure 6

Error distribution for prediction of the thermal conductivity ratio by a MLP, b RBF, and c LSSVM models

Full size image

As it can be seen in Table 2, the R2 was obtained greater than 0.98 for all the developed methods, which indicates these models are valid and acceptable. Since the RBF method owns the best performance, Fig. 7 shows just the cross-plot for the RBF method. In using the correlation coefficient to evaluate the performance of the method, it is enough to consider two things: firstly, the approach of the R2 to value 1 and secondly the closeness of accumulation of data points to the 45° line. In the RBF model, the R2 value is obtained 0.995, and the location of most of the data points is close to the 45° line. This indicates the RBF is the best predictor for the thermal conductivity ratio. Figure 8 is drawn to indicate the relative deviations of predicted values of the RBF model versus the measured thermal resistance data points. Moreover, Fig. 9 shows a very close match between the RBF model prediction and target values versus the index of the data points. As it is shown in this figure, there is a great agreement between the predicted and measured data for the RBF model. Notably, Fig. 8 compares the accuracy of the model against the target values, which not only validated the model but also shows that the model is not noisy. As can be seen, the target values overlap the model prediction line showing that the model has sufficient accuracy.

Fig. 7
figure 7

Plot for the RBF model

Full size image
Fig. 8
figure 8

Relative error of the predicted thermal conductivity ratio

Full size image
Fig. 9
figure 9

Simultaneous representations of the experimental data and predicted thermal conductivity ratio

Full size image

5 Conclusion

The objective of this study was to predict the thermal conductivity ratio of ZnO-MWCNT/EG-water hybrid nanofluid. In this regard, three intelligent models, including MLP, RBF, and LSSVM, were utilized. In all the developed models, the same dataset, which included wide ranges of volume concentration, temperature, and thermal conductivity ratio values, was used for training and testing the developed networks. The aim of using these three intelligent models was to access a model with the best quality for predicting the thermal conductivity ratio. In this study, the graphical graphs and statistical parameters were utilized to evaluate the accuracy of the mentioned methods. Comparing the MLP, RBF, and LSSVM models, it was revealed that the RBF model was the most accurate one.