Extended Sliding Mode Observer-Based Output Constraint Nonlinear Control Scheme for Electro-hydraulic Actuators with System Uncertainties

Abstract

To achieve high performance of the electro-hydraulic servo system (EHSS), how to well handle system uncertainties is quietly meaningful in designing various controllers. As a result, the state-space representation of the EHSS is established by considering system uncertainties including the external load force, the friction force, the parameter uncertainties, the structural vibrations, and the unmodeled characteristics. Based on the state model, an extended sliding mode observer (ESMO) for the EHSS is detailly designed to estimate and compensate for the matched and the mismatched system uncertainties. Proper saturation functions are employed in the ESMO to deal with the high-frequency interferences caused by the chattering phenomenon. With two estimation values from the ESMO, an output constraint nonlinear control scheme (OCNCS) is designed for the position output constraint control of the EHSS based on the barrier Lyapunov function (BLF). The state-space model and the proposed control algorithm are then developed in MATLAB/Simulink. Subsequently, some simulation studies are conducted to verify the control performance. What’s more, an experimental bench is established and the control algorithms are then downloaded into the target computer through the internet to drive the bench in real-time. The results from simulation and experiment indicate that the proposed control method outperforms the extended sliding mode observer (ESMO)-based robust adaptive backstepping controller (RABC), the OCNCS, and the backstepping controller (BC). The peak tracking error is reduced by 99.11%, 51.93%, and 37.46% in simulation and 93.54%, 78.98%, and 15.89% in experimental compared to the ESMO-based RABC, the OCNCS, and the BC, respectively.

1 Introduction

Electro-hydraulic servo systems (EHSSs) are widely used in various industrial applications due to their high-power density, fast response, and precise control capabilities. Despite significant nonlinearities, uncertainties, dead zones, constraints, saturation, and other complex behaviors, the development of advanced closed-loop controllers for hydraulic systems has been relentless. These sophisticated controllers aim to address the uncertainties, including both uncertain nonlinearities and parametric uncertainties, to fulfill the ever-growing demands for precise control performance. Adaptive control methods [1,2,3], have been innovated to counteract parametric uncertainties effectively. However, they fall short when it comes to handling uncertain nonlinearities that encompass modeling errors and external disturbances. These nonlinearities, when they become dominant, can significantly degrade the tracking accuracy of the EHSS. To bolster the robustness of adaptive control and to enhance tracking performance, an integration of robust and adaptive controls has been pursued. This integrated approach has given rise to a number of advanced algorithms, such as robust adaptive control [4], RISE-based adaptive control [5, 6], adaptive sliding mode control [7, 8], neural network control [9, 10], which have been effectively applied to hydraulic systems. One of the challenges with these methods is their reliance on high-gain feedback to achieve desired performance outcomes. However, high-gain feedback is generally avoided in practical scenarios due to its propensity to amplify high-frequency dynamics and measurement noise. Consequently, control strategies tend to be overly conservative, particularly when the system encounters large disturbances [11, 12]. To improve the systems’ ability to withstand disturbances, an array of disturbance rejection control strategies has been derived[13, 14]. Disturbance observers are particularly favored due to their simplicity and compatibility with various control methods. These observers [9,10,11,12,13,14,15,16], aid in enhancing control performance by estimating and compensating for parametric uncertainties and disturbances, which are treated as lumped disturbances, thereby mitigating their impacts without resorting to high-gain feedback mechanisms. In addition, these estimation values directly from analog sensors usually have heavy noise, which will increase the control input ripples and result in poor steady tracking performance. A notable example is the extended state observer (ESO) [17]. The ESO excels in disturbance estimation with minimal reliance on model information and is distinguished by its simple structure with only a handful of parameters that are straightforward to tune. This has led to its widespread application in the field, as seen in references [18,19,20].

Another significant achievement is the extended sliding mode observer (ESMO) [21], which is derived from sliding mode observers with the concept of sliding mode control. Therefore, the ESMO has an inherent robustness to disturbances. The initial ESMO in [21] employs $\left( {x_{i} - \hat{x}_{i} } \right)$ with properly tuning gains to compensate for the estimation error in system states estimations and discontinuous function ${\text{sign}}\left( {x_{i} - \hat{x}_{i} } \right)$ with control gains to improve the estimation accuracy in the extended states. Subsequently, the enhanced ESMO is proposed with discontinuous functions ${\text{sign}}\left( {x_{i} - \hat{x}_{i} } \right)$ to compensate for both the system states and the extended states [22]. The ESMO is also compared with disturbance observers in [4] and the ESO in [23, 24], whose results prove that the ESMO’s estimation values have less noise than disturbance observers and the ESMO conducts a better performance than the ESO. The ESMO gives researchers a basic alternative requirement when designing the disturbance rejection control schemes.

Despite these advances, a critical limitation remains: these controllers often overlook the output constraint of hydraulic systems. Addressing this gap presents a key opportunity for future research and development in hydraulic control systems. Output constraint control is of great significance in practical applications, as it guarantees the safety and stability of the controlled system [25]. In recent years, considerable research efforts have been devoted to the development of control strategies for EHSSs to address these challenges [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26]. The enforcement of the output constraint is effectively realized through the use of a barrier lyapunov function (BLF), as an alternative to the conventional quadratic lyapunov function. The efficiency of the BLF has been proved in many quality controls of hydraulic systems. D. Won [15] employs the BLF combined with disturbance observers to constrain the output in a desired boundary. Furthermore, the research presented in [27, 28] proposes a state-constrained control approach for single-rod hydraulic actuators, designed to maintain the states within prescribed limits in the channels, even in the absence of disturbances. The important aspect is the design of control schemes that can handle system uncertainties and ensure the satisfaction of output constraints. In practical engineering, especially, in real hydraulic servo systems, the BLF gives an explosive calculation to the computer. It requires a computer with large memory and a high-speed processor, which increases the cost of the actual system.

The anticipated outcome of the proposed controller is to ensure that the system’s control performance indices—such as overshoot, steady-state tracking error, and convergence speed—align with the actual performance requirements [28]. Nevertheless, there appears to be a lack of focus on the system’s transient tracking performance, even though the aforementioned controllers can secure commendable steady-state control performance. In this study, an extended sliding mode observer (ESMO)-based control scheme is proposed for EHSSs with system uncertainties. The ESMO is designed to estimate the matched and mismatched unmeasured states of the EHSS, which are essential for feedback control. By incorporating the estimated states into the control law, the proposed scheme is capable of compensating for system uncertainties and achieving accurate tracking of desired output trajectories. Furthermore, the control scheme incorporates output constraint enforcement to ensure that the controlled EHSS operates within predefined limits. This is achieved by designing appropriate control laws that regulate the output of the actuator while maintaining stability and performance. Some simulation and experimental studies are conducted in the presence of system uncertainties to verify the performance of the proposed controller. Comparative results show the efficiency of the proposed control scheme. With the ESMO’s compensation, the maximum position tracking error is 9.6837 × 10^–5 m in the experimental study, which is almost the measurement noise of the analog displacement sensor.

The remainder of this paper is organized as follows: Sect. 2 provides the problem formulation and preliminaries for the EHSSs and the challenges associated with their control. Section 3 details the theoretical derivation of the ESMO and the output constraint nonlinear control scheme (OCNCS) based on the BLF. Simulation results and discussions are presented in Sect. 4. Finally, conclusions and future research directions are outlined in Sect. 5.

Through the development of this control scheme, it is expected that enhanced control performance, robustness against system uncertainties, and improved output constraint enforcement can be achieved for EHSSs. These advancements will contribute to the effective utilization of EHSSs in various industrial applications.

2 Problem Formulation and Preliminaries

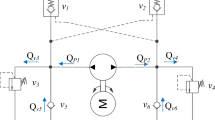
Figure 1 presents the configuration schematic of the EHSS. By applying Newton’s second law, the force balance equation yields

$$- m\ddot{x}_{{\text{p}}} - B_{{\text{p}}} \dot{x}_{{\text{p}}} + A_{{\text{p}}} p_{{\text{L}}} = F_{{\text{L}}} { + }F_{{\text{F}}}$$

(1)

where, m—the mass of the load, x_p—the piston rod displacement, B_p—the viscous damping coefficient of the oil, A_p—the effective area, p_L—the load pressure p_L = p₁-p₂, F_L—the external load force, F_F—the coulomb friction force.

Fig. 1

Configuration schematic of the EHSS

With the flow continuity equation, the load flow Q_L from the servo valve to two actuator chambers yields

$$Q_{{\text{L}}} = {{\left( {Q_{1} + Q_{2} } \right)} \mathord{\left/ {\vphantom {{\left( {Q_{1} + Q_{2} } \right)} 2}} \right. \kern-0pt} 2}{ = }A_{{\text{p}}} \dot{x}_{{\text{p}}} + C_{{{\text{tl}}}} p_{{\text{L}}} + \dot{p}_{{\text{L}}} {{V_{{\text{t}}} } \mathord{\left/ {\vphantom {{V_{{\varvec{t}}} } {4\beta_{{\varvec{e}}} }}} \right. \kern-0pt} {4\beta_{{\text{e}}} }}$$

(2)

where, Q_L—the load flow from the servo valve to the actuator chambers, C_tl—the total leakage coefficient, V_t—the total volume of two champers, β_e—the effective bulk modulus of the oil.

The load flow of the hydraulic cylinder is determined by the servo valve spool displacement.

$$Q_{{\text{L}}} = C_{{\text{d}}} {\text{w}}x_{{\text{v}}} \sqrt {{{\left[ {p_{{\text{s}}} - {\text{sign}} (x_{{\text{v}}} )p_{{\text{L}}} } \right]} \mathord{\left/ {\vphantom {{\left[ {p_{{\varvec{s}}} - {\text{sign}} (x_{{\text{v}}} )p_{{\text{L}}} } \right]} \rho }} \right. \kern-0pt} \rho }}$$

(3)

where,, x_v—the servo valve spool displacement, C_d—the discharge coefficient of the servo valve, w—the area gradient of the servo valve spool, ρ—the density of the oil, p_s—the pressure of the supply of oil.

According to [4], the EHSS’s control input for the servo valve can be presented as

$$u_\text{L} = u_{\max } \sqrt {{{\Delta p_\text{r} } \mathord{\left/ {\vphantom {{\Delta p_{r} } {\left[ {p_\text{s} - {\text{sign}} (Q_\text{L} )p_\text{L} } \right]}}} \right. \kern-0pt} {\left[ {p_\text{s} - {\text{sign}} (Q_\text{L} )p_\text{L} } \right]}}} {{Q_{\text{L}} } \mathord{\left/ {\vphantom {{Q_{\text{L}} } {Q_\text{r} }}} \right. \kern-0pt} {Q_\text{r} }}$$

(4)

where, u_L—the control voltage, u_max–the maximum control voltage, Δp_r—the rated load pressure of the servo valve, Q_r—the rated flow of the servo valve.

Define the system state vector as ${\varvec{x}} = [x_{1} ,x_{2} ,x_{3} ]^{T}$$= [x_\text{p} ,\dot{x}_\text{p} ,p_\text{L} ]^{T}$, therefore, the state space representation of the EHSS yields

$$\left\{ {\begin{array}{*{20}l} {\dot{x}_{1} = x_{2} } \hfill \\ {\dot{x}_{2} = \underbrace {{\theta_{1} x_{3} - \theta_{2} x_{2} }}_{{f_{1} \left( {x_{2} ,x_{3} } \right)}}\underbrace {{ + \Delta \theta_{1} x_{3} - \Delta \theta_{2} x_{2} - {{F_{L} } \mathord{\left/ {\vphantom {{F_\text{L} } m}} \right. \kern-0pt} m} - {{F_\text{F} } \mathord{\left/ {\vphantom {{F_{F} } m}} \right. \kern-0pt} m} + \mu }}_{{\Delta_{1} }}} \hfill \\ {\dot{x}_{3} = \underbrace {{ - \theta_{3} x_{2} - \theta_{4} x_{3} }}_{{f_{2} \left( {x_{2} ,x_{3} } \right)}} + \theta_{5} Q_\text{L} \underbrace {{ - \Delta \theta_{3} x_{2} - \Delta \theta_{4} x_{3} }}_{{\Delta_{2} }}} \hfill \\ {\dot{\Delta }_{1} = \Upsilon_{1} } \hfill \\ {\dot{\Delta }_{2} = \Upsilon_{2} } \hfill \\ {y = x_{1} } \hfill \\ \end{array} } \right.$$

(5)

where, θ₁ = A_p/m, θ₂ = B_p/m, θ₃ = 4A_pβ_e/V_t, θ₄ = 4C_tlβ_e/V_t, θ₅ = 4β_e/V_t, Actually, the viscous damping coefficient of the hydraulic oil $B_\text{p}$, the effective bulk modulus of the oil $\beta_\text{e}$ and the total leakage coefficient of the hydraulic actuator $C_\text{tl}$ in real hydraulic system are all estimated values. Due to the measurement errors in the physical parameters of the hydraulic cylinder and the errors in other parameters (such as the viscosity damping system B_p of the hydraulic oil, the total leakage coefficient C_tl of the hydraulic cylinder, and the volume elasticity modulus β_e of the hydraulic oil), there are differences between the parameters in the system state equation and the actual physical system. Therefore, parameter variations are considered in the system’s state equation, where Δθ₁, Δθ₂, Δθ₃ and Δθ₄ represent the parameter variations of θ₁, θ₂, θ₃ and θ₄, respectively. In addition, the structural vibration caused by the movement of the piston rod and some unmodeled characteristics of the hydraulic oil nonlinearity (collectively represented as μ) are included. Collectively, Δ₁ represents the system uncertainty caused by external disturbance forces, friction forces, parameter variations, structural vibrations, and unmodeled characteristics, Δ₁ = -F_L/m-F_F/m + Δθ₁x₃-Δθ₂x₂ + μ. Δ₂ represents the system uncertainty caused by parameter variations of θ₃ and θ₄, Δ₂ = -Δθ₃x₂-Δθ₄x₃. Δ₁ represents the load fluctuation of the hydraulic cylinder piston rod caused by system uncertainty, and Δ₂ represents the pressure fluctuation in the two chambers of the hydraulic cylinder caused by system uncertainty. Υ_j are variation rates of Δ_j. y = x₁ is the output of the displacement output, f₁(x₂, x₃) = θ₁x₃-θ₂x₂, f₂(x₂,x₃) = -θ₃x₂-θ₄x₃.

Assumption 1

The desired displacement of the EHSS $y_\text{d}$, and its first, second, and third-order time derivative $\dot{y}_\text{d}$, $\ddot{y}_\text{d}$ and $\dddot y_\text{d}$ are all bounded. Δ_j, and their variation rate Υ_j are all bounded, i.e., $\Delta_{j} \le \Delta_{j\max }$, $\Upsilon_{j} \le \Upsilon_{j\max }$.

Assumption 2

Functions f_j(x₂, x₃) are Lipschitz with respect to x₂ and x₃. There exist four Lipschitz constants γ_1i, γ₂, γ₃ and γ₄, which makes the following inequations hold.

$$\begin{aligned} &\left| {f_{1} \left( {x_{2} ,x_{3} } \right) - \hat{f}_{1} \left( {\hat{x}_{2} ,\hat{x}_{3} } \right)} \right| \\ &\quad= \left| {\hat{f}_{1} \left( {\hat{x}_{2} ,\hat{x}_{3} } \right)} \right| \le \gamma_{1} \left| {x_{2} - \hat{x}_{2} } \right| + \gamma_{2} \left| {x_{3} - \hat{x}_{3} } \right| \\ &\quad = \gamma_{1} \left| {\tilde{x}_{2} } \right| + \gamma_{2} \left| {\tilde{x}_{3} } \right|\end{aligned}$$

(6)

$$\begin{aligned} &\left| {f_{2} \left( {x_{2} ,x_{3} } \right) - \hat{f}_{2} \left( {\hat{x}_{2} ,\hat{x}_{3} } \right)} \right| \\ &\quad= \left| {\tilde{f}_{2} \left( {\tilde{x}_{2} ,\tilde{x}_{3} } \right)} \right| \le \gamma_{3} \left| {x_{2} - \hat{x}_{2} } \right| + \gamma_{4} \left| {x_{3} - \hat{x}_{3} } \right| \\ &\quad= \gamma_{3} \left| {\tilde{x}_{2} } \right| + \gamma_{4} \left| {\tilde{x}_{3} } \right|\end{aligned}$$

(7)

where, $\hat{x}_{i}$ and $\tilde{x}_{i}$, i = 1,2,3. Will be defined in the next section.

3 Controller Design

3.1 Development of the ESMO

With the state representation (5), consider the following five-order ESMO.

$$\begin{gathered} \left\{ {\begin{array}{*{20}l} {\dot{\hat{x}}_{1} = \hat{x}_{2} - L_{1} {\text{sign}}\left( {x_{1} - \hat{x}_{1} } \right)} \hfill \\ {\dot{\hat{x}}_{2} = \theta_{1} \hat{x}_{3} - \theta_{2} \hat{x}_{2} - L_{2} {\text{sign}}\left( {x_{2} - \hat{x}_{2} } \right) + \hat{\Delta }_{1} } \hfill \\ {\dot{\hat{x}}_{3} = - \theta_{3} \hat{x}_{2} - \theta_{4} \hat{x}_{3} + \theta_{5} Q_\text{L} - L_{3} {\text{sign}}\left( {x_{3} - \hat{x}_{3} } \right) + \hat{\Delta }_{2} } \hfill \\ \end{array} } \right. \hfill \\ \dot{\hat{\Delta }}_{1} = L_{4} L_{2} {\text{sign}}\left( {x_{2} - \hat{x}_{2} } \right) \hfill \\ \dot{\hat{\Delta }}_{2} = L_{5} L_{3} {\text{sign}}\left( {x_{3} - \hat{x}_{3} } \right) \hfill \\ \end{gathered}$$

(8)

where, $\hat{x}_{i}$ are estimation values of $x_{i}$, $\hat{\Delta }_{j}$ are estimation values of Δ_j, L₁, L₂, L₃, L₄ and L₅ are the control gains of the ESMO. $\tilde{\user2{X}} = \left[ {\tilde{x}_{1} ,\tilde{x}_{2} ,\tilde{x}_{3} ,\tilde{\Delta }_{1} ,\tilde{\Delta }_{2} } \right]^{T} = \left[ {x_{1} - \hat{x}_{1} ,x_{2} - \hat{x}_{2} ,x_{3} - \hat{x}_{3} ,\Delta_{1} - \hat{\Delta }_{1} ,\Delta_{2} - \hat{\Delta }_{2} } \right]^{T}$, one can obtain the estimation error dynamics yields

$$\begin{gathered} \left\{ {\begin{array}{*{20}l} {\dot{\tilde{x}}_{1} = \tilde{x}_{2} - L_{1} {\text{sign}}\left( {\tilde{x}_{1} } \right)} \hfill \\ {\dot{\tilde{x}}_{2} = \theta_{1} \tilde{x}_{3} - \theta_{2} \tilde{x}_{2} - L_{2} {\text{sign}}\left( {\tilde{x}_{2} } \right) + \tilde{\Delta }_{1} } \hfill \\ {\dot{\tilde{x}}_{3} = - \theta_{3} \tilde{x}_{2} - \theta_{4} \tilde{x}_{3} - L_{3} {\text{sign}}\left( {\tilde{x}_{3} } \right) + \tilde{\Delta }_{2} } \hfill \\ \end{array} } \right. \hfill \\ \dot{\tilde{\Delta }}_{1} = L_{4} L_{2} {\text{sign}}\left( {\tilde{x}_{2} } \right) - \Upsilon_{1} \hfill \\ \dot{\tilde{\Delta }}_{2} = L_{5} L_{3} {\text{sign}}\left( {\tilde{x}_{3} } \right) - \Upsilon_{2} \hfill \\ \end{gathered}$$

(9)

Lemma

[4] If the control gains L₁, L₂, L₃, L₄ and L₅ are selected large enough such that $L_{1} > \left| {\tilde{x}_{2} } \right| + \sigma_{1}$, $L_{2} > \gamma_{1} \left| {\tilde{x}_{2} } \right| + \gamma_{2} \left| {\tilde{x}_{3} } \right| + \left| {\tilde{\Delta }_{1} } \right| + \sigma_{2}$, $L_{3} > \gamma_{3} \left| {\tilde{x}_{2} } \right| + \gamma_{4} \left| {\tilde{x}_{3} } \right| + \left| {\tilde{\Delta }_{2} } \right| + \sigma_{3}$, $L_{4} > 0$, $L_{5} > 0$, and $\sigma_{i}$ are three small positive real constants, which can guarantee the estimation error $\tilde{\user2{X}}$ convergence to zero in a finite time T > 0.

Proof

Consider the following three sliding mode surfaces as $S_{i} = \tilde{x}_{i}$. According to the estimation error dynamics (9), the time derivative of S_i yield.

$$\left\{ \begin{aligned} \dot{S}_{1} & = \dot{\tilde{x}}_{1} = \tilde{x}_{2} - L_{1} {\text{sign}}\left( {\tilde{x}_{1} } \right) \\ \dot{S}_{2} & = \dot{\tilde{x}}_{2} = \tilde{f}_{1} \left( {\tilde{x}_{2} ,\tilde{x}_{3} } \right) - L_{2} {\text{sign}}\left( {\tilde{x}_{2} } \right) + \tilde{\Delta }_{1} \\ \dot{S}_{3} & = \dot{\tilde{x}}_{3} = \tilde{f}_{2} \left( {\tilde{x}_{2} ,\tilde{x}_{3} } \right) - L_{3} {\text{sign}}\left( {\tilde{x}_{3} } \right) + \tilde{\Delta }_{2} \\ \end{aligned} \right.$$

(10)

If we focus specifically on the first equation in (10), the following inequality can be derived:

$$S_{1} \dot{S}_{1} = \tilde{x}_{1} \dot{\tilde{x}}_{1} = \tilde{x}_{1} \left[ {\tilde{x}_{2} - L_{1} {\text{sign}}\left( {\tilde{x}_{1} } \right)} \right] \le \left| {\tilde{x}_{1} } \right|\left[ {\left| {\tilde{x}_{2} } \right| - L_{1} } \right]$$

(11)

Therefore, if one properly selects the control gain L₁ as $L_{1} > \left| {\tilde{x}_{2} } \right| + \sigma_{1}$, where $\sigma_{1}$ is a small positive real constant, then Eq. (11) can be rewritten as

$$S_{1} \dot{S}_{1} < \sigma_{1} \left| {\tilde{x}_{1} } \right| \le 0$$

(12)

One can conclude that $S_{1}$ will reach a sliding mode manifold in a finite time T₁ > 0, and $\tilde{x}_{1} = \dot{\tilde{x}}_{1} = 0$. We can further derive

$$\tilde{x}_{1} = \dot{\tilde{x}}_{1} = \tilde{x}_{2} - L_{1} {\text{sign}}\left( {\tilde{x}_{1} } \right) = 0$$

(13)

then,

$$\tilde{x}_{2} = L_{1} {\text{sign}}\left( {\tilde{x}_{1} } \right)$$

(14)

The following inequality can be derived in terms of the dynamics of S₂ in (10).

$$S_{2} \dot{S}_{2} = \tilde{x}_{2} \dot{\tilde{x}}_{2} = \tilde{x}_{2} \left( {\tilde{f}_{1} \left( {\tilde{x}_{2} ,\tilde{x}_{3} } \right) - L_{2} {\text{sign}}\left( {\tilde{x}_{2} } \right) + \tilde{\Delta }_{1} } \right)$$

(15)

Based on Assumption 2 (6), thus one can obtain

$$\begin{aligned}S_{2} \dot{S}_{2} & \le \left| {\tilde{x}_{2} } \right|\left[ {\left| {\tilde{f}_{1} \left( {\tilde{x}_{2} ,\tilde{x}_{3} } \right)} \right| - L_{2} + \left| {\tilde{\Delta }_{1} } \right|} \right] \\ &\le \left| {\tilde{x}_{2} } \right|\left[ {\gamma_{1} \left| {\tilde{x}_{2} } \right| + \gamma_{2} \left| {\tilde{x}_{3} } \right| - L_{2} + \left| {\tilde{\Delta }_{1} } \right|} \right] \end{aligned}$$

(16)

If the control gain $L_{2}$ is properly selected such that

$$L_{2} > \gamma_{1} \left| {\tilde{x}_{2} } \right| + \gamma_{2} \left| {\tilde{x}_{3} } \right| + \left| {\tilde{\Delta }_{1} } \right| + \sigma_{2}$$

(17)

where $\sigma_{2}$ is a small positive real constant. By substituting Eq. (17) into Eq. (16), one can derive the following equation.

$$S_{2} \dot{S}_{2} < - \sigma_{2} \left| {\tilde{x}_{2} } \right| \le 0$$

(18)

Therefore, the estimation error $\tilde{x}_{2}$ will converge to zero in a finite time T₂ > 0 and $\tilde{x}_{2} = \dot{\tilde{x}}_{2} = 0$. The dynamics of $\tilde{x}_{2}$ in (9) can be rewritten as

$$\dot{\tilde{x}}_{2} = \theta_{1} \tilde{x}_{3} - \theta_{2} \tilde{x}_{2} - L_{2} {\text{sign}}\left( {\tilde{x}_{2} } \right) + \tilde{\Delta }_{1} = 0$$

(19)

Then, $\theta_{1} \tilde{x}_{3} + \tilde{\Delta }_{1} = - L_{2} {\text{sign}}\left( {\tilde{x}_{2} } \right)$. With the above results, the dynamics of $\tilde{\Delta }_{1}$ in (9) becomes

$$\dot{\tilde{\Delta }}_{1} = L_{4} L_{2} {\text{sign}}\left( {\tilde{x}_{2} } \right) - \Upsilon_{1} = L_{4} \left( { - \tilde{\Delta }_{1} - \theta_{1} \tilde{x}_{3} } \right) - \Upsilon_{1}$$

(20)

Likewise, consider the dynamics of $S_{3}$, one can derive the following inequality.

$$S_{3} \dot{S}_{3} = \tilde{x}_{3} \dot{\tilde{x}}_{3} = \tilde{x}_{3} \left( {\tilde{f}_{2} \left( {\tilde{x}_{2} ,\tilde{x}_{3} } \right) - L_{3} {\text{sign}}\left( {\tilde{x}_{3} } \right) + \tilde{\Delta }_{2} } \right)$$

(21)

Based on Assumption 2 (7),

$$\begin{aligned} S_{3} \dot{S}_{3} & \le \left| {\tilde{x}_{3} } \right|\left[ {\left| {\tilde{f}_{2} \left( {\tilde{x}_{2} ,\tilde{x}_{3} } \right)} \right| - L_{3} + \left| {\tilde{\Delta }_{2} } \right|} \right] \\ & \le \left| {\tilde{x}_{3} } \right|\left[ {\gamma_{3} \left| {\tilde{x}_{2} } \right| + \gamma_{4} \left| {\tilde{x}_{3} } \right| - L_{3} + \left| {\tilde{\Delta }_{2} } \right|} \right]\end{aligned}$$

(22)

Therefore, if we properly select the control gain L₃ as

$$L_{3} > \gamma_{3} \left| {\tilde{x}_{2} } \right| + \gamma_{4} \left| {\tilde{x}_{3} } \right| + \left| {\tilde{\Delta }_{2} } \right| + \sigma_{3}$$

(23)

where $\sigma_{3}$ is a small positive real constant. Then $S_{3} \dot{S}_{3} < - \sigma_{3} \left| {\tilde{x}_{3} } \right| \le 0$, $\tilde{x}_{3}$ will converge to zero in a finite time T₃ > 0 and $\tilde{x}_{3} = \dot{\tilde{x}}_{3} = 0$. Therefore, the dynamics of $\tilde{x}_{3}$ in (9) can be rewritten as

$$\dot{\tilde{x}}_{3} = - \theta_{3} \tilde{x}_{2} - \theta_{4} \tilde{x}_{3} - L_{3} {\text{sign}}\left( {\tilde{x}_{3} } \right) + \tilde{\Delta }_{2} = 0$$

(24)

Furtherly, one can derive $\tilde{\Delta }_{2} = - L_{3} {\text{sign}}\left( {\tilde{x}_{3} } \right)$, with $\dot{\tilde{\Delta }}_{2} = L_{5} L_{3} {\text{sign}}\left( {\tilde{x}_{3} } \right) - \Upsilon_{1}$ in (9), the following equation can be obtained.

$$\dot{\tilde{\Delta }}_{2} + L_{5} \tilde{\Delta }_{2} + \Upsilon_{1} = 0$$

(25)

It can be seen that $\dot{\tilde{\Delta }}_{2} + L_{5} \tilde{\Delta }_{2} + \Upsilon_{1} = 0$ is a first-order derivative equation, the solution for Eq. (25) is

$$\tilde{\Delta }_{2} = e^{{ - L_{5} t}} \left( {C + \int {\Upsilon_{1} e^{{ - L_{5} t}} } dt} \right)$$

(26)

As long as the control gain $L_{5} > 0$, $\tilde{\Delta }_{2}$ will converge to zero in a finite time T₄ > 0. Obviously, the convergence of $\tilde{x}_{3}$ is irrelated to that of $\dot{\tilde{\Delta }}_{1}$, therefore, Eq. (20) can be rewritten as

$$\dot{\tilde{\Delta }}_{1} = L_{4} \left( { - \tilde{\Delta }_{1} - \theta_{1} \tilde{x}_{3} } \right) - \Upsilon_{1} = - L_{4} \tilde{\Delta }_{1} - \Upsilon_{1}$$

(27)

Similar to Eq. (25), both of them are first-order derivative equations. Therefore, as long as the control gain $L_{4} > 0$, $\tilde{\Delta }_{1}$ will converge to zero in a finite time T₅ > 0. Define a new variable T as

$$T = {\text{sup}}\left\{ {T_{{1}} ,T_{{2}} ,T_{{3}} ,T_{{4}} ,T_{{5}} } \right\}$$

(28)

From all above, $\tilde{\user2{x}}$ will converge to zero in a finite time T > 0. The ESMO is finite-time stable. End of the proof.

Remark 1

The principle of equivalence and saturation functions can be employed in the ESMO, and the final formula of the ESMO can be presented as [4]

$$\begin{gathered} \left\{ \begin{gathered} \dot{\hat{x}}_{1} = \hat{x}_{2} + L_{1} \frac{{x_{1} - \hat{x}_{1} }}{{\left| {x_{1} - \hat{x}_{1} } \right| + \delta_{1} }} \hfill \\ v_{2eq} = L_{1} \frac{{x_{1} - \hat{x}_{1} }}{{\left| {x_{1} - \hat{x}_{1} } \right| + \delta_{1} }} \hfill \\ \dot{\hat{x}}_{2} = \theta_{1} \hat{x}_{3} - \theta_{2} \hat{x}_{2} + L_{2} \frac{{v_{2eq} }}{{\left| {v_{2eq} } \right| + \delta_{2} }} + \hat{\Delta }_{1} \hfill \\ \dot{\hat{x}}_{3} = - \theta_{3} \hat{x}_{2} - \theta_{4} \hat{x}_{3} + \theta_{5} Q_\text{L} + L_{3} \frac{{x_{3} - \hat{x}_{3} }}{{\left| {x_{3} - \hat{x}_{3} } \right| + \delta_{3} }} + \hat{\Delta }_{2} \hfill \\ \end{gathered} \right. \hfill \\ \dot{\hat{\Delta }}_{1} = L_{4} L_{2} \frac{{v_{2eq} }}{{\left| {v_{2eq} } \right| + \delta_{2} }} \hfill \\ \dot{\hat{\Delta }}_{2} = L_{5} L_{3} \frac{{x_{3} - \hat{x}_{3} }}{{\left| {x_{3} - \hat{x}_{3} } \right| + \delta_{3} }} \hfill \\ \end{gathered}$$

(29)

where, δ_i are three small positive real constants, which can eliminate the chattering phenomenon in sliding mode surface.

Remark 2

It needs to be emphasized that even if the saturation function can suppress high-frequency disturbances in the ESMO, there will inevitably be estimation noise in the estimated values of the observer. The main reasons are as follows:

• 1. The ESMO inherently uses a discontinuous control action to drive the system states onto the sliding surface S_i. This can result in high-frequency oscillations around the sliding surface, known as chattering, which may manifest as noises in the estimation.

• 2. The real hydraulic control system depends on analog feedback sensors (the displacement sensor, and two pressure sensors). Therefore, the ESMO also relies on these sensors with measurement noises as inputs, this noise can propagate through the observer dynamics and affect the state estimates. Although ESMO is robust against disturbances, it is not completely immune to measurement noise.

• 3. According to the model of the EHSS, there are model errors between the real hydraulic system dynamics and the model used in the ESMO, especially these errors might be dynamic or stochastic in nature. These factors can introduce errors in the state estimation of the ESMO, which might be perceived as estimation noise.

• 4. In addition, the ESMO’s too-large control gains, incomplete resistance to external disturbances, and, numerical computational errors or computational delays could be reflected as noise in the state estimation.

3.2 Development of the OCNCS

Define the system state tracking error vector as

$$z = \left[ {z_{{1}} ,z_{{2}} ,z_{{3}} } \right]^{T} = [x_{{1}} - y_{{\text{d}}} ,x_{{2}} - \alpha_{{1}} ,x_{{3}} - \alpha_{{2}} ]^{T}$$

(30)

where, z₁ denotes the displacement tracking error and |z₁|< k_b, k_b is the system output tracking error constraint, and the system output k_cl < x₁ < k_cu, k_cu is the system output upper boundary k_cu = y_d + k_b,, k_cl is the system output lower boundary, k_cl = y_d-k_b, α₁ and α₂ are two virtual control laws in the controller design.

Theorem

Combining the system state representation Eq. (5) and two estimation values $\hat{\Delta }_{1}$ and $\hat{\Delta }_{2}$ from the ESMO, there exists the following control law, which will make the output tracking error meet |z₁|< k_b, ∀t > 0.

$$\left\{ \begin{aligned} z_{1} & = x_{1} - y_{{\text{d}}} , \\ \alpha_{1} & = - k_{1} z_{1} \left( {k_{{\text{b}}}^{{\text{2}}} - z_{1}^{2} } \right) + \dot{y}_\text{d} , \\ z_{2} & = x_{2} - \alpha_{1} , \\ \alpha_{2} & = {{\left( {\theta_{2} x_{2} - k_{2} z_{2} + \dot{\alpha }_{1} - {{z_{1} } \mathord{\left/ {\vphantom {{z_{1} } {\left( {k_{{\text{b}}}^{{\text{2}}} - z_{1}^{2} } \right)}}} \right. \kern-0pt} {\left( {k_{{\text{b}}}^{{\text{2}}} - z_{1}^{2} } \right)}} - \hat{\Delta }_{1} } \right)} \mathord{\left/ {\vphantom {{\left( {\theta_{2} x_{2} - k_{2} z_{2} + \dot{\alpha }_{1} - {{z_{1} } \mathord{\left/ {\vphantom {{z_{1} } {\left( {k_{{\varvec{b}}}^{{\varvec{2}}} - z_{1}^{2} } \right)}}} \right. \kern-0pt} {\left( {k_{{\varvec{b}}}^{{\varvec{2}}} - z_{1}^{2} } \right)}} - \hat{\Delta }_{1} } \right)} {\theta_{1} ,}}} \right. \kern-0pt} {\theta_{1} ,}} \\ z_{3} & = x_{3} - \alpha_{2} , \\ Q_\text{L} & = {{\left( {\theta_{3} x_{2} + \theta_{4} x_{3} - \hat{\Delta }_{2} + \dot{\alpha }_{2} - k_{3} z_{3} - \theta_{1} z_{2} } \right)} \mathord{\left/ {\vphantom {{\left( {\theta_{3} x_{2} + \theta_{4} x_{3} - \hat{\Delta }_{2} + \dot{\alpha }_{2} - k_{3} z_{3} - \theta_{1} z_{2} } \right)} {\theta_{5} .}}} \right. \kern-0pt} {\theta_{5} .}} \\ \end{aligned} \right.$$

(31)

where, k_i are three positive control gains. If control gains L_j+3 are properly chosen such L_j+3 > 1/4k_j+1, then, |z₁|< k_b, and z enters in a bounded hypersphere ball H_r, and holds in H_r, ∀t > 0, ∀t > t₀.

$$\begin{aligned} H_\text{r} &= - k_{1} z_{1}^{2} - \sum\limits_{i = 1}^{2} {k_{j + 1} \left( {z_{j + 1} - \frac{1}{{2k_{j + 1} }}\tilde{\Delta }_{j} } \right)^{2} } \\ &\quad - \sum\limits_{j = 1}^{2} {\xi_{j} \left( {\tilde{\Delta }_{j} - \frac{1}{{2\xi_{j} }}\Upsilon_{j} } \right)^{2} } + \sum\limits_{j = 1}^{2} {\frac{1}{{4\xi_{j} }}\Upsilon_{j\max }^{2} } \end{aligned}$$

(32)

where, ξ_j = L_j+3–1/4k_j+1.

Proof

Step 1: Consider the BLF as.

$$\chi_{1} { = }\frac{1}{2}\ln \frac{{k_{{\text{b}}}^{{\text{2}}} }}{{k_{{\text{b}}}^{{\text{2}}} - z_{1}^{2} }}$$

(33)

The time derivative of $\chi_{1}$ yields

$$\dot{\chi }_{1} { = }\frac{{z_{1} \dot{z}_{1} }}{{k_{{\text{b}}}^{{\text{2}}} - z_{1}^{2} }}$$

(34)

The time derivative of $z_{1}$ can be derived by Eq. (30).

$$\dot{z}_{1} = \dot{x}_{1} - \dot{y}_{{\text{d}}} = x_{2} - \dot{y}_{{\text{d}}}$$

(35)

Therefore, Eq. (34) can be rewritten as

$$\dot{\chi }_{1} { = }\frac{{z_{1} \left( {z_{2} + \alpha_{1} - \dot{y}_{{\text{d}}} } \right)}}{{k_{{\text{b}}}^{{\text{2}}} - z_{1}^{2} }}$$

(36)

With the virtual control law α₁ in (22), one can obtain

$$\dot{\chi }_{1} = - k_{1} z_{1}^{2} + \frac{{z_{1} z_{2} }}{{k_\text{b}^{2} - z_{1}^{2} }}$$

(37)

Step 2: Considering the tracking error $z_{2}$ and the estimation error $\tilde{\Delta }_{1}$, define the following Lyapunov function as

$$\chi_{2} = \chi_{1} + \frac{{z_{2}^{2} }}{2} + \frac{{\tilde{\Delta }_{1}^{2} }}{2}$$

(38)

Given $\dot{\chi }_{1}$ in (37), the time derivative of $\chi_{2}$ yields

$$\dot{\chi }_{2} { = } - k_{1} z_{1}^{2} + \frac{{z_{1} z_{2} }}{{k_\text{b}^{2} - z_{1}^{2} }} + z_{2} \dot{z}_{2} + \tilde{\Delta }_{1} \dot{\tilde{\Delta }}_{1}$$

(39)

The $\dot{z}_{2}$ can be derived from Eq. (30).

$$\dot{z}_{2} = \dot{x}_{2} - \dot{\alpha }_{1}$$

(40)

With the dynamics $\dot{x}_{2} = \theta_{1} x_{3} - \theta_{2} x_{2} + \Delta_{1}$ in (5) and $\Delta_{1} = \hat{\Delta }_{1} + \tilde{\Delta }_{1}$, Eq. (40) can be rewritten as

$$\dot{z}_{2} = \theta_{1} x_{3} - \theta_{2} x_{2} + \hat{\Delta }_{1} + \tilde{\Delta }_{1} - \dot{\alpha }_{1}$$

(41)

Equation (39) can be rewritten in terms of Eq. (41).

$$\begin{aligned} \dot{\chi }_{2} & = - k_{1} z_{1}^{2} + \frac{{z_{1} z_{2} }}{{k_\text{b}^{2} - z_{1}^{2} }} + z_{2} \Big( \theta_{1} z_{3} + \theta_{1} \alpha_{2} - \theta_{2} x_{2} \\ &\quad+ \hat{\Delta }_{1} + \tilde{\Delta }_{1} - \dot{\alpha }_{1} \Big) + \tilde{\Delta }_{1} \dot{\tilde{\Delta }}_{1}\end{aligned}$$

(42)

With the virtual control law $\alpha_{2}$ in (22) and $\dot{\tilde{\Delta }}_{1} = - L_{4} \tilde{\Delta }_{1} - \Upsilon_{1}$ in (27), one can obtain

$$\dot{\chi }_{2} = - k_{1} z_{1}^{2} - k_{2} z_{2}^{2} + \theta_{1} z_{2} z_{3} + z_{2} \tilde{\Delta }_{1} + \tilde{\Delta }_{1} \left( { - L_{4} \tilde{\Delta }_{1} - \Upsilon_{1} } \right)$$

(43)

Step 3: The following Lyapunov function can be defined in terms of the tracking error $z_{3}$ and the estimation error $\tilde{\Delta }_{2}$.

$$\chi_{3} { = }\chi_{2} + \frac{{z_{3}^{2} }}{2} + \frac{{\tilde{\Delta }_{2}^{2} }}{2}$$

(44)

Given $\dot{\chi }_{2}$ in (43), the time derivative of $\chi_{3}$ yields

$$\begin{aligned} \chi_{3}& = - k_{1} z_{1}^{2} - k_{2} z_{2}^{2} + \theta_{1} z_{2} z_{3} + z_{2} \tilde{\Delta }_{1} \\ &\quad+ \tilde{\Delta }_{1} \left( { - L_{4} \tilde{\Delta }_{1} - \Upsilon_{1} } \right) + z_{3} \dot{z}_{3} + \tilde{\Delta }_{2} \dot{\tilde{\Delta }}_{2} \end{aligned}$$

(45)

$\dot{z}_{3}$ in (45) can be obtained by Eq. (30).

$$\dot{z}_{3} = \dot{x}_{3} - \dot{\alpha }_{2}$$

(46)

$\dot{x}_{3}$ in (46) can be obtained by Eq. (5), $\dot{x}_{3} = - \theta_{3} x_{2} - \theta_{4} x_{3} + \theta_{5} Q_\text{L} + \Delta_{2}$, with $\Delta_{2} = \hat{\Delta }_{2} + \tilde{\Delta }_{2}$, Eq. (46) can be rewritten as

$$\dot{z}_{3} = - \theta_{3} x_{2} - \theta_{4} x_{3} + \theta_{5} Q_\text{L} + \hat{\Delta }_{2} + \tilde{\Delta }_{2} - \dot{\alpha }_{2}$$

(47)

Furtherly, Eq. (45) can be rewritten as

$$\begin{aligned} \chi_{3} = & - k_{1} z_{1}^{2} - k_{2} z_{2}^{2} + \theta_{1} z_{2} z_{3} + z_{2} \tilde{\Delta }_{1} + \tilde{\Delta }_{1} \left( { - L_{4} \tilde{\Delta }_{1} - \Upsilon_{1} } \right) \\ & + z_{3} \left( { - \theta_{3} x_{2} - \theta_{4} x_{3} + \theta_{5} Q_\text{L} + \hat{\Delta }_{2} + \tilde{\Delta }_{2} - \dot{\alpha }_{2} } \right) + \tilde{\Delta }_{2} \dot{\tilde{\Delta }}_{2} \\ \end{aligned}$$

(48)

With the real control law $Q_\text{L}$ in (31) and $\dot{\tilde{\Delta }}_{2} = - L_{5} \tilde{\Delta }_{2} - \Upsilon_{2}$ in (25), one can obtain

$$\begin{aligned} \dot{\chi }_{3} & = - k_{1} z_{1}^{2} - k_{2} z_{2}^{2} - k_{3} z_{3}^{2} + z_{2} \tilde{\Delta }_{1} - L_{4} \tilde{\Delta }_{1}^{2} - \tilde{\Delta }_{1} \Upsilon_{1} \\ &\quad + z_{3} \tilde{\Delta }_{2} + \tilde{\Delta }_{2} \left( { - L_{5} \tilde{\Delta }_{2} - \Upsilon_{2} } \right) \\ &= - k_{1} z_{1}^{2} - k_{2} \left( {z_{2} - \frac{1}{{2k_{2} }}\tilde{\Delta }_{1} } \right)^{2} - k_{3} \left( {z_{3} - \frac{1}{{2k_{3} }}\tilde{\Delta }_{2} } \right)^{2}\\ &\quad - \left( {L_{4} - 1/4k_{2} } \right)\left( {\tilde{\Delta }_{1}- \frac{1}{{2\left( {L_{4} - 1/4k_{2} } \right)}}\Upsilon_{1} } \right)^{2} \\ &\quad - \left( {L_{5} - 1/4k_{3} } \right)\left( {\tilde{\Delta }_{2} - \frac{1}{{2\left( {L_{5} - 1/4k_{3} } \right)}}\Upsilon_{2} } \right)^{2} \\ &\quad + \frac{1}{{4\left( {L_{4} - 1/4k_{2} } \right)}}\Upsilon_{1}^{2} + \frac{1}{{4\left( {L_{5} - 1/4k_{3} } \right)}}\Upsilon_{2}^{2} \\ \end{aligned}$$

(49)

With $\xi_{1} = L_{4} - 1/4k_{2}$ and $\xi_{2} = L_{5} - 1/4k_{3}$, Eq. (49) can be rewritten as

$$\begin{aligned} \dot{\chi }_{3} &= - k_{1} z_{1}^{2} - k_{2} \left( {z_{2} - \frac{1}{{2k_{2} }}\tilde{\Delta }_{1} } \right)^{2} - k_{3} \left( {z_{3} - \frac{1}{{2k_{3} }}\tilde{\Delta }_{2} } \right)^{2} \\ &\quad- \xi_{1} \left( {\tilde{\Delta }_{1} - \frac{1}{{2\xi_{1} }}\Upsilon_{1} } \right)^{2} - \xi_{2} \left( {\tilde{\Delta }_{2} - \frac{1}{{2\xi_{2} }}\Upsilon_{2} } \right)^{2} \\ &\quad+ \frac{1}{{4\xi_{1} }}\Upsilon_{1}^{2} + \frac{1}{{4\xi_{2} }}\Upsilon_{2}^{2} \\ = & - k_{1} z_{1}^{2} - \sum\limits_{j = 1}^{2} {k_{j + 1} \left( {z_{j + 1} - \frac{1}{{2k_{j + 1} }}\tilde{\Delta }_{j} } \right)^{2} } \\ &\quad- \sum\limits_{j = 1}^{2} {\xi_{j} \left( {\tilde{\Delta }_{j} - \frac{1}{{2\xi_{j} }}\Upsilon_{j} } \right)^{2} } + \sum\limits_{j = 1}^{2} {\frac{1}{{4\xi_{j} }}\Upsilon_{j\max }^{2} } \\ \end{aligned}$$

(50)

Therefore, if we properly select control gains k_i > 0 and $\xi_{j} > 0$, thus there is only one positive term $\sum\limits_{j = 1}^{2} {\frac{1}{{4\xi_{j} }}\Upsilon_{j\max }^{2} }$ in (50) and the other terms are all negative so that these negative terms can guarantee $\dot{\chi }_{3} < 0$. The closed-loop is bounded stable. The tracking error vector z can be guaranteed to enter in H_r in a finite time t₁ > 0 and holds in H_r, ∀t > t₀; furtherly, the system output tracking error |z₁|< k_b, ∀t > t₀. End of the proof.

3.3 Stability of the Closed-loop

To prove the stability of the closed loop, we define an overall Lyapunov function as

$$\chi_{{\text{h}}} { = }\frac{1}{2}\ln \frac{{k_\text{b}^{2} }}{{k_\text{b}^{2} - z_{1}^{2} }} + \frac{{z_{2}^{2} }}{2} + \frac{{z_{3}^{2} }}{2} + \frac{{\tilde{\Delta }_{1}^{2} }}{2} + \frac{{\tilde{\Delta }_{2}^{2} }}{2} + \frac{{S_{1}^{2} }}{2} + \frac{{S_{2}^{2} }}{2} + \frac{{S_{3}^{2} }}{2}$$

(51)

Thus, one can derive the time derivative of $\chi_{{\varvec{h}}}$ yields

$$\begin{aligned} \dot{\chi }_{{\text{h}}} & { = }\frac{{z_{1} \dot{z}_{1} }}{{k_{{\text{b}}}^{{\text{2}}} - z_{1}^{2} }} + z_{2} \dot{z}_{2} + z_{3} \dot{z}_{3} + \tilde{\Delta }_{1} \dot{\tilde{\Delta }}_{1} + \tilde{\Delta }_{2} \dot{\tilde{\Delta }}_{2} \\ &\quad+ S_{1} \dot{S}_{1} + S_{2} \dot{S}_{2} + S_{3} \dot{S}_{3}\end{aligned}$$

(52)

According to the stability proof for the ESMO, Eq. (52) can be rewritten with results of Eq. (11), (16), and (22) yields

$$\begin{aligned} \dot{\chi }_{{\text{h}}} &< \frac{{z_{1} \dot{z}_{1} }}{{k_{{\text{b}}}^{{\text{2}}} - z_{1}^{2} }} + z_{2} \dot{z}_{2} + z_{3} \dot{z}_{3} + \tilde{\Delta }_{1} \dot{\tilde{\Delta }}_{1} + \tilde{\Delta }_{2} \dot{\tilde{\Delta }}_{2} \\ &\quad{ + }\left| {\tilde{x}_{1} } \right|\left[ {\left| {\tilde{x}_{2} } \right| - L_{1} } \right] + \left| {\tilde{x}_{2} } \right|\left[ {\gamma_{1} \left| {\tilde{x}_{2} } \right| + \gamma_{2} \left| {\tilde{x}_{3} } \right| - L_{2} + \left| {\tilde{\Delta }_{1} } \right|} \right] \\ &\quad+ \left| {\tilde{x}_{3} } \right|\left[ {\gamma_{3} \left| {\tilde{x}_{2} } \right| + \gamma_{4} \left| {\tilde{x}_{3} } \right| - L_{3} + \left| {\tilde{\Delta }_{2} } \right|} \right] \hfill \\ \end{aligned}$$

(53)

Furtherly, based on the stability proof for the OCNCS, Eq. (53) can be rewritten with Eq. (49) yields

$$\begin{aligned} \dot{\chi }_{{\text{h}}} &= - k_{1} z_{1}^{2} - k_{2} z_{2}^{2} - k_{3} z_{3}^{2} + z_{2} \tilde{\Delta }_{1} - L_{4} \tilde{\Delta }_{1}^{2} - \tilde{\Delta }_{1} \Upsilon_{1} \\ &\quad+ z_{3} \tilde{\Delta }_{2} + \tilde{\Delta }_{2} \left( { - L_{5} \tilde{\Delta }_{2} - \Upsilon_{2} } \right) + \left| {\tilde{x}_{1} } \right|\left[ {\left| {\tilde{x}_{2} } \right| - L_{1} } \right] \\ &\quad + \left| {\tilde{x}_{2} } \right|\left[ {\gamma_{1} \left| {\tilde{x}_{2} } \right| + \gamma_{2} \left| {\tilde{x}_{3} } \right| - L_{2} + \left| {\tilde{\Delta }_{1} } \right|} \right] \\ &\quad + \left| {\tilde{x}_{3} } \right|\left[ {\gamma_{3} \left| {\tilde{x}_{2} } \right| + \gamma_{4} \left| {\tilde{x}_{3} } \right| - L_{3} + \left| {\tilde{\Delta }_{2} } \right|} \right] \\ &= - k_{1} z_{1}^{2} - k_{2} \left( {z_{2} - \frac{1}{{2k_{2} }}\tilde{\Delta }_{1} } \right)^{2} - k_{3} \left( {z_{3} - \frac{1}{{2k_{3} }}\tilde{\Delta }_{2} } \right)^{2} \\ &\quad - \xi_{1} \left( {\tilde{\Delta }_{1} - \frac{1}{{2\xi_{1} }}\Upsilon_{1} } \right)^{2} - \xi_{2} \left( {\tilde{\Delta }_{2} - \frac{1}{{2\xi_{2} }}\Upsilon_{2} } \right)^{2} \\ & \quad + \frac{1}{{4\xi_{1} }}\Upsilon_{1\max }^{2} + \frac{1}{{4\xi_{2} }}\Upsilon_{2\max }^{2} { + }\left| {\tilde{x}_{1} } \right|\left[ {\left| {\tilde{x}_{2} } \right| - L_{1} } \right] \\ &\quad + \left| {\tilde{x}_{2} } \right|\left[ {\gamma_{1} \left| {\tilde{x}_{2} } \right| + \gamma_{2} \left| {\tilde{x}_{3} } \right| - L_{2} + \left| {\tilde{\Delta }_{1} } \right|} \right] \\ &\quad + \left| {\tilde{x}_{3} } \right|\left[ {\gamma_{3} \left| {\tilde{x}_{2} } \right| + \gamma_{4} \left| {\tilde{x}_{3} } \right| - L_{3} + \left| {\tilde{\Delta }_{2} } \right|} \right] \\ \end{aligned}$$

(54)

Thus, if one properly selects the control gains as k_i > 0, $L_{1} > \left| {\tilde{x}_{2} } \right| + \sigma_{1}$, $L_{2} > \gamma_{1} \left| {\tilde{x}_{2} } \right| + \gamma_{2} \left| {\tilde{x}_{2} } \right| + \left| {\tilde{\Delta }_{1} } \right| + \sigma_{2}$, $L_{3} > \gamma_{3} \left| {\tilde{x}_{2} } \right| + \gamma_{4} \left| {\tilde{x}_{3} } \right| + \left| {\tilde{\Delta }_{2} } \right| + \sigma_{3}$, $\xi_{1} = L_{4} - 1/4k_{2} > 0$ and $\xi_{2} = L_{5} - 1/4k_{3} > 0$, one can obtain

$$\begin{aligned} \dot{\chi }_{{\text{h}}} & < - k_{1} z_{1}^{2} - \sum\limits_{j = 1}^{2} {k_{j + 1} \left( {z_{j + 1} - {{\tilde{\Delta }_{j} } \mathord{\left/ {\vphantom {{\tilde{\Delta }_{j} } {2k_{j + 1} }}} \right. \kern-0pt} {2k_{j + 1} }}} \right)^{2} } \\ &\quad- \sum\limits_{j = 1}^{2} {\xi_{j} \left( {\tilde{\Delta }_{j} - {{\Upsilon_{j} } \mathord{\left/ {\vphantom {{\Upsilon_{j} } {2\xi_{j} }}} \right. \kern-0pt} {2\xi_{j} }}} \right)^{2} } + \sum\limits_{j = 1}^{2} {{{\Upsilon_{j\max }^{2} } \mathord{\left/ {\vphantom {{\Upsilon_{j\max }^{2} } {4\xi_{j} }}} \right. \kern-0pt} {4\xi_{j} }}} \\ &\quad- \sum\limits_{i = 1}^{2} {\sigma_{i} \left| {x_{i} } \right|}\end{aligned}$$

(55)

It can be seen that only the term $\sum\limits_{j = 1}^{2} {{{\Upsilon_{j\max }^{2} } \mathord{\left/ {\vphantom {{\Upsilon_{j\max }^{2} } {4\xi_{j} }}} \right. \kern-0pt} {4\xi_{j} }}}$ is positive, other terms are all negative. These negative terms can guarantee the stability of the closed-loop in the presence of $\sum\limits_{j = 1}^{2} {{{\Upsilon_{j\max }^{2} } \mathord{\left/ {\vphantom {{\Upsilon_{j\max }^{2} } {4\xi_{j} }}} \right. \kern-0pt} {4\xi_{j} }}}$.

Remark 3

The convergence of the proposed controller depends on the positive term $\sum\limits_{j = 1}^{2} {{{\Upsilon_{j\max }^{2} } \mathord{\left/ {\vphantom {{\Upsilon_{j\max }^{2} } {4\xi_{j} }}} \right. \kern-0pt} {4\xi_{j} }}}$. There is only one positive term in $\dot{\chi }_{{\text{h}}}$, other terms are all negative. If all the control gains are properly selected large enough, which will shrink the hypersphere ball H_r, the convergence of the proposed control scheme can be guaranteed. In addition, if the system uncertainties $\Delta_{j}$ vary slowly or are two constants so that $\Upsilon_{j} \approx 0$, thus Eq. (55) becomes.

$$\begin{aligned} \dot{\chi }_{3} &\approx - k_{1} z_{1}^{2} - \sum\limits_{j = 1}^{2} {k_{j + 1} \left( {z_{j + 1} - \frac{1}{{2k_{j + 1} }}\tilde{\Delta }_{j} } \right)^{2} } \\ &\quad- \sum\limits_{j = 1}^{2} {\xi_{j} \left( {\tilde{\Delta }_{j} - \frac{1}{{2\xi_{j} }}\Upsilon_{j} } \right)^{2} } \sum\limits_{i = 1}^{2} {\sigma_{i} \left| {x_{i} } \right|} \le 0\end{aligned}$$

(56)

Therefore, the closed-loop is bounded stable. Therefore, the overall architecture of the proposed control scheme can be presented.

4 Comparative Simulation and Experimental Study

In the simulation and experimental study, the desired displacement y_d is a sine wave signal with an amplitude of 0.01 m and a frequency of 1 Hz. Table 1 presents the key hydraulic parameters. In the simulation study, Δ₁ = 2sin(2πωt), Δ₂ = 2 × 10⁹sin(2πωt) (Fig. 2).

Table 1 Key hydraulic parameters

Fig. 2

The overall architecture of the closed loop

i. The BC: With the state representation, the control law is $\alpha_{1} = - k_{1} z_{1} + \dot{y}_{\text{d}}$, $\alpha_{2} = {{\left( {k_{2} z_{2} + z{}_{1} + \theta_{2} x_{2} + \dot{\alpha }_{1} } \right)} \mathord{\left/ {\vphantom {{\left( {k_{2} z_{2} + z{}_{1} + \theta_{2} x_{2} + \dot{\alpha }_{1} } \right)} {\theta_{1} }}} \right. \kern-0pt} {\theta_{1} }}$, $Q_{\text{L}} = {{\left( {\theta_{1} z_{2} + k_{3} z_{3} + \dot{\alpha }_{2} + \theta_{3} x_{2} + \theta_{4} x_{3} } \right)} \mathord{\left/ {\vphantom {{\left( {\theta_{1} z_{2} + k_{3} z_{3} + \dot{\alpha }_{2} + \theta_{3} x_{2} + \theta_{4} x_{3} } \right)} {\theta_{5} }}} \right. \kern-0pt} {\theta_{5} }}$, where, $\alpha_{1}$ and $\alpha_{2}$ are the virtual control law in the BC. In the simulation study, k₁ = 319, k₂ = 300, k₃ = 300. In the experimental study, k₁ = 130, k₂ = 125, k₃ = 110. Results are presented in Fig. 3 (simulation) and Fig. 9 (experiment) respectively.

Fig. 3

The BC’s tracking performance

ii. The OCNCS: With $\hat{\Delta }_{j} = 0$, the OCNCS is conducted on the EHSS. In the simulation study, k₁ = 200, k₂ = 2000, k₃ = 200. In the experimental study, k₁ = 130, k₂ = 400, k₃ = 130. Results are presented in Fig. 4 (simulation) and Fig. 10 (experiment) respectively.

Fig. 4

The OCNCS’ tracking performance

iii. The ESMO-based RABC: This controller was presented in [4], and its control law yields.

The ESMO:

$$\begin{gathered} \left\{ {\begin{array}{*{20}l} {\dot{\hat{x}}_{1} = \hat{x}_{2} + L_{1} {{\left( {x_{1} - \hat{x}_{1} } \right)} \mathord{\left/ {\vphantom {{\left( {x_{1} - \hat{x}_{1} } \right)} {\left( {\left| {x_{1} - \hat{x}_{1} } \right| + \delta_{1} } \right)}}} \right. \kern-0pt} {\left( {\left| {x_{1} - \hat{x}_{1} } \right| + \delta_{1} } \right)}}} \hfill \\ {v_\text{2eq} = L_{1} {{\left( {x_{1} - \hat{x}_{1} } \right)} \mathord{\left/ {\vphantom {{\left( {x_{1} - \hat{x}_{1} } \right)} {\left( {\left| {x_{1} - \hat{x}_{1} } \right| + \delta_{1} } \right)}}} \right. \kern-0pt} {\left( {\left| {x_{1} - \hat{x}_{1} } \right| + \delta_{1} } \right)}}} \hfill \\ {\dot{\hat{x}}_{2} = \theta_{1} \hat{x}_{3} - \theta_{2} \hat{x}_{2} + L_{2} {{v_\text{2eq} } \mathord{\left/ {\vphantom {{v_\text{2eq} } {\left( {\left| {v_\text{2eq} } \right| + \delta_{2} } \right)}}} \right. \kern-0pt} {\left( {\left| {v_\text{2eq} } \right| + \delta_{2} } \right)}} + \hat{\Delta }_{1} } \hfill \\ {\dot{\hat{x}}_{3} = - \theta_{3} \hat{x}_{2} - \theta_{4} \hat{x}_{3} + \theta_{5} Q_\text{L} + L_{3} {{\left( {P_\text{L} - \hat{x}_{3} } \right)} \mathord{\left/ {\vphantom {{\left( {P_\text{L} - \hat{x}_{3} } \right)} {\left( {\left| {P_\text{L} - \hat{x}_{3} } \right| + \delta_{3} } \right)}}} \right. \kern-0pt} {\left( {\left| {P_\text{L} - \hat{x}_{3} } \right| + \delta_{3} } \right)}} + \hat{\Delta }_{2} } \hfill \\ \end{array} } \right. \hfill \\ \dot{\hat{\Delta }}_{1} = L_{4} L_{2} {{v_\text{2eq} } \mathord{\left/ {\vphantom {{v_\text{2eq} } {\left( {\left| {v_\text{2eq} } \right| + \delta_{2} } \right)}}} \right. \kern-0pt} {\left( {\left| {v_\text{2eq} } \right| + \delta_{2} } \right)}} \hfill \\ \dot{\hat{\Delta }}_{2} = L_{5} L_{3} {{\left( {x_{3} - \hat{x}_{3} } \right)} \mathord{\left/ {\vphantom {{\left( {x_{3} - \hat{x}_{3} } \right)} {\left( {\left| {x_{3} - \hat{x}_{3} } \right| + \delta_{3} } \right)}}} \right. \kern-0pt} {\left( {\left| {x_{3} - \hat{x}_{3} } \right| + \delta_{3} } \right)}} \hfill \\ \end{gathered}$$

(57)

The RABC control law:

$$\left\{ {\begin{array}{*{20}l} {\left[ {z_{1} ,z_{2} ,z_{3} } \right]^{T} = \left[ {x_{1} - x_{pr} ,x_{2} - \alpha_{1} ,x_{3} - \alpha_{2} } \right]^{T} } \hfill \\ {Q_\text{L} = \frac{1}{{\theta_{5} }}\left( { - k_{3} z_{3} + \theta_{1} z_{2} + \hat{\theta }_{3} x_{2} + \hat{\theta }_{4} x_{3} - \hat{\Delta }_{2} + \dot{\alpha }_\text{2c} } \right)} \hfill \\ {\dot{\hat{\theta }}_{2} = \tau_{2} \varphi_{2} ,\,\dot{\hat{\theta }}_{3} = \tau_{3} \varphi_{3} ,\,\dot{\hat{\theta }}_{4} = \tau_{4} \varphi_{4} } \hfill \\ \end{array} } \right.$$

(58)

where, L₁ = 5, L₂ = 0.8, L₃ = 30, L₄ = 45, L₅ = 4 × 10⁹, δ₁ = 0.001, δ₂ = 0.003, δ₃ = 0.0005, k₁ = 130, k₂ = 125, k₃ = 120 and τ₂ = τ₃ = τ₄ = 1 × 10^–15. Results are presented in Fig. 5 (simulation) and Fig. 11 (experiment) respectively.

Fig. 5

The ESMO-based RABC’s tracking performance

iv. The ESMO-based OCNCS (proposed): With estimation values of $\hat{\Delta }_{j}$ from the ESMO, the proposed control law is conducted on the EHSS. In the simulation study, L₁ = 70, L₂ = 5 × 10³, L₃ = 9 × 10⁹, L₄ = 400, L₅ = 200, δ₁ = δ₂ = 0.01, δ₃ = 0.05, k₁ = 200, k₂ = 2000 and k₃ = 200. In the experimental study, L₁ = 5, L₂ = 0.8, L₃ = 30, L₄ = 45, L₅ = 4 × 10⁹, δ₁ = 0.001, δ₂ = 0.003, δ₃ = 0.0005, k₁ = 130, k₂ = 400 and k₃ = 130. Results are presented in Fig. 6, Fig. 7 (simulation) and Fig. 12, Fig. 13 (experiment) respectively.

Fig. 6

The ESMO-based OCNCS’s tracking performance

Fig. 7

The ESMO’s performance: a the estimation of x₁, b the estimation of x₂, c the estimation of x₃, d the estimation of Δ₁, e the estimation of Δ₂

Remark 4

It’s crucial to recognize that some experimental system parameters are not directly measured, but rather inferred from estimates. Some key parameters such as the viscous damping coefficient of the hydraulic oil B_p, the effective bulk modulus of the oil β_e, and the hydraulic actuator’s total leakage coefficient C_tl are all based on estimated values. Consequently, the EHSS is subject to parameter uncertainties due to variations in these estimates. The unaccounted disturbance, denoted as qt, originates from pressure fluctuations within the hydraulic cylinder chambers. These fluctuations are attributed to several factors, including discrepancies between the modeled and actual parameters of the EHSS experimental setup, vibrations of the mechanical structure tied to the piston rod’s motion, and the nonlinear behavior of the hydraulic oil. Frictional forces referred to as F_F, occur at the contact interface between the piston rod and the cylinder. In parallel, an external disturbance force F_L, is induced by a 2 V control signal applied by the control system to the force-loading hydraulic cylinder, adding another layer of complexity to the system’s dynamic behavior.

4.1 Comparative Simulation Results

As is shown in Fig. 3, it can be seen that the BC can’t constrain the tracking error within k_b = 0.001 m in the presence of sinusoidal disturbances, which reveals the BC has poor robustness. As is shown in Fig. 4, the OCNCS has strong robustness when faced with sinusoidal disturbances, which robustly confines the tracking error within a threshold of k_b = 0.001. As is shown in Fig. 5, the ESMO-based RABC employs the ESMO to estimate and compensate for the sinusoidal disturbances. Therefore, it conducts an excellent tracking performance. Likewise, as is shown in Fig. 6, the proposed controller also shows excellent tracking performance due to the ESMO estimating and compensating for the system uncertainties (Fig. 7).

The peak error (PE) and root mean square error (RMSE) can illustrate the performance of four controllers.

$${\text{PE}} = \mathop {{\text{max}}}\limits_{1 \to n} \left\{ {|z_{1} |} \right\},\,\,{\text{RMSE}} = \sqrt {\frac{{\sum\limits_{i}^{n} {\left( {R_{in,i} - R_{out,i} } \right)^{2} } }}{n}}$$

(59)

where R_in,i denotes the reference signal, R_out,i denotes the displacement sensor signal, and n denotes the length. The PE of |z₁| and the RMSE results are presented in Table 2. In addition, the R-squared, the NSE (Nash–Sutcliffe efficiency) and the RSR (ratio of standard deviation) of the four controllers are also presented in Table 2. What’s more, the mean, the median, the skewness, the kurtosis, the CV (Coefficient of Variation) and the CI (confidence intervals) are also analyzed in Table 3. As is present in Table 2 and Table 3, the comprehensive performance metrics demonstrate that the proposed controller outperforms the ESMO-based RABC, the OCNCS and the BC in the simulation study.

Table 2 The performance indicator for four controllers

Table 3 The statistical properties of four controllers

Remark 5

It can be seen that in the estimation of x₁, x₂, x₃, Δ₁, and Δ₂ of the ESMO, noise appears to varying degrees. Most of the noise is concentrated at the peak positions, with the estimation of × 2 being the most severely affected because the true feedback value of x₂ is derived directly from the differentiation of x₁. The emergence of noise is mainly due to the following aspects: 1) The ESMO inherently uses a discontinuous control action, 2) The ESMO’s high control gains, 3) Incomplete resistance to external disturbances, 4) Basically, the normal operation of the ESMO relies on the controller trying to maintain the consistency between the system feedback displacement and the ideal displacement. However, the OCNCS needs great computation, especially under k_b = 0.001 m, which will bring unexpected computational errors or computational delays. These factors could be reflected as noise in the ESMO’s estimation.

4.2 Comparative experimental results

Figure 8 presents the real control system. The real control system’s hardware consists primarily of a host computer, a target computer, an A/D board PCI-1716, a D/A board ACL-6126, and a signal conditioning system. The displacement signal from the displacement sensor and two pressure signals from two pressure sensors with current signals from 4 to 20 mA will be optimized by the signal conditioning system and converted into voltage signals from 2 to 10 V, then these will be acquired by the PCI-1716 board in the target computer. The control input voltage from -10 V to 10 V from the ACL-6126 board, which is conducted by the control algorithm, will be optimized by the signal conditioning system and converted into a current signal from − 40 mA to 40 mA to drive the servo valve. Based on the MATLAB xPC target fast prototyping technology, the host computer is connected with the target computer (IPC-610) by the TCP/IP. To operate the experimental bench in real-time, the control algorithm, which was created by the MATLAB/Simulink in the host computer, will be converted into a C program and then downloaded into the target computer. The sample time of the control system is 1 ms.

Fig. 8

The real control system of the EHSS

As is shown in Fig. 9, just as in the simulations, the BC is unable to maintain the tracking error within the range of k_b = 0.001 in the experiments. Whereas, the OCNCS can robustly hold the tracking error within k_b = 0.001 m, which shows better robustness (Fig. 10). With the ESMO compensating for the system uncertainties, the ESMO-based RABC produces an excellent tracking performance (Fig. 11). Combining the inherent robust OCNCS, the ESMO-based OCNCS also conducts an excellent tracking performance with smaller tracking errors. The performance indicators and the statistical properties are presented in Tables 4 and 5 respectively. The data from both Tables 4 and 5 all point to the conclusion that the performance of the proposed controller is better than the ESMO-based RABC, the OCNCS, and the BC.

Fig. 9

The BC’s tracking performance

Fig. 10

The OCNCS’s performance

Fig. 11

The ESMO-based RABC’s tracking performance

Table 4 The performance indicators for four controllers

Table 5 The statistical properties of four controllers

In summary, we can conclude from the simulation and the experiment that the tracking performance of the proposed control scheme is better than that of the ESMO-based RABC, the OCNCS, and the BC.

Remark 6

It can be seen that the noise in the experiment is more severe than that in the simulation. In experiments, the reasons for the noise are more complex. The main reason is that the analog sensors used in the experiments contain a large amount of measurement noise. Similarly, in experiments, the value of x₂ is obtained by directly differentiating the analog displacement sensor. However, the ESMO has a filtering effect, therefore, the estimated values contain less noise than the actual values. The estimation error of x₃ is larger, mainly due to the differences between the theoretical model and the actual system model. In addition, complex data calculations, computational errors, delays in network data transmission, and the computational speed of computers in the actual control system can all exacerbate the noise in the estimated values (Fig. 12).

Fig. 12

The ESMO-based OCNCS’s tracking performance

5 Conclusion

The paper presents a comprehensive study on the challenges of system uncertainties in EHSSs and proposes an innovative solution to mitigate these issues using advanced control methods. The core of the proposed solution is the ESMO, which is a sophisticated tool capable of discerning not only the complete state of the system but also differentiating between the types of uncertainties the system encounters—namely, matched and mismatched uncertainties. The ESMO’s ability to estimate both types of uncertainties presents a novel approach to online estimation that is particularly useful for dynamic systems like EHSS that need real-time adjustments to maintain high performance.

In conjunction with the ESMO, the paper discusses the integration of a BLF. This approach is rooted in nonlinear control theory and is particularly effective in dealing with output constraints. BLF is typically used to methodically achieve desired control objectives and, when combined with the ESMO’s estimation capabilities, forms a robust control strategy.

The advancement brought forth by the paper is encapsulated in the OCNCS for EHSS. OCNCS is designed to optimize the system’s performance in the face of uncertainties, ensuring the hydraulic system functions efficiently and effectively. The paper validates the proposed control scheme through rigorous simulation and experimental studies, demonstrating its superior performance when benchmarked against existing control methods such as ESMO-based RABC, the standalone OCNCS, and the BC. The outcome of this research presents a significant leap in the EHSS’s ability to operate with higher accuracy, stability, and reliability, which is critical in applications where precision and responsiveness are paramount (Fig. 13).

Fig. 13

The ESMO’s performance: a the estimation of x₁, b the estimation of x₂, c the estimation of x₃, d the estimation of Δ₁ and Δ₂

Finally, the paper outlines the trajectory for future research. The authors express an intention to combine the ESMO with a full state constraint control methodology, which would provide an even more robust framework for handling uncertainties by accounting for all possible states of the system. Additionally, the paper hints at exploring fractional-order extended sliding mode observers, which represent an extension to the traditional sliding mode control techniques and have the potential to offer finer control over system dynamics due to their non-integer order differentiation capability. This exploration into fractional-order control methods indicates a forward-thinking approach to control theory, pushing the boundaries of how precision can be achieved in systems with inherent uncertainties such as EHSS.