Buckling Behavior of Nonuniform-Friction Piles with Linear Distribution of Subgrade Reaction

Abstract

A novel analytical approach for predicting the buckling load with its mode shape of friction piles fully embedded in soil is proposed, in which the lateral subgrade and axial friction resistances change linearly. The proposed approach considers uniform rectangular piles that are either free or pinned or fixed at the pile and toe. The differential equation that governs the mode shape of the buckling pile along with the boundary conditions was analytically derived and numerically solved using the Runge–Kutta method and the Regula-Falsi method. The buckling loads of this study agreed well with those reported in the literature. The buckling behavior of piles was discussed as factors affecting the end condition, aspect ratio, subgrade ratio, friction ratio, subgrade parameter and friction parameter.

1 Introduction

Piles embedded in soil are widely used in geotechnical engineering to sustainably support axial compressive loads [1]. In addition, piles are often used in large-scale projects for the purpose of reinforcing soft ground by permanently using it as the ground for plant and marine engineering [2]. It is well known that, due to the wide cross-sectional shape of the width and perimeter, the compressive load capacity of the embedded pile can be effectively increased by the lateral subgrade reaction force and the axial friction resistance.

From this point of view, until recently, many studies investigating the static behavior of pile foundations have been actively conducted. The typical works related to this study are reviewed herein: Chen et al. [3] studied the laterally loaded piles based on Cusp Catastrophe Theory for sudden failure of structural mechanisms; Ng and Lei [4] developed the database of compression load test for 15 piles in Hong Kong and analyzed the pile skin friction with respect to local displacement, N-value in the standard penetration test, and effective stress principle; Ho and Tang [5] studied axial compressive load tests on piles embedded in polymer slurries, where maximum vertical skin friction was proposed; Ng et al. [6] tested the lateral earth pressures affected by pore water pressure for the well-instrumented piles and observed that a sudden substantial reduction in both pressures resulted upon the initiation of slip at soil-pile interface; Rabaiotti and Malecki [7] conducted full-scale pullout tests of piles in layered rock and quantified the contact strength between rock and concrete; Poulos et al. [8] evaluated the feasibility of simple method for analyzing a rectangular pile by converting it into an equivalent circular pile in finite element modeling; and Znamenskii et al. [9] assessed the load-bearing capacity of embedded piles for a 56-story apartment building.

In addition, the static behavior of pile foundation discussed above, understanding the buckling behavior of piles, is an important part of the pile design, in order to support the axially compressive load arising from the concentrated load, surcharge load and self-weight. In particular, the buckling analysis is essential to avoid lateral bending, which can eventually cause collapse. Many studies were devoted to developing the analytical approach for the buckling of axially loaded piles based on elastic foundation approach [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26]: Berezantzev et al. [10] developed the load bearing capacity which has been frequently used by many engineers in the foundation engineering; Liang et al. [11] analyzed the buckling stability of the bridge piers after the scoured soil layer was removed, ignoring possible increments/decrements in the stress–strain history of the soil; Seo and Prezzi [12] investigated an explicit solution of the load–deflection relationship for a single pile embedded in the multilayered ground under a vertical load based on the energy principle to derive governing differential equations; Lee [13] conducted an experimental loading test on the 1/4 to 1/2 inch diameter piles partially embedded in dry soil, in which all piles failed by buckling; Prakash [14] determined the first buckling load of a fully embedded pile that produced lateral resistance due to lateral deflection depending on the linearly variable stiffness of the soil; West et al. [15] investigated the clustering pattern of the buckling mode of end-bearing piles supported by elastic Winkler foundations with horizontal subgrade reaction forces that vary linearly with pile depth; Gabr et al. [16] developed the subgrade reaction coefficient using the general power distribution function to predict the critical buckling load of slender piles with vertical lateral friction effect; Bhattacharya et al. [17] studied buckling instability caused destructive forms of pile failure, which discussed the different cases where local buckling and collapse mechanisms of offshore piles should be considered in pile design; Shields [18] developed a general design method for small diameter grout piles (micro-piles), assuming that the lateral stiffness is sufficient to protect against buckling of piles fully embedded in soil; Vogt et al. [19] presented a new analytical concept that can compute the first buckling load of a pile based on buckling experiments on micro-pile embedded with a length of 4 m in soft clay with nonlinear material properties; Catal [20] used the small displacement theory to calculate the buckling load of Timoshenko piles with linear-elastic rotating springs at the pile head partially embedded in elastic soil following the Winkler hypothesis; Jesmani et al. [21] studied the three-dimensional finite element buckling of embedded concrete piles partially and fully in sandy soil subjected to an external compressive load; Ma et al. [22] used Hamilton’s principle to calculate the exact solution of the buckling load with the buckling mode shape of a single pile embedded in elastic soils and obtained a nonlinear buckling equation; Lee [23] presented an integrated model that can calculate both the natural frequency and the buckling load of partially embedded end-bearing piles with an axial compressive load; Muravyeva and Vatin [24] studied longitudinal buckling of offshore gas pipelines from the perspective of pipeline construction that experiences severe temperature changes that cause equilibrium disturbances of longitudinal buckling; Ghadban et al. [25] investigated the buckling behavior of nonuniform compressive beams with arbitrary end restraints on elastic soils with variable elastic stiffnesses; and Gatto and Montrasio [26] analyzed the inference of slenderness ratio on the ultimate behavior of piles with a very small diameter employed in soil reinforcement.

The literature reviewed above has covered a number of interesting effects on buckling behavior used in pile design, construction and maintenance. These studies are related to end-bearing piles that do not contain lateral friction or relatively low lateral friction. However, in order to construct a pile with a relatively large perimeter to withstand the vertical load caused by axial friction resistance, it is necessary to consider the transmission of frictional resistance along the axis of the pile.

In this study, a novel analytical and numerical approach to predict the bucking load and its mode shape of friction piles fully embedded in elastic soil is suggested, which captures the effect of linear variation in lateral subgrade reaction and axial friction resistance along its depth. The differential equation that governs the buckling mode shape and the boundary conditions in the interactive soil-pile system were analytically derived and numerically solved using the Runge–Kutta method in conjunction with the Regula-Falsi method. The results of the current solution were compared to the existing solution in the literature. Numerical experiments were provided to demonstrate the versatility of the assay.

2 Mathematical Modeling

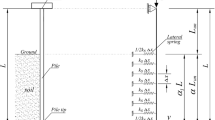
A fully embedded pile of length $l$ loaded with an external compressive force $P$ is shown in Fig. 1a. At the head and toe, the end of the pile is free or pinned or fixed. Thus, a total of nine combinations of end supports are possible such as ‘free-free,’ ‘free-pinned,’ ‘free-fixed’ and so on. When expressing the end condition of a pile, the former refers to the head of the pile, and the latter refers to the toe of the pile. If the compressive load $P$ is less than the buckling load ${P}_{B}$, that is, $P<{P}_{B}$, the pile remains straight. However, when the load $P$ gradually increases and reaches ${P}_{B}$, the pile eventually buckles, and the pile axis forms a buckling elastic curve called the mode shape described in Cartesian coordinates $(x,y)$ with the origin $O$ at the pile head. As shown in Fig. 1a, the stress resultants obviously consist of the axial force $N$, the shear force $V$ and the bending moment $M$ caused by the lateral deflection $y$ at the material point $(x,y)$ of the buckling pile. In addition, the external lateral reaction ${R}_{k}$ and axial friction resistance ${F}_{f}$ are loaded to the buckling pile by $y$.

Fig. 1

Problem statement: a Geometry of pile parameters, b Linear function of soil parameters and c Pile element subjected to forces

The pile material is linear elastic with a uniform rectangular cross section of width $d$ and height $h$, as shown in Fig. 1a, where the bending axis is $z$-axis (see Fig. 1c).

The aspect ratio $\lambda$ of the cross section is a ratio of $h$ to $d$, defined as

$$\lambda =\frac{h}{d}$$

(1)

Then, the cross-sectional area $A$ and width $d$ are expressed, respectively, as

$$A=dh={\lambda d}^{2}$$

(2.1)

$$d=\sqrt{\frac{A}{\lambda }}$$

(2.2)

Using Eqs. (1) and (2), the cross-sectional perimeter $u$ and the second moment of inertia $I$ are obtained in terms of $\lambda$ and $A$:

$$u=2\left(d+h\right)=2\left(\lambda +1\right)\sqrt{\frac{A}{\lambda }}$$

(3)

$$I=\frac{d{h}^{3}}{12}=\frac{\lambda {A}^{2}}{12}$$

(4)

The pile is laterally supported by elastic soil with the lateral subgrade reaction coefficient $k$ expressed in the dimension of $[{\mathrm{FL}}^{-3}]$. Shown in Fig. 1b is the distribution of coefficient $k$ changed linearly, starting ${k}_{h}$ at $x=0$ of the pile head and ending ${k}_{t}$ at $x=l$ of the pile toe. The subgrade ratio $\kappa$ is defined as

$$\kappa =\frac{{k}_{t}}{{k}_{h}}$$

(5)

Using Eq. (5) yields the linear function of $k$ at any coordinate $x$, or

$$k={k}_{h}\left[\left(\kappa -1\right)\frac{x}{l}+1\right]$$

(6)

When a compressive load $P(={P}_{B})$ is applied externally to the pile head, the pile is axially resisted by the friction force between pile surface and soil with the friction resistance coefficient $f$ expressed in the dimension of $[{\mathrm{FL}}^{-2}]$. The distribution of coefficient $f$ changes linearly from ${f}_{h}$ of the pile head to ${f}_{t}$ of the pile toe as shown in Fig. 1b. The friction ratio $\psi$ is defined as

$$\psi =\frac{{f}_{t}}{{f}_{h}}$$

(7)

Using Eq. (7) gives the linear function of $f$ at any coordinate $x$, or

$$f={f}_{h}\left[\left(\psi -1\right)\frac{x}{l}+1\right]$$

(8)

Figure 1c shows the internal forces ($N,V,M$) and external forces (${R}_{k},{F}_{f}$) subjected to the buckling element. In relation to the free body diagram in Fig. 1c, where $z$-axis is the bending axis, the equilibrium equations of the pile element are obtained by setting $\sum {F}_{x}=0$, $\sum {F}_{y}=0$ and $\sum M=0$:

$$\frac{dN}{dx}+{F}_{f}=0$$

(9)

$$\frac{dV}{dx}+{R}_{k}=0$$

(10)

$$\frac{dM}{dx}+V-N\frac{dy}{dx}=0$$

(11)

The intensity of the lateral subgrade reaction ${R}_{k}$ related to the lateral deflection $y$ is given by

$${R}_{k}=dky={k}_{h}\sqrt{\frac{A}{\lambda }}\left[\left(\kappa -1\right)\frac{x}{l}+1\right]y$$

(12)

The intensity of the frictional resistance ${F}_{f}$ on the pile shaft is taken in the form

$${F}_{f}=uf=2\left(\lambda +1\right){f}_{h}\sqrt{\frac{A}{\lambda }}\left[\left(\psi -1\right)\frac{x}{l}+1\right]$$

(13)

The axial force $N$ of the buckling pile is determined by Eq. (9) with the integration coefficient ${P}_{B}$ as follows [25].

$$N={P}_{B}-{\int }_{0}^{x}{F}_{f}dx={P}_{B}-\left(\lambda +1\right){f}_{h}\sqrt{\frac{A}{\lambda }}\left[\left(\psi -1\right)\frac{{x}^{2}}{l}+2x\right]$$

(14)

If $V$ in Eq. (11) is removed using Eqs. (10) and this result is combined with Eq. (9), it gives

$$\frac{{d}^{2}M}{d{x}^{2}}-N\frac{{d}^{2}y}{d{x}^{2}}+{F}_{f}\frac{dy}{dx}-{R}_{k}=0$$

(15)

By using the load–deflection relationship, the bending moment $M$ is given by Eq. (16.1) [27] and its second derivative can be obtained as Eq. (16.2):

$$M=-EI\frac{{d}^{2}y}{d{x}^{2}}$$

(16.1)

$$\frac{{d}^{2}M}{d{x}^{2}}=-EI\frac{{d}^{4}y}{d{x}^{4}}$$

(16.2)

where $E$ is the Young’s modulus of the pile material.

When substituting Eqs. (12)–(14) into Eq. (15), a single ordinary fourth-order differential equation governing the mode shape of the buckling pile is yielded:

$$\frac{\lambda E{A}^{2}}{12}\frac{{d}^{4}y}{d{x}^{4}}-\left\{\frac{4\left(\lambda +1\right){f}_{m}}{\psi +1}\sqrt{\frac{A}{\lambda }}\left[\left(\psi -1\right)\frac{{x}^{2}}{2l}+x\right]-{P}_{B}\right\}\frac{{d}^{2}y}{d{x}^{2}}$$

$$-\frac{4\left(\lambda +1\right){f}_{m}}{\psi +1}\sqrt{\frac{A}{\lambda }}\left[\left(\psi -1\right)\frac{x}{l}+1\right]\frac{dy}{dx}+\frac{2{k}_{m}}{\kappa +1}\sqrt{\frac{A}{\lambda }}\left[\left(\kappa -1\right)\frac{x}{l}+1\right]y=0$$

(17)

where ${k}_{m}$ and ${f}_{m}$ are $k$ and $f$ at the mid-span at $x=l/2$, defined as

$${k}_{m}=\frac{1}{2}\left({k}_{h}+{k}_{t}\right)=\frac{{k}_{h}}{2}\left(\kappa +1\right)$$

(18)

$${f}_{m}=\frac{1}{2}\left({f}_{h}+{f}_{t}\right)=\frac{{f}_{h}}{2}\left(\psi +1\right)$$

(19)

For dimensionless analysis of buckling behavior, the dimensionless parameters are introduced as follows.

$$ \xi = \frac{x}{l};\eta = \frac{y}{l};\alpha = \frac{{k_{m} l^{4} }}{{EA^{1.5} }};\beta = \frac{{f_{m} l^{3} }}{{EA^{1.5} }};p_{B,i} = \frac{{P_{B,i} l^{2} }}{{EA^{2} }} $$

(20)

where ($\xi ,\eta$) are the normalized Cartesian coordinates ($x,y$), $\alpha$ is the subgrade parameter, $\beta$ is the friction parameter and ${p}_{B,i}$ is the buckling load parameter with the integer mode number $i=\mathrm{1,2},3,\cdots$.

Combination with Eqs. (17) and (20) provides a nondimensional differential equation that governs the mode shape for the interactive soil-pile system considered in this study:

$$\begin{aligned} & \frac{{d}^{4}\eta }{d{\xi }^{4}} =\left\{\frac{24\left(\lambda +1\right)\beta }{{\lambda }^{1.5}(\psi +1)}\left[\left(\psi -1\right){\xi }^{2}+2\xi \right]-\frac{12}{\lambda }{p}_{B,i}\right\}\frac{{d}^{2}\eta }{d{\xi }^{2}}\\ & \quad +\frac{48\left(\lambda +1\right)\beta }{{\lambda }^{1.5}(\psi +1)}\left[\left(\psi -1\right)\xi +1\right]\frac{d\eta }{d\xi }-\frac{24\alpha }{{\lambda }^{1.5}(\kappa +1)}\left[\left(\kappa -1\right)\xi +1\right]\eta \end{aligned}$$

(21)

It is noted that ${p}_{B,i}$ is the eigenvalue of Eq. (21) which will be determined using the boundary conditions described below. If the pile is degenerated into a column, i.e., not embedded pile, Eq. (21) is reduced to ${d}^{4}\eta /d{\xi }^{4}=-(12{p}_{B,i}/\lambda ){d}^{2}\eta /d{\xi }^{2}$ identical to the result of Timoshenko and Gere [28].

Now, the boundary conditions for Eq. (21) are considered. For free ends of the pile head ($x=0)$ and toe ($x=l)$, $M$ and $V$ become zero and the boundary conditions of the dimensionless form are

$$ \frac{{d^{2} \eta }}{{d\xi^{2} }} = 0; \frac{{d^{3} \eta }}{{d\xi^{3} }} + \frac{{12{ }p_{B,i} }}{\lambda }\frac{d\eta }{{d\xi }} = 0\;{\text{for}}\;\xi = 0 $$

(22.1)

$$ \frac{{d^{2} \eta }}{{d\xi^{2} }} = 0; \frac{{d^{3} \eta }}{{d\xi^{3} }}{ } + \left\{ {\frac{{12{ }p_{B,i} }}{\lambda } - \frac{{24\left( {\lambda + 1} \right)\beta }}{{\lambda^{1.5} }}} \right\}\frac{d\eta }{{d\xi }} = 0\;{\text{for}}\;\xi = 1 $$

(22.2)

For pinned ends of the pile head ($x=0)$ and toe ($x=l)$, $y$ and $M$ become zero and the corresponding nondimensional boundary conditions are expressed as

$$ \eta = 0; \frac{{d^{2} \eta }}{{d\xi^{2} }} = 0. $$

(23)

For fixed ends of the pile, head ($x=0)$ and toe ($x=l)$, $y$ and $dy/dx$ become zero and the corresponding boundary conditions are given by

$$\eta =0; \frac{d\eta }{d\xi }=0$$

(24)

3 Numerical Solution Methods and Validation

A computer program applying FORTRAN language was self-coded to calculate the buckling load parameters ${p}_{B,i}$ with their buckling mode shapes ${(\xi ,\eta )}_{i}$ based on the mathematical modeling developed in this study. The input pile parameters are the end condition, the aspect ratio $\lambda$, the subgrade ratio $\kappa$, the friction ratio $\psi$, the subgrade parameter $\alpha$ and the friction parameter $\beta$. An iterative trial and error method was developed to solve the differential equation, Eq. (21), subjected to Eqs. (22)–(24) of the boundary conditions as initial and boundary problems. First, to calculate the buckling mode shape of the pile, the direct numerical integration method such as fourth order Runge–Kutta method [29] was used. Second, in order to find ${p}_{B,i}$ in the eigenvalue problem, the numerical method for solving nonlinear equations such as the Regula-Falsi method [29] was used. Shown in Fig. 2 is the block diagram of program algorithm of this study. A detailed numerical method can be referred to in the works [23, 30].

Fig. 2

Block diagram of program algorithm

Convergence experiment was performed by changing the step size $\Delta \xi$ dividing the entire pile length to obtain sufficient accuracy of the solution during numerical integration, and the results are given in Fig. 3. In all end conditions of the pile, numerical solutions of ${p}_{B,1}$ give good convergence for $1/\Delta \xi =30$, i.e., 30 divisions. See, for example, the pinned–pinned pile indicated by the circle mark ●, where ${p}_{B,1}=1.3625$ with $1/\Delta \xi =30$ converges to ${p}_{B,1}=1.3654$ with $1/\Delta \xi =100$, respectively, with 3-digit accuracy. Considering the results of Fig. 3, in this study, $1/\Delta \xi =50$ was used for further numerical calculation, and in this case, ${p}_{B,1}=1.3643$ was obtained which was more advanced to ${p}_{B,1}=1.3654$ with $1/\Delta \xi =100$. Additionally, all solutions with $1/\Delta \xi =50$ were calculated on a graphics-capable PC within 0.1 s of computation time per problem.

Fig. 3

Convergence experiment

For verification, the first buckling load ${P}_{B,1}$ calculated in this study was compared with that reported in open literature [28] and the finite element analysis (FEA). First, the degenerated pile to the column, not embedded in soil, was considered. For solving the reduced differential equation of ${d}^{4}\eta /d{\xi }^{4}=-(12{p}_{B,i}/\lambda ){d}^{2}\eta /d{\xi }^{2}$ in the absence of soil properties, column parameters are $l=15$ m, $d=2$ m, $h=1$ m and $E=30$ GPa. The ${P}_{B,1}$ in MN of this study and reference for the four end conditions are given in Table 1. Note that, ${P}_{B,1}$ in reference are the closed-form solutions. Even though ${P}_{B,1}$ of this study is an approximate numerical solution, but the two results of ${P}_{B,1}$ were identical within 5-digit of accuracy. Second, ${P}_{B,1}$ of the pile fully embedded in soil of this study and the FEA using ABAQUS software were considered. In FEA calculations, the subgrade reaction was modeled as a spring element and the friction resistance was modeled as a linearly distributed upward axial load. These two terms are then subjected to the FEA software to calculate the buckling load. The pile parameters are $l=15$ m, $d=2$ m, $h=1$ m, $E=30$ GPa for concrete pile, ${k}_{h}=10$ MN/m³, ${k}_{t}=12$ MN/m³, ${f}_{h}=150$ kPa and ${f}_{t}=225$ kPa, and its nondimensional pile parameters were converted as $\lambda =0.5, \kappa =1.2, \psi =1.5, \alpha =6.56$ and $\beta =0.0075$. The comparison results for ${P}_{B,1}$ with the six end conditions are shown in Table 2 as being in good agreement with an average error of 4.96%. These two comparisons in Tables 1 and 2 validate the mathematical modeling and solution methods of this study. If the distributions of $k$ and $f$ are uniform with $\kappa =1$ and $\psi =1$, ${P}_{B,i}$ of piles with opposite end conditions, e.g., free-pinned and pinned-free and so on, are the same. The computer program in this study performed these characteristics accurately, suggesting that mathematical modeling and numerical methods were accurate.

Table 1 Comparison^a of first buckling load ${P}_{B,1}$ in this study and reference

Table 2 Comparison^a of first buckling load ${P}_{B,1}$ in this study and FEA

4 Numerical Experiments and Discussion

In numerical experiments of the buckling load parameters ${p}_{B,i}$ of piles with the shape ${(\xi ,\eta )}_{i}$, the effects of aspect ratio $\lambda$, subgrade ratio $\kappa$ and friction ratio $\psi$ are examined including nine end conditions. The domains of nondimensional parameters used in the analysis are $\lambda =0 -1.5$, $\kappa =0- 2$, $\psi =0- 2$, $\alpha =0- 15$ and $\beta =0- 0.1$. These values are designed to simulate realistic material and geometrical properties of soil-pile systems [31, 32]. The numerical results obtained in this study for the parametric study are shown in Table 3 and Figs. 4, 5, 6, 7, 8, 9, 10, where the lowest three ${p}_{B,i}$ are shown with the specified pile parameters.

Table 3 Effect of end condition on buckling load parameter ${p}_{B,i}$

Fig. 4

${p}_{B,i}$ versus $\uplambda$ curve: a free-free, b pinned–pinned and c fixed–fixed pile

Table 3 presents the buckling load parameters ${p}_{B,i}$ with the different set of the nine end conditions. The pile parameters are $\lambda =0.5, \kappa =1.2, \psi =1.5, \alpha =6.56$ and $\beta =0.0075$. Regardless of the mode number, the lowest and highest values of ${p}_{B,i}$ are achieved in free-free and fixed–fixed piles, respectively. The higher the degree of end fixity of piles, the higher ${p}_{B,i}$ occurs, and if degrees of end fixity, e.g., free-pinned and pinned-free, are different, the end conditions supported by the larger $k$ and $f$ at the smaller degree of end fixity, the higher ${p}_{B,i}$ occurs. From this fact, it can be seen that the end condition of the pile is one of the most dominant influences in determining ${p}_{B,i}$. This table can be used in benchmark tests for calculations of interesting readers.

Figure 4 shows the relationship between the buckling load parameter ${p}_{B,i=\mathrm{1,2},3}$ and the aspect ratio $\lambda$ for the three end conditions of the pile: free-free, pinned–pinned, and fixed–fixed. Here, the rest of the pile parameters are shown in the legend. In general, ${p}_{B,i}$ increases with increasing $\lambda$, but in certain domains of $\lambda$, ${p}_{B,i}$ decreases. It is noted that the increasing slope of ${p}_{B,i}$ is greater in the higher mode. It is interesting that the relationship between ${p}_{B,i}$ and $\lambda$ is almost linear over the larger domain of $\lambda$, but not exactly linear. For example, for the fixed–fixed pile, $\lambda <0.25$ or so. In Fig. 4b, i.e., for the pinned–pinned pile, the buckling load curves of ${p}_{B,2}$ and ${p}_{B,3}$ intersect each other at $(\mathrm{0.202,1.6792})$, denoted by ■, implying that at $\lambda =0.202$, the double root of ${p}_{B,2}= {p}_{B,3}$ exist with different mode shapes of ${(\xi ,\eta )}_{i=2}$ and ${(\xi ,\eta )}_{i=3}$, respectively. Also, for the free-free and fixed–fixed piles, adjacent double root of ${p}_{B,i}={p}_{B,i+1}$ exists, which are not shown in Fig. 4a and c. The phenomenon of the occurrence of the double root of eigenvalues has already been reported in previous studies [33, 34] related to the natural frequencies of the free vibration problem, and also, as in this study, a double root of the eigenvalue of the buckling load parameter ${p}_{B,i}$ can occur in relation to the buckling problem.

Hereafter, subsequent numerical experiments consider only the first buckling load parameter ${p}_{B,1}$ of piles, where the pile has collapsed and is no longer able to withstand external loads, so a higher ${p}_{B,i}$ with $i>2$ in practical engineering is less important than ${p}_{B,1}$ [35]. Figure 5 shows the first ${p}_{B,1}$ versus aspect ratio $\lambda$ curves for piles with free, pinned, and fixed pile heads ($\xi =0$) and free, pinned, and fixed pile toes ($\xi =1$). Regardless of end condition, in general, ${p}_{B,1}$ increases with increase in $\lambda$, similar to Fig. 4. This can be stated that the greater $\lambda$ creates the greater $I(=\lambda {A}^{2}/12)$ of the cross section in the same area $A$ and consequently the greater flexural rigidity $EI$ causes the higher ${p}_{B,1}$. It can be seen that when $\lambda$ is smaller than a certain value, the effect of end condition is very insignificant. For example, in the case of the head-free end of Fig. 5a, when $\lambda <0.25$, the ${p}_{B,1}$ value of the three end conditions is almost the same.

Fig. 5

${p}_{B,1}$ versus $\uplambda$ curve: a head-free, b head-pinned and c head-fixed pile

The effect of the subgrade ratio $\kappa$ on ${p}_{B,1}$ is shown in Fig. 6. Here, the value $\kappa$ varies from 0 to 2, representing $\kappa =0$ as cohesive soil and linearly increasing $\kappa =2$ in cohesionless soil along the pile axis [14]. The ${p}_{B,1}$ value exhibits the decreasing or the increasing tendency as $\kappa$ value increases for the head-free and head-pinned piles, whereas ${p}_{B,1}$ value consistently exhibits the increasing tendency as $\kappa$ value increases for the head-fixed piles. Interestingly, ${p}_{B,1}$ of the free-free and free-pinned piles in Fig. 6a is the same when about $\kappa >0.75$. For free-free pile, an optimal value of $\kappa$ exists, which means that ${p}_{B,1}=0.602$ is the largest for $\kappa =0.881$ as indicated by ▲.

Fig. 6

${p}_{B,1}$ versus $\kappa$ curve: a head-free, b head-pinned and c head-fixed pile

The effect of the friction ratio $\psi$ on ${p}_{B,1}$ is shown in Fig. 7, where $\psi <1$ denotes the linearly decreasing unit side friction and $\psi >1$ denotes the linearly increasing unit side friction, as described by Kyfor et al. [36]. The ${p}_{B,1}$ value decreases as $\psi$ value increases. In Fig. 7a and b, ${p}_{B,1}$ does not show a significant difference between free-free and free-pinned and between pinned–pinned and pinned-fixed pile, respectively. The decreasing slops of ${p}_{B,1}$ are very small, so that the effect of $\psi$ on ${p}_{B,1}$ may be negligible. For this reason, it is reasonable to choose $\psi =1$, i.e., a uniform frictional resistance $f$, for easy and economical earthwork when installing piles.

Fig. 7

${p}_{B,1}$ versus $\varphi$ curve: a head-free, b head-pinned and c head-fixed pile

Figure 8 shows the effect of subgrade parameter $\alpha$ on ${p}_{B,1}$. The greater value of ${p}_{B,1}$ is displayed as $\alpha$ value increases, as expected. It is attributed to the fact that a high soil stiffness, i.e., a high subgrade reaction, produces less pile deflection and hence piles can carry the higher ${p}_{B,1}$. Similar observation was reported by Gabr et al. [16] and Lee [23] for the end bearing piles, i.e., piles where axial frictional resistance is not considered.

Fig. 8

${p}_{B,1}$ versus $\alpha$ curve: a head-free, b head-pinned and c head-fixed pile

The effect of friction parameter $\beta$ on ${p}_{B,1}$ is shown in Fig. 9, where $\beta =0$ corresponds to end bearing pile and $\beta >0$ corresponds to floating piles. The result reveals that ${p}_{B,1}$ value for end bearing piles is lower than that for floating piles, regardless of end condition, and ${p}_{B,1}$ value increases with increasing $\beta$ value, as expected. This is because the vertical side friction reduces axial compressive force throughout the pile shaft, contributing to high buckling load. The variation according to changing is almost linear, but not exactly linear, as shown in Fig. 9. The changing fashion of ${p}_{B,1}$ with a change in $\beta$ is almost linear, but not exactly linear as shown in Fig. 8.

Fig. 9

${p}_{B,1}$ versus $\beta$ curve: a head-free, b head-pinned and c head-fixed pile

The value of ${p}_{B,1}$ is dominantly dependent on $\alpha$ and $\beta$, as shown in Figs. 8 and 9 above. Once the surface map of ${p}_{B,1}$ is expressed as a graph by changing $\alpha$ and $\beta$, it is easy to understand the change of ${p}_{B,1}$ at a glance in the actual engineering field. For illustrative purposes, in Fig. 10, the surface map of ${p}_{B,1}$ is reported as in the region of $0<\alpha \le 15$ and $0<\beta \le 0.1$ with $\lambda =0.5$, $\kappa =1.2$ and $\psi =1.5$ for the free-free, pinned–pinned and fixed–fixed piles. These surface maps show that ${p}_{B,1}$ increases with increasing $\alpha$ and $\beta$. As expected from this result, the largest value of ${p}_{B,1}$ occurs at the largest values of $\alpha =15$ and $\beta =0.1$. For the free-free and pinned–pinned piles, the surface map is clearly a curved plane, whereas for the fixed–fixed pile, the surface is a linear plane.

Fig. 10

Surface map of $\left({p}_{B,1}, \alpha , \beta \right)$: a free-free, b pinned–pinned and c fixed–fixed pile

Figure 11 shows the typical first mode shape ${(\xi ,\eta )}_{i=1}$ with the corresponding ${p}_{B,1}$ of buckling piles affected by the end conditions expressed in Eqs. (22)–(24). This kind of mode shape provides the relative deflection and the locations of maximum deflection and the nodal point, i.e., zero deflection, for the buckling pile geometry as useful information in pile construction and maintenance.

Fig. 11

Example of mode shape: a free-free end, b pinned–pinned and c fixed–fixed pile

5 Summary and Conclusions

A novel numerical approach was presented for calculating buckling loads of the friction pile fully embedded in soil, taking into account the lateral subgrade reaction and the axial frictional resistance. The differential equation for buckling piles of rectangular cross section embedded in soil with linearly varying soil parameters was derived, associated with boundary conditions related to the pile end condition, and numerical methods solving the buckling load with the buckled mode shape were developed. Numerical experiments were provided to illustrate the variability of geotechnical engineering applications with the various pile parameters. Summarizing the results obtained through numerical experiments, the conclusions of this study are as follows.

• (1) Thirty divisions of the entire pile length in the Runge–Kutta method were sufficient to achieve 4-digit accuracy of the buckling load parameter ${p}_{B,i}$.

• (2) Solutions of ${p}_{B,i}$ were efficiently computed on PC, meaning that the computation time per problem is less than 0.1 s.

• (3) Solutions of ${p}_{B,i}$ matched very well with the closed-form solution in the literature and solutions using the finite element analysis.

• (4) There can be double roots of ${p}_{B,i}$ with different mode shapes in a single aspect ratio $\lambda$.

• (5) Increasing the aspect ratio $\lambda$ increases ${p}_{B,i}$. This is because the greater $\lambda$, the greater the moment of inertia of the pile cross section.

• (6) A trend of increasing ${p}_{B,i}$ was observed with increasing the subgrade parameter $\alpha$. This is because it reduces the lateral deflection, leading to a greater ${p}_{B,i}$ of the pile.

• (7) A trend of increasing ${p}_{B,i}$ was observed with increasing the friction parameter $\beta$. This is because it transmits less load along the pile axis, leading to a greater ${p}_{B,i}$ of the pile.

For further study, other intrinsic properties of piles in geotechnical engineering including variable cross section, partially embedded piles and free vibration issues should also be investigated.