1 Introduction

Due to the wide range of uncertainties in the process of seismic analysis of structures, the best and most reasonable method seems to be the probabilistic approach (Ang & Tang, 2007). In this regard, reliability and fragility analysis are the most effective approaches. The development of fragility curves requires a statistic and probabilistic analysis that can be performed by different methodologies (including analytical, experimental, and combined methods and even methods based on engineering judgment) depending on the desired accuracy (Baharvand & Ranjbaran, 2020; Zuo et al., 2019). However, the analytical techniques are frequently used in the case of accurate computer models due to acceptable accuracy and ease in controlling data and the attained statistical sets.

Considering the special features of Incremental Dynamic Analysis (IDA) in dealing with the inherent uncertainties of ground motions records and providing an appropriate statistical population, this approach is usually used in the development of fragility curves (Vamvatsikos & Cornell, 2002, 2004).

Assuming that parameter r represents the structural response, R stands for the limit state corresponding to a predefined damage level, IM designates the earthquake intensity measure, and im is a given excitation intensity, then a fragility curve in the form of Eq. 1 determines the probability that the response exceeds the limit states for the given intensity:

$${\text{Fragility}} = P[r \ge R|{\text{IM}} = {\text{im}}]$$
(1)

Fragility curves are the cumulative distribution function of damage (Hao, 2011). There are generally two approaches of constant damage level (IM-based; IM stands for Intensity Measure) and constant hazard level (EDP-based; EDP stands for Engineering Demand Parameter) methods for fragility analysis (Mohsenian et al., 2021c; Zareian et al., 2010). In the first approach (IM-based), the probability of exceeding from limit responses corresponding to a predefined performance level is determined for various earthquake intensity levels. In this method, which is more common, the intensity measure corresponding to the considered performance level is used for establishing a statistical population. On the other hand, in the EDP-based method, which is deemed more appropriate for seismic retrofitting purposes, the probability of exceeding different performance levels for a given intensity of the applied excitation is determined. In this approach, the structural response is considered as statistical data. In some cases, the fragility curves may be established using both methods. For this purpose, the exceedance probabilities for different intensities are derived discretely using the EDP-based approach. Then, using the IM-based method, the fragility curve is described as the best curve fitted to the extracted points in the previous step.

The development of fragility curves provides a powerful means for evaluating the influence of different parameters on the seismic responses of structures. Accordingly, fragility analysis has been performed by various investigators for different purposes. For instance, some researchers utilized the fragility curves for seismic performance evaluation of different structural systems under different types of excitations (Ghowsi & Sahoo, 2013; Kim & Leon, 2013; Lee et al., 2018; Mohsenian, Filizadeh, et al., 2021). Fragility curves are also powerful tools for assessing the effectiveness of different retrofitting and strengthening methods on the seismic response of damaged or weak structures (Mohsenian et al., 2020, 2021b). For instance, Ahmadi and Ebadi Jamkhaneh (2021) utilized fragility analysis to evaluate the effectiveness of the energy dissipation devices on improving the seismic performance of structures with a soft story. Shafaei and Naderpour (2020) utilized fragility analysis to evaluate the seismic performance of reinforced concrete frame structures retrofitted by FRP and subjected to main shock-after shock sequence. Montazeri et al. (2021) performed fragility analysis to assess the seismic performance of retrofitted conventional bridges. Kima and Shinozuka (2004) developed fragility curves for bridges retrofitted by steel jacketing.

A review of previous studies shows the extensive applications of fragility analysis. Evaluations showed that in most of the past investigations, the fragility curves were developed assuming a probabilistic distribution for the statistical data. However, the log-normal distribution is a more common assumption, but the normal distribution has also been used in previous studies for fragility curve development (Mohsenian et al., 2021c). Although the accuracy of the fragility analysis directly depends on such assumption, its validity is not verified and even in some cases, investigators attempted to propose alternative methods to prevent making such assumptions (Sudret et al., 2014). Needless to say, in a project depending on the size and importance, the accuracy of the results can considerably affect the safety and economical aspects. According to the authors’ best knowledge, the only available study that evaluates the validity of assumptions regarding the distribution of statistical data used in fragility curve development is the research performed by Shinozuka et al. (2000). In this study, the authors tested the goodness of fit of the fragility curves developed by assuming two-parameter log-normal distribution and estimated the confidence intervals of the two parameters (median and log-standard deviation) of the distribution. However, this study was performed on a bridge structure.

The present study tends to evaluate the accuracy of the assumptions of normal and log-normal distribution for the data used in fragility curve development in building structures, and also determine the sensitivity of the results of fragility analysis to these assumptions. What makes this study distinctive from the previous similar research works and the major novelties of the present paper are its focus on the building structures, the utilized performance-based viewpoint, and a clear and applicable methodology. Moreover, assessment of the sensitivity of fragility curves to different assumed distributions (normal or log-normal) is another novelty of the present study. For this purpose, six multi-story moment-resisting steel frames with 3, 5, 7, 10, 12, and 15 stories are designed. Considering different performance and hazard levels, fragility curves are developed assuming both normal and log-normal distributions for the data derived from Incremental Dynamic Analysis (IDA). Different numerical tests such as Shapiro–Wilk and Kolmogorov–Smirnov, as well as the graphical and descriptive tests, are performed on the utilized data sets for fragility curve development to assess the validity of the assumed distributions, and according to the outcomes of the performed statistical tests, the assumption of the log-normal distribution is more reliable, although the normal assumption is also not incorrect for all of the performance levels.

This study is organized into six sections. Sections 2 and 3 present the details of the studied models and the adopted assumptions for nonlinear modeling of the structures. The hierarchy of incremental dynamic analysis and fragility analysis of the studied frame structures using both normal and log-normal assumptions are discussed in Sect. 4. The performed tests on the attained data for fragility curve development to determine the appropriate statistical distribution and the attained results are presented in Sect. 5. Finally, Sect. 6 concludes this study.

2 Characteristics of the Studied Models

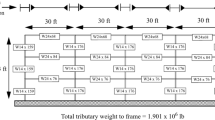
In this study, 2-dimensional intermediate moment-resisting steel frame structures, depicted in Fig. 1, are used. The gravitational dead (QD) and live (QL) loads in the stories are 31.5 and 10 kN/m2, respectively. The roof live load (QL) is 7.5 kN/m2. The span length and story heights are identical for all the structures and equal to 5 and 3.2 m, respectively. To investigate the effect of structural height, 3, 5, 7, 10, 12, and 15-story structures are designed. The selected heights for the modeled structures are in the range of allowable height range for the moment-resisting steel frame system (a maximum of 50 m from the base level).

Fig. 1
figure 1

Geometrical properties and loading details of the studied structures

Full size image

It is assumed in the design phase that the structures belong to the category of ordinary buildings and are located in a site with high seismicity (PGA = 0.35 g). The site soil is considered to be type C according to ASCE7 (ASCE, 2010) categorization (stiff soil with the shear wave velocity between 375 to 750 m/s). The frame structures are designed according to AISC360 (AISC, 2010) using ETABS software (CSI, 2015).

For the beams and columns, I-shaped and box sections are used, respectively. The properties of the beam and columns sections, which are specified by Bi and Ci in Fig. 1, are presented in Table 1.

Table 1 Geometrical properties of the beam and column section of the designed structures (dimensions are in mm)
Full size table

It is noteworthy that the geometry, member sections, and loading of the frame structures are symmetrical relative to the z-axis (see Fig. 1). Rigid diaphragms are also considered at each story level. A360 steel grade with the yield stress, Poisson’s ratio, and modulus of elasticity equal to 250 MPa, 0.26, and 210 GPa is considered for the structural components of the designed buildings (ASTM, 2019).

3 Modeling Nonlinear Behavior of Structures

PERFORM-3D software (CSI, 2017) is used for 2-dimensional nonlinear modeling and analysis of the structure. The gravitational loading assumptions for the nonlinear model are the same as the linear model. It should be noted that in the combination of gravitational and lateral loads, the effects of the gravitational loads (QG) is considered according to Eq. 2, in which QD and QL stand for the dead and live loads, respectively (ASCE, 2017):

$$Q_{G} = Q_{D} + 0.25Q_{L}$$
(2)

The generalized load-deformation curve depicted in Fig. 2 is used for nonlinear modeling of beams and columns of the frame structures. The parameters a, b, and c in this figure are extracted from the table of acceptance criteria of steel members according to the yielding mode and compactness of the structural elements (ASCE, 2017). According to Fig. 2, the slope of the initial hardening stage of steel, tg(α), is set to be the 3% of the slope of the elastic branch, tg(β). (ASCE, 2017). In this figure, θ represents the plastic hinge rotation.

Fig. 2
figure 2

The generalized force–deformation curve of steel structural elements (ASCE, 2017)

Full size image

The maximum expected strength, QCE, of the beams is derived from Eq. 6, while for the columns Eqs. 4 and 5 are used:

$$Q_{CE} = ZF_{ye}$$
(3)
$$Q_{CE} = ZF_{ye} \left( {1 - \frac{\left| P \right|}{{2P_{ye} }}} \right)\, \text(for)\, \left( {\frac{\left| P \right|}{{P_{ye} }} < 0.2} \right)$$
(4)
$$Q_{CE} = ZF_{ye} \frac{9}{8}\left( {1 - \frac{\left| P \right|}{{P_{ye} }}} \right) \, \text(for)\, \left( {\frac{\left| P \right|}{{P_{ye} }} \ge 0.2} \right)$$
(5)

In these equations, \(Z\) and \({F}_{ye}\) are the plastic section modulus and the expected yield stress of materials, respectively. \(P\) stands for the axial force of the member at the beginning of the dynamic analysis, \({P}_{ye}\) is the axial load corresponding to the axial yielding of the column, which is derived by multiplying the cross-section of the element by the expected yield stress of materials (\({P}_{ye}=A{F}_{ye}\)).

It is also noteworthy that concentrated flexural-axial hinges are considered for the beam and column elements at the critical locations (both ends).

4 Developing Fragility Curves Using Incremental Dynamic Analysis

First, the selected ground motions are applied to the structure and the modeled structures are analyzed using the Incremental Dynamic Analysis (IDA). 30 pairs of ground motion records corresponding to the site condition (the shear wave velocity between 375 to 750 m/s) are extracted from the PEER database (PEER, http://peer.berkeley.edu/peer-ground-motion-database). It is obvious that the number of utilized records is much greater than the minimum required number of ground motion records for IDA analysis (Shome, 1999). It should be noted that the minimum required number of records should also comply with the limitations of normality tests as well (Ghasemi & Zahediasl, 2012). This issue is completely discussed in Sect. 5. However, given the significant reduction in the inherent uncertainties due to the number of records used in this study, the results of IDA are expected to be sufficiently reliable.

The selected records and properties of their main components are given in Table 2. The selected records are classified as far-fault ground motions. Between the horizontal components of each ground motion, the one with the maximum highest spectral acceleration in the vibration frequency range of frame structures is selected as the main component and used in IDA. According to Fig. 3, these records are selected such that their average spectrums have a good agreement with the site design spectrum. As it is evident in this figure, the difference between the design spectrum and the average spectrum of the records in the governing mode of each frame is negligible.

Table 2 Properties of the main component of the selected ground motion records for IDA
Full size table
Fig. 3
figure 3

Comparison of the average spectrum of the selected ground motion records with the site design spectrum

Full size image

For IDA, the Peak Ground Acceleration (PGA(g)) and the maximum inter-story drifts are opted as the Intensity (IM) and Demand Measures (DM), respectively. The IDA results in a graphical relationship between DM and IM, which is called the IDA curve. In order to improve accuracy of the analysis, the increment of IM measure in the analysis is selected equal to 0.05 g. Accordingly, the peak ground acceleration of the record in nth step (PGAn) is derived from Eq. (6). Given PGA0 as the initial peak ground acceleration of ground motion records (see Table 2), the scale factor in nth step (SFn) is derived from Eq. (7) (Mohsenian & Mortezaei, 2019)

$$PGA_{n} \left( g \right) = 0.0{\text{5n}}$$
(6)
$$SF_{n} = PGA_{n} /PGA_{0}$$
(7)

The IDA curves for the studied structures are demonstrated in Fig. 4. The limit states corresponding to different performance levels of the Immediate Occupancy (IO), Life Safety (LS), and Collapse Prevention (CP) are also depicted in this figure (ASCE, 2017). However, since this study aims to compare the results of two different assumptions for the statistical distribution of data used in fragility curve development, other arbitrary limit states can also be used.

Fig. 4
figure 4

IDA curves and the limit states corresponding to different performance levels of a 3- b 5- c 7- d 10- e 12- and f 15-story frames

Full size image

Having the results of IDA in hand, the subsequent steps are followed to develop the fragility curves:

  1. i.

    According to Fig. 5, the intensity measure corresponding to a given performance level of the system (in this study the IO, LS, and CP performance levels) is extracted from the IDA curves. At this step, for each performance level, a statistical community containing 30 members will be available.

    Fig. 5
    figure 5

    Calculation of the exceedance probability for a certain performance level under a given intensity (x0) using IDA results

    Full size image
  2. ii.

    Assuming normal or log-normal distribution for the collected data sets in the previous step, after calculating the mean value (\(\mu\)) and standard deviation (\(\sigma\)), the density probability functions are established using Eqs. 8 and 9 (Nowak & Collins, 2012):

    $$f\left( x \right) = \frac{1}{{\sigma \sqrt {2\pi } }}EXP\left( {\frac{{\left( {x - \mu } \right)^{2} }}{{ - 2\sigma^{2} }}} \right)$$
    (8)
    $$f\left( x \right) = \frac{1}{{x\sigma \sqrt {2\pi } }}EXP\left( {\frac{{(\left( {{\text{ln}}\left( x \right) - \mu } \right)^{2} }}{{ - 2\sigma^{2} }}} \right)$$
    (9)
  3. iii.

    According to Fig. 5, taking \({x}_{0}\) as a specific intensity, the integral of the probability density function (the area under the curve) from \(-\infty\) to \({x}_{0}\) determines the exceedance probability (P) for the considered damage level. This means that at this specific intensity, there is a probability of P that the structural response exceeds the response corresponding to the considered damage (performance) level.

  4. iv.

    Subtracting P from 1 gives the reliability (P0) of the system for the considered damage (performance) level, and this means that at a certain intensity, there is a probability of P0 that the structure does not experience the considered performance level (Mohsenian, Filizadeh et al., 2021).

The fragility curves are derived for different performance levels of the studied structures according to the described methodology, assuming normal and log-normal distributions. The attained fragility curves are demonstrated in Fig. 6.

Fig. 6
figure 6

The extracted fragility curves for different performance levels using IDA results a 3- b 5- c 7- d 10- e 12- and f 15-story frames

Full size image

As evident in Fig. 6, however, there are differences between the curves derived from different distribution assumptions, but there is no clear trend for these differences. In most cases, for higher seismic intensities, the normal distribution assumptions result in lower exceedance probabilities. This is more evident for taller frame structures and higher performance levels. Vice versa, under lower seismic intensities, the log-normal assumption gives lower exceedance probabilities.

In the following, the maximum differences between the fragility curves for each performance level (DIO, DLS, and DCP) of the frame structures are extracted up to the peak ground acceleration of 1.0 g (PGA = 1.0 g). The attained results are presented in Fig. 7 (\(Difference=({Fragility}_{Normal}-{Fragility}_{Log-Normal})\times 100\)).

Fig. 7
figure 7

The curves of difference percentage between the developed fragility curves using normal and log-normal distribution assumptions a 3- b 5- c 7- d 10- e 12- and f 15-story frames

Full size image

For the IO performance level, the maximum difference between the curves is about 10%. According to Fig. 7, most of the differences occur around the intensity of 0.35 g, which indicates the design basis earthquake according to many of the design codes. For the LS and CP performance levels, the maximum differences between the curves are 10 and 13.5%, respectively. These maximums for the mentioned performance levels have occurred around the ground motion intensities of 0.95 and 0.8 g, which are higher than the intensity corresponding to the maximum considered earthquake (0.55 g) (see Fig. 7).

5 Evaluation of the Assumed Statistical Distributions

Controlling the dispersion and central tendencies of parts of the data (sample variables) and consequently providing a suitable distribution function are among the valid statistical methods that are often used for the probabilistic evaluation of larger communities. When a statistical population has a normal distribution, the normality of data is evaluated using different methods that fall into three broad categories: numerical (significance tests), descriptive, and graphical (Mishra et al., 2019). In this section, the mentioned methods are first briefly described and defined. Then, using these methods, the accuracy of the normal and log-normal assumptions of the data derived from IDA analysis will be evaluated. SPSS Statistics software (Statistics, 2013) is used for this purpose.

5.1 Numerical Normality Test Methods

The numerical normality test methods usually use well-known statistics such as Kolmogorov–Smirnov (K-S), Lilliefors corrected (K-S), Shapiro–Wilk, and Anderson–Darling (Barton, 2005; Öztuna et al., 2006; Shapiro & Wilk, 1965).

Although the estimation accuracy of all statistics depends on the sample size (small sample size leads to estimation error), studies have shown that for all possible distributions and sample sizes, the Shapiro–Wilk statistic has the highest accuracy in the estimation process, and Kolmogorov–Smirnov statistics is in the second place (Razali & Wah, 2011). Thus, for the small sample size, the Shapiro–Wilk statistic is usually recommended. The high computational volume of IDA, which is a time-consuming process, encourages the authors to utilize the minimum possible number of ground motion records (Han & Chopra, 2006; Vamvatsikos & Allin Cornell, 2006). Accordingly, the utilized sample size in this study is small (all samples consist of 30 data points which guarantee the minimum required number of data points for the utilized tests (Ghasemi & Zahediasl, 2012)). According to the provided explanations, in the present study, only the Shapiro–Wilk and Kolmogorov–Smirnov tests were used. For each frame, the results of the mentioned tests were for both normal and log-normal distribution assumptions are presented in Tables 3 and 4. In these tables, column df stands for the “degrees of freedom” which is equal to the sample size. The two other columns are used to check whether the normality (or log-normality) assumption is correct or not. Sig. represents the significance, and the significance values lower than 0.05 mean that the data set do not follow normal (or log-normal) distribution. However, for the tests with significance values higher than 0.05, there is a higher probability of normal (log-normal) distribution provided that the value of the statistics (first column) is closer to 1.

Table 3 The results of Shapiro–Wilk and Kolmogorov–Smirnov tests for controlling the assumption of the normal distribution of data used in fragility curve development
Full size table
Table 4 The results of Shapiro–Wilk and Kolmogorov–Smirnov tests for controlling the assumption of the log-normal distribution of data used in fragility curve development
Full size table

As mentioned, achieving the significance values (Sig.) Less than 0.05 in the statistics (which is the acceptable limit in statistical analysis) means rejecting the normality (log-normality) assumption of the distribution function governing the statistical population, and higher significance values (closer to 1) means more reliable assumptions. As evident in Table 3, the assumption of a normal distribution is ruled out in many cases (see the yellow cells) and is also a weak assumption for other cases based on the statistics values. In comparison, the log-normal distribution assumption for the data is much stronger (see Table 4). As can be seen, both statistics agree on the accuracy of the log-normal distribution assumption for the data. Given the explanations provided, the log-normal distribution is preferable.

5.2 Descriptive Normality Test Method

The descriptive method is based on evaluating the frequency, mean (µ), and standard deviation (σ) of the data. The normal distribution has a symmetrical bell-shaped curve, and for the normal distribution in a statistical population, 68.2, 99.7 and 95.4% of the observations would be between µ ± σ, µ ± 2σ, and µ ± 3σ, respectively (Altman & Bland, 1995). Skewness and kurtosis are the important parameters that describe asymmetry. Since the values of these two parameters in a normal distribution are zero, a significant deviation of them from zero will undermine the normality assumption (Thode, 2002). Converting these parameters to a Z score, and providing a tolerance interval would be a good measure of normality. In the latter case, the results obtained between + 1.96 and  1.96 indicate the correctness of the normality assumption for the statistical population (Ghasemi & Zahediasl, 2012).

The results of the descriptive test for the studied frames at different performance levels for both normal and log-normal distributions are as presented in Table 5. It should be noted that in the case of log-normal assumption, the tests are performed on the logarithm of the data derived from IDA analysis. If the normal assumption is verified for those values, the main data has a log-normal distribution. According to the results, both assumptions for the distribution of data are in the significance intervals, but in comparison, the assumption of the log-normal distribution of data is certainly more reliable, given the lower values of the score statistic.

Table 5 The results of the descriptive tests for controlling the normal and log-normal distribution assumptions of data used in developing fragility curves of different performance levels
Full size table

5.3 Graphical Normality Test Methods

The graphical methods are the approximate approaches for examining the hypothesis of normality distribution. Due to the low reliability of this method, it is used only as an auxiliary tool along with other methods (Öztuna et al., 2006) In these approaches, histograms, stem-and-leaf plots, boxplots, and quantile–quantile (Q-Q) plots are used to evaluate the hypothesis. As mentioned earlier, for a normal distribution, the histogram is bell-shaped and symmetrical related to the mean (Ghasemi & Zahediasl, 2012).

The stem and leaf diagrams are similar to the histograms and are used to illustrate the probability distribution shape of quantitative data (Das & Imon, 2016). Since the use of this diagram requires the availability of large-size samples, this method is not very common. Accordingly, it has not been used in the present study. For the studied frames, histogram diagrams are for both normal and log-normal (normality of the logarithms of the attained data from IDA) assumptions are shown in Figs. 8, 9, 10, 11, 12, 13.

Fig. 8
figure 8

The histogram diagrams at different performance levels for 3-story frame (a, b and c) log-normal distribution (d, e and f) normal distribution

Full size image
Fig. 9
figure 9

The histogram diagrams at different performance levels for 5-story frame (a, b and c) log-normal distribution (d, e and f) normal distribution

Full size image
Fig. 10
figure 10

The histogram diagrams at different performance levels for 7-story frame (a, b and c) log-normal distribution (d, e and f) normal distribution

Full size image
Fig. 11
figure 11

The histogram diagrams at different performance levels for 10-story frame (a, b and c) log-normal distribution (d, e and f) normal distribution

Full size image
Fig. 12
figure 12

The histogram diagrams at different performance levels for 12-story frame (a, b and c) log-normal distribution (d, e and f) normal distribution

Full size image
Fig. 13
figure 13

The histogram diagrams at different performance levels for 15-story frame (a, b and c) log-normal distribution (d, e and f) normal distribution

Full size image

As mentioned, histograms are a way to show the shape of the distribution of experimental data. The closer the histogram shape is to the Gaussian or bell-shaped distribution, the more the data fit the normal distribution. As evident from Figs. 8, 9, 10, 11, 12, 13, the histograms attained for the logarithms of the data sample are closer to the Gaussian distribution shape. Therefore, it is concluded that the log-normal distribution is a stronger assumption for all the studied structures and different considered performance levels. This finding is in agreement with the results numerical and descriptive tests results.

The Q-Q plots show the observed and expected values. In a normal distribution, the observed values are almost equal to the expected values. Deviation from this correspondence will reduce the validity of the normal distribution. Figures 14, 15, 16, 17, 18, 19 depict the attained Q-Q plots for the normal and log-normal assumptions. If the data belongs to the normal distribution, the points should be around a straight line, otherwise, this shows a null hypothesis, which means the data will not follow the normal distribution. According to Figs. 14, 15, 16, 17, 18, 19, the log-normal assumption seems a more valid hypothesis.

Fig. 14
figure 14

The Q-Q plots for 3-story frame (a, b and c) log-normal distribution (d, e and f) normal distribution

Full size image
Fig. 15
figure 15

The Q-Q plots for 5-story frame (a, b and c) log-normal distribution (d, e and f) normal distribution

Full size image
Fig. 16
figure 16

The Q-Q plots for 7-story frame (a, b and c) log-normal distribution (d, e and f) normal distribution

Full size image
Fig. 17
figure 17

The Q-Q plots for 10-story frame (a, b and c) log-normal distribution (d, e and f) normal distribution

Full size image
Fig. 18
figure 18

The Q-Q plots for 12-story frame (a, b and c) log-normal distribution (d, e and f) normal distribution

Full size image
Fig. 19
figure 19

The Q-Q plots for 15-story frame (a, b and c) log-normal distribution (d, e and f) normal distribution

Full size image

In a box diagram, the mean of the statistical population is drawn as a line inside the box, and the range between the first and third quartiles of frequency is considered as the length of the box (Altman & Bland, 1995). If the box is symmetric relative to the mean line, the assumption of a normal distribution for the data is supported. For the studied frames, considering the different performance levels and different hypotheses for the normal and log-normal distribution of the data, the mentioned diagrams are extracted for the IDA results and their logarithm values. The attained results are depicted in Fig. 20. Considering the box plots of normal distribution assumptions, it seems there is a low probability that the statistical data has a normal distribution, but by for the log-normal assumption (box diagrams on the right) the logarithm of the IDA results follow a normal distribution with a high probability, i.e., it is assumed that the statistical data follow the log-normal distribution. This finding is in agreement with the results of the graphical tests, as well as numerical and descriptive methods.

Fig. 20
figure 20

The box plots at different performance levels of the studied structures (a, c, e, g, i and k) normal distribution (b, d, f, h, j and l) log-normal distribution

Full size image

6 Conclusion

In this study, the reliability of the normal and log-normal probability distribution assumptions for the fragility curve development has been investigated considering different performance levels in the structural system. For this purpose, three numerical (significance), descriptive and graphical test methods have been utilized. To evaluate the effects of the statistical distribution on the accuracy of the analysis, the attained fragility curves using both assumptions have been compared. Based on the adopted assumptions, the following conclusions can be made:

  1. 1.

    Although the fragility curves derived from both normal and log-normal distribution assumptions are similar, for different earthquakes intensities, up to 13% difference is observed between them. Studies have shown that the differences in the distribution of probability values in both assumptions do not follow a specific trend.

  2. 2.

    Based on the results of numerical tests (significance tests) and descriptive methods, the assumption of normal distribution for the data is not false, but it is not a strong hypothesis. Because the results of the numerical test oppose this assumption in some cases. Moreover, in some other cases, the results of numerical and descriptive methods for this assumption are not in agreement. Therefore, it is concluded that the findings do not support the assumption of normal distribution for the data used in fragility curve development.

  3. 3.

    The results of both numerical tests, i.e., Shapiro–Wilk and Kolmogorov–Smirnov confirm the accuracy of the log-normal distribution assumption for statistical data with a high probability. In this regard, the results of descriptive tests also confirm the accuracy of this assumption. In addition, there is consistency between the findings of both numerical and descriptive and graphical tests. Accordingly, the log-normal distribution assumption for statistical data used in the process fragility curve development is verified.