1 Introduction

With the revitalization of the old industrial base in Northeast China, jacketing structure, a new construction technique used to add stories to the existing buildings, has been drawing lots of attentions (Ji et al. 2018). Jacketing structure includes mainly two forms: synergy and separation (Zheng and Ji 2008a, b). The separating jacketing structure is separated from the original building to independently bear and transfer the load from the adding stories to the new foundation. Hence, the separating jacketing structure is suitable for storey adding of low existing buildings. Although steel structure has been widely applied in industrial and civilian buildings because of its light weight, high bearing capacity, and good economic (Zhang et al. 2014; Patton and Singh 2017), it cannot meet the requirements of jacketing structure which needs to span over the existing building with larger span length. For this reason, a new form of steel frame structure is proposed which connects composite column (i.e., the H type honeycomb composite column (Ji et al. 2017) with concrete-filled rectangular steel tube flanges) with composite beam (i.e., the I-shaped honeycomb composite beam with concrete-filled rectangular steel tube flanges) using integral joint. In order to reduce the deflection of the composite beam, the prestressed reinforcements can be located in the lower steel tube flange, pre-tensioned and anchored at the end of the integral joint.

The rectangular steel tube flange of this kind of columns is filled with concrete, under the action of axial load the steel tube exerts lateral restraint on the compressive concrete, which makes the concrete in the three direction compressive stress state, retards the occurrence and development of its longitudinal microfracture, thereby improves its compressive strength and compression deformation ability. Then, with the support of the concrete, the geometric stability of the steel tube wall is enhanced and the instability mode of the steel tube is changed, thus the bearing capacity of the steel tube is improved. The concrete-filled steel tube uses the interaction between the steel tube and concrete, namely the restraining effect of the steel tube on the concrete makes the concrete under the state of complex stress, as a result, the strength of concrete is improved, and the plasticity and toughness are greatly improved. At the same time, the local buckling can be avoided or delayed because of the existence of concrete. In addition, during the construction process of CFST, the steel tube can also serve as a template for pouring its core concrete. In short, CFST is formed by combination between steel tube and concrete, which not only can make up for the shortcomings of the two materials, but also bring the advantages of two materials into full play. Furthermore, the honeycombed web connecting the two CFST columns can reduce the self-weight of the composite columns effectively and make the building beautiful when exposed to the outside. The rigidity of the cross section is no longer constant along the longitudinal direction after opening in the web, but for a honeycomb column with regular openings, the stiffness changes are characterized by repeated regularity because of the overall stiffness of each opening unit is equal. Therefore, the whole column can still be regarded as a column of equal stiffness from the macroscopic point of view.

Numerous researches have been conducted on I-beam with steel tube flanges or CFST flanges. Hassanein and Silvestre (2013) studied the lateral–distortional buckling of hollow steel tube flange plate girders with slender unstiffened webs (HTFPG). The good agreement between the obtained experimental results of the buckling capacity with the predictions provided by European code verified the rationality of method provided by the code. Then, they provided some design suggestions. Liang (2016) in our group carried out the experimental study on the overall stability of I-beams with rectangular CFST flange and proposed a formula to predict their ultimate bending moment. With the help of 1stOpt software, the non-dimensional critical moment formula of the lateral-torsional buckling of cantilever beam with tip lateral elastic brace is obtained by Zhang et al. (2016) based on stability theory. Then, the accuracy of the formula is verified by ADINA finite element software. The studies on the CFST composite columns are mainly focused on the conventional CFST columns and the latticed columns. Lama and Gardner (2008) conducted axial compression tests on 16 hollow stainless steel tube and concrete-filled stainless steel tube columns to investigate the influences of different parameters on the bearing capacity of the columns and established a formula to predict the bearing capacity of the column. The correctness of the proposed formula was verified through comparing with the predictions calculated by EC4 and ACI. Ellobody and Ghazym (2012) carried out the experimental investigation of axially and eccentrically loaded plain and fibre rein-forced (FR) concrete-filled stainless steel circular tubular columns. The test ultimate loads were compared with the design ultimate loads calculated using the Eurocode 4 for composite columns and the results showed that the EC4 accurately predicted the ultimate loads of axially loaded concrete-filled stainless steel circular tubular columns, but were quite conservative for predicting the ultimate loads of the eccentrically loaded columns. Lastly, the test results provide useful information regarding the behaviour of FR concrete-filled stainless steel columns. Zhong (2010) studied the stability of CFST latticed columns based on stability theory, derived a calculation method of the equivalent slenderness ratio and proposed a formula to predict the stability bearing capacity of the column. Zhou (2012) conducted the axial compression, bending and pseudo-static tests on square CFST columns to investigate the influence of structural form on the bearing capacity and the seismic performance of the column and proposed a formula to estimate the bearing capacity of the column. Yang et al. (2016) carried out the experimental investigation to study the effects of slenderness ratio, eccentricity and column slope on the load-carrying capacities and failure modes of variable and uniform concrete filled steel tubular (CFST) latticed columns under axial and eccentric compression. The results clearly showed that all the CFST latticed columns with variable cross section exhibited an overall failure, which is similar to that of CFST latticed columns with a uniform cross section. For the eccentrically compressed variable CFST latticed columns, the strain of the columns at the loading side, as well as the difference in the strain, increases from the bottom to the cap, and a more significant increase in strain is observed in the cross section closer to the column cap. Our group carried out the eigenvalue analysis of 18 H-type honeycomb composite columns with rectangular concrete-filled steel tube flanges (STHCC) (Ji et al. 2017), introduced the influence factor β of concrete and established a formula to predict the eigenvalue buckling load of this kind of composite columns based on Euler formula.

The STHCC column not only exhibits the characteristics of double-legged CFST latticed column, but also yields the weak stability of H-type honeycombed steel column. Up to now, there have been few researches on the nonlinear buckling analysis of STHCC, and the corresponding design methods are not perfect. Therefore it is significant to conduct the nonlinear buckling analysis of the STHCC. Based on the former eigenvalue analysis (Ji et al. 2017) developed by our group, 30 finite element models of STHCC are established by using finite element software ABAQUS. The influences of different parameters including the concrete strength grade, the nominal slenderness ratio, the hoop coefficient and the flange width on the nonlinear buckling capacity of STHCC columns are investigated. In addition, a formula is proposed to predict the nonlinear buckling load of STHCC column through regression analysis based on the results of parameter study.

2 Specimens Design

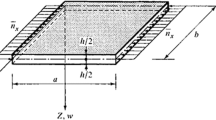
In order to study the nonlinear overall stability of STHCC, the concrete strength grade f k cu, the nominal slenderness ratio λt, the hoop coefficients ξ and the flange width h1 are selected as the main parameters. 30 STHCC specimens with different parameters are designed. The specific parameters of each specimen are listed in Table 1. The slenderness ratio of the composite columns is calculated according to the equation of the nominal slenderness ratio of the steel column (Eq. 1) proposed by Strength of Materials (James and Barry 2011) and the physical meaning of each symbol can be referred to the design code for steel structure (BS EN 1993-1-1 2005). Due to both ends of the specimen are hinged, the calculated length factor μ is equal to 1 and the calculated length l0 is l. The honeycomb web is formed by opening holes on steel webs with the diameter to height ratio d/hw of 0.7, and the space between two holes to height ratio s/hw of 0.3. The connection between the flange and web is welded. The section size of the specimen is shown in Fig. 1, and the three-dimensional figure of the specimen is shown in Fig. 2.

$$ \lambda_{\text{t}} = \frac{{l_{0} }}{i} = \frac{{l_{0} }}{{\sqrt {\left( {I_{\text{s}} + 0.8\frac{{E_{\text{c}} }}{{E_{\text{s}} }}I_{\text{c}} } \right)/\left( {A_{\text{s}} + 0.8\frac{{E_{\text{c}} }}{{E_{\text{s}} }}A_{\text{c}} } \right)} }} $$
(1)
Table 1 Parameters of 30 STHCC specimens
Full size table
Fig. 1
figure 1

The section size of H-type steel column with honeycombed web and hollow flanges

Full size image
Fig. 2
figure 2

The three-dimensional figure of specimen

Full size image

3 Stress Mechanism

CFST flanges are formed by filling concrete into the hollow flange steel tube. Figure 3 shows the three-dimensional stress state of the steel tube as well as the inner concrete. Under the longitudinal axial compression P, the longitudinal compressive strain can be calculated as follows:

$$ \varepsilon_{{ 1 {\text{s}}}} = \mu_{\text{s}} \varepsilon_{3} \, ; \, \varepsilon_{{ 1 {\text{c}}}} = \mu_{\text{c}} \varepsilon_{3} $$
(2)

where, μs and μc are the Poisson’s ratio of steel and concrete respectively. ε1s and ε1c are transverse strain of steel and concrete respectively.

Fig. 3
figure 3

Three-dimensional stress states of steel tube and concrete

Full size image

The relationship between the Poisson’s ratio of steel and concrete of the CFST flange of STHCC specimen was changed during the loading process. At the beginning, the Poisson’ ratio of concrete was smaller than that of the steel (i.e., μc < μs); when the longitudinal compressive stress of the steel reached its proportional limit (i.e., δ3 ≈ fp), the Poisson’ ratio of concrete was similar with that of the steel (μc ≈ μs); then, with further increase of the compression load P, the stress of the steel exceeded its proportional limit (i.e., δ3 > fp), in this case, the Poisson’ ratio of concrete became larger than that of the steel (i.e., μc > μs), hence, the corresponding strain of concrete was also larger than that of steel according to Eq. 2 (i.e., ε1c > ε1s), which mean that the expansion of core concrete was larger than that of the steel tube. Therefore, the core concrete was restrained by the steel tube and its lateral expansion was hindered. The interaction force generated between the steel tube and the core concrete, as shown in Fig. 3a. The longitudinal compression stress (δ3), the radial compression stress (δ2), the circumferential tension stress (δ1) of the steel tube and the longitudinal, radial and circumferential compression stress of core concrete (δ ′3 , δ ′2 , δ ′1 ) are presented in Fig. 3b. Due to the deformation of the steel tube caused by the hoop force, the hoop force was significantly reduced in the middle of the edge, as shown in Fig. 4a. In addition, the circumferential shear stress τ and the normal stress pointing to the honeycomb of web were produced when subjected to compression P, as shown in Fig. 4b.

Fig. 4
figure 4

Stress distribution state of CFST flange and web. a CFST flange, b web

Full size image

When the CFST is subjected to axial compression, the hoop effect would occur. The steel tube and the core concrete are under the three-directional stress state which is different from the uniaxial compression state, and the material properties are changed at the same time. With the increase of the hoop effect, the compressive strength of concrete increases gradually, and similarly, the elastic modulus. In addition, the plastic deformation ability of concrete also increases obviously and the concrete transforms from brittle material to plastic material. In addition, the local stability of CFST flange is improved because of supporting provided by the core concrete, hence the yield strength of steel can be fully utilized.

4 Finite Element Model and Model Verification

4.1 Constitutive Models of Steel and Concrete

4.1.1 Constitutive Model of Concrete

The nonlinear constitutive model of concrete proposed by Han (2016) considering the hoop effect is adopted in present research as shown in Fig. 5a.

Fig. 5
figure 5

Constitutive models of concrete and steel. a Constitutive model of concrete (Han 2016), b Constitutive model of steel

Full size image

The stress–strain relationship of core concrete of CFST under compression is expressed as follows:

$$ y = \left\{ {\begin{array}{*{20}l} \hfill {2 \cdot x - x^{2} \,\quad (x \le 1)} \\ \hfill {\frac{x}{{\beta_{0} \cdot (x - 1)^{\eta } + x}} \, \quad(x > 1)} \\ \end{array} } \right. $$
(3)

\( x = \frac{\varepsilon }{{\varepsilon_{0} }} , { }y = \frac{\delta }{{\delta_{0} }} \) , \( \delta_{0} = f_{\text{c}} ({\text{N/mm}}^{ 2} ) \). The constant \( \varepsilon_{0} \) can be obtained from formulae (4) and (5).

$$ \varepsilon_{\text{c}} = (1300 + 12.5 \cdot f_{\text{c}} ) \cdot 10^{ - 6} $$
(4)
$$ \varepsilon_{0} = \varepsilon_{\text{c}} + 800 \cdot \xi^{0.2} \cdot 10^{ - 6} $$
(5)

where, ξ is hoop effect coefficient which can be calculated by formula (6).

$$ \xi = \frac{{A_{\text{s}} f_{\text{y}} }}{{A_{\text{c}} f_{\text{ck}} }} $$
(6)

The coefficients (\( \beta_{0} \) and \( \eta \)) in formula 1 can be calculated by formulae (7) and (8) as follows.

$$ \eta = \left\{ \begin{array}{ll} \, 2&\quad{\text{ Circular CFST}} \hfill \\ 1.6 + 1.5/x&\quad{\text{ Rectangular CFST}} \hfill \\ \end{array} \right. $$
(7)
$$ \beta_{0} = \left\{ \begin{array}{ll} ( 2. 3 6\times 1 0^{ - 5} )^{{\left[ {0.25 + (\xi - 0.5)^{7} } \right]}} \cdot f_{c}^{0.5} \cdot 0. 5\ge 0. 1 2&\quad {\text{ Circular CFST}} \hfill \\ \, \frac{{f_{\text{c}}^{0.1} }}{{1.2\sqrt {1 + \xi } }}&\quad{\text{ Rectangular CFST }} \hfill \\ \end{array} \right. $$
(8)

The stress–strain relationship of core concrete of CFST under tension is expressed as follows:

$$ y = \left\{ {\begin{array}{ll} 1.2 \cdot x - 0.2 \cdot x^{6}& \quad (x \le 1) \\ \frac{x}{{0.31 \cdot \delta_{\text{p}}^{ 2} \cdot (x - 1)^{1.7} + x}} &\quad (x > 1) \\ \end{array} } \right. $$
(9)

where, \( x = \frac{{\varepsilon_{\text{c}} }}{{\varepsilon_{\text{p}} }};{\text{ y = }}\frac{{\delta_{\text{c}} }}{{\delta_{\text{p}} }}; \, \delta_{\text{p}} = 0.26 \cdot (1.25 \cdot f_{\text{c}} )^{2/3} ; \, \varepsilon_{\text{p}} = 43.1 \cdot \delta_{\text{p}} (\mu \varepsilon ). \)

The damage factor is inputted into concrete constitutive model in ABAQUS software to form the concrete damage plasticity model, which are calculated by the formula (10) and (11) from the reference (Li 2011).

$$d_{\text{c}}=1-\frac{{\left(\delta_{\text{c}}+2\delta_{{\text{c}}_{0} } \right)}}{{E_{\text{c}} (2\delta_{{\text{c}}_{0}} /E_{\text{c}} + \varepsilon_{\text{c}} )}} (d_{\text{c}} \ge 0 )$$
(10)
$$ d_{\text{t}} = 1 - \frac{{\left( {\delta_{\text{t}} + \delta_{{\text{t}}_{0}} } \right)}}{{E_{\text{c}} (\delta_{{{\text{t}}_{0} }} /E_{\text{c}} + \varepsilon_{\text{t}} )}}{ (}d_{\text{t}} \ge 0 ) $$
(11)

where, \( d_{\text{c}} \) , \( d_{\text{t}} \) is the compression damage factor and the tensile damage factor, respectively; \( E_{\text{c}} \) is the initial elastic modulus of concrete (Han 2016).

4.1.2 Constitutive Model of Steel

The stress–strain curve of steel is generally divided into five stages: elastic, elastic–plastic, plastic, strengthening and second plastic flow. The STHCC columns conducted in this paper are all long columns hence the strengthening stage of steel can be neglected. Therefore, the ideal elastoplastic constitutive model shown in Fig. 5b is adopted.

4.2 Finite Element Model

ABAQUS software (ABAQUS Inc. 2006) is used to establish the finite element models of STHCC specimens. In order to obtain the stress distributions of steel and concrete, 8-node brick elements (C3D8R) with three translation degrees of freedom at each node were adopted to simulate steel and concrete. Through arranging the hexahedral seeds, the fine mesh of the composite columns was achieved. The plastic damage model was used to describe the material property of concrete which was achieved by inputting the coordinates of the points in the constitutive model of concrete as shown in Fig. 5a. The interface between steel tube and concrete is simulated by contact element, which is composed of normal contact and tangential bond-slip. The hard contact in ABAQUS is chosen as the normal contact behavior between the steel tube and concrete, and the tangential contact is modeled by the Coulomb friction model, and the friction coefficient is 0.25.

Both the top and bottom ends of the columns were fixed against all displacement except for the vertical displacement at the loaded end and all rotation angles to realize hinge connection. The axial load was applied on the top of column through the line displacement of the reference point RP. The FE model of one typical specimen is shown in Fig. 6. This initial geometric imperfection of the column specimens was simulated in the model as the first buckling mode shape of the hinged column multiplied by an amplification factor. Hence, a previous eigenvalue analysis of the model was conducted. Once the initial shape of the column was obtained, it was imported to the model as the initial imperfection. The imperfection amplitude value of L/1000 employed by the majority of researchers for the amplification factor was used. The nonlinear buckling simulation analysis of composite columns was carried out by using Riks method.

Fig. 6
figure 6

FE model of specimen

Full size image

4.3 Model Verification

According to the above method, the nonlinear buckling analyses of 17 CFST columns (Han 2016) and 4 CFSFB (Ren 2015; Liang 2016) were conducted, and the parameters of them and the overall stability bearing capacity obtained by test (Nue) and nonlinear buckling simulation analysis (Nusn) are listed in Tables 2 and 3.

Table 2 The comparison of stability bearing capacity of 17 CFST columns
Full size table
Table 3 The comparison of stability bearing capacity of 4 CFSFB
Full size table

The comparison of the load–displacement curves obtained by experiments and FE simulations for 21 specimens is shown in Fig. 7.

Fig. 7
figure 7

Load-displacement curves of specimens. a Sc154-1 and Sc154-2, b Sc154-3 and Sc154-4, c Sc149-1 and Sc149-2, d Sc141-1 and Sc141-2, e Sc130-1 and Sc130-2, f Sc130-3, g scz1-1-1 and scz1-1-2, h scz1-1-3, i scz1-2-1, j scz1-2-2, k scz1-2-3, l L-2, m CFSFB-1, n CFSFB-2, o CFSFB-3

Full size image

It can be seen from Fig. 7, Tables 2 and 3 that the FE outcomes obtained by adopting Han’s constitutive model of concrete consist better with the experimental results in forms of load–displacement curves and overall stability capacity when compared with those obtained by using the concrete constitutive models proposed by GB (2014) or Yu (2003). Therefore, the concrete constitutive model proposed by Han is adopted to conduct FE analysis. In addition, the feasibility of the modeling method proposed above for the buckling analysis of CFST columns and CFSFB is also verified. The STHCC specimens in this paper are similar to CFST columns and CFSFB, hence the same modeling method can be used to analyze the overall stability of STHCC specimens.

5 Nonlinear Buckling Analysis of the STHCC

Nonlinear buckling analysis of 30 STFCC columns was carried out by using ABAQUS finite element software. The relationships between the vertical load and horizontal displacement in mid-height of the specimens were extracted. The influences of the concrete strength grade, the nominal slenderness ratio, the hoop coefficient and the flange width on the nonlinear stability bearing capacity of composite columns were investigated.

5.1 Concrete Strength Grade (f cu k)

The load–displacement (N-μm) curves of STHCC specimens with different concrete strength grades (i.e., 30, 40, 50, 60 and 70) are shown in Fig. 8, and the stability bearing capacity is listed in Table 4. It can be seen from Fig. 8 that with the increase of the concrete strength grade, the stability bearing capacity of the column increases gradually. However, the increase of the stability bearing capacity with concrete strength is not significant. It can be seen from Table 4 that the stability bearing capacity increases from 1058.83 to 1139.27 kN with an increase of 7.60% when the concrete strength grade increase from 30 to 70. Hence, through increasing the concrete strength grade to improve the stability bearing capacity of the column is limited.

Fig. 8
figure 8

The load–displacement (N-μm) curves of STHCC specimens with different concrete strength grades

Full size image
Table 4 The stability bearing capacity of specimens
Full size table

5.2 Nominal Slenderness Ratio (λ t)

Figure 9 depicts the predicted load–displacement (N-μm) curves of the STHCC specimens with different nominal slenderness ratios (i.e., 110.84, 129.31, 147.78, 166.26, 184.73, 221.68 and 240.15). The obtained stability bearing capacity is listed in Table 5. It can be seen from Fig. 9 that with the increase of the nominal slenderness ratio, the stability bearing capacity of the composite column decreases obviously. It can be seen from Table 5 that the stability bearing capacity of the composite column is 3328.21 kN when the nominal slenderness ratio is 110.84 while this value decreases to 771.16 kN (i.e., 76.83% decrease) when the nominal slenderness ratio increases to 240.15, indicating that the nominal slenderness ratio has great influence on the stability of composite columns. In addition, it can be seen from Fig. 9 that with the increase of the nominal slenderness ratio, the curve after the peak load decreases more smoothly, indicating a better the ductility of the column. Therefore, the selection of a reasonable the nominal slenderness ratio is crucial to the safety of the structure.

Fig. 9
figure 9

The load–displacement (N-μm) curves of STHCC specimens with different nominal slenderness ratios

Full size image
Table 5 The stability bearing capacity of specimens
Full size table

5.3 Hoop Coefficients (ξ)

The variation of the load–displacement (N-μm) curves of the STHCC specimens with hoop coefficients (i.e., 7.60, 8.54, 9.55, 10.61, 11.74 and 12.95) are shown in Fig. 10. The stability bearing capacity of the composite column with different hoop coefficients is listed in Table 6.

Fig. 10
figure 10

The load–displacement (N-μm) curves of STHCC specimens with different hoop coefficients

Full size image
Table 6 The stability bearing capacity of specimens
Full size table

It can be seen from Fig. 10 that with the increase of the hoop coefficient, the stability bearing capacity of the composite column increases significantly. For instance, the stability bearing capacity of the composite column increases from 1128.11 to 1389.95 kN with 23.21% increase when the hoop coefficient increases from 7.60 to 12.95 (Table 6). In addition, it can be seen from Fig. 10 that the load–displacement curves seem to be elevated integrally without ductility loss with the increase of hoop coefficient.

5.4 Flange Width (h 1)

The influences of the flange width on the stability of the STHCC specimens are shown in Fig. 11 and the stability bearing capacity is listed in Table 7. With the increase of the flange width from 120 to 200 mm (l = 11 m), it can be seen from Table 7 that the stability bearing capacity increases from 1215.56 to 1800.92 kN (i.e., 48.16% increase). Therefore, with a constant flange length b, the stability of STHCC is significantly improved with the increase of the flange width.

Fig. 11
figure 11

The load–displacement (N-μm) curves of STHCC specimens with different flange width. a C-19, 22, 25, 28 (l = 11 m), b C-20, 23, 26, 29 (l = 12 m), c C-21, 24, 27, 30 (l = 13 m)

Full size image
Table 7 The stability bearing capacity of specimens
Full size table

5.5 Comparison Between Eigenvalue Analysis/Nonlinear Buckling Analysis and Test Result

Only the von Mises stress nephograms of eigenvalue analysis and nonlinear buckling analysis of specimen C-19 are shown in Fig. 12 for other specimens exhibit the similar von Mises stress nephograms. It can be seen from the Fig. 12a that the deformation of the composite column obtained from the eigenvalue analysis is more uniform and smoother than that of the nonlinear bulking analysis because that the initial imperfection and material nonlinearity are not considered. However, the von Mises stress and buckling capacity are all larger than those of the actual value. In addition, it can be seen from Fig. 12b that the deformation near the ends of the composite column obtained from the nonlinear bulking analysis is relatively smaller while the mid-span deformation is larger compared with those gained from the eigenvalue analysis because of considering the geometric nonlinearity and material nonlinearity, and is consistent with its actual experimental deformation (Fig. 12c). Therefore, the nonlinear buckling analysis accounting the influence of the initial imperfection can be used to predict the stability of composite column STHCC.

Fig. 12
figure 12

The deformation diagram obtained from eigenvalue buckling analysis, nonlinear buckling analysis and test. a Eigenvalue buckling, b nonlinear buckling, c Test

Full size image

6 Formula for Nonlinear Buckling Load N u, cr

6.1 Formula Establishment

The stability capacity Nusn of the STHCC column with different parameters predicted through using FE analysis based on 30 specimens (C-1 ~ C-30) is listed in Table 8. A formula is proposed to predict the stability bearing capacity of the composite columns (STHCC) considering the influences of the concrete strength grade, the nominal slenderness ratio, the hoop coefficient and the flange width by superposition method. In addition, the composite effect correction value βc based on the stability formula of CFST column proposed by Han (2016) is also introduced.

Table 8 Simulated value Nusn of nonlinear buckling and the composite effect correction value βc
Full size table

A formula proposed to predict the stability bearing capacity Nu, cr of STHCC is expressed as follows:

$$ N_{\text{u, cr}} = \frac{2d}{{\left( {\lambda + 35} \right)^{2} }}A_{\text{sc}} \left( {1.18 + 0.85\xi } \right)f_{\text{ck}} + \frac{{\pi^{2} k_{\text{y}} EI}}{{\left( {\mu l} \right)^{2} }} - \beta_{\text{c}} $$
(12)
$$ d = \left[ {13500 + 4810 \cdot \ln \left(\frac{235}{{f_{\text{y}} }}\right)} \right] \cdot \left(\frac{25}{{f_{\text{ck}} + 5}}\right)^{0.3} \cdot \left(\frac{\alpha }{0.1}\right)^{0.05} $$
(13)
$$ \lambda = \frac{2\sqrt 3 l}{b} $$
(14)

where, λ is the slenderness ratio of CFST flange; Asc is the cross section area of single CFST flange; ξ is the hoop coefficient; f ck is the standard value of concrete axial compressive strength; fy is the yield strength of steel; βc is the composite effect correction value; μ is the calculation length factor; α is the steel content; ky is the reduction factor of the moment of inertia of the web (Zhang 2008).

The composite effect correction values βc of 30 specimens (C-1 ~ C-30) are obtained by using Eq. 12 (i.e., Nusn = Nu, cr) and the results are listed in Table 8.

The cross section characteristic parameter γ related to the section size of the specimen is introduced, and can be calculated by Eq. 15.

$$ \gamma = \frac{{\left( {b - h_{1} - 10} \right)}}{100} $$
(15)

As shown in Fig. 13, through statistical regression analysis, the relationship between the composite effect correction value βc and the cross section characteristic parameter γ is established as Eq. 16.

$$ \beta_{\text{c}} = 115.57\left[ {\frac{{\left( {b - h_{1} - 10} \right)}}{100}} \right]^{2} + 171.85\frac{{\left( {b - h_{1} - 10} \right)}}{100} + 0.92 $$
(16)

where, b is flange length, and h1 is flange width.

Fig. 13
figure 13

Relationship between βc and γ

Full size image

Substituting Eq. 16 into Eq. 12, the formula for predicting the nonlinear stability bearing capacity of STHCC is derived as follows:

$$ N_{\text{u, cr}} = \frac{2d}{{\left( {\lambda + 35} \right)^{2} }}A_{\text{sc}} \left( {1.18 + 0.85\xi } \right)f_{\text{ck}} + \frac{{\pi^{2} k_{\text{y}} EI}}{{\left( {\mu l} \right)^{2} }} - \left( {115.57\left[ {\frac{{\left( {b - h_{1} - 10} \right)}}{100}} \right]^{2} + 171.85\frac{{\left( {b - h_{1} - 10} \right)}}{100} + 0.92} \right) $$
(17)

6.2 Formula Verification

Lastly, the FE models of other 22 STHCC columns (C-31-C-52) were established to verify the reasonableness of the formula for nonlinear buckling load Nu, cr. The parameters of the specimens, the simulated value Nusn and the calculated value Nu, cr of nonlinear buckling load are listed in Table 9. It can be seen from Table 9 that the formula outcomes obtained by Eq. 17 has high reliability.

Table 9 The comparison of stability bearing capacity of 26 STHCC columns
Full size table

7 Conclusions

A systematic study was conducted on the stability properties of STHCC columns through FE analysis using ABAQUS. Firstly, the correctness of the FE model was verified by comparing with the experimental results conducted by former researchers. Then, the nonlinear buckling analyses of 30 STHCC specimens were carried out to investigate the influences of the concrete strength grade, the nominal slenderness ratio, the hoop coefficient and the flange width on the nonlinear bulking capacity of STHCC columns. A formula considering the above parameters was proposed to predict the nonlinear bulking capacity of STHCC column Nu, cr based on the equation proposed by Han for the stability capacity of the CFST columns. Based on the results of FE analyses of the STHCC specimens, the following conclusions can be drawn:

  1. 1.

    The established formula can be used to predict the lower boundary of the stability bearing capacity of STHCC columns, namely the nonlinear buckling load.

  2. 2.

    The STHCC column is deformed along the strong axis of the CFST flange. Therefore, it is effective to improve the stability of the column by connecting the two independent CFST columns into a whole by using connecting plate in practice.

  3. 3.

    When the flange thickness increases from 11 mm to 16 mm (i.e., the corresponding hoop coefficient increases from 7.60 to 12.95), the stability bearing capacity of STHCC column increased by 23.21%. Hence, the stability of the column can be improved by increasing the thickness of the flange appropriately.

  4. 4.

    With the increase of concrete strength grade, the improvement of the stability capacity of STHCC column is slight.