Global Buckling Behavior of Intermittently Fastened Cold-Formed Steel Built-Up Columns

Abstract

In the load-bearing wall frame system, built-up sections are utilized over single section to enhance the performance of Cold-Formed Steel (CFS) structural systems. Built-up CFS sections can be formed in different shapes by the use of intermittently connected fasteners in the longitudinal direction. The spacings of these intermittent fasteners can alter the global buckling behavior of built-up CFS columns, and hence, they are investigated in the present study. The change of global buckling load from a single section CFS column to a built-up section CFS column is studied with different fastener spacing. In this chapter, a numerical methodology using a compound spline finite strip method is developed to compute the elastic critical buckling load of CFS built-up columns. The results of buckling analysis are compared with FE-based software ABAQUS and results are found to be in good agreement. Parametric studies on back-to-back connected I section with different web to flange ratios have been carried out, and it is found that global buckling behavior of open built-up sections will move toward fully composite section buckling behavior with the reduction in the fastener spacing.

1 Introduction

In the load-bearing wall frame system, cold-formed steel (CFS) columns are subjected to high in-plane loading. These members should have sufficient axial and flexural rigidity, and built-up CFS sections are most suitable for such conditions. These compound sections can be formed by connecting two or more single CFS sections by fasteners or welds. The presence of fasteners in the longitudinal direction will affect the buckling behavior of built-up members, especially in global buckling mode. In the design standards, the equations for computing the ultimate global buckling strength of CFS columns have been verified with different experimental works reported in literature [6, 8]. To compute the ultimate global buckling strength for built-up CFS columns, it becomes important to compute the critical global buckling stress accurately. The focus of this study is to comprehend the composite action generated by the discrete fastener arrangement on the critical global buckling stress of built-up columns. In the design provisions, AISI: S100 [4] provides modified slenderness ratios to accommodate the effect of discrete fastener on the global buckling of built-up sections (Eq. 1).

$$\left( {\frac{{{\text{KL}}}}{r}} \right)_{ms} = \sqrt {\left( {{\raise0.7ex\hbox{${{\text{KL}}}$} \!\mathord{\left/ {\vphantom {{{\text{KL}}} r}}\right.\kern-0pt} \!\lower0.7ex\hbox{$r$}}} \right)_{o}^{2} + \left( {{\raise0.7ex\hbox{$s$} \!\mathord{\left/ {\vphantom {s {r_{yc} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${r_{yc} }$}}} \right)^{2} }$$

(1)

For which, $\left( {{\raise0.7ex\hbox{$s$} \!\mathord{\left/ {\vphantom {s {r_{yc} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${r_{yc} }$}}} \right) \le 0.5 \times \left( {{\raise0.7ex\hbox{${KL}$} \!\mathord{\left/ {\vphantom {{KL} r}}\right.\kern-0pt} \!\lower0.7ex\hbox{$r$}}} \right)_{o}$

where s is spacing between fasteners, r_yc is the minimum radius of gyration of a single section, r_o is the minimum radius of gyration of the compound section, and KL is the effective length of the member.

The above recommendation is experimentally evaluated by Stone and LaBoube [12] on back-to-back connected channel sections. It is found that when the thickness is high (more than 1 mm), a modified slenderness ratio with minimum screw spacing does not affect the ultimate capacity. In the context of plug welds, Whittle and Ramseyer [14] did an experimental study on closed built-up columns made by face-to-face connected lipped plain channels. The dimension of specimens is selected such as the sections are locally and distortionally stable and flexural buckling is the natural mode of buckling. It is found that for plug welded built-up sections, a modified slenderness ratio will predict conservative results. Reyes and Guzmán [10] studied the effect of weld spacing, fixed, and flexible support conditions on the ultimate strength of box CFS columns. It is found that the ultimate capacity of the box CFS column does not vary much with weld spacing and rigid or flexible end condition. Fratamico et al. [7] studied the composite action generated by screw fasteners on the global buckling behavior of built-up columns using a semi-analytical screw fastener element. Abbasi et al. [2] developed a compound finite strip-based numerical formulation for buckling stress computation of CFS built-up columns. The effect of fastener spacing, in context of beams is reported by Wang and Young [13], where open and closed shape built-up sections are studied.

In the literature, the effect of the modified slenderness ratio on the ultimate capacity of globally buckling columns has been studied by experimental work. The composite action generated by different fastener spacing needs to be studied to get the optimum number of fasteners for forming a fully composite action. In this study, a spline finite strip-based numerical formulation is formed to incorporate the effect of fasteners on the buckling behavior of CFS columns. By applying specific constraints on the numerical model, pure global buckling mode can be captured. The details of numerical formulations are given in the next sections.

2 Numerical Framework

The theory of classical finite strip method and spline finite method for single section CFS members are well documented in the literature [5], Lau and Hancock [9]. However, in this study, an extension to the pre-existed spline finite framework is presented for the buckling analysis of built-up CFS sections. The Direct Strength Method (DSM), which is a simple non-iterative design procedure [11], uses the critical buckling stress to compute the ultimate strength of the CFS member. In this chapter, a numerical framework is presented to capture the effect of discrete fasteners on the stability behavior of built-up CFS sections. A compound methodology is adopted to incorporate fasteners as three-dimensional beam elements into the SFSM-based numerical model of thin plates. In this chapter, this numerical framework will be referred to as the Compound Spline Finite Strip Method (CSFSM). To avoid the occurrence of distortional buckling and a consequential global-distortional buckling interaction at any length, a constraint model is also developed and presented in this study. The stiffness and stability matrices can be derived as per the conventional spline finite strip method [9].

2.1 Compound Spline Finite Strip Method

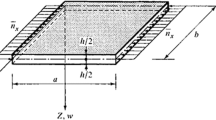
For a typical plate strip, the generalized displacement field at the mid surface in local coordinates d(x, y) is given by the displacement functions at its nodal lines. For the application of specific boundary conditions at ends, the local amendment property of splines is used. In this study, cubic spline functions (B3) are used in the longitudinal direction to get continuous curvature. For membrane and flexural deformations, linear and Hermitian cubic interpolation functions are adopted in the transverse direction. A generalized displacement field at mid surface is as follows,

$${\mathbf{d}}\left( {{\text{x}},{\text{y}}} \right) = \left\{ {u,v,w} \right\}^{{\text{T}}} = \left[ {N_{x} } \right][\phi_{y} ]\left\{ \delta \right\}$$

(2)

where, [N_x] is the matrix of transverse shape functions, [ϕ_y] is the matrix of spline functions in longitudinal direction, and {δ} = {u_i, v_i, w_i, θ_i, u_j, v_j, w_j, θ_j}^T is displacement vector of strip (Figs. 1 and 2).

Fig. 1

Spline finite strip with the coordinate axis

Fig. 2

Local B3 cubic spline function

2.1.1 Fastener Element

To form the tangent stiffness matrix of the compound section, the strain energy of the fasteners present in the system needs to be added in the total strain energy of the folded plate system. The local stiffness matrix of a three-dimensional beam element needs to be transformed about the plate’s displacement field so that the additional strain energy of the fastener element can be computed. The displacement field of a two-node beam element with six degrees of freedom at each node can be expressed as,

$$\left\{ {\delta_{b}^{L} } \right\} = \left\{ {u_{b}^{i} ,v_{b}^{i} ,w_{b}^{i} ,\theta_{bx}^{i} ,\theta_{by}^{i} ,\theta_{bz}^{i} ,u_{b}^{j} ,v_{b}^{j} ,w_{b}^{j} ,\theta_{bx}^{j} ,\theta_{by}^{j} ,\theta_{bz}^{j} } \right\}^{{\text{T}}}$$

(3)

The symmetric stiffness matrix of a beam element in the local coordinate system can be written as (Fig. 3),

$$\left[ {K_{b}^{L} } \right] = { }\left[ {\begin{array}{*{20}c} {\left[ {K_{ii} } \right]} & {\left[ {K_{ij} } \right]} \\ {\left[ {K_{ji} } \right]} & {\left[ {K_{jj} } \right]} \\ \end{array} } \right]$$

(4)

$$\begin{aligned} K_{1,1} & = \frac{{{\text{EA}}}}{L}; K_{1,7} = \frac{{ - {\text{EA}}}}{L}; K_{2,2} = \frac{{12{\text{EI}}_{z} }}{{L^{3} }}; K_{2,6} = \frac{{6{\text{EI}}_{z} }}{{L^{2} }}; K_{2,8} \\ & = \frac{{ - 12{\text{EI}}_{z} }}{{L^{3} }}; K_{2,12} = \frac{{6{\text{EI}}_{z} }}{{L^{2} }} \\ \end{aligned}$$

$$K_{3,3} = \frac{{12{\text{EI}}_{y} }}{{L^{3} }}; K_{3,5} = \frac{{ - 6{\text{EI}}_{y} }}{{L^{2} }}; K_{3,9} = \frac{{ - 12{\text{EI}}_{y} }}{{L^{3} }}; K_{3,11} = \frac{{ - 6{\text{EI}}_{y} }}{{L^{2} }}; K_{4,4} = \frac{{{\text{GJ}}}}{L};$$

$$K_{4,10} = - \frac{{{\text{GJ}}}}{L}; K_{5,5} = \frac{{4{\text{EI}}_{y} }}{L}; K_{5,9} = \frac{{ - 6{\text{EI}}_{y} }}{{L^{2} }};K_{5,11} = \frac{{2{\text{EI}}_{y} }}{L}; K_{6,6} = \frac{{4{\text{EI}}_{z} }}{L};$$

$$K_{7,7} = \frac{{{\text{EA}}}}{L}; K_{8,8} = \frac{{12{\text{EI}}_{z} }}{{L^{3} }}; K_{8,12} = \frac{{ - 6{\text{EI}}_{z} }}{{L^{2} }}; K_{9,9} = \frac{{12{\text{EI}}_{y} }}{{L^{3} }}; K_{9,11} = \frac{{6{\text{EI}}_{y} }}{{L^{2} }};$$

$$K_{10,10} = \frac{{{\text{GJ}}}}{L}; K_{11,11} = \frac{{4{\text{EI}}_{y} }}{L};K_{12,12} = \frac{{4{\text{EI}}_{z} }}{L}$$

Fig. 3

Beam element in the local coordinate axis

2.1.2 Compound Framework

The beam stiffness matrix is added to the global stiffness matrix by making the appropriate transformation of axes and interpolating the beam displacement vector to the plate’s displacement vector with the relationship given below (Fig. 4).

Fig. 4

Compound section connected by beam element and strip orientations in global coordinate axes

$$\Pi_{b} = \frac{1}{2} \left\{ {\delta_{b}^{G} } \right\}^{T} \left[ {K_{b}^{G} } \right]\left\{ {\delta_{b}^{G} } \right\}$$

(5)

$$\left\{ {\begin{array}{*{20}c} {\{ \delta_{b}^{i} \} } \\ {\{ \delta_{b}^{j} \} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {\left[ {Tr_{{b_{i} q}} } \right]} & 0 \\ 0 & {\left[ {Tr_{{b_{j} r}} } \right]} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\{ \delta_{q} \} } \\ {\left\{ {\delta_{r} } \right\}} \\ \end{array} } \right\}$$

(6)

$$\left[ {Tr_{ii} } \right] = \left[ {\begin{array}{*{20}c} {N_{ui} \phi_{ui} } & {} & {} & {} & {N_{uj} \phi_{uj} } & {} & {} & {} \\ {} & {N_{vi} \phi_{vi} } & {} & {} & {} & {N_{vj} \phi_{vj} } & {} & {} \\ {} & {} & {N_{wi} \phi_{wi} } & {N_{\theta i} \phi_{\theta i} } & {} & {} & {N_{wj} \phi_{wj} } & {N_{\theta j} \phi_{\theta j} } \\ {} & {} & {N_{wi} \phi ^{\prime}_{wi} } & {N_{\theta i} \phi ^{\prime}_{\theta i} } & {} & {} & {N_{wj} \phi ^{\prime}_{wj} } & {N_{\theta j} \phi ^{\prime}_{\theta j} } \\ {} & {} & {N^{\prime}_{wi} \phi_{wi} } & {N^{\prime}_{\theta i} \phi_{\theta i} } & {} & {} & {N^{\prime}_{wj} \phi_{wj} } & {N^{\prime}_{\theta j} \phi_{\theta j} } \\ 0 & {} & {} & {} & 0 & {} & {} & {} \\ \end{array} } \right]$$

(7)

2.2 Constrained Model

In this study, a constrained model is developed in the CSFSM to compute the pure elastic critical global buckling stress of the built-up section. By constraining the transverse displacements of folded corner lines, the distortional deformations can be eliminated. To allow only the minor axis deformations, lateral displacements of the corner nodes will be kept free. This model will be able to restrict distortional buckling mode efficiently, but local buckling cannot be eliminated. To avoid the occurrence of local buckling in the deformed configuration, the width to thickness ratio of stiffened and un-stiffened elements can be selected such as critical local buckling stress will be more than the yield stress of the material. In this study, all the sections are selected such as the local buckling stress will be higher than the global buckling stress at any length. The constrained model is as shown in Fig. 5.

Fig. 5

Constrained model adopted for allowing only minor axis buckling mode

3 Numerical Examples

3.1 Verification of CSFSM

A built-up I section formed by two back-to-back connected lipped channel sections subjected to uniform compression is considered in this study (Fig. 6). The buckling analysis results obtained from the current numerical method are compared with finite element-based software ABAQUS [1]. The geometric and material properties of the lipped channel section are presented in Table 1. All the results are obtained for generally adopted boundary conditions, i.e., simply-supported and clamped–clamped ends. The fastener spacing is kept fixed at one-third of the length of the member for both boundary conditions. To obtain symmetrical deformed shape, warping free and warping restrained deformations are imposed to both ends for simply-supported and clamped–clamped boundary conditions, respectively. All the results are plotted in Fig. 7 for different numbers of spline knots.

Table 1 Geometrical and material properties of lipped channel section

Fig. 6

A typical single lipped channel and built-up section

Fig. 7

Verification and convergence of CSFSM for the built-up section for simply-supported and clamped–clamped boundary conditions

In the Fig. 7, critical buckling stress obtained by CSFSM is normalized with yield stress, and plotted for different lengths by keeping a fixed fastener spacing. The number of spline knots required for the convergence is found to be almost same for both Simply-Supported (SS) and Clamped–Clamped (CC) boundary conditions. In both the cases, especially for global buckling range, CSFSM results move toward FEA results with increase in numbers of spline knots.

3.2 Verification of the Constrained Model

To verify the results obtained from the constrained model for global buckling mode, constrained finite strip method (cFSM) [3] is used. A single lipped channel section discussed in Table 2 is used for verification. All the results presented in Fig. 8 are for lengths more than 1000 mm with simply-supported boundary condition. From the results, it can be seen that constrained model results match with the cFSM outputs.

Table 2 Geometrical and material properties of lipped channel section (in Fig. 8)

Fig. 8

Verification of the constrained model for lipped channel section with cFSM

3.3 Effect of Fastener Spacing

The presence of discrete fasteners will result in an intermediate-composite curve, which moves toward the fully composite curve in the global buckling region. To understand the stability behavior of built-up sections, different fastener spacing is adopted in this study (s = L/3, and L/5). All the built-up sections are generated by using two sets of fastener rows at one-third of the web height, as shown in Fig. 9. All the results presented here are of built-up section deforming under minor axis buckling only. By decreasing the fastener spacing, an enhanced composite behavior is obtained and the corresponding buckling stress outputs shift toward the fully composite curve. The properties of the lipped channel section are given in Table 2. The increment in critical buckling stress due to the reduction in fastener spacing is presented in Table 3 for different sections.

Fig. 9

Built-up section and plan diagram

Table 3 Numerical results for different (h/b) ratio

4 Discussion

The presence of a discrete fastener system in the built-up section provides an intermediate-composite action, which depends upon the fastener spacing and their arrangement. The above-discussed CSFSM can incorporate the effect of fastener on the stability behavior of the system. It can be seen from the results presented in the above sections that with a specific fastener spacing, the composite action of the built-up section matches the buckling behavior of a fully composite section. Other fastener spacing results in a buckling behavior, which is in between the single and fully composite section behavior.

AISI: S100 predictions can also be presented for the above-discussed sections. The modified slenderness ratio for different fastener spacing is presented in Fig. 10. For minimum suggested fastener spacing, modified slenderness ratio gives unconservative predictions, but for low fastener spacing or spacing for which buckling behavior is near to composite section behavior, modified slenderness ratio gives conservative predictions.

Fig. 10

Comparison of actual buckling stress and AISI: S100 buckling stress predictions

5 Conclusions

In this study, a numerical framework based upon compound methodology to incorporate the effect of fastener on buckling behavior of CFS built-up members is presented. The numerical model is verified with ABAQUS outputs, and a sensitivity study is performed for generally adopted boundary conditions. To understand the effect of different fastener spacing, a numerical study is performed with a constrained model to capture only the minor axis buckling mode. It is found that for the built-up I section, the fastener spacing of L/5 will provide the buckling behavior similar to a fully composite section buckling behavior. For other higher spacing, buckling behavior of the built-up section will result in an intermediate-composite buckling behavior.

AISI: S100 provides a modified slenderness formulation to incorporate the loss of shear rigidity on the global buckling behavior of CFS built-up columns. The results from the current study are compared with the modified slenderness formulation, and it is found that AISI buckling load prediction for the built-up section is conservative around 10% when fully composite buckling behavior is ensured. In this study, the versatility of the current numerical formulation is presented, and this framework can be extended to compute the effect of discrete fastener on other buckling modes, i.e., local and distortional buckling modes.