Reducing large graphs to small supergraphs: a unified approach

Abstract

Summarizing a large graph with a much smaller graph is critical for applications like speeding up intensive graph algorithms and interactive visualization. In this paper, we propose CONditional Diversified Network Summarization (CondeNSe), a Minimum Description Length-based method that summarizes a given graph with approximate “supergraphs” conditioned on a set of diverse, predefined structural patterns. CondeNSe features a unified pattern discovery module and a set of effective summary assembly methods, including a powerful parallel approach, k-Step, that creates high-quality summaries not biased toward specific graph structures. By leveraging CondeNSe ’s ability to efficiently handle overlapping structures, we contribute a novel evaluation of seven existing clustering techniques by going beyond classic cluster quality measures. Extensive empirical evaluation on real networks in terms of compression, runtime, and summary quality shows that CondeNSe finds 30–50% more compact summaries than baselines, with up to 75–90% fewer structures and equally good node coverage.

1 Introduction

In an era of continuous generation of large amounts of data, summarization techniques are becoming increasingly crucial to help abstract away noise, uncover patterns, and inform human decision processes. Here we focus on the summarization of graphs, which are powerful structures that capture a number of phenomena, from communication between people (Leskovec et al. 2005; Backstrom et al. 2006; Koutra et al. 2013) to links between webpages (Kleinberg et al. 1999), to interactions between neurons in our brains (OCP 2014; Safavi et al. 2017). In general, graph summarization or coarsening approaches (Liu et al. 2016) seek to find a concise representation of the input graph that reveals patterns in the original data, while usually preserving specific network properties. As graph summaries are application-dependent, they can be defined with respect to various aspects: they can preserve specific structural patterns, focus on some entities in the network, preserve the answers to a specific set of queries, or maintain the distributions of some graph properties. Graph summarization leads to the reduction of data volume, speedup of graph algorithms, improved storage and query time, and interactive visualization. Its major challenges are in effectively handling the volume and complexity of data, defining the interestingness of patterns, evaluating the proposed summarization techniques, and capturing network structural changes over time. The graph mining community has mainly studied summarization techniques for the structure of static, plain graphs (Chierichetti et al. 2009; Navlakha et al. 2008) and to a smaller extent, methods for attributed or dynamic networks (Shah et al. 2015).

Fig. 1

CondeNSe generates simpler and more compact supergraphs than baselines. Yellow, red, and green nodes for stars, cliques, and bipartite cores, respectively (color figure online)

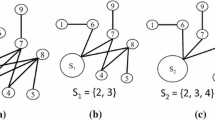
Our method, ConDeNSe or CONditional Diversified Network Summarization, summarizes the structure of a given large-scale network by selecting a small set of its most informative structural patterns. Inspired by recent work (Navlakha et al. 2008; Koutra et al. 2014), we formulate graph summarization as an information-theoretic optimization problem in search of local structures that collectively minimize the description of the graph. CondeNSe is a unified, edge-overlap-aware graph summarization method that summarizes a given graph with approximate “supergraphs” conditioned on diverse, predefined structural patterns. An example is shown in Fig. 1, where the (super)nodes in Fig. 1b correspond to sets of nodes in the original graph. Specifically, the predefined patterns include structures that have well-understood graph-theoretical properties and are found in many real-world graphs (Kleinberg et al. 1999; Araujo et al. 2014; Faloutsos et al. 1999; Prakash et al. 2010): cliques, stars, bipartite cores, chains, and patterns with skewed degree distribution.

Our work effectively addresses three main shortcomings of prior summarization work (Koutra et al. 2014; Koutra and Faloutsos 2017), namely: (1) its heavy dependence on the structural pattern discovery method and intrinsic tendency, or bias, to select star-like structures in the final summary; (2) its inability to handle edge-overlapping patterns in the summary; and (3) its dependence on the order in which candidate structures are considered for the final summary. Our proposed unified approach effectively handles these issues and results in robust, compact summaries with 5–10× fewer structural patterns (or supernodes) and up to 50% better compression.

CondeNSe consists of three modules that address the aforementioned shortcomings. (1) A unified structural pattern discovery module leverages the strengths of various popular graph clustering methods (e.g., Louvain Blondel et al. 2008, METIS Karypis and Kumar 1999) to address the biases toward specific structures per clustering method; (2) A Minimum Description Length-based (MDL) formulation with a penalty term effectively minimizes redundancy in edge coverage by the structural patterns included in the summary. This term is paramount when the candidate structural patterns have significant edge overlap, such as in the case of our unified structure discovery module; (3) An iterative, multi-threaded, and divide-and-conquer-based summary assembly module further reduces structure selection bias during the summary creation process by being independent of the order in which the candidate structural patterns are considered. This parallel module is up to 53× faster than its serial counterpart on a 6-core machine.

Our contributions in this paper are as follows:

• Approach We introduce ConDeNSe, an effective unified, edge-overlap-aware graph summarization approach. ConDeNSe includes a powerful parallel summary assembly module, k-Step, that creates compact and easy-to-understand graph summaries with high node coverage and low redundancy.

• Novel metric We propose a way to leverage ConDeNSe as a proxy to compare graph clustering methods with respect to their summarization performance on large, real-world graphs. Our work complements the usual evaluation metrics in the related literature (e.g., modularity, conductance).

• Experiments We present a thorough empirical analysis on real networks to evaluate the summary quality and runtime, and study the properties of seven clustering methods.

For reproducibility, the code is available online at https://github.com/yikeliu/ConDeNSe. Next, we present the related work and necessary background.

2 Related work and background

Our work is related to (1) graph summarization methods, (2) compression and specifically MDL, (3) graph clustering, and (4) graph sampling. We briefly review each of these topics next.

Graph summarization

Most research efforts in graph summarization (Liu et al. 2016) focus on plain graphs and can be broadly classified as group-based (LeFevre and Terzi 2010; Raghavan and Garcia-Molina 2003), compression-based (Chierichetti et al. 2009; Navlakha et al. 2008; Goonetilleke et al. 2017), simplification-based, influence-based, and pattern-based (Cook and Holder 1994). Dynamic graph summarization has been studied to a much smaller extent (Shah et al. 2015; Jin and Koutra 2017). Beyond the classic definition of graph summarization, there are also approaches that summarize networks in terms of structural properties (e.g., degree, PageRank) by automatically leveraging domain knowledge (Jin and Koutra 2017; Jin et al. 2017). Most related to our work are the ideas of node grouping and graph compression. Built on these ideas, two representative methods, MDL-summarization (Navlakha et al. 2008) and VoG (Koutra et al. 2014), are MDL-based summarization methods that compress the graphs by finding near-structures [e.g., (near-) cliques, (near-) bipartite cores]. MDL-summarization, which iteratively combines neighbors into supernodes as long as it helps with minimizing the compression cost, includes mostly cliques and cores in the summaries, and has high runtime complexity.

On the other hand, VoG finds structures by employing SlashBurn (Kang and Faloutsos 2011) (explained below) and hence is particularly biased toward selecting star structures. Moreover, it creates summaries (i.e., lists of structures) using a greedy heuristic on a pre-ordered set of structures (cf. Sect. 4.3). Unlike these methods, CondeNSe performs ensemble pattern discovery and handles edge-overlapping structures. Furthermore, its summary assembly is robust to the ordering of structures.

MDL in graph mining

Many data mining problems are related to summarization and pattern discovery, and, thus, to Kolmogorov complexity (Faloutsos and Megalooikonomou 2007), which can be practically implemented by the MDL principle (Rissanen 1983). Applications include clustering (Cilibrasi and Vitányi 2005), community detection (Chakrabarti et al. 2004), pattern discovery in static and dynamic networks (Koutra et al. 2014; Shah et al. 2015), and more.

Graph clustering

Graph clustering and community detection are of great interest to many domains, including social, biological, and web sciences (Girvan and Newman 2002; Backstrom et al. 2008; Fortunato 2010). Here, we leverage several graph clustering methods to obtain diversified graph summaries, since each method is biased toward certain types of structures, such as cliques and bipartite cores (Blondel et al. 2008; Karypis and Kumar 1999; Yang and Leskovec 2013) or stars (Kang and Faloutsos 2011). Unlike the existing literature (Leskovec et al. 2010) where clustering methods are compared with respect to classic quality measures, we also propose to use ConDeNSe as a vessel to evaluate the methods’ summarization power. We leverage seven decomposition methods, compared quantitatively in Table 1

Table 1 Qualitative comparison of the graph clustering techniques included in ConDeNSe

:

• SlashBurn Kang and Faloutsos (2011) is a node reordering algorithm initially developed for graph compression. It performs two steps iteratively: (1) It removes high-centrality nodes from the graph; (2) It reorders nodes such that high-degree nodes are assigned the lowest IDs and nodes from disconnected components get the highest IDs. The process is repeated on the giant connected component. We use SlashBurn by identifying structures from the egonet of each high-centrality node, and the disconnected components, as subgraphs.

• Louvain Blondel et al. (2008) is a modularity-based partitioning method for detecting hierarchical community structure. Like SlashBurn, Louvain is iterative: (1) Each node is placed in its own community. Then, the neighbors j of each node i are considered, and i is moved to j’s community if the move produces the maximum modularity gain. The process is applied repeatedly until no further gain is possible. (2) A new graph is built whose supernodes represent communities, and superedges are weighted by the sum of weights of links between the two communities. The algorithm typically converges in a few passes.

• Spectral clustering refers to a class of algorithms that rely on eigen-decomposition to identify community structure. We use one such spectral clustering algorithm (Hespanha 2004), which partitions a graph by performing k-means clustering on the top-k eigenvectors of the input graph. The idea behind this clustering is that nodes with similar connectivity have similar eigen-scores in the top-k vectors and form clusters.

• METIS Karypis and Kumar (1999) is a cut-based k-way multilevel graph partitioning scheme based on multilevel recursive bisection (MLRB). Until the graph size is substantially reduced, it first coarsens the input graph by grouping nodes into supernodes iteratively such that the edge-cut is preserved. Next, the coarsened graph is partitioned using MLRB, and the partitioning is projected onto the original input graph G through backtracking. The method produces k roughly equally sized partitions.

• HyCoM Araujo et al. (2014) is a parameter-free algorithm that detects communities with hyperbolic structure. It approximates the optimal solution by iteratively detecting important communities. The key idea is to find in each step a single community that minimizes an MDL-based objective function given the previously detected communities. The iterative procedure consists of three steps: community candidates, community construction, and matrix deflation.

• BigClam Yang and Leskovec (2013) is a scalable overlapping community detection method. It is built on the observation that overlaps between communities are densely connected. By explicitly modeling the affiliation strength of each node-community pair, the latter is assigned a nonnegative latent factor which represents the degree of membership to the community. Next, the probability of an edge is modeled as a function of the shared community affiliations. The identification of network communities is done by fitting BigClam to a given undirected network G.

• KCBC Liu et al. (2015) is inspired by the k-cores algorithm Giatsidis et al. (2011), which unveils densely connected structures. A k-core is a maximal subgraph for which each node is connected to at least k other nodes. KCBC iteratively removes k-cores starting by setting k equal to the maximum core number (the max value k for which the node is present in the resulting subgraph) across all nodes. Each connected component in the induced subgraphs is identified as a cluster, and is removed from the original graph. The process is repeated on the remaining graph.

Other clustering methods that we considered (e.g., Weighted Stochastic Block Model or WSBM) are not included in ConDeNSe due to lack of scalability. For instance, WSBM took more than a week to finish on our smallest dataset.

Graph sampling

Sampling graph nodes and/or edges may be considered an alternative method of graph compression, and as such these techniques relate to graph summarization (Hübler et al. 2008; Batson et al. 2013). Graph sampling techniques have been extensively studied and reviewed (Mathioudakis et al. 2011; Ahmed et al. 2013; Hasan et al. 2016). Node sampling methods include sampling according to degree, PageRank score, or substructures like spanning trees. Edge sampling techniques include uniform sampling and sampling according to edge weights or effective resistance (Spielman and Srivastava 2011) to maintain node reachability (Aho et al. 1972) or the graph spectrum up to some multiplicative error. Graph sampling can also be used to approximate queries with theoretical guarantees.

That said, the fundamental goals of graph sampling and summarization differ. Sampling focuses on obtaining sparse subgraphs that maintain properties of the original input graph, like degree distribution, size distribution of connected components, diameter, or community structure (Maiya and Berger-Wolf 2010). Unlike graph summarization, sampling is less concerned with identifying succinct patterns or structures that represent the input graph and assist user understanding. Although sampling has been shown to support visualization (Rafiei and Curial 2005), these methods usually operate on individual nodes/edges instead of collective patterns. Furthermore, the results of graph sampling algorithms may require additional processing for interpretability.

3 ConDeNSe: proposed model

Table 2 Major symbols and definitions

We formulate the graph summarization problem as a graph compression problem. Let $G({\mathcal {V}}, {\mathcal {E}})$ be a graph with $n = |{\mathcal {V}}|$ nodes and $m = |{\mathcal {E}}|$ edges, without self-loops. The Minimum Description Length (MDL) problem, which is a practical version of Kolmogorov Complexity (Faloutsos and Megalooikonomou 2007), aims to find the best model M in a given family of models ${\mathcal {M}}$ for some observed data ${\mathcal {D}}$ such that it minimizes $L(M) + L({\mathcal {D}} | M)$, where L(M) is the description length of M in bits and $L({\mathcal {D}} | M)$ is the description length of ${\mathcal {D}}$ which is encoded by the chosen model M. Table 2 provides the definitions of the recurrent symbols used in this section.

We consider summaries in the model family ${\mathcal {M}}$, which consists of all possible permutations of subsets of structural patterns in $\Omega$. One option is to populate $\Omega$ with the frequent patterns that occur in the input graph (in a data-driven manner), but frequent subgraph mining is NP-complete and does not scale well. Moreover, even efficient approximate approaches are not applicable to unlabeled graphs and can only handle small graphs with a few tens or hundreds of nodes. To circumvent this problem, we choose set $\Omega$ with five patterns that are common in real-world static graphs (Kleinberg et al. 1999; Araujo et al. 2014), correspond to interesting real behaviors, and can (approximately) describe a wide range of structural patterns: stars (st), full cliques (fc), bipartite cores (bc), chains (ch), and hyperbolic structures with skewed degree distribution (hs). Under the MDL principle, any approximate structures (e.g., near-cliques) can be easily encoded as their corresponding exact structures (e.g., fc) with some errors. Since many communities have hyperbolic structure (Araujo et al. 2014) and it cannot be expressed as a simple composition of the other structural patterns in $\Omega$, we consider it separately. Motivated by real-world discoveries, we focus on structures that are commonly found in networks, but our framework is not restricted to them; it can be readily extended to other, application-dependent types of structures as well.

Formally, we tackle the following problem:

Problem 1

Given a graph G with adjacency matrix ${\mathbf {A}}$ and structural pattern types $\Omega$, we seek to find the model M that minimizes the encoding length of the graph and the redundancy in edge coverage:

$$L(G,M) = L(M) + L({\mathbf {E}})+L({\mathbf {O}})$$

(1)

where ${\mathbf {M}}$ is ${\mathbf {A}}$’s approximation induced by M, ${\mathbf {E}} = {\mathbf {M}} \oplus {\mathbf {A}}$ is the error matrix to correct for edges that were erroneously described by M, $\oplus$ is exclusive OR, and ${\mathbf {O}}$ is the edge-overlap matrix to penalize edges covered by many patterns.

Model M induces a supergraph with each $s \in M$ as an (approximate) supernode, and weighted superedges between them. Before we further formalize the task of encoding the model, the error matrix, and the edge-overlap penalty matrix, we provide a visual illustration of our MDL objective.

An illustrative example

Figure 2 shows the original adjacency matrix ${\mathbf {A}}$ of an input graph, which is encoded as (1) ${\mathbf {M}}$ (the matrix that is induced by the model M), and (2) the error matrix E (which captures additional/missing edges that are not properly described in M). In this example, there are 6 structures in the model (from the top left corner to the bottom right corner: a star, a large clique, a small clique, a bipartite core, a chain, and a hyperbolic structure), where the cliques and the bipartite core have overlapping nodes and edges.

Fig. 2

Illustration of MDL encoding

3.1 Encoding the model

To fully describe a model $M \in {\mathcal {M}}$ for the input graph G, we encode it as L(M):

$$L(M) = L_{\mathbb {N}}(|M|+1) + \log _2 \left( {\begin{array}{c}|M|+|\Omega |-1\\ |\Omega |-1\end{array}}\right) + \sum _{s \in M}{\big ( -\log \Pr (x(s) \mid M) + L(s) \big )}$$

(2)

where in the first two terms we encode the number of structural patterns in M using Rissanen’s optimal encoding for integers (Rissanen 1983) and the number of patterns per type in $\Omega$, respectively. Then, for each structure $s \in M$, we encode its type x(s) using optimal prefix codes (Cover and Thomas 2012), and its connectivity L(s). Next, we introduce the MDL encoding per type of structure in $\Omega$.

• Stars A star consists of a “hub” node connected to two or more “spoke” nodes. We encode it as:

  $$L(st) = L_{\mathbb {N}}(|st| - 1) + \log _2 n + \log _2 {{n-1} \atopwithdelims (){|st|-1}}$$

  (3)

  where we encode in order the number of spokes, the hub ID (we identify it out of n nodes using an index over the combinatorial number system), and the spoke IDs.

• Cliques A clique is a densely connected set of nodes with:

  $$L(fc) = L_{\mathbb {N}}(|fc|) + \log _2 {n \atopwithdelims ()|fc|}$$

  (4)

  where we encode its number of nodes followed by their IDs.

• Bipartite cores A bipartite core consists of two nonempty sets of nodes, L and R, which have edges only between them, and $L \cap R = \emptyset$. Stars are a special case of bipartite cores with $|L| = 1$. The encoding cost is given as:

  $$L(bc) = L_{\mathbb {N}}(|L|) + L_{\mathbb {N}}(|R|) + \log _2{n \atopwithdelims ()|L|} + \log _2{n \atopwithdelims ()|R|},$$

  (5)

  where we encode the number of nodes in L and R followed by the node IDs in each set.

• Chains A chain is a series of nodes that are linked consecutively—e.g., node-set $\{a,b,c,d\}$ in which a is connected to b, b is connected to c, and c is connected to d. Its encoding cost, L(ch), is:

  $$L(ch) = L_{\mathbb {N}}(|ch| - 1) + \sum _{i=1}^{|ch|} \log _2(n-i+1)$$

  (6)

  where we encode its number of nodes, followed by their node IDs in order of connection.

• Hyperbolic structures A hyperbolic structure or community (Araujo et al. 2014) has skewed degree distribution which often follows a power law with exponent between − 0.6 and − 1.5. The encoding length of a hyperbolic structure hs is given as:

  $$L({ hs }) = k + L_{\mathbb {N}}(|{ hs }|) + \log _2 \left( {\begin{array}{c}n\\ |{ hs }|\end{array}}\right) + \log _2(|{\mathbf {A}}(hs)|) + ||{ hs }|| l_1 + ||{ hs }||' l_0$$

  (7)

  where we first encode the power-law exponent (using Rissanen’s encoding (Rissanen 1983) for the integer part, the number of decimal values, and the decimal part), followed by the number of nodes and their IDs. Then, we encode the number of edges in the structure (=$|{\mathbf {A}}(hs)|$), and use optimal prefix codes, $l_0, l_1$, for the missing ($||{ hs }||'$) and present ($||{ hs }||$) edges, respectively. Specifically, $l_1 = -\log ((||{ hs }|| / (||{ hs }|| + ||{ hs }||'))$, and $l_0$ is defined similarly.

3.2 Encoding the errors

Given that M is a summary, and ${\mathbf {M}}$ is only an approximation of ${\mathbf {A}}$, we also need to encode errors of the model. For instance, a near-clique is represented as a full clique in the model, and, thus, contributes some edges to the error matrix (i.e., the missing edges from the real data). We encode the error ${\mathbf {E}} = {\mathbf {M}} \oplus {\mathbf {A}}$ in two parts, ${\mathbf {E}}^+$ and ${\mathbf {E}}^-$, since they likely follow different distributions (Koutra et al. 2014). The former encodes the edges induced by M which were not in the original graph, and the latter the original edges that are missing in M:

$$L({\mathbf {E}}^+) = \log _2(|{\mathbf {E}}^+|) + ||{\mathbf {E}}^+||l_1 + ||{\mathbf {E}}^+||'l_0$$

(8)

$$L({\mathbf {E}}^-) = \log _2(|{\mathbf {E}}^-|) + ||{\mathbf {E}}^-||l_1 + ||{\mathbf {E}}^-||'l_0$$

(9)

where we encode the number of 1s in ${\mathbf {E}}^+$ (or ${\mathbf {E}}^-$), followed by the actual 1s and 0s using optimal prefix codes (as before).

3.3 Encoding the edge-overlap penalty

Several of the graph decomposition methods that we consider (e.g., SlashBurn, KCBC in Table 1) generate edge-overlapping patterns. The MDL model we have presented so far naturally handles node overlaps—if two structures consist of the same large set of nodes, only one of the them will be chosen during the encoding cost minimization process, because their combination would lead to higher encoding cost. However, up to this point, the model considers a binary state for each edge: that is, an edge is described by the model M, or not described by it. This could lead to summaries with high redundancy in edge coverage, as we show next with an illustrative example.

To explicitly handle extensive edge overlaps in the graph summaries (which can lead to low node/edge coverage), we add a penalty term, $L({\mathbf {O}})$, in the optimization function in Eq. (1). We introduce the matrix ${\mathbf {O}}$, which maintains the number of times each edge is described by M, i.e., the number of selected structures in which the edge occurs. We encode the description length of ${\mathbf {O}}$ as:

$$L({\mathbf {O}})=\log _2(|{\mathbf {O}}|)+||{\mathbf {O}}||l_1+||{\mathbf {O}}||'l_0+\sum _{o \in {\mathcal {E}}({\mathbf {O}})} L_{{\mathbb {N}}}(|o|)$$

(10)

where we first encode the number of distinct overlaps, and then use the optimal prefix code to encode the number of the present and missing entries in ${\mathbf {O}}$. As before, $l_0$ and $l_1$ are the lengths of the optimal prefix codes for the present and missing entries, respectively. Finally, we encode the weights in ${\mathbf {O}}$ using the optimal encoding for integers $L_{{\mathbb {N}}}$ (Rissanen 1983). We denote with ${\mathcal {E}}({\mathbf {O}})$ the set of nonnegative entries in matrix ${\mathbf {O}}$.

An illustrative example

Let us assume that the output of an edge-overlapping graph clustering method consists of three full cliques: (1) full clique 1 with nodes 1–20; (2) full clique 2 with nodes 11–30; and (3) full clique 3 with nodes 21–40. The encoding that does not account for overlaps (which is based on the modeling described in Sects. 3.1 and 3.2) includes all three structures in the summary, which clearly yields both redundant nodes and edges. Despite the overlap, the description length of the graph given the model above is calculated as 441 bits, since edges that are covered multiple times are not penalized. For reference, the graph needs 652 bits under the null (empty) model, where all the original edges are captured in the error matrix ${\mathbf {E}}$. Ideally, we want a method that penalizes extensive overlaps and maximizes the node/edge coverage.

In the example that we described above, by leveraging the full optimization function in Eq. (1), which includes the edge-overlap penalty term, we obtain a summary with only the first two cliques, as desired. The encoding of our proposed method has a length of 518 bits, which is higher than the number of bits of the non edge-overlap aware encoding (441 bits). The reason is that in the former (edge-overlap-aware) summary, some edges have remained unexplained (edges from nodes 11–20 to nodes 21–40), and thus are encoded as error. On the other hand, the latter summary encodes all the nodes and edges (without errors), but explains many edges twice (e.g., the nodes 11–20 and the edges between them, the edges between nodes 11–20 and 21–30) without accounting for the redundancy-related bits twice.

Our proposed edge-overlap-aware encoding can effectively handle a family model ${\mathcal {M}}$ that consists of subsets of node- and edge-overlapping structural patterns, and can choose a model M that describes the input graph well, and also minimizes redundant modeling of nodes and edges.

4 ConDeNSe: our proposed algorithm

Based on the model from Sect. 3, we propose CondeNSe, an ensemble, edge-overlap-aware algorithm that summarizes a graph with a compact supergraph consisting of a diverse set of structural patterns (e.g., fc, hs). CondeNSe consists of four modules (Algorithm 1), described in detail next.

4.1 Module A: Unified pattern discovery module

As we mentioned earlier, in our formulation, we consider summaries in the model family ${\mathcal {M}}$, which consists of all possible permutations of subsets of structural patterns in $\Omega$ (e.g., a summary with 10 full cliques, 3 bipartite cores, 5 stars and 9 hyperbolic structures). Toward this goal, the first step is to discover subgraphs in the input graph. These can then be used to build its summary. To find the “perfect” graph summary, we would need to generate all possible ($2^n$) patterns for a given graph G, and then, from all possible ($2^{2^n}$) combinations of these patterns pick the set that minimizes Eq. (1). This is intractable even for small graphs. For example, for $n=100$ nodes, there are more than $2^{\text {nonillion}}$ (1 nonillion $=10^{30}$) possible summaries. We reduce the search space by considering patterns that are found via graph clustering methods, and are likely to fit the structural patterns in $\Omega$ well.

The literature is rich in graph clustering methods (Blondel et al. 2008; Karypis and Kumar 1999; Yang and Leskovec 2013; Kang and Faloutsos 2011). However, each approach is biased toward identifying specific types of graph structures, which are most often cliques and bipartite cores. Choosing a decomposition method to generate patterns for the summary depends on the domain, the expected patterns (e.g., mainly clique- or star-like structures), and runtime constraints. To mitigate biases introduced by individual clustering methods, and to consider a diverse set of candidate patterns, we propose a unified approach that leverages seven existing clustering methods: SlashBurn, Louvain, Spectral, METIS, HyCoM, BigClam, and KCBC (Sect. 2). In Table 1, we present the qualitative advantages, disadvantages, and biases of the methods. Specifically, SlashBurn tends to provide excellent graph coverage and biased summaries in which stars dominate. Conversely, most other approaches produce primarily full cliques and stars, and some bipartite cores. HyCoM finds mainly hyperbolic communities with skewed degree distributions.

Our proposed unified approach (Algorithm 1, lines 2–4) is expected to lead to summaries with a better balanced set of structures (i.e., a good mix of exact and approximate cliques, bipartite cores, stars, chains and hyperbolic structures), and lower encoding cost than any standalone graph clustering method. At the same time, it is expected to take longer to generate all the patterns (although the clustering methods can trivially run in parallel) and the search space for the summary becomes larger, equal to the union of all the subgraphs that the clustering methods generate.

In the experimental evaluation, we use CondeNSe to empirically compare the impact of these methods on the summary quality and evaluate their summarization power.

4.2 Module B: Structural pattern identification module

This module (Algorithm 1, lines 5–12) identifies and assigns an identifier structural pattern in $\Omega$ to all the subgraphs found in module A. In other words, this module seeks to characterize each cluster with its best suited pattern in $\Omega = \{fc, st, bc, ch, hs\}$. Let g be the induced graph of a pattern generated in Step 1, and $\omega$ be a pattern in $\Omega$. Following the reasoning in Sect. 3, we use MDL as a selection criterion. To model g with $\omega$, we first model g with its best representation as structure type $\omega$ (explained in detail next), $r(g,\omega )$, and define its encoding cost as $L_{r(g,\omega }(g,\omega ) = L(\omega ) + L(g|\omega ) = L(\omega ) + L(E^+_\omega ) + L(E^-_\omega )$, where $E^+_\omega$ and $E^-_\omega$ encode the erroneously modeled and unmodeled edges of g. The pattern type in $\omega$ that leads to the smallest MDL cost is used as the identifier of the corresponding subgraph g (lines 11–12 in Algorithm 1).

Finding the best representation $r(g,\omega )$

Per pattern type $\omega$, each pattern g can be represented by a family of structures—e.g., we can represent g with as many bipartite cores as can be induced on all possible permutations of g’s nodes into two sets L (left node-set) and R (right node-set). The only exception is the full clique (fc) pattern, which has a unique (unordered) set of nodes. To make the problem tractable, we use the graph-theoretical properties of the pattern types in $\Omega$ in order to choose the representation of g which minimizes the incorrectly modeled edges.

Specifically, we represent g as a star by identifying its highest degree node as the hub and all other nodes as spokes. Representing g as a bipartite core reduces to finding the maximum bipartite pattern, which is NP-hard. To scale-up the computation, we approximate it with semi-supervised classification with two classes L and R, and the prior information that the highest degree node belongs to L and its neighbors to R. For the classification, we use Fast Belief Propagation (Koutra et al. 2011) with heterophily between neighbors. Similarly, representing g as a chain reduces to finding its longest path, which is also NP-hard. By starting from a random node, we perform breadth-first search two times, and end on nodes $v_1$ and $v_2$, respectively. Then, we consider the path $v_1$ to $v_2$ (based on BFS), and perform local search to further expand it. For the hyperbolic structures, we used power-law fitting (http://tuvalu.santafe.edu/~aaronc/powerlaws/ by Clauset et al.). Lines 7-10 in Algorithm 1 succinctly describe the search of the best representation r for every subgraph g and pattern type $\omega$.

4.3 Module C: Structural pattern selection module

This module is key for creating compact summaries and is described in lines 13–14 of Algorithm 1. Ideally, we would consider all possible combinations of the previously identified structures and pick the subset that minimizes the encoding cost in Eq. (1). If $|{\mathcal {S}}|$ structures have been found and identified in the previous steps, finding the optimal summary from $2^{|{\mathcal {S}}|}$ possibilities is not tractable. For reference, we have seen empirically that graphs with about 100,000 nodes, have over 50K structures. The optimization function is neither monotonic nor submodular, in which case a greedy hill climbing approach would give a $(1 - \frac{1}{\epsilon })$-approximation of the optimal.

Instead of considering all possible combinations of structures for the summary, prior work has proposed GnF, a heuristic that considers the structures in decreasing order of “local” encoding benefit and includes in the model the ones that help further decrease the graph’s encoding cost L(G, M). The local encoding benefit (Koutra et al. 2014) is defined as $L(g,\emptyset )-L(g,\omega )$, where $L(g,\emptyset )$ represents the encoding of g as noise (i.e., empty model). Although it is efficient, its output summary and performance heavily depend on the structure order. To overcome these shortcomings and obtain more compact summaries, we propose a new structural pattern selection method, Step, as well as a faster serial version and three parallel variants: Step-P, Step-PA, and k-Step.

• Step This method iteratively sifts through all the structures in ${\mathcal {S}}$ and includes in the summary the structure that decreases the cost in Eq. (1) the most, until no structure further decreases the cost. Formally, if ${\mathcal {S}}_i$ is the set of structures that have not been included in the summary at iteration i, Step chooses structure $s_i^*$ s.t.

  $$s_i^* = arg\min _{s\in {\mathcal {S}}_i}{L(G,M_{i-1} \cup \{s\})}$$

  where $M_{i-1}$ is the model at iteration $i-1$, and $M_0=\emptyset$ is the empty model. CondeNSe with Step finds up to $30\%$ more compact summaries than baseline methods, but its quadratic runtime $O(|{\mathcal {S}}|^2)$ makes it less ideal for large datasets with many structures ${\mathcal {S}}$ produced by module A. Therefore, we propose four methods that significantly reduce Step ’s runtime while maintaining its summary quality.

• Step-P The goal of Step-P is to speed up the computation of Step by iteratively solving smaller, “local” versions of Step in parallel. Step-P begins by dividing the nodes of the graph into p partitions using METIS. Next, each candidate structural pattern is assigned to the partition with the maximal node overlap. Step-P then iterates until convergence, with each iteration consisting of two phases:

  1.:

  Parallelize In parallel, a process is spawned for each partition and is tasked with finding the structure that would lower the encoding cost in Eq. (1) the most out of all the structures in its partition. For any given partition, there may be no structure that lowers the global encoding cost.

  2.:

  Sync From all structures returned in phase 1, the one that minimizes Eq. (1) the most is added to the summary. If no structure reduces the encoding cost, the algorithm has converged. If not, phase 1 is repeated.

• Step-PA In addition to parallelizing Step, we introduce the idea of “inactive” partitions, which is an optimization designed to reduce the number of processes that are spawned by Step-P. Step-PA differs from Step-P by designating every partition of the graph as active, then if a partition fails x times to find a structure that lowers the cost in Eq. (1), that partition is declared inactive and is not visited in future iterations. Thus, the partitions with structures not likely to decrease the overall encoding cost of the model get x chances (e.g., 3) before being eventually ruled out, effectively reducing the number of processes spawned for each iteration of Step-PA after the first x iterations.

• k-Step The pseudocode of this variant is given in Algorithm 2. k-Step further speeds up Step while maintaining high-quality summaries. This algorithm has two phases: the first applies Step-P k times (lines 3–5) to guarantee that the initial structural patterns included in the summary are of good quality. The second expands the summary by building local solutions of Step-P per active partition (lines 8–9). If a partition does not return any solution, it is flagged as inactive (lines 10–11). For the partitions that returned nonempty solutions, the best structure per partition is added into a temporary list (line 13), and a parallel “glocal” step applies Step-P over that list and populates the summary (lines 14–16). We refer to this step as “glocal” because it is a global step within the local stage. The local stage is repeated until no active partitions are left.

4.4 Module D: Approximate supergraph creation module

In the empirical analysis (Sect. 5), we show that Step results in graph summaries with up to 80–90% fewer structures than the baselines, and thus can be leveraged for tractable graph visualization. The last and fourth module of CondeNSe (Algorithm 1, lines 15–18), instead of merely outputting a list of structures, creates an “approximate” supergraph which gives a high-level but informative view of large graphs. An exact supergraph, $G_S({\mathcal {V}}_S,{\mathcal {E}}_S)$, of a graph $G({\mathcal {V}},{\mathcal {E}})$ consists of a set of supernodes ${\mathcal {V}}_S=P({\mathcal {V}})$ which is a power set (i.e., family of sets) over ${\mathcal {V}}$ and a set of superedges ${\mathcal {E}}_S$. The superweight is often defined as the sum of edge weights between the supernodes’ constituent nodes.

Unlike most prior work, CondeNSe creates “approximate,” yet powerful supergraphs: (1) the supernodes do not necessarily correspond to a set of nodes with the same connectivity, but to rich structural patterns (including hyperbolic structures and chains); (2) the supernodes may have node overlap, which helps to pinpoint bridge nodes (i.e., nodes that span multiple communities); (3) the supernodes may show deviations from the perfect corresponding structural patterns (i.e., they correspond to near-structures).

Definition

A CondeNSe approximate supergraph of G is a supergraph with supernodes that correspond to possibly overlapping structural patterns in $\Omega$. These patterns are approximations of clusters in $G$.

In other words, the CondeNSe supergraphs consist of supernodes that are fc, st, ch, bc, and hs. To obtain an approximate supergraph, we map the structural patterns returned in module C to approximate supernodes. Then, for every pair of supernodes, we add a superedge if there were edges between their constituent nodes in ${\mathcal {V}}$ and set its superweight equal to the number of such (unweighted) edges, as shown in line 18 of Algorithm 1.

To evaluate the edge overlap in the summaries, and hence the effectiveness of our overlap-aware encoding, we use the normalized overlap metric. The normalized overlap between two supernodes is their Jaccard similarity. It is 0 if the supernodes do not share any nodes, and close to 1 if they share many nodes compared to their sizes. Although it is not the focus of the current paper, the CondeNSe supergraphs can be used for visualization and potentially for approximation of algorithms on large networks (without specific theoretical guarantees, at least in the general form).

4.5 CondeNSe: complexity analysis

We discuss the complexity of CondeNSe by considering each module separately:

The first module has complexity $O(n^3)$, which corresponds to Spectral. However, in practice, HyCoM is often slower than Spectral, likely due to implementation differences (JAVA vs. MATLAB). The complexity of this module can be lowered by selecting the fastest methods. Module B is linear on the number of edges of the discovered patterns. Given that they are overlapping, the computation of L(G, M) is done in $T = O(|M|^2 + m)$, which is O(m) for real graphs with $|M|^2<<m$. In module C, Step has complexity $O(|S|^2\times T)$, where S is the set of labeled structures. Step-P and Step-PA are $O(t\times \frac{|S|^2}{p}\times T)$, where p is the number of METIS partitions (‘active’ partitions for Step-PA) and t is the number of iterations. k-Step is a combination of Step-P and a local stage, so it runs in $O(K\times \frac{|S|^2}{p}\times T+ t_{lcl}\times (\frac{|S|^2}{p_{active}} + p_{active}^2)\times T)$, where $t_{lcl}$ is the iterations of its local stage. Finally, the supergraph (module D) can be generated in O(m).

5 Empirical analysis

We conduct thorough experimental analysis to answer three main questions:

• How effective is CondeNSe?

• Does it scale with the size of the input graph?

• How do the clustering methods compare in terms of summarization power?

Setup We ran experiments on the real graphs given in Table 3.

With regards to clustering parameters, we choose the number of SlashBurn hub nodes to slash per iteration $h_{slash}=2$ to achieve better granularity of clusters. For Louvain, we choose resolution $\tau =0.0001$ as it generates a number of clusters comparable with other clustering methods for all our datasets. For Spectral and METIS, the number of clusters k are set to $\sqrt{n/2}$ according to a rule of thumb (clusterMaker 2018), where n is the number of nodes in the graph. The other clustering methods are parameter-free. Unless otherwise specified, we followed the same rule of thumb for setting the number of input METIS partitions p for all the Step variants. In Sects. 5.1 and 5.2, we set the number of chances $x=3$ for Step-PA.

Table 3 Summary of graphs used in our experiments

5.1 Effectiveness of CondeNSe

Ideally, we want a summary to be: (1) concise, with a small number of structures/supernodes; (2) minimally redundant, i.e., capturing dependencies such as overlapping supernodes, but without overly encoding overlaps; and (3) covering in terms of nodes and edges. We perform experiments on the real data in Table 3 to evaluate CondeNSe ’s performance with regard to these criteria. We note that we do not evaluate the effectiveness of CondeNSe by comparing structural properties of the compressed graph to those of the original graph, since the goal of our method is to detect ‘important’ structures (which can help with better understanding the underlying patterns) and does not optimize for specific graph properties or queries (that is usually the goal of graph sampling techniques).

Baselines

The first baseline is VoG (Koutra et al. 2014), which we describe in Sect. 2. For our experiments, we used the code that is online at https://github.com/GemsLab/VoG_Graph_Summarization. The second baseline is our proposed method, CondeNSe, combined with the GnF heuristic (Sect. 4.3).

A1. Conciseness

In Table 4, we compare our proposed method (for different structure selection methods) and the baselines with respect to their compression rates, i.e., the percentage of bits needed to encode a graph with the composed summary over the number of bits needed to encode the corresponding graph with an empty model/summary (that is, all its edges are in the error matrix). In parentheses, we also give the total number of structures in the summaries. We find that compared to baselines, CondeNSe with the Step variants yields significantly more compact summaries, with 30–50% lower compression rate and about 80–90% fewer structures. The Step variants give comparable results in summarization power.

Table 4 ConDeNSe: Compression rate with respect to the empty model (i.e., percentage of bits used with the model versus the empty model)

Table 5 Overlapping supernode pairs and average similarity in parentheses

A2. Minimal redundancy

In Figs. 1 and 3, we visualize the supergraphs for AS-Oregon and Choc, which are generated from the selected structures of VoG and CondeNSe-Step. It is visually evident that the CondeNSe supergraphs are significantly more compact. In Table 5, we also provide information about the number of overlapping supernode pairs and their average Jaccard similarity, as an overlap quantifier (in parentheses). For brevity, we only give results for k-Step, since the results of the rest Step series are similar. We observe that CondeNSe has significantly fewer supernode overlaps, and the overlaps are smaller in magnitude. We also note that the overlap encoding module achieves 10–20% reduction in overlapping edges, showing its effectiveness for minimizing redundancy.

Fig. 3

Choc: CondeNSe-Step generates more compact supergraphs. (b, c) The full supergraphs by VoG-GnF, and CondeNSe-Step, resp. Yellow for stars, red for cliques, green for bipartite cores. The edge weights correspond to the number of inter-supernode edges (color figure online)

A3. Coverage

We give the summary node/edge coverage as a ratio of the original for different assembly methods in Fig. 4. We observe that the baselines have better edge coverage than the Step variants, which is expected as they include significantly more structures in their summaries. However, in most cases, k-Step and Step-PA achieve better node coverage than the baselines. Taking into account the (contradicting) desired property for summary conciseness, CondeNSe with Step variants has better performance, balancing coverage and summary size well.

Fig. 4

Node coverage versus edge coverage—marker size corresponds to the graph size. Step variants have better node coverage, and handle the summary coverage-conciseness trade-off well

What other properties do the various summaries have? What are the main structures found in different types of networks (e.g., email vs. routing networks)? In Table 6, we show the number of in-summary structures per type. We note that no chains and hyperbolic structures were included in the summaries of the networks that we show here (although some were found by the pattern discovery module, and there are synthetic examples in which they are included in the final summaries). This is possibly because stars are extreme cases of hyperbolic structures, and the encoding of (approximate) hyperbolic structures is of the same order, yet often more expensive than the encoding of stars with errors. As for chains, they are not ‘typical’ clusters found by popular clustering methods, but rather by-products of the decomposition methods that we consider. Moreover, given that the chain encoding considers the sequence of node IDs, and errors in the real data increase the encoding cost, very often encoding them in the error matrix yields better compression. One observation is that Step gives less biased summaries than the baselines. For email networks, we see that stars are dominant (e.g., users emailing multiple employees that do not contact each other), with considerable number of cliques and bipartite cores too. For routing networks (AS-Caida and AS-Oregon), we mostly see cliques (e.g., “hot-potato” routing), and a few stars and bipartite cores. In collaboration networks, cliques are the most common structures, followed by stars (e.g., administrators). VoG and CondeNSe-GnF are biased toward stars, which exceed the other structures by an order of magnitude. Overall, CondeNSe fares well with respect to the desired properties for graph summaries.

Table 6 ConDeNSe: Number of structures per type in the summaries in the format [fc, st, bc], for VoG we have [$fc+nc,st,bc+nb$], where nc is near-clique and nb is near-bipartite core

5.2 Runtime analysis of CondeNSe

We give the runtime of pattern discovery and the Step methods in Fig. 5. As we discussed in the complexity analysis, the modules of our summarization method depend on the number of edges and selected structures. Thus, in the figure we plot the runtime of our variants with respect to the number of edges in the input graphs.“Discovery” represents the maximum time of the clustering methods, and “Disc.Fast” corresponds to the slowest among the fastest methods (KCBC, Louvain, METIS, BigClam). We ran the experiment on an Intel(R) Xeon(R) CPU E5-1650 at 3.50 GHz, and 256 GB memory.

We see that the fast unified discovery is up to 80× faster than the original one. As expected, Step is the slowest method. The parallel variants Step-P, Step-PA, and k-Step are more scalable, with k-Step being the most efficient. Taking into account the similarity of the heuristics in both conciseness and coverage, Fig. 5 further suggests that k-Step is the best performing heuristic given that it exhibits the shortest runtime.

Fig. 5

Runtime versus # of edges: k-Step is more efficient than the other methods, and scales to larger graphs

5.3 Sensitivity analysis of CondeNSe: agreement between Step and Step variants

Our analysis so far has shown that k-Step leads to the best combination of high compression and low runtime compared to the other methods. But how well does it approximate Step in terms of the generated summary? To answer this question, we evaluate the “agreement” between the generated summaries, which in this section we view as ordered lists of structures based on the iteration they were included in the final summary (which defines the rank of each structure). Many measures have been proposed to quantify the correlation between sequences, including the famous Pearson’s product-moment coefficient. And when it comes to rank correlation measures, Spearman’s $\rho$ and Kendall’s $\tau$ are the popular ones, while others are mostly ad hoc and not pervasive. These measures, however, only work on permuted lists or lists of the same length, while the generated summaries can have different constituent structures and lengths. Other measures that are popular in information retrieval, such as precision, cannot explain in detail the level of disagreement between two models (i.e., ranked lists) as they treat each summary as an unordered set of structures. In our evaluation, we want a measure that (1) effectively handles summaries of different lengths, and (2) penalizes with different, adaptive weights ‘rank’ disagreement between structures included in both summaries, and disagreement for missing structures from one summary. Thus, we propose a new measure of agreement between models, which we call AG. Let $M_1$ and $M_2$ be the two summaries, and $rank(s,M_i)$ be the ranking of structure s in summary $M_i$ [i.e., the order in which it was included in the summary while minimizing Eq. (1)]. We define the agreement of the two summaries as:

$$AG(M_1,M_2) = {1 - \text {normalized disagreement}} = 1 - \frac{1}{Z} [\alpha D+(1-\frac{\alpha }{2})D_1+(1-\frac{\alpha }{2})D_2]$$

where the disagreement has three components: (1) $D=\sum _{s \in M_1 \cap M_2} |rank(s,M_1)-rank(s,M_2)|$ is the rank disagreement for structures that are in both summaries, (2) $D_1=\sum _{s \in M_1 \cap M_2'}|(|M_2|+1)-rank(s,M_1)|$ is the disagreement for structures in $M_1$ but not in $M_2$, and (3) $D_2$ is defined analogously to capture the disagreement for structures in $M_2$ but not in $M_1$. Finally, Z is a normalization factor that guarantees that the normalized disagreement, and thus AG, are in [0, 1]: $Z=(1-\frac{\alpha }{2})\sum _{s \in M_1}|(|M_2|+1)-rank(s,M_1)|+\sum _{s \in M_2}|(|M_1|+1)-rank(s,M_2)|$. Based on the definition above, $AG=1$ for identical summaries, while 0 for completely different summaries. In order to penalize more the structures that appear in one summary but not in the other, we set $\alpha =0.3$ (the results are consistent for other values of $\alpha$). In Table 7, we give the agreement between Step and its faster variants. As a side note, the agreement with VoG is almost 0 in all the cases. As expected, Step-P produces the same summaries as Step, while Step-PA and k-Step preserve the agreement well.

Table 7 Agreement of Step and its variants

5.4 Sensitivity to the number of partitions

All parallel variants of Step take p METIS partitions as input. To analyze the effects of varying p on runtime and agreement, we ran k-Step and increased p from 12 to 96 in increments of 12.

We only give the results on AS-Oregon, since other datasets lead to similar results. We observe that while agreement is robust, runtime decreases as p increases and especially so with the smaller values of p. This observation is consistent with our motivation for parallelizing Step: by decreasing the number of structures in any given partition, the “local” subproblems of Step become smaller and thus less time-consuming. Figure 6 shows the effect of the number of partitions on runtime and agreement, both averaged over three trials.

5.5 Sensitivity of Step-PA

We also experimented with varying the number of “chances” allowed for partitions in the Step-PA variant. Step-PA speeds up Step-P by forcing partitions to drop out after not returning structures for a certain number of attempts (x). However, while giving partitions fewer chances can speed up the algorithm, smaller values of x can compromise compression and agreement.

In Fig. 6, we give the agreement and runtime of Step-PA on Choc and AS-Oregon setting $x=\{1,2,3,4,5\}$. We found that both runtime and agreement increased with x, and plateaued after $x=3$. This suggests that forcing partitions to drop out early, while better for runtime, can lead to the loss of candidate structures that may be useful for compression later.

Fig. 6

The agreement is robust to the number of partitions, while the runtime decreases

5.6 CondeNSe as a clustering evaluation metric

Given the independence of Step from the structure ordering, we use CondeNSe to evaluate the different clustering methods and give their individual compression rates in Table 8.

Table 8 CondeNSe as an evaluation metric: Compression rate of clustering methods with respect to the empty model (i.e., percentage of bits for encoding the graph given the chosen model versus the empty model)

For number and type of structures we give our observations based on AS-Oregon (Fig. 7), which is consistent with other datasets. As we see in the case of AS-Oregon (which is consistent with the other networks), SlashBurn mainly finds stars (136 out of 138 structures); Louvain, Spectral, KCBC, and BigClam reveal mostly cliques (9/9, 15/17, 9/9, and 28/29, respectively); METIS has a less biased distribution (18 cliques, 12 stars), and HyCoM, though looks for hyperbolic structures, tends to find cliques in our experiments (45 out of 52 structures). Also, SlashBurn and BigClam discover more structural patterns than other methods, which partially explains their good compression rate in Table 8.

Fig. 7

Number of structures found by the clustering methods for AS-Oregon. Transparent/solid rectangles for before/after the structure selection step. Notation: fc: full clique, st: star, ch: chain, bc: bipartite core, hs: hyperbolic structure

We perform an ablation study to evaluate the graph clustering methods in the context of summarization. Specifically, we create a leave-one-out unified model for each clustering method and evaluate the contribution of each clustering method to the final summary. The results are shown in Table 9. We see that Louvain appears to be the most important method: when included, it contributes the most; and when dropped, the compression rate reduces (worse). When KCBC is dropped, SlashBurn gets to the top, but Louvain also has considerable contribution. In the missing-Louvain case, the contribution gets redistributed among other clustering methods to make up for it, this effect differs by dataset, e.g., METIS gets boosted for AS-Oregon, while it is Spectral for Choc.

Table 9 Ablation study for AS-Oregon. Louvain and SlashBurn contribute most to the CondeNSe summaries

In terms of runtime, for modules A and B (pattern discovery and identification), Spectral and HyCoM take the longest time, while KCBC, Louvain, METIS, and BigClam are the fastest ones, with SlashBurn falling in the middle. For Module C (summary assembly), the trade-off between runtime and candidate structures is given in the complexity analysis (Sect. 4.5). In practice, HyCoM usually takes the longest time, followed by Spectral and SlashBurn.

6 Conclusion

In this work we proposed ConDeNSe, a method that summarizes large graphs as small, approximate and high-quality supergraphs conditioned on diverse pattern types. CondeNSe features a new selection method, Step, which generates summaries with high compression and node coverage. However, this comes at the cost of increased runtime, which we addressed by introducing faster parallel approximations to Step. We provided a thorough empirical analysis of CondeNSe, and contributed a novel evaluation of clustering methods in terms of summarization power, complementing the literature that focuses on classic quality measures. We showed that each clustering approach has its strengths and weaknesses and make different contributions to the final summary. Moreover, CondeNSe leverages their strengths, handles edge-overlapping structures, and shows results superior to baselines, including significant improvement in the bias of summaries with respect to the considered pattern types.

Ideally without the constraint of time, we naturally recommend the application of as many clustering methods in Module A of CondeNSe. On the other hand, to deal with the additional complexity of having more structures, we recommend choosing faster clustering methods or a mixture of fast and ‘useful’ methods (depending on the application at hand) that contribute good structures, as shown in our analysis.