Optimal allocation model and method for parallel ‘reservoir and pumping station’ irrigation system under insufficient irrigation conditions

Abstract

The effective regulation and storage of water resources by reservoirs in arid and semi-arid areas is important for alleviating water resource shortages. In this paper, multiple irrigation reservoirs and pumping stations are evaluated, according to their special hydraulic connections and used to establish the water resources optimal allocation model of the parallel ‘reservoir and pumping station’ irrigation system. The mathematical model takes the maximum total income of the whole irrigation area as the objective function, the water supply and spill of the reservoir and the water replenishment of the pumping station as the decision variables, and the system water supply, agricultural water rights, reservoir operation criteria as the constraints. A new multilevel decomposition aggregation dynamic programming (MDADP) algorithm is proposed to solve the complex nonlinear model and is compared with the real-coded genetic algorithm, particle swarm optimization, cat swarm optimization and whale optimization algorithm. From the analysis of optimality and the applicability of the algorithm, MDADP was found to be more suitable than the above heuristic models for solving problems in the field of the optimal allocation of water resources.

Introduction

As global warming and the increase of human activities, the amount of available water resources in the world is decreasing sharply, while the distribution of water resources was becoming increasingly uneven (Ashofteh et al. 2012; Haddeland et al. 2014). Agriculture accounts for approximately 70% of the world’s fresh water resources uses (Li et al. 2018), and the serious shortage of water for irrigation was of great concern.

Common water resource projects include reservoirs, ponds, pumping stations and wells. The joint operation of these projects can effectively ensure irrigation in dry years. Therefore, a lot of research focused on the joint regulation of multi-reservoirs (Ashrafi and Dariane 2017; Wan et al. 2017; Louati et al. 2011) and surface water and groundwater (Wan et al. 2018; Alizadeh et al. 2017; Ketabchi and Ataie-Ashtiani 2015). In addition, considering river agricultural water rights, pumping stations can also replenish water resources outside of the local region to supplement irrigation reservoirs or irrigated areas, but the joint investigation of multiple reservoirs and multiple pumping stations was rare.

Many kinds of constraints, such as the water balance equation, hydraulic linkage and dispatching criterion, should be considered in the joint dispatching model of multi-water source engineering. Therefore, due to these coupling constraints and the size of the system, the galway coupling model was usually applied, which presents a nonlinear coupling problem (Pérez-Díaz et al. 2010; Mo et al. 2013; Afshar 2013). To solve this problem, many methods, including linear programming (LP) (Reis et al. 2006; Azamathulla et al. 2008), nonlinear programming (NLP) (Martin 1983; Lund and Ferreira 1996; Barros et al. 2003), dynamic programming (DP) (Kumar and Baliarsingh 2003; Goor et al. 2011; Li et al. 2011) and progressive optimization methods (POA) (Cheng et al. 2012), have been proposed and discussed in past decades. In addition to the above classical methods of function optimization, various heuristic models were also proposed, such as the genetic algorithm (Cinar et al. 2010; Hincal et al. 2011), ant colony algorithm (Jalali et al. 2007; Deep et al. 2009), simulated annealing algorithm (Georgiou et al. 2006), and particle swarm optimization algorithm (Lu et al. 2010; Wang et al. 2010). These function optimization methods and intelligent optimization algorithms were widely used in the water resources optimal scheduling field. However, due to the existence of complex constraints in the system, the complexity of the mathematical model required has increased. There are drawbacks when applying the above methods/algorithms to solve the problem. For example, although LP can solve high-dimensional problems in theory, it needs long operation time; NLP cannot deal with non-convexity problems and the convergence is poor (Afshar 2013); DP was easily affected by ‘Curse of dimensionality’ (Cheng et al. 2012). It was difficult to obtain an initial feasible solution for a complex system, which leads to the local optimal solution of the POA, and the common heuristic methods have difficulty dealing with the equality constraint and the judgment constraint (Cheng et al. 2013), there was no strict mathematical proof of the optimal solution (Samanipour and Jelovica 2020).

The decomposition-aggregation method, also known as the two-level algorithm, has been widely used to solve complex large-scale system problems. Through decomposition, the large-scale system was divided into a series of subsystems, which can be solved by the traditional function optimization method, and then a series of subsystems are aggregated by constructing regression equations, from which the global optimal solution of the large-scale system is obtained. On this basis, Gong and Cheng (2018) and Gong et al. (2019) took the coordination variable in the process of decomposition-aggregation as the decision variable, and aggregated a series of subsystems into a dynamic programming model of large-scale systems according to the recursive principle of DP, thus proposing a large-scale system decomposition aggregation dynamic programming (DADP) method.

In this research, an irrigation system composed of many irrigation reservoirs and pumping stations was studied, from which an optimal allocation model of water resources for a ‘reservoir and pumping station’ irrigation system was proposed. The model established in this paper has the following characteristics: firstly, when the total amount of agricultural water rights was determined, the allocation of water rights in sub-irrigation areas was taken as a decision-making variable. Then, the optimal allocation model of parallel ‘reservoir and pumping station’ irrigation systems can be decomposed into N ‘single reservoir and single pumping station’ irrigation system. Secondly, the irrigation water quantity of each sub-irrigation area for two kinds of dry crops that are rotated was taken as the decision variable in the water-deficient irrigation area, then the optimal water allocation model of a ‘single reservoir and single pumping station’ irrigation system can be decomposed into two optimal water allocation models of a single crop irrigation system. Therefore, based on the DADP algorithm, a multilevel decomposition aggregation dynamic programming (MDADP) algorithm was proposed to solve the model of a parallel ‘reservoir and pumping station’ irrigation system. In addition, two classic heuristic [real-coded genetic algorithm (RGA) and particle swarm optimization (PSO)] and two new heuristic [cat swarm algorithm (CSO) and whale optimization algorithm (WOA)] models were used and compared with the proposed MDADP algorithm, and the optimality and the applicability of these algorithms were verified with an example.

Model and method

Model construction

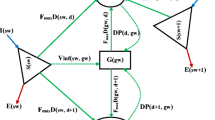
The water resource shortage area north of the Huai River in Jiangsu Province, China, were used as the study area; this irrigation area is usually planted with wheat and corn. The two dry crops undergo rotation cultivation (the growth stages do not overlap). The entire growth period of wheat is usually from October to May, while the entire growth period of corn is usually from June to September. Therefore, the combined total duration of the growth period for the two dry crops is consistent with the whole hydrological year of the irrigation reservoir (i.e., from October to September). Therefore, in the process of mathematical model optimization, the growth stage of the dry crops was taken as the optimal operation stage of the irrigation reservoir and pumping station. The parallel ‘reservoir and pumping station’ system is shown in Fig. 1.

Fig. 1

Schematic diagram of irrigation system

where: i is the number of the reservoir or pumping station; N is the total number of reservoirs or pumping stations; j is the crop type (j = 1,2); k is the crop growth stage; X_i,j,k is the actual water supply of i reservoir to the k growth stage of j crops, MCM; Y_i,j,k is the water replenishment of i pumping station at the k growth stage of j crops, MCM; LS_i,j,k is the inflow of i reservoir at the k growth stage of crop j, MCM; PS_i,j,k is the water spill of i reservoir at the k growth stage of crop j, MCM; EF_i,j,k is the evaporation capacity of i reservoir at the k growth stage of crop j, MCM. (Note: MCM is million cubic meters).

Objective function

The water supply strategy of irrigation reservoirs is usually optimized as an effective method to ensure the efficient utilization of limited water resources. There is a complex relationship between the reservoir water supply and crop yield. On one hand, it shows the impact of full and insufficient irrigation on the maximum and actual yield of final crops; on the other hand, it shows the effect of water stress caused by water deficit at a certain growth stage on crop transpiration and actual yield. The relationship between water and yield proposed by Jensen (1968) and Doorenbos and Kassam (1979) is whidely used to represent this relationship. Based on the water production function given by Jensen, the objective function of maximizing the total agricultural income in the whole irrigation area was established in the current study. Simultaneously, to facilitate the joint operation calculation of the parallel ‘reservoir and pumping station’ irrigation system, the ratio of the actual evapotranspiration generation and the potential evapotranspiration generation in the model was converted into the ratio of the reservoir water supply and the crop water demand (Wardlaw and Barnes 1999).

For irrigated areas where two major crops are rotated, the objective function can be expressed as:

$$ \max G = \sum\limits_{i = 1}^{N} {\sum\limits_{j = 1}^{2} {\left\{ {\prod\limits_{k = 1}^{{M_{j} }} {\left( {\frac{{X_{i,j,k} }}{{YS_{i,j,k} }}} \right)^{{h_{i.j,k} }} \cdot (Y_{m} )_{i,j} \cdot A_{i,j} \cdot P_{i,j} } } \right\}} } $$

(1)

where: G is the total income of the whole irrigation area, 10⁴ rmb; M_j is the total number of j crop growth stages; (Y_m)_i,j is the maximum yield of j crops when the reservoir is fully supplied with water, kg/hm²; h_i,j,k is the sensitivity index of the k growth stage yield of the j crop irrigated by i reservoir under water shortage; YS_i,j,k is the maximum water demand of the k growth stage of the j crop irrigated by reservoir i, MCM; A_i,j is the planting area of the j crop irrigated by reservoir i, hm²; Pi,j is the unit price of the j crop irrigated by reservoir i, kg/rmb. (Note: rmb is the legal currency of China).

Constraints

(1) System water supply constraints:

1) Total water supply constraints of the system:

$$ \sum\limits_{i = 1}^{N} {\left( {SK_{i} + BZ_{i} } \right)} \le SW $$

(2)

2) “Single reservoir-single station” irrigation system annual total water supply constraints:

$$ \sum\limits_{j = 1}^{2} {\sum\limits_{k = 1}^{{M_{j} }} {X_{i,j,k} \le SK_{i} + BZ_{i} } } \left( {i = 1,2,...,N} \right) $$

(3)

3) Water supply constraints during the whole growth period of a single crop:

$$ \sum\limits_{k = 1}^{{M_{j} }} {X_{i,j,k} \le IW_{i,j} } \left( {i = 1,2,...,N;j = 1,2} \right) $$

(4)

where: SK_i is the total annual water supply of i reservoir, MCM; BZ_i is the total water replenishment of i pumping station, that is, the maximum agricultural water right that the pumping station can draw in a year, MCM; SW is the total water supply of the system, MCM; IW_i,j is the total irrigation water of the whole growth period of j crop irrigated by i reservoir, MCM.

(2) Pumping station constraints:

1) Total water replenishment of pumping stations:

$$ \sum\limits_{i = 1}^{N} {BZ_{i} } \le SQ $$

(5)

2) Allowable water replenishment of each pump station:

$$ \sum\limits_{j}^{2} {\sum\limits_{k}^{{M_{j} }} {Y_{i,j,k} \le BZ_{i} } } $$

(6)

3) Capacity constraint of pumping station:

$$ Y_{i,j,k} \le Q_{i} \cdot N_{i,j,k} \times 10^{ - 4} $$

(7)

where, SQ is the total amount of water replenishment by the pumping station (water right); $Q_{i}$ is the design flow of the i pump station, m³/s; $N_{i,j,k}$ is the maximum operating time of the i pump station in the k growth stage of the j crop, h.

(3) Constraints of reservoir operation criteria:

$$ V_{i,j,k}^{\min } \le V_{i,j,k} \le V_{i,j,k}^{\max } $$

(8)

Among these, V_i,j,k was determined by the water balance equation:

$$ V_{i,j,k} = V_{i,j,k - 1} + LS_{i,j,k} + Y_{i,j,k} - X_{i,j,k} - EF_{i,j,k} - PS_{i,j,k} $$

(9)

where, V_i,j,k is i reservoir water storage at the end of the k growth stage, which should be the corresponding time between the maximum and minimum water storage.

1) If $V_{i,j,k} \le V_{i,j,k}^{\min }$, then the reservoir needed to replenish water through the pumping station, and replenish water to the lower limit of the reservoir water storage, The water replenishment of the pumping station is shown in formula (10).

$$ Y_{i,j,k} = V_{i,j,k}^{\min } - V_{i,j,k} $$

(10)

The water spill of the reservoir is shown in formula (11).

$$ PS_{i,j,k} = 0 $$

(11)

2) If $V_{i,j,k} \ge V_{i,j,k}^{\max }$, then the pumping station did not need to replenish water, and the water spill of the reservoir is shown in formula (12).

$$ PS_{i,j,k} = V_{i,j,k} - V_{i,j,k}^{\max } $$

(12)

3) If $V_{i,j,k}^{\min } \le V_{i,j,k} \le V_{i,j,k}^{\max }$, the reservoir did not need to replenish water or spill water.

$$ Y_{i,j,k} = PS_{i,j,k} = 0 $$

(13)

(4) Crop water demand constraints:

$$ YS_{i,j,k}^{\min } \le X_{i,j,k} \le YS_{i,j,k} $$

(14)

where: $YS_{i,j,k}^{\min }$ is the minimum water demand of the j crop in the k growth stage irrigated by the i reservoir, MCM.

(5) Initial and boundary conditions:

$$ V_{0} { = }V_{end} $$

(15)

where: V₀ is the initial storage capacity of the reservoir; V_end is the ending storage capacity after reservoir regulation and storage.

Model solution

Multilevel decomposition aggregation dynamic programming (MDADP)

The optimal allocation model of water resources for a parallel ‘reservoir and pumping station’ irrigation system established in this study has the following characteristics. Firstly, to distribute the total amount of water raised by the pumping station (the total water right) to each sub-irrigation area, the water resources optimal allocation model of parallel ‘reservoir and pumping station’ irrigation system can be decomposed into N ‘single reservoir and single pumping station’ irrigation system; Secondly, the optimal water allocation model of a ‘single reservoir and single pumping station’ irrigation system can be decomposed into two optimal water allocation models for dry crop irrigation.

Considering that the optimal allocation model of water resources for the parallel ‘reservoir and pumping station’ irrigation system is a stage divisible high dimensional dynamic programming model, the conventional function optimization method is subject to problems such as ‘Curse of dimensionality’ (Cheng et al. 2012), which is difficult to solve. Therefore, the use of DADP to solve the high dynamic programming model is proposed. As shown in Fig. 2, DADP combines the decomposition-aggregation (DA) and DP (Bellman and Dreyfus 1964) approaches: first, the large-scale system model is decomposed into a series of subsystem optimization models, which are solved by DP, then, the coordination variables of each subsystem are taken as decision variables. According to the recursive principle of DP, a series of subsystem models can be aggregated into a large-scale system DP model, and the global optimal solution can be obtained by examining the optimal solution of each subsystem from the optimal solution of the DP model of a large-scale system.

Fig. 2

a Is the schematic diagram of DP; b is the schematic diagram of DADP

Obviously, the DADP algorithm only needs one decomposition and aggregation operation to solve the conventional large-scale system mathematical model. However, the parallel ‘reservoir and pumping station’ irrigation system built in the current study has multi-level decomposition, so a MDADP was proposed based on the DADP algorithm, the algorithm flow of which is shown in Fig. 3. The MDADP solution steps are as follows:

Fig. 3

MDADP algorithm flowchart

Step1: first-level decomposition of large systems. By determining the total amount of agricultural water rights in the transit river, and discretizing the allowable allocation of water rights in each sub-irrigation area, the first level decomposition can decompose the water resources optimal allocation model of the parallel ‘reservoir and pumping station’ irrigation system into N “single reservoir and single pumping station” irrigation systems (level I subsystem model); the model is as follows:

Objective function:

$$ \max F_{i} = \sum\limits_{j = 1}^{2} {\left\{ {\prod\limits_{k = 1}^{{M_{j} }} {\left( {\frac{{X_{i,j,k} }}{{YS_{i,j,k} }}} \right)^{{h_{i.j,k} }} \cdot (Y_{m} )_{i,j} \cdot A_{i,j} \cdot P_{i,j} } } \right\}} \left( {i = 1,2,...,N} \right) $$

(16)

where: F_i is the annual output value of the irrigation area where i reservoir is located.

Constraints:

$$ \sum\limits_{j = 1}^{2} {\sum\limits_{k = 1}^{{M_{j} }} {X_{i,j,k} \le SK_{i} + BZ_{i} } } \left( {i = 1,2,...,N} \right) $$

(17)

Step2: second-level decomposition of large systems. In the current study, the effects of water stress on the final yield of dry crops was studied, and the water competition of two types of dry crops under the condition of limited water resources was also considered. The optimal water allocation model of any ‘single reservoir and single pumping station’ irrigation system was decomposed into two optimal water allocation models of a single dry crop (level II subsystem model), which were as follows:

Objective function:

$$ \max f_{i,j} = \prod\limits_{k = 1}^{{M_{j} }} {\left( {\frac{{X_{i,j,k} }}{{YS_{i,j,k} }}} \right)^{{h_{i.j,k} }} } \cdot (Y_{m} )_{i,j} \cdot A_{i,j} \cdot P_{i,j} \left( {i = 1,2,...,N;j = 1,2} \right) $$

(18)

where: F_i,j is the output value of j crop irrigated by i reservoir.

Constraints:

$$ \sum\limits_{k = 1}^{{M_{j} }} {X_{i,j,k} \le IW_{i,j} } \left( {i = 1,2,...,N;j = 1,2} \right) $$

(19)

In addition, the level II subsystem model must satisfy the constraints of the dispatching criterion, pumping station capacity, crop water demand and reservoir boundary conditions.

Step3: Level II subsystem solution. The decomposed subsystems belonged to a one-dimensional DP model, which could be solved by the classical DP method. The state variables λ_i,j,k are the total water supply of the reservoir to a single crop during the whole growth period, and were discrete in a fixed step d in [0, IW_i,j]. For each state variable λ_i,j,k, the decision variable X_i,j,k was discretized in its feasible region [0, λ_i,j,k] by the step length d. The optimal water supply process of a reservoir to each growth stage of dry crops in the subsystem can was obtained by using the sequential recursion and the state transfer equationλ_i,j,k-1 = λ_i,j,k − X_i,j,k (i = 1, 2, …, N; j = 1, 2; k = 1, 2, …, M_j) and the value of the objective function F_i,j, according to the optimal water supply process of the reservoir, the optimal spill water process of the reservoir PS_i,j,k (i = 1, 2, …, N; j = 1, 2; k = 1, 2, …, M_j) and the optimal water replenishment process of the pumping station Y_i,j,k (i = 1, 2, …, N; j = 1, 2; k = 1, 2, …, M_j).

Step4: Level II subsystem aggregation. A series of corresponding relationships of IW_i,j ~ f_{i, j} (IW_i,j) (i = 1, 2, …, N; j = 1, 2) could be obtained by solving the subsystems of level II, according to the recursive principle of DP, then N level II aggregation models were obtained by aggregating the two level II subsystems which that belonged to the same subarea.

Objective function:

$$ \max F_{i} = f_{i,1} (IW_{i,1} ) + f_{i,2} (IW_{i,2} )\left( {i = 1,2,...,N} \right) $$

(20)

Constraints:

$$ IW_{i,1} + IW_{i,2} \le SK_{i} + BZ_{i} \left( {i = 1,2,...,N} \right) $$

(21)

Step5: Level I subsystem aggregation. The water rights BZ_i(i = 1, 2, …, N) of each sub-irrigation area were discretized, and the discrete values were substituted into the level II aggregation model, then a series of corresponding relationships of BZ_i ~ F_i (BZ_i) (i = 1, 2, …, N) could be obtained. Similarly, according to the recursive principle of DP, N level II aggregation models could be re-aggregated into level I aggregation models, resulting in the level I aggregation model becoming a large-scale system model.

Objective function:

$$ \max G = F_{1} (BZ_{1} ) + F_{2} (BZ_{2} ) + \cdot \cdot \cdot + F_{N} (BZ_{N} ) $$

(22)

Constraints:

$$ BZ_{1} + BZ_{2} + \cdot \cdot \cdot + BZ_{N} \le SQ $$

(23)

By using the classical DP method to solve the level I aggregation model, the optimal annual output value G^* of the whole irrigation area and the optimal allocation water right BZ_i^*(i = 1, 2, …, N) of each sub-irrigation area could be obtained according to the results of BZ_i^*(i = 1, 2, …, N). From the reexamination of the level II aggregation model, the optimal total irrigation water for different dry crops could be obtained by IW_i,j^*(i = 1, 2, …, N; j = 1, 2); Finally, according to the optimal total irrigation water quantity of dryland crops, the optimal water supply process X_i,j,k^*(i = 1, 2, …, N; j = 1, 2; k = 1, 2, …, M_j) and water spill process PS_i,j,k^*(i = 1, 2, …, N; j = 1, 2; k = 1, 2, …, M_j) of the reservoirs in the whole growth period of the different dryland crops could be obtained, along with the optimal replenishment water process of the pumping station Y_i,j,k^*( i = 1, 2, …, N; j = 1, 2; k = 1, 2, …, M_j).

Real-coded genetic algorithm (RGA)

Wright (1991) proposed a RGA, which is a real-to-individual coding method that can achieve better optimization results than binary-coded genetic algorithms.

For a given optimization problem with m variables, the n initial solution sets $\left( {x_{i}^{1} ,x_{i}^{2} ,...,x_{i}^{m} } \right)$ are usually generated in a random manner when the RGA is used to solve the problem, where the process of population iteration, selection, crossover and mutation are adopted to ensure the evolution of the population. In this study, a roulette wheel was used for the selection operation, and random single-point method was used for cross operation. First, a sequence number t smaller than m was randomly generated, and then the sequence numbers corresponding to a pair of genes t to m were exchanged with each other to complete the crossover operation. For example: a pair of genomes $X_{1} = \left( {x_{1}^{1} ,...,x_{1}^{t} ,...,x_{1}^{m} } \right)$ and $X_{2} = \left( {x_{2}^{1} ,...,x_{2}^{t} ,...,x_{2}^{m} } \right)$ will become $X_{1}{\prime} = \left( {x_{1}^{1} ,...,x_{2}^{t} ,...,x_{2}^{m} } \right)$ and $X_{2}{\prime} = \left( {x_{2}^{1} ,...,x_{1}^{t} ,...,x_{1}^{m} } \right)$ through the cross operation; The mutation operation was completed by random single point mutation.

Considering that the mathematical model established in this study contains many constraints, in the process of solving RGA, the penalty term was constructed to deal with many these constraints, as follows:

$$ p_{1} (x) = \left\{ {\begin{array}{*{20}c} {\mu_{1} } & {\begin{array}{*{20}c} {} & {} \\ \end{array} if\begin{array}{*{20}c} {} & {V_{i,j,k} > V_{i,j,k}^{\max } } \\ \end{array} } \\ 0 & { otherwise\begin{array}{*{20}c} {} & {} \\ \end{array} } \\ \end{array} } \right. $$

(24)

$$ p_{2} (x) = \left\{ {\begin{array}{*{20}c} {\mu_{2} } & {\begin{array}{*{20}c} {} & {} \\ \end{array} if\begin{array}{*{20}c} {} & {V_{i,j,k} > V_{i,j,k}^{\min } } \\ \end{array} } \\ 0 & { otherwise\begin{array}{*{20}c} {} & {} \\ \end{array} } \\ \end{array} } \right. $$

(25)

$$ p_{3} (x) = \left\{ {\begin{array}{*{20}c} {\mu_{3} } & {\begin{array}{*{20}c} {} & {} \\ \end{array} if\begin{array}{*{20}c} {} & {\sum\limits_{j = 1}^{2} {\sum\limits_{k = 1}^{{M_{j} }} {Y_{j,k} } > BZ_{i} } } \\ \end{array} } \\ 0 & {otherwise\begin{array}{*{20}c} {} & {} \\ \end{array} } \\ \end{array} } \right. $$

(26)

$$ p_{4} (x) = \left\{ {\begin{array}{*{20}c} {\mu_{4} } & {\begin{array}{*{20}c} {} & {} \\ \end{array} if\begin{array}{*{20}c} {} & {\sum\limits_{i = 1}^{N} {BZ_{i} } > SQ} \\ \end{array} } \\ 0 & { otherwise\begin{array}{*{20}c} {} & {} \\ \end{array} } \\ \end{array} } \right. $$

(27)

where, P₁, P₂, P₃, and P₄ are the penalty functions of the upper and lower limits of reservoir capacity, the water right constraints of sub-regions and the agricultural total water right constraints of the whole irrigation area respectively, and μ₁, μ₂, μ₃, and μ₄ are the penalty factors respectively, in the actual solution process, the penalty factors are all taken as − 10,000,000.

By integrating the objective function of the model with the penalty term, the fitness function of the RGA was constructed as follows:

$$ W = G + P_{1} + P_{2} + P_{3} + P_{4} $$

(28)

where: W is the fitness function value.

Particle swarm optimization (PSO)

J. Kennedy first proposed the PSO algorithm, which originated from bird predation behavior research. The algorithm abstracts each bird as a particle, and the location of the food is the optimal solution of the problem. The distance between the bird and the food is the objective function of the current particle. Each particle s has its own position vector θ_s (containing components X, Y, PS, etc.) and velocity vector υ_s, which are updated according to Eqs. (29) and (30) during each iteration, until the iteration termination condition is met. Similarly, in the process of solving PSO, the penalty term shown in the constructive formulae (24)–(27) is needed to deal with the constraint.

$$ \upsilon_{s} (k) = \omega \upsilon_{s} (k - 1) + c_{1} r_{1} (p_{s} (k - 1) - \theta_{s} (k - 1)) + c_{2} r_{2} (g(k - 1) - \theta_{s} (k - 1)) $$

(29)

$$ \theta_{s} (k) = \theta_{s} (k - 1) + \upsilon_{s} (k) $$

(30)

where: ω is the inertia factor, is a non-negative number, usually the size of ω, and the global and local search ability of the algorithm; c₁ and c₂ as acceleration factors.

Cat swarm algorithm (CSO)

Chu and Tsai (2007) proposed a CSO by observing the daily behavior of cats. Each cat of the algorithm corresponds to a set of solutions to the optimization problem, and the cat attributes consist of speed, fitness, and tracking or searching mode flag values (usually 0 or 1). Each cat is in its initial position, and the cat’s signature values are used to determine whether the cat is in tracking or searching mode. If, in tracking mode, the position of the cat is changed by changing the speed of each dimension of the cat according to Eqs. (31) and (32); if in search mode, n cats first copy their position and then perform mutation operations, making each cat occupy a new position; the fitness is then calculated again from the 2n cat position to select the cat with the highest fitness to replace the current cat, completing the position update. Finally, the cat is placed in a new position and the optimal cat is retained until the termination condition is satisfied. Similarly, in the process of solving CSO, the penalty term shown in the constructive formula (24) ~ (27) are needed to deal with the constraint.

$$ v_{k}^{d} \left( {t + 1} \right) = v_{k}^{d} \left( t \right) + c \cdot rand \cdot \left( {X_{best}^{d} \left( t \right) - X_{k}^{d} \left( t \right)} \right)\quad d = 1,2,...,l $$

(31)

$$ X_{k}^{d} \left( {t + 1} \right) = X_{k}^{d} \left( t \right) + v_{k}^{d} \left( {t + 1} \right) $$

(32)

where: $v_{k}^{d} \left( {t + 1} \right)$ is the d-th dimensional velocity vector of the k-th cat after updating; l is the dimension of the solution; $X_{best}^{d} \left( t \right)$ is the d-th dimension component of the current optimal solution; $X_{k}^{d} \left( t \right)$ is the d-th dimension component of the current position of the k-th cat; c is a constant and a random number of [0,1].

Whale optimization algorithm (WOA)

The WOA is a kind of heuristic optimization algorithm that simulates the hunting behavior of the humpback whale (Mirjalili and Lewis 2016). The algorithm mainly includes three important stages: encircling prey, catching prey with a bubble net, and searching for prey. In the algorithm, each humpback whale represents a set of solution sets, and the global optimal solution is obtained by continuously updating the whale’s position in the solution space.

(1) Stalking prey. The WOA algorithm first assumes the target prey or an approximate optimal solution, i. e. the optimal whale position is defined, and then the other whales update their positions to the optimal whale according to the formulae (33)–(36).

$$ D = \left| {C \cdot X^{*} \left( t \right) - X\left( t \right)} \right| $$

(33)

$$ X\left( {t + 1} \right) = X^{*} \left( t \right) - A \cdot D $$

(34)

$$ A = 2a \cdot r_{1} - a $$

(35)

$$ C = 2 \cdot r_{2} $$

(36)

where: D is the position of the current individual and the optimal solution; t is the number of iterations; A and C are the vector coefficients; X^*(t) is the position vector of the current optimal solution. In the iterative process, a drops linearly from 2 to 0, and r₁ and r₂ are [0,1] random numbers.

(2) Bubble net predation. As the whales feed in the bubble net, they move along a spiral path. Therefore, the position update between the whale and prey is expressed by a logarithmic spiral equation, as shown in Eqs. (37) and (38).

$$ D{\prime} = \left| {X^{*} \left( t \right) - X\left( t \right)} \right| $$

(37)

$$ X\left( {t + 1} \right) = D \cdot e^{bl} \cdot \cos \left( {2\pi l} \right) + X^{*} \left( t \right) $$

(38)

where: b is the helix shape parameter and l is the random number of the uniform distribution in the range [-1, 1]. Usually in WOA, the probability p is used to choose between bubble net predator and stalking predator.

(3) Search for prey. To ensure that the whale is fully searched in solution space, when |A|≥ 1, the searching individual moves toward the whale in a random position, as shown in Eqs. (39) and (40).

$$ D^{^{\prime\prime}} = \left| {C \cdot X_{rand} \left( t \right) - X\left( t \right)} \right| $$

(39)

$$ X\left( {t + 1} \right) = X_{rand} \left( t \right) - A \cdot D $$

(40)

Similarly, the WOA needs to construct the penalty term shown in Eqs. (24) to (27) to deal with the constraint.

Case analysis

Study area

Xinyi City is located at the northern edge of Jiangsu Province, China. Its geographical position is 117° 59ʹ–119° 39ʹE and 34° 06ʹ–34°26ʹN. It belongs to an arid and water deficient area in Huaibei, Jiangsu Province. The location of the research area is shown in Fig. 4. There are two irrigation areas in the Yibei district and the Gao'a district. The irrigation area is limited by the natural conditions in the hilly and mountainous areas. The crops are mainly dry crops, usually wheat and corn varieties. The wheat planting area in the Gao'a irrigation area is 1.54 × 10³ hm², while the corn planting area is 1.63 × 10³ hm². The wheat planting area in the Yibei irrigation area is 1.26 × 10³ hm², while the corn planting area is 1.47 × 10³ hm².

Fig. 4

Location of study area

The distribution of rainfall in the study area is uneven, the rainfall in the flood season accounts for 68% of the annual rainfall. The average annual evaporation is 968.0 mm, and the irrigation water use coefficient is 0.65. The main irrigation water source of the Gaotang (GT) Reservoir is 15 MCM and the lower limit of reservoir capacity is 3 MCM in the Gao'a irrigation area. The main irrigation water source of the Shadun (SD) Reservoir is 7 MCM and the lower limit of the reservoir capacity is 3 MCM in the Yibei irrigation area.

The two main dry crops (wheat and corn) planted in the study area, which was affected by topographic factors, underwent crop rotation. Considering that the growing cycle of wheat is usually from October to May while that of corn is usually from June to September, the total duration of the growth period of the two crops is basically consistent with that of the whole hydrological year (from October to September of the following year). Therefore, in this study the regulation and storage periods of the GT reservoir and SD reservoir were divided according to the growth stages of the crops. The inflow, rainfall, measured evaporation of E₆₀₁ and crop water demand of the reservoir are shown in Fig. 5. The crop parameters for the irrigation areas are shown in Tables 1 and 2.

Fig. 5

Inflow, rainfall, evaporation and demand

Table 1 Wheat test parameters

Table 2 Corn test parameters

Because of the high topography of the study area, the water demand of the irrigation area cannot be met only by gravity diversion and reservoir impoundment. Therefore, through the transformation, upgrading, and modernization of the irrigation district, new water source projects (such as pump stations) are used to ensure the irrigation needs of the district are met in drought years. The existing Shengli (SL) and Haohu (HH) pumping stations, which are designed to operate at 1m³/s for 20 h/day, provide supplementary irrigation to the GT and SD reservoirs by drawing water from Shu River. According to Xinyi’s water resources planning data, the total amount of river agricultural water rights in a typical year is 12 MCM.

The evaporation loss water volume of the two irrigation reservoirs was determined according to the evaporation depth and the average water area of the reservoir in this period. The evaporation depth was determined by the measured evaporation data of the E₆₀₁ evaporator and corrected by the conversion coefficient w_i,j. while the water area was determined according to the reservoir area storage capacity relationship function provided by the reservoir management personnel.

$$ EF_{i,j,k} = 0.1 \times w_{i,j,k} \times E_{i,j,k} \times \left( {\alpha V_{i,j,k} + \beta } \right) $$

(41)

where: EF_i,j,k is the evaporation capacity of reservoir i at the k growth stage of crop j, MCM; E_i,j,k is the evaporation capacity of the evaporator, mm; w_i,j,k is the conversion coefficient of the water surface evaporation of i reservoir at the k growth stage of j crops; α and β are the coefficients (GT Reservoir: α = 1.963 × 10^–3, β = 2.013; SD Reservoir: α = 2.117 × 10^–3, β = 1.863).

Evaluation indicators

The reliability of water supply guarantee rate of reservoir and vulnerability index of water shortage index (Chanda et al. 2014) are used to further evaluate the water supply guarantee ability of irrigation system after optimized solution of five algorithms. The water supply guarantee rate represents the satisfaction degree of irrigation system water demand, and is expressed as the ratio of actual water supply to water demand, and calculated according to Formula (42); the water shortage index represents the severity of water shortage in irrigation system, and is calculated according to Formula (43).

$$ {\text{Re}} l = \frac{{\sum\limits_{i = 1}^{N} {\sum\limits_{j = 1}^{2} {\sum\limits_{k = 1}^{{M_{j} }} {X_{i,j,k} } } } }}{{\sum\limits_{i = 1}^{N} {\sum\limits_{j = 1}^{2} {\sum\limits_{k = 1}^{{M_{j} }} {YS_{i,j,k} } } } }} $$

(42)

$$ Vul = \max \left\{ {1 - \frac{{X_{i,j,k} }}{{YS_{i,j,k} }}} \right\} $$

(43)

Results and analysis

Algorithm optimality

In order to compare the performance of the MDADP, RGA, PSO, CSO and WOA algorithms, their optimality was compared from four aspects: the optimality of the objective function, the stability of the algorithm, the convergence of the algorithm, and the solving speed of the algorithm.

To compare the optimality of the objective function, the sensitivity analysis of the parameters of the five algorithms was needed first. As shown in Table 3, the optimal value of the objective function for the MDADP was 6.76E + 07 rmb, with no parameters to be calibrated. For the RGA, the optimal value of the objective function was 6.68E + 07 rmb, with a population size of 100 and a crossover rate of 0.6 for pm, while the variation rate pe was 0.2. For PSO, the optimal value of the objective function was (6.67E + 07) rmb, at which time the population size was 60, the inertia weight ω was 0.7, and the acceleration factor (c₁ = c₂) was 1.2. For the CSO, the optimal value of the objective function is 6.67E + 07 rmb, when the population size was 80, MR is 0.4, CDC and SRD were both 0.3. For the WOA, when the population size was 100, the optimal value of the objective function is 6.70E + 07 rmb, the initial value of convergence factor a was 2, and the shape parameter b was 1. Although the objective function values of the above algorithms are close, the MDADP was still slightly better than the other heuristic algorithm. At the same time, the MDADP did not need calibration parameters in the solution process, while the other four intelligent algorithms all had 2–3 parameters needing sensitivity analysis. The essence of the MDADP algorithm is that many dynamic programs are nested in each other and the result is not affected by the additional parameters, so it has better operability.

Table 3 Sensitivity analysis of MDADP, RGA, PSO, CSO and WOA

According to the parameters measured in Table 3, the five algorithms were run 10 times to verify the stability of each algorithm. As shown in Table 4 and over 10 runs, the MDADP achieved an optimal value for the objective function, and still outperformed the RGA, PSO, CSO, and WOA for the optimal solution, the worst solution, the mean, and the standard deviation. Therefore, the results show that the proposed MDADP has better stability than the other algorithm.

Table 4 Results of ten runs of five algorithms

Figure 6a shows the convergence trends of the five algorithms. It is known that the running of the MDADP algorithm is independent of the number of iterations of the algorithm, and the optimal objective function value can be obtained in one run. Therefore, the MDADP converged much faster than the RGA, PSO, CSO, and WOA. Figure 6b shows the run time of the five algorithms. Although running time of the RGA, PSO, CSO and WOA algorithms increased as the number of iterations increased, they still saved compared with the MDADP. Therefore, the MDADP algorithm has the disadvantages of requiring large storage and a long computation time.

Fig. 6

a Is the convergence trend of the five algorithms; b is the running solution time of the five algorithms

In general, although the running of the MDADP algorithm takes longer, it is more outstanding in the optimization of the objective function, the stability of the algorithm and the convergence of the algorithm compared with RGA, PSO, CSO and WOA algorithms, resulting in better algorithm optimality.

Algorithm applicability

The applicability of the MDADP, RGA, PSO, CSO and WOA algorithms was compared and analyzed. The operation process and results of the parallel ‘reservoir and pumping station’ irrigation system are considered here.

Figure 7a and b show the water supply process of the SD and GT reservoirs after the optimization solution. It was obvious that the water supply trends of the two reservoirs obtained by the five algorithms were basically similar; there were only subtle differences in how much water was supplied at each stage. Table 5 shows that the MDADP algorithm obtained the largest total water supply and the smallest water shortage. Compared with the RGA, PSO, CSO, and WOA algorithms, the MDADP algorithm increased the water supply by 0.3%, 0.9%, 2.5% and 1.0%, respectively, and reduced the water shortage by 2.8%, 7.3%, 18.4% and 8.4%, respectively, while the total income of irrigation area increased by 1.2%, 1.3%, 1.3% and 0.9%, respectively.

Fig. 7

a Is the water supply process of SD reservoir; b is the water supply process of GT reservoir; c is the storage capacity curve of SD reservoir; d is the storage capacity curve of GT reservoir; e is the water replenishment process of HH pumping station; f is the water replenishment process of SL pumping station

Table 5 Dispatching results of irrigation system (10⁴m³)

Figure 7c and d show the changes in the storage capacity of the two reservoirs. The capacity curves obtained by the MDADP were lower than those by the RGA, PSO, CSO and WOA, especially for the SD Reservoir. It was also evident that at the end of the storage period of the SD reservoir, the MDADP guaranteed V_end = V₀, while the other four heuristic algorithms were all V_end > V₀. The re-analysis of Fig. 7e and f shows that the main reasons leading to the termination of the reservoir was that the agricultural water rights allocated to the SD Reservoir by the RGA, PSO, CSO, and WOA are too much. However, the total water supply of the final irrigation system was less than that of the MDADP, indicating that the excess water rights allocated by the RGA, PSO, CSO, and WOA algorithms were stored in the reservoir, resulting in V_end > V₀. It also meant that heuristic irrigation systems did not work as well as reservoirs and pumping stations, and scarce water was not used effectively.

In contrast, usually the initial set of solutions of a heuristic algorithms was randomly generated in the feasible region, whereas for a linear constraint containing d decision variables, such as $x_{1} + x_{2} + ... + x_{d} \le B\left( {B \in R} \right)$, if the intelligent algorithm wants to deal with this constraint, it needs to construct a penalty function to ensure that the sum of the d decision variables was less than or equal to B. Obviously, satisfying the condition that the sum of d random numbers is equal to B is the strict, therefore, most of the solutions in the initial solution set ultimately satisfied the condition that the sum of d random numbers was less than B. The above was also the key reason for V_end > V₀ after solving by the RGA, PSO, CSO and WOA algorithms. The MDADP algorithm guaranteed V_end = V₀, mainly because the essence of this algorithm was the multiple nested solution process of the DP algorithm, and according to the state transition equation of DP, the sum of d random numbers was guaranteed to be equal to B.

Table 6 shows the water supply guarantee rate and water shortage index of two reservoirs obtained by the five algorithms. It was clear that the irrigation system should be as large as possible in terms of the guaranteed water supply and the water shortage index should be as small as possible. Compared with the RGA, PSO, CSO, and WOA, the MDADP improved the water supply guarantee rate by 0.2%, 7.3%, 11.2% and 1.7%, respectively, and reduced the water shortage index by 3.9%, 19.4%, 2.0% and 26.0%, respectively. For GT Reservoir, the water supply guarantee rate of the MDADP was increased by 2.0%, 14.1%, and 0.5% compared with RGA, PSO and WOA, respectively, while it decreased by 4.0% compared with the CSO. Compared with RGA and WOA, the water deficit index decreased by 11.2% and 26.7%, and increased by 30.3% compared with PSO and CSO. Therefore, the MDADP algorithm can be used to solve the model to obtain a higher water supply guarantee rate and a smaller water shortage index.

Table 6 Evaluation indicators

Overall, it was found that the proposed MDADP algorithm was more reasonable than the RGA, PSO, CSO and WOA algorithms by analyzing the operation process and operation results of the parallel ‘reservoir and pumping station’ irrigation system. It was more suitable for solving the optimal allocation model of water resources in the joint operation of reservoirs and pumping stations.

Conclusion

Research on the optimal operation of reservoir water resources is of great significance importance for the comprehensive development and management of water resources. By focusing on several irrigation reservoirs and pumping stations, defining the hydraulic connection between reservoirs and pumping stations, and accounting for the restriction of river agricultural water rights, a parallel ‘reservoir and pumping station’ irrigation system model for the optimal allocation of water resources was established, and a new MDADP algorithm was proposed and compared with the RGA, PSO, CSO and WOA heuristic algorithms.

The optimality analysis showed that the MDADP performed better than the RGA, PSO, CSO and WOA in the optimality, stability and convergence of the objective function, moreover, the MDADP algorithm did not need the calibration parameter, and the operability of the algorithm was also good. However, the MDADP algorithm also had the disadvantages of requiring large storage and a long computation time, and needs additional methods to improve its performance. The applicability analysis showed that the MDADP algorithm was more effective than the above heuristic algorithms in improving the efficiency of water resources in terms of the scheduling process and the scheduling results of irrigation systems, increasing the total revenue of the whole irrigation area. Therefore, the MDADP algorithm is a practical optimization algorithm to solve the complex water source engineering joint dispatching problem, and popularization and application values.