1 Introduction

During the past 70 years, the proportional-integral-derivative (PID) controller has been adopted in a variety of control loops due to its simplicity and usefulness (Ziegler and Nichols 1942; Ray 1989; Rivera et al. 1986; Åström et al. 1993; O'Dwyer 2006). Numerous modified versions of the standard form and their tuning methods have been proposed for improving the closed-loop response (O'Dwyer 2006). This improvement of the PID control technique has significantly impacted automation in the process industries.

The settings of a PID controller are mainly done in the time domain or the frequency domain. Some methods use information regarding the transient response of a step setpoint or the approximated model of a process. Other methods use some knowledge about the ultimate frequency values of a process. Although being initially well set, fixed-gain PID controllers often behave poorly due to process variations or uncertainties. For this reason, periodical retuning is required to maintain the desired closed-loop behavior. These shortcomings of PID controllers in dealing with complex process dynamics have resulted in challenges for research works on auto-tuning and self-tuning PID control that can deal effectively with a wide range of process control problems (Lee et al. 2017; Sun et al. 2020; Hernández-Alvarado et al. 2016; Pongfai et al. 2020; Ashida et al. 2017; Simorgh et al. 2020; Zhao and Xi 2020).

Lee et al. (2017) conducted a case study based on PID auto-tuning for the molten carbonate fuel cell (MCFC) operation framework. The tuning rules were computed based on the fractional-order plus time delay model. In an automatic mechanical transmission system application, Sun et al. (2020) used a powertrain mathematical model to tune PID controller parameters automatically by minimizing the cost function in relationship with the outputs’ tracking errors by incorporating the Nelder-Mead method. Based on neural networks, Hernández-Alvarado et al. (2016) implemented an auto-tune PID controller on remotely operated vehicles for trajectory tracking with unknown disturbances. Pongfai et al. (2020) designed a novel optimal PID auto-tuning controller based on a swarm learning process in which results were performed by comparing ant colony optimization with a new constrained Nelder–Mead algorithm, the genetic algorithm, the particle swarm optimization algorithm, and a neural network. Ashida et al. (2017) proposed a parameter tuning law for an implicit self-tuning PID control scheme to track the desired reference model output from the system output. In a highly nonlinear process such as a continuously stirred tank reactor (CSTR), Simorgh et al. (2020) designed a self-tuning PID controller using Ziegler–Nichols tuning algorithm based on online estimation methods by incorporating the noise, disturbance and variations in system dynamics. Zhao and Xi (2020) compared the manually tuning PID controller and the PID controller comprising the adaptive genetic algorithm.

Recently, to overcome the fixed-gain PID controller's poor performance, nonlinear PID control strategies using nonlinear functions to modify the structure of the conventional PID controller have been actively conducted (Seraji 1998, 1997; Han 2009; Guerrero et al. 2019; Hua et al. 2020). Seraji (1998, 1997) introduced a class of nonlinear PID controllers which consist of a nonlinear gain in cascade with a linear PID controller to scale the error. Han (2009) proposed a nonlinear PID controller with nonlinear gain functions combining e(t), ∫e(t)dt and \(\dot{e}(t)\) to achieve better tracking and noise rejection. An approach based on a novel nonlinear PID-type controller with an auto gain tuning mechanism was proposed by Guerrero et al. (2019) for a rotorcraft-based transportation system, which can achieve efficient payload positioning and aggressive maneuvering control. A decoupled nonlinear PID controller was developed via the Lyapunov design by Hua et al. (2020) for trajectory tracking control of an underwater vehicle, which proved the stability of the closed-loop system and improved robustness.

By the introduction of nonlinearities in their PID controller structure, the responses were successfully improved for some types of processes. Nevertheless, in most cases, the number of parameters to be tuned is greater than that of the standard PID controller, which causes difficulties in both tuning and implementation.

For this reason, the author introduced a nonlinear PID (NPID) controller that scales the error inputted by the integrator in the standard PID controller frame and the setpoint tracking rules for the first-order plus time delay (FOPTD) model based on the Integral of Squared Error (ISE), the Integral of Absolute Error (IAE), and the Integral of Time multiply Absolute Error (ITAE) performance indices (Jin 2019). In this controller structure, the number of the tuning parameters is kept at 3, and the integrator wind-up can be partially prevented by scaling down large errors. Still, due to the use of the pure derivative term, there is a possibility that abrupt setpoint change or high-frequency noises will cause Derivative Kick.

In order to alleviate this limitation, we present an NPID controller that is of the form employed in industrial sites by supplementing the ideal derivative term with a first-order filter. Since many industrial processes can be approximated by the FOPTD model and PID controllers are usually tuned to fit for either setpoint tracking or disturbance rejection, we propose new tuning formulas for setpoint tracking and disturbance rejection for the NPID controller based on a genetic algorithm for optimization, and the least squares method for curve fitting. Three steps are here adopted. The first step involves using the dimensionless approach to express the parameters of the NPID controller in terms of the ratio L/τ of the time delay L to the time constant τ in the FOPDT process model. The second step produces the optimum NPID parameters to minimize the IAE performance criterion. Repeated optimizations are performed for different values of L/τ and N to obtain their averaged values. The last step obtains the tuning formulas using the least squares method with together the calculated values and the rule formulas.

The paper is organized as follows: Sect. 1 shows the direction of this study through a survey of existing methods. Section 2 gives a brief overview of the author's previous NPID controller and proposes an enhanced NPID controller. Section 3 obtains new tuning formulas for the NPID controller. Section 4 verifies the effectiveness of the proposed method through simulation of five processes, and finally, Sect. 5 offers concluding remarks.

2 Nonlinear PID controller

2.1 Structure of the NPID controller

NPID controller, which employs a nonlinear gain in cascade with the integral action of a conventional PID controller. Figure 1 shows the NPID control system. In Fig. 1, ys denotes the setpoint, y the output (or the process variable) and u the control input, e the error between the setpoint and the output, v the scaled error, and Gp(s) the process. (1)-(2) are the linear part transfer functions of the NPID controller, given by

$$\frac{{U_{pd} }}{E(s)} = K_{p} {(1 + }T_{d} s{)}$$
(1)
$$\frac{{U_{i} (s)}}{V(s)} = \frac{{K_{p} }}{{T_{i} s}}$$
(2)

where Kp, Ti and Td are the proportional gain, the integral time and the derivative time, respectively. The scaled error v(t) in the integral term is described by

$$v(t{)} = k(e)e(t{)}$$
(3)

k(e) is a nonlinear gain defined by

$$k(e) = \exp \left( { - \frac{{e^{2} }}{{2\sigma ^{2} }}} \right)$$
(4)

where σ denotes the difference between the current setpoint value and the previous value in the step-type setpoint or does dGp(0) in the step-type disturbance d and Gp(0) is the steady-state gain of the process.

Fig. 1
figure 1

The NPID control system

Full size image

The disadvantage of the ideal derivative term in (1) is that a sudden change in the setpoint or/and high-frequency noises coming into control loops will cause a phenomenon known as Derivative Kick. Due to this, in many field applications, PID controllers with a first-order filter in the derivative term are mainly adopted. In this paper, we propose an NPID controller, as shown in Fig. 2, which is an improvement of the NPID controller in Fig. 1.

Fig. 2
figure 2

The proposed NPID control system

Full size image

The time-domain equation of the proposed NPID controller is given by

$$\begin{aligned} u(t) = & u_{p} (t) + u_{i} (t) + u_{d} (t), \\ u_{p} (t) = & K_{p} e(t), \\ u_{i} (t) = & \frac{{K_{p} }}{{T_{i} }}\int {v(t)dt} , \\ \frac{{T_{d} }}{N}\frac{{du_{d} (t)}}{dt} + u_{d} (t) = & K_{p} T_{d} \frac{de(t)}{{dt}} \\ \end{aligned}$$
(5)

where upi and ud denote the PI action and the D action, respectively and N is a user-defined parameter. By using the approximation of a differentiator, the magnitude of its frequency \(K_{p} T_{d} \omega /\sqrt {1 + T_{d}^{2} \omega^{2} /N^{2} }\) limited to NKp as ω → ∞. This means that high-frequency measurement noise is amplified at most by a factor NKp. N is appropriately selected according to the noise environment and typical values of N are 5 to 30 (O'Dwyer 2006; Åström et al. 1998).

The NPID controller given by (3)—(5) can be applied to linear and nonlinear processes, but many industrial processes can be approximated with the FOPTD model, i.e., a commonly used model. So we obtain new tuning rules based on the FOPTD process model given by

$$\tau \frac{dy(t)}{{dt}} + y(t) = Ku(t - L)$$
(6)

where K, τ, and L denote the steady-state gain, the time constant, and the time delay, respectively.

2.2 Dimensionless NPID control system

Defining dimensionless variable t′ = t/τ and letting u(τt′) = \(\overline{u}(t^{\prime})\), e(τt′) = \(\overline{e}(t^{\prime})\) and v(τt′) = \(\overline{v}(t^{\prime})\) to simplify the linear parts of the NPID controller in (5) gives

$$\begin{aligned} \overline{u}(t^{\prime}) = & \overline{u}_{p} (t^{\prime}) + \overline{u}_{i} (t^{\prime}) + \overline{u}_{d} (t^{\prime}), \\ \overline{u}_{p} (t^{\prime}) = & K_{p} \overline{e}(t^{\prime}), \\ \overline{u}_{i} (t^{\prime}) = & \frac{{K_{p} \tau }}{{T_{i} }}\int {\overline{v}} (t^{\prime})dt^{\prime}, \\ \frac{{T_{d} }}{N\tau }\frac{{d\overline{u}_{d} (t^{\prime})}}{dt^{\prime}} + \overline{u}_{d} (t^{\prime}) = & \frac{{K_{p} T_{d} }}{\tau }\frac{{d\overline{e}(t^{\prime})}}{dt^{\prime}}. \\ \end{aligned}$$
(7)

In a similar fashion, applying the dimensionless approach with defining y(τt′) = \(\overline{y}(t^{\prime})\) to (6) yields

$$\frac{{d\bar{y}(t^{'} )}}{{dt^{'} }} + \bar{y}(t^{'} ) = K\bar{u}\left( {t^{'} - \frac{L}{\tau }} \right)$$
(8)

(7) and (8) can be expressed in the form of the transfer function as

$$\overline{U}(s) = K_{p} [\overline{E}(s) + \frac{1}{{\overline{T}_{i} s}}\overline{V}(s) + \frac{{\overline{T}_{d} s}}{{1 + \frac{{\overline{T}_{d} }}{N}s}}\overline{E}(s)]$$
(9)
$$\frac{{\overline{Y}(s)}}{{\overline{U}(s)}} = \frac{{Ke^{{ - \overline{L}s}} }}{s + 1}$$
(10)

where \(\overline{T}_{i} = T_{i} /\tau\), \(\overline{T}_{d} = T_{d} /\tau\), and \(\overline{L} = L/\tau\).

Combining the process gain K with the proportional gain Kp of the NPID controller and applying a disturbance on the input side yields the block diagram of the dimensionless NPID control system. By doing this, the number of process parameters becomes only one, and the tuning parameters KKp, \(\overline{T}_{i}\) and \(\overline{T}_{d}\) of the NPID controller become functions of \(\overline{L}\) = L/τ.

3 Tuning formulas of the NPID controller

3.1 Performance Index

When tuning one degree of freedom PID controllers, it is difficult to simultaneously achieve good transient behavior toward changes in setpoint and an appropriate reduction of disturbances. The following shows an example of this. With K = 1, τ = 1, L = 1, and N = 10 in Fig. 2, the result of applying a non dominated sorting genetic algorithm (NSGA-II) to the multiobjective problem of minimizing a setpoint tracking performance index and another disturbance rejection performance index is shown in Fig. 3. It can be seen from the optimal Pareto front in Fig. 3 and responses in Fig. 4 that are tuning for good setpoint tracking degrades disturbance rejection, whereas tuning for fast disturbance rejection results in poor setpoint tracking. Therefore, they are usually tuned to fit for either setpoint tracking or disturbance rejection, depending on the purpose of long-term use.

Fig. 3
figure 3

Optimal Pareto front

Full size image
Fig. 4
figure 4

Responses at three points on optimal Pareto front

Full size image

As seen in Fig. 5 with a choice of N, the NPID controller has three tuning parameters tuning parameters KKp, \(\overline{T}_{i} ( = T_{i} /\tau )\) and \(\overline{T}_{d} ( = T_{d} /\tau )\) functions of \(\overline{L}( = L/\tau )\). Finding tuning formulas for the FOPTD process model provides the smallest overshoot, fastest rise time, or quickest settling time leads to optimization problems. Applying a GA to these optimization problems is one of the most challenging steps and requires the design of objective functions. In order to combine all of these objectives, we use a single performance index in terms of the integral of the absolute value of the error (IAE) as

$$IAE = \int_{0}^{\infty } {\mid y_{s} (t^{\prime}) - \overline{y}(t^{\prime})\mid dt^{\prime}}$$
(11)

where \(\overline{y}(t^{\prime})\) is the output of the dimensionless system.

Fig. 5
figure 5

Dimensionless NPID control system

Full size image

3.2 Optimum parameters

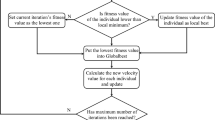
The average of 20 repeated calculations was performed for each value over the ranges of 0.01 to 1 and 1 to 3 of L/τ and over the ranges of 5 to 30 of N to obtain a set of optimal parameters that minimize IAE and was plotted in Fig. 6 for setpoint tracking and Fig. 7 for disturbance rejection, respectively. The points marked ‘◯’ in the figures denote the averaged results.

Fig. 6
figure 6

Optimal parameter values for setpoint tracking

Full size image
Fig. 7
figure 7

Optimal parameter values for disturbance rejection

Full size image

3.3 Tuning rule formulas

With the optimally calculated values, the following empirical formulas of the form used in O'Dwyer (2006), Zhuang and Atherton (1993) were adopted as the models of the curve fitting.

$$K_{p} = a_{1} \left( {\frac{L}{\tau }} \right)^{{b_{1} }} ,\frac{{T_{i} }}{\tau } = a_{2} + b_{2} \left( {\frac{L}{\tau }} \right)\;{\text{and}}\;\frac{{T_{d} }}{\tau } = a_{3} \left( {\frac{L}{\tau }} \right)^{{b_{3} }} \;{\text{for setpoint tracking}}$$
(12)
$$K_{p} = a_{1} \left( {\frac{L}{\tau }} \right)^{{b_{1} }} ,\frac{{T_{i} }}{\tau } = a_{2} \left( {\frac{L}{\tau }} \right)^{{b_{2} }} \;and\;\frac{{T_{d} }}{\tau } = a_{3} \left( {\frac{L}{\tau }} \right)^{{b_{3} }} \;{\text{for disturbance rejection}}$$
(13)

By using the least squares method, the parameters of these formulas over the given ranges of L/τ and N were obtained for setpoint tracking and disturbance rejection and listed in Tables 1, 2, 3, 4, respectively.

Table 1 NPID controller tuning rules for setpoint tracking (0.01 ≤ L/τ < 1)
Full size table
Table 2 NPID controller tuning rules for setpoint tracking (1 ≤ L/τ < 3)
Full size table
Table 3 NPID controller tuning rules for disturbance rejection (0.01 ≤ L/τ < 1)
Full size table
Table 4 NPID controller tuning rules for disturbance rejection (1 ≤ L/τ < 3)
Full size table

Figures 8–9 show the 3D surfaces of the interpolated tuning rules combining Table 1 with Table 2, and Table 3 with Table 4, respectively. The figures imply that there are differences to some extent for N, but not large.

Fig. 8
figure 8

Tuning rule surfaces for setpoint tracking: a KKp versus L/τ and N; b Ti/τ versus L/τ and N; c Td/τ versus L/τ and N

Full size image
Fig. 9
figure 9

Tuning rule surfaces for disturbance rejection: a KKp versus L/τ and N; b Ti/τ versus L/τ and N; c Td/τ versus L/τ and N

Full size image

4 Simulation results

The objective of simulation works on five processes including a nonlinear CSTR process is to compare the responses of the proposed method with those of the PID controllers proposed by the Lopez setting (hereafter referred to as PID-Lopez) (Lopez and Murril 1967) and the CHR setting (hereafter referred to as PID-CHR) (Chien et al. 1972). In the case of the CSTR process, the response of the proposed method is compared with that of the adaptive controller proposed by Chen and Peng ( 1999) (hereafter referred to as AC-Chen). N is set to 10 for the NPID controller.

4.1 Case 1: FOPTD processes

The transfer functions of the FOPTD processes are given by

$$G_{p1} (s) = \frac{{e^{ - 5s} }}{1 + 10s}$$
(14)
$$G_{p2} (s) = \frac{{e^{ - 10s} }}{1 + 10s}$$
(15)
$$G_{p3} (s) = \frac{{e^{ - 20s} }}{1 + 10s}$$
(16)

The ratio L/τ of the time delay to the time constant in each process Gp1(s), Gp2(s), and Gp3(s) is 0.5, 1, and 2, respectively. The controller settings for these three processes using the PID-Lopez method, the PID-CHR method and the proposed method are summarized in Table 5. The responses for unit step changes in setpoint or disturbance using these settings are plotted in Figs. 10, 11, 12.

Table 5 Settings for setpoint tracking and disturbance rejection on Processes 1–3
Full size table
Fig. 10
figure 10

Unit step responses of the three methods on Process 1: a setpoint b disturbance

Full size image
Fig. 11
figure 11

Unit step responses of the three methods on Process 2: a setpoint b disturbance

Full size image
Fig. 12
figure 12

Unit step responses of the three methods on Process 3: a setpoint b disturbance

Full size image

In order to assess the performance of the three methods quantitatively, rise time tr = t95–t5, overshoot Mp, 2% settling time ts, and the integral of absolute error \(IAE = \int_{0}^{\infty } {|e(t)|} dt\) were obtained for setpoint tracking and perturbance peak Mpeak, recovery time trcy and IAE for disturbance rejection. Mpeak denotes |ymax-ys| or |ymin-ys| and trcy does the time that it takes for y to recover within 2% of ys. It is evident in the figures that the responses are faster when using the NPID controller, without a significant increase of the overshoot and settling time. More precisely, compared with the other methods in Table 6, tr of the NPID controller is smaller while IAE is least, and both Mp and ts are reasonable in the case of setpoint tracking. Both the PID-Lopez method and the proposed method give better closed-loop responses with smaller IAE and shorter trcy. In contrast, the PID-CHR method yields sluggish disturbance rejection performances with larger IAE and longer trcy.

Table 6 Performance comparison of the three methods on Processes 1–3
Full size table

4.2 Case 2: Fourth-order process

Consider a 4th-order process used in Åström et al. (1998):

$$G_{p4} (s) = \frac{{0.36(1 - s)e^{ - s} }}{(12s + 1)(3s + 1)(0.2s + 1)(0.05s + 1)}$$
(17)

There are several parameter estimation techniques for approximating the 4th-order process to a FOPTD model (Skogestad 2004; Young 1981).The estimates of the FOPTD model are K = 0.36, τ = 12.28, and L = 5.20. These values were used for the settings of the PID controller and (17) was used for the NPID controller tuning and simulation. Controller settings are summarized in Table 7. Figure 13 shows a comparison of the unit step responses of the PID and NPID control systems. It is seen in Fig. 13 that the response of the NPID controller is clearly better than those of the others. Tables 8 and 9 list the quantitative results obtained from simulation.

Table 7 Controller settings for Process 4
Full size table
Fig. 13
figure 13

Unit step responses of the three methods on Process 4: a setpoint b disturbance

Full size image
Table 8 Performance comparison of the three methods on Process 4
Full size table
Table 9 Performance comparison of the two methods on the CSTR process
Full size table

4.3 Case 3: CSTR process

Consider a CSTR model used in Chen and Peng (1999). The mathematical model is given by

$$\dot{x}_{1} = - x_{1} + D_{a} (1 - x_{1} )\exp \left( {\frac{{x_{2} }}{{1 + x_{2} /\gamma }}} \right) + d_{1} ,$$
(18a)
$$\dot{x}_{2} = - (1 + \beta )x_{2} + HD_{a} (1 - x_{1} )\exp \left( {\frac{{x_{2} }}{{1 + x_{2} /\gamma }}} \right) + \beta u + d_{2} ,$$
(18b)
$$y = x_{2} ,$$
(18c)

where x1 and x2 are the concentration C and the temperature T, respectively; y and u are the outlet temperature of the reactant and the temperature of cooling water, respectively; d1 and d2 disturbances; Da is the Damökhler number; H is the heat of reaction; β the heat transfer coefficient; γ = E ̸ RTf, E activation energy [cal/mol]; and R is the gas constant [cal/mol–K]. x1, x2, u, and t are non–dimensionalized by

$$x_{1} = \frac{{C_{f} - C}}{{C_{f} }}, \, x_{2} = \frac{{T - T_{f} }}{{T_{f} }}\gamma , \, u = \frac{{T_{c} - T_{f} }}{{T_{f} }}\gamma , \, t = t^{\prime}\frac{{F_{f} }}{V}.$$
(19)

where Cf, Tf, Ff and C, T, F denote the concentration [mol/m3], temperature [K], and flow [m3/sec] at the inlet and outlet of the reactant, respectively. Tcf, Fcf and Tc, Fc are the temperature and flow at the inlet and outlet of cooling water, respectively. V is the volume of the CSTR [m3]. The open-loop process has nominal values Da = 0.072, γ = 20, H = 8, and β = 0.3 (Chen and Peng 1999). With these nominal values, the process has two stable equilibrium points xa = [0.144, 0.886]T and xc = [0.765, 4.705]T, and one unstable equilibrium point xb = [0.447, 2.752]T.

In the case of an exothermic reaction, a coolant stream needs to be passed through the cooling jacket to remove the extra heat and maintain the reaction temperature. As the flow–changing valve operation as a control input for controlling the outlet temperature Tc of the jacket has a physical limit, the input saturation is limited between umin = -5 and umax = 5. In the case of the AC-Chen method, the parameters η = 0.2, m = 5, and sign(∂y/∂x) = 1 were used for the adaptive controller.

4.3.1 Setpoint tracking response

Since the CSTR process in (18) is highly nonlinear, the NPID controller was directly tuned using a GA while step setpoint signals were changed from 0.886 to 2.752 at t = 1 and from 2.752 to 4.705 at t = 16 and vice versa, as shown in Fig. 14. This tuning results in the settings Kp = 91.056, Ki = 0.026 and Kd = 11.561 for setpoint tracking.

Fig. 14
figure 14

Step responses of the two methods for changes in setpoint: a ys = 0.886 → 2.752 → 4.705, b ys = 4.705 → 2.752 → 0.886.

Full size image

Again, it is seen that the response of the proposed method is better than that of the AC-Chen method. Table 5, which summarizes the quantitative results, also proves this.

4.3.2 Disturbance rejection response

The settings of the NPID controller were obtained in a similar manner while applying step disturbances d1 = 0.2, d2 = 0.2 at t = 1 and then d1 = -0.2, d2 = -0.2 at t = 16 with constant ys of 2.752. The results are Kp = 64.997, Ki = 129.999 and Kd = 20.002 for disturbance rejection. The response of the proposed method is shown in Fig. 15, together with that of the AC-Chen method.

Fig. 15
figure 15

Responses of the two methods for changes in disturbances on the CSTR process

Full size image

From Fig. 15 and Table 10, it is seen that Mpeak, trcy and IAE of the proposed method are better than those of the AC-Chen method.

Table 10 Performance comparison of the two methods on the CSTR process
Full size table

4.3.3 Noise elimination response

In order to validate the robustness of the proposed method against noise, a Gaussian noise N(0,0.032) equivalent to about 15% of the change in the setpoint value was applied to the output stage. Figure 16 shows the responses of the two methods.

Fig. 16
figure 16

Step responses of the two methods under noise

Full size image

Comparing Fig. 16 with Fig. 14(a) without noise, the proposed method shows a satisfactory response even in a noisy environment.

5 Conclusion

This paper has proposed an enhanced NPID controller to improve setpoint tracking or disturbance rejection responses and avoid possible Derivative Kick. The parameters of the NPID controller were expressed in terms of L/τ using the dimensionless approach. Repeated optimizations of 20 were performed for each value over the ranges of 0.01 to 1 and 1 to 3 of L/τ and over the ranges of 5 to 30 of N to obtain the averaged parameter values that minimize the IAE criterion. By using the least-squares method with together the calculated values and the rule formulae, the new tuning rules have been obtained. A set of simulation works on the five processes have depicted that the proposed method demonstrated good tracking and disturbance performance and robustness against noise than the other methods. The proposed method worked well for particularly the higher-order process and the nonlinear process. In future works, the proposed rules can be applied to an auto-tuning approach.