1 Introduction

Wind energy is a form of solar energy which results from the uneven distribution of heat and pressure in the atmosphere. Because of the irregularities of the surface of the earth, wind patterns change from one location to another. Wind is an abundant renewable energy source however it is intermittent and unpredictable.

Until the end of 2013, electricity production from wind energy was estimated at 3.5% (320 GW) of the global electricity production (Zin et al. 2013).

Different types of generators have been developed for wind energy conversion systems. Among them, the Double Fed Induction Generator (DFIG) is widely used because of their advantages such as variable speed operation, reduced cost of the converter and simplicity of control of the power flow at the point coupling common (PCC) in the grid (Akel et al. 2014; Merahi and Berkouk 2013).

The power control of the DFIG has been the subject of extensive research. Field Oriented Control (FOC) is the most popular control used for decoupled the active and reactive powers of the DFIG by the orientation of the stator flux along the d-axis of Park frame (Merahi et al. 2014). In this context, Direct Control of Power is currently the most popular method in the literature to control the real and reactive powers of the DFIG due to its ease of implementation. However, since this control approach is characterized by a single loop (power), therefore it is difficult to evaluate the rotor current in the DFIG (Janssens et al. 2007). In this paper, we propose to use the Indirect Control of Power, which consists of two loops, an internal loop to control the rotor current and an external loop for the control of the two powers. This control scheme protects the DFIG against overcurrent and ensures a good performance.

Several controllers have been proposed in the literature to control the two loops of powers and rotor currents. Conventional controllers using Proportional-Integral (PI) are the most commonly used due to their simple implementation. However, these controllers lack robustness and may not produce satisfactory performance under challenging operating conditions such as parameter variations of the DFIG.

Robust nonlinear controllers based on Lyapunov stability theory of have been proposed in the literature to improve the performance of the DFIG under challenging operating conditions. Among them, the Sliding Mode Controller (SMC) has been widely applied. However, the main disadvantage of SMC is the chattering problem (Jeong et al. 2008; Zhang 2014; Lu et al. 2014).

Several approach have been described in the literature to eliminate the problem of chattering such as High-Order Sliding Mode Control (HOSMC) (Beltran et al. 2012; Benbouzid et al. 2014; Susperregui et al. 2011), Fuzzy Sliding Mode Control (FSMC) (Mohammadi and Nafar 2013) and super-twisting sliding mode control (STSMC) (Swikir and Utkin 2016; Chalanga et al. 2016; Salgado et al. 2014). The HOSMC generalizes the basic idea of SMC by acting on the high-order time derivatives of the sliding mode, which guarantees that the first-time derivative of the sliding mode is continuous. In this way, the chattering phenomenon can be completely eliminated. However, the major disadvantage of HOSMC is that it requires the knowledge of the time derivatives of the sliding variable (Chalanga et al. 2016). The FSMC approach combines the advantages of SMC and Fuzzy Logic Control (FLC). In this way, the phenomenon of chattering can be decreased. The STSMC is a viable alternative to the conventional SMC in order to avoid the chattering phenomenon without compromising the tracking performance (Swikir and Utkin 2016; Horch et al. 2015). Other control laws derived from the Lyapunov approach are well suited for the control of power and rotor current of DFIG such as the back-stepping control (BSC) (Reddak et al. 2016). Extensive research works have also focused on assessing the stability and the state estimation problems of the whole system. In In this paper, the nonlinear BSC is used to control the power and rotor current of the DFIG (Tarek et al. 2015) and its performance is compared with STSMC.

The amount of power that can captured from a wind turbine depends on several parameters including the wind turbine characteristics and wind variability, which depends of on the geographical location. Maximum Power Point Tacking (MPPT) algorithms are designed to search for the optimum operating point that allows the wind turbine to extract the maximum power from the available wind energy (Boutoubat et al. 2013; Hinkkanen 2004; Amimeur et al. 2012). Several MPPT control strategies have been proposed in the literature (Hong et al. 2013; Wu et al. 2013; Eltamaly and Farh 2013; Belmokhtar et al. 2014). The MPPT used in this work based on the Tip Speed Ratio (TSR) control, which regulates the rotor speed, while keeping the TSR at its optimum value to capture the maximum wind power. This method requires an accurate knowledge of the wind turbine parameters and measurement of the wind speed in order to determine the required generator’s speed to extract the maximum power (Eltamaly and Farh 2013; Belmokhtar et al. 2014; Lin and Hong 2010).

Sensor-less speed control of DFIG has been addressed by several authors (Akel et al. 2014; Forchetti et al. 2009; Lin et al. 2011). The model reference adaptive system (MRAS)-based observer has been the most popular in DFIG mechanical speed estimation due to its simplicity and ease of implementation. However, the MRAS approach does give satisfactory performance under challenging operating conditions such as parameter variations of the DFIG. An Adaptive Sliding Mode Observer (ASMO) is used in this paper to further improve the robustness of the observer against parameter variations in the DFIG.

The main objective of this contribution is to propose an enhanced nonlinear control scheme for the DFIG. The control scheme consists of: (1) a BSC controller to regulate the current rotor and power of DFIG, (2) ASMO observer to estimate the mechanical speed of the DFIG, (3) an MPPT algorithm to search for the optimum operating point that allows the wind turbine to extract the maximum power from the available wind energy.

The rest of the paper is organized as follows: Sect. 2 presents a description and modeling of the wind turbine with DFIG. In Sect. 3, the proposed control algorithms for the wind, DFIG and observer are derived. Finally, simulation results and conclusions are presented in Sects. 4 and 5 respectively.

2 Modeling of the studied system

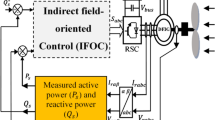
The configuration of studied system is illustrated in Fig. 1. Which consists to a variable speed wind turbine with MPPT controller, a DFIG and inverter.

Fig. 1
figure 1

Structure and control scheme of the studied system

Full size image

2.1 Wind turbine model and characteristics

The wind turbine converts the kinetic energy from the wind into aerodynamic power \( P_{a} \) which expressed by the following equation:

$$ P_{a} = \frac{1}{2}C_{p} \left( {\lambda ,\beta } \right)\rho \pi R^{2} V^{3} $$
(1)
$$ \lambda = \frac{{R\Omega _{t} }}{V} $$
(2)

The aerodynamic torque is given by:

$$ T_{a} = \frac{{P_{a} }}{{\Omega _{t} }} $$
(3)

The Wind Turbine (WT) model structure is depicted in Fig. 2. The coupling of the shaft between the wind turbine and a DFIG requires a gearbox system (G). Therefore, the speed and torque delivered to the generator are related by the following equation:

$$ \Omega _{t} = \frac{{\Omega _{mec} }}{G} $$
(4)
$$ T_{g} = \frac{{T_{a} }}{G} $$
(5)
Fig. 2
figure 2

Block diagram of the modeling of a WT

Full size image

2.2 Modelling of the DFIG

The classical DFIG model described in the Park reference frame is given by the following set of equations of voltages and flux linkages for the stator and rotor respectively:

$$ \left\{ {\begin{array}{*{20}c} {V_{ds} = R_{s} i_{ds} + \frac{{d\psi_{ds} }}{dt} - \omega_{s} \psi_{qs} } \\ {V_{qs} = R_{s} i_{qs} + \frac{{d\psi_{qs} }}{dt} + \omega_{s} \psi_{ds} } \\ {V_{dr} = R_{r} i_{dr} + \frac{{d\psi_{dr} }}{dt} - \omega_{r} \psi_{qr} } \\ {V_{qr} = R_{r} i_{qr} + \frac{{d\psi_{qr} }}{dt} - \omega_{r} \psi_{dr} } \\ \end{array} } \right. $$
(6)
$$ \left\{ {\begin{array}{*{20}c} {\psi_{ds} = L_{s} i_{ds} + L_{m} i_{dr} } \\ {\psi_{qs} = L_{s} i_{qs} + L_{m} i_{qr} } \\ {\psi_{dr} = L_{r} i_{dr} + L_{m} i_{ds} } \\ {\psi_{qr} = L_{r} i_{qr} + L_{m} i_{qs} } \\ \end{array} } \right. $$
(7)

The electromagnetic torque is given by:

$$ T_{em} = \frac{3}{2}\frac{{P.L_{m} }}{{L_{s} }}\left( {\psi_{qs} i_{dr} - \psi_{ds} i_{qr} } \right) $$
(8)

The active and reactive powers of the DFIG are:

$$ \left\{ {\begin{array}{*{20}c} {P_{s} = V_{ds} .\,i_{ds} + V_{qs} .\,i_{qs} } \\ {Q_{s} = V_{qs} .\,i_{ds} - V_{ds} .\,i_{qs} } \\ \end{array} } \right. $$
(9)

2.3 DFIG with stator field orientation strategy

To make the control of the DFIG equivalent to that of the DC machine, for which a natural decoupling exists between the flux and torque, an orientation strategy of the stator flux following the d-axis is applied. One can write:

$$ \left\{ {\begin{array}{*{20}c} {\psi_{ds} = \psi_{s} } \\ {\psi_{qs} = 0} \\ \end{array} } \right. $$
(10)
$$ \left\{ {\begin{array}{*{20}l} {V_{ds} = 0} \hfill \\ {V_{qs} = V_{s} \approx \omega_{s} \psi_{s} } \hfill \\ \end{array} } \right. $$
(11)
$$ \left\{ {\begin{array}{*{20}c} {\psi_{s} = L_{s} i_{ds} + L_{m} i_{dr} } \\ {0 = L_{s} i_{qs} + L_{m} i_{qr} } \\ \end{array} } \right. $$
(12)
$$ T_{em} = - \frac{3}{2}\frac{{P.L_{m} }}{{L_{s} }}\psi_{ds} i_{qr} $$
(13)

The equations relating the stator currents to the rotor currents are deduced as:

$$ \left\{ {\begin{array}{*{20}l} {i_{ds} = \frac{{V_{s} }}{{\omega_{s} L_{s} }} - \frac{{L_{m} }}{{L_{s} }}i_{dr} } \hfill \\ {i_{ds} = - \frac{{L_{m} }}{{L_{s} }}i_{qr} } \hfill \\ \end{array} } \right. $$
(14)

Hence, the rotor voltage equations can be written as:

$$ \left\{ {\begin{array}{*{20}c} {V_{dr} = R_{r} \,i_{dr} + L_{r} \,\sigma \,\frac{{di_{dr} }}{dt} - F_{emd} } \\ {V_{qr} = R_{r} \,i_{qr} + L_{r} \,\sigma \,\frac{{di_{qr} }}{dt} + F_{emq} } \\ \end{array} } \right. $$
(15)

with

$$ \left\{ {\begin{array}{*{20}l} {F_{emd} = g\,\omega_{s} \,L_{r} \,\sigma \,i_{qr} } \hfill \\ {F_{emq} = g\,\omega_{s} \,L_{r} \,\sigma \,i_{dr} + g\frac{{L_{m} \,V_{s} }}{{L_{s} }}} \hfill \\ \end{array} } \right.;\quad \sigma = 1 - \frac{{L_{m}^{2} }}{{L_{r} L_{s} }} $$

Finally, Eq. (9) becomes:

$$ \left\{ {\begin{array}{*{20}l} {P_{s} = - \frac{{V_{s} \,L_{m} }}{{L_{s} }}i_{qr} } \hfill \\ {Q_{s} = - \frac{{V_{s} \,L_{m} }}{{L_{s} }}i_{dr} + \frac{{V_{s}^{2} }}{{L_{s} \,\omega_{s} }}} \hfill \\ \end{array} } \right. $$
(16)

3 Control strategies

This section provides a detailed description and derivation steps of the different control strategies shown in Fig. 1.

3.1 MPPT with speed control

The goal of the MPPT strategy is to extract the maximum power from the wind. The TSR is the most widely used method for MPPT. Figure 3 shows that the optimum turbine speed is first compared with the actual value and the difference is then fed into PI controller to obtain the reference of electromagnetic torque. The optimal turbine speed is achieved when TSR is maintained at its optimal value.

$$ \Omega _{t}^{*} = \frac{{\lambda_{opt} \cdot V}}{R} $$
(17)
Fig. 3
figure 3

MPPT with speed control

Full size image

Under these conditions, the maximum power is given by:

$$ P_{opt} = \frac{{C_{p\_\hbox{max} } }}{{\lambda_{opt}^{3} }}\frac{{\rho \,\pi \,R^{5} }}{2}\frac{{\varOmega_{mec}^{3} }}{{G^{3} }} $$
(18)

3.2 Nonlinear control design for DFIG

In this section, two nonlinear control laws for the control of the DFIG rotor currents and power are derived namely the back-stepping control (BSC) and super-twisting sliding mode control (STSMC).

3.2.1 Back-stepping control

The control by Back-Stepping tries to find a stabilizing control for the closed-loop nonlinear system in the sense of Lyapunov stability theory. The design steps of the BSC for the DFIG model are:

Step 1 Active and reactive power control

Defining the active and reactive power errors as:

$$ \left\{ {\begin{array}{*{20}c} {e_{1} = P_{s}^{*} - P_{s} } \\ {e_{3} = Q_{s}^{*} - Q_{s} } \\ \end{array} } \right. $$
(19)

The derivative of the error is as:

$$ \left\{ {\begin{array}{*{20}c} {\dot{e}_{1} = \dot{P}_{s}^{*} - \dot{P}_{s} } \\ {\dot{e}_{3} = \dot{Q}_{s}^{*} - \dot{Q}_{s} } \\ \end{array} } \right. $$
(20)

The first Lyapunov function is chosen as:

$$ V_{1} = \frac{1}{2}e_{1}^{2} + \frac{1}{2}e_{3}^{2} $$
(21)

The derivative of the function V1 is expressed as:

$$ \dot{V}_{1} = e_{1} \dot{e}_{1} + e_{3} \dot{e}_{3} $$
(22)

Which can be rewritten as follows:

$$ \dot{V}_{1} = - K_{1} e_{1}^{2} - K_{3} e_{3}^{2} $$
(23)

To ensure that the derivative of V1 is negative, the constants of K1 and K3 should be positive. Equation (20) can be rewritten as follows:

$$ \left\{ {\begin{array}{*{20}c} {\dot{e}_{1} = \left( {\dot{P}_{s}^{*} + \frac{{V_{s} L_{m} }}{{L_{s} }}\dot{i}_{qr} } \right) = - K_{1} e_{1} } \\ {\dot{e}_{3} = \left( {\dot{Q}_{s}^{*} + \frac{{V_{s} L_{m} }}{{L_{s} }}\dot{i}_{dr} } \right) = - K_{3} e_{3} } \\ \end{array} } \right. $$
(24)

Finally, the direct and quadratic of rotor currents of DFIG chosen as:

$$ \left\{ {\begin{array}{*{20}c} {\dot{i}_{dr}^{*} = \frac{{L_{s} }}{{V_{s} L_{m} }}\left( { - \dot{Q}_{s}^{*} - K_{3} e_{3} } \right)} \\ {\dot{i}_{qr}^{*} = \frac{{L_{s} }}{{V_{s} L_{m} }}\left( { - \dot{P}_{s}^{*} - K_{1} e_{1} } \right)} \\ \end{array} } \right. $$
(25)

Step 2 Rotor currents control

Defining the rotor currents errors as:

$$ \left\{ {\begin{array}{*{20}c} {e_{2} = i_{qr}^{*} - i_{qr} } \\ {e_{4} = i_{dr}^{*} - i_{dr} } \\ \end{array} } \right. $$
(26)

The derivative of the error is:

$$ \left\{ {\begin{array}{*{20}c} {\dot{e}_{2} = \dot{i}_{qr}^{*} - \dot{i}_{qr} } \\ {\dot{e}_{4} = \dot{i}_{dr}^{*} - \dot{i}_{dr} } \\ \end{array} } \right. $$
(27)

with

$$ \left\{ {\begin{array}{*{20}c} {\dot{i}_{dr} = \frac{1}{{L_{r} \sigma }}\left( {V_{dr} - R_{r} i_{dr} } \right)} \\ {\dot{i}_{qr} = \frac{1}{{L_{r} \sigma }}\left( {V_{qr} - R_{r} i_{qr} } \right)} \\ \end{array} } \right. $$
(28)

The second Lyapunov function is chosen such as:

$$ V_{2} = \frac{1}{2}\left( {e_{1}^{2} + e_{2}^{2} + e_{3}^{2} + e_{4}^{2} } \right) $$
(29)

The derivative of the function V2 is expressed as:

$$ \dot{V}_{2} = e_{1} \dot{e}_{1} + e_{2} \dot{e}_{2} + e_{3} \dot{e}_{3} + e_{4} \dot{e}_{4} $$
(30)

Equation (30) can be rewritten as follows:

$$ \dot{V}_{2} = - K_{1} e_{1}^{2} - K_{2} e_{2}^{2} - K_{3} e_{3}^{2} - K_{4} e_{4}^{2} $$
(31)

Again, to ensure that the derivative of V2 is negative, K2 and K4 are selected as positive constants. Equation (26) can be rewritten as follows:

$$ \left\{ {\begin{array}{*{20}c} {\dot{e}_{2} = \left( {\left( {\frac{{L_{s} }}{{V_{s} L_{m} }}\left( { - \dot{P}_{s}^{*} - K_{1} e_{1} } \right)} \right) - \left( {\frac{1}{{L_{r} \sigma }}\left( {V_{qr} - R_{r} i_{qr} } \right)} \right)} \right) = - K_{2} e_{2} } \\ {\dot{e}_{4} = \left( {\left( {\frac{{L_{s} }}{{V_{s} L_{m} }}\left( { - \dot{Q}_{s}^{*} - K_{3} e_{3} } \right)} \right) - \left( {\frac{1}{{L_{r} \sigma }}\left( {V_{dr} - R_{r} i_{dr} } \right)} \right)} \right) = - K_{4} e_{4} } \\ \end{array} } \right. $$
(32)

Finally, the direct and quadratic of rotor voltage of the DFIG are chosen as:

$$ \left\{ {\begin{array}{*{20}c} {V_{dr} = L_{r} \sigma \left( {\left( {\frac{{L_{s} }}{{V_{s} L_{m} }}\left( { - \dot{Q}_{s}^{*} - K_{3} e_{3} } \right)} \right) + \frac{{R_{r} }}{{L_{r} \sigma }}i_{dr} + K_{4} e_{4} } \right)} \\ {V_{qr} = L_{r} \sigma \left( {\left( {\frac{{L_{s} }}{{V_{s} L_{m} }}\left( { - \dot{P}_{s}^{*} - K_{1} e_{1} } \right)} \right) + \frac{{R_{r} }}{{L_{r} \sigma }}i_{qr} + K_{2} e_{2} } \right)} \\ \end{array} } \right. $$
(33)

A block diagram of the BSC used in this section is illustrated in Fig. 4.

Fig. 4
figure 4

Block diagram of the back-stepping control

Full size image

3.2.2 Super-twisting sliding mode control (STSMC)

In this section, the basic principle and design procedure of the STSMC scheme used to control the active and reactive powers and the rotor currents of DFIG are discussed.

STSMC is a controller like the Second Order Sliding Mode Control (SOSMC) attempts to eliminate the chattering effect. However, STSMC is more advantageous compared to SOSMC because it retains the same tracking performance and robustness of the conventional Sliding Mode Control (SMC) and it depends strongly on the sliding surface.

STSMC scheme consists of two terms: the equivalent control Uequ and super twisting control Ust.

$$ u\left( t \right) = u_{equ} \left( t \right) + u_{st} \left( t \right) $$
(34)

with

$$ u_{st} \left( t \right) = u_{1} \left( t \right) + u_{2} \left( t \right) $$
(35)
$$ \left\{ {\begin{array}{*{20}l} {u_{1} (t) = - \lambda .\left| S \right|^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \cdot \text{sgn} (S)} \hfill \\ {\dot{u}_{2} (t) = - \gamma \cdot \text{sgn} (S)} \hfill \\ \end{array} } \right. $$
(36)

where λ and γ are positive constants and the fixed-gain can be chosen as:

$$ \left\{ {\begin{array}{*{20}l} {\lambda \rangle \frac{\phi }{{\Gamma _{\hbox{min} } }}} \hfill \\ {\gamma^{2} \ge \frac{4\phi }{{\Gamma _{\hbox{min} }^{2} }}\frac{{\Gamma _{\hbox{max} } \left( {\lambda + \phi } \right)}}{{\Gamma _{\hbox{min} } \left( {\lambda - \phi } \right)}}} \hfill \\ \end{array} } \right. $$
(37)

with: Φ, Γmin, Γmax are the positive constants.

For the equivalent control of STSMC, the same procedure is used as for the conventional SMC. The design procedure applied for a model of the DFIG include the following steps:

Step 1 Active and reactive power control

A. Equivalent control

The active and reactive powers switching surface is designed as:

$$ \left\{ {\begin{array}{*{20}l} {S\left( P \right) = P_{s}^{*} - P_{s} } \hfill \\ {S\left( Q \right) = Q_{s}^{*} - Q_{s} } \hfill \\ \end{array} } \right. $$
(38)

In order to guarantee the existence of a sliding mode and ensure convergence, the condition on Lyapunov function must be fulfilled:

$$ \left\{ {\begin{array}{*{20}l} {\dot{S}\left( P \right) \cdot S\left( P \right) \le 0} \hfill \\ {\dot{S}\left( Q \right) \cdot S\left( Q \right) \le 0} \hfill \\ \end{array} } \right. $$
(39)
$$ \left\{ {\begin{array}{*{20}l} {\dot{S}\left( P \right) = \dot{P}_{s}^{*} - \dot{P}_{s} = \dot{P}_{s}^{*} + \frac{{L_{s} }}{{V_{s} \cdot L_{m} }}\dot{i}_{qr}^{*} } \hfill \\ {\dot{S}\left( Q \right) = \dot{Q}_{s}^{*} - \dot{Q}_{s} = \dot{Q}_{s}^{*} + \frac{{L_{s} }}{{V_{s} \cdot L_{m} }}\dot{i}_{dr}^{*} } \hfill \\ \end{array} } \right. $$
(40)

The outputs powers controllers by STSMC are the rotor currents references of DFIG, so, the equivalent control is given by:

$$ \left\{ {\begin{array}{*{20}l} {\dot{S}\left( P \right) = 0 \Leftrightarrow \dot{i}_{qr}^{*} = - \frac{{V_{s} \cdot L_{m} }}{{L_{s} }}\dot{P}_{s}^{*} } \hfill \\ {\dot{S}\left( Q \right) = 0 \Leftrightarrow \dot{i}_{dr}^{*} = - \frac{{V_{s} \cdot L_{m} }}{{L_{s} }}\dot{Q}_{s}^{*} } \hfill \\ \end{array} } \right. $$
(41)

B. Super-Twisting Control (STC)

In this work, the hyperbolic tangent surface is used for the STC due to its robustness and fast convergence. The STC terms can written as:

$$ \left\{ \begin{aligned} i_{qr(st)} \left( t \right) = - \lambda_{P} \cdot \left| S \right|^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \cdot \tanh (S) - \int {\gamma_{P} \cdot \tanh (S)dt} \hfill \\ i_{dr(st)} \left( t \right) = - \lambda_{Q} \cdot \left| S \right|^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \cdot \tanh (S) - \int {\gamma_{Q} \cdot \tanh (S)dt} \hfill \\ \end{aligned} \right. $$
(42)

To respect the condition of convergence, the positive gains for λp, λQ, γp and γQ are chosen appropriately.

Step 2 Rotor current control

A. Equivalent control

The rotor current switching surface is designed as:

$$ \left\{ {\begin{array}{*{20}l} {S\left( {i_{dr} } \right) = i_{dr}^{*} - i_{dr} } \hfill \\ {S\left( {i_{qr} } \right) = i_{qr}^{*} - i_{qr} } \hfill \\ \end{array} } \right. $$
(43)

In order to guarantee the existence of a sliding mode and ensure convergence, the condition on Lyapunov function must be fulfilled:

$$ \left\{ {\begin{array}{*{20}l} {\dot{S}\left( {i_{dr} } \right) \cdot S\left( {i_{dr} } \right) \le 0} \hfill \\ {\dot{S}\left( {i_{qr} } \right) \cdot S\left( {i_{qr} } \right) \le 0} \hfill \\ \end{array} } \right. $$
(44)
$$ \left\{ {\begin{array}{*{20}l} {\dot{S}\left( {i_{dr} } \right) = \dot{i}_{dr}^{*} - \dot{i}_{dr} = \dot{i}_{dr}^{*} - \frac{1}{{\sigma \cdot L_{r} }}\left( {V_{dr} - R_{r} \cdot i_{dr} } \right)} \hfill \\ {\dot{S}\left( {i_{qr} } \right) = \dot{i}_{qr}^{*} - \dot{i}_{qr} = \dot{i}_{qr}^{*} - \frac{1}{{\sigma \cdot L_{r} }}\left( {V_{qr} - R_{r} \cdot i_{qr} } \right)} \hfill \\ \end{array} } \right. $$
(45)

The outputs rotor currents controllers by STSMC are the rotor voltages references of the DFIG, therefore, the equivalent control is given by:

$$ \left\{ {\begin{array}{*{20}l} {\dot{S}\left( {i_{dr} } \right) = 0 \Leftrightarrow V_{dr}^{*} = \sigma \cdot L_{r} \cdot \dot{i}_{dr}^{*} + R_{r} \cdot i_{dr} } \hfill \\ {\dot{S}\left( {i_{qr} } \right) = 0 \Leftrightarrow V_{qr}^{*} = \sigma \cdot L_{r} \cdot \dot{i}_{qr}^{*} + R_{r} \cdot i_{qr} } \hfill \\ \end{array} } \right. $$
(46)

B. Super-Twisting Control (STC)

The STC terms used for the control of the rotor voltage of the DFIG can written as:

$$ \left\{ \begin{aligned} V_{dr(st)} \left( t \right) = - \lambda_{d} \cdot \left| S \right|^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \cdot \tanh (S) - \int {\gamma_{d} \cdot \tanh (S)dt} \hfill \\ i_{qr(st)} \left( t \right) = - \lambda_{q} \cdot \left| S \right|^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \cdot \tanh (S) - \int {\gamma_{q} \cdot \tanh (S)dt} \hfill \\ \end{aligned} \right. $$
(47)

Similarly, to respect the condition of convergence, we have chosen the positive gains for λd, λq, γd and γq.

A block diagram of the STSMC used in this section illustrated in Fig. 5.

Fig. 5
figure 5

Block diagram of the STSMC

Full size image

3.3 Adaptive sliding mode observer (ASMO)

For the DFIG, speed sensorless operation is desirable in practice, because the use of a sensor of speed has several drawbacks in term of cost and robustness.

In this paper, we have developed a Sensor-less system based on ASMO to estimate the mechanical speed of the DFIG. Firstly, the sliding mode observer for the DFIG will represented in the stationary reference frame and is defined as:

$$ \left\{ {\begin{array}{*{20}l} {\dot{\hat{x}}_{1} = - \lambda x_{1} + a\hat{x}_{3} + pK\hat{x}_{5} \hat{x}_{4} + \frac{1}{{\sigma L_{s} }}V_{\alpha s} - KV_{\alpha r} +\Lambda _{1} I_{s} } \hfill \\ {\dot{\hat{x}}_{2} = - \lambda x_{2} + a\hat{x}_{4} - pK\hat{x}_{5} \hat{x}_{3} + \frac{1}{{\sigma L_{s} }}V_{\beta s} - KV_{\beta r} +\Lambda _{2} I_{s} } \hfill \\ {\dot{\hat{x}}_{3} = bx_{1} - c\hat{x}_{3} - p\hat{x}_{5} \hat{x}_{4} + V_{\alpha r} +\Lambda _{3} I_{s} } \hfill \\ {\dot{\hat{x}}_{4} = bx_{2} - c\hat{x}_{4} - p\hat{x}_{5} \hat{x}_{3} + V_{\beta r} +\Lambda _{4} I_{s} } \hfill \\ \end{array} } \right. $$
(48)

Secondly, with the adaptation mechanism based on a simple conventional PI-type controller, we can determine the Mechanical Speed Observer (MSO) of the DFIG. So, the MSO expressed by:

$$ \left\{ \begin{aligned} e_{i\alpha s} = x_{1} - \hat{x}_{1} \hfill \\ e_{i\beta s} = x_{2} - \hat{x}_{2} \hfill \\ e_{\varphi \alpha r} = x_{3} - \hat{x}_{3} \hfill \\ e_{\varphi \beta r} = x_{4} - \hat{x}_{4} \hfill \\ \end{aligned} \right. $$
(49)
$$ \varepsilon = e_{i\alpha s} \hat{x}_{4} - e_{i\beta s} \hat{x}_{3} $$
(50)
$$ \dot{\hat{x}}_{5} = K_{p} \varepsilon + K_{i} \int\limits_{0}^{t} {\varepsilon dt} $$
(51)

where

$$ \begin{aligned} \hat{x} & = \left[ {\hat{i}_{\alpha s} \quad \hat{i}_{\beta s} \quad \hat{\varphi }_{\alpha r} \quad \hat{\varphi }_{\beta r} \quad \hat{\omega }_{r} } \right]^{T} \\ \lambda & = \frac{{R_{s} }}{{\sigma \,L_{s} }} + \frac{{R_{r} \,L_{m}^{2} }}{{\sigma \,L_{s} \,L_{r}^{2} }},\quad \tau_{r} = \frac{{L_{r} }}{{R_{r} }},\quad K = \frac{{L_{r} }}{{\sigma \,L_{s} \,L_{r} }},\quad a = \frac{K}{{\tau_{r} }},\quad b = \frac{{L_{m} }}{{\tau_{r} }},\quad c = \frac{1}{{\tau_{r} }} \\ \end{aligned} $$

S1, S2 represent the sliding surfaces. In this work, the hyperbolic tangent surface is used due to its robustness and fast convergence.

$$ I_{s} = \left[ {sign\,\left( {S_{1} } \right)\quad sign\,\left( {S_{2} } \right)} \right]^{T} $$
(52)
$$ \left\{ \begin{aligned} S_{1} = x_{1} - \hat{x}_{1} \hfill \\ S_{2} = x_{2} - \hat{x}_{2} \hfill \\ \end{aligned} \right. $$
(53)

The gains Λ1, Λ2, Λ3, Λ4: are calculated to ensure the convergence of errors observer. The gains are derived as Belabbas et al. (2016):

$$ \left[ \begin{aligned}\Lambda _{11} \quad\Lambda _{12} \hfill \\ \varLambda_{21} \quad \varLambda_{22} \hfill \\ \end{aligned} \right] =\Gamma ^{ - 1} \left[ \begin{aligned} \delta_{1} \quad 0 \hfill \\ 0\quad \delta_{2} \hfill \\ \end{aligned} \right] $$
(54)
$$ \Gamma = \frac{1}{{a^{2} + \left( {K\,p\,x_{5} } \right)^{2} }}\left[ {\begin{array}{*{20}c} a & { - K\,p\,x_{5} } \\ {K\,p\,x_{5} } & a \\ \end{array} } \right] $$
(55)
$$ \left[ \begin{aligned}\Lambda _{31} \quad\Lambda _{32} \hfill \\\Lambda _{41} \quad\Lambda _{42} \hfill \\ \end{aligned} \right] = \left[ {\begin{array}{*{20}c} {\left( {q_{1} - c} \right)} & { - px_{5} } \\ {px_{5} } & {\left( {q_{2} - c} \right)} \\ \end{array} } \right].\left[ \begin{aligned} \delta_{1} \quad 0 \hfill \\ 0\quad \delta_{2} \hfill \\ \end{aligned} \right] $$
(56)

Such as:

$$ \left\{ \begin{aligned} \delta_{1} \rangle \left| {e_{3} } \right|_{\hbox{max} } \hfill \\ \delta_{2} \rangle \left| {e_{4} } \right|_{\hbox{max} } \hfill \\ \end{aligned} \right.\quad and\quad \left\{ \begin{aligned} q_{1} \rangle 0 \hfill \\ q_{2} \rangle 0 \hfill \\ \end{aligned} \right. $$

4 Simulation results and discussion

To test the performance of the BSC controller used to regulate the two powers (active, reactive) and rotor current of the DFIG. A simulation study of the DFIG model and control schemes was done using MATLAB and Simulink with the parameter’s values listed in the “Appendix”. To better illustrate the advantages and performance of BSC, four tests are performed and the results are presented in the following subsections:

4.1 Control the power and rotor current by BSC

In this section, BSC is used to control the two powers and rotor current of the DFIG. The system is initially simulated with the variable wind speed profile shown in Fig. 6. The reference mechanical speed, the real measure speed and the estimated speed from the Adaptive Sliding Mode Observer (ASMO) are shown in Fig. 7. The results demonstrate fast convergence and good tracking performance of the real mechanical speed during the whole wind speed profile. The error between the estimated speed from the ASMO and the real speed is very small.

Fig. 6
figure 6

Wind profile

Full size image
Fig. 7
figure 7

Mechanical speed: reference (blue), actual (red), observed (green) (color figure online)

Full size image

The d- and q-axis stator flux components of the DFIG are illustrated in Fig. 8. Note that the q-axis stator flux is zero in steady-state, which demonstrate that the stator flux is perfectly oriented along the d-axis.

Fig. 8
figure 8

Stator flux of DFIG: d- and q-axis components

Full size image

The optimal power extracted from the wind turbine according to the wind speed is obtained from the MPPT algorithm and is used as the reference power. Thus, in order to ensure a unit power factor, it is necessary to choose a reference of zero for the reactive power.

Figures 9a and b show the response of two powers (Active, Reactive) of the DFIG respectively. It can be noted that the two powers follow these references successfully, and with a quick response time. These results clearly demonstrate the effectiveness of the BSC controller to regulate the two powers of the DFIG.

Fig. 9
figure 9

Powers of DFIG controlled by BSC: a active and b reactive

Full size image

Figure 10a and b show the response of the rotor current in the d-q Park coordinate respectively. It is also observed that the rotor currents follow these references perfectly and no steady-state errors. Thus, the rotor currents in the d- and q-axis of Park coordinate are the images of the reactive power real power respectively. These results demonstrate the advantage and performance of BSC to control the DFIG powers and rotor current.

Fig. 10
figure 10

Rotor current of DFIG controlled by BSC: a direct and b quadrature

Full size image

From these results, it can be concluded that the BSC leads to faster transient response and zero steady-state error.

The electromagnetic torque shown in the Fig. 11 responds quickly to an active power demand while it is independent of the reactive power.

Fig. 11
figure 11

Electromagnetic torque

Full size image

4.2 Comparative study between BSC and STSMC

In this second section of these simulation results, which was based on a comparative study between BSC and STSMC used to control the rotor currents and the two powers of the DFIG. STSMC can eliminate the chattering phenomena characterizing the conventional SMC and presents good convergence towards the desired reference.

Figures 12a and b show the responses of the active and reactive powers of the DFIG respectively. From these results, it can be concluded that both BSC and STSMC are able to perfectly control the two powers with good steady-state performance. However, in the transient regime, the BSC is more effective as compared to the STSMC, because with the BSC the two powers converge rapidly towards their references and do not exhibit any overshoot or oscillation. On the other hand, it can be noticed that with the STSMC both power responses have some overshoot during the transient. In summary, BSC provide more accurate control and has a faster convergence than STSMC.

Fig. 12
figure 12

Powers of DFIG: a active and b reactive

Full size image

From this comparison, it can be concluded that both controllers give good overall performances however BSC gives a faster transient response than STSMC.

4.3 Control system under parameter variations

In this section, a robustness test of the BSC controller against parameters variations of the DFIG is carried out. For this, the stator and rotor resistances of the DFIG are varied by 30% and by 50% of their nominal values.

Figures 13a and b present the responses of the two powers of the DFIG respectively. It can be observed that the responses of the two powers are not affected by these parameters variations of the DFIG which confirms the robustness of BSC.

Fig. 13
figure 13

Powers of DFIG under the parameters variations of the DFIG: a active and b reactive

Full size image

This test clearly demonstrate that BSC can effectivelly compensate for parametric variations of the DFIG.

4.4 Control system under actuator modelling error

This test aims to evaluate the degree of robustness of the BSC against modelling errors. This test was performed by introducing two Transfer Functions (TF) ΔG of the second degree, which were characterized by the presence of a pulsation ωn. The TF was placed at the input of DFIG as shown in the Fig. 14. In addition, the increase in the value of the pulsation indicates that there is an important modelling error in the system studied.

$$ \Delta G = \frac{{\omega_{n}^{2} }}{{S^{2} + 4S + \omega_{n}^{2} }} $$
(57)

where S is the Laplace transform.

Fig. 14
figure 14

Proposed of DFIG structure based on BSC controller with modelling error

Full size image

Figure 15 shows the response of the powers of the DFIG under the simulated modelling error scenario. To further demonstrate the performance of the BSC controller, a comparison was made between the case with no-modelling error (i.e. ωn = 0 rad/s) and when the system has a modelling error for different pulsation values of 10, 50 and 100 rad/s.

Fig. 15
figure 15

Powers of DFIG under actuator modeling error of the DFIG: a active and b reactive

Full size image

From these simulation results, it is clear that the response of the powers has not changed and has not been influenced by the presence of the modelling error. These results confirm the performance and robustness of the BSC controller and its suitability for wind energy systems applications.

Table 1 summarizes the comparative results of the BSC and STSMC controller under the different scenarios considered in these simulation studies.

Table 1 BSC and STSMC comparison
Full size table

5 Conclusion

This proposed some robust control strategies for wind energy conversion systems (WECS) based on a speed sensorless doubly-fed induction generator (DFIG). Two control methods have been proposed based on back-stepping control (BSC) and super-twisting sliding mode control (STSMC) to regulate the real and reactive powers and the rotor current of the DFIG. To achieve a fast convergence of the observer and preserve the desired tracking performance under model uncertainties, an ASMO model is employed to estimate the mechanical speed. The aim of this proposed control scheme is to improve the performance, robustness, and efficiency of the WECS while maximizing the power extracted from the wind. Various simulation scenarios have been presented to evaluate the proposed control structure under different operating conditions. Overall, the proposed BSC strategy provides a fast-transient response and offers better performance, robustness against parametric uncertainties. The control structure can be extended and applied to large power systems with grid-connected wind farms.