1 Introduction

One of the concerns of managers and owners of various industries is to be able to maintain the reliability and availability of systems and meanwhile to decrease maintenance and operating costs. The importance of the maintenance management has greatly gained a large attention in all sectors of manufacturing and service organizations. When a machine fails to operate in a system, it does not only delay the completion time of the operations assigned on it but also affect all the other planned operations in the system. Consequently, the missions cannot be finished on time and it will induce penalties and bad reputation to the company (Chung et al. 2009). As much as 1/3 of maintenance costs are due to bad planning, overtime costs, and limited or misuse of preventive maintenance, and are therefore unnecessary (Wireman 1989). Others estimate these expenses to 15–70% (Coetzee 2004; Bevilacqua and Braglia 2000). Maintenance management could have benefited from the advent of a large area in operations research, called maintenance optimization (Dekker 1996, 1998). The interest in development and implementation of maintenance optimization started in the early 1960s (Dekker 1996; Sandve and aven 1999). There is an attempt to find the optimum balance between the cost of maintenance and the associated cost which is called maintenance optimization model (Sandve and aven 1999). So maintenance optimization plan has been always considered as one of the main interests of researchers and several papers have been presented in this regard. In the view of optimization approach, the studies fall into two categories: analytical/numerical optimization methods and meta-heuristic methods.

There are considerable works about analytical/numerical optimization methods in maintenance optimization problems, such as Fattahi et al. (2014), Niazi et al. (2012), Baslis et al. (2012) and Latify et al. (2013). These methods have some obvious deficiencies such as convergence problems, time-consuming solution and error in linearization of nonlinear problems. Analytical/numerical optimization methods are always in two states; either finding a global solution or not having a solution. In other words, they consequently could not represent local solutions.

Meta-heuristic methods has also been considered in solving maintenance optimization (Ezzinbi et al. 2014; Marković et al. 2013; Otsmani et al. 2013). Among this kind of optimization methods, genetic algorithm (GA) has always been in center of interest for solving such problems and has been successfully applied in several papers, (Martorell et al. 2005; Morcous and Lounis 2005; Ilgin and Tunali 2007; Okasha and Frangopol 2009). GA is well-known due to their robust search capabilities that help reduce the computational complexity of large optimization problems (Kobbacy 2008; Coit and Smith 1994; Busacca et al. 2001) and overwhelm numerical methods mentioned inadequacies.

Today’s competitive world and increasing customer demand for highly reliable energy producers makes availability measure more challenging task especially in gas turbines. This is led to get more interest among researchers to optimize maintenance plan effectively to reduce cost and downtime especially in industrial gas turbines. Numerical optimization methods have been applied for optimization purpose to get outage time reduction, availability improvement and cost reduction in this field of interest (Bohlin et al. 2009, 2010; Wärja et al. 2008; Bohlin and Wärja 2015). These studies, however, are not exempt from mentioned shortcomings of numerical methods. To get rid of numerical method deficiencies, an intelligent tool for optimizing maintenance decisions has been developed in which genetic algorithm (GA) is used as the optimization algorithm.

The rest of this paper is organized as follows. Second Section provides the mathematical modeling of Gas turbine maintenance planning. In third Section, a general overview of proposed genetic algorithm is presented. Numerical results are given and discussed in forth Section. Finally, the conclusion is presented in last Section.

2 Gas turbine maintenance optimization formulation

The maintenance scheduling problem of a gas turbine is formulated in this section. Optimization of maintenance plan is a mixed integer programming (MIP) Model and like other optimization problems, involves an objective function and a set of constraints.

Aircraft model is a general optimization model which was applied to the replacement of components in aircraft engines (Andréasson 2004). The model is a MIP with components \(i = 1, \ldots ,N\), and time units \(t = 1, \ldots ,T\), and it uses two binary variables for replacement and maintenance called \(x_{it}\) and \(z_{t}\) respectively which are formulated in Eqs. (2) and (3) (Andréasson 2004).

$$x_{it} = \left\{ {\begin{array}{*{20}c} 1 & {\text{if part i is to be replaced at time t}} \\ 0 & {\text{else}} \\ \end{array} } \right.$$
(1)
$$z_{t} = \left\{ {\begin{array}{*{20}c} 1 & {\text{if some parts is to be replaced at time t,}} \\ 0 & {{\text{else}} .} \\ \end{array} } \right.$$
(2)

The constant cost for performing maintenance \(d\) multiplied by the binary variable for maintenance \(z_{t}\), and the cost for replacement, that is the spare part cost, \(c\) multiplied by the binary variable for replacement \(x_{it}\) makes the sum of costs, the objective function that is represented in Eq. (3) (Andréasson 2004).

$$\hbox{min} \sum\limits_{t = 1}^{T} {\left( {dz_{t} + c\sum\limits_{i = 1}^{N} {x_{it} } } \right)}$$
(3)

The first constraint represented in Eq. (4) says that every time the replacement of some part is trigged a fixed cost must be paid. This means that if a replacement is carried out then maintenance is performed. The constraint pushes the binary variable \(z_{t}\) to be one if it \(x_{it}\) is one as stated in Eq. (5) (Andréasson 2004).

$$x_{it} \le z_{t} ,\quad i \in N,\,t \in T$$
(4)
$$x_{it} ,\,z_{t} \in \left\{ {0,\left. 1 \right\}} \right.,\quad i \in N,\,t \in T,$$
(5)

Each component has a fixed life length \(T_{i}\), and each component must be replaced within its life length. The fact that the part must be replaced at least once every \(T_{i}\) time step yields the constraint with Eq. (6) (Andréasson 2004).

$$\sum\limits_{t = l}^{{l + T_{i} - 1}} {x_{it} \ge 1,\quad i \in N,\,l = 1, \ldots ,T - T_{i} + 1}$$
(6)

According to Bohlin and Wärja (2015), this general model can be modified for applying in gas turbine maintenance scheduling. The modification, performed on the objective function and the constraints, are described as follows.

  1. (a)

    Objective function

The objective function of this optimization problem is the cost of the maintenance schedule which consists of maintenance cost, base cost, downtime cost. Decision variable of the problem is a binary-coded matrix of which rows are the maintenance plan of individual components; \(x_{i1} ,x_{i2} , \ldots ,x_{iT}\) the \(y_{t}\) is another decision variable that shows occurrence of maintenance at occasion t. Each item has a maintenance cost \(C_{i}\) consisting of direct and indirect cost of the maintenance activity. In addition, the value of production per hour at an occasion \(t\) is denoted \(Dt\). This value is used for calculating the downtime cost which is the product of production value and downtime hours. A base cost \(St\) is also used for each occasion \(t\). The base cost is associated with shared setup costs not related to the down time of the occasion \(t\) and includes some of the costs for shutting down and restarting the gas turbine, travel expenses, and other shared costs that cannot be modeled using material, work, or down time costs (Holland 1975). This objective function can be presented in the form of Eq. (7) that is modified form of Eq. (6).

$$\hbox{min} f = \sum\limits_{i = 1}^{I} {\sum\limits_{t = 1}^{H} {c_{i} } } x_{it} + \sum\limits_{t = }^{H} {S_{t} y_{t} + \sum\limits_{t = 1}^{H} {D_{t} d_{t} } }$$
(7)

In this case, Gas turbine downtime \(dt\) is calculated as follows:

$$w_{t} = \sum\limits_{p = 1}^{P} {\hbox{max} (\Delta_{pi} x_{it} )}$$
(8)
$$NR_{t} = (24 - A)\left\lceil {\frac{{w_{t} }}{A} - 1} \right\rceil \times y_{t}$$
(9)
$$WR_{t} = 24(7 - W)\left\lceil {\frac{{w_{t} }}{WA} - 1} \right\rceil \times y_{t}$$
(10)
$$R_{t} = NR_{t} + WR_{t}$$
(11)
$$d_{t} = w_{t} + R_{t}$$
(12)

According to Eq. (12), gas turbine downtime can be estimated as the sum of work time and rest time. Work time is the time that doing maintenance activities take at a maintenance stop. It is assumed that each maintenance activity is divided into P parallel phases. The total work time is the sum of the maximum work time in each phase. The rest time at a maintenance stop consists of the night-rest and week-rest which are calculated using (9) and (10), respectively. For more detail, reader is referred to Bohlin and Wärja (2015).

  1. (b)

    Constraints

The set of constraints to be considered in maintenance optimization problem is specified below, in Eqs. (13) to (16). Equation (13) ensures that each maintenance activity \(i\) must be done at least once within an interval of length \(Ti\). \(H\) is the horizon of the scheduling. Remaining life of individual component, \(Oi\) is modeled in Eq. (14). Dependency between maintenance activities is also an important factor in maintenance scheduling and is displayed in Eqs. (15) and (16) (Bohlin and Wärja 2015).

$$\sum\limits_{j = t}^{t + Ti} {x_{ij} } \ge 1\begin{array}{*{20}c} {\begin{array}{*{20}c} {} & {} \\ \end{array} } & {\forall i,t} \\ \end{array} \begin{array}{*{20}c} {where} & {t \in } \\ \end{array} 1 \ldots H - Ti$$
(13)
$$\sum\limits_{j = 1}^{{Ti - O_{i} }} {x_{ij} } \ge 1\begin{array}{*{20}c} {\begin{array}{*{20}c} {} & {\forall i} \\ \end{array} } & {\begin{array}{*{20}c} {where} & {} \\ \end{array} Ti - Oi \le H} \\ \end{array}$$
(14)
$$\begin{aligned} &\sum\limits_{j = t}^{{t + Ti_{i} }} {(x_{ij} + \sum\limits_{i' \in Ni} {x_{i'j} } )} \ge 1 \hfill \\ &\quad {\forall i,\,t} \quad {where}\quad t \in 1 \ldots H - Ti \end{aligned}$$
(15)
$$\begin{aligned} &\sum\limits_{j = 1}^{{Ti - O_{i} }} {(x_{ij} } + \sum\limits_{i' \in Ni} {x_{{i{\prime }j}} } ) \ge 1 \hfill \\ &\quad {\forall i} \quad {where} \quad Ti - Oi \le H \end{aligned}$$
(16)

Gas turbine availability plays an important role in system operation and management and it’s essential to be guaranteed. System availability constraint is given in (17) (Bohlin and Wärja 2015).

$$Avail. < 1 - \frac{{\sum\nolimits_{t = 1}^{H} {d_{t} } }}{24*7*H}$$
(17)

where Avail. is the required availability of Gas turbine.

3 Proposed binary coded genetic algorithm

Genetic algorithm is one of the most famous and efficient meta-heuristic optimization methods which models genetic evolution pattern for solving problems. It was first formalized as an optimization method by Holland (1975) in 1960s as a search tool (Mitchell 1998).This algorithm is an effective search method in large-scale solution spaces that ultimately led to finding the optimum solution. Genetic algorithms have been most commonly applied to solve combinatorial optimization problems.

In genetic algorithm, each solution of the optimization problem would be represented by a vector X of the decision variables, which is coded in a so-called chromosome. Both binary-coded and real-coded chromosome is used in solving optimization problems.

The GA search usually starts with a random initial population of potential solutions. Then, these individuals are evaluated in terms of their so-called finesses, which are their corresponding objective function values. This initial population is called first generation which is used to producing next generations by four main genetic operators (Lee and El-Sharkawi 2008):

  • Selection of a pair of individuals as parents;

  • Crossover of the parents, to generate two children;

  • Repair operator; to modify generated children,

  • Genetic mutation.

In this paper a binary-coded genetic algorithm (BCGA) which is described as follows.

Chromosome definition In the proposed BCGA, the chromosome consists of a sequence of 0/1 bits, representing the maintenance occasion. Chromosomes are in form of matrix X with I × H bits. Figure 1 shows the sample chromosomes for typical maintenance scheduling. In order to create of the new generation of solutions, it is needed to evaluate proposed solution by fitness value. In proposed BCGA fitness value is estimated by the objective function of maintenance optimization problem.

Fig. 1
figure 1

Sample chromosomes for BCGA

Full size image

Selection Parents are selected using the one of selection algorithms. In this paper, the roulette wheel is used for parent selection in which the chance of a chromosome to be selected for reproduction is proportional to its fitness. It means the lower the cost is, the higher the chance will be. After the selection, two new children are produced by means of crossover and mutation.

Crossover Two crossover operators are used in BCGA; window crossover and two point crossover. In window crossover, two rows and two columns would be randomly selected and area between would be swapped in associated matrix. Two point crossover only two columns would be selected.

Mutation In BCGA, the standard mutation scheme that changes a bit from 0 to 1 and vice versa is used.

Repair operators As mentioned before, the solution to maintenance optimization problem should satisfy a set of constraints. In BCGA, a special kind of operator is developed which grantees constraints (Marković et al. 2013; Morcous and Lounis 2005) to be satisfied. These operators apply to the produced children resulting from mutation and crossovers. This operator checks whether the new children satisfy the mentioned time constraints. If mentioned requirements are not satisfied, then these operators will change it to an acceptable solution.

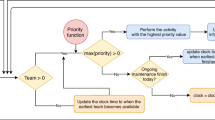
The Genetic algorithm evolution would be continued until a specific number of generations. The flowchart of the BCGA is shown in Fig. 2.

Fig. 2
figure 2

Flowchart of proposed genetic algorithm

Full size image

4 Numerical results and discussions

Numerical results, based on a SGT-600 maintenance case study, are reported in this section. The case study consists of 17 components of SGT-600 Gas turbine which has 25 maintenance activities. Scheduling horizon, H, is 15 years. Details of each activity include time interval, duration and cost, are given in Table 1 in Bohlin and Wärja (2015).

Table 1 Production scenarios
Full size table

In order to study the effect of remaining life of components, two aging patterns are defined: uniform aging and random aging. In random aging, the remaining life of each component is a random number between 0 and Ti-1. While in uniform aging scenario, the remaining life of each component is calculated based on Eq. (13) in which X is a random number between 0 and \(\max_{i = 1}^{I} T_{i} - 1\).

$$O_{i} = \left\lfloor X \right\rfloor \begin{array}{*{20}c} {} & {\bmod } \\ \end{array} \begin{array}{*{20}c} {} & k \\ \end{array} T_{i}$$
(18)

where k equals 0.9.

The maintenance plan is optimized for four scenarios A to D. In scenario A, the production value is $10 k US per hour. In scenario B, the production value in 10% of the occasions is zero. These occasions would be selected randomly. In the third Scenario, production value is randomly selected using a Gaussian distribution with expected value $10 k US and a standard deviation of $5 k US. Scenarios C and D are the same, however in the latter case, 10% of the occasions have zero production value. Details of these four scenarios are shown in Table 1.

The results of implementation proposed genetic algorithm is given in Tables 2 and 3 which are respectively related to uniform and random aging scenarios. The presented results are average results of 50 sample GA runs for each case which consist of maintenance cost, production loss cost and availability in both conventional and optimized maintenance schedule. It should be noted that the conventional plan includes fixed intervals without any optimization.

Table 2 BCGA Results of Uniform aging
Full size table
Table 3 Results proposed BCGA of random aging
Full size table

4.1 Comparing result of conventional and optimized maintenance schedule

The results of implementation proposed genetic algorithm is given in Tables 2 and 3 which are respectively related to random and uniform aging scenarios. The presented results are average results of 50 sample GA runs for each case which consist of maintenance cost, production loss cost and availability in both conventional and optimized maintenance schedule. Input maintenance intervals for performing PM tasks in optimized model are constant, while in optimized maintenance plan it is possible that the time for an activity differs from its interval due to reduction of cost.

Comparing the results of conventional and optimized maintenance schedule indicate a significant improvement in the latter case, since the total cost is decreased and the availability is increased. This improvement is mainly due to two important points. The first point is maintenance grouping which means to make two or more maintenance activities to be done in one occasion. By parallel execution of maintenance activities, the total shared base cost will be decreased. Grouping, however, can increase the total number maintenance stops. Besides, improvement in optimized plan comes from using opportunistic maintenance scheduling which results in cost savings due to downtime reduction.

Comparison of maintenance cost, production loss cost and availability is shown in Tables 4 and 5 and revealed in Figs. 3, 4 and 5. Figure 3 reveals a slight raise in availability due to optimization of conventional plan in both life patterns roughly 2% due to reducing outage time. This growth would benefit the production unit to be affected less loss of production. Besides, reduction in total cost including maintenance costs and production loss cost is also shown in tables. This has been represented in Fig. 4 in which optimization of maintenance plan, would result in a large reduction in production loss, almost more than 80%. It should be noted that maintenance cost is increased by 5% which is due to increase of number of maintenance activities.

Table 4 Comparison of optimized and conventional plan (Uniform aging)
Full size table
Table 5 Comparison of optimized and conventional plan (Random aging)
Full size table
Fig. 3
figure 3

Availability comparison of conventional and optimized maintenance plans

Full size image
Fig. 4
figure 4

Production loss reduction due to optimization of maintenance plan

Full size image
Fig. 5
figure 5

Comparison of maintenance cost between conventional and optimized plans

Full size image

4.2 Verification and validation

As the final study, the results are compared to reported results in Bohlin and Wärja (2015). The differences between two results are presented in Tables 6 and 7. Negative numbers show that GA result is lower. It is shown there are acceptable Note that due to stochastic nature of input data (life patterns and production scenarios), having zero difference is not expected or even logical. In all cases availability of proposed algorithm is in better condition, while the results of Bohlin and Wärja (2015) have lower maintenance cost.

Table 6 Difference between BCGA and Ref. (Bohlin and Wärja 2015) (Uniform aging)
Full size table
Table 7 Difference between BCGA and Ref. (Bohlin and Wärja 2015) (Random aging)
Full size table

5 Conclusion

In this paper, a proposed genetic algorithm for Gas Turbine maintenance optimization is presented. The main purpose of proposed algorithm is to make the balance between maintenance costs (i.e. direct and indirect) and down time cost while maintaining system availability on predefined level. In order to handle optimization constraints, new repair operators are applied. The results of proposed GA on a SGT-600 case study are discussed. It is shown that compared to conventional maintenance plan, in the optimized maintenance plan availability is increased and meanwhile the total cost is reduced. These improvements are mainly due to grouping of maintenance activities. The proposed algorithm is also verified using a Cplex maintenance optimization (Boschian et al. 2009; Ghosh and Roy 2009; Garg and Deshmukh 2006; Maintenance NRC 2008; R. Corporation; Smith and Hinchcliffe 2004; Bloom 2006).