1 Introduction

This paper adds information to the knowledge of stability and controllability in control theory by means of a study of dispersiveness in nilpotent control systems. Dispersiveness is a dynamic property characterized by the absence of recursiveness, which implies non occurrence of periodic trajectories, mixing, or transitivity. It relates to the orbital Lyapunov stability and parallelizability, being suitable for problems concerning the behavior of close trajectories [7, 8]. The control theoretical formalism of dispersiveness was introduced in [21, 22]. The prolongational limit criterion states that a control system is dispersive if and only if every prolongational limit set is empty. This criterion was used in various studies on dispersive concepts in the control framework. In [20], sufficient conditions for dispersiveness of invariant control systems on the Heisenberg group were presented. In [13], one of the main results shown that a dispersive control affine system (with piecewise constant controls) has absolutely stable semiorbits. The paper [19] proved that a control affine system with piecewise constant controls is dispersive if and only if its associated control flow is parallelizable. One has discovered that the dispersiveness contrasts with the controllability, since the absence of transitivity means non existence of any control set [19].

Invariant control systems on nilpotent Lie groups have received quite some attention in the last forty years, becoming important mathematical models in physics and engineering applications. The main subjects in this framework are controllability, equivalence, classification in low-dimension, optimal control problems, mechanical systems, particle physics, and quantum theory (as references source we mention [1,2,3,4,5,6, 9,10,11, 14, 15, 17, 18, 24] ). The contribution of the present paper consists of furnishing sufficient condition for dispersiveness of the nilpotent control systems, promoting a classification of homogeneous and inhomogeneous systems.

The insight for the main result of this paper came into the planar system \( \dot{x}=\dfrac{\partial }{\partial x_{1}}\left( x\right) +u\left( t\right) \dfrac{\partial }{\partial x_{2}}\left( x\right) \), \(x\in \mathbb {R}^{2}\). This system is dispersive, essentially because the flow of a partial derivative vector is dispersive, and \(\dfrac{\partial }{\partial x_{1}}\) does not depend linearly on \(\dfrac{\partial }{\partial x_{2}}\). In the general case, we consider a simply connected nilpotent Lie group G and an invariant control system

$$\begin{aligned} \dot{x}=X_{0}\left( x\right) +\underset{i=1}{\overset{m}{\sum }}u_{i}\left( t\right) X_{i}\left( x\right) ,\qquad x\in G, \end{aligned}$$

with right invariant vector fields and piecewise constant controls. Every non trivial invariant vector field on a nilpotent Lie group has a dispersive flow [12]. Thus, the nominal invariant system \(\dot{x}=X_{0}\left( x\right) \) is dispersive. By adding the controlled vectors, the problem consists of finding sufficient conditions for the perturbed system to preserve the dispersiveness. The main theorem of this paper shows that the nilpotent control system is dispersive if the drift vector \(X_{0}\) does not belong to the greatest \(ad_{X_{0}}\)-invariant ideal \(\mathcal {L}_{0}\) that contains the controlled vectors \(X_{1},\ldots ,X_{m}\) (Theorem 3.1).

This result can be applied to the studies of stability and controllability. If \(X_{0}\notin \mathcal {L}_{0}\) (inhomogeneous system), the nilpotent control system is dispersive, hence all orbits are absolutely stable and the control flow is parallelizable [13, 19]. The nilpotent control system is dispersive if, and only if, it has no control set [19]. If the intention of adding the controlled vectors is the rise of control sets, the dispersiveness should be broken, which needs \(X_{0}\in \mathcal {L}_{0}\) (homogeneous system). A classical result assures that the strong accessibility rank condition (\(\dim \mathcal {L}_{0}=\dim G\)) is necessary for the controllability of the system [23]. We show that the condition \(X_{0}\in \mathcal {L}_{0}\) is necessary for the existence of a control sets. All these possibilities distinguish the invariant control systems on nilpotent Lie groups

2 Preliminaries

This section contains the basic definitions of invariant control systems on nilpotent Lie groups. We show the properties and differences of dispersiveness and controllability.

Assume that G is a simply connected nilpotent Lie group with the Lie algebra \(\mathfrak {g}\) of the right invariant vector fields on G. It is well-known that G is isomorphic with \(\mathfrak {g}\) via the exponential map \(\exp :\mathfrak {g}\rightarrow G\) and the Baker–Campbell–Hausdorff product in \(\mathfrak {g}\) defined as

$$\begin{aligned} A*B=A+B+R_{2}+\cdots +R_{k} \end{aligned}$$

with \(R_{i}\) given by the Lie brackets of \(A,B\in \mathfrak {g}\), and \( R_{i}\in \mathfrak {g}^{i}\), where \(0=\mathfrak {g}^{k+1}\subset \mathfrak {g} ^{k}\subset \ldots \subset \mathfrak {g}^{2}\subset \mathfrak {g}\) is the descending central series of \(\mathfrak {g}\). This means in particular that \( \exp \) is a global diffeomorfism of manifolds.

For a given right invariant vector field X on G, we consider its associated vector field \(X^{*}\) on \(\mathfrak {g}\) given by

$$\begin{aligned} X^{*}\left( Y\right) =\exp _{*}X\left( Y\right) =d\left( \exp ^{-1}\right) _{\exp \left( Y\right) }\left( X\left( \exp \left( Y\right) \right) \right) ,\qquad Y\in \mathfrak {g}. \end{aligned}$$

The corresponding flow \(X_{t}^{*}\) on \(\mathfrak {g}\) is the map

$$\begin{aligned} X_{t}^{*}\left( Z\right) =tX*Z,\quad \left( t,Z\right) \in \mathbb {R} \times \mathfrak {g}, \end{aligned}$$

and satisfies \(\exp \left( X_{t}^{*}\left( Z\right) \right) =\exp \left( tX\right) \exp \left( Z\right) \). This means that the exponential map is a conjugation between the flow of \(X^{*}\) on \(\mathfrak {g}\) and the flow of X on G.

Assume \(X\ne 0\) and consider the positive integer j such that \(X\in \mathfrak {g}^{j}\) but \(X\notin \mathfrak {g}^{j+1}\). Take a hyperplane \(h_{X}\) of \(\mathfrak {g}\) containing \(\mathfrak {g}^{j+1}\) but not containing X. We know that \(h_{X}\) is a global section for the flow \(X_{t}^{*}\), which means there is a continuous map \(\tau _{X}:\mathfrak {g}\rightarrow \mathbb {R} \) such that for every \(Z\in \mathfrak {g}\), \(X_{t}^{*}\left( Z\right) \in h_{X}\) if, and only if \(t=\tau _{X}\left( Z\right) \) (see [12, Proposition 1]). This means that the flow \(X_{t}^{*}\) on \(\mathfrak {g}\) is parallelizable, or in other words, it is dispersive. By conjugation, it follows that the flow \(\exp \left( tX\right) \) on G is dispersive.

We now consider an invariant control system on G given by

with control range \(U\subset \mathbb {R}^{m}\) and right invariant vector fields \(X_{0},X_{1},...,X_{m}\) in \(\mathfrak {g}\). The solutions \(\varphi \left( t,x,u\right) \) of this system satisfy the cocycle property:

$$\begin{aligned} \varphi \left( t+s,x,u\right) =\varphi \left( t,\varphi \left( s,x,u\right) ,u\cdot s\right) ,\qquad t,s\in \mathbb {R},x\in G,u\in \mathcal {U}_{pc}, \end{aligned}$$

where \(u\cdot s\) is the shift \(u\cdot s\left( \tau \right) =u\left( s+\tau \right) \), and they satisfy the right invariance property:

where 1 is the identity of G.

For every \(x\in G\) and \(T\ge 0\), we define the sets

The sets \(\mathcal {O}^{+}\left( x\right) \), \(\omega ^{+}\left( x\right) \), and \(J^{+}\left( x\right) \) are called respectively positive semi-orbit , positive limit set, and positive prolongational limit set of x.

Definition 2.1

The control system \(\Sigma _{G}\) is said to be dispersive if, for every pair of points \(x,y\in G\) there are neighborhoods \(U_{x}\) of x and \(U_{y}\) of y and a constant \(T>0\) such that \(U_{x}\cap \varphi \left( t,U_{y},u\right) =\emptyset \), for all t and u, with \(\left| t\right| >T\).

In general, a control system is dispersive if, and only if, \(J^{+}\left( x\right) =\emptyset \) for all state x ([21, Theorem 3.1]). In the invariant case, the right invariance property Ri implies

$$\begin{aligned} J^{+}\left( x\right) =\omega ^{+}\left( x\right) =\omega ^{+}\left( 1\right) x, \quad \text { for all }x\in G. \end{aligned}$$

Thus, the invariant control system \(\Sigma _{G}\) is dispersive if, and only if, \(\omega ^{+}\left( 1\right) =\emptyset \) (see [19]). In this case, for each constant control function u, the autonomous differential equation \(\dot{x}=X_{0}\left( x\right) +\sum _{i=1}^{m} u_{i}X_{i}\left( x\right) \) defines a parallelizable dynamical system, and the solution \(\varphi \left( t,x,u\right) \) is orbitally Lyapunov stable with respect to a compatible metric [19].

Definition 2.2

A nonempty set \(D\subset G\) is a control set of the system \(\Sigma _{G}\) if it satisfies the conditions:

  1. (1)

    For each \(x\in D\), there is a control function \(u\in \mathcal {U}_{pc}\) with \(\varphi \left( t,x,u\right) \in D\) for all \(t\ge 0\);

  2. (2)

    \(D\subset \textrm{cl}\left( \mathcal {O}^{+}(x)\right) \) for every \( x\in D\);

  3. (3)

    D is maximal satisfying both the properties \(\left( 1\right) \) and \( \left( 2\right) \).

The control system is called controllable if the whole space G is a control set itself, and \(D\subset \textrm{cl}\left( \mathcal {O} ^{+}(x)\right) \)

By the right invariance property Ri, there are two distinct conditions for the invariant control system on G:

  1. (1)

    The control sets form a partition of G. In this case, the control set \(D_{1}\) containing the identity 1 is a Lie subgroup (\(D_{1}=\textrm{cl} \left( \mathcal {O}^{+}(x)\right) \cap \textrm{cl}\left( \mathcal {O} ^{-}(x)\right) \)), and all other control sets are the right cosets \(D_{1}x\), with \(x\in G\).

  2. (2)

    There is no control set.

The first condition includes the controllable case \(D_{1}=G\). The second condition is called complete uncontrollability, and is equivalent to the dispersiveness ([19, Section 3]). Indeed, if D is a control set, by the conditions \(\left( 1\right) \) and \(\left( 2\right) \) of Definition 2.2, there is a control function \(u\in \mathcal {U}_{pc}\) such that \(D\subset \textrm{cl}\left( \mathcal {O}_{>0}^{+}(\varphi \left( t,x,u\right) )\right) \subset \textrm{cl}\left( \mathcal {O} _{>t}^{+}(x)\right) \) for all \(t\ge 0\). This means that \(D\subset \omega ^{+}\left( x\right) \) for every \(x\in D\).

3 Main results

For the main results of this paper, we consider a fixed nilpotent control system of the form \(\Sigma _{G}\) with drift \(X_{0}\ne 0\). The nominal system \( \dot{\textrm{x}}=X_{0}\left( x\right) \) on G is dispersive. The problem can be viewed from two distinct points of view. By interpreting the control system \(\Sigma _{G}\) as a perturbation of \(X_{0}\) by the vector fields \( X_{1},...,X_{m}\), the problem consists of providing conditions for the system to preserve the dispersiveness. On the other view, since the dispersiveness is opposite to the controllability, the problem consists of providing conditions for breaking the dispersiveness, permitting the rise of control sets.

The strategy is to investigate a conjugate control system on the Lie algebra \(\mathfrak {g}\). The system \(\Sigma _{G}\) on G is associated to the following system on \(\mathfrak {g}\):

The general solution \(\varphi ^{*}\left( t,X,u\right) \) of the system \(\Sigma _{\mathfrak {g}}\) satisfies the relation

In other words, the exponential map is a conjugation of the systems \(\Sigma _{\mathfrak {g}}\) and \(\Sigma _{G}\). As a consequence, the solutions of \(\Sigma _{\mathfrak {g}}\) are completely determined by the solutions through the origin, which means the right invariance property:

We often denote by \(\omega _{*}^{+}\left( X\right) \) and \(J_{*}^{+}\left( X\right) \) respectively the positive limit set and the positive prolongational limit set of \(X\in \mathfrak {g}\). Since the exponential map is a conjugation, the properties \(P^{*}1\) and \(P^{*}2\) imply the following relations:

$$\begin{aligned} \exp \left( J_{*}^{+}\left( X\right) \right) =J^{+}\left( \exp \left( X\right) \right) ,\quad \omega _{*}^{+}\left( X\right) =J_{*}^{+}\left( X\right) ,\quad J_{*}^{+}\left( X\right) =J_{*}^{+}\left( 0\right) *X. \end{aligned}$$

Thus, the control system \(\Sigma _{G}\) is dispersive if, and only if, its associated control system \(\Sigma _{\mathfrak {g}}\) is dispersive, which is equivalent to \( \omega _{*}^{+}\left( 0\right) =\emptyset \).

We now are able to show the main theorem of this paper. Let \(ad_{X}\) denote the adjoint map of \(\mathfrak {g}\), \(ad_{X}\left( Y\right) =\left[ X,Y\right] \) for \(X,Y\in \mathfrak {g}\).

Theorem 3.1

Let \(\mathcal {L}_{0}\subset \mathfrak {g}\) be the Lie subalgebra generated by all vector fields of the form \(ad_{X_{0}}^{k}\left( X_{i}\right) \), with \(k\ge 0\) and \(i=1,\ldots ,m\). The nilpotent control system \(\Sigma _{G}\) is dispersive, if \(X_{0}\notin \mathcal {L}_{0}\).

Proof

For each constant \(u\in U\), define the vector field \(\textrm{X}_{u}=\textrm{X}\left( \cdot ,u\right) \) and set \(\mathcal {F}=\left\{ \textrm{X}_{u}:u\in U\right\} \). The system semigroup \(\mathcal {S}^{*}\) of \(\Sigma _{\mathfrak {g}}\) is given by

$$\begin{aligned} \mathcal {S}^{*}=\left\{ F_{t_{1}}^{1*}\circ \cdots \circ F_{t_{n}}^{n*}:F^{i}\in \mathcal {F},t_{i}\ge 0,n\in \mathbb {N}\right\} . \end{aligned}$$

Since the control functions are piecewise constant, the system semigroup \( \mathcal {S}^{*}\) determines all the trajectories of the control system \(\Sigma _{\mathfrak {g}}\).

For \(u\in \mathcal {U}_{pc}\) and \(t>0\), there are then sequences \( t_{1},...,t_{n}>0\) and \(F^{1},\ldots ,F^{n}\in \mathcal {F}\) such that \( t=\sum _{i=1}^{n}t_{i}\) and

$$\begin{aligned} \varphi ^{*}\left( t,X,u\right) =F_{t_{1}}^{1*}\circ \cdots \circ F_{t_{n}}^{n*}\left( X\right) ,\qquad X\in \mathfrak {g}. \end{aligned}$$

For \(X=0\), we have

$$\begin{aligned} F_{t_{n}}^{n*}\left( 0\right) =t_{n}F^{n}*0=t_{n}F^{n} \end{aligned}$$

and then

$$\begin{aligned} F_{t_{n-1}}^{n-1*}\circ F_{t_{n}}^{n*}\left( 0\right) =t_{n-1}F^{n-1}*t_{n}F^{n}=t_{n-1}F^{n-1}+t_{n}F^{n}+R_{2}^{1}+\cdots +R_{k}^{1} \end{aligned}$$

where \(R_{i}\) is given by the Lie brackets of \(t_{n-1}F^{n-1}\) and \( t_{n}F^{n}\):

$$\begin{aligned} R_{2}^{1}= & \frac{1}{2}\left[ t_{n-1}F^{n-1},t_{n}F^{n}\right] =\frac{ t_{n-1}t_{n}}{2}\left[ F^{n-1},F^{n}\right] \\ R_{3}^{1}= & \frac{1}{12}\left[ t_{n-1}F^{n-1},\left[ t_{n-1}F^{n-1},t_{n}F^{n}\right] \right] -\frac{1}{12}\left[ t_{n}F^{n},\left[ t_{n-1}F^{n-1},t_{n}F^{n}\right] \right] \\= & \frac{t_{n-1}^{2}t_{n}}{12}\left[ F^{n-1},\left[ F^{n-1},F^{n}\right] \right] -\frac{t_{n-1}t_{n}^{2}}{12}\left[ F^{n},\left[ F^{n-1},F^{n}\right] \right] \\ & \vdots \end{aligned}$$

Following by induction, we obtain

where \(R_{i}\left( t,u\right) \) depends on the Lie brackets of \( t_{1}F^{1},\ldots ,t_{n}F^{n}\). Take \(u_{j}^{i}\in U\) such that

$$\begin{aligned} F^{i}=X_{0}+\underset{j=1}{\overset{m}{\sum }}u_{j}^{i}X_{j},\qquad i=1,\ldots ,n. \end{aligned}$$

By the equation \(E_{1}\), we have

where we used \(t=\sum _{i=1}^{n}t_{i}\). We notice that

$$\begin{aligned} \left[ F^{i},F^{k}\right] =\underset{j=1}{\overset{m}{\sum }} u_{j}^{k}ad_{X_{0}}\left( X_{j}\right) -\underset{j=1}{\overset{m}{\sum }} u_{j}^{i}ad_{X_{0}}\left( X_{j}\right) +\underset{j=1}{\overset{m}{\sum }} \underset{l=1}{\overset{m}{\sum }}u_{j}^{i}u_{l}^{k}\left[ X_{j},X_{l}\right] \end{aligned}$$

hence \(\left[ F^{i},F^{k}\right] \in \mathcal {L}_{0}\). Recursively, we have \( R_{l}\left( t,u\right) \in \mathcal {L}_{0}\).

Now, suppose that \(\omega _{*}^{+}\left( 0\right) \) is nonempty and take \(Z\in \omega _{*}^{+}\left( 0\right) \). There are sequences \( t_{n}\rightarrow +\infty \) and \(\left( u_{n}\right) \) such that \(\varphi ^{*}\left( t_{n},0,u_{n}\right) \rightarrow Z\). By the equation \(E_{2}\), we may write

$$\begin{aligned} \varphi ^{*}\left( t_{n},0,u_{n}\right) =t_{n}X_{0}+\sum _{i=1}^{l_{n}} \underset{j=1}{\overset{m}{\sum }}t_{i}^{n}u_{j}^{n,i}X_{j}+ \sum _{l=2}^{k}R_{l}\left( t_{n},u_{n}\right) \end{aligned}$$

where \(t_{n}=\sum _{i=1}^{l_{n}}t_{i}^{n}\). We then have \(\dfrac{1}{t_{n}} \varphi ^{*}\left( t_{n},0,u_{n}\right) \rightarrow 0\), which means

$$\begin{aligned} X_{0}+\sum _{i=1}^{l_{n}}\underset{j=1}{\overset{m}{\sum }}\frac{ t_{i}^{n}u_{j}^{n,i}}{t_{n}}X_{j}+\sum _{l=2}^{k}\frac{1}{t_{n}}R_{l}\left( t_{n},u_{n}\right) \longrightarrow 0. \end{aligned}$$

As \(\sum _{i=1}^{l_{n}}\sum _{j=1}^{m} \frac{ t_{i}^{n}u_{j}^{n,i}}{t_{n}}X_{j}+\sum _{l=2}^{k}\frac{1}{t_{n}}R_{l}\left( t_{n},u_{n}\right) \in \mathcal {L}_{0}\), it follows that \(X_{0}\in \mathcal {L }_{0}\). Thus, \(\omega _{*}^{+}\left( 0\right) \) is empty, if \( X_{0}\notin \mathcal {L}_{0}\). This proves the theorem. \(\square \)

An immediate consequence of Theorem 3.1 is that the condition \( X_{0}\in \mathcal {L}_{0}\) is necessary for the existence of control sets. Recall that the system satisfies the strong accessibility rank condition if \(\dim \mathcal {L}_{0}=\dim \mathfrak {g}\), that is, \(\mathcal {L} _{0}=\mathfrak {g}\) [23]. By assuming a locally path connected control range \(U\subset \mathbb {R}^{m}\), the strong accessibility rank condition is necessary for the controllability of the system \(\Sigma _{G}\) ([23, Theorem 4.10]). The hypothesis from Theorem 3.1 implies the system does not satisfy the strong accessibility rank condition. Clearly, the converse does not hold.

3.1 Classification of nilpotent control systems

We now discuss all possible properties of nilpotent control systems in view of dispersiveness and controllability. It should be remembered that the system \(\Sigma _{G}\) is called homogeneous if the drift \(X_{0}\) is an element of \(\mathcal {L}_{0}\); otherwise, the system is called inhomogeneous. By Theorem 3.1, every inhomogeneous nilpotent control system is dispersive. In the homogeneous case, there are three possibilities:

3.1.1 \(X_{0}\in \mathcal {L}_{0}\) and the system is dispersive

For instance, let \(G=H_{3}\) be the Heisenberg group

$$\begin{aligned} H_{3}=\left\{ \begin{pmatrix} 1 & \quad a & \quad b \\ 0 & \quad 1 & \quad c \\ 0 & \quad 0 & \quad 1 \end{pmatrix} :a,b,c\in \mathbb {R}\right\} , \end{aligned}$$

and consider the invariant control system \(\dot{\textrm{x}}=X_{0}\left( x\right) +u\left( t\right) X_{1}\left( x\right) \), with control range \(U= \left[ 0,1\right] \), and

$$\begin{aligned} X_{0}= \begin{pmatrix} 0 & \quad 2 & \quad 0 \\ 0 & \quad 0 & \quad 0 \\ 0 & \quad 0 & \quad 0 \end{pmatrix} ,\quad X_{1}= \begin{pmatrix} 0 & \quad -1 & \quad 0 \\ 0 & \quad 0 & \quad 0 \\ 0 & \quad 0 & \quad 0 \end{pmatrix} . \end{aligned}$$

We have the fundamental solution

$$\begin{aligned} \varphi \left( t,1,u\right) = \begin{pmatrix} 1 & \quad 2t-\int _{0}^{t}u\left( s\right) \,ds & \quad 0 \\ 0 & \quad 1 & \quad 0 \\ 0 & \quad 0 & \quad 1 \end{pmatrix} . \end{aligned}$$

Since \(t\le 2t-\int _{0}^{t}u\left( s\right) \,ds\), it follows that \( \underset{t\rightarrow +\infty }{\lim }\left( 2t-\int _{0}^{t}u\left( s\right) \,ds\right) =+\infty \). Hence, \(\omega ^{+}\left( 1\right) =\emptyset \).

3.1.2 \(X_{0}\in \mathcal {L}_{0}\) and the system is controllable

This occurs when an invariant control system, with unrestricted controls, satisfies the strong accessibility rank condition.

3.1.3 \(X_{0}\in \mathcal {L}_{0}\) and the system is neither dispersive nor controllable

In this case, there are many control sets, every point of G is contained in a control set, the identity control set \(D_{1}\) is a Lie subgroup of G, and G is foliated by cosets of \(D_{1}\). For example, consider again the invariant control system \(\dot{x}=X_{0}\left( x\right) +u\left( t\right) X_{1}\left( x\right) \) on the Heisenberg group \(H_{3}\) as above, with control range \(U=\left[ 0,3\right] \) instead. We have \(\textrm{X}\left( x,2\right) =0\) for all \(x\in H_{3}\). Hence, every point is stationary with respect to the constant control function \(u\equiv 2\). The control set \(D_{1}\) containing the identity is the Lie subgroup

$$\begin{aligned} D_{1}=\left\{ \begin{pmatrix} 1 & \quad a & \quad 0 \\ 0 & \quad 1 & \quad 0 \\ 0 & \quad 0 & \quad 1 \end{pmatrix} :a\in \mathbb {R}\right\} \end{aligned}$$

and all other control sets are the right cosets \(D_{1}x\), \(x\in H_{3}\).

The dynamics of the non-dispersive nilpotent systems are determined by the Lie subgroups of G. A summary of all cases is expressed in Fig. 1.

Fig. 1
figure 1

Classification of nilpotent control systems

Full size image

3.2 Examples

Next, we present some examples and illustrations for the main result of this paper.

Example 3.1

Let G be the simply connected Lie group with Lie algebra \(\mathfrak {g} =\left\{ \begin{pmatrix} a & x \\ 0 & a \end{pmatrix}:a,x\in \mathbb {R}\right\} \). Consider the invariant control system on G given by

$$\begin{aligned} \begin{array}{l} \dot{x}=X_{0}\left( x\right) +u\left( t\right) X_{1}\left( x\right) ,\qquad x\in G, \\ u\in \mathcal {U}_{pc}=\{u:\mathbb {R}\rightarrow \left[ -1,1\right] :u\text { piecewise constant}\}. \end{array} \end{aligned}$$

where

$$\begin{aligned} X_{0}= \begin{pmatrix} 1 & \quad 2 \\ 0 & \quad 1 \end{pmatrix} ,\hspace{1cm}X_{1}= \begin{pmatrix} 1 & \quad -1 \\ 0 & \quad 1 \end{pmatrix} . \end{aligned}$$

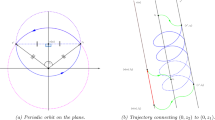
Since \(\mathfrak {g}\) is an abelian Lie algebra, and \(X_{0}\) does not depend linearly on \(X_{1}\), this control system is dispersive, by Theorem 3.1. Figure 2 illustrates the trajectories of the associated control system on the algebra \(\mathfrak {g}\).

Fig. 2
figure 2

Trajectories of the control system \(\dot{X}= \begin{pmatrix} 1 & 2\\ 0 & 1 \end{pmatrix} +u\left( t\right) \begin{pmatrix} 1 & -1\\ 0 & 1 \end{pmatrix} \) on the Lie algebra \(\mathfrak {g}=\left\{ \begin{pmatrix} a & x\\ 0 & a \end{pmatrix} :a,x\in \mathbb {R}\right\} \), with control range \(U=\left[ -1,1\right] \), control function \(u\left( t\right) =\left\{ \begin{array}{l} -1,\qquad \text { if }t\le -1\\ 0\text {, if }-1<t\le 0\\ 1, \qquad \text { if }t>0 \end{array} \right. .\)

Full size image

Example 3.2

Let G be the simply connected Lie group with Lie algebra \(\mathfrak {g} =\left\{ \begin{pmatrix} a & x & y \\ 0 & a & z \\ 0 & 0 & a \end{pmatrix} :a,x,y,z\in \mathbb {R}\right\} \). We have \(\mathfrak {g}^{2}=\left\{ \begin{pmatrix} 0 & 0 & b \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix} :b\in \mathbb {R}\right\} \) and \(\mathfrak {g}^{3}=0\). Consider the invariant control system on G given by

$$\begin{aligned} \begin{array}{l} \dot{x}=X_{0}\left( x\right) +u_{1}\left( t\right) X_{1}\left( x\right) +u_{2}\left( t\right) X_{2}\left( x\right) ,\qquad x\in G, \\ u\in \mathcal {U}_{pc}=\{u:\mathbb {R}\rightarrow \left[ 0,1\right] \times \left[ -1,0\right] :u\text { piecewise constant}\}. \end{array} \end{aligned}$$

where

$$\begin{aligned} X_{0}= \begin{pmatrix} 0 & \quad 1 & \quad 0 \\ 0 & \quad 0 & \quad 1 \\ 0 & \quad 0 & \quad 0 \end{pmatrix} ,\hspace{1cm}X_{1}= \begin{pmatrix} 0 & \quad 2 & \quad -3 \\ 0 & \quad 0 & \quad 1 \\ 0 & \quad 0 & \quad 0 \end{pmatrix} ,\hspace{1cm}X_{2}= \begin{pmatrix} 0 & \quad 4 & \quad 0 \\ 0 & \quad 0 & \quad 2 \\ 0 & \quad 0 & \quad 0 \end{pmatrix} . \end{aligned}$$

It is easily seen that \(X_{0}\notin \mathcal {L}_{0}\). Therefore, this control system is dispersive, by Theorem 3.1. Each 3-dimensional shape \(\mathbb {R}_{a}^{3}=\left\{ \begin{pmatrix} a & x & y \\ 0 & a & z \\ 0 & 0 & a \end{pmatrix} \in \mathfrak {g}:\left( x,y,z\right) \in \mathbb {R}^{3}\right\} \) is invariant by the system. The trajectories of the associated system on the algebra \(\mathfrak {g}\), with respect to a constant control function u, are lines given by

$$\begin{aligned} \varphi ^{*}\left( t,X,u\right) = \begin{pmatrix} a & x+\left( 1+2u_{1}+4u_{2}\right) t & y+\dfrac{z-x+\left( 2z-x-6\right) u_{1}+\left( 4z-2x\right) u_{2}}{2}t \\ 0 & a & z+\left( 1+u_{1}+2u_{2}\right) t \\ 0 & 0 & a \end{pmatrix} . \end{aligned}$$

Concatenations of these trajectories make all the trajectories of the system (see Fig. 3).

Fig. 3
figure 3

Trajectories of the system \( \dot{X}=X_{0}^{*}\left( X\right) +u_{1}\left( t\right) X_{1}^{*}\left( X\right) +u_{2}\left( t\right) X_{2}^{*}\left( X\right) \) on the Lie algebra \(\mathfrak {g}=\left\{ \begin{pmatrix} a & x & y\\ 0 & a & z\\ 0 & 0 & a \end{pmatrix} :a,x,y,z\in \mathbb {R}\right\} \), with \(X_{0}= \begin{pmatrix} 0 & 1 & 0\\ 0 & 0 & 1\\ 0 & 0 & 0 \end{pmatrix} ,X_{1}= \begin{pmatrix} 0 & 2 & -3\\ 0 & 0 & 1\\ 0 & 0 & 0 \end{pmatrix} ,X_{2}= \begin{pmatrix} 0 & 4 & 0\\ 0 & 0 & 2\\ 0 & 0 & 0 \end{pmatrix} \), control range \(U=\left[ 0,1\right] \times \left[ -1,0\right] \), control function \(u\left( t\right) =\left\{ \begin{array}{l} \left( 1,-1\right) ,\text { for }t\le 1\\ \left( 0,0\right) ,\text { for }1<t\le 5\\ \left( 1,0\right) ,\text { for }5<t \end{array} \right. .\)

Full size image

Example 3.3

Consider an invariant control system \(\dot{x}=X_{0}\left( x\right) +\sum _{i=1}^{m} u_{i}\left( t\right) X_{i}\left( x\right) \) on the Heisenberg group \(H_{2n+1}\) of the \(\left( n+2\right) \times \left( n+2\right) \) real matrices

$$\begin{aligned} \begin{pmatrix} 1 & \quad \textrm{v} & \quad c \\ 0 & \quad I_{n} & \quad \textrm{w} \\ 0 & \quad 0 & \quad 1 \end{pmatrix} \end{aligned}$$

where \(\textrm{v}\) is a row vector of length n, \(\textrm{w}\) is a column vector of length n, and \(I_{n}\) is the identity matrix of size n. Take the element E in the Heisenberg algebra \(\mathfrak {h}_{2n+1}\) given by

$$\begin{aligned} E= \begin{pmatrix} 0 & \quad \textrm{0} & \quad 1 \\ 0 & \quad 0_{n} & \quad \textrm{0} \\ 0 & \quad 0 & \quad 0 \end{pmatrix} . \end{aligned}$$

We have \(\mathfrak {h}_{2n+1}^{2}=\left\{ aE:a\in \mathbb {R}\right\} \). By Theorem 3.1, it follows that the control system is dispersive, if the drift \(X_{0}\) is not of the form \(aE+\sum _{i=1}{m} a_{i}X_{i}\). This was previously proved in [20], using an alternative method.

4 Final comments

The paper [19] shows that a necessary and sufficient condition for dispersiveness of an invariant control system is the parallelizability of the control flow. It also assures that the existence of a functional that diverges on the system semigroup is sufficient for dispersiveness. The condition for dispersiveness given in the present paper may be simpler of checking, since it consists of analyzing the linear dependence of the drift vector on the controlled vectors and the Lie brackets of all the vector fields of the system. A dispersive control system has absolutely stable orbits. An open question of this paper asks about the converse theorem: Is the dispersiveness a necessary condition for absolutely stable orbits?