Revisited convexity notions for $L^\infty$ variational problems

Abstract

We address a detailed study of the convexity notions that arise in the study of weak* lower semicontinuity of supremal functionals, as well as those arising by the $L^p$-approximation, as $p \rightarrow +\infty$ of such functionals. Our quest is motivated by the knowledge we have on the analogous integral functionals and aims at establishing a solid groundwork underlying further research in the $L^\infty$ context.

1 Introduction

In the past decades there has been a growing interest towards $L^\infty$ variational problems, partly because of their main applications. Indeed, in the first instance, they appeared empirically in the search for bounds in optimal design problems such as determining the yield set of a polycrystal, or the first failure of a dielectric, in particular, in connection with power-law ($L^p$-) approximation. This latter method has shown to be a quite efficient procedure to describe the mentioned phenomena. In fact, not only it was adopted in physics literature (see [58, 78,79,80]) but, later on, a rigorous mathematical justification was provided, see [1, 12, 23, 25,26,27,28,29,30, 33, 39, 48, 53, 55, 65, 70, 74].

Variational models in $L^\infty$ have also emerged in connection with Lipschitz extension problems [24, 47, 61], or more general minimization problems (in these frameworks absolute minimizers are the appropriate solutions to look for, see [39, Definition 1.1] and [60]). The $L^\infty$ setting can also be used to provide an energy formulation of non linear partial differential equations (see for, by now, classical results [6,7,8,9], the more recent contributions, [14, 18] and the higher order problems contained in [10, 40, 41] and the bibliography contained therein).

Since then, a wide literature has been developed, also in the non-Euclidean setting, starting from [61] and its quoting literature, in connection with Dirichlet forms, pre-fractal sets, Finsler structures, etc., see [36, 37, 56, 57, 66], among a much wider scientific production.

It is worth recalling that these mathematical models play also an important role in the context of optimal transport, game theory, partial differential equations, non-local problems also in connection with artificial intelligence problems, etc., see e.g. [15, 31, 34, 35, 52, 67, 68].

Many of the above models are formulated in terms of what is called a supremal functional

$$\begin{aligned} F(u,O)={\text {*}}{ess\,sup}_{x\in O} f(x, u(x), D u(x)),\ O\subseteq \Omega \text { open },\ u\in W^{1,\infty }(O;\mathbb {R}^N)\nonumber \\ \end{aligned}$$

(1.1)

where $\Omega$ is an open and bounded set in $\mathbb {R}^n$ and $f:\Omega \times \mathbb {R}^n\times \mathbb {R}^{N\times n}\longrightarrow \mathbb {R}$ is a Carathéodory function. We call the function f supremand. For both the minimization and the $L^p$- approximation, a crucial property which emerges in the application of the Direct Methods of the Calculus of Variations is the lower semicontinuity with respect to the weak* topology of $W^{1,\infty }$ of the functional F in (1.1). Consequently it is crucial to look for necessary and sufficient conditions on the supremand f for this lower semicontinuity. These conditions reflect, as in the integral setting, on appropriate convexity notions of $f(x, u, \cdot )$ (see, e.g. [2, 21] among a wider literature), rather than the convexity of the functional F. For what concerns the convexity properties inherited by F, we refer to [56]. The main goal of our paper is to develop a deep understanding of the convexity notions of the supremands f. We trust the present paper provides a clear baseline to researchers dealing with problems in the field, as it gathers many properties and results dispersed in the literature, clarifying some features of the concepts under study, adding also novel insights contributing to a unified approach to the study of supremal problems.

Indeed, in the seminal paper by Barron et al. [21], a necessary and sufficient condition on the supremand f for the sequential weak* lower semicontinuity of $F(\cdot ,\Omega )$ was found. The condition was named strong Morrey quasiconvexity and it is renamed in Definition 3.1 as strong BJW-quasi-level convexity in honor to Barron, Jensen, and Wang. To facilitate checking this condition in applications, necessary and sufficient conditions for strong BJW-quasi-level convexity were also introduced. Namely, the sufficient condition of poly-level convexity and the necessary conditions of weak BJW-quasi-level convexity and rank-one level convexity. It is also worth taking into account that problem (1.1) was already interesting in the scalar setting, i.e. $n=1$ or $N=1$, with the necessary and sufficient condition for the sequential weak* lower semicontinuity of $F(\cdot ,\Omega )$ on the supremand f detected by [14, 19, 20] and known in the optimization literature as quasiconvexity and later on named level convexity by [2, 72, 73], and used for the supremal representation in [16, 17, 38].

Broadly speaking, one has the following

$$\begin{aligned} \begin{array}{c}f \text { level convex }\Rightarrow \ f\text { poly-level convex}\Rightarrow \ f\text { strong BJW-quasi-level convex} \\ \Rightarrow \ f\text { weak BJW-quasi-level convex}\Rightarrow \ f\text { rank-one level convex}.\end{array} \end{aligned}$$

If one is acquainted with the Direct Method of the Calculus of Variations in the context of integral minimization and the related theory for vectorial problems, the previous chain of implications seems familiar and natural. As we will see, the specificity of supremal problems brings into play new features and, even the above implications shall be read with care under appropriate additional assumptions. Besides, the treatment of minimization problems through $L^p$-approximation, cf. [4, 5, 39, 74], brought into play other relevant conditions.

Another target of this work consists of a full revision of these later concepts, unveiling new perspectives on the subject. We also believe that this is a fundamental step to further proceed to our ultimate goal, that we postpone for a future work, which is to extend to the vectorial setting the previous work of the authors [75], namely, to provide conditions to ensure the existence of minimizers when the supremand f fails to satisfy the strong BJW-quasi-level convexity and the Direct Methods cannot be applied.

Next, we describe how the paper is organized, as well as the ideas and questions that have driven our analysis. We note that, with the exception of Appendix B, in all our work we restrict to supremands depending on the gradient variable only. This allows to distinguish whether additional assumptions that one finds in the literature are intrinsic, or not, to the property under study.

Section 2 is devoted to the integral notion of quasiconvexity (see Definition 2.1) which is the fundamental property associated with the sequential weak* lower semicontinuity in $W^{1,\infty }(\Omega ;\mathbb {R}^N)$ of functionals of the form

$$\begin{aligned} I(u):=\int _\Omega f(Du(x))\,dx,\quad u\in u_0+W_0^{1,\infty }(\Omega ;\mathbb {R}^N) \end{aligned}$$

for a given function $f:\mathbb {R}^{N\times n}\rightarrow \mathbb {R}.$ Essentially, we recall existing results and, despite the different context, this will be useful in the subsequent sections. In order to formulate our results with the greatest possible generality in the later sections, we refer to the presentation of the forthcoming monograph [50], while in a slightly more restrictive setting the same statements could be made by referring to [43]. Let us highlight, that, in Proposition 2.3, we establish a new characterization of quasiconvexity, motivated by the supremal notion of strong BJW-quasi-level convexity treated later on, in Sect. 3.

In Sect. 3 we consider in detail the notions introduced by Barron, Jensen, and Wang, previously mentioned. Several of the questions that we address in this section are motivated by properties that are well known in the integral setting. In particular, we observe that the convexity notions emerging in the integral setting inherit also the lower semicontinuity, while, as we will see in Proposition 3.5, among the notions considered in Sect. 3 for the supremal setting, only the strong BJW-quasi-level convexity encodes this property.

Another question that led our investigation was, whether in the case the supremand f is strong BJW-quasi-level convex and the boundary condition $u_0$ is an affine map, $u_0$ is also a minimizer for the functional $F(u,\Omega )$ in (1.1). The analogue to this in the integral setting is well known and amounts to the fact that the quasiconvexity notion is independent of the domain where the integral is considered. Therefore, we are led to the question of the independence of domain for strong BJW-quasi-level convex functions. If we return to the starting point of this discussion, our question is precisely equivalent to the independence of domain for weak BJW-quasi-level convex functions. While for weak BJW-quasi-level convexity we obtained a positive answer, cf. Proposition 3.7, and thus, we get that affine boundary conditions are minimizers to the problem described above, cf. Corollary 3.8, the independence of domain for strong BJW-quasi-level convexity was only ensured under some conditions on the sets, in particular, its convexity, see Proposition 3.10. We note that the result on independence of the domain in the definition of strong BJW-quasi-level convexity has been obtained by exploiting the lower semicontinuity of the related supremal functional, requiring to adapt results from [21]. This is left to Appendix A. We just observe here that the independence of the domain in the convexity notions combines well with the fact that, in the nonhomogeneous setting, the supremal representation in terms of suitably ‘convex’ densities requires weakly* lower semicontinuity in every domain [38, 71, 72, see counterexamples] and the bibliography contained therein.

A deeper understanding of minimization of integral functionals shows that the condition which is intrinsic to the weak* lower semicontinuity is the equivalent condition to quasiconvexity which is given by (2.1), but testing on periodic functions. This is another direction that warrants investigation: whether in the notion of strong BJW-quasi-level convexity, periodic functions can be considered. At this point, our analysis is not conclusive, motivating us to introduce the concept of periodic-weak BJW-quasi-level convexity.

Still in Sect. 3, we investigate how do the notions of convexity introduced in this section relate to each other. Our aim is to obtain an exhaustive study of these relations, therefore, whenever possible, we also provide counter-examples and we end the section with a list of the relations for which a satisfactory answer was not obtained. Also a proof of a characterization in terms of supremal Jensen’s inequality involving probability measures under very mild assumptions is given in Appendix C.

In Sect. 4, our interest is to relate strong BJW-quasi-level convexity with the convexity concepts raised by power-law approximation, “namely $L^p$-approximation as $p \rightarrow +\infty$”, not only as a way to deal with lower semicontinuity of $L^\infty$-variational problems, but also in order to rigorously obtain the latter ones by means of variational convergence emanating from $L^p$- type norm functionals. More precisely, we relate strong BJW-quasi-level convexity with the notions of $\textrm{curl}_{(p>1)}$-Young quasiconvexity, $\textrm{curl}$-Young quasiconvexity, and $\textrm{curl}-\infty$ quasiconvexity, cf. Definition 4.2, not necessarily under these names in the literature. As in Sect. 3, we also provide some counterexamples and we list some open questions of interest. In particular, we will see that coercivity always plays a crucial role. To this end, we start recalling the counterexamples to representation of weakly* lower semicontinuous supremal functionals, depending on gradients, in terms of non-homogeneous level convex densities (of the form $f(x,\xi )$) already in the scalar case, see [72] and the bibliography contained therein. Thus it arises naturally the question of comparing the notions providing sufficient conditions for representation of lower semicontinuous supremal functionals under coercivity hypotheses. Finally, due to the deep connections with Young measures, appearing already in some definitions, we will provide in Appendix B a new proof of sufficiency of $\textrm{curl}$-Young quasiconvexity for weak* lower semicontinuity of supremal functionals (also in the nonhomogeneous setting).

For the sake of completeness, we consider, in Sect. 5, the interplay between the convexity notions arising in the integral and the supremal settings.

We will leave for further studies the comparison with supremal convexity notions using the duality theory in Convex analysis as in [22] and [71] or making use of the intrinsic distances as, e.g., in [54] and [56], or rephrasing the notions exploiting the connections with variational unbounded integral functionals and/or differential inclusions, see [68, 74, 81].

1.1 Notation

In the sequel we will make use of the following notation

• We denote by Q the unit cube of ${\mathbb {R}}^n$ centered at the origin with side length 1, i.e. $Q:= \left( -\frac{1}{2}, \frac{1}{2}\right) ^n$.

• By ${\mathcal {L}}^n$ we denote the n-dimensional Lebesgue measure.

• For any set $E\subset {\mathbb {R}}^d$, $\chi _E$ denotes its characteristic function, i.e. $\chi _E(x)=\left\{ \begin{array}{ll} 1 & \hbox { if } x \in E,\\ 0 & \hbox {otherwise.}\end{array}\right.$

• For every open set $\Omega \subset {\mathbb {R}}^n$ we denote by $W^{1,\infty }_0(\Omega ;{\mathbb {R}}^N)$ as in [43, Definition 12.9 (iv)], the set $W^{1,\infty }(\Omega ;{\mathbb {R}}^N)\cap W^{1,1}_0(\Omega ;{\mathbb {R}}^N)$, where the latter set is the $W^{1,1}$-closure of $C^\infty _c(\Omega ;{\mathbb {R}}^N)$, recalling that when $\Omega$ is a bounded, connected and with Lipschitz boundary set, $W^{1,\infty }_0(\Omega ;{\mathbb {R}}^N)$ coincides with the set of (globally) Lipschitz maps wich are null at the boundary $\partial \Omega$, i.e.

  $$\begin{aligned} \textrm{Lip}_0(\Omega ;\mathbb {R}^N):=\left\{ \varphi :\Omega \longrightarrow \mathbb {R}^N\Big |\ \varphi \text { is Lipschitz in }\overline{\Omega }\text { and }\varphi =0 \text { on the boundary}\right\} . \end{aligned}$$

• For any cube $C\subset {\mathbb {R}}^n$, by $W^{1,\infty }_\textrm{per}(C;{\mathbb {R}}^N)$ we denote the subset of $W^{1,\infty }({\mathbb {R}}^n;{\mathbb {R}}^N)$, made by C-periodic functions.

2 A review of the integral notion of quasiconvexity and of some of its properties

We recall the definition of quasiconvex functions, fundamental in the minimization of vectorial integral functionals. A classic reference on this subject is the monograph [43]. In the sequel we sometimes refer to the forthcoming monograph [50] where the quasiconvexity notion is given without requiring a priori the local boundedness of the function. This shall be useful below when dealing with curl-$\infty$ quasiconvex functions. We call the attention for the new characterization of quasiconvexity established in Proposition 2.3.

Definition 2.1

A Borel measurable function $g:{\mathbb {R}}^{N \times n} \rightarrow {\mathbb {R}}$ is called quasiconvex if

$$\begin{aligned} g(\xi )\le \int _Q g(\xi +D \varphi (x))\,dx \end{aligned}$$

(2.1)

for every $\xi \in \mathbb {R}^{N\times n}$ and for every $\varphi \in W^{1,\infty }_0(Q;{\mathbb {R}}^N)$, where $Q:= \left( -\frac{1}{2}, \frac{1}{2}\right) ^n$.

Remark 2.2

• (i) In the definition of quasiconvexity, one can also consider functions taking values in $[-\infty ,\infty ]$ but many properties may fail in this case. (See [13].)

• (ii) In the forthcoming monograph [50] it has been shown that if g is real valued then it is locally-Lipschitz, i.e. for every $\xi \in {\mathbb {R}}^{N\times n}$ and every $R>0$, there exists a constant $L \equiv L(\xi , R)$ such that

  $$\begin{aligned} |g(\zeta )-g(\zeta ')|\le L |\zeta -\zeta '| \hbox { for every }\zeta , \zeta ' \in B_R(\xi ) \end{aligned}$$

  hence continuous and locally bounded, thus, a posteriori Definition 2.1 coincides with [43, Definition 5.1, (ii)].

• (iii) In (2.1) the cube $Q:=\left( -\frac{1}{2},\frac{1}{2}\right) ^n$ can be replaced by any bounded open set $\Omega$ (averaging the integral in (2.1) by the measure of $\Omega$), cf. [43, Proposition 5.11]. On the other hand in [50] it has been proven that Definition 2.1 can be equivalently given by testing with functions $\varphi \in \textrm{Lip}_0(O;\mathbb {R}^N)$ only requiring the set O to be open and bounded, with ${\mathcal {L}}^n(\partial O)=0$..

• (iv) If g is real valued (then it is locally bounded) one can replace in the definition of quasiconvexity, via reverse Fatou’s lemma, $W^{1,\infty }_0$ by $C_c^\infty$.

• (v) We can replace $W^{1,\infty }_0(Q;{\mathbb {R}}^N)$ by $W^{1,\infty }_\textrm{per}(Q;{\mathbb {R}}^N)$ as well as, by $\big \{\varphi \in W^{1,\infty }_\mathrm{{loc}}(\mathbb R^n;{\mathbb {R}}^N)|\ D\varphi \text { is } Q\hbox {-periodic and }\int _Q D\varphi (x)\,dx=0\big \}$. Moreover, the unit cube Q can be replaced by any cube, provided that the integral in (2.1) is averaged by the measure of the cube.

• (vi) The notion of quasiconvexity coincides with the $\mathcal {A}$-quasiconvexity (cf. [51, Remark 3.3]) in the case $\mathcal {A}=\textrm{curl}$.

Next we provide a new characterization of quasiconvexity, stemming from the results from [21], in particular Proposition 2.4. We present the proof for the readers’ convenience.

Proposition 2.3

Let $g:\mathbb {R}^{N\times n}\longrightarrow \mathbb {R}$ be a Borel measurable function. Consider the following condition

$$\begin{aligned} \forall \ \varepsilon>0\ \forall \ \xi \in \mathbb {R}^{N\times n}\ \forall \ K>0\ \exists \ \delta =\delta (\varepsilon , K,\xi )>0: \end{aligned}$$

$$\begin{aligned} \left. \begin{array}{l}\varphi \in W^{1,\infty }(Q;\mathbb {R}^N)\\ ||D\varphi ||_{L^\infty (Q)}\le K\\ \max _{x\in \partial Q}|\varphi (x)|\le \delta \end{array}\right\} \Longrightarrow g(\xi )\le \int _Q g(\xi +D\varphi (x))\,dx+\varepsilon . \end{aligned}$$

(2.2)

One has that g is quasiconvex if and only if g satisfies (2.2).

Proof

Quasiconvexity follows immediately from (2.2) applied to test functions $\varphi \in W^{1,\infty }_0(Q;\mathbb {R}^N)$, letting $\varepsilon \rightarrow 0$.

To prove the reverse implication let $\varepsilon >0$, $\xi \in \mathbb {R}^{N\times n}$ and $K>0$ be arbitrary. Let $\varphi \in W^{1,\infty }(Q;\mathbb {R}^N)$ be such that $\Vert D \varphi \Vert _{L^\infty (Q)}\le K$ and $\max _{x \in \partial Q}|\varphi (x)|\le \delta$ for some $\delta$ to be chosen later. Then, having in mind that, by the Lipschitz continuity of $\varphi$ in Q, $|\varphi (y)-\varphi (x)|\le K|y-x|$ for any $x\in \partial Q$ and $y\in Q$, one has $|\varphi (y)| \le 2 \delta$ for any $y =(y_1,\dots , y_n) \in Q$, with $|y_i | \ge 1/2 - \eta$ for some $1 \le i \le n$, provided that $\eta \le \frac{\delta }{K}$.

Now, given $\eta >0$ small, let $\psi _\eta \in C^1({\mathbb {R}}^n)$ be such that $0\le \psi _\eta (y)\le 1$ for all $y\in {\mathbb {R}}^n$, $\psi _\eta \equiv 1$ for $y \in (1 -\eta )Q$, $\psi _\eta \equiv 0$ for $y \not \in Q$, and $|D\psi _\eta (y)|< \frac{c_0}{\eta }$ for every $y\in \mathbb {R}^n$ for some constant $c_0$ independent of $\eta$.

The quasiconvexity of g entails that

$$\begin{aligned} g(\xi )&\le \int _Q g(\xi +D(\psi _\eta \varphi )(x))\,dx\\&= \int _Q g(\xi +D \varphi (x))\,dx + \int _{Q\setminus (1-\eta )Q} (g(\xi + D(\psi _\eta \varphi )(x))-g(\xi +D\varphi (x)))\,dx. \end{aligned}$$

To conclude the proof it suffices to estimate the latter integral on the right hand side by $\varepsilon$. To achieve this, observe that, since g is quasiconvex, by (ii) in Remark 2.2, it is locally Lipschitz, thus, in particular, choosing $R:=K(1+4\,c_0)$, there exists a constant L depending on $\xi$ and K above such that

$$\begin{aligned} |g(\zeta )- g(\zeta ')|\le L |\zeta -\zeta '| \hbox { for every } \zeta , \zeta ' \in B_R(\xi ). \end{aligned}$$

(2.3)

Observe that $\Vert D \varphi \Vert _{L^\infty (Q)}\le K\le R$ and, if we take $\eta =\frac{\delta }{2\, K}$, then $\Vert D(\psi _\eta \varphi )\Vert _{L^\infty (Q)}\le (2 c_0+1)K\le R$. Therefore, by (2.3), and observing that $\mathcal {L}^n(Q\setminus (1-\eta )Q)\le c_1\eta$, for some constant $c_1$ only depending on the dimension n, one gets

$$\begin{aligned}&\int _{Q\setminus (1-\eta )Q}\left| g(\xi + D(\psi _\eta \varphi )(x))-g(\xi + D \varphi (x)) \right| \,dx\\&\quad \le L \int _{Q\setminus (1-\eta )Q} (|D \varphi (x)| + |D \psi _\eta (x)|\,|\varphi (x)|)\,dx\\&\quad \le L (K c_1\eta + 2c_0c_1 \delta )= c_1L( \tfrac{1}{2} + 2c_0) \delta . \end{aligned}$$

Then it suffices to take $\delta$ sufficiently small so that the last term is smaller than $\varepsilon$. $\square$

Definition 2.4

Let $g:{\mathbb {R}}^{N \times n} \rightarrow \mathbb {R}$ be a Borel measurable function. The greatest quasiconvex function below g is called the quasiconvex envelope of g and it is denoted by ${\mathcal {Q}} g$, i.e. ${\mathcal {Q}} g:{\mathbb {R}}^{N\times n}\rightarrow [-\infty ,+\infty )$ is such that

$$\begin{aligned} {\mathcal {Q}} g(\xi ):=\sup \left\{ h(\xi )\Big |\ h:{\mathbb {R}}^{N \times n} \rightarrow {\mathbb {R}},\ h(\xi ) \le g(\xi ) \text { for all }\xi \in {\mathbb {R}}^{N \times n},\ h \hbox { is quasiconvex}\right\} . \end{aligned}$$

Remark 2.5

Note that, ${\mathcal {Q}} g$ is well defined and it is a Borel measurable function, see [43].

The following lemma will be useful in the remaining part of this paper. It relies on the notion of strong quasiconvexity introduced in [50]. Indeed, a Borel function $f: \mathbb R^{N\times n}\rightarrow {\mathbb {R}}$ is called strongly quasiconvex at $\xi \in {\mathbb {R}}^{N\times n}$ if

$$\begin{aligned} f\left( \xi + \int _C D \varphi (x) \,dx\right) \le \int _C f(\xi +D \varphi (x))\,dx \end{aligned}$$

for every unit cube $C \subset {\mathbb {R}}^N$ and for all functions $\varphi \in W^{1,\infty }_\textrm{loc}( {\mathbb {R}}^N; {\mathbb {R}}^n )$ with $D \varphi$ C-periodic. The function f is called strongly quasiconvex if it is strongly quasiconvex at every $\xi \in {\mathbb {R}}^{N \times n}$.

Lemma 2.6

Let $g:\mathbb {R}^{N\times n}\longrightarrow \mathbb {R}$ be a Borel measurable function. Then, for every $\xi \in \mathbb {R}^{N\times n}$, one has

$$\begin{aligned} {\mathcal {Q}} g(\xi )&= \inf \left\{ \int _Q g(\xi +D \varphi (x))\,dx: \varphi \in W^{1,\infty }_\textrm{loc}({\mathbb {R}}^n;{\mathbb {R}}^N),\hbox { with }D\varphi \ Q\hbox {-periodic and }\right. \\&\quad \quad \quad \quad \left. \int _QD \varphi (x)\,dx=0\right\} \\&= \inf \left\{ \int _Q g(\xi +D \varphi (x))\,dx: \varphi \in W^{1,\infty }_\textrm{per}( Q;{\mathbb {R}}^N)\right\} \\&= \inf \left\{ \int _Q g(\xi +D \varphi (x))\,dx: \varphi \in W^{1,\infty }_0( Q;{\mathbb {R}}^N)\right\} \\&= \inf \left\{ \frac{1}{{\mathcal {L}}^n(\Omega )}\int _\Omega g(\xi +D \varphi (x))\,dx: \varphi \in W^{1,\infty }_0(\Omega ;\mathbb R^N)\right\} \end{aligned}$$

if $\Omega \subseteq \mathbb {R}^n$ is open and bounded with $\mathcal L^n(\partial \Omega )=0$.

Proof

Explicit constructions together with Riemann-Lebesgue lemma allow to prove that any quasiconvex function is strongly quasiconvex (details about this proof can be found in the forthcoming monograph [50]) hence the quasiconvex envelope is strongly quasiconvex, and thus

$$\begin{aligned} {\mathcal {Q}} g(\xi )&\le \inf \left\{ \int _Q \mathcal Qg(\xi +D \varphi (x))\,dx: \varphi \in W^{1,\infty }_\textrm{loc}({\mathbb {R}}^n;{\mathbb {R}}^N),\hbox { with }D\varphi \ Q\hbox {-periodic and }\right. \\&\quad \quad \quad \quad \left. \int _QD \varphi (x)\,dx=0\right\} \\&\le \inf \left\{ \int _Q g(\xi +D \varphi (x))\,dx: \varphi \in W^{1,\infty }_\textrm{loc}({\mathbb {R}}^n;{\mathbb {R}}^N),\hbox { with }D\varphi \ Q\hbox {-periodic and }\right. \\&\quad \quad \quad \quad \left. \int _QD \varphi (x)\,dx=0\right\} \\&\le \inf \left\{ \int _Q g(\xi +D \varphi (x))\,dx: \varphi \in W^{1,\infty }_\textrm{per}( Q;{\mathbb {R}}^N)\right\} \\&\le \inf \left\{ \int _Q g(\xi +D \varphi (x))\,dx: \varphi \in W^{1,\infty }_0( Q;{\mathbb {R}}^N)\right\} \\&\le {\mathcal {Q}} g(\xi ), \end{aligned}$$

where in the last inequality we argue as in [43]. Thus all the formulas above coincide. Moreover, in view of Remark 2.2 (iii) exploiting similar arguments as in the chain of inequalities above, and the invariance of the domain, proven in [43], $Q g(\xi )$ also coincides with

$$\begin{aligned} \inf \left\{ \frac{1}{{\mathcal {L}}^n(\Omega )}\int _\Omega g(\xi +D \varphi (x))\,dx: \varphi \in W^{1,\infty }_0(\Omega ;{\mathbb {R}}^N)\right\} \end{aligned}$$

and with

$$\begin{aligned} \inf \left\{ \frac{1}{{\mathcal {L}}^n(\Omega )}\int _\Omega g(\xi +D \varphi (x))\,dx: \varphi \in \textrm{Lip}_0( \Omega ;{\mathbb {R}}^N)\right\} \end{aligned}$$

provided $\Omega \subseteq \mathbb {R}^n$ is open and bounded with ${\mathcal {L}}^n(\partial \Omega )=0$ (see [50]). $\square$

The following definition has been introduced by Ball and Murat (cf. [13, Definition 2.1]).

Definition 2.7

Let $1\le p \le \infty$. A Borel function $g: {\mathbb {R}}^{N \times n}\rightarrow {\mathbb {R}}$ is $W^{1,p}$-quasiconvex at $\xi \in {\mathbb {R}}^{N \times n}$ if

$$\begin{aligned} g(\xi ) \le \int _Q g(\xi + D \varphi (x))\,dx \end{aligned}$$

for every $\varphi \in W^{1,p}_0(Q;{\mathbb {R}}^{N})$. We say that g is $W^{1,p}$-quasiconvex if it is $W^{1,p}$-quasiconvex at every $\xi \in {\mathbb {R}}^{N\times n}$.

Remark 2.8

• (i) Note that $W^{1,\infty }$-quasiconvexity is the quasiconvexity introduced in Definition 2.1.

• (ii) The above definition can be given also when the range of g is $[-\infty ,+\infty ]$.

• (iii) The set Q can be replaced by any bounded open set $\Omega$ such that ${\mathcal {L}}^n(\partial \Omega )=0$ replacing the integral by an averaged integral in $\Omega$.

• (iv) If g is $W^{1,p}$-quasiconvex for some $1 \le p \le +\infty$, then it is $W^{1,q}$-quasiconvex for all $p \le q \le +\infty$ (cf. [13, Remark 2.2]). Thus quasiconvexity and $W^{1,1}$-quasiconvexity are, respectively, the weakest and the strongest condition.

• (v) If $g: {\mathbb {R}}^{N\times n} \rightarrow \mathbb {R}$ and satisfies the following growth condition: there exist $C>0$ and $1\le p<+\infty$, such that

  $$\begin{aligned} g(\eta )\le C(1+ |\eta |^p) \end{aligned}$$

  (2.4)

  for all $\eta \in {\mathbb {R}}^{N\times n}$, then g is $W^{1,p}$-quasiconvex at $\xi$ if and only if for every bounded and open set $\Omega$,

  $$\begin{aligned} g(\xi )\le \frac{1}{{\mathcal {L}}^{n}(\Omega )}\int _\Omega g(\xi + D \varphi (x))\,dx \end{aligned}$$

  for every $\varphi \in C^\infty _c(\Omega ;{\mathbb {R}}^{N})$.

• (vi) Also, if g is $W^{1,p}$-quasiconvex and satisfies the following coercivity condition: there exist $C' > 0$, and $1< p < +\infty$ such that

  $$\begin{aligned} g(\eta ) \ge C'(|\eta |^p -1) \end{aligned}$$

  for all $\eta \in {\mathbb {R}}^{N\times n}$, then g is $W^{1,1}$-quasiconvex.

The previous remark allows to state, in the spirit of the characterizations obtained in Lemma 2.6 for the quasiconvex envelope of a function, an alternative formula in terms of $W^{1,p}_0(\Omega ;{\mathbb {R}}^N)$ test functions.

Lemma 2.9

Let $1 \le p < +\infty ,$ and let $g:\mathbb {R}^{N\times n}\longrightarrow \mathbb {R}$ be a Borel measurable function satisfying the growth condition (2.4). Let $\Omega$ be open, bounded with $\mathcal {L}^n(\partial \Omega )=0$. Then

$$\begin{aligned} {\mathcal {Q}} g(\xi ) = \inf \left\{ \frac{1}{\mathcal L^n(\Omega )}\int _\Omega g(\xi +D \varphi (x))\,dx: \varphi \in W^{1,p}_0( \Omega ;{\mathbb {R}}^N)\right\} . \end{aligned}$$

Furthermore, under the extra assumption that g is upper semicontinuous, one has

$$\begin{aligned} {\mathcal {Q}} g(\xi ) = \inf \left\{ \int _Q g(\xi +D \varphi (x))\,dx: \varphi \in W^{1,p}_\textrm{per}(Q;{\mathbb {R}}^N)\right\} . \end{aligned}$$

Proof

The first statement follows from the previous remark, observing that under our assumptions ${\mathcal {Q}} g$ is Borel measurable, quasiconvex and satisfies the same growth condition as g. Indeed, by Remark 2.8 (v) and then by (iii) one has

$$\begin{aligned} {\mathcal {Q}} g(\xi )&\le \inf \left\{ \frac{1}{\mathcal {L}^n(\Omega )}\int _\Omega \mathcal Qg(\xi +D \varphi (x))\,dx: \varphi \in W^{1,p}_0(\Omega ;{\mathbb {R}}^N)\right\} \\&\le \inf \left\{ \frac{1}{\mathcal {L}^n(\Omega )}\int _\Omega g(\xi +D \varphi (x))\,dx: \varphi \in W^{1,p}_0( \Omega ;{\mathbb {R}}^N)\right\} \\&\le \inf \left\{ \frac{1}{\mathcal {L}^n(\Omega )}\int _\Omega g(\xi +D \varphi (x))\,dx: \varphi \in W^{1,\infty }_0( \Omega ;{\mathbb {R}}^N)\right\} \\&= \mathcal Qg(\xi ) \end{aligned}$$

invoking the characterization of ${\mathcal {Q}} g$ provided in Lemma 2.6 to obtain the last identity.

For the second statement, we start by observing that one inequality follows from the fact that $W^{1,\infty }_\textrm{per}(Q;\mathbb {R}^N)$ $\subseteq$ $W^{1,p}_\textrm{per}(Q;\mathbb {R}^N)$ and by the characterization of ${\mathcal {Q}} g$ provided by Lemma 2.6. For the other inequality, consider for a fixed function $\varphi \in W^{1,p}_\textrm{per}(Q;{\mathbb {R}}^N)$, the convolution with a sequence of mollifiers $(\rho _\varepsilon )_{\varepsilon }$, defined as $\rho _\varepsilon (x):= \frac{1}{\varepsilon ^n}\rho \Big (\frac{x}{\varepsilon }\Big ),$ where

$$\begin{aligned} \rho \in C_c^\infty ({\mathbb {R}}^n), \quad \textrm{supp} \rho \subset B_1,\quad \rho \ge 0,\quad \rho (-x)=\varrho (x), \quad \text {and} \quad \int _{B_1} \rho (x)\,d x=1, \end{aligned}$$

denoting $B_1$ the unit ball in ${\mathbb {R}}^n$ centered at the origin. Note that $\varphi *\rho _\varepsilon$ is still a periodic function and moreover it belongs to $W^{1,\infty }(\mathbb {R}^n;\mathbb {R}^N)$. Then by the quasiconvexity of ${\mathcal {Q}} g$, one has

$$\begin{aligned} {\mathcal {Q}} g(\xi )\le \limsup _{\varepsilon \rightarrow 0} \int _Q g(\xi +D(\varphi *\rho _\varepsilon )(x))\,dx. \end{aligned}$$

Note that, by (2.4), the right-hand side in the previous inequality is bounded. This allows to use the reversed Fatou’s lemma and get

$$\begin{aligned} {\mathcal {Q}} g(\xi )\le \int _Q \limsup _{\varepsilon \rightarrow 0} g(\xi +D(\varphi *\rho _\varepsilon )(x))\,dx. \end{aligned}$$

Finally, the upper semicontinuity assumption ensures that the integrand converges pointwise to $g(\xi +D\varphi (x))$, as desired. $\square$

3 On some convexity notions for functions and sequential weak* lower semicontinuity of $L^\infty$ functionals

In this section we revisit some convexity notions previously introduced by Barron et al. [21] in the context of $L^\infty$ functionals. The notions of strong (respectively weak) Morrey quasiconvexity are renamed to strong (respectively weak) BJW-quasi-level convexity in honour to Barron, Jensen, and Wang, while the the notions of polyquasiconvexity and rank-one quasiconvexity are renamed to poly-level convexity and rank-one level convexity as previously done in [4]. These notions are related to the problem of existence of minimizers for supremal functionals and to the not fully understood notion of quasiconvexity for unbounded integral functionals (see [21, Lemma 1.4] and the last section in [59]). Our goal, in this section, is to better understand each of these notions as well as the relations between them. The questions addressed here are motivated by the knowledge on the analogous notions in the context of integral minimization problems.

Once the convexity notions are introduced, we consider, in a first moment, some properties that are intrinsic to them. Namely, lower semicontinuity and invariance on the domain. For this last property we achieve, as in the integral setting, that the cube Q can be replaced by other open and bounded sets $\Omega$, satisfying further suitable restrictions according to the specific notion under analysis. We also get a characterization of periodic-weak BJW-quasi-level convexity and existence of minimizers for some class of supremal problems. Afterwards, in Sect. 3.1, we explore which are the conditions that are sufficient and which are necessary.

Definition 3.1

Let $N, n \in {\mathbb {N}}$ and let $f:\mathbb {R}^{N\times n}\longrightarrow \mathbb {R}$.

• (1) The function f is said to be level convex if, for every $\xi ,\eta \in \mathbb {R}^{N\times n}$ and for every $0<\lambda <1$, one has

  $$\begin{aligned} f(\lambda \xi +(1-\lambda )\eta )\le \max \{f(\xi ),f(\eta )\}, \end{aligned}$$

  namely for every $t \in {\mathbb {R}}$, the sublevel sets $L_t(f):=\{\xi \in {\mathbb {R}}^{N\times n}:f(\xi ) \le t\}$ are convex.

• (2) The function f is said to be poly-level convex if, there exists a level convex function $g:\mathbb {R}^{\tau (n,N)}$ $\longrightarrow \mathbb {R}$ such that, for every $\xi \in \mathbb {R}^{N\times n}$,

  $$\begin{aligned} f(\xi )=g(T(\xi )), \end{aligned}$$

  where

  $$\begin{aligned} \tau (n,N):=\sum _{s=1}^{\min \{n,N\}}\sigma (s),\quad \text {with}\quad \sigma (s)=\left( {\begin{array}{c}N\\ s\end{array}}\right) \left( {\begin{array}{c}n\\ s\end{array}}\right) =\frac{N!\,n!}{(s!)^2(N-s)!(n-s)!} \end{aligned}$$

  and $T(\xi )$ is a vector with all the minors of $\xi$, namely

  $$\begin{aligned} T(\xi ):=(\xi ,\textrm{adj}_2\xi ,\ldots ,\textrm{adj}_{\min \{n,N\}}\xi ) \end{aligned}$$

  being $\textrm{adj}_s\xi$ $(2\le s\le \min \{n,N\})$ the matrix of all $s\times s$ minors of $\xi$.

• (3) Assume that the function f is Borel measurable. We say that f is strong BJW-quasi-level convex if

  $$\begin{aligned} \forall \ \varepsilon>0\ \forall \ \xi \in \mathbb {R}^{N\times n}\ \forall \ K>0\ \exists \ \delta =\delta (\varepsilon , K,\xi )>0: \\ \left. \begin{array}{l}\varphi \in W^{1,\infty }(Q;\mathbb {R}^N)\\ ||D\varphi ||_{L^\infty (Q;\mathbb {R}^{N\times n})}\le K \\ \max _{x\in \partial Q}|\varphi (x)|\le \delta \end{array}\right\} \Longrightarrow f(\xi )\le {\text {*}}{ess\,sup}_{x\in Q} f(\xi +D\varphi (x))+\varepsilon . \end{aligned}$$

• (4) Assume that the function f is Borel measurable. We say that f is weak BJW-quasi-level convex if

  $$\begin{aligned} \displaystyle f(\xi )\le {\text {*}}{ess\,sup}_{x\in Q}f\left( \xi + D\varphi \left( x\right) \right) ,\ \forall \ \xi \in \mathbb {R}^{N\times n},\ \forall \ \varphi \in W_{0}^{1,\infty }(Q;\mathbb {R}^N). \end{aligned}$$

• (5) Assume that the function f is Borel measurable. We say that f is periodic-weak BJW-quasi-level convex if, for every $\xi \in \mathbb {R}^{N\times n}$ and for every $\varphi \in W_\mathrm{{per}}^{1,\infty }(Q;\mathbb {R}^N)$,

  $$\begin{aligned} \displaystyle f(\xi )\le {\text {*}}{ess\,sup}_{x\in Q}f\left( \xi + D\varphi \left( x\right) \right) . \end{aligned}$$

• (6) The function f is said to be rank-one level convex if, for every $\xi ,\eta \in \mathbb {R}^{N\times n}$ such that $\textrm{rank}(\xi -\eta )=1$ and for every $0<\lambda <1$, one has

  $$\begin{aligned} f(\lambda \xi +(1-\lambda )\eta )\le \max \{f(\xi ),f(\eta )\}, \end{aligned}$$

  i.e. for every $t \in {\mathbb {R}}$, $L_t(f)$ contains all segments $[\xi , \eta ]$ connected through a rank-one matrix.

Remark 3.2

• (i) Regarding the notion of strong BJW-quasi-level convexity, to ease the parallel with the integral setting, one shall have in mind the characterization of quasiconvexity provided in Proposition 2.3. In this way, we obtain that the supremal version of (2.2) provides the notion of strong BJW-quasi-level convexity, while the supremal version of (2.1) leads to weak BJW-quasi-level convexity. As we shall see in Proposition 3.17 these two notions, weak and strong BJW-quasi-level convexity, do not coincide.

• (ii) We will work with the conditions defining strong BJW-quasi-level convexity and weak BJW - quasi-level convexity on domains other than the cube Q, namely $\Omega \subseteq \mathbb {R}^n$. In that case we will refer to those conditions as strong BJW-quasi-level convexity in $\Omega$ or weak BJW-quasi-level convexity in $\Omega$. In Propositions 3.7 and 3.10 we will see these notions are independent of the domain in some appropriate classes of sets. In an analogous way, we will also refer to periodic-weak BJW-quasi-level convexity in a cube $C\subseteq \mathbb {R}^n$ if the inequality in (3) is valid for test functions in $W^{1,\infty }_\textrm{per}(C;\mathbb {R}^N).$

• (iii) The definition of periodic-weak BJW-quasi-level convexity is new as a definition, but it was already used in [21, Lemma 2.8] through a formulation, that we will prove to be equivalent in Proposition 3.6. It appears as an intermediate step to prove that sequential weak* lower semicontinuity of a supremal functional of the form $F(\cdot ,\Omega )$, as in (1.1), implies weak BJW-quasi-level convexity. Example 3.15 below provides a counter-example to the reverse implication. The notion of periodic-weak BJW-quasi-level convexity also coincides with the notion of $\mathcal {A}$-weak quasiconvexity considered in [4] in the case of the $\textrm{curl}$ operator, since by Proposition 3.6, periodic-weak BJW-quasi-level convexity can be tested on functions with periodic gradients.

Having in mind the relevant convexity notions to treat minimization problems of integral form (see [43]), one should note that since convex functions are continuous in their effective domain, the lower semicontinuity is encoded in polyconvexity, quasiconvexity and rank-one convexity. This is not the case in the context under our attention here. Indeed, there exist level convex, poly-level convex, weak and periodic-weak BJW-quasi-level convex, and rank-one level convex functions that are not lower semicontinuous. On the other hand, it will be seen, cf. Proposition 3.5, that strong BJW-quasi-level convex functions are always lower semi-continuous. To this end, we start by recalling the following preparatory result (see [21, Proposition 2.5]), which proof is presented for the convenience of the reader.

Lemma 3.3

Let $f:\mathbb {R}^{N\times n}\longrightarrow \mathbb {R}$ be a Borel measurable function that is strong Morrey quasiconvex on a bounded and open set $\Omega \subseteq \mathbb {R}^n$ with Lipschitz boundary i.e.

$$\begin{aligned}&\forall \ \varepsilon>0\ \forall \ \xi \in \mathbb {R}^{N\times n}\ \forall \ K>0\ \exists \ \delta =\delta (\varepsilon , K,\xi )>0: \nonumber \\&\left. \begin{array}{l}\varphi \in W^{1,\infty }(\Omega ;\mathbb {R}^N)\\ ||D\varphi ||_{L^\infty (\Omega ;\mathbb {R}^{N\times n})}\le K \\ \max _{x\in \partial \Omega }|\varphi (x)|\le \delta \end{array}\right\} \Longrightarrow f(\xi )\le {\text {*}}{ess\,sup}_{x\in \Omega } f(\xi +D\varphi (x))+\varepsilon . \end{aligned}$$

(3.1)

Then, for every $\xi \in {\mathbb {R}}^{N\times n}$ and for every sequence $(\varphi _k)_{k\in \mathbb {N}}\subseteq W^{1,\infty }(\Omega ;{\mathbb {R}}^N)$ weakly* converging to 0 in $W^{1,\infty }(\Omega ;{\mathbb {R}}^N)$, it follows that

$$\begin{aligned} f(\xi )\le \liminf _{k \rightarrow \infty }{\text {*}}{ess\,sup}_{x\in \Omega } f(\xi + D \varphi _k(x)). \end{aligned}$$

Proof

The weak* convergence of $\varphi _k$ to 0 in $W^{1,\infty }(\Omega ;{\mathbb {R}}^N)$ entails that $(\varphi _k)_{k\in \mathbb {N}}$ is bounded in $W^{1,\infty }(\Omega ;{\mathbb {R}}^N)$. In particular, there exists $K>0$ such that $\Vert D\varphi _k\Vert _{L^\infty (\Omega ;\mathbb {R}^{N\times n})}\le K$, for every $k \in {\mathbb {N}}$. Moreover, by Rellich-Kondrachov theorem (see [32, Theorem IX.16], which holds since $\Omega$ is a bounded and open set with Lipschitz boundary) or, equivalently, by applying Arzelà-Ascoli theorem), $\varphi _k\in C(\overline{\Omega };\mathbb {R}^N)$ and $\varphi _k \rightarrow 0$ strongly in $L^\infty (\Omega ;{\mathbb {R}}^N)$. Therefore, given $\xi \in {\mathbb {R}}^{N\times n}$, $\varepsilon >0$, and $\delta =\delta (\varepsilon , K,\xi )>0$ as in the assumption, one has, for sufficiently large k, $\sup _{x \in \partial \Omega } |\varphi _k(x)|\le \delta (\varepsilon , K,\xi )$. Thus, the strong BJW-quasi-level convexity of f implies that

$$\begin{aligned} f(\xi )\le {\text {*}}{ess\,sup}_{x\in \Omega }f(\xi + D\varphi _k)+ \varepsilon , \end{aligned}$$

for k sufficiently large. Passing to the limit on k we obtain

$$\begin{aligned} f(\xi )\le \liminf _{k\rightarrow \infty } {\text {*}}{ess\,sup}_{x\in \Omega }f(\xi +D\varphi _k)+\varepsilon . \end{aligned}$$

The arbitrariness of $\varepsilon$ concludes the proof. $\square$

The following example shows that lower semicontinuity is not a necessary condition of functions enjoying the other convexity notions.

Example 3.4

Let $f:\mathbb {R}^{N\times n}\longrightarrow \mathbb {R}$ be such that $f=\chi _A$ where $A=\{\xi \in \mathbb {R}^{N\times n}:\ \xi _1^1\ge 1\}$ and for every $\eta \in {\mathbb {R}}^{N\times n}$, $\eta ^1_1$ denotes the first entry of the matrix $\eta$. Note that f is not lower semicontinuous. Indeed, considering the sequence $(\xi _k)_{k\in \mathbb {N}}\subseteq \mathbb {R}^{N\times n}$ such that $(\xi _k)_1^1=1-\frac{1}{k}$ and all the other components are zero, one has $\lim \xi _k=\xi$ where $\xi _1^1=1$, being all the other components of $\xi$ equal to zero. However,

$$\begin{aligned} f(\xi )=1>0=\lim \inf f(\xi _k). \end{aligned}$$

On the other hand, one can easily get that f is level convex as well as poly-level convex, weak BJW-quasi-level convex, periodic-weak BJW-quasi-level convex and rank-one level convex, (see also Theorem 3.12 below). Observe that f is not strong BJW-quasi-level convex because f is not lower semicontinuous, (cf. Proposition 3.5 below).

Proposition 3.5

Let $N,n\ge 1$.

• (i) If $f:{\mathbb {R}}^{N\times n}\longrightarrow \mathbb {R}$ is strong BJW-quasi-level convex in a bounded and open set $\Omega$ with Lipschitz boundary, then it is lower semicontinuous.

• (ii) There are functions $f:\mathbb {R}^{N\times n}\longrightarrow \mathbb {R}$ that are not lower semicontinuous but that are either level convex, poly-level convex, weak BJW-quasi-level convex, periodic-weak BJW-quasi-level convex or rank-one level convex.

Proof

The proof of (i) follows by Lemma 3.3. Indeed, taken a sequence $\xi _k \rightarrow 0$ in ${\mathbb {R}}^{N \times n}$, we can define for every $x \in \Omega$, $\varphi _k(x):= \xi _k x$. This sequence of functions lying in $W^{1,\infty }(\Omega ;{\mathbb {R}}^N)$ converges strongly to 0 in $W^{1,\infty }(\Omega ;\mathbb {R^N})$, hence, by the previous proposition it follows that

$$\begin{aligned} f(\xi )\le \liminf _{k\rightarrow \infty } f(\xi + \xi _k). \end{aligned}$$

Condition (ii) is a consequence of Example 3.4. $\square$

We now prove an equivalent formulation to periodic-weak BJW-quasi-level convexity.

Proposition 3.6

(Periodic-weak BJW-quasi-level convexity.) Let $f:\mathbb {R}^{N\times n}\longrightarrow \mathbb {R}$ and let $C\subseteq \mathbb {R}^n$ be a cube. Then f is periodic-weak BJW-quasi-level convex in C if and only if for every $\varphi \in W_\mathrm{{loc}}^{1,\infty }(\mathbb {R}^n;\mathbb {R}^N)$, such that $D\varphi$ is C-periodic, one has

$$\begin{aligned} \displaystyle f(\zeta )\le {\text {*}}{ess\,sup}_{x\in C}f\left( D\varphi \left( x\right) \right) , \end{aligned}$$

where $\zeta =\frac{1}{\mathcal {L}^n(C)}\int _C D\varphi (x)\,dx$.

Proof

For the non-trivial implication, let $\varphi \in W_\mathrm{{loc}}^{1,\infty }(\mathbb {R}^n;\mathbb {R}^N)$ be a function with C-periodic gradient and let $\zeta =\frac{1}{\mathcal {L}^n(C)}\int _C D\varphi (x)\,dx$. By an argument similar to that in Lemma 2.6 (see the forthcoming monograph [50] fro details), the function defined in C by $w(x):=\varphi (x)-\zeta \cdot x$ can be extended by C-periodicity to an element in $W^{1,\infty }_\textrm{per}(C;\mathbb {R}^N)$. Using the hypothesis of periodic-weak BJW-quasi-level convexity in C, one gets

$$\begin{aligned} \displaystyle f(\zeta )\le {\text {*}}{ess\,sup}_{x\in C}f\left( \zeta + Dw\left( x\right) \right) ={\text {*}}{ess\,sup}_{x\in C}f\left( D\varphi (x) \right) , \end{aligned}$$

as whished. $\square$

Next we are going to address the question of independence of domain in the notions of weak BJW-quasi-level convexity and strong BJW-quasi-level convexity. We observe that the class of sets that we can achieve in an equivalent notion of weak BJW-quasi-level convexity is more general than for strong BJW-quasi-level convexity. Actually, while in the first setting (cf. Proposition 3.7) the argument relies on Vitali’s covering argument, in the second one, the proof of Proposition 3.10 exploits the lower semicontinuity of the associated supremal functional as a necesssary condition to the strong BJW-quasi-level convexity of the supremand (cf. Proposition A.1) that involves a strong version of Besicovitch derivation theorem constraining the class of admissible sets.

Proposition 3.7

The notion of weak BJW-quasi-level convexity remains unchangeable if the set Q is replaced by any other bounded and open set in $\mathbb {R}^n$ with boundary of null $\mathcal {L}^n$-measure.

Proof

We need to show that, if $f:\mathbb {R}^{N\times n}\longrightarrow \mathbb {R}$ is a Borel measurable function such that

$$\begin{aligned} \displaystyle f(\xi )\le {\text {*}}{ess\,sup}_{x\in O}f\left( \xi + D\varphi \left( x\right) \right) ,\ \forall \ \xi \in \mathbb {R}^{N\times n},\ \forall \ \varphi \in W_{0}^{1,\infty }(O;\mathbb {R}^N) \end{aligned}$$

where O is a given open set in $\mathbb {R}^n$, then, for any bounded open set $\Omega$ of $\mathbb {R}^n$ whose boundary has null ${\mathcal {L}}^n$-measure, one has

$$\begin{aligned} \displaystyle f(\xi )\le {\text {*}}{ess\,sup}_{x\in \Omega }f\left( \xi + D\psi \left( x\right) \right) ,\ \forall \ \xi \in \mathbb {R}^{N\times n},\ \forall \ \psi \in W_{0}^{1,\infty }(\Omega ;\mathbb {R}^N). \end{aligned}$$

Let O and f be as above and let $\Omega$ be a bounded and open set with $\mathcal {L}^n(\partial \Omega )=0$. Let $\xi \in \mathbb {R}^{N\times n}$ and $\psi \in W_{0}^{1,\infty }(\Omega ;\mathbb {R}^N).$ Without loss of generality, assume $\Omega$ is connected, otherwise consider one of its connected components.

Let $x_0\in \Omega$ and define $\Omega _0=\{x-x_0: x \in \Omega \}:=\Omega -x_0$. Consider, $\mathcal {G}$, the collection of open sets $a+\varepsilon \,\Omega _0$, for $a\in \mathbb {R}^n$ and $\varepsilon >0$. By the Vitali covering theorem (see [44, Corollary 10.5]), up to a set of measure zero, the set O can be covered with a countable number of sets $G\in \mathcal {G}$ with disjoint closures. More precisely, for some countable collection $\mathcal {G}'\subseteq \mathcal {G}$,

$$\begin{aligned} \bigcup _{G\in \mathcal {G}'}G\subseteq O,\qquad \mathcal {L}^n\left( O{\setminus }\bigcup _{G\in \mathcal {G}'}G\right) =0, \end{aligned}$$

and $G\cap F=\emptyset$ for $G,F\in \mathcal {G}'$ with $G\ne F$.

Each set $G\in \mathcal {G}'$ has the form $a+\varepsilon \,\Omega _0$. On each of these sets, define a function $\psi _{a,\varepsilon }$ as

$$\begin{aligned} \psi _{a,\varepsilon }(y)=\varepsilon \psi \left( \frac{y-a}{\varepsilon }+x_0\right) . \end{aligned}$$

Observe that

$$\begin{aligned} D\psi _{a,\varepsilon }(y)=D\psi \left( \frac{y-a}{\varepsilon }+x_0\right) . \end{aligned}$$

Patching these functions together, we construct a function $\varphi$ defined on O as $\varphi =\psi _{a,\varepsilon }$ in each $a+\varepsilon \,\Omega _0\in \mathcal {G}'$, and $\varphi =0$ in $O{\setminus } \cup _{G\in \mathcal {G}'}G$. In this way, one gets $\varphi \in W_{0}^{1,\infty }(O;\mathbb {R}^N)$, and thus, using the hypothesis, we get

$$\begin{aligned} \displaystyle f(\xi )\le {\text {*}}{ess\,sup}_{y\in O}f\left( \xi + D\varphi \left( y\right) \right) \le {\text {*}}{ess\,sup}_{x\in \Omega }f\left( \xi + D\psi \left( x\right) \right) , \end{aligned}$$

as desired. $\square$

Proposition 3.7 provides an answer to the question raised in the introduction regarding the minimization of some supremal functionals on a set of functions with a prescribed affine boundary condition. This is stated in the next corollary, and is an immediate consequence of the previous result.

Corollary 3.8

Let $\Omega$ be a bounded open set with boundary of null $\mathcal {L}^n$-measure and let $f:\mathbb {R}^{N\times n}\longrightarrow \mathbb {R}$ be a Borel measurable function. Consider the functional

$$\begin{aligned} I(u)={\text {*}}{ess\,sup}_{x\in \Omega } f(Du(x)), \text { for } u\in W^{1,\infty }(\Omega ;\mathbb {R}^N). \end{aligned}$$

Let $\xi \in \mathbb {R}^{N\times n}$ and denote by $u_\xi$ an affine (vector-)function with gradient $\xi$.

If f is weak BJW-quasi-level convex, then $u_\xi$ minimizes I on $u_\xi +W_0^{1,\infty }(\Omega ;\mathbb {R}^N)$.

Next we address the invariance of domain in the notion of strong BJW-quasi-level convexity. We start with translation of sets.

Remark 3.9

If $f:\mathbb {R}^{N\times n}\longrightarrow \mathbb {R}$ is strong BJW-quasi-level convex in a bounded open set $\Omega \subseteq \mathbb {R}^n$

then, it is also strong BJW-quasi-level convex in any translation of $\Omega$. That is, for any $x_0\in \mathbb {R}^n$

$$\begin{aligned} & \forall \ \varepsilon>0\ \forall \ \xi \in \mathbb {R}^{N\times n}\ \forall \ K>0\ \exists \ \delta =\delta (\varepsilon , K,\xi )>0: \nonumber \\ & \left. \begin{array}{l}\varphi \in W^{1,\infty }(x_0+\Omega ;\mathbb {R}^N)\\ ||D\varphi ||_{L^\infty (x_0+\Omega ;\mathbb {R}^{N\times n})}\le K\vspace{0.2cm}\\ \max _{x\in \partial (x_0+\Omega )}|\varphi (x)|\le \delta \end{array}\right\} \Longrightarrow f(\xi )\le {\text {*}}{ess\,sup}_{x\in x_0+\Omega } f(\xi +D\varphi (x))+\varepsilon , \end{aligned}$$

(3.2)

where $x_0+\Omega$ denotes the translation of the set $\Omega$ by the vector $x_0$. Observe that $\partial (x_0+\Omega )=x_0+\partial \Omega$ and that $x_0 +\Omega$ is also bounded and open. Also, observe that for every function $\varphi \in W^{1,\infty }(x_0+\Omega ;{\mathbb {R}}^N)$, defining $\psi (x):= \varphi (x_0+x)$ for $x \in \Omega$, one has $\psi \in W^{1,\infty }(\Omega ;{\mathbb {R}}^N)$. If $\Vert D \varphi \Vert _{L^\infty (x_0+\Omega ;\mathbb {R}^{N\times n})}\le K$, it results

$$\begin{aligned} \Vert D \psi \Vert _{L^\infty (\Omega ;\mathbb {R}^{N\times n})}\Vert =\Vert D \varphi \Vert _{L^\infty (x_0+\Omega ;\mathbb {R}^{N\times n})}\le K, \end{aligned}$$

and, if $\max _{x\in \partial (x_0+\Omega )}|\varphi (x)|\le \delta$, then

$$\begin{aligned} \max _{x \in \partial \Omega }|\psi (x)|=\max _{x \in \partial (x_0+\Omega )}|\varphi (x)|\le \delta . \end{aligned}$$

Thus, by (3.1), we have for every $\varepsilon >0,$ $\xi \in {\mathbb {R}}^{N\times n}$, $K>0$ that there exists a $\delta \equiv \delta (\varepsilon , K, \xi )>0$ such that

$$\begin{aligned} f(\xi )\le {\text {*}}{ess\,sup}_{x\in \Omega } f(\xi +D\psi (x))+\varepsilon = {\text {*}}{ess\,sup}_{x\in x_0+\Omega } f(\xi +D\varphi (x))+\varepsilon , \end{aligned}$$

thus proving (3.2).

Our next goal is to address more general cases. On the one hand, it is hard to deal with the strong BJW-quasi-level convexity notion directly. But, on the other hand, we can relate it with lower semicontinuity of supremal functionals, independently of their domain of definition, (see Propositions A.1 and A.2 in the Appendix). Therefore to achieve our goal we pass through properties of supremal functionals.

Proposition 3.10

In the notion of strong BJW-quasi-level convexity, the set Q can be replaced by any other bounded, open, and convex set in $\mathbb {R}^n$.

Proof

Assume that f is strong BJW-quasi-level convex in a bounded, convex, and open set $\Omega \subseteq \mathbb {R}^n$. By Proposition A.1 one has that $F(u,O):={\text {*}}{ess\,sup}_{x\in \Omega }f\left( Du\left( x\right) \right)$ is sequentially weakly* lower semicontinuous in $W^{1,\infty }(O;\mathbb {R}^N)$ for any bounded and open set $O\subseteq \mathbb {R}^n$. Then it suffices to invoke Proposition A.2 to conclude that f is also strong BJW-quasi-level convex in O. $\square$

As a side result, we also get that the sequential weak* lower semicontinuity of F is independent of the domain $\Omega$ in the class of bounded, open and convex sets.

Proposition 3.11

$$\begin{aligned} F(u,\Omega ):={\text {*}}{ess\,sup}_{x\in \Omega }f\left( Du\left( x\right) \right) , \end{aligned}$$

where $\Omega$ is a bounded open set in $\mathbb {R}^n$ and $u\in W^{1,\infty }(\Omega ;\mathbb {R}^N)$.

If $F(\cdot ,\mathcal {O}_1)$ is sequentially weakly* lower semicontinuous in $W^{1,\infty }(\mathcal {O}_1;\mathbb {R}^N)$ with $\mathcal {O}_1$ bounded, convex, and open, then $F(\cdot ,\mathcal {O}_2)$ is sequentially weakly* lower semicontinuous in $W^{1,\infty }(\mathcal {O}_2;\mathbb {R}^N)$ for any bounded open set $\mathcal {O}_2$.

In particular, the sequential weak* lower semicontinuity of $F(\cdot ,\Omega )$ is independent of the domain $\Omega$ in the class of bounded, convex, and open sets.

Proof

The result follows directly from the Propositions A.1 and A.2. $\square$

3.1 Hierarchy of convexity notions

The convexity notions related to the lower semicontinuity of the supremal functionals under consideration having been introduced, we investigate in the sequel how they are interconnected with each other. We retake the work by [21] and we try to make an exhaustive study of the notions of convexity introduced above in terms of necessary and sufficient conditions to each of them. We review the properties stated therein, we establish other relations and we provide counter-examples whenever possible. The section finishes with a list of questions that remain open.

Theorem 3.12

Let $N, n \in {\mathbb {N}}$ and let $f:\mathbb {R}^{N\times n}\longrightarrow \mathbb {R}$.

• (1) If f is level convex then f is poly-level convex and rank-one level convex. If f is also Borel measurable then f is weak and periodic-weak BJW-quasi-level convex. Moreover, if f is additionally lower semicontinuous, then f is strong BJW-quasi-level convex.

• (2) Assume that f is poly-level convex and satisfies one of the following hypotheses:

  • (i) $f=g\circ T$, where T is as in the definition of poly-level convexity and $g:\mathbb {R}^{\tau (n,N)}\longrightarrow \mathbb {R}$ is level convex and lower semicontinuous;

  • (ii) f is lower semicontinuous and $\lim _{|\xi |\rightarrow +\infty }f(\xi )=+\infty$,

  then f is strong BJW-quasi-level convex. If f is poly-level convex and $f=g\circ T$, with g level convex and Borel measurable, then f is weak and periodic-weak BJW-quasi-level convex. If f is poly-level convex then f is rank-one level convex.

• (3) If f is strong BJW-quasi-level convex then f is weak and periodic-weak BJW-quasi-level convex.

• (4) If f is periodic-weak BJW-quasi-level convex then f is weak BJW-quasi-level convex.

• (5) If f is weak BJW-quasi-level convex and upper semi-continuous then f is rank-one level convex.

• (6) If f is periodic-weak BJW-quasi-level convex in any cube $C\subseteq \mathbb {R}^n$ then f is rank-one level convex. In particular, if f is strong BJW-quasi-level convex then f is rank-one level convex.

• (7) Let $n=1$ or $N=1$. Then f is level convex if and only if it is poly-level convex and if and only if it is rank-one level convex. Furthermore

  • (i) if f is lower semicontinuous, then f is level convex if and only if it is strong BJW-quasi-level convex,

  • (ii) if f is upper semicontinuous then f is level convex if and only if f is weak BJW-quasi-level convex, and if and only if it is periodic-weak BJW-quasi-level convex.

  In particular, if f is continuous, all the notions are equivalent. If $n=1$, the upper semicontinuity can be replaced by Borel measurability, to get that f is level convex if and only if f is weak BJW-quasi-level convex and if and only f is periodic-weak BJW-quasi-level convex.

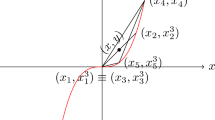
To ease the reading of the theorem, consider the following figure (Fig. 1).

Fig. 1

The figure shall be considered to accompany Theorem 3.12. Namely, the labels to each implications refer to the items in the theorem containing the referred implication and, when additional hypotheses are required, the label is signed with $^*$

Remark 3.13

• (1) As observed earlier, strong BJW-quasi-level convex functions are lower semicontinuous while poly-level convex functions may fail to enjoy this property. For that reason we considered in (2) of the previous proposition lower semicontinuity assumptions. As we will see in Proposition 3.17 the upper semicontinuity hypothesis cannot be removed in (5).

• (2) With respect to (6), observe that if we only assume f is periodic-weak BJW-quasi-level convex (in the cube Q) then we can only get the rank-one level convexity of f in some rank-onedirections, namely those that are given by matrices with only one non-null column. Note that this is what is established by Ansini and Prinari in [4, Proposition 5.1 (i)] in the case of the $\textrm{curl}$ operator. Actually, as already mentioned, $\mathrm curl$-weak quasiconvexity in [4] is what we called periodic-weak BJW-quasi-level convexity. According to [4, Proposition 5.1 (i)], this ensures the level convexity inequality in the directions of the kernel of the $\textrm{curl}$ operator that are the directions that we find in our argument (cf. Remark 3.2 (iii)).

• (3) Contrary to the case $n=1$, where weak BJW-quasi-level convexity and periodic-weak BJW-quasi-level convexity imply level convexity, we shall see in Proposition 3.17, that in the case $N=1$, this is not true for weak BJW-quasi-level convexity, even if the function f is lower semicontinuous, while it is currently open in the periodic-weak BJW-quasi-level convex setting.

Proof

Conditions (1), (3), (4) and (6) follow from standard arguments, as well as the last two assertions of (2). For the first statement of (1), it suffices to make use of the first component of the vector function T. The second assertion of (1) follows by restricting to rank-one connected matrices. The next two assertions of (1) follow from Jensen’s inequality (cf. Theorem C.1) applied with $\varphi = \xi + D\psi$, for $\psi \in W_0^{1,\infty }(Q;\mathbb {R}^N)$ or $\psi \in W_\textrm{per}^{1,\infty }(Q;\mathbb {R}^N)$, $\Omega = Q$, and $\mu$ the Lebesgue measure restricted to the cube Q if we observe that, either $W_0^{1,\infty }(Q;\mathbb {R}^N)$ and $W_\textrm{per}^{1,\infty }(Q;\mathbb {R}^N)$ have zero integral average. The last assertion of (1) follows from the previous ones and (2) (i), once this is proved.

With respect to (3), given $\varphi \in W_\mathrm{{per}}^{1,\infty }(Q;\mathbb {R}^N)$, define $\varphi _n(x):=\frac{1}{n}\varphi (nx)$. Then let $\varepsilon =\frac{1}{n}$, $K=||D\varphi ||_{L^{\infty }(Q;\mathbb {R}^{N\times n})}$, and $\xi \in \mathbb {R}^{N\times n}$. Consider the constant $\delta >0$ provided by the assumption of strong BJW-quasi-level convexity. Note that, for sufficiently large n, $\max _{x\in \partial Q}|\varphi _n(x)|\le \delta$. Therefore, applying the assumption, one gets

$$\begin{aligned} f(\xi )\le {\text {*}}{ess\,sup}_{x\in Q} f(\xi +D\varphi _n(x))+\frac{1}{n}={\text {*}}{ess\,sup}_{x\in Q} f(\xi +D\varphi (x))+\frac{1}{n}, \end{aligned}$$

and the desired inequality is achieved by letting $n\rightarrow \infty$. Regarding (4), it suffices to observe that $W_{0}^{1,\infty }(Q;\mathbb {R}^N)\subseteq W_\mathrm{{per}}^{1,\infty }(Q;\mathbb {R}^N)$. With respect to the second assertion in (2), let $\xi \in \mathbb {R}^{N\times n}$ and $\varphi \in W_\textrm{per}^{1,\infty }(Q;\mathbb {R}^N)$. Since $\textrm{adj}_s$, $2\le s\le \min \{n,N\}$, are quasiaffine functions (in the sense of [43, Definition 1.5]),

$$\begin{aligned} T(\xi )=\int _QT(\xi +D\varphi (x))\,dx \end{aligned}$$

and thus, by Theorem C.1,

$$\begin{aligned} f(\xi )= & g(T(\xi ))=g\left( \int _QT(\xi +D\varphi (x))\,dx\right) \le {\text {*}}{ess\,sup}_{x\in Q}g\left( T(\xi + D\varphi \left( x\right) ) \right) \\= & {\text {*}}{ess\,sup}_{x\in Q}f\left( \xi + D\varphi \left( x\right) \right) . \end{aligned}$$

In this way we proved that f is periodic-weak BJW-quasi-level convex. Next, we prove the last assertion of (2). Let $\xi ,\eta \in \mathbb {R}^{N\times n}$ such that $\textrm{rank}(\xi -\eta )=1$. Then, for some level convex function $g:\mathbb {R}^{\tau (n,N)}\longrightarrow \mathbb {R}$, $f=g\circ T$ and

$$\begin{aligned} f(\lambda \xi +(1-\lambda )\eta )=&g(T(\lambda \xi +(1-\lambda )\eta )) =g(\lambda T(\xi )+(1-\lambda )T(\eta ))\\ \le&\max \{g(T(\xi )),g(T(\eta ))\} =\max \{f(\xi ),f(\eta )\} \end{aligned}$$

where we have used [43, Lemma 5.5] and the level convexity of g, achieving the rank-one level convexity of f. Finally, we prove (6). It follows as in [43, proof of Theorem 7.7 (ii)]. Let $\xi ,\eta \in \mathbb {R}^{N\times n}$ be such that $\textrm{rank}(\xi -\eta )=1$. Then $\xi -\eta =a\otimes \nu$ for some $a\in \mathbb {R}^N$ and $\nu \in \mathbb {R}^n$ is a unit vector. Let $R\in \mathcal{S}\mathcal{O}(n)$ be a special orthogonal matrix such that $R e_1=\nu$, where $e_1$ is the first vector of the canonical basis of $\mathbb {R}^n$, and denote by C the cube RQ. Then, we can construct a function $\varphi \in W^{1,\infty }_\textrm{per}(C;\mathbb {R}^N)$ such that $D\varphi \in \{(1-\lambda )(\xi -\eta ),-\lambda (\xi -\eta )\}$ a.e. in C. Therefore, applying the periodic-weak assumption on f in every cube, one gets

$$\begin{aligned} f(\lambda \xi +(1-\lambda )\eta )\le {\text {*}}{ess\,sup}_{x\in C}f(\lambda \xi +(1-\lambda )\eta +D\varphi )=\max \{f(\xi ),f(\eta )\}, \end{aligned}$$

proving the rank-one level convexity. The statement regarding strong BJW-quasi-level convexity, follows from Proposition 3.10 combined with the previous.

Condition (5) was proved in [75, Theorem A.5]. Regarding (7), it suffices to observe that level convexity is equivalent to rank-one level convexity and poly-level convexity. All the previous points guarantee the remaining equivalences, up to the last assertion, which follows by standard arguments.

It remains to prove the first part of (2).

This relies on results regarding lower semicontinuity of functionals presented in the Appendix. By Proposition A.2 combined with Proposition 3.10, it suffices to show that, under each of the two set of hypotheses, the functional $F(u,O):={\text {*}}{ess\,sup}_{x\in \Omega }f\left( Du\left( x\right) \right)$ is sequentially weakly* lower semicontinuous in $W^{1,\infty }(O;\mathbb {R}^N)$.

First we present the proof of the sequential weak* lower semicontinuity of the functional F under assumption (i). Let $(u_k)_{k\in \mathbb {N}}\subseteq W^{1,\infty }(O,\mathbb {R}^N)$ be an arbitrary sequence weakly* converging to some function u in $W^{1,\infty }(O,\mathbb {R}^N)$. We want to show that

$$\begin{aligned} F(u,O) \le \liminf _{k\rightarrow \infty }F(u_k,O). \end{aligned}$$

Since, by [43, Theorem 8.20, Remark 8.21 (iv)], $T(Du_k)$ weakly* converges to T(Du) in $L^\infty (O;\mathbb {R}^{\tau (n,N)})$, it suffices to show that

$$\begin{aligned} G(V,O):={\text {*}}{ess\,sup}_{x\in O}g\left( V\left( x\right) \right) ,\qquad V\in L^\infty (O;\mathbb {R}^{\tau (n,N)}) \end{aligned}$$

is sequential weak* lower semicontinuous in $L^\infty (O;\mathbb {R}^{\tau (n,N)}).$ Let then $(V_k)_{k\in \mathbb {N}}\subseteq L^\infty (O;\mathbb {R}^{\tau (n,N)})$ be an arbitrary sequence weakly* converging in $L^\infty (O;\mathbb {R}^{\tau (n,N)})$ to some function V.

Let $r:=\liminf _{k\rightarrow \infty }G(V_k,O)=\lim _{i\rightarrow \infty }G(V_{k_i},O)$ for some subsequence $(V_{k_i})_{i\in \mathbb {N}}$ of $(V_k)_{k\in \mathbb {N}}$. Then, by definition of limit, for arbitrary $\varepsilon >0$, there is $i_0\in \mathbb {N}$ such that, for $i\ge i_0$,

$$\begin{aligned} g(V_{k_i}(x))\le {\text {*}}{ess\,sup}_{x\in O}g\left( V_{k_i}\left( x\right) \right) =G(V_{k_i},O)\le r+\varepsilon \qquad \text {for}\ a.e.\ x\in O. \end{aligned}$$

That is, denoting $E_{r+\varepsilon }:=\{S\in \mathbb {R}^{\tau (n,N)}:\ g(S)\le r+\varepsilon \}$ one has, for $i\ge i_0$, $V_{k_i}(x)\in E_{r+\varepsilon }\ \text {for}\ a.e.\ x\in O$ and thus $\textrm{d}(V_{k_i}(x),E_{r+\varepsilon })=0\ \text {for}\ a.e.\ x\in O,$ where $\textrm{d}(\cdot ,E_{r+\varepsilon })$ denotes the distance function to the set $E_{r+\varepsilon }$. Since g is level convex, the set $E_{r+\varepsilon }$ is convex and by [49, Theorem 5.14] the functional

$$\begin{aligned} D(V,O):=\int _O\textrm{d}\left( V(x);E_{r+\varepsilon }\right) \,dx \end{aligned}$$

is sequentially weakly* lower semicontinuous in $L^\infty (O;\mathbb {R}^{\tau (n,N)})$. Therefore,

$$\begin{aligned} 0\le \int _O\textrm{d}\left( V(x);E_{r+\varepsilon }\right) \,dx\le \liminf _{i\rightarrow \infty }\int _O\textrm{d}\left( V_{k_i}(x);E_{r+\varepsilon }\right) \,dx=0 \end{aligned}$$

and $\textrm{d}\left( V(x);E_{r+\varepsilon }\right)$ for $a.e.\ x\in O$. Using the hypothesis that g is lower semicontinuous we have that $E_{r+\varepsilon }$ is closed and thus $V(x)\in E_{r+\varepsilon }$ for $a.e.\ x\in O$ that gives

$$\begin{aligned} {\text {*}}{ess\,sup}_{x\in O}g\left( V\left( x\right) \right) \le r+\varepsilon \end{aligned}$$

ensuring the desired condition by letting $\varepsilon \rightarrow 0$ and recalling the definition of r.

Finally, we prove the sequential weak* lower semicontinuity of the functional F under condition (ii). As before, let $(u_k)_{k\in \mathbb {N}}\subseteq W^{1,\infty }(O,\mathbb {R}^N)$ be an arbitrary sequence weakly* converging to some function u in $W^{1,\infty }(O,\mathbb {R}^N)$. Let $(u_{k_i})_{i\in \mathbb {N}}$ be a subsequence of $(u_k)_{k\in \mathbb {N}}$ such that $\liminf _{k\rightarrow \infty }F(u_k,O)=\lim _{i\rightarrow \infty }F(u_{k_i},O)$ and let $r:=\lim _{i\rightarrow \infty }F(u_{k_i},O)$. Defining $E_{r+\varepsilon }:=\{\xi \in \mathbb {R}^{N\times n}:\ f(\xi )\le r+\varepsilon \}$, one has that, given $\varepsilon >0$, there is $i_0\in \mathbb {N}$ such that, for $i\ge i_0$,

$$\begin{aligned} T(Du_{k_i}(x))\in T(E_{r+\varepsilon })\ \text {for}\ a.e.\ x\in O. \end{aligned}$$

In particular, $\textrm{d}(T(Du_{k_i}(x)),T(E_{r+\varepsilon }))=0\ \text {for}\ a.e.\ x\in O$ and also

$$\begin{aligned} \textrm{d}(T(Du_{k_i}(x)),\textrm{co}(T(E_{r+\varepsilon })))=0\ \text {for}\ a.e.\ x\in O. \end{aligned}$$

Now we invoke, as above, the sequential weak* lower semicontinuity in $L^\infty (O;\mathbb {R}^{\tau (n,N)})$ of the functional

$$\begin{aligned} B(V,O):=\int _O\textrm{d}\left( V(x);\textrm{co}(T(E_{r+\varepsilon }))\right) \,dx. \end{aligned}$$

Since, $T(Du_{k_i})$ weakly* converges to T(Du) in $L^\infty (O;\mathbb {R}^{\tau (n,N)})$,

$$\begin{aligned} 0 & \le \int _O\textrm{d}\left( T(Du(x));\textrm{co}(T(E_{r+\varepsilon }))\right) \,dx \\ & \le \liminf _{i\rightarrow \infty }\int _O\textrm{d}\left( T(Du_{k_i}(x));\textrm{co}(T(E_{r+\varepsilon }))\right) \,dx=0 \end{aligned}$$

giving

$$\begin{aligned} \textrm{d}\left( T(Du(x));\textrm{co}(T(E_{r+\varepsilon }))\right) =0\ \text {for }a.e.\ x\in O. \end{aligned}$$

(3.3)

Since f is lower semicontinuous, the set $E_{r+\varepsilon }$ is closed. Moreover, the growth assumption on f, ensures that $E_{r+\varepsilon }$ is bounded and thus compact. Therefore, $T(E_{r+\varepsilon })$ is also compact and we can apply [43, Theorem 2.14] to ensure that $\textrm{co}(T(E_{r+\varepsilon }))$ is closed. This, together with (3.3) entails that

$$\begin{aligned} T(Du(x))\in \textrm{co}(T(E_{r+\varepsilon }))\ \text {for }a.e.\ x\in O. \end{aligned}$$

It is now enough to show that

$$\begin{aligned} \{\xi \in \mathbb {R}^{N\times n}:\ T(\xi )\in \textrm{co}(T(E_{r+\varepsilon }))\}=E_{r+\varepsilon } \end{aligned}$$

(3.4)

to conclude that $Du(x)\in E_{r+\varepsilon }\ \text {for }a.e.\ x\in O$ that, in turn, ensures $f(Du(x))\le r\ \text {for }a.e.\ x\in O$ as wished.

Regarding (3.4), it follows from [43, Theorem 7.4 (iii)] and the fact that $E_{r+\varepsilon }$ is polyconvex in the sense of [43, Definition 7.2 (ii)], by [43, Theorem 7.4 (ii)] and the poly-level convexity of f. $\square$

We give, next, several examples of functions enjoying or not the convexity notions discussed above. These examples, besides the interest in itself, will be useful to discuss in Proposition 3.17 below the validity of the counter-implications of the previous proposition.

Example 3.14

Let $g:\mathbb {R}\longrightarrow \mathbb {R}$ be the characteristic function $g=\chi _{]1,\infty )}$ and, for $n >1$, define $f:\mathbb {R}^{n\times n}\longrightarrow \mathbb {R}$ as $f(\xi )=g(\det (\xi ))$. Trivially, since g is level convex, f is poly-level convex. However, one can easily see that f is not level convex. Moreover, f is lower semicontinuous because g is lower semicontinuous and the determinant is a continuous function.

Example 3.15

This example was given in [75, Example A.3]. Exploiting it further, it also serves to discuss periodic-weak BJW-quasi-level convexity. Let $N\ge 1$ and $n>1$. Let $S:=\{\xi , \eta \}\subset \mathbb {R}^{N\times n}$ such that $\textrm{rank}(\xi -\eta )=1$ and let $f:=1-\chi _S$, where $\chi _S$ is the characteristic function of S. As proved in [75, Example A.3], the function f is not rank-one level convex, but it is weak BJW-quasi-level convex. In particular, as noticed in [73, Example 2.7], f is not strong BJW-quasi-level convex. Note also, that f is lower semicontinuous (although it is not continuous).

Moreover, if we choose $\xi$ and $\eta$ such that $\xi -\eta =a\otimes e_1$ for some $a\in \mathbb {R}^N$ ($e_1$ being the first vector of the canonical basis in $\mathbb {R}^n$), arguing as in [45, proof of Theorem 3.2 (ii)] (see also [43, page 319]) we conclude that f is not periodic-weak BJW-quasi-level convex. (Note that here we need to construct a function $\varphi \in W_\mathrm{{per}}^{1,\infty }(Q;\mathbb {R}^N)$ and that is the reason to choose $\xi$ and $\eta$ so that $\xi -\eta$ is compatible with the cube Q.) In an analogous way, considering appropriate matrices $\xi$ and $\eta$ we can ensure that f is not periodic-weak BJW-quasi-level convex in a given cube C.

Example 3.16

According to a result proved by Kirchheim [64] (see also [43, Theorem 7.12]), if $N\ge 2$ and $n\ge 2$, there is a finite number of $N\times n$ matrices, $\xi _1,\ldots ,\xi _m\in \mathbb {R}^{N\times n}$, such that ${\text {*}}{rank}(\xi _i-\xi _j)>1,\ \forall \ i\ne j$ and there exist $\xi _0\notin \{\xi _1,\ldots ,\xi _m\}$ and $u\in u_{\xi _0}+W_0^{1,\infty }(Q;\mathbb {R}^N)$ (where $u_{\xi _0}$ denotes an affine function verifying $Du_{\xi _0}(x)\equiv \xi _0$) with $Du(x)\in \{\xi _1,\ldots ,\xi _m\},\ a.e.$ in Q. Consider then the function $f=1-\chi _S$ where $S=\{\xi _1-\xi _0,\ldots ,\xi _m-\xi _0\}$ and $\chi _S$ is the characteristic function of S. Of course f is lower semi-continuous and, by the properties stated above it is rank-one level convex, but not strong BJW-quasi-level convex. To show this last statement, it’s enough to consider $\varphi :=u-u_{\xi _0}\in W_0^{1,\infty }(Q;\mathbb {R}^N)$ to get a contradiction to strong BJW-quasi-level convexity. Indeed, take $\varepsilon \in (0,1)$, $\xi =0$, and $K=\max \{|\xi _0-\xi _1|,\ldots ,|\xi _0-\xi _m|\}$ and observe that $f(0)=1>\varepsilon = {\text {*}}{ess\,sup}_{x\in Q}f(0+D\varphi (x))+\varepsilon$.

Proposition 3.17

Let $N,n\in \mathbb {N}$ and denote by f a real valued function defined in $\mathbb {R}^{N\times n}$.

• (i) If $N, n>1$, there exist (lower semicontinuous) non-level convex functions f that are poly-level convex, strong BJW-quasi-level convex, periodic-weak BJW-quasi-level convex, weak BJW- quasi-level convex, and rank-one level convex.

• (ii) For $N\ge 1$ and $n>1$, there exist (lower semicontinuous) functions f that are weak BJW-quasi-level convex, but neither poly-level convex, nor strong BJW-quasi-level convex, nor rank-one level convex, nor periodic-weak BJW-quasi-level convex in a fixed cube C. In particular, taking $C=Q$, there exist non periodic-weak BJW-quasi-level convex functions satisfying all the previous properties.

• (iii) If $N, n >1$, there exist (lower semicontinuous) rank-one level convex functions f that are not strong BJW-quasi-level convex.

Proof

Statement (i) is proved by Example 3.14 having in mind the implications (2) (i), (3) and (5), stated in Theorem 3.12. Observe that this example can be easily adapted to the case $N \not = n$. Statement (ii) is proved by Example 3.15 having in mind Theorem 3.12 (2). Finally, statement (iii) is proved by Example 3.16. $\square$

Example 3.18

If $f:{\mathbb {R}}^{N\times n}\rightarrow {\mathbb {R}}$ is a lower semicontinuous poly-level convex function, satisfying $\lim _{|\xi |\rightarrow +\infty }$ $f(\xi )=+\infty$, then the bounded function $\arctan (f):{\mathbb {R}}^{N\times n}\rightarrow (-\pi /2,\pi /2)$ is poly-level convex and strong BJW-quasi-level convex.

The previous analysis leaves open several questions that we list below.

• (1) Example 3.18 shows that the assumptions of Theorem 3.12 (2)(ii) are not sharp. We can wonder if the coercivity condition $\lim _{|\xi |\rightarrow +\infty } f(\xi )=+\infty$ can be removed in general. Recall also that if we assume f is level convex and lower semicontinuous ( which in particular is poly-level convex) then f is strong BJW-quasi-level convex with no need of any growth assumption.

• (2) Can we obtain an example showing that strong BJW-quasi-level convexity does not imply poly-level convexity? Recall that in the integral setting there exist examples of quasiconvex functions which are not polyconvex ([43, Theorem 5.51].

• (3) Does periodic-weak BJW-quasi-level convexity imply poly-level convexity?

• (4) Does periodic-weak BJW-quasi-level convexity in any cube C together with lower semicontinuity imply strong BJW-quasi-level convexity? (This being the case, then the two conditions are equivalent.)

• (5) Does weak BJW-quasi-level convexity together with the continuity of the function imply strong BJW-quasi-level convexity?

• (6) The results of next section suggest that necessary and sufficient conditions may be obtained under a coercivity assumption. In particular does weak BJW-quasi-level convexity imply rank-one or strong BJW-quasi-level convexity in the class of coercive functions?

Questions (3) and (4) are open even in the scalar case $N=1$.

4 Convexity notions arising in connection with $L^p$- approximation

In this section, we address the comparison between definitions of the previous sections and those arising in the context of so-called power-law (i.e. $L^p$-) approximation, in particular the notions of $\textrm{curl}-\infty$ quasiconvexity and $\textrm{curl}$-Young quasiconvexity (see Definition 4.2). The importance of these notions goes beyond the lower semicontinuity of supremal functionals and we review, in the next introductory paragraphs, the context of their introduction in the literature as well as the motivation to our analysis. Having in mind the scope of power-law approximation in the applications (see the list of references in Sect. 1), we start our discussion focusing on its interplay with the broader notion of $\mathcal A-\infty$ quasiconvexity, ${\mathcal {A}}$ denoting a generic differential constraint (e.g. ${\mathcal {A}}= \mathrm div$, in the case of plasticity, or ${\mathcal {A}}=(\mathrm curl,\mathrm div)$ in the case of micromagnetics, or ${\mathcal {A}}= \mathrm curl$, as in our subsequent analysis).

At this point it is worth to recall that the theory of $\mathcal A$-quasiconvexity has been introduced by Dacorogna, (see e.g. [42, pp. 100–102]), the theory was later formalized in [51], in the case of constant rank operators, (to which we refer for a detailed treatment of the subject). It has been then extended to the context of $L^\infty$ problems, first in the case when ${\mathcal {A}}=\textrm{div}$ treated by Bocea and Nesi [29] and later, with much wider generality, by Ansini and Prinari in [4, 5], giving particular emphasis to power-law approximation.

Indeed, departing from the material science’s results already mentioned in the introduction, where it was satisfactory to provide sufficient conditions on a supremand $f:\Omega \times \mathbb R^{m}\rightarrow [0,+\infty )$, in order to guarantee the variational convergence, as $p\rightarrow +\infty$, of functionals of the type

$$\begin{aligned} v \mapsto \left( \int _\Omega f^p(x, v(x))\,dx\right) ^{\frac{1}{p}} \end{aligned}$$

(4.1)

towards

$$\begin{aligned} v \mapsto {\text {*}}{ess\,sup}_{x \in \Omega } f(x, v(x)), \end{aligned}$$

(4.2)

with v possibly satisfying ${\mathcal {A}} v=0$ (cf. [25, 29, 39, 48, 53] among a wider literature), the asymptotic behaviour of functionals of the type (4.1) has been object of investigation, leading to limiting $L^\infty$ energies different from (4.2), see for instance [4, 5, 11, 33, 74].

In particular, in [4, Theorem 4.2], the $\Gamma$-limit with respect to the $L^\infty$-weak* convergence of (4.1), has been computed for Carathéodory integrands, under a generic differential constraint ${\mathcal {A}}$ on the fields v and a linear coercivity condition on f on the second variable, i.e. when there exists $\alpha >0$ such that

$$\begin{aligned} f(x,\xi ) \ge \alpha |\xi |, \end{aligned}$$

(4.3)

for every $\xi \in {\mathbb {R}}^{m}$ and a.e. $x \in \Omega$. Having in mind the case of ${\mathcal {A}}= \mathrm curl$ and $m=N\times n$, the obtained limit energy has the form

$$\begin{aligned} v \mapsto {\text {*}}{ess\,sup}_{x \in \Omega } Q_\infty f(x, v(x)), \end{aligned}$$

where the density $Q_\infty f$ is the so-called $\mathrm curl-\infty$ quasiconvex envelope of $f(x,\cdot )$, namely the greatest $\mathrm curl-\infty$ quasiconvex minorant of $f(x,\cdot )$ (see [4, Section 3.2] and [5] for definitions and proofs of this result in a more general framework and (4.11) below for an equivalent definition). More precisely, in [4, Theorem 4.4] it has been proven that the $\textrm{curl}-\infty$ quasiconvexity of f is necessary and sufficient for the $L^p$- approximation of (4.2) in terms of (4.1) in the continuous, homogeneous (and $\mathrm curl$-free, among more general operators ${\mathcal {A}}$) setting, assuming (4.3).

With $\textrm{curl}-\infty$ quasiconvexity playing a crucial role for the attainment of a variational limit with supremal form, the question of comparing this notion with the other (necessary and) sufficient conditions for this variational convergence, arises naturally and consequently the question of necessary and sufficient conditions for lower semicontinuity of supremal functionals given in Sect. 3. It is worth, indeed, to recall that, from the theoretical stand-point, the variational power-law approximation (for instance obtained via $\Gamma$-convergence), guarantees that the limit functional is weakly* lower semicontinuous (see [46]). This entails that the ‘convexity’ hypotheses which provide power-law approximation are sufficient conditions for the lower semicontinuity of the limiting supremal functional, however leaving open the necessity condition. With the aim of adopting power-law approximation to get lower semicontinuity of their limiting supremal functionals, the definition of generalized Jensen’s inequality has been introduced in [39], later revisited by [5] (for general operators ${\mathcal {A}}$), leading to the notion of $\mathrm curl$-Young quasiconvexity, and $\mathrm curl_{(p>1)}$-Young quasiconvexity (see Definition 4.2). Hence the question of comparing and establishing a hierarchy among the notions of $\textrm{curl}_{(p>1)}$-Young, $\textrm{curl}-\infty$ and $\textrm{curl}$-Young quasiconvexity (and those introduced in Sect. 3) emerges as well. At this point it should be emphasized that the question was already completely solved in the scalar case $n=1$ in [22], using three different approaches. Performing an $L^p$-approximation, by means of the duality theory in Convex Analysis, and making use of Young measures, level convex envelopes appear as densities of relaxed functionals. It is not yet known how to obtain the relaxation in the vectorial framework, and, at the same time, how to deal with the three approaches mentioned above.

In order to introduce some of the mentioned properties we will need the concept of (gradient) Young measures. We start recalling the fundamental theorem of Young measure theory, which we present as in [76, Theorem 4.1].

Denote by $\mathcal Pr({\mathbb {R}}^{m})$ the set of Borel probability measures defined in ${\mathbb {R}}^{m}$.

Theorem 4.1

Let $\Omega \subseteq \mathbb {R}^n$ be an open, bounded, connected set with Lipschitz boundary. Let $(V_j)_{j\in \mathbb {N}}$ be a sequence bounded in $L^p(\Omega ;{\mathbb {R}}^m)$, where $p \in [1,+\infty ]$. Then, there exists a subsequence (not explicitly labeled) and a family of probability measures, $\{\nu _x\}_{x \in \Omega }\subset {\mathcal Pr}({\mathbb {R}}^m)$, called the $(L^p)$-Young measure generated by the (sub)sequence $(V_j)_{j\in \mathbb {N}}$, such that the following assertions are true:

• (i) The family $\{\nu _x\}_{x \in \Omega }$ is weakly* measurable, that is, for all Carathéodory integrands $f: \Omega \times {\mathbb {R}}^m \rightarrow {\mathbb {R}}$, the compound function

  $$\begin{aligned} x\mapsto \langle f (x, \cdot ), \nu _x\rangle =\int _{{\mathbb {R}}^m} f(x, \xi )\,d \nu _x(\xi ), \; x \in \Omega \end{aligned}$$

  is Lebesgue measurable,

• (ii) If $p \in [1,+\infty )$, it holds that $\int _\Omega \int _{\mathbb R^{m}}|\xi |^p\,d\nu _x(\xi )\,dx <+\infty ,$ or, if $p =\infty$, there exists a compact set $K \subset {\mathbb {R}}^m$ such that $\textrm{supp}\,\nu _x \subset K$ for a.e. $x \in \Omega$.

• (iii) For all Carathéodory integrands $f: \Omega \times {\mathbb {R}}^m \rightarrow {\mathbb {R}}$ with the property that the family $(f (x, V_j ))_{j\in \mathbb {N}}$ is uniformly bounded in $L^1$ and equiintegrable, it holds that $f(x,V_j)\rightharpoonup \left( x \mapsto \int _{{\mathbb {R}}^m}f(x,\xi )\,d\nu _x(\xi )\right)$ in $L^1$.

In the case $p<\infty$, (iii) follows by (i) and (ii), (cf. [76, Problem 4.3]) and thus we will refer to ($L^p$)-Young measure to any family of parametrized measures $\nu =\{\nu _x\}_{x\in \Omega }$ satisfying (i) and (ii), either if $p \in [1,+\infty )$ or $p=+\infty$.

We will write $V_j\overset{Y}{\rightarrow }\nu$ to refer to the sequence $(V_j)_{j\in \mathbb {N}}$ which generates the Young measure $\nu$. The Young measure $\nu$ is said to be homogeneous if there is a measure $\nu _0 \in \mathcal Pr({\mathbb {R}}^m)$ such that $\nu _x = \nu _0$ for ${\mathcal {L}}^n$- a.e. $x \in \Omega .$

In the sequel, we will be interested in Young measures that are generated by sequences of gradients. Recall that, given an $(L^p)$-Young measure $\nu \equiv \{\nu _x\}_{x\in \Omega }$ we say that $\nu$ is a $W^{1,p}$-gradient Young measure, $p \in [1,+\infty ]$, if there exists $u_j \in W^{1,p}(\Omega )$ such that $D u_j$ generates $\nu \equiv \{\nu _x\}_{x \in \Omega }$. If $p=+\infty$ we can simply say that $\{\nu _x\}_{x\in \Omega }$ is a gradient Young measure (we refer to Kinderlehrer and Pedregal [62, 63], and to Rindler [76], where these measures are called $W^{1,\infty }$-gradient Young measures). A homogeneous $W^{1,p}$-gradient Young measure (homogeneous gradient Young measure respectively) is a $W^{1,p}$-gradient Young measure (a gradient Young measure respectively) which is homogeneous in the above mentioned sense.

Having in mind the more general setting of ${\mathcal {A}}$- free fields in $L^p$, and in order to understand the results available in literature dealing with $L^p$-approximation, the Fundamental Theorem can be considered also to justify the introduction of $\mathcal A-\infty$ Young measures, as in [51, Section 2] and [5]. Indeed, without loss of generality, these are measures generated by sequences in $L^\infty (\Omega ; \mathbb R^{d\times N}) \cap \textrm{Ker} {\mathcal {A}}$ (where $\textrm{Ker}\mathcal A$ denotes the kernel of the operator ${\mathcal {A}}$) uniformly bounded in the $L^\infty$ norm (or equivalently, possibly passing to a subsequence, weakly* converging in $L^\infty$ (see [51, Section 2])). In the case ${\mathcal {A}}= \textrm{curl}$, it results that $\textrm{curl} -\infty$ Young measures are gradient Young measures. In the following, we will adopt the latter terminology.

Definition 4.2

Let $f:\mathbb {R}^{N\times n}\longrightarrow \mathbb {R}$ be a Borel measurable function.

• (1) Assume that f is lower semicontinuous and bounded from below. We say that f is $\textrm{curl}_{(p>1)}$-Young quasiconvex, if

  $$\begin{aligned} {\text {*}}{ess\,sup}_{x \in Q}f\left( \int _{\mathbb R^{N\times n}}\xi \, d\nu _x(\xi ) \right) \le {\text {*}}{ess\,sup}_{x \in Q} \left( \mathop {\nu _x - \mathrm ess\,sup}_{\xi \in {\mathbb {R}}^{N\times n}}f(\xi )\right) , \end{aligned}$$

  (4.4)

  whenever $\nu \equiv \{\nu _x\}_{x \in Q}$ is a $W^{1,p}$-gradient Young measure for every $p\in (1,\infty )$.

• (2) Assume that f is lower semicontinuous and bounded from below. We say that f is $\textrm{curl}$-Young quasiconvex, if

  $$\begin{aligned} {\text {*}}{ess\,sup}_{x \in Q}f\left( \int _{{\mathbb {R}}^{N\times n}}\xi \, d\nu _x(\xi ) \right) \le {\text {*}}{ess\,sup}_{x \in Q} \left( \mathop {\nu _x - \mathrm ess\,sup}_{\xi \in {\mathbb {R}}^{N\times n}}f(\xi )\right) , \end{aligned}$$

  (4.5)

  whenever $\nu \equiv \{\nu _x\}_{x \in Q}$ is a gradient Young measure.

• (3) Assume that f is non-negative. We say that f is $\mathbf {\textrm{curl}-\infty }$ quasiconvex if for every $\xi \in {\mathbb {R}}^{N\times n}$

  $$\begin{aligned} f(\xi ) = \lim _{p\rightarrow +\infty } \inf \left\{ \left( \int _Q f^p(\xi + D u (x))\,dx\right) ^{\tfrac{1}{p}}: u \in W^{1,\infty }_\textrm{per} (Q; {\mathbb {R}}^N)\right\} . \end{aligned}$$

Remark 4.3

• (i) We observe that the double essential suprema in (4.4) and (4.5) of the previous definition are meaningful because the function f is assumed to be lower semicontinuous and bounded from below. In principle, one can give definitions of $\textrm{curl}_{(p>1)}$-Young and $\textrm{curl}$-Young quasiconvexity without these assumptions, adding the condition that the right-hand sides of (4.4) and (4.5) make sense. This may be the approach done in [5, 39]. Next, we describe why the assumptions of lower semicontinuity and boundedness from below are sufficient for this goal. We first observe that there is no loss of generality assuming the bound from below is zero. In that case,

  $$\begin{aligned} \mathop {\nu _y - \mathrm ess\,sup}_{\xi \in {\mathbb {R}}^{N\times n}}f(\xi )=\lim _{k\rightarrow \infty }||f||_{L^k(\mathbb {R}^{N\times n};\nu _y)}. \end{aligned}$$

  This identity ensures the Lebesgue measurability of $y\mapsto \mathop {\nu _y - \mathrm ess\,sup}_{\xi \in {\mathbb {R}}^{N\times n}}f(\xi )$ in view of the Lebesgue measurability of

  $$\begin{aligned} y\mapsto \int _{\mathbb {R}^{N\times n}}|f(\xi )|^k\,d\nu _y \end{aligned}$$

  which follows from Theorem 4.1 (i), extended to normal integrands by using [49, Corollary 6.30].

• (ii) The notion of $\textrm{curl}_{(p>1)}$-Young quasiconvexity already appeared in [39, Eq. (3.1) in Theorem 3.1, under the name of ’generalized Jensen’s inequality’]. There, the function f is considered with also x and u dependence.

• (iii) Note that, if $1\le p<q\le \infty$, then every $W^{1,q}$-gradient Young measure (gradient Young measure if $q=\infty$) is also a $W^{1,p}$-gradient Young measure. Therefore, to verify $\textrm{curl}_{(p>1)}-$Young quasiconvexity it suffices to check (4.4) for parametrized measures that are $W^{1,p}$-gradient Young measures for every $p\in (p_0,\infty )$ with $p_0>1$.

• (iv) The set Q in the definition of $\textrm{curl}$-Young quasiconvexity can be replaced by any other bounded open set as observed in [5, Remark 4.3] in the context of ${\mathcal {A}} -$quasiconvexity under a coercivity assumption.

• (v) the notion of $\textrm{curl}-\infty$ quasiconvexity can be found in [4, Definition 3.3], with ${\mathcal {A}}= \textrm{curl}$.

Next we provide some characterizations of $\textrm{curl}_{(p>1)}$-Young quasiconvexity and of $\textrm{curl}$-Young quasiconvexity.

Proposition 4.4

Let $f:\mathbb {R}^{N\times n}\longrightarrow \mathbb {R}$ be a lower semicontinuous function and bounded from below. Then the following conditions are equivalent

• (i) f is $\textrm{curl}_{(p>1)}$-Young quasiconvex;

• (ii) f satisfies

  $$\begin{aligned} f\left( \int _{{\mathbb {R}}^{N \times n}}\xi \,d\nu _x(\xi )\right) \le \mathop {\nu _x - \mathrm ess\,sup}_{\xi \in {\mathbb {R}}^{N\times n}} f(\xi )\ \hbox { for a.e. } x \in Q \end{aligned}$$

  whenever $\nu \equiv \{\nu _x\}_{x \in Q}$ is a $W^{1,p}$-gradient Young measure for every $p\in (1,\infty )$;

• (iii) f satisfies

  $$\begin{aligned} f\left( \int _{{\mathbb {R}}^{N \times n}}\xi \,d\nu (\xi )\right) \le \mathop {\nu - \mathrm ess\,sup}_{\xi \in {\mathbb {R}}^{N\times n}} f(\xi ) \end{aligned}$$

  (4.6)

  whenever $\nu$ is a homogeneous $W^{1,p}$-gradient Young measure for every $p\in (1,\infty )$.

Moreover, in the definition of $\textrm{curl}_{(p>1)}$-Young quasiconvexity the domain Q can be replaced by any open, bounded, connected set $\Omega \subseteq \mathbb {R}^n$, with Lipschitz boundary.

An analogous statement holds by replacing $\textrm{curl}_{(p>1)}$-Young quasiconvexity by $\textrm{curl}$-Young quasiconvexity and $W^{1,p}$-gradient Young measures for every $p\in (1,\infty )$ by gradient Young measures.

Remark 4.5

We observe that the result just stated is still true without the lower semicontinuity and boundedness from below assumptions, if conditions (4.4) and (4.5) are meaningful in the sense of Remark 4.3 (i).

Proof

Clearly (ii) entails (i). On the other hand, (i) is equivalent to (iii). Indeed, (i) implies (iii) because homogeneous $W^{1,p}$-gradient Young measures are particular cases of $W^{1,p}$-gradient Young measures. In turn, (iii) implies (i) taking into account that given an arbitrary $W^{1,p}$-gradient Young measure $\{\nu _x\}_{x \in Q}$, each $\nu _x$ (for almost every x fixed) is a homogeneous $W^{1,p}$-gradient Young measure (cf. [76, Proposition 5.14 and Remark 5.15]). Similarly, (i) implies (ii).

In particular, by (iii), we conclude that (i) does not depend on the domain Q. Actually, reasoning as above we can show that (iii) is equivalent to

$$\begin{aligned} f\left( \int _{{\mathbb {R}}^{N\times n}}\xi \, d\nu _x(\xi ) \right) \le {\text {*}}{ess\,sup}_{y \in \Omega } \left( \mathop {\nu _y - \mathrm ess\,sup}_{\xi \in {\mathbb {R}}^{N\times n}}f(\xi )\right) ,\ \mathrm {a.e.}\ x\in \Omega \end{aligned}$$

whenever $\nu \equiv \{\nu _x\}_{x \in \Omega }$ is a $W^{1,p}$-gradient Young measure for every $p\in (1,\infty )$ where $\Omega \subseteq \mathbb {R}^n$ is any open, bounded, connected set with Lipschitz boundary.

The proof of the case of $\textrm{curl}$-Young quasiconvex functions is analogous to the previous one. $\square$

Next we provide a characterization of $\textrm{curl}-\infty$ quasiconvexity through a power-law approximation of quasiconvex hulls.

Proposition 4.6

Let $f:\mathbb {R}^{N\times n}\longrightarrow [0,\infty )$ be a Borel measurable function. Then f is $\mathrm curl-\infty$ quasiconvex if and only if

$$\begin{aligned} f(\xi )= \lim _{p\rightarrow +\infty } ({\mathcal {Q}} (f^p))^{1/p}(\xi ), \end{aligned}$$

(4.7)

where ${\mathcal {Q}} (f^p)$ stands for the quasiconvex envelope of $f^p$. In particular, if f is $\mathrm curl-\infty$ quasiconvex then f is lower semicontinuous and locally bounded.

Remark 4.7

Note that, combining (4.7) with the several characterizations of a quasiconvex envelope provided in Lemmas 2.6 and 2.9 (this second lemma applies to functions with linear growth), we can explicit $\mathrm curl-\infty$ quasiconvex functions in terms of a limit of several type of minimization problems.

Proof

The characterization of $\mathrm curl-\infty$ quasiconvexity follows from Lemma 2.6 applied to $f^p$.

Now assume that f is a $\mathrm curl-\infty$ quasiconvex function. By Remark 2.2 (ii), $\mathcal Q (f^p)$ is lower semicontinuous. Therefore, also $({\mathcal {Q}} (f^p))^{1/p}$ is lower semicontinuous and thus, f being the limit of a monotone increasing family of lower semicontinuous functions, it is also lower semicontinuous. Finally, to show that f is locally bounded, we invoke [3, Exercise 5.11]. Indeed, since ${\mathcal {Q}} (f^p)$ is quasiconvex, it is also separately convex and we get that, for $h\in \mathbb {N}$,

$$\begin{aligned} \sup _{\xi \in [-h,h]^{N\times n}} {\mathcal {Q}} (f^p)(\xi )&\le (2^{N\times n+1}-1)\max \left\{ Q (f^p)(\zeta ):\ \zeta \in [-h-1,h+1]^{N\times n}\cap \mathbb {Z}^{N\times n}\right\} \\&\le (2^{N\times n+1}-1)\max \left\{ f^p(\zeta ):\ \zeta \in [-h-1,h+1]^{N\times n}\cap \mathbb {Z}^{N\times n}\right\} . \end{aligned}$$

implying

$$\begin{aligned} \sup _{\xi \in [-h,h]^{N\times n}} \mathcal (Q (f^p))^{1/p}(\xi )&\le (2^{N\times n+1}-1)^{1/p}\max \\&\quad \ \left\{ f(\zeta ):\ \zeta \in [-h-1,h+1]^{N\times n}\cap \mathbb {Z}^{N\times n}\right\} \end{aligned}$$

that provides a local bound for f if we have in mind (4.7). $\square$

As a complement to Theorem 3.12, we state a result, establishing some relations between the convexity notions introduced above and those of the previous section. We will consider the following growth and coercivity conditions

$$\begin{aligned}&(G) \qquad \exists \ C>0:\ f(\xi ) \le C(1+|\xi |)\; \hbox { for every }\xi \in {\mathbb {R}}^{N\times n} \\&(C) \qquad \exists \ \alpha , \beta >0:\ f(\xi )\ge \alpha |\xi |-\beta \; \hbox { for every }\xi \in {\mathbb {R}}^{N\times n}. \end{aligned}$$

Theorem 4.8

Let $f:{\mathbb {R}}^{N\times n}\rightarrow {\mathbb {R}}$ be a Borel measurable function, bounded from below.

• (1) If f is level convex then it satisfies inequality (4.6) for every $W^{1,p}$-gradient Young measure, for $p \in (1,+\infty ]$. In particular, if it is also lower semicontinuous then f is $\textrm{curl}_{(p>1)}-$Young quasiconvex and $\textrm{curl}$-Young quasiconvex.

• (2) If $f:{\mathbb {R}}^{N\times n}\rightarrow [0,+\infty )$ is level convex, lower semicontinuous, and satisfies the coercivity condition (C), then f is $\mathrm curl-\infty$ quasiconvex.

• (3) If $f: {\mathbb {R}}^{N\times n}\rightarrow [0, +\infty )$ and poly-level convex with $f=g\circ T$, for $g:\mathbb {R}^{\tau (n,N)}\longrightarrow \mathbb {R}$ level convex and lower semicontinuous and satisfying (C) in $\mathbb {R}^{\tau (n,N)}$ then f is $\textrm{curl}-\infty$ quasiconvex.

• (4) If f is poly-level convex with $f=g\circ T$, for $g:\mathbb {R}^{\tau (n,N)}\longrightarrow \mathbb {R}$ level convex then f satisfies (4.6) for every $W^{1,p}$-gradient Young measure for $p \in (1,+\infty ]$. In particular, if f is also lower semicontinuous then f is $\textrm{curl}_{(p>1)}-$Young quasiconvex and $\textrm{curl}$-Young quasiconvex.

• (5) If f is $\textrm{curl}_{(p>1)}-$Young quasiconvex, then f is $\textrm{curl}-$Young quasiconvex.

• (6) Let $f:{\mathbb {R}}^{N\times n}\rightarrow [0,+\infty )$ be a $\textrm{curl}_{(p>1)}-$Young quasiconvex function satisfying the coercivity condition (C). If, moreover, either f is upper semi-continuous or f satisfies the growth condition (G), then f is $\mathrm curl-\infty$ quasiconvex.

• (7) If $f:{\mathbb {R}}^{N\times n}\rightarrow [0,+\infty )$ is $\textrm{curl}-\infty$ quasiconvex then f is $\textrm{curl}-$Young quasiconvex. Moreover if it also satisfies the growth condition (G), then f is $\textrm{curl}_{(p>1)}-$Young quasiconvex.

• (8) If $f:{\mathbb {R}}^{N\times n}\rightarrow [0,+\infty )$ is $\mathrm curl-$Young quasiconvex and locally bounded and satisfies the coercivity condition (C), then f is also $\mathrm curl-\infty$ quasiconvex. Moreover, if f satisfies the growth condition (G), then f is $\mathrm curl_{(p>1)}$- Young quasiconvex.

• (9) If f is either $\textrm{curl}$-Young quasiconvex or $\textrm{curl}_{(p>1)}-$Young quasiconvex then f is strong BJW-quasi-level convex. Moreover, if we only assume (4.6) for every $W^{1,p}$-gradient Young measure with $p>1$ or for any gradient Young measure, then f is weak BJW-quasi-level convex. Also, if f satisfies (4.6) for every gradient Young measure, or for every $W^{1,p}$-gradient Young measure for every $p>1$ then f is rank-one level convex.

• (10) If $f:{\mathbb {R}}^{N\times n}\rightarrow [0,+\infty )$ is $\mathrm curl-\infty$ quasiconvex, then f is strong BJW-quasi-level convex. In particular, it is periodic-weak BJW-quasi-level convex in any cube $C\subset {\mathbb {R}}^n$, weak BJW-quasi-level convex, and rank-one level convex.

Fig. 2, above depicts the implications stated in Theorem 4.8 concerning the notions introduced in this section. Note that the theorem contains broader results.

Fig. 2

The figure shall be considered to accompany Theorem 4.8. Namely, the labels to each implications refer to the items in the theorem containing the referred implication and, when additional hypotheses are required, the label is signed with $^*$. The subscript + means that the corresponding implication only applies to nonnegative functions

Remark 4.9

• (i) In view of (5), (1) improves [5, Proposition 3.3 (2)] in the case of ${\mathcal {A}}=\mathrm curl$. Observe also that the proof of (1) ensures that level convex functions satisfy condition (4.6) without any assumption of lower semicontinuity nor on the sign of the function. These assumptions are only needed to relate with $\textrm{curl}_{(p>1)}-$Young quasiconvexity.

• (ii) As a by-product of the proof of (2), we have obtained a generalization of [74, Proposition 5.1] asserting

  $$\begin{aligned} \lim _{p\rightarrow +\infty }\left( (f^p)^{**}\right) ^{1/p}=f \end{aligned}$$

  under the weaker coercivity assumption (C). (The notation $(f^p)^{**}$ stands, as usual, for the bidual of $f^p$, cf. [43, Definition 2.41 (ii)].

• (ii) We observe that (3) has been already proven under continuity assumptions of g in [4, Proposition 5.7].

• (iv) Regarding (4), the fact that a poly-level convex function is also $\textrm{curl}$-Young quasiconvex has been already proven in [5, Proposition 6.3] in the case of a nonnegative and a lower senjcontinuous g, since their argument exploits our first implication of (7).

• (v) We observe that the first implication of (7) in the above result has been proved in [5, Proposition 3.4], in the more general setting of ${\mathcal {A}}-\infty$-Young measures, under the continuity assumption on f. As seen in (7), this extra requirement can be removed in the case ${\mathcal {A}}= \mathrm curl$. Note, however that, in this case, as observed in Remark 4.6, f is lower semicontinuous.

• (vi) The assertion of (9) related to rank-one level convexity has been proved in [5, Proposition 6.4 (3)] under the extra lower semicontinuity assumption.

• (vii) If $n=1$ or $N=1$, f is level convex if and only if it satisfies (4.6) for every $W^{1,p}$-gradient Young measure, for any $p \in (1,+\infty ]$. In particular, if f is also lower semicontinuous it is level convex (equivalently strong BJW-quasi-level convex) if and only if it is $\mathrm curl_{(p>1)}$-Young quasiconvex and if and only if it is $\mathrm curl$-Young quasiconvex. The above considerations follow by (1) and (9), recalling that in the scalar case, rank-one level convexity reduces to level convexity. Note, however, that, with this restriction, in the proof of (9) we can invoke the zig-zag lemma, cf. [46, Lemma 20.2], in place of the construction of approximate solutions. We recall that if $N=1$ there exist lower semicontinuous functions which are weak BJW-quasi-level convex but neither $\textrm{curl}_{(p>1)}$-Young quasiconvex nor $\textrm{curl}$-Young quasiconvex.

• (viii) If $n=1$ or $N=1$ and $f:{\mathbb {R}}^{N\times n}\rightarrow [0,+\infty )$ satisfies (C), then it is level convex, lower semicontinuous (equivalently strong BJW-quasi-level convex) if and only if it is $\mathrm curl-\infty$ quasiconvex.

Proof

• (1) The argument to prove this implication follows from the fact that level convexity and Borel measurability entail the supremal Jensen’s inequality. Namely

  $$\begin{aligned} f\left( \int _\Omega \varphi \,d\mu \right) \le \mu -{\text {*}}{ess\,sup}_{x\in \Omega } f(\varphi (x)) \end{aligned}$$

  for every probability measure $\mu$ on $\mathbb {R}^{d}$ supported on the open set $\Omega \subseteq \mathbb {R}^{d}$, and every $\varphi \in L^1_\mu (\Omega ;\mathbb {R}^{n})$ (see Theorem C.1 for a proof). We apply the previous inequality with $\varphi = id$, $\Omega = {\mathbb {R}}^{N\times n}$, and $\mu$ any probability measure in $\mathbb {R}^{N\times n}$. In particular, we observe that f satisfies (4.6), whenever $\nu$ is a homogeneous $W^{1,p}$-gradient Young measure for every $p\in (1,\infty ]$ which, by Proposition 4.4, implies that f is $\textrm{curl}_p-$Young quasiconvex and $\textrm{curl}$-Young quasiconvex provided f is also lower semicontinuous.

• (2) This result has been obtained under the requirement that $f(\xi )\ge \alpha |\xi |$, for every $\xi \in {\mathbb {R}}^{N\times n}$ in [5, Proposition 2.9]. Here we observe that this condition can be relaxed. We start observing that

  $$\begin{aligned} \limsup _{p\rightarrow +\infty } ({\mathcal {Q}} (f^p)(\xi ))^{1/p}\le f(\xi ). \end{aligned}$$

  Having in mind that $(f^p)^{**}\le {\mathcal {Q}} (f^p)$, we will prove the opposite inequality, showing that

  $$\begin{aligned} f(\xi )\le \limsup _{p\rightarrow +\infty } ((f^p)^{**}(\xi ))^{1/p}. \end{aligned}$$

  To this end we will invoke [72, Corollary 3.11] which relies on the relaxation result [72, Theorem 3.9] where the coercivity is only needed to ensure boundedness of gradients. Therefore [72, Corollary 3.11] can be generalized to the coercivity condition $f(\xi )\ge \alpha |\xi |-\beta$. However, [72, Corollary 3.11] requires continuity and linear growth from above. To deal with these assumptions, we replace f by its Pasch-Hausdorff transform, as in [5, Proposition 2.9]. This is defined as $f_\lambda (\xi ):=\inf \{\max \{f(\eta ), \lambda |\xi -\eta |\}: \eta \in {\mathbb {R}}^{N\times n}\}$ for every $\lambda >0$ and it turns out that $f_\lambda$ is level convex, continuous and $f=\sup _{\lambda >0} f_\lambda$. Moreover $f_\lambda (\xi )\le \max \{f(0), \lambda |\xi |\} \le f(0)+ \lambda |\xi |$, so it has linear growth from above. For what concerns the coercivity condition, it results that

  $$\begin{aligned} f_\lambda (\xi )&\ge \inf \left\{ \max \{\alpha |\eta |-\beta , \lambda |\xi -\eta |-\beta \}: \eta \in {\mathbb {R}}^{N\times n}\right\} \\&=\inf \left\{ \max \{\alpha |\eta |,\lambda |\eta -\xi |\}: \eta \in {\mathbb {R}}^{N\times n}\right\} -\beta \\&\ge \inf \left\{ \max \{\alpha |\eta |,\alpha |\eta -\xi |\}: \eta \in {\mathbb {R}}^{N\times n}\right\} - \beta ; \hbox { for } \lambda \ge \alpha . \end{aligned}$$

  Then, in view of the level convexity of $|\cdot |$,

  $$\begin{aligned} f_\lambda (\xi )\ge \frac{1}{2}\alpha |\xi |-\beta , \hbox { for } \lambda \ge \alpha . \end{aligned}$$

  Applying [72, Corollary 3.11] to $f_\lambda$, we have the same chain of inequalities as in [5, Proposition 2.9], i.e.

  $$\begin{aligned} f(\xi )&=\sup _{\lambda>0}f_\lambda (\xi )=\sup _{\lambda>0}(\sup _{p>1}(((f_\lambda )^p)^{**}(\xi ))^{1/p}&\\&=\sup _{p>1}\sup _{\lambda>0}(((f_\lambda )^p)^{**}(\xi ))^{1/p}\le \sup _{p>1}((f^p)^{**}(\xi ))^{1/p}. \end{aligned}$$

  Finally, observe that, since $\{((f^p)^{**}(\xi ))^{1/p}\}$ is nondecreasing,

  $$\begin{aligned} \sup _{p>1}((f^p)^{**}(\xi ))^{1/p}=\lim _{p\rightarrow +\infty } ((f^p)^{**}(\xi ))^{1/p} \end{aligned}$$

  concluding the proof.

• (3) The proof develops along the lines of [4, Proposition 5.7]. Taking into account the arguments developed in (2), we can deal with the weaker assumptions of our statement, allowing us to write

  $$\begin{aligned} \lim _{p\rightarrow +\infty }\left( (g^p)^{**}\right) ^{1/p}(T(\xi ))= g(T(\xi ))= f(\xi ). \end{aligned}$$

  On the other hand,

  $$\begin{aligned} f(\xi ) = g(T (\xi )) = \lim _{p\rightarrow +\infty } ((g^p)^ {**})^{1/p}(T (\xi )) \le \lim _{p\rightarrow +\infty } f_p(\xi ) \le f(\xi ),\qquad \end{aligned}$$

  (4.8)

  where, adopting the same notation as in [5] and [4],

  $$\begin{aligned} f_p(\xi ):=\inf \left\{ \left( \int _Q f^p(\xi + D u (x))\,dx\right) ^{\tfrac{1}{p}}: u \in W^{1,\infty }_\textrm{per} (Q; {\mathbb {R}}^N)\right\} . \end{aligned}$$

  Indeed the polyconvex function $(g^p)^{**}(T(\xi ))\le g^p(T(\xi ))=f^p(\xi )$, from which the first inequality in (4.8) follows. Finally, (4.8) concludes the proof of the statement.

• (4) If follows as the proof of (1), by applying Jensen’s inequality with $W^{1,p}$-gradient Young measures, ($p \in [1,\infty ]$) to the function g, recalling that T is quasiaffine and invoking [76, Corollary 5.12].

• (5) As observed in Remark 4.3, gradient Young measures are $W^{1,p}$-gradient Young measures for every $1\le p\le \infty$. This entails the desired implication.

• (6) In the case f is upper semicontinuous, the result follows from [39, Theorem 3.1] together with [4, Theorem 4.4] (note that these results are still valid under the current weaker coercivity assumption). We stress that Theorem 4.4 in [4] requires the continuity of the function. Regarding the other case, first we invoke [74, Theorem 2.2, (61), and Remarks 3.3 and 5.1], where it has been proven that the $\Gamma$-limit with respect to the uniform ($L^\infty$) convergence in $C(\overline{Q};{\mathbb {R}}^N)$ of

  $$\begin{aligned} F_p(u):=\left\{ \begin{array}{ll} \displaystyle \left( \int _Q f^p(D u(x))\,dx\right) ^\frac{1}{p} & \hbox { if }u \in W^{1,p}(Q;{\mathbb {R}}^N)\cap C(\overline{Q};{\mathbb {R}}^N),\vspace{0.2cm}\\ + \infty & \hbox { otherwise} \end{array}\right. \end{aligned}$$

  (4.9)

  is given by

  $$\begin{aligned} F(u)=\left\{ \begin{array}{ll}\displaystyle {\text {*}}{ess\,sup}_{x \in Q} \mathcal {Q}_\infty f(D u) & \hbox { if }u \in W^{1,\infty }(Q;{\mathbb {R}}^N)\cap C(\overline{Q};{\mathbb {R}}^N),\vspace{0.2cm}\\ + \infty & \hbox { otherwise} \end{array}\right. \end{aligned}$$

  (4.10)

  where

  $$\begin{aligned} \mathcal {Q}_\infty f(\xi ):=\sup _{n \in \mathbb {N}} (\mathcal {Q}(f^n)(\xi ))^{1/n}=\lim _{p\rightarrow \infty }(\mathcal {Q}(f^p)(\xi ))^{1/p}. \end{aligned}$$

  (4.11)

  On the other hand, since f is $\mathrm curl_{(p>1)}$-Young quasiconvex, by [39, Theorem 3.1], the $\Gamma$-limit (with respect to the uniform convergence in $C(\overline{Q};{\mathbb {R}}^N)$) of the functionals $F_p$ coincides with ${\text {*}}{ess\,sup}_{x\in Q}f(D u(x))$, when $u\in W^{1,\infty }(Q;{\mathbb {R}}^N)\cap C(\overline{Q};{\mathbb {R}}^N)$. Therefore we can conclude that

  $$\begin{aligned} {\text {*}}{ess\,sup}_{x \in Q} f(D u(x))= {\text {*}}{ess\,sup}_{x \in Q} {\mathcal {Q}}_\infty f(D u(x)), \end{aligned}$$

  for every $u \in W^{1,\infty }(Q;{\mathbb {R}}^N)\cap C(\overline{Q};{\mathbb {R}}^N)$. Applying the equality to linear fuctions u with $D u=\xi$ arbitrary, we obtain

  $$\begin{aligned} f(\xi )= {\mathcal {Q}}_\infty f(\xi ). \end{aligned}$$

  Having in mind the characterization of $\mathrm curl-\infty$ quasiconvexity provided by (4.7) and recalling (4.11), this proves our claim.

• (7) We prove the second part of the statement, the first being very similar, just observing that [76, Theorem 7.15] applies to gradient Young measures with no need of any growth condition. Let $\{\nu _x\}_{x\in Q}$ be a parametrized measure that is a $W^{1,p}$-gradient Young measure for every $p\in (1,\infty )$. The growth assumption (G) allows to apply [76, Theorem 7.15] to get,

  $$\begin{aligned} {\mathcal {Q}} (f^p)\left( \int _{{\mathbb {R}}^{N\times n}} \xi \,d \nu _x(\xi )\right) \le \int _{{\mathbb {R}}^{N\times n}} f^p(\xi )\,d \nu _x(\xi ). \end{aligned}$$

  Therefore

  $$\begin{aligned} {\mathcal {Q}} (f^p)\left( \int _{{\mathbb {R}}^{N\times n}} \xi \,d \nu _x(\xi )\right) \le \int _{{\mathbb {R}}^{N\times n}} f^p(\xi )\,d \nu _x(\xi )\le \mathop {\nu _x - \mathrm ess\,sup}_{\xi \in {\mathbb {R}}^{N\times n}} f^p(\xi ). \end{aligned}$$

  Taking the power $\tfrac{1}{p}$ on this inequality and passing to the limit as $p\rightarrow \infty$ we get the $\textrm{curl}_{(p>1)}-$Young quasiconvexity of f, having in mind the assumption that f is $\textrm{curl}-\infty$ quasiconvex and condition (4.7).

• (8) The last assertion follows by the first part and (7). For the first part, start considering the functionals $F_p$ and F introduced in (4.9) and (4.10), as in the proof of (6). First, observe that [74, (5) in Remark 5.2] guarantees that the $\Gamma$-limit with respect to the $L^\infty$ convergence of the restriction of the functionals $F_p$ to $W^{1,\infty }(Q;{\mathbb {R}}^N)$ is given by the functional F in (4.10). Therefore, if we consider, for every $u \in W^{1,\infty }(Q;{\mathbb {R}}^N)$, the functional

  $$\begin{aligned}&{\mathcal {F}}(u):=\inf \left\{ \liminf _{p \rightarrow +\infty } \left( \int _Q f^p(D u_p)\,dx\right) ^{\frac{1}{p}}:\ u_p \in W^{1,\infty }(Q;\mathbb R^N), \right. \nonumber \\&\quad \left. \sup _ p\Vert u_p\Vert _{W^{1,\infty }} <+\infty , u_p \rightarrow u \hbox { in }L^\infty \right\} , \end{aligned}$$

  (4.12)

  one has

  $$\begin{aligned} {\text {*}}{ess\,sup}_{x \in Q} {\mathcal {Q}}_\infty f(D u(x))=F(u) \le {\mathcal {F}}(u) \hbox { for every }u \in W^{1,\infty }(Q;\mathbb R^N). \end{aligned}$$

  In order to prove the opposite inequality, i.e.

  $$\begin{aligned} {\mathcal {F}}(u) \le {\text {*}}{ess\,sup}_{x \in Q} \mathcal Q_\infty f(D u(x)) \hbox { for every }u \in W^{1,\infty }(Q;\mathbb R^N), \end{aligned}$$

  we start observing that, under our coercivity (C) assumptions on f, by [43, Theorem 9.1] and [46, Proposition 6.16], for every p, the functional

  $$\begin{aligned}&\inf \left\{ \liminf _{n \rightarrow +\infty }\left( \int _Q f^p(D u_n(x))\right) ^{\frac{1}{p}}: \sup _n\Vert u_n\Vert _{W^{1,\infty }}\!<\!+\infty , u_n \!\rightarrow \! u \hbox { in }L^\infty \right\} \nonumber \\&\quad =\left( \int _Q Q(f^p)(D u(x))\,dx\right) ^{\frac{1}{p}}. \end{aligned}$$

  (4.13)

  Hence, by [46, Proposition 6.11], in view of (4.13), (4.12) can be written as

  $$\begin{aligned}&{\mathcal {F}}(u)= \inf \left\{ \liminf _{p \rightarrow +\infty } \left( \int _Q Q(f^p)(D u_p)\,dx\right) ^{\frac{1}{p}}:\ u_p \in W^{1,\infty }(Q;{\mathbb {R}}^N), \right. \\&\quad \left. \sup _ p\Vert u_p\Vert _{W^{1,\infty }} <+\infty , u_p \rightarrow u \hbox { in }L^\infty \right\} . \end{aligned}$$

  Thus,

  $$\begin{aligned} {\mathcal {F}}(u)&\le \liminf _{p\rightarrow +\infty } \left( \int _Q Q(f^p)(D u(x))\,dx\right) ^{\frac{1}{p}}\\&\le \liminf _{p\rightarrow +\infty } \left( {\text {*}}{ess\,sup}_{x \in Q} Q(f^p) (D u(x))\right) ^{\frac{1}{p}} \\&=\liminf _{p\rightarrow +\infty }{\text {*}}{ess\,sup}_{x \in Q} (Q(f^p))^{\frac{1}{p}}(D u(x))\\&\le {\text {*}}{ess\,sup}_{x \in Q}{\mathcal {Q}}_\infty f(D u(x)) \end{aligned}$$

  where we have exploited [46, Proposition 6.8 and 6.11], and the definition of ${\mathcal {Q}}_{\infty } f$ and the monotonicity of $(Q(f^p))^{1/p}$. Now we have that

  $$\begin{aligned}&{\mathcal {F}}(u)=\inf \left\{ \liminf _{p \rightarrow +\infty } \left( \int _Q f^p(D u_p(x))\,dx\right) ^{1/p}: u_p \in W^{1,\infty }(Q;{\mathbb {R}}^N), \right. \nonumber \\&\quad \left. \sup _ p\Vert u_p\Vert _{W^{1,\infty }} <+\infty , u_p \overset{*}{\rightharpoonup }\ u \hbox { in }W^{1,\infty }(Q;\mathbb R^N) \right\} , \end{aligned}$$

  (4.14)

  Indeed, the inequality ‘$\le$’ is consequence of Rellich theorem and the opposite one follows by Banach-Alaoglu-Bourbaki theorem. To finish our proof, we recall that, under the assumption of $\mathrm curl$-Young quasiconvexity on f, [5, Theorem 4.1] provides

  $$\begin{aligned} {\text {*}}{ess\,sup}_{x \in Q} f(D u(x)) \le \liminf _{p \rightarrow +\infty } \left( \int _Q f^p(D u_p(x))\,dx \right) ^{1/p}, \end{aligned}$$

  for every $u_p \overset{*}{\rightharpoonup }\ u$ in $W^{1,\infty }(Q;{\mathbb {R}}^N)$, i.e.

  $$\begin{aligned} {\text {*}}{ess\,sup}_{x \in Q} f(D u(x)) \le {\mathcal {F}}(u) \hbox { for every }u \in W^{1,\infty }(Q;{\mathbb {R}}^N). \end{aligned}$$

  The opposite inequality is a consequence of the standard approximation of $L^\infty$ norm by the $L^p$ one, i.e.

  $$\begin{aligned} {\mathcal {F}}(u) \le \liminf _{p\rightarrow +\infty }\left( \int _Q f^p(D u(x))\,dx\right) ^{\frac{1}{p}}={\text {*}}{ess\,sup}_{x \in Q }f(D u(x)). \end{aligned}$$

  Finally, putting together the representations for ${\mathcal {F}}$, obtained for (4.12) and its equivalent (4.14), we can conclude that

  $$\begin{aligned} {\text {*}}{ess\,sup}_{x \in Q} f(D u(x)) = {\text {*}}{ess\,sup}_{x \in Q} {\mathcal {Q}}_\infty f(D u(x)) \end{aligned}$$

  for every $u \in W^{1,\infty }(Q;{\mathbb {R}}^N)$. This, in turn, provides the equality $f(\xi )= {\mathcal {Q}}_\infty f(\xi )$ for every $\xi \in {\mathbb {R}}^{N \times n}$, which proves the $\mathrm curl-\infty$ quasiconvexity of f.

• (9) By (5), to prove the first statement it suffices to consider the case f is $\textrm{curl}$-Young quasiconvex. Then the result follows from [5, Proposition 6.1], which in turn relies on the lower semicontinuity result in Theorem B.2 (see also [5, Theorem 4.2] for another argument). For what concerns the second implication, let $\xi \in \mathbb {R}^{N\times n}$, $\varphi \in W_0^{1,\infty }(Q;\mathbb {R}^{N})$, $u(x)=\xi \cdot x+\varphi (x)$ and the push-forward measure $\nu =D u_{\sharp }\mathcal {L}^{N\times n}$. As observed in [3, p. 60], the measure $\nu$ coincides with the generalized product $\mathcal {L}^n\otimes \delta _{Du(x)}$. Considering [62, Theorem 2.1], we observe that this latter measure is a homogeneous gradient Young measure whose barycenter is $\xi$. Hence, by (4.6),

  $$\begin{aligned} f(\xi )=f\left( \int _Q Du(x)\,dx\right) =f\left( \int _{\mathbb {R}^{N\times n}} \xi \,d\nu (\xi )\right) \le {\text {*}}{\nu -ess\,sup}_{\xi \in \mathbb {R}^{N\times n}}f(\xi )=\\ ={\text {*}}{\mathcal {L}^n\otimes \delta _{Du(x)}-ess\,sup}_{(x,\xi ) \in Q\times \mathbb {R}^{N\times n}}f(\xi )= {\text {*}}{ess\,sup}_{x \in Q}f(Du(x)) \end{aligned}$$

  proving the weak BJW-quasi-level convexity. For the next implication, let $\xi ,\eta \in \mathbb {R}^{N\times n}$ be such that $\textrm{rank}(\xi -\eta )=1$ and let $0<\lambda <1$. One needs to show that

  $$\begin{aligned} f(\lambda \xi +(1-\lambda )\eta )\le \max \{f(\xi ),f(\eta )\}. \end{aligned}$$

  Considering the construction of approximate solutions carried out in [69, p. 97], one gets a sequence $(u_j)\subseteq W^{1,\infty }(Q;\mathbb {R}^N)$ such that $u_j(x)=(\lambda \xi +(1-\lambda )\eta )\cdot x$ on $\partial Q$ and $\textrm{dist}(Du_j,\{\xi ,\eta \})\rightarrow 0$ in measure in Q. As discussed in [69, p. 120], $Du_j$ generates the homogeneous Young measure $\nu _x=\lambda \delta _\xi +(1-\lambda )\delta _\eta$. This measure has $\lambda \xi +(1-\lambda )\eta$ as barycenter, thus

  $$\begin{aligned} f(\lambda \xi \!+\!(1\!-\!\lambda )\eta )\!=\!f\left( \int _{\mathbb {R}^{N\times n}}\zeta \,d\nu _x(\zeta )\right) \!\le \! {\text {*}}{\nu _x-ess\,sup}_{\zeta \in \mathbb {R}^{N\times n}} f(\zeta )\!=\!\max \{f(\xi ),f(\eta )\}. \end{aligned}$$

  where we have also used (4.6).

• (10) The first implication is a consequence of [74, Proposition 5.2] together with (4.7). For what concerns the second implication since f is strong BJW-quasi-level convex and, invoking Proposition 3.10, we get that f is also strong BJW-quasi-level convex in any other cube C. Hence, using (3) in Theorem 3.12, we conclude that f is periodic-weak BJW-quasi-level convex in the cube C. The last parts are also consequences of (3) and (6) in Theorem 3.12.

$\square$

We observe that many implications in Theorem 4.8 do not invert. Indeed, we have the following result.

Example 4.10

• (1) In [5, Example 6.6] it has been shown that the function ${\arctan }(\textrm{det}): \xi \in {\mathbb {R}}^{2 \times 2} \rightarrow [-\pi /2,\pi /2]$ is poly-level convex (hence $\textrm{curl}$-Young quasiconvex) but not level convex.

• (2) The example provided in [5, Example 6.7] shows that to ensure that a $\textrm{curl}$-Young quasiconvex function is $\textrm{curl}-\infty$ quasiconvex, some additional assumption, like (C) in (8) of Theorem 4.8, should be imposed. Indeed the function $W:{\mathbb {R}}^{2 \times 2} \rightarrow \mathbb [0,+\infty )$, defined as

  $$\begin{aligned} W(\xi )= \sup \{h(|\xi |), k(\xi )\}, \end{aligned}$$

  with h and k given by $k(\xi ):= \arctan (\mathrm det \xi )$ and $h(t)= \left\{ \begin{array}{ll} 0 & \hbox { if } t \le 1, \\ t-1 & \hbox { if } 1 \le t \le 2,\\ 1 & \hbox { if }t \ge 2\end{array} \right.$ is $\textrm{curl}$-Young quasiconvex but neither $\textrm{curl}-\infty$ quasiconvex, nor quasiconvex, nor level convex.

• (3) In [4, Proposition 5.9] it has been observed that the continuous function $f: {\mathbb {R}} \rightarrow [0,+\infty )$ given by $f(t):=\left\{ \begin{array}{ll} 0 & \hbox { if } t \le 0,\\ t & \hbox { if } 0 \le t\le 1,\\ 1 & \hbox { if } t \ge 1. \end{array} \right.$ is periodic-weak BJW-quasi-level convex and strong BJW- quasi-level convex since it is level convex. On the other hand, it has been proven that f is not $\textrm{curl}-\infty$ quasiconvex.

Proposition 4.11

• (1) There exist $\textrm{curl}$-Young quasiconvex functions which are not level convex, i.e. (1) in Proposition 4.8 does not invert.

• (2) There exist level convex and poly-level convex functions which are not $\textrm{curl}-\infty$ quasiconvex.

• (3) A function f which satisfies (4.6) for every homogeneous gradient Young measure is not necessarily $\textrm{curl}-\infty$ quasiconvex. Moreover, even if the function is assumed lower semicontinuous and bounded from below, (4.6) does not imply that the function is $\textrm{curl}-\infty$ quasiconvex, i.e. $\mathrm curl$-Young quasiconvexity does not imply $\textrm{curl}-\infty$ quasiconvexity.

• (4) There exist lower semicontinuous level convex (hence lower semicontinuous and poly-level convex, strong BJW-quasi-level convex, periodic-weak BJW-quasi-level convex, weak BJW-quasi-level convex and rank-one level convex) functions which are not $\textrm{curl}-\infty$ quasiconvex.

Proof

Condition (1) follows from Example 4.10(1).

Condition (2) relies on the fact that $\textrm{curl}-\infty$ quasiconvex functions are lower semicontinuous (cf. Proposition 4.6), while level convexity and poly-level convexity do not entail lower semicontinuity (cf. Example 3.4).

The first part of (3) follows by the same argument as in (2). Indeed, condition (4.6) follows from (1) in Theorem 4.8 and by Proposition 4.6, a function that is not lower semicontinuous, it is not $\textrm{curl}-\infty$ quasiconvex. To prove the second assertion of (3), it suffices to refer to Example 4.10(2).

The proof of (4) follows by Example 4.10(3). $\square$

In the following result we show a partial converse of (3) in Proposition 4.8. It utilises ideas from [13, Theorem 4.1] and [43, Theorem 5.46].

Proposition 4.12

Let $f:{\mathbb {R}}^{N\times n}\rightarrow [0,+\infty )$ be a $\textrm{curl}-\infty$ quasiconvex function, of the form

$$\begin{aligned} f(\xi )= g(\alpha + \langle \beta , T(\xi ) \rangle ), \end{aligned}$$

with $\alpha \in {\mathbb {R}}$ and $\beta \in {\mathbb {R}}^{\tau (N, n)}$ (see [43, Theorem 5.46]), or in particular $f:\mathbb R^{N\times N}\rightarrow [0,+\infty )$

$$\begin{aligned} f(\xi ):=g (\det \xi ), \end{aligned}$$

(4.15)

where $g:{\mathbb {R}}\rightarrow [0,+\infty )$ is a lower semicontinuous function and there exist $a_1 >0, a_2 \in {\mathbb {R}}$ such that for every $\delta \in {\mathbb {R}}$

$$\begin{aligned} g(\delta )\ge a_1 |\delta |+ a_2. \end{aligned}$$

Then g is level convex, hence f is poly-level convex.

Proof

By (4.7), [43, Theorem 6.24], [74, Proposition 5.1] and the arguments used in (2) of Proposition 4.8 to weaken the coercivity condition,

$$\begin{aligned} f(\xi )&= \lim _{p\rightarrow +\infty } \left( \mathcal {Q}(f^p)(\xi )\right) ^{\frac{1}{p}} = \lim _{p\rightarrow +\infty } (\mathcal {Q}(g^p(\alpha + \langle \beta , T(\xi )\rangle )))^\frac{1}{p} \nonumber \\&= \lim _{p\rightarrow +\infty } ((g^p)^{**}(\alpha + \langle \beta , T(\xi )\rangle )))^{\frac{1}{p}} = g^\textrm{lslc}(\alpha + \langle \beta , T(\xi )\rangle )), \end{aligned}$$

(4.16)

where $g^\textrm{lslc}$ denotes the lower semicontinuous and level convex envelope of g (see [75]). Hence f is poly-level convex. Putting together (4.15) and (4.16), from the arbitrariness of $\alpha + \langle \beta , T(\xi )\rangle \in {\mathbb {R}}$, we obtain the level convexity of g. $\square$

The previous analysis leaves several open questions about the convexity notions treated in this section.

• (1) We have seen that $\textrm{curl}_{(p>1)}$-Young quasiconvexity, $\textrm{curl}-$Young quasiconvexity, $\textrm{curl}-\infty$ quasiconvexity, imply strong BJW-quasi-level convexity. One may wonder if strong BJW-quasi-level convexity is indeed below in this hierarchy, in the class of coercive functions. Note that the function in Example 4.10 (3) is not coercive. In the same spirit one may wonder if weak BJW-quasi-level convexity entails $\textrm{curl}-\infty$ quasiconvexity in the class of functions satisfying (C).

• (2) In (7) and (8) we have proven that $\textrm{curl}_{(p>1)}$-Young quasiconvexity, $\textrm{curl}-$Young quasiconvexity and $\textrm{curl}-\infty$ quasiconvexity are equivalent, but it is not known if the assumptions are sharp.

• (3) In (8) we obtained that $\textrm{curl}$-Young quasiconvex functions are $\textrm{curl}_{(p>1)}$-Young quasiconvex requiring that f is non-negative since our proof relies on proving that f is also $\textrm{curl}-\infty$ quasiconvex. One may wonder if a direct proof can be provided removing this artificial assumption.

Remark 4.13

In regard to question (1) dealing with coercivity, it is worth to recall that [4, Theorem 4.2] in the $\mathrm curl$-free setting, has been improved in [74, Theorem 2.2]. Indeed, the Carathéodory assumption has been relaxed to Lebesgue $\otimes$ Borel-measurability for f, but under a linear growth constraint from above and below on $f(x, \cdot )$ for a.e. $x \in \Omega$, obtaining a strong BJW-quasi-level convex limiting density, $f_\infty$ (see [74, Eq. (61) and (62)]), i.e. $\Gamma -\lim _{p\rightarrow +\infty }(\int _\Omega f^p(x, D u(x))dx)^\frac{1}{p} = {\text {*}}{ess\,sup}_{x \in \Omega } f_\infty (x,D u(x))$. Moreover, it has been proven that $f_\infty$ coincides with $Q_\infty f$ either assuming in addition upper semicontinuity on $f(x,\cdot$) or in the homogeneous setting, requiring just Borel measurability and (up to a constant) (4.3) (see [74, Remark 5.2]). This latter case reinforces the curiosity towards proving (or disproving) that strong BJW-quasi-level convexity and coercivity could imply $\textrm{curl}-\infty$ quasiconvexity.

Moreover by the above mentioned $\Gamma$-convergence results from [4] and [74], it follows that $\textrm{curl}-\infty$ quasiconvexity is necessary and sufficient for the $L^p$-approximation under continuity and coercivity assumptions, but it is not completely clear if this notion is really necessary under the sole assumption of lower semicontinuity.

Then, question (1) above can be rephrased as follows:

in the vectorial case the relaxation of supremal functionals of the type (1.1) (namely the characterization of the greatest $L^\infty$ lower semicontinuous functional below a given one) is currently open. The $\textrm{curl}-\infty$ quasiconvexity (and $\textrm{curl}$-Young quasiconvexity) of the supremand appears only as a sufficient condition for the lower semicontinuity of such functionals, but it is not known if this is also a necessary condition, even under coercivity assumptions.

In the same order of ideas, emanating from the results in [74] one can observe that strong-BJW-quasi-level convexity is necessary for power-law approximations, while its sufficiency is currently open.

Finally, regarding the scalar case, we underline that, in the homogeneous and scalar case in [74, Remark 5.2], i.e. $v(x)=D u(x)\in {\mathbb {R}}^{n\times N}$, with either $n=1$ or $N=1$, the limiting density $f_\infty$ coincides with the level convex and lower semicontinuous envelope of f, thus recovering the results in [5], cf. Proposition 2.9 and Theorem 2.10 therein, and the particular cases discussed in [11, 33, 39, 53], and leads by means of power-law approximation strategies, to the same conclusions as (viii) in Remark 4.9.

5 Relating convexity definitions from the integral and supremal settings

It is easily seen that convexity is a sufficient condition to level convexity. Indeed, we will see that the convexity notions arising on the minimization of integral functionals are strictly stronger than the corresponding ones appearing in the minimization of supremal functionals.

Proposition 5.1

• (1) If f is polyconvex, i.e., for some convex function $g:\mathbb {R}^{\tau (n,N)}\longrightarrow \mathbb {R}$,

  $$\begin{aligned} f(\xi )=g(T(\xi )), \forall \ \xi \in \mathbb {R}^{N\times n} \end{aligned}$$

  being $\tau (n,N)$ and $T(\xi )$ as in Definition 3.1, then f is poly-level convex.

• (2) If f is quasiconvex, then f is $\textrm{curl}$-Young quasiconvex.

• (3) If f is quasiconvex, then f is strong BJW-quasi-level convex.

• (4) If f is quasiconvex and non-negative then f is $\textrm{curl}-\infty$ quasiconvex.

• (5) If f is rank-one convex, i.e. f is convex along rank-one directions, then f is rank-one level convex.

Remark 5.2

The proof of (4) is presented for the reader’s convenience since it is given by [4, Proposition 3.6] for the ${\mathcal {A}}$-free setting, under the extra explicit assumptions of local boundedness and upper semicontinuity. These requirements are not needed in the $\textrm{curl}$-free setting, since they are granted for any quasiconvex function, see (ii) in Remark 2.2.

Proof

(1) and (5) The results follow immediately from the fact that convex functions are also level convex.

(2) The proof is in [5, Proposition 3.3 (1)], in the more general case of the operator $\textrm{curl}$ replaced by a generic partial differential operator ${\mathcal {A}}$ with constant rank and under the extra assumption that f is continuous. By (ii) in Remark 2.2, the continuity is implicitly guaranteed by the quasiconvexity of f.

(3) Having in mind Proposition 2.3 it suffices to observe that a function satisfying (2.2) is strong BJW-quasi-level convex. To obtain this, it suffices to estimate the integral by the essential supremum.

(4) It follows by the equalities

$$\begin{aligned} f(\xi )=f^p(\xi )^{1/p}=\left( \inf \left\{ \int _Q f^p(\xi + D \varphi (y))dy:\varphi \in W^{1,\infty }_0(Q;{\mathbb {R}}^N)\right\} \right) ^{1/p} \end{aligned}$$

where in the second one it has been exploited the quasiconvexity of $f^p$ due to the quasiconvexity of f, which follows from the increasing monotonicity of $(\cdot )^p$, the Jensen’s inequality applied to this latter function, and the fact that $\inf$ and $\frac{1}{p}$ power interchanges. Hence it suffices to pass to the limit as $p \rightarrow +\infty$ to get the assertion. $\square$

In view of the previous proposition, one might wonder if the supremal convexity notions imply some integral convexity notions. This is not likely to happen since clearly level convexity does not imply rank-one level convexity. The next example taken from [4, Example 5.5] proves our claim considering a continuous, non-negative function with linear growth defined in ${\mathbb {R}}^{N\times n}$.

Example 5.3

Let $f: {\mathbb {R}}^{N\times n} \rightarrow [0,+\infty )$ be the continuous function given by

$$\begin{aligned} f(\xi ):=\left\{ \begin{array}{ll} |\xi | & \hbox { if } |\xi |\le 1,\\ 1 & \hbox { if } 1\le |\xi |\le 2,\\ \frac{1}{2}|\xi | & \hbox { if } |\xi | \ge 2. \end{array} \right. \end{aligned}$$

Then f is level convex (see (2) in Theorem 4.8) but it is not rank-one level convex.

Proposition 5.4

There exist functions which are level convex (and thus poly-level convex, $\textrm{curl}-\infty$ quasiconvex, $\textrm{curl}_{(p>1)}$ quasiconvex, $\textrm{curl}$-Young quasiconvex, strong BJW-quasi-level convex, rank-one level convex) which are not rank-one level convex (hence neither convex, nor polyconvex, nor quasiconvex).

Proof

The result follows from Example 5.3, Proposition 4.8 and Theorem 3.12, and [43, Theorem 5.3]. $\square$

Appendices

Appendix A

In [21] it was proven that a necessary and sufficient condition to the sequential weak* lower semicontinuity in $W^{1,\infty }(\Omega ,\mathbb {R}^N)$ of a functional

$$\begin{aligned} F(u):={\text {*}}{ess\,sup}_{x\in \Omega }f\left( Du\left( x\right) \right) ,\quad u\in W^{1,\infty }(\Omega ,\mathbb {R}^N) \end{aligned}$$

is the strong BJW-quasi-level convexity of the supremand f. Here, we exploit the arguments employed to achieve this statement, with the ultimate goal of showing that the cube Q in the definition of strong BJW-quasi-level convexity can be replaced by other sets in an appropriate class, cf. Proposition 3.10.

Proposition A.1

Let $\Omega \subseteq \mathbb {R}^{n}$ be a bounded, convex, and open set, and let $f:\mathbb {R}^{N\times n}\longrightarrow \mathbb {R}$ be a strong BJW-quasi-level convex on the set $\Omega$. That is, f satisfies (3.1).

Let $O\subseteq \mathbb {R}^{n}$ be a bounded open set. Then, the functional $F(u,O):={\text {*}}{ess\,sup}_{x\in O}\!f\!\left( Du\left( x\right) \right)$ is sequentially weakly* lower semicontinuous in $W^{1,\infty }(O,\mathbb {R}^N)$.

Proof

The result follows as in [21, Theorem 2.6]. By Remark 3.2, we can reduce to the case that $\Omega$ contains the origin. Then invoking the strong version of Besicovitch derivation theorem (cf. [3, Theorem 5.52]) that allows to work with more general sets than the cube, that need to be convex. Moreover we make use of Lemma 3.3 instead of [21, Proposition 2.5]. Note that bounded, open, convex sets have Lipschitz boundary thus the hypotheses of the lemma are fulfilled. $\square$

The next goal is to show that strong BJW-quasi-level convexity is also a necessary condition to sequential weak* lower semicontinuity of $F(\cdot ,O)$ in $W^{1,\infty }(O;\mathbb {R}^N)$. Again, we follow the same procedure of the proof of [21, Theorem 2.7, Lemma 2.8.]. We stress that we don’t require the sequential weak* lower semicontinuity in any set as in [21] because we work in the same set, either in the sequential weak* lower semicontinuity of the functional and in the strong BJW-quasi-level convexity. This is not a restriction if we combine it with Proposition A.1, as it will be made clear in Proposition3.10.

The following result can be proven.

Proposition A.2

Let $f:\mathbb {R}^{N\times n}\longrightarrow \mathbb {R}$ be a Borel measurable function and consider the functional

$$\begin{aligned} F(u,\Omega ):={\text {*}}{ess\,sup}_{x\in \Omega }f\left( Du\left( x\right) \right) , \end{aligned}$$

where $\Omega$ is a bounded open set in $\mathbb {R}^n$. If $F(\cdot ,\Omega )$ is sequentially weakly* lower semicontinuous in $W^{1,\infty }(\Omega ;\mathbb {R}^N)$ then

• (i) f is lower semicontinuous and it is periodic-weak BJW-quasi-level convex (considering any cube in place of Q). In particular, f is also weak BJW-quasi-level convex (considering also any cube in place of Q).

• (ii) If additionally we have that $\partial \Omega$ is Lipschitz, then f is strong BJW-quasi-level convex.

Remark A.3

Item (i) above, together with the Proposition 3.7 entail that, if F is sequentially weakly* lower semicontinuous in $W^{1,\infty }(\Omega ;\mathbb {R}^N)$, then f is weak BJW-quasi-level convex in any bounded and open set $\Omega$ with boundary of null $\mathcal {L}^n$-measure.

Proof

The proof of (i) follows as in [21, Lemma 2.8]. The lower semicontinuity of f follows simply considering, for a given sequence $(\xi _k)_{k\in \mathbb {N}}\subseteq \mathbb {R}^{N\times n}$ converging to $\xi \in \mathbb {R}^{N\times n}$, the sequence of affine functions $u_k(x)=\xi _k\, x$ that converges to $u(x):=\xi \, x$ in $W^{1,\infty }(\Omega ;\mathbb {R}^N)$ since $\Omega$ is bounded.

It remains to prove that f is periodic-weak BJW-quasi-level convex since, in view of Theorem 3.12 (4), the weak BJW-quasi-level convexity then follows immediately. Let C be any cube in $\mathbb {R}^n$, $\xi \in \mathbb {R}^{N\times n}$, and $\varphi \in W_{\textrm{per}}^{1,\infty }(C;\mathbb {R}^N).$ We want to show that

$$\begin{aligned} \displaystyle f(\xi )\le {\text {*}}{ess\,sup}_{x\in C}f\left( \xi + D\varphi \left( x\right) \right) . \end{aligned}$$

Then consider $\varphi _\varepsilon (x):=\varepsilon \varphi \left( \frac{x}{\varepsilon }\right)$. Of course, as $\varepsilon$ tends to 0, $\varphi _\varepsilon$ converges weakly* in $W^{1,\infty }(\Omega ;\mathbb {R}^N)$ to 0. Therefore $u_\varepsilon (x):=\xi x+ \varphi _\varepsilon (x)$ converges weakly* in $W^{1,\infty }(\Omega ;\mathbb {R}^N)$ to $u_\xi (x):=\xi \,x$, as $\varepsilon$ tends to 0. Applying the sequential weak* lower semicontinuity of $F(\cdot ,\Omega )$, one gets

$$\begin{aligned} f(\xi )= & {\text {*}}{ess\,sup}_{x\in \Omega }f\left( Du_\xi \left( x\right) \right) \le \liminf _{\varepsilon \rightarrow 0}{\text {*}}{ess\,sup}_{x\in \Omega }f\left( Du_\varepsilon \left( x\right) \right) \\= & \liminf _{\varepsilon \rightarrow 0}{\text {*}}{ess\,sup}_{x\in \Omega }f\left( \xi + D \varphi \left( \frac{x}{\varepsilon }\right) \right) \le {\text {*}}{ess\,sup}_{z\in C}f\left( \xi +D\varphi \left( z\right) \right) \end{aligned}$$

where we used in the last inequality the periodicity of $\varphi$.

The proof of (ii) is the same as the one of [21, Theorem 2.7]. That is, assume by contradiction that there exist $\varepsilon >0$, $\xi \in \mathbb {R}^{N\times n}$, and $K>0$ such that, for every $\delta >0$ there is a function

$$\begin{aligned} \varphi _\delta \in W^{1,\infty }(\Omega ;\mathbb {R}^N) \end{aligned}$$

such that

$$\begin{aligned} ||D\varphi _\delta ||_{L^\infty (\Omega )}\le K,\quad \max _{x\in \partial \Omega }|\varphi _\delta (x)|\le \delta \quad \text {and}\quad f(\xi )> {\text {*}}{ess\,sup}_{x\in \Omega } f(\xi +D\varphi _\delta (x))+\varepsilon . \end{aligned}$$

It can be ensured that, up to a subsequence, $\varphi _\delta$ weakly* converges in $W^{1,\infty }(\Omega ;\mathbb {R}^N)$ to some function $\varphi \in W^{1,\infty }_0(\Omega ;\mathbb {R}^N)$. Indeed, $\Omega$ being a bounded open set with Lipschitz boundary, by Sobolev’s embedding theorems, $\varphi _\delta \in C(\overline{\Omega };{\mathbb {R}}^N)$. Moreover, the functions $\varphi _\delta$ are Lipschitz continuous with Lipschitz constant bounded by $||D\varphi _\delta ||_{L^\infty (\Omega )}\le K$. Therefore, the sequence $\varphi _\delta$ is equicontinuous and by Ascoli-Arzelá’s theorem, up to a subsequence, $\varphi _\delta$ converges uniformly to a function $\varphi \in C(\overline{\Omega };{\mathbb {R}}^N)$. On the other hand, the Lipschitz inequality enjoyed by the functions $\varphi _\delta$, together with $\max _{x\in \partial \Omega }|\varphi _\delta (x)|\le \delta$, ensure that $\varphi _\delta$ is a bounded sequence in $W^{1,\infty }(\Omega ;{\mathbb {R}}^N)$. Thus, up to a subsequence, it converges weakly* in $W^{1,\infty }(\Omega ;{\mathbb {R}}^N)$. We can then conclude that the uniform limit, $\varphi$, belongs to $W^{1,\infty }(\Omega ;{\mathbb {R}}^N)$ and it is also the weak* limit in $W^{1,\infty }(\Omega ;{\mathbb {R}}^N)$. Finally the estimates on the traces on $\partial \Omega$ of $\varphi _\delta$, also imlpy that $\varphi \in W^{1,\infty }_0(\Omega ;{\mathbb {R}}^N)$.

Then, by the sequential weak* lower semicontinuity of $F(\cdot ,\Omega )$, one gets

$$\begin{aligned} {\text {*}}{ess\,sup}_{x\in \Omega }f\left( \xi + D\varphi \left( x\right) \right) \le \liminf _{\delta \rightarrow 0} {\text {*}}{ess\,sup}_{x\in \Omega }f\left( \xi +D\varphi _\delta \left( x\right) \right)<f(\xi )-\varepsilon <f(\xi ). \end{aligned}$$

This contradicts the fact that, by (i) and Proposition  3.7,

$$\begin{aligned} \displaystyle f(\xi )\le {\text {*}}{ess\,sup}_{x\in \Omega }f\left( \xi + D\psi \left( x\right) \right) ,\ \forall \ \xi \in \mathbb {R}^{N\times n},\ \forall \ \psi \in W_0^{1,\infty }(\Omega ;\mathbb {R}^N), \end{aligned}$$

where we used the fact that we are assuming $\Omega$ bounded, open, and with Lipschitz, thus with boundary of null measure. $\square$

Appendix B

The following result is a key tool to provide an alternative argument to the proof of [5, Theorem 4.2]. It extends to the inhomogeneous setting [68, Lemma 2.5], where the continuity assumption of [14, Theorem 34] was relaxed.

Lemma B.1

Let $U\subset {\mathbb {R}}^n$ be an open set with finite measure and let $f:U\times \mathbb {R}^m\rightarrow \mathbb {R}$ be a normal integrand ( i.e., f is Lebesgue $\otimes$ Borel-measurable; and $f(x,\cdot )$ is lower semicontinuous for a.e. $x\in U$), bounded from below. Further, let $(u_k)_{k\in \mathbb {N}}$ be a uniformly bounded sequence of functions in $L^\infty (U;{\mathbb {R}}^m)$ generating a Young measure $\nu =\{\nu _x\}_{x\in U}$. Then,

$$\begin{aligned} \liminf _{k \rightarrow \infty }{\text {*}}{ess\,sup}_{x\in U} f(x,u_k(x)) \ge {\text {*}}{ess\,sup}_{x\in U}\bar{f}(x), \end{aligned}$$

where $\bar{f}(x):= {\text {*}}{\nu _x-ess\,sup}_{\xi \in \mathbb {R}^m} f(x,\xi )$ for $x\in U$.

Proof

We give the details of the proof for the reader’s convenience, which follows the lines of [68, Lemma 2.5].

Without loss of generality we can assume that f is non negative. Let $\varepsilon >0$ be fixed, and choose a set $S\subset U$ with positive Lebesgue measure such that $\bar{f}(x)\ge \Vert \bar{f}\Vert _{L^\infty (U)}-2\varepsilon$ for all $x\in S$. Next, we show that there exists a measurable subset $S'\subset S$ with ${\mathcal {L}}^n(S')>0$ such that

$$\begin{aligned} \Bigl (\int _{\mathbb {R}^m} |f(x,\xi )|^p \,d\nu _x(\xi )\Bigr )^{\frac{1}{p}} \ge \Vert \bar{f}\Vert _{L^\infty (U)}-\varepsilon \end{aligned}$$

(5.1)

for all $x\in S'$ and $p>1$ sufficiently large. Indeed, with

$$\begin{aligned} S_k:= \Bigl \{x \in S: \bigl (\textstyle \int _{{\mathbb {R}}^m}f(x,\xi )^p d\nu _x(\xi )\bigr )^{\frac{1}{p}} \ge \Vert \bar{f}\Vert _{L^\infty (\Omega )} - \varepsilon \hbox { for all}\ p \ge k\Bigr \} \end{aligned}$$

for $k \in \mathbb N$, one has that $S= \bigcup _{k=1}^\infty S_k$. Since $\mathcal L^n(S) > 0$, there must be at least one $k'$ for which $\mathcal L^n(S_{k'}) > 0$, and setting $S':= S_{k'}$ shows (5.1).

We take the inequality in (5.1) to the pth power and integrate over $S'$. Along with Theorem 4.1 (i), extended to normal integrands by using [49, Corollary 6.30], it follows that

$$\begin{aligned} {\mathcal {L}}^n(S') (\Vert \bar{f}\Vert _{L^\infty (\Omega )}-\varepsilon )^p&\le \int _{S'} \int _{\mathbb {R}^m} |f(x, \xi )|^p\, d\nu _x(\xi ) \, dx \\&\le \liminf _{k\rightarrow \infty } \int _U |f(x, u_k(x))|^p \, dx \\&\le \liminf _{k\rightarrow \infty } \Vert f(\cdot , u_k(\cdot ))\Vert _{L^\infty (U)}^p {\mathcal {L}}^n (U). \end{aligned}$$

Hence,

$$\begin{aligned} \liminf _{k\rightarrow \infty } \Vert f(\cdot , u_k(\cdot ))\Vert _{L^\infty (U)} \ge \Bigl (\frac{{\mathcal {L}}^n(S')}{{\mathcal {L}}^n (U)}\Bigr )^{\frac{1}{p}}\bigl (\Vert \bar{f}\Vert _{L^\infty (U)}-\varepsilon \bigr ) \end{aligned}$$

for $p>1$ sufficiently large. Letting $p\rightarrow \infty$ and recalling that $\varepsilon >0$ is arbitrary concludes the proof. $\square$

We are in position to prove that $\mathrm curl$-Young quasiconvexity is a sufficient condition for the lower semicontinuity of supremal functionals. The result can be trivially extended to the ${\mathcal {A}}$-free setting, thus providing an alternative argument to the one proposed in [5, Theorem 4.2].

Theorem B.2

Let $f:\Omega \times {\mathbb {R}}^{N\times n} \rightarrow {\mathbb {R}}$ be a normal integrand, bounded from below and such that $f(x,\cdot )$ is $\textrm{curl}-$ Young quasiconvex for a.e. $x \in \Omega$. Let $F:W^{1,\infty }(\Omega ;{\mathbb {R}}^N)\rightarrow {\mathbb {R}}$ be the functional defined by

$$\begin{aligned} F(u)= {{\,\mathrm{ess\,sup}\,}}_{x \in \Omega }f(x,D u(x)). \end{aligned}$$

Then F is sequentially weakly* lower semicontinuous in $W^{1,\infty }(\Omega ;{\mathbb {R}}^N)$.

Proof

The result follows from Lemma B.1 and Definition 4.2 (2). Without loss of generality we can assume that f is non negative.

Indeed, taken any sequence $(u_k)$ weakly* converging to u in $W^{1,\infty }(\Omega ;{\mathbb {R}}^N)$, which generates a $W^{1,\infty }$-gradient Young measure, $\nu _x$ with baricenter Du(x), we have

$$\begin{aligned} \liminf _{k\rightarrow \infty }F(u_k)&\ge {{\,\mathrm{ess\,sup}\,}}_{x \in \Omega }\nu _x-{{\,\mathrm{ess\,sup}\,}}_{\xi \in {\mathbb {R}}^{N\times n}} f(x,\xi )\\&\ge f\left( x,\int _{{\mathbb {R}}^{N\times n}} \xi d \nu _x(\xi )\right) \hbox { for a.e.} x \in \Omega . \end{aligned}$$

Consequently

$$\begin{aligned} \liminf _{k\rightarrow \infty } F(u_k) \ge {{\,\mathrm{ess\,sup}\,}}_{x \in \Omega }f(x,D u(x))= F(u), \end{aligned}$$

which proves the desired lower semicontinuity result. $\square$

Appendix C

The result below relates the level convexity of a function with a generalization of Jensen’s inequality in the supremal setting. A proof can be found in Barron [14, Theorem 30], (see [21, Theorem 1.2], where the theorem is stated under a lower semicontinuity hypothesis, and [20, Lemma 2.4] where one implication has been shown in order to provide a Hopf-Lax formula). It is possible to avoid this condition as already mentioned without proof in [75]. For convenience of the reader we include the proof here.

Theorem C.1

A Borel measurable function $f:{\mathbb {R}}^{n}\rightarrow {\mathbb {R}}$ is level convex if and only if it satisfies the supremal Jensen’s inequality:

$$\begin{aligned} f\left( \int _\Omega \varphi \,d\mu \right) \le \mu -{\text {*}}{ess\,sup}_{x\in \Omega } f(\varphi (x)) \end{aligned}$$

for every probability measure $\mu$ on $\mathbb {R}^{d}$ supported on the open set $\Omega \subseteq \mathbb {R}^{d}$, and every $\varphi \in L^1_\mu (\Omega ;\mathbb {R}^{n})$.

In particular, considering the Lebesgue measure, if $\Omega$ is a set with finite Lebesgue measure,

$$\begin{aligned} f\left( \frac{1}{\mathcal L^n(\Omega )}\int _\Omega \varphi (x)\,dx\right) \le {\text {*}}{ess\,sup}_{x\in \Omega }f(\varphi (x)),\ \forall \ \varphi \in L^1(\Omega ;\mathbb {R}^n). \end{aligned}$$

Proof

To show that a function satisfying the supremal Jensen’s inequality is level convex, it suffices to take for every $t \in [0,1]$ a function $\varphi$ whose values are $\xi$ on a set of $\mu$-measure t and $\eta$ on a set of $\mu$-measure $1-t$.

Now we prove that, if f is level convex then it satisfies supremal Jensen’s inequality. To this end it suffices to prove that, given an open set $\Omega \subseteq \mathbb {R}^{d}$, for every probability measure $\mu$ on $\mathbb {R}^{d}$ supported on $\Omega$, if $\varphi \in L^1_\mu (\Omega ;\mathbb {R}^{n})$ is such that $\varphi (x) \in C$, $\mu$-a.e. $x\in \Omega$ with $C\subset \mathbb {R}^{n}$ a convex set with finite dimension, then

$$\begin{aligned} \int _\Omega \varphi \, d \mu \in C. \end{aligned}$$

(5.2)

Indeed, once this is proved we obtain supremal Jensen’s inequality taking C as the level set of f corresponding to $\displaystyle \mu -{\text {*}}{ess\,sup}_{x\in \Omega } f(\varphi (x))$, symbolised by $\displaystyle \left\{ f \le \mu -{\text {*}}{ess\,sup}_{x\in \Omega } f(\varphi (x)) \right\}$ which is convex under the level convexity assumption on f.

Thus, it remains to prove that under the above assumptions (5.2) holds. We argue by an inductive argument on the dimension N of the convex set C. Clearly there is nothing to prove if $N=0$. Assume that C is a convex set of dimension $N>0$, that is the smallest affine space containing C has dimension N. If $\varphi (x) \in C$ for $\mu$-a.e. $x \in \Omega$, clearly

$$\begin{aligned} \xi _0:=\int _\Omega \varphi \,d \mu \in \overline{C}, \end{aligned}$$

which is still convex. The thesis is obvious if $\xi _0$ belongs to the interior of C relative to the smallest affine subset containing C, in symbols $\xi _0\in \mathrm{rel\,int}\,C$, thus we can reduce ourselves to the case when $\xi _0 \in \overline{C}{\setminus } \mathrm{rel\,int}\,C$, the relative boundary of C. By [77, Theorem 6.3], $\xi _0 \in \overline{C}{\setminus } \mathrm{rel\,int}\,\overline{C}$ and thus, [77, Theorem 11.6] ensures the existence of a non trivial supporting hyperplane $H=\{\xi \in \mathbb {R}^{n}:\ \langle \alpha ,\xi \rangle =c\}$ to $\overline{C}$ containing $\xi _0$. That is, $\langle \alpha ,\xi _0\rangle =c$ and $\langle \alpha ,\xi \rangle \ge c,\ \forall \ \xi \in \overline{C}$. Therefore

$$\begin{aligned} \langle \alpha ,\xi -\xi _0 \rangle \ge 0,\ \forall \ \xi \in \overline{C} \end{aligned}$$

and taking, in particular, $\xi =\varphi (x)$, we get

$$\begin{aligned} \langle \alpha ,\varphi (x)-\xi _0\rangle \ge 0,\ \mu -a.e.\ x\in \Omega . \end{aligned}$$

Integrating in $\Omega$, it results

$$\begin{aligned} \int _\Omega \langle \alpha ,\varphi (x)-\xi _0\rangle \,d\mu (x)=\langle \alpha ,\int _\Omega \varphi (x)-\xi _0\,d\mu (x)\rangle =0. \end{aligned}$$

Therefore, $\langle \alpha ,\varphi (x)-\xi _0\rangle = 0,\ \mu -a.e.\ x\in \Omega$ which means that $\mu -a.e.\ x \in \Omega$, $\varphi (x)\in H \cap C$ which is a convex set with dimension less than N, thus by induction hypothesis $\xi _0 \in H\cap C$, and thus it is also in C. That concludes the proof. $\square$