Two theorems on the intersections of horospheres in asymptotically harmonic spaces

Abstract

We use Busemann functions to construct volume preserving mappings in an asymptotically harmonic manifold. If the asymptotically harmonic manifold satisfies the visibility condition, we construct mappings which preserve distances in some directions. We also prove that some integrals on the intersection of horospheres are independent of the differences between the values of the corresponding Busemann functions and we establish an upper bound of the volume of the intersection of two horospheres which is independent of the difference between values of corresponding Busemann functions.

1 Introduction

Let (M, g) be a simply connected, complete Riemannian manifold without con- jugate points. Let d(p, q) be the distance between $p,q\in M$. For each unit tangent vector v to M, the Busemann function $b_v: M\rightarrow {\mathbb {R}}$ on (M, g) is defined by

$$\begin{aligned} b_v(x)=\lim _{t\rightarrow \infty }(d(x,\gamma _v(t))-t), \end{aligned}$$

where $\gamma _v: [0,\infty )\rightarrow M$ is a geodesic ray such that $\gamma _v'(0)=v$. Busemann functions are convex and $C^2$ [7, 10]. The level hypersurfaces of Busemann functions are called horospheres. A Riemannian manifold is called harmonic, if, about any point, the geodesic spheres of sufficiently small radii are of constant mean curvature. A simply connected, complete Riemannian manifold (M, g) without conjugate points is called asymptotically harmonic if the mean curvatures of the horospheres are constant [9, 14]. Szabó [18] proved that a compact harmonic manifolds with a finite fundamental group is locally symmetric. Knieper [13] proved that a compact harmonic manifold with an infinite fundamental group is locally symmetric provided that the harmonic manifold has non-positive curvature or the fundamental group is Gromov hyperbolic. Ranjan and Shah [17] proved that a non-compact harmonic manifold with subexponential volume growth is flat. We refer to [14] for further results, including asymptotically harmonic manifolds. All harmonic manifolds are asymptotically harmonic, and all known asymptotically harmonic manifolds are harmonic and homogeneous [9]. It is also remarkable that the following question is remained open: Is a harmonic manifold homogeneous?

To consider the homogeneousness of a harmonic manifold and, more generally, of an asymptotically harmonic manifold, we construct a volume preserving mapping which maps one point to another point. For this construction, we use the mean curvature of horospheres and the variation of the volume density for the flow in the orthogonal direction to horospheres.

Let $C_c(M)$ be the set of continuous functions with compact support and $T^1M$ be a unit tangent bundle. We obtain the following theorem.

Theorem 1.1

Let (M, g) be an asymptotically harmonic manifold. Then, for all points $p\ne q\in M$, there exists a diffeomorphism $F:M\rightarrow M$ such that $F(p)=q$ and

$$\begin{aligned} \int _M f(x)d\mu (x) = \int _M f(F(x))d\mu (x), \end{aligned}$$

for all $f\in C_c(M)$, where $d\mu$ is the Riemannian measure on M.

Szabó [18] proved that a Riemannian manifold is a harmonic manifold if and only if the volume of the intersection of geodesic spheres depends only on the radii and the distance between the centers of the geodesic spheres. Csikós and M. Horváth [4, 5] proved that the intersections can be restricted to the cases with the same radii, and they also proved that the volume of a tubular neighborhood about a geodesic depends only on the length of the geodesic and the radius if and only if the Riemannian manifold is harmonic. In addition, some relations between integrals and measures on a harmonic manifold and its ideal boundary were found by Itoh and Satoh [11] and by Rouviére [16]. Knieper and Peyerimhoff [12] also considered the integrals and measures on harmonic manifolds to find a solution of the Dirichlet problem at infinity, and Biswas, Knieper, and Peyerimhoff [2] proved that there exists a Fourier transform between harmonic manifolds and its ideal boundary.

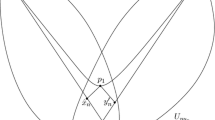
A Hadamard manifold (M, g) is a simply connected, complete Riemannian manifold of non-positive sectional curvature, and it is called a a visibility manifold (or satisfies the visibility condition) if, for any two different points $v_1$, $v_2$ at infinity, there is a geodesic $\gamma : {\mathbb {R}} \rightarrow M$ with $\gamma (\infty ) = v_1$, $\gamma (-\infty ) = v_2$ (see Sect. 2). All intersections of two horospheres in a Hadamard manifold are bounded if and only if the Hadamard manifold is a visibility manifold (see Definition 2.6 and Lemma 2.7). We note that the volume of an intersection of two horospheres in a visibility manifold is finite. In particular, for every harmonic manifold which satisfies the visibility condition, the volume of the intersection $b_{v_1}^{-1}(c_1)\cap b_{v_2}^{-1}(c_2)$ of two horospheres is independent of $c_1-c_2$. For asymptotically harmonic manifolds which satisfy the visibility condition (i.e., asymptotically harmonic, visibility manifolds), in this article, we prove that some integrals on the intersection of two horospheres are independent of the difference between values of corresponding Busemann functions. We also obtain an upper bound of the volume of the intersection of two horospheres. Throughout this paper, we assume that the dimension of the manifold is $n\ge 2$. Our main theorem is the following:

Theorem 1.2

Let (M, g) be an asymptotically harmonic, visibility manifold. Let $p\in M$, $v_1\ne v_2\in T_p^1M$, and $c\in {\mathbb {R}}$. Then there exists a constant $C>0$ such that the $(n-2)$-dimensional volume of the intersection $b_{v_1}^{-1}(c-t)\cap b_{v_2}^{-1}(c+t)$ is less than C, for all $t\in {\mathbb {R}}$.

2 Preliminary

The integration of a function on a connected Riemannian manifold (M, g) can be computed in terms of the integrals on hypersurfaces:

Proposition 2.1

[6] Let (M, g) be a connected Riemannian manifold. Let $\varphi :M\rightarrow {\mathbb {R}}$ be a $C^1$ function such that $\nabla \varphi$ is non-vanishing on M, and let $S_t$ be the hypersuface defined by $S_t=\{x\in M:\varphi (x)=t\}$, for all $t\in {\mathbb {R}}$. Then, for all $f\in C_c(M)$ and $t\in {\mathbb {R}}$,

$$\begin{aligned} \int _M f(x)d\mu (x)=\int _{{\mathbb {R}}}\int _{S_t}\frac{f(x)}{\Vert \nabla \varphi (x)\Vert }d\mu _t(x)dt, \end{aligned}$$

where $d\mu$ is the Riemannian measure on M and $d\mu _t$ is the induced Riemannian measure on $S_t$.

We introduce an infinitesimal “volume preserving” mapping on (M, g) in [8]. We say that a vector field X on M is volume preserving if $L_X(d\mu )=0$, where $L_X$ is the Lie derivative with respect to X. If $\phi _t$ is the flow generated by X, then we call $\phi _t$ volume preserving if X is volume preserving. In that case, we have $(\phi _t)^*(d\mu )=d\mu .$ This flows preserve integrals on a Riemannian manifold (M, g) since it preserves the Riemannian measure if it is a diffeomorphism.

Proposition 2.2

Let $\phi _t$ be a flow on a Riemannian manifold (M, g) and suppose that $\phi _t$ is a diffeomorphism on M for all $t\in {\mathbb {R}}$. Then $\phi _t$ is volume preserving if and only if

$$\begin{aligned} \int _M f(x) d\mu (x) = \int _M f(\phi _t(x)) d\mu (x), \end{aligned}$$

(1)

for all $f\in C_c(M)$, where $d\mu$ is the Riemannian measure on M.

Proof

If $\phi _t$ is volume preserving, then, clearly, Eq. (1) holds. Now, suppose that Eq. (1) holds for all $f\in C_c(M)$. Then

$$\begin{aligned} \int _M f(\phi _t(x))d\mu (x)=\int _M f(x)d\mu (x)=\int _M f(\phi _t(x))(\phi _t)^*(d\mu )(x) \end{aligned}$$

(2)

for all $f\in C_c(M)$. We denote $(\phi _t)^*(d\mu )=f_0 \, d\mu$ for some function $f_0$. Then, by Eq. (2), $f_0=1$ and $(\phi _t)^*(d\mu )=d\mu$. $\square$

Now, we define asymptotic geodesic rays:

Definition 2.3

[3] Let (M, g) be a Hadamard manifold, and $\gamma _1,\gamma _2:[0,\infty )\rightarrow M$ geodesic rays. $\gamma _1,\gamma _2$ are said to be asymptotic if there exists a constant $C>0$ such that

$$\begin{aligned} d(\gamma _1(t),\gamma _2(t))\le C, \end{aligned}$$

for all $t\ge 0$.

This gives an equivalence relation on geodesic rays: two geodesic rays are equivalent if and only if they are asymptotic. The set $\partial _{\infty } M$ of points at infinity is the set of equivalence classes of this relation. This is also called the ideal boundary of (M, g). Consequently, there exists a set of distance functions from each point and their limits. Let C(M) be the space of continuous functions on M equipped with the topology of uniform convergence on bounded subsets. Let $C_*(M)$ denote the quotient of C(M) by the 1-dimensional subspace of constant functions. For all $v\in T^1M$ and $t\in {\mathbb {R}}$,

$$\begin{aligned} \nabla b_v(\gamma (t))=-\gamma '(t), \end{aligned}$$

where $\gamma$ is a geodesic ray in (M, g) asymptotic to $\gamma _v$. In particular, the image of Busemann functions in $C_*(M)$ can be associated to geodesic rays. The points at infinity also corresponds to the images of Busemann functions in $C_*(M)$.

Proposition 2.4

[3] Let (M, g) be a Hadamard manifold. Then the Busemann functions associated to asymptotic geodesic rays in M are equal up to addition of a constant.

Proposition 2.5

[3] Let (M, g) be a Hadamard manifold, $\theta \in \partial _{\infty }M$, and $x\in M$. Then there exists a unique geodesic ray $\gamma \in \theta$ from x.

By the propositions, points at infinity bijectively correspond to images of Busemann functions in $C_*(M)$.

For two elements of $\partial _{\infty }M$, there could exist a geodesic from one direction to another direction. If such geodesic exists for all pairs of distinct elements of $\partial _{\infty }M$, then we call such a Hadamard manifold a visibility manifold:

Definition 2.6

[1] A Hadamard manifold (M, g) is called a visibility manifold if, for all $p\in M$ and $v_1\ne v_2\in T_p^1M$, there exists a geodesic ray $\gamma$ such that $\gamma$ is a asymptotic to $\gamma _{v_1}$, and the geodesic ray $t\mapsto \gamma (-t)$ is asymptotic to $\gamma _{v_2}$.

Such geodesic ray $\gamma$ is said to be bi-asymptotic to $v_1,v_2$. There exist several equivalent conditions for the visibility, one of which is as follows.

Lemma 2.7

[1] Let (M, g) be a Hadamard manifold. Then the following statements are equivalent:

• (i) (M, g) is a visibility manifold.

• (ii) $b_{v_1}^{-1}((-\infty , c_1))\cap b_{v_2}^{-1}((-\infty ,c_2))$ is bounded for all $p\in M$, $v_1\ne v_2\in T_p^1M$, and $c_1,c_2\in {\mathbb {R}}$.

For example, if a Hadamard manifold (M, g) satisfies the curvature condition $K\le -a^2<0$, for some $a\in {\mathbb {R}}$, then (M, g) is a visibility manifold [1]. In a Hadamard manifold, bi-asymptotic geodesics are normal geodesics of some intersection of horospheres of the form $b_v^{-1}(0)\cap b_{-v}^{-1}(0)$:

Proposition 2.8

[7] Let (M, g) be a Hadamard manifold. Then, for every $v\in T^1M$, $b_v^{-1}(0)\cap b_{-v}^{-1}(0)$ is connected,

$$\begin{aligned} \nabla b_v(x)+\nabla b_{-v}(x)=0, \end{aligned}$$

for all $x\in b_v^{-1}(0)\cap b_{-v}^{-1}(0)$, and the geodesics which is asymptotic to $\gamma _v$ and intersects $b_v^{-1}(0)\cap b_{-v}^{-1}(0)$ orthogonally at a point are bi-asymptotic to $v,-v$.

Consequently, for two distinct bi-asymptotic geodesics, there exists a 2-dimensional flat, totally geodesic embedding containing them:

Theorem 2.9

[7] Let (M, g) be a Hadamard manifold. Then, for all $v\in T^1M$, the Busemann function $b_v$ is convex, and the set $b_v^{-1}(0)\cap b_{-v}^{-1}(0)$ is convex. If two geodesics $\gamma _1,\gamma _2$ are bi-asymptotic, there exists $a>0$ and a totally geodesic, isometric embedding $F:[0,a]\times {\mathbb {R}}\rightarrow M$ such that $\gamma _1=\left. F\right| _{\{0\}\times {\mathbb {R}}}$ and $\gamma _2=\left. F\right| _{\{a\}\times {\mathbb {R}}}$.

Let $p\in M$, $v_1\ne v_2\in T_p^1M$, and

$$\begin{aligned} D=\{x\in M: \nabla b_{v_1}(x)+\nabla b_{v_2}(x)=0\}. \end{aligned}$$

Note that D is closed and D is nonempty if (M, g) is a visibility manifold. For every point $x\in D$, by Proposition 2.5, there exists a unique geodesic ray from x which is asymptotic to $v_1$, so it is bi-asymptotic to $v_1,v_2$. In particular, by Theorem 2.9, D is connected. Suppose that D is nonempty, so D contains a bi-asymptotic geodesic to $v_1,v_2$. Let $c_0$ be the constant value of $b_{v_1}+b_{v_2}$ on D. If $c_1,c_2\in {\mathbb {R}}$ and $c_1+c_2=c_0$, then there exists a point x on each bi-asymptotic geodesic $\gamma$ such that $b_{v_1}(x)=c_1$ and $b_{v_2}(x)=c_2$ since $\gamma$ is contained in D which implies $b_{v_1}(\gamma (0))+b_{v_2}(\gamma (0))=c_0=c_1+c_2$, and $\gamma '(t)=-\nabla b_{v_1}(\gamma (t))=\nabla b_{v_2}(\gamma (t))$ which implies

$$\begin{aligned} b_{v_1}(x)=b_{v_1}(\gamma (0))-t=c_1, \,\,\, b_{v_2}(x)=b_{v_2}(\gamma (0))+t=c_2, \end{aligned}$$

where $t=b_{v_1}(\gamma (0))-c_1=c_2-b_{v_2}(\gamma (0))$ and $x=\gamma (t)$. Set $v=\nabla b_{v_1}(x)$. Then, since $v=-\gamma '(t)$ and $\gamma$ is bi-asymptotic to $v_1$ and $v_2$, $-v$ and v are asymptotic to $v_1$ and $v_2$, respectively. By Proposition 2.4, the equations

$$\begin{aligned} b_{-v}=b_{v_1}-c_1, \,\,\, b_v=b_{v_2}-c_2 \end{aligned}$$

hold. Consequently, by Proposition 2.8,

$$\begin{aligned} b_{v_1}^{-1}(c_1)\cap b_{v_2}^{-1}(c_2)=b_v^{-1}(0)\cap b_{-v}^{-1}(0)\subseteq D \end{aligned}$$

(3)

holds.

3 Proof of Theorem 1.1

Let $p,q\in M$. Since (M, g) is connected and complete, there exists a unit-speed geodesic $\gamma$ such that $\gamma (0)=p$, $\gamma (t_0)=q$ for some $t_0>0$. Set $v=-\gamma '(0)$. Let $S_t=b_v^{-1}(t)$ be the level set of $b_v$ for all $t\in {\mathbb {R}}$. Consider a diffeomorphism $\phi :{\mathbb {R}}\times S_0\rightarrow M$ defined by

$$\begin{aligned} \phi _t(x)=\phi (t,x):=\exp _x\left( t \nabla b_v(x)\right) , \end{aligned}$$

for all $(t,x)\in {\mathbb {R}}\times S_0$.

For all $w\in T^1M$, we denote the space of orthogonal tangent vectors to w by $w^{\perp }$. Define $U=U(t):\nabla b_v(\phi _t(x))^{\perp }\rightarrow \nabla b_v(\phi _t(x))^{\perp }$ by

$$\begin{aligned} U(w):=\nabla _w \nabla b_v, \end{aligned}$$

for all $t\in {\mathbb {R}}$ and $w\in \nabla b_v(\phi _t(x))^{\perp }$. Since (M, g) is asymptotically harmonic, ${\text {tr}}U=-\Delta b_v=h$ for some constant $h\in {\mathbb {R}}$. Since $b_v$ is convex, $h\ge 0$.

Lemma 3.1

For every $t\in {\mathbb {R}}$,

$$\begin{aligned} (\phi _t)^*(d\mu _t)=e^{ht}d\mu _0. \end{aligned}$$

We note that Lemma 3.1 was given in [15]. Here, we provide the proof for the reader’s convenience.

Proof

For all $(t,x)\in {\mathbb {R}}\times S_0$,

$$\begin{aligned} \left. (\phi _t)_*\right| _x\left( \frac{\partial }{\partial t}\right) =\nabla b_v(\phi _t(x)). \end{aligned}$$

Then

$$\begin{aligned} \left. (\phi _t)_*\right| _x(w)=\left. \exp _*\right| _{t\nabla b_v(x)}\left( w,t U(w)\right) . \end{aligned}$$

(4)

Set $x\in S_0$ and $w\in \nabla b_v(x)^{\perp }$. Define

$$\begin{aligned} \Gamma (s,t):=\exp _{\sigma (s)}(t\nabla b_v(\sigma (s))), \end{aligned}$$

for all $s\in (-\varepsilon ,\varepsilon )$ and $t\in {\mathbb {R}}$, where $\sigma =\sigma (s)$ is the curve in $S_0$ such that $\sigma (0)=x$ and $\sigma '(0)=w$ and $\varepsilon >0$.

We denote $\partial _t\Gamma =\Gamma _*\left( \frac{\partial }{\partial t}\right)$, $\partial _s\Gamma =\Gamma _*\left( \frac{\partial }{\partial s}\right)$, and $J(t)=\partial _s\Gamma (0,t)$, for all $t\in {\mathbb {R}}$. So, $\left. (\phi _t)_*\right| _x\left( \frac{\partial }{\partial t}\right) =\nabla b_v(\phi _t(x))$ and $\left. (\phi _t)_*\right| _x(w)=J(t)$, for all $t\in {\mathbb {R}}$. Then, from Eq. (4), we have

$$\begin{aligned} U(J(t))=\nabla _{\partial _s\Gamma (0,t)}\partial _t\Gamma =\nabla _{\partial _t\Gamma (0,t)}\partial _s\Gamma =J'(t), \end{aligned}$$

for all $t\in {\mathbb {R}}$. Thus, we get

$$\begin{aligned} U=A'A^{-1}, \end{aligned}$$

on $\nabla b_v(\phi _t(x))^{\perp }$, where $t\in {\mathbb {R}}$, $R_t$ is the Jacobi operator along $t\mapsto \phi _t(x)$, and $A=A(t)$ is the (1, 1) tensor field on $\nabla b_v(\phi _t(x))^{\perp }$ such that $A^{\prime \prime }+R_tA=0$. Since (M, g) is asymptotically harmonic, ${\text {tr}}U=h$ is constant. So,

$$\begin{aligned} (\ln (\det A(t)))'={\text {tr}}U(t)=h, \end{aligned}$$

and $\det A(t)=e^{ht}$. Hence,

$$\begin{aligned} (\phi _t)^*(d\mu _t(\phi _t(x)))= & {} d\mu _t\left( \left. (\phi _t)_*\right| _x(w_1),\ldots ,\left. (\phi _t)_*\right| _x(w_{n-1}) \right) d\mu _0(x) \\= & {} \det A(t) \, d\mu _0(x)=e^{ht}d\mu _0(x), \end{aligned}$$

where $w_1,\ldots ,w_{n-1}$ are orthonormal tangent vectors to $S_0$ at x. $\square$

Define $F:M\rightarrow M$ by

$$\begin{aligned} F(\phi (t,x)):=\phi (\alpha (t),x), \end{aligned}$$

for all $(t,x)\in {\mathbb {R}}\times S_0$, where $\alpha =\alpha (t)$ is a smooth function on ${\mathbb {R}}$ such that $\alpha (0)=t_0$.

Corollary 3.2

For every $t\in {\mathbb {R}}$,

$$\begin{aligned} F^*(d\mu _{\alpha (t)})=e^{h\alpha (t)-ht}d\mu _t. \end{aligned}$$

Proof

For all points $x\in S_t$,

$$\begin{aligned} F(x)=\exp _x((\alpha (t)-t)\nabla b_v(x)), \end{aligned}$$

So, similarly to Lemma 3.1, Corollary 3.2 holds. $\square$

Therefore, by Proposition 2.1 and Corollary 3.2,

$$\begin{aligned} \int _Mf(x)d\mu (x)= & {} \int _{{\mathbb {R}}}\int _{S_s}f(x)d\mu _s(x)ds\\= & {} \int _{{\mathbb {R}}}\int _{F^{-1}{(S_s)}}f(F(x))F^*(d\mu _s)(x)ds\\= & {} \int _{{\mathbb {R}}}\int _{S_t}f(F(x))\alpha '(t)F^*(d\mu _{\alpha (t)})(x)dt\\= & {} \int _{{\mathbb {R}}}\int _{S_t}f(F(x))\alpha '(t)e^{h\alpha (t)-ht}d\mu _t(x)dt\\= & {} \int _{{\mathbb {R}}}\int _{S_t}f(F(x))d\mu _t(x)dt\\= & {} \int _Mf(F(x))d\mu (x), \end{aligned}$$

if $\alpha$ is strictly monotonic and

$$\begin{aligned} \alpha '(t)e^{h\alpha (t)-ht}=1 \end{aligned}$$

(5)

for all $t\in {\mathbb {R}}$. Consider two cases. First assume that $h=0$. Then, Eq. (5) holds if $\alpha (t)=t+t_0$. Thus $F=\phi _{t_0}$. Now assume that $h>0$. Then Eq. (5) holds if and only if

$$\begin{aligned} \alpha '(t)e^{h\alpha (t)}=e^{ht}, \end{aligned}$$

or, equivalently,

$$\begin{aligned} \frac{e^{h\alpha (t)}-e^{ht_0}}{h}=\frac{e^{ht}-1}{h}, \end{aligned}$$

so

$$\begin{aligned} \alpha (t)=\frac{1}{h}\ln \left( e^{ht}+e^{ht_0}-1\right) . \end{aligned}$$

Therefore,

$$\begin{aligned} F(\phi (t,x))=\phi \left( \frac{1}{h}\ln \left( e^{ht}+e^{ht_0}-1\right) ,x\right) . \end{aligned}$$

$\square$

Remark

If $h=0$, then $F=\phi _{t_0}$ is just a translation in ${\mathbb {R}}^n$, so it is an isometry. On the other hand, if $h>0$, then

$$\begin{aligned} F_*(\nabla b_v(\phi _t(x)))=\alpha '(t)\nabla b_v(\phi _{\alpha (t)}(x)), \end{aligned}$$

so F is not an isometry since

$$\begin{aligned} \alpha '(t)=\frac{he^{ht}}{h(e^{ht}+e^{ht_0}-1)}=\frac{e^{ht}}{e^{ht}+e^{ht_0}-1}<1. \end{aligned}$$

Also, $\alpha (t)-t$ is a strictly monotone decreasing function on ${\mathbb {R}}$, and F is well-defined.

4 Proof of Theorem 1.2

For asymptotically harmonic manifolds, we can find a volume preserving mapping from two Busemann functions directly.

Lemma 4.1

Let (M, g) be an asymptotically harmonic manifold, $p\in M$, and $v_1\ne v_2\in T_p^1M$. Then the vector field $X=\nabla b_{v_1}-\nabla b_{v_2}$ is volume preserving.

Proof

Note that X is non-vanishing since $v_1\ne v_2$ and

$$\begin{aligned} {\text {div}}X=-\Delta b_{v_1}+\Delta b_{v_2}. \end{aligned}$$

In particular, since (M, g) is asymptotically harmonic, $L_X(d\mu )=({\text {div}}X)d\mu =0$. $\square$

Consequently, this vector field derives a flow such that it preserves $d b_{v_1}$ and $d b_{v_2}$, and the flow is not volume preserving in general.

Lemma 4.2

Let (M, g) be an asymptotically harmonic manifold, $p\in M$, $v_1\ne v_2\in T_p^1M$, and

$$\begin{aligned} X=\frac{1}{\Vert \nabla b_{v_1}-\nabla b_{v_2}\Vert ^2}(\nabla b_{v_1}-\nabla b_{v_2}). \end{aligned}$$

Then the flow $\phi _t$ of X satisfies

$$\begin{aligned} (\phi _t)^*(d b_{v_1})=d b_{v_1}, \,\,\, (\phi _t)^*(d b_{v_2})=d b_{v_2}, \end{aligned}$$

(6)

for all $t\in {\mathbb {R}}$.

Proof

We denote $\beta =g(\nabla b_{v_1},\nabla b_{v_2})$ and set

$$\begin{aligned} X:=\frac{1}{\Vert \nabla b_{v_1}-\nabla b_{v_2}\Vert ^2}(\nabla b_{v_1}-\nabla b_{v_2})=\frac{1}{2-2\beta }(\nabla b_{v_1}-\nabla b_{v_2}). \end{aligned}$$

(7)

Then, since $g(X,\nabla b_{v_1}-\nabla b_{v_2})=1$ and $g(X,\nabla b_{v_1}+\nabla b_{v_2})=0$,

$$\begin{aligned} b_{v_1}(\phi _t(x))=b_{v_1}(x)+\frac{t}{2}, \,\,\, b_{v_2}(\phi _t(x))=b_{v_2}(x)-\frac{t}{2}, \end{aligned}$$

(8)

for all $t\in {\mathbb {R}}$ and $x\in M$, where $\phi _t$ is the flow of X. In particular,

$$\begin{aligned} (\phi _t)^*(d b_{v_1})=d b_{v_1}, \,\,\, (\phi _t)^*(d b_{v_2})=d b_{v_2}, \end{aligned}$$

for all $t\in {\mathbb {R}}$. $\square$

By Eq. (8), for all $c_1,c_2\in {\mathbb {R}}$,

$$\begin{aligned} \phi _t(b_{v_1}^{-1}(c_1)\cap b_{v_2}^{-1}(c_2))=b_{v_1}^{-1}\left( c_1+\frac{t}{2}\right) \cap b_{v_2}^{-1}\left( c_2-\frac{t}{2}\right) . \end{aligned}$$

It means that the flow in Lemma 4.2 maps one intersection of two horospheres onto another intersection of two horospheres, and the intersection $\phi _t(b_{v_1}^{-1}(c_1)\cap b_{v_2}^{-1}(c_2))$ of two horospheres is orthogonal to each gradient of the Busemann function, $\nabla b_{v_1}$,$\nabla b_{v_2}$, for all $c_1,c_2\in {\mathbb {R}}$. Similarly, we consider the flow of $\frac{1}{2+2\beta }(\nabla b_{v_1}+\nabla b_{v_2})$:

Proposition 4.3

Let (M, g) be a visibility manifold, $p\in M$, and $v_1\ne v_2\in T_p^1M$. Then there exists a constant $c_0\in {\mathbb {R}}$ such that, for every $x\in M$,

$$\begin{aligned} b_{v_1}(x)+b_{v_2}(x)\ge c_0. \end{aligned}$$

In addition, if $b_{v_1}(x)+b_{v_2}(x)=c_0$, then $\nabla b_{v_1}(x)+\nabla b_{v_2}(x)=0$, for any $x\in M$.

Proof

Let $v_1\ne v_2\in T_p^1M$,

$$\begin{aligned} D:=\{x\in M:\nabla b_{v_1}(x)+\nabla b_{v_2}(x)=0\}, \end{aligned}$$

and let $c_0$ be the value of $b_{v_1}+b_{v_2}$ on D. Note that $D\ne \emptyset$ since (M, g) is a visibility manifold. Set

$$\begin{aligned} Y:=\frac{1}{\Vert \nabla b_{v_1}+\nabla b_{v_2}\Vert ^2}(\nabla b_{v_1}+\nabla b_{v_2})=\frac{1}{2+2\beta }(\nabla b_{v_1}+\nabla b_{v_2}), \end{aligned}$$

on $M-D$, where $\beta =g(\nabla b_{v_1},\nabla b_{v_2})$. For all $x\in M$, if $b_{v_1}(x)+b_{v_2}(x)=c_0$, then, by Eq. (3), $x\in D$, so Y is not defined at x. Conversely, if $b_{v_1}(x)+b_{v_2}(x)\ne c_0$, then $x\notin D$, so Y is well-defined at x. For all $x\in M$ and $s\in {\mathbb {R}}$, $(b_{v_1}+b_{v_2})(\psi _{s'}(x))=b_{v_1}(x)+b_{v_2}(x)+s'\ne c_0$ for all $s'$ between 0 and s if and only if both $(b_{v_1}+b_{v_2})(x)$ and $(b_{v_1}+b_{v_2})(\psi _s(x))$ are larger than $c_0$, or both of them are smaller than $c_0$, which is equivalent to the following inequality

$$\begin{aligned} (b_{v_1}(x)+b_{v_2}(x)-c_0)(b_{v_1}(x)+b_{v_2}(x)+s-c_0)>0. \end{aligned}$$

Since $g(Y,\nabla b_{v_1}+\nabla b_{v_2})=1$ and $g(Y,\nabla b_{v_1}-\nabla b_{v_2})=0$, for all $s\in {\mathbb {R}}$ and $x\in M$ satisfying $(b_{v_1}(x)+b_{v_2}(x)-c_0)(b_{v_1}(x)+b_{v_2}(x)+s-c_0)>0$, we have

$$\begin{aligned} b_{v_1}(\psi _s(x))=b_{v_1}(x)+\frac{s}{2}, \,\,\, b_{v_2}(\psi _s(x))=b_{v_2}(x)+\frac{s}{2}, \end{aligned}$$

(9)

where $\psi _s$ is the flow of Y.

Now, suppose that $b_{v_1}(x)+b_{v_2}(x)=c<c_0$ for some $x\in M$. Let $U_i$ be the (0, 2)-tensor field on M defined by

$$\begin{aligned} U_i(w_1,w_2):=g\left( \nabla _{w_1}\nabla b_{v_i},w_2\right) \end{aligned}$$

for all $x'\in M$ and $w_1,w_2\in T_{x'}M$, where $i=1,2$. Since $b_{v_i}$ is convex, $U_i$ is positive semi-definite. Consequently,

$$\begin{aligned} Y[\beta ]= & {} \frac{(\nabla b_{v_1}+\nabla b_{v_2})\left[ g\left( \nabla b_{v_1},\nabla b_{v_2}\right) \right] }{2+2\beta } \nonumber \\= & {} \frac{g\left( \nabla _{\nabla b_{v_1}}\nabla b_{v_2},\nabla b_{v_1}\right) +g\left( \nabla _{\nabla b_{v_2}}\nabla b_{v_1},\nabla b_{v_2}\right) }{2+2\beta } \nonumber \\= & {} \frac{U_2(\nabla b_{v_1},\nabla b_{v_1})+U_1(\nabla b_{v_2},\nabla b_{v_2})}{2+2\beta }\ge 0. \end{aligned}$$

(10)

Hence, $s\mapsto \beta (\psi _s(x))$ is non-decreasing. By Lemma 2.7,

$$\begin{aligned} (b_{v_1}+b_{v_2})^{-1}((-\infty ,c_0])\cap (b_{v_1}-b_{v_2})^{-1}(t) \end{aligned}$$

is compact and, since $(b_{v_1}+b_{v_2})(\psi _s(x))=(b_{v_1}+b_{v_2})(x)+s=c+s<c_0$ and $(b_{v_1}-b_{v_2})(\psi _s(x))=(b_{v_1}-b_{v_2})(x)=t$, it contains $\psi _s(x)$ for all $s\in (0,c_0-c)$, where $t=b_{v_1}(x)-b_{v_2}(x)$. Thus, there exists a sequence $s_i\in (0,c_0-c)$, $i=1,2,\ldots$, such that $\lim _{i\rightarrow \infty }s_i=c_0-c$ and the limit $x_0:=\lim _{i\rightarrow \infty }\psi _{s_i}(x)$ exists. Since

$$\begin{aligned} (b_{v_1}+b_{v_2})(x_0)=(b_{v_1}+b_{v_2})(x)+c_0-c=c_0, \end{aligned}$$

by Eq. (3), we have $x_0\in D$ so that $\beta (x_0)=-1$. Thus, since $s\mapsto \beta (\psi _s(x))$ is non-decreasing, we have

$$\begin{aligned} -1\le \beta (x)\le \beta (x_0)=-1, \end{aligned}$$

which implies $x \in D$ and $c=c_0$. It is a contradiction to $c<c_0$. $\square$

To prove Theorem 1.2, we need the following theorem:

Theorem 4.4

Let (M, g) be an asymptotically harmonic, visibility manifold. Let $p\in M$, $v_1\ne v_2\in T_p^1M$, and $c_1,c_2\in {\mathbb {R}}$. Let S be the intersection $b_{v_1}^{-1}(c_1)\cap b_{v_2}^{-1}(c_2)$ of horospheres and $\nabla b_{v_1}(x)+\nabla b_{v_2}(x)\ne 0$ for all points $x\in S$. Then the following integrals are independent of $c_1-c_2$:

$$\begin{aligned} \int _S \sqrt{\frac{1-g(\nabla b_{v_1},\nabla b_{v_2})}{1+g(\nabla b_{v_1},\nabla b_{v_2})}}d\mu ', \,\,\, \int _S \sqrt{\frac{1+g(\nabla b_{v_1},\nabla b_{v_2})}{1-g(\nabla b_{v_1},\nabla b_{v_2})}} d\mu ', \end{aligned}$$

where $d\mu '$ is the induced measure on the submanifold S of (M, g).

Proof

We adopt the notations

$$\begin{aligned} \beta ,X,Y,\phi _t,\psi _s,D,c_0,U_1,U_2 \end{aligned}$$

in the proof of Lemma 4.2 and Proposition 4.3.

Note that D is closed. If there exists a neighborhood V of $x\in D$ in M such that $V\subseteq D$, then, for every geodesic $\gamma$ with $\gamma (0)\in V$ and $\gamma '(0)\perp \nabla b_{v_1}(\gamma (0))$, by Theorem 2.9, there exists a totally geodesic, isometric embedding $F:[0,a]\times {\mathbb {R}}\rightarrow M$ between $\gamma _1$, $\gamma _2$ where $a>0$ is a sufficiently small constant for $\gamma ([0,a])\subseteq V$, $\gamma _1$ and $\gamma _2$ are unique asymptotic geodesics to $v_1$ with $\gamma _1(0)=\gamma (0)$ and $\gamma _2(0)=\gamma (a)$, respectively. By the uniqueness of a geodesic joining two points in a Hadamard manifold, $F(s,0)=\gamma (s)$ for all $s\in [0,a]$. Since F is a totally geodesic, isometric embedding, $d(\gamma _1(t),F(s,t))=s$ for all $s\in [0,a]$, so the curve $t\in {\mathbb {R}}\mapsto F(s,t)$ is asymptotic to $\gamma _1$, so it is asymptotic to $v_1$, for all $s\in [0,a]$. Since F is isometric, $\gamma$ is orthogonal to the unique asymptotic curve $t\in {\mathbb {R}}\mapsto F(s,t)$ to $v_1$ at $\gamma (s)$, for all $s\in [0,a]$. Hence, $\gamma ([0,a])$ is contained in the level set of $b_{v_1}$. It means that the level set of $b_{v_1}$ containing x in V is totally geodesic, thus $h=-\Delta b_v=0$, for all $v\in T^1M$. Let $v\in T^1M$ and let U be the (0, 2)-tensor field defined by $U(w_1,w_2):=g(\nabla _{w_1}\nabla b_v,w_2)$ for all $x\in M$ and $w_1,w_2\in T_xM$. So, U is symmetric, and, since a Busemann function is convex, U is positive semi-definite. Also, since ${\text {tr}}U=h=0$, $U=0$. By the Riccati equation for horospheres,

$$\begin{aligned} \nabla _{\nabla b_v}U+U^2+R_{\nabla b_v}=R_{\nabla b_v}=0, \end{aligned}$$

where $R_{\nabla b_v}$ is the Jacobi operator along a geodesic with the velocity vector $\nabla b_v$. Thus, $R_v=R_{\nabla b_{-v}(x)}=0$ for all $x\in M$ and $v\in T^1_xM$. Therefore, (M, g) is flat. Hence, (M, g) is not a visibility manifold which contradicts the assumption of Theorem 4.4.

Suppose that $h\ne 0$. We note that $b_{v_1}+b_{v_2}\ge c_0$ by Proposition 4.3. By Eqs. (8) and (9), the flows $\phi _t,\psi _s$ map one intersection $b_{v_1}^{-1}(c_1)\cap b_{v_2}^{-1}(c_2)$ of horospheres onto another intersection, where $c_1,c_2\in {\mathbb {R}}$ and $c_1+c_2> c_0$. Let $E_1,\ldots ,E_n$ be a positively oriented, orthonormal frame on $M-D$, and $\theta _1,\ldots ,\theta _n$ be the dual 1-forms of the frame field such that $E_1,E_2$ spans a subbundle containing $\nabla b_{v_1}$,$\nabla b_{v_2}$, and $d b_{v_1}\wedge d b_{v_2}=\sqrt{1-\beta ^2}\,\theta _1\wedge \theta _2$. There always exists such frame $E_1,\ldots ,E_n$ on $M-D$. For example, if $E_1=\nabla b_{v_1}$ and $E_2=\frac{1}{\Vert \nabla b_{v_2}-\beta \nabla b_{v_1}\Vert }(\nabla b_{v_2}-\beta \nabla b_{v_1})$, then, since $\Vert \nabla b_{v_2}-\beta \nabla b_{v_1}\Vert =\sqrt{1-\beta ^2}$, $\theta _1=db_{v_1}$ and

$$\begin{aligned} \theta _2(w)=\frac{1}{\sqrt{1-\beta ^2}}g(w,\nabla b_{v_2}-\beta \nabla b_{v_1})=\frac{1}{\sqrt{1-\beta ^2}}(db_{v_2}-\beta db_{v_1})(w), \end{aligned}$$

for all $x\in M-D$ and $w\in T_xM$. Thus, $\theta _2=\frac{1}{\sqrt{1-\beta ^2}}(db_{v_2}-\beta db_{v_1})$ and $\theta _1\wedge \theta _2=\frac{1}{\sqrt{1-\beta ^2}}db_{v_1}\wedge db_{v_2}$.

By Eq. (6), we have $(\phi _t)^*(db_{v_i})=db_{v_i}$ for $i=1,2$, so $(\phi _t)^*(db_{v_1}\wedge db_{v_2})=(\phi _t)^*(db_{v_1})\wedge (\phi _t)^*(db_{v_2})=db_{v_1}\wedge db_{v_2}$. Also, from Eq. (9), we have $(\psi _s)^*(db_{v_i})=db_{v_i}$ for $i=1,2$, so $(\psi _s)^*(db_{v_1}\wedge db_{v_2})=db_{v_1}\wedge db_{v_2}$. Thus, $db_{v_1}\wedge db_{v_2}$ is invariant under the pullback of $\phi _t$ and $\psi _s$, so that, for all $s> 0$ and $t\in {\mathbb {R}}$,

$$\begin{aligned} (\phi _t)^*(\theta _1\wedge \theta _2)= & {} (\phi _t)^*\left( \frac{1}{\sqrt{1-\beta ^2}}\,db_{v_1}\wedge db_{v_2}\right) \nonumber \\= & {} \frac{1}{\sqrt{1-\beta ^2(\phi _t)}}\,(\phi _t)^*(db_{v_1}\wedge db_{v_2}) \nonumber \\= & {} \frac{1}{\sqrt{1-\beta ^2(\phi _t)}}\,db_{v_1}\wedge db_{v_2} \nonumber \\= & {} \sqrt{\frac{1-\beta ^2}{1-\beta ^2(\phi _t)}}\,\theta _1\wedge \theta _2, \end{aligned}$$

(11)

$$\begin{aligned} (\psi _s)^*(\theta _1\wedge \theta _2)= & {} \sqrt{\frac{1-\beta ^2}{1-\beta ^2(\psi _s)}}\,\theta _1\wedge \theta _2. \end{aligned}$$

(12)

on $M-D$. Since (M, g) is asymptotically harmonic,

$$\begin{aligned} {\text {div}}\left( \nabla b_{v_1}-\nabla b_{v_2}\right) =0, \,\,\, {\text {div}}\left( \nabla b_{v_1}+\nabla b_{v_2}\right) =2h. \end{aligned}$$

Thus, we obtain

$$\begin{aligned} {\text {div}}X= & {} {\text {div}}\left( \frac{1}{2-2\beta }\left( \nabla b_{v_1}-\nabla b_{v_2}\right) \right) \nonumber \\= & {} \left( \nabla b_{v_1}-\nabla b_{v_2}\right) \left[ \frac{1}{2-2\beta }\right] +\frac{1}{2-2\beta }{\text {div}}\left( \nabla b_{v_1}-\nabla b_{v_2}\right) \nonumber \\= & {} -\frac{\left( \nabla b_{v_1}-\nabla b_{v_2}\right) [2-2\beta ]}{(2-2\beta )^2}=-\frac{X[2-2\beta ]}{2-2\beta }\nonumber \\= & {} -X\left[ \ln (2-2\beta )\right] \nonumber \\= & {} X\left[ \ln \left( \frac{1}{1-\beta }\right) \right] , \end{aligned}$$

(13)

and

$$\begin{aligned} {\text {div}}Y= & {} {\text {div}}\left( \frac{1}{2+2\beta }\left( \nabla b_{v_1}+\nabla b_{v_2}\right) \right) \nonumber \\= & {} \left( \nabla b_{v_1}+\nabla b_{v_2}\right) \left[ \frac{1}{2+2\beta }\right] +\frac{1}{2+2\beta }{\text {div}}\left( \nabla b_{v_1}+\nabla b_{v_2}\right) \nonumber \\= & {} -\frac{\left( \nabla b_{v_1}+\nabla b_{v_2}\right) [2+2\beta ]}{(2+2\beta )^2}+\frac{2h}{2+2\beta }\nonumber \\= & {} -\frac{Y[2+2\beta ]}{2+2\beta }+\frac{h}{1+\beta }\nonumber \\= & {} Y\left[ \ln \left( \frac{1}{1+\beta }\right) \right] +\frac{h}{1+\beta }. \end{aligned}$$

(14)

Consequently, for the induced Riemannian measure $d\mu$ on $M-D$, the following equations hold:

$$\begin{aligned} \frac{\partial }{\partial t}(\phi _t)^*(d\mu )= & {} (\phi _t)^*(L_X(d\mu ))=(\phi _t)^*\left( {\text {div}}Xd\mu \right) \\= & {} \left( {\text {div}}X\circ \phi _t\right) (\phi _t)^*(d\mu ),\\ \frac{\partial }{\partial s}(\psi _s)^*(d\mu )= & {} \left( {\text {div}}Y\circ \psi _s\right) (\psi _s)^*(d\mu ). \end{aligned}$$

Set $(\phi _t)^*(d\mu )=f_t \, d\mu$ where $f_t\in C^{\infty }(M-D)$. Then

$$\begin{aligned} \frac{\partial }{\partial t}f_t \, d\mu =&\left( {\text {div}}X\circ \phi _t\right) f_t\, d\mu ,\\ \frac{\partial }{\partial t}\ln f_t=&{\text {div}}X\circ \phi _t. \end{aligned}$$

Note that $X[f](\phi _t)=\frac{\partial }{\partial t}f(\phi _t)$ for all $f\in C^{\infty }(M-D)$. Thus, since $f_0=1$, from Eq. (13), we get

$$\begin{aligned} f_t=\frac{1-\beta }{1-\beta (\phi _t)}. \end{aligned}$$

Hence,

$$\begin{aligned} (\phi _t)^*(d\mu )=\frac{1-\beta }{1-\beta (\phi _t)}d\mu . \end{aligned}$$

(15)

Similarly, when $(\psi _s)^*(d\mu )=g_s \, d\mu$ for some $g_s\in C^{\infty }(M-D)$, by Eq. (14),

$$\begin{aligned} \ln g_s=\ln \left( \frac{1+\beta }{1+\beta (\psi _s)}\right) +\int _0^s\frac{h}{1+\beta (\psi _k)}dk, \end{aligned}$$

so

$$\begin{aligned} (\psi _s)^*(d\mu )=\exp \left( \int _0^s\frac{h}{1+\beta (\psi _k)}dk\right) \frac{1+\beta }{1+\beta (\psi _s)}d\mu . \end{aligned}$$

(16)

Set $d\mu ':=\theta _3\wedge \cdots \wedge \theta _n$. Since $E_1$,$E_2$ span a subbundle containing $\nabla b_{v_1}$,$\nabla b_{v_2}$, $E_3,\ldots ,E_n$ are tangent to the intersection $b_{v_1}^{-1}(c_1)\cap b_{v_2}^{-1}(c_2)$ of horospheres for all $c_1,c_2\in {\mathbb {R}}$ such that $c_1+c_2>c_0$. That is, $E_3,\ldots ,E_n$ is an orthonormal frame on the intersection of horospheres and $d\mu '$ is the induced Riemannian measure on the intersection of horospheres. Since $\phi _t$ maps the intersection $b_{v_1}^{-1}(c_1)\cap b_{v_2}^{-1}(c_2)$ of horospheres onto another intersection of horospheres which is orthogonal to $\nabla b_{v_1}$ and $\nabla b_{v_2}$ for all $c_1,c_2\in {\mathbb {R}}$ such that $c_1+c_2> c_0$, $(\phi _t)^*(d\mu ')=f\,d\mu '$ for some function $f\in C^{\infty }(M-D)$. By Eqs. (11) and (15),

$$\begin{aligned} \frac{1-\beta }{1-\beta (\phi _t)}d\mu= & {} (\phi _t)^*(d\mu )=(\phi _t)^*(\theta _1\wedge \theta _2)\wedge (\phi _t)^*(d\mu ') \\= & {} \sqrt{\frac{1-\beta ^2}{1-\beta ^2(\phi _t)}}\theta _1\wedge \theta _2\wedge (\phi _t)^*(d\mu '), \end{aligned}$$

so

$$\begin{aligned} (\phi _t)^*(d\mu ')=\sqrt{\frac{(1-\beta )(1+\beta (\phi _t))}{(1+\beta )(1-\beta (\phi _t))}}d\mu '. \end{aligned}$$

Similarly, since $\psi _s$ maps the intersection of horospheres onto another intersection of horospheres, by Eqs. (12) and (16), we have

$$\begin{aligned} (\psi _s)^*(d\mu ')=\exp \left( \int _0^s\frac{h}{1+\beta (\psi _k)}dk\right) \sqrt{\frac{(1+\beta )(1-\beta (\psi _s))}{(1-\beta )(1+\beta (\psi _s))}}d\mu ', \end{aligned}$$

or, equivalently,

$$\begin{aligned} \sqrt{\frac{1-\beta (\phi _t)}{1+\beta (\phi _t)}}\,(\phi _t)^*(d\mu ')= & {} \sqrt{\frac{1-\beta }{1+\beta }}d\mu ', \end{aligned}$$

(17)

$$\begin{aligned} \sqrt{\frac{1+\beta (\psi _s)}{1-\beta (\psi _s)}}\,(\psi _s)^*(d\mu ')= & {} \exp \left( \int _0^s\frac{h}{1+\beta (\psi _k)}dk\right) \sqrt{\frac{1+\beta }{1-\beta }}d\mu '. \end{aligned}$$

(18)

Now, let

$$\begin{aligned} S(s,t):=b_{v_1}^{-1}\left( \frac{s+c_0+t}{2}\right) \cap b_{v_2}^{-1}\left( \frac{s+c_0-t}{2}\right) , \end{aligned}$$

for all $s\ge 0$ and $t\in {\mathbb {R}}$. Note that

$$\begin{aligned} S(c_1+c_2-c_0,c_1-c_2)=b_{v_1}^{-1}(c_1)\cap b_{v_2}^{-1}(c_2), \end{aligned}$$

for all $c_1,c_2\in {\mathbb {R}}$ such that $c_1+c_2\ge c_0$. Set

$$\begin{aligned} V(s,t):= & {} \int _{S(s,t)}\sqrt{\frac{1-\beta }{1+\beta }}d\mu ',\\ W(s,t):= & {} \int _{S(s,t)}\sqrt{\frac{1+\beta }{1-\beta }}d\mu ', \end{aligned}$$

for all $s>0$ and $t\in {\mathbb {R}}$. Then, $x\in S(s,t)$ holds if and only if $b_{v_1}(x)+b_{v_2}(x)=s+c_0$ and $b_{v_1}(x)-b_{v_2}(x)=t$, for all $s>0$, $t\in {\mathbb {R}}$, and $x\in M$. From Eq. (8), we have

$$\begin{aligned} (b_{v_1}+b_{v_2})(\phi _t(x))= & {} (b_{v_1}+b_{v_2})(x), \\ (b_{v_1}-b_{v_2})(\phi _t(x))= & {} (b_{v_1}-b_{v_2})(x)+t, \end{aligned}$$

for all $t\in {\mathbb {R}}$ and $x\in M$. Thus, $\phi _t(S(s,t_0))=S(s,t_0+t)$ holds for all $s>0$ and $t_0,t\in {\mathbb {R}}$. Also, from Eq. (9),

$$\begin{aligned} (b_{v_1}+b_{v_2})(\psi _s(x))= & {} (b_{v_1}+b_{v_2})(x)+s, \\ (b_{v_1}-b_{v_2})(\psi _s(x))= & {} (b_{v_1}-b_{v_2})(x), \end{aligned}$$

for all $s>0$ and $x\in M-D$. Hence, $\psi _s(S(\varepsilon ,t))=S(s+\varepsilon ,t)$ holds, for all $s,\varepsilon >0$ and $t\in {\mathbb {R}}$. By Eq. (17),

$$\begin{aligned} V(s,t)= & {} \int _{\phi _t(S(s,0))}\sqrt{\frac{1-\beta }{1+\beta }}d\mu ' \nonumber \\= & {} \int _{S(s,0)}\sqrt{\frac{1-\beta (\phi _t)}{1+\beta (\phi _t)}}\,(\phi _t)^*(d\mu ') \nonumber \\= & {} \int _{S(s,0)}\sqrt{\frac{1-\beta }{1+\beta }}d\mu ' \nonumber \\= & {} V(s,0), \end{aligned}$$

(19)

for all $s>0$ and $t\in {\mathbb {R}}$. For all $s,\varepsilon >0$ and $t\in {\mathbb {R}}$, from Eq. (18), we obtain

$$\begin{aligned} W(s+\varepsilon ,t)= & {} \int _{\psi _s(S(\varepsilon ,t))}\sqrt{\frac{1+\beta }{1-\beta }}d\mu '\\= & {} \int _{S(\varepsilon ,t)}\sqrt{\frac{1+\beta (\psi _s)}{1-\beta (\psi _s)}}\,(\psi _s)^*(d\mu ')\\= & {} \int _{S(\varepsilon ,t)}\exp \left( \int _0^s\frac{h}{1+\beta (\psi _k)}dk\right) \sqrt{\frac{1+\beta }{1-\beta }}d\mu '. \end{aligned}$$

By differentiating it for s, we get

$$\begin{aligned} \frac{\partial }{\partial s}W(s+\varepsilon ,t)= & {} \int _{S(\varepsilon ,t)}\frac{h}{1+\beta (\psi _s)}\exp \left( \int _0^s\frac{h}{1+\beta (\psi _k)}dk\right) \sqrt{\frac{1+\beta }{1-\beta }}d\mu '\\= & {} \int _{S(\varepsilon ,t)}\frac{h}{1+\beta (\psi _s)}\sqrt{\frac{1+\beta (\psi _s)}{1-\beta (\psi _s)}}\,(\psi _s)^*(d\mu ')\\= & {} \int _{S(s+\varepsilon ,t)}\frac{h}{\sqrt{1-\beta ^2}}d\mu '. \end{aligned}$$

By Eq. (19), we have

$$\begin{aligned} \frac{\partial }{\partial t}V(s,t)= & {} 0, \end{aligned}$$

(20)

$$\begin{aligned} \frac{\partial }{\partial s}W(s,t)= & {} \int _{S(s,t)}\frac{h}{\sqrt{1-\beta ^2}}d\mu ' \nonumber \\= & {} \frac{h}{2}W(s,t)+\frac{h}{2}V(s,t). \end{aligned}$$

(21)

By differentiating Eq. (21) for t, from Eq. (20), the following equation holds:

$$\begin{aligned} \frac{\partial ^2}{\partial s\partial t}W(s,t)=\frac{h}{2}\frac{\partial }{\partial t}W(s,t), \end{aligned}$$

which implies, for all $s,\varepsilon >0$ and $t\in {\mathbb {R}}$,

$$\begin{aligned} \frac{\partial }{\partial t}W(s+\varepsilon ,t)=e^{hs/2}\frac{\partial }{\partial t}W(\varepsilon ,t). \end{aligned}$$

(22)

By Eq. (17),

$$\begin{aligned} W(s,t)= & {} \int _{\phi _t(S(s,0))}\sqrt{\frac{1+\beta }{1-\beta }}d\mu '\\= & {} \int _{S(s,0)}\sqrt{\frac{1+\beta (\phi _t)}{1-\beta (\phi _t)}}\,(\phi _t)^*(d\mu ')\\= & {} \int _{S(s,0)}\frac{1+\beta (\phi _t)}{1-\beta (\phi _t)}\sqrt{\frac{1-\beta (\phi _t)}{1+\beta (\phi _t)}}\,(\phi _t)^*(d\mu ') \\= & {} \int _{S(s,0)}\frac{1+\beta (\phi _t)}{1-\beta (\phi _t)}\sqrt{\frac{1-\beta }{1+\beta }}d\mu '\\= & {} \int _{S(s,0)}\left( -1+\frac{2}{1-\beta (\phi _t)}\right) \sqrt{\frac{1-\beta }{1+\beta }}d\mu '. \end{aligned}$$

Thus we obtain

$$\begin{aligned} \frac{\partial }{\partial t}W(s,t)= & {} \int _{S(s,0)}\frac{2 X[\beta ](\phi _t)}{(1-\beta (\phi _t))^2}\sqrt{\frac{1-\beta }{1+\beta }}d\mu '\\= & {} \int _{S(s,0)}\frac{2 X[\beta ](\phi _t)}{(1-\beta (\phi _t))^2}\sqrt{\frac{1-\beta (\phi _t)}{1+\beta (\phi _t)}}\,(\phi _t)^*(d\mu ')\\= & {} \int _{S(s,t)}\frac{2X[\beta ]}{(1-\beta )\sqrt{1-\beta ^2}}d\mu '. \end{aligned}$$

Now, we get, from Eq. (7),

$$\begin{aligned} X[\beta ]= & {} \frac{1}{2-2\beta }(\nabla b_{v_1}-\nabla b_{v_2})\left[ g(\nabla b_{v_1},\nabla b_{v_2})\right] \nonumber \\= & {} \frac{1}{2-2\beta }\left( U_2(\nabla b_{v_1},\nabla b_{v_1})-U_1(\nabla b_{v_2},\nabla b_{v_2})\right) . \end{aligned}$$

(23)

Consequently, we have

$$\begin{aligned} \frac{\partial }{\partial t}W(s,t)= & {} \int _{S(s,t)}\frac{\sqrt{1-\beta ^2}}{(1-\beta )^2} \frac{U_2(\nabla b_{v_1},\nabla b_{v_1})-U_1(\nabla b_{v_2},\nabla b_{v_2})}{1-g(\nabla b_{v_1},\nabla b_{v_2})^2}d\mu '\\= & {} \int _{S(s,t)}\frac{\sqrt{1-\beta ^2}}{(1-\beta )^2}\frac{U_2(\nabla b_{v_1}-\beta \nabla b_{v_2},\nabla b_{v_1}-\beta \nabla b_{v_2})}{\Vert \nabla b_{v_1}-\beta \nabla b_{v_2}\Vert ^2}d\mu ' \\{} & {} -\int _{S(s,t)}\frac{\sqrt{1-\beta ^2}}{(1-\beta )^2}\frac{U_1(\nabla b_{v_2}-\beta \nabla b_{v_1},\nabla b_{v_2}-\beta \nabla b_{v_1})}{\Vert \nabla b_{v_2}-\beta \nabla b_{v_1}\Vert ^2}d\mu ', \end{aligned}$$

since $\nabla _{\nabla b_{v_1}}\nabla b_{v_1}=0=\nabla _{\nabla b_{v_2}}\nabla b_{v_2}$,

$$\begin{aligned} U_1(\nabla b_{v_1},w)=U_1(w,\nabla b_{v_1})= & {} g(\nabla _{\nabla b_{v_1}}\nabla b_{v_1},w)=0,\\ U_2(\nabla b_{v_2},w)=U_2(w,\nabla b_{v_2})= & {} g(\nabla _{\nabla b_{v_2}}\nabla b_{v_2},w)=0, \end{aligned}$$

for all $w\in TM$,

$$\begin{aligned} U_1(\nabla b_{v_2},\nabla b_{v_2})= & {} U_1(\nabla b_{v_2},\nabla b_{v_2})-2\beta U_1(\nabla b_{v_1},\nabla b_{v_2})+\beta ^2 U_1(\nabla b_{v_1},\nabla b_{v_1})\\= & {} U_1(\nabla b_{v_2}-\beta \nabla b_{v_1},\nabla b_{v_2}-\beta \nabla b_{v_1}),\\ U_2(\nabla b_{v_1},\nabla b_{v_1})= & {} U_2(\nabla b_{v_1},\nabla b_{v_1})-2\beta U_2(\nabla b_{v_1},\nabla b_{v_2})+\beta ^2 U_2(\nabla b_{v_2},\nabla b_{v_2})\\= & {} U_2(\nabla b_{v_1}-\beta \nabla b_{v_2},\nabla b_{v_1}-\beta \nabla b_{v_2}), \end{aligned}$$

and $1-g(\nabla b_{v_1},\nabla b_{v_2})^2=1-\beta ^2=\Vert \nabla b_{v_1}-\beta \nabla b_{v_2}\Vert ^2=\Vert \nabla b_{v_2}-\beta \nabla b_{v_1}\Vert ^2$.

Now, use the following lemma:

Lemma 4.5

Let (M, g) be an asymptotically harmonic manifold. Then, for all $v,w\in T^1M$,

$$\begin{aligned} g(\nabla _w\nabla b_v,w)\le h, \end{aligned}$$

(24)

where $h=-\Delta b_v$.

Proof

Let U be the (0, 2)-tensor field defined by $U(w_1,w_2):=g(\nabla _{w_1}\nabla b_v,w_2)$ for all $x\in M$ and $w_1,w_2\in T_xM$. Then U is symmetric, positive semi-definite, and ${\text {tr}}U=h$. Thus, every eigenvalue of U is real, non-negative, and less than or equal to h. In particular, Eq. (24) holds. $\square$

By Lemma 4.5,

$$\begin{aligned} \begin{aligned}&0\le \frac{U_1(\nabla b_{v_2},\nabla b_{v_2})}{1-\beta ^2}=\frac{U_1(\nabla b_{v_2}-\beta \nabla b_{v_1},\nabla b_{v_2}-\beta \nabla b_{v_1})}{\Vert \nabla b_{v_2}-\beta \nabla b_{v_1}\Vert ^2}\le h, \\&0\le \frac{U_2(\nabla b_{v_1},\nabla b_{v_1})}{1-\beta ^2}=\frac{U_2(\nabla b_{v_1}-\beta \nabla b_{v_2},\nabla b_{v_1}-\beta \nabla b_{v_2})}{\Vert \nabla b_{v_1}-\beta \nabla b_{v_2}\Vert ^2} \le h. \end{aligned}\nonumber \\ \end{aligned}$$

(25)

Hence, by Eqs. (23) and (25), $\frac{X[\beta ]}{1+\beta }$ is bounded. By Lemma 2.7, $\bigcup _{\varepsilon \in [0,s]}S(\varepsilon ,t)$ is compact for all $s >0$. Fix $s>0$. Then $\beta$ has a maximum value on the compact set $\bigcup _{\varepsilon \in [0,s]}S(\varepsilon ,t)$. In particular, there exists a constant $C>0$ such that, for all $\varepsilon \in (0,s)$,

$$\begin{aligned} \left| \frac{\partial }{\partial t}W(\varepsilon ,t)\right| \le C \int _{S(\varepsilon ,t)}\sqrt{1+\beta }\,d\mu '. \end{aligned}$$

(26)

Now, we use the following lemma:

Lemma 4.6

The $(n-2)$-dimensional volume ${\text {vol}}_{n-2}S(s,t)$ of S(s, t) is non-decreasing for $s>0$ where $t\in {\mathbb {R}}$ is fixed, and, for all $s>0$ and $x\in S(s,t)$,

$$\begin{aligned} \beta (x)\le -2e^{-hs}+1. \end{aligned}$$

Proof

For all $s,\varepsilon >0$ and $t\in {\mathbb {R}}$,

$$\begin{aligned} \begin{aligned} {\text {vol}}_{n-2}S(s+\varepsilon ,t)&= \int _{\psi _s(S(\varepsilon ,t))}d\mu '=\int _{S(\varepsilon ,t)}(\psi _s)^*(d\mu ')\\&=\int _{S(\varepsilon ,t)}\exp \left( \int _0^s\frac{h}{1+\beta (\psi _k)}dk\right) \sqrt{\frac{(1+\beta )(1-\beta (\psi _s))}{(1-\beta )(1+\beta (\psi _s))}}\,d\mu '. \end{aligned} \end{aligned}$$

Thus, we obtain

$$\begin{aligned} \frac{\partial }{\partial s}{\text {vol}}_{n-2}S(s+\varepsilon ,t)= & {} \int _{S(\varepsilon ,t)}\left( \frac{h}{1+\beta (\psi _s)}-\frac{Y[\beta ](\psi _s)}{1-\beta ^2(\psi _s)}\right) (\psi _s)^*(d\mu ')\\= & {} \int _{S(s+\varepsilon ,t)}\left( \frac{h}{1+\beta }-\frac{Y[\beta ]}{1-\beta ^2}\right) d\mu ' \\= & {} \int _{S(s+\varepsilon ,t)}\frac{1}{1+\beta }\left( h-\frac{Y[\beta ]}{1-\beta }\right) d\mu ' \end{aligned}$$

Hence, we have

$$\begin{aligned} \frac{\partial }{\partial s}{\text {vol}}_{n-2}S(s,t) = \int _{S(s,t)}\frac{1}{1+\beta }\left( h-\frac{Y[\beta ]}{1-\beta }\right) d\mu '. \end{aligned}$$

(27)

By Eqs. (10) and (25),

$$\begin{aligned} Y\left[ \ln \left( \frac{1}{1-\beta }\right) \right] =\frac{Y[\beta ]}{1-\beta }\le h, \end{aligned}$$

(28)

and we obtain

$$\begin{aligned} \ln \left( \frac{1-\beta (x)}{1-\beta (\psi _s(x))}\right) \le hs \end{aligned}$$

and

$$\begin{aligned} \beta (\psi _s(x))\le e^{-hs}\beta (x) + 1 - e^{-hs}, \end{aligned}$$

for all $s>0$ and $x\in M-D$. Since, $\lim _{k\rightarrow s-}\beta (\psi _{-k}(x))=-1$ for all $x\in S(s,t)$, by considering $\beta (x)=\beta (\psi _s(\psi _{-s}(x)))$, we obtain, for all $s>0$ and $x\in S(s,t)$,

$$\begin{aligned} \beta (x)\le -2 e^{-hs}+1. \end{aligned}$$

(29)

Thus, by Eqs. (27), (28), and (29),

$$\begin{aligned} \frac{\partial }{\partial s}{\text {vol}}_{n-2}S(s,t) \ge \frac{1}{2(1-e^{-hs})}\left( h-h\right) {\text {vol}}_{n-2}S(s,t)= 0. \end{aligned}$$

(30)

Thus, ${\text {vol}}_{n-2}S(s,t)$ is non-decreasing for $s>0$. $\square$

By Eq. (26) and Lemma 4.6, for small $\varepsilon >0$, ${\text {vol}}_{n-2}S(\varepsilon ,t)$ is bounded, and for some constant $C>0$

$$\begin{aligned} \left| \frac{\partial }{\partial t}W(\varepsilon ,t)\right| \le C\sqrt{2-2e^{-h\varepsilon }}. \end{aligned}$$

Then we obtain

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0+}\frac{\partial }{\partial t}W(\varepsilon ,t)=0, \end{aligned}$$

(31)

and, by Eqs. (22) and (31), we have

$$\begin{aligned} \frac{\partial }{\partial t}W(s,t)=0 \end{aligned}$$

(32)

By Eqs. (20) and (32), Theorem 4.4 is proved. $\square$

Proof of Theorem 1.2

Since $\beta = -1$ on D, the notations X, $\phi _t$ can be extended to M, and, by Eq. (15), we have

$$\begin{aligned} {\text {vol}}_{n-2}S(0,t)= \int _{S(0,0)}(\phi _t)^*(d\mu ')=\int _{S(0,0)}d\mu '={\text {vol}}_{n-2}S(0,0). \end{aligned}$$

By setting a constant $C={\text {vol}}_{n-2}S(0,0)+1$, Theorem 1.2 is proved for $2c=c_0$. Now, suppose that $c_1+c_2\ne c_0$. The $(n-2)$-dimensional volume of the intersection $S=b_{v_1}^{-1}(c_1)\cap b_{v_2}^{-1}(c_2)$ satisfies

$$\begin{aligned} {\text {vol}}_{n-2}S=\int _S d\mu ' \le \int _S \frac{1}{\sqrt{1-\beta ^2}}d\mu '=\frac{1}{2}(V(s,t)+W(s,t)), \end{aligned}$$

where $s=c_1+c_2-c_0$, $t=c_1-c_2$, and $V(s,t)+W(s,t)$ is independent of t by Theorem 4.4. By setting $C=\frac{1}{2}(V(s,t)+W(s,t)+1)$, the proof is completed. Such C has a minimum value when $\nabla b_{v_1}$ and $\nabla b_{v_2}$ are orthogonal, and increases if the angle between $\nabla b_{v_1}$ and $\nabla b_{v_2}$ approaches to 0 or $\pi$. $\square$

Now, we give an example which supports the main theorem.

Example

Consider the Poincaré upper-half plane model $\{(x,y,z)\in {\mathbb {R}}^3:z>0\}$ with the metric:

$$\begin{aligned} g=\frac{dx^2+dy^2+dz^2}{z^2}. \end{aligned}$$

The distance between two points $(x_1,y_1,z_1)$, $(x_2,y_2,z_2)$ is

$$\begin{aligned} d((x_1,y_1,z_1),(x_2,y_2,z_2))=2{\text {arcsinh}}\left( \frac{\sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2}}{2\sqrt{z_1z_2}}\right) , \end{aligned}$$

We consider the volume of the intersections of horospheres for the case: $v_1=\left. \frac{\partial }{\partial x}\right| _{(0,0,1)}$ and $v_2=-\left. \frac{\partial }{\partial x}\right| _{(0,0,1)}$. The geodesic $\gamma _{v_1}$ is the unit circle centered at (0, 0, 0) and the equation of the geodesic sphere centered at $(\cos r,0,\sin r)$ containing (0, 0, 2) is

$$\begin{aligned} \frac{(x-\cos r)^2+y^2+(z-\sin r)^2}{4\sin r \, z}=\frac{5-4\sin r}{8\sin r}, \end{aligned}$$

or equivalently,

$$\begin{aligned} (x-\cos r)^2+y^2+\left( z-\frac{5}{4}\right) ^2=\frac{9}{16}. \end{aligned}$$

Every point (x, y, z) of the intersection of the geodesic spheres centered at $(\cos r,0,\sin r)$ and $(-\cos r,0,\sin r)$ containing (0, 0, 2) satisfies

$$\begin{aligned} x=0, \,\, y^2+\left( z-\frac{5}{4}\right) ^2=\frac{9}{16}. \end{aligned}$$

It is also the equation of the intersection of horospheres. Write $y=\frac{3}{4}\cos t$ and $z=\frac{3}{4}\sin t+\frac{5}{4}$. Then the volume of the intersection of horospheres is

$$\begin{aligned} \int _0^{2\pi } \frac{3}{3\sin t + 5}dt < 3\pi . \end{aligned}$$

Remark

Let (M, g) be an asymptotically harmonic, visibility manifold. Let $c_1,c_2\in {\mathbb {R}}$ such that $c_1+c_2>c_0$ and $r>0$. The set $b_{v_1}^{-1}([c_1,c_1+r])\cap b_{v_2}^{-1}([c_2,c_2+r])$ is the union of countably many sets of the form

$$\begin{aligned} S=\{x\in M: a_1+c_0\le b_{v_1}+b_{v_2}\le a_2+c_0, \,\, a_3\le b_{v_1}-b_{v_2}\le a_4\}, \end{aligned}$$

where $a_1,a_2\ge 0$ and $a_3,a_4\in {\mathbb {R}}$. It can be obtained by taking the middle points of each sides of the square $[c_1,c_1+r]\times [c_2,c_2+r]$ repeatedly. The n-dimensional volume of a set of the form equals

$$\begin{aligned} \begin{aligned} \int _S d\mu&= \int _S \theta _1\wedge \theta _2\wedge d\mu ' \\&=\int _S db_{v_1}\wedge db_{v_2}\wedge \left( \frac{1}{\sqrt{1-\beta ^2}}d\mu '\right) \\&=\frac{1}{2}\int _{a_1}^{a_2}\int _{a_3}^{a_4}\int _{S(s,t)}\frac{1}{\sqrt{1-\beta ^2}}d\mu '\,dt\,ds. \end{aligned} \end{aligned}$$

By Theorem 4.4,

$$\begin{aligned} \int _S d\mu = \frac{a_4-a_3}{2}\int _{a_1}^{a_2}\int _{S(s,0)}\frac{1}{\sqrt{1-\beta ^2}}d\mu '\,ds. \end{aligned}$$

Therefore, the n-dimensional volume of $b_{v_1}^{-1}([c_1,c_1+r])\cap b_{v_2}^{-1}([c_2,c_2+r])$ is independent of $c_1-c_2$.