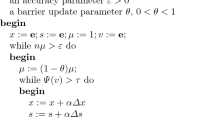A polynomial interior-point algorithm with improved iteration bounds for linear optimization

Abstract

In this paper, we present a polynomial primal-dual interior-point algorithm for linear optimization based on a modified logarithmic barrier kernel function. Iteration bounds for the large-update interior-point method and the small-update interior-point method are derived. It is shown that the large-update interior-point method has the same polynomial complexity as the small-update interior-point method, which is the best known iteration bounds. Our result closes a long-existing gap in the theoretical complexity bounds for large-update interior-point method and small-update interior-point method.

1 Introduction

The field of interior-point methods (IPMs) for linear optimization (LO) originated with the Karmarkar’s paper [1] that was proved to have much better polynomial complexity than the Khacian’s ellipsoidal method, the first method with polynomial complexity for LO. Motivated by the success of Karmarkar’s method for LO, many researchers have proposed and analyzed various IPMs for LO [2,3,4,5,6], second-order cone optimization (SOCO) [7], semidefinite optimization (SDO) [8], and linear complementarity problem (LCP) [9,10,11]. Other relevant references are [12,13,14,15,16,17,18]. In this paper, we restrict ourselves to the primal-dual IPMs for the class of LOs.

The primal-dual IPMs use the Newton direction as a search direction, which is derived from the well-known primal-dual logarithmic barrier function. There is a gap between the practical behavior and the theoretical performance results of these algorithm [19], especially for the so-called large-update methods. In practice, large-update methods are much more efficient than the so-called small-update methods [12,13,14,15,16,17,18]. However, small-update methods have better iteration bound in theory than large-update methods.

Several strategies have been proposed to improve the theoretical complexity of large-update IPMs. Hung and Ye [20], Jansen et al. [21] and Monteiro et al. [22] use higher order methods to improve the complexity of large-update IPMs. However, there is a price to pay for the reduced complexity; higher order methods are computationally more expensive per iteration than first order methods, since some additional equation systems need to be solved with the same coefficient matrix at each iteration. Subsequently Peng et al. [2, 3] improved the theoretical complexity for large-update IPMs using a class of self-regular kernel functions to determine the proximity measure and search direction, which are the crucial factors for the analysis of IPMs. Bai et al. [5, 23,24,25,26] consider several specific kernel functions and analyzed complexity of corresponding IPMs. In [6] Bai et al. proposed a new class of kernel functions, called eligible kernel functions that are neither logarithmic nor self-regular, and they presented a unified framework to analyze the complexity of the corresponding IPMs.

Motivated by the above-mentioned papers, in this paper we introduce a new kernel function $\psi (t)$ as follows:

$$\begin{aligned} \psi (t)=\frac{t^2-1}{2}+2\ln \left( 1+\frac{1}{t}\right) -2\ln 2,~~~ t>0. \end{aligned}$$

(1)

The new kernel function leads to the best known complexity bound of $O(\sqrt{n}\log \frac{n}{\epsilon })$ for the large-update primal-dual IPM, which is as good as iteration bound for small-update primal-dual IPM, hence, improving the theoretical complexity of large-update IPMs.

The paper is organized as follows. In Sect. 2, the generic primal-dual IPM based on the kernel function is described. In Sect. 3, we give the properties of the new kernel function which plays a crucial role in the complexity analysis of algorithm. In Sect. 4, the estimation of the step-size is discussed. The iteration bounds of the algorithm with large-updates and small-updates, are derived in Sect. 5. Finally, Sect. 6 contains some concluding remarks.

Some notation used throughout the paper is as follows. First, $\Re ^n$, $\Re ^{n}_{+}$ and $\Re ^{n}_{++}$ denote the set of vectors with n components, the set of nonnegative vectors and the set of positive vectors, respectively. The 2-norm and the infinity norm are denoted by $\Vert \cdot \Vert$ and ${\Vert \cdot \Vert }_\infty$, respectively. If $x,s\in \Re ^n$, then xs denotes the componentwise (or Hadamard) product of the vectors x and s. Furthermore, e denotes the all-one vector of length n. If $z\in \Re ^n_+$ and $f:\Re _+\rightarrow \Re _+$, then f(z) denotes the vector in $\Re ^n_+$ whose ith component is $f(z_i)$, with $1\le i\le n$. We write $f(x)=O(g(x))$ if $f(x)\le cg(x)$ for some positive constant c and $f(x)=\Theta (g(x))$ if $c_1g(x)\le f(x)\le c_2g(x)$ for positive constants $c_1$ and $c_2$.

2 The generic interior-point algorithm

In this paper, we consider the LO problem, which takes the following standard form

$$\begin{aligned} (P)\ \ \ \ \ \ \min \{c^Tx:Ax=b,x\ge 0\}, \end{aligned}$$

where $A\in \textbf{R}^{m\times n}$, rank$(A)=m, b\in \textbf{R}^m$, $c\in \textbf{R}^n$, and its dual problem

$$\begin{aligned} (D)\ \ \ \ \ \ \max \{b^Ty:A^Ty+s=c,s\ge 0\}. \end{aligned}$$

Without loss of generality, we assume that both (P) and (D) satisfy the interior point condition (IPC), i.e., there exists $(x^0, s^0, y^0)$ such that

$$\begin{aligned} Ax^0=b,~~x^0>0,~~A^Ty^0+s^0=c,~~s^0>0. \end{aligned}$$

If the IPC holds, finding an optimal solution of (P) and (D) is equivalent to solving the system of optimality conditions

$$\begin{aligned} Ax= & {} b, x\ge 0, \nonumber \\ A^Ty+s= & {} c, s\ge 0, \nonumber \\ xs= & {} 0, \end{aligned}$$

(2)

where xs denotes the coordinatewise product of the vectors x and s. The basic idea of primal-dual IPMs is to replace the third equation in (2), the so-called complementarity condition for (P) and (D), by the parameterized equation $xs = \mu e,$ with $e = (1,..., 1)^T, \mu >0$. This leads to the following system

$$\begin{aligned} Ax= & {} b, x\ge 0, \nonumber \\ A^Ty+s= & {} c, s\ge 0, \nonumber \\ xs= & {} \mu e. \end{aligned}$$

(3)

If the IPC holds, then for each $\mu >0$, system (3) has a unique solution $(x(\mu ), y(\mu ), s(\mu ))$, which is called the $\mu$-center of the primal-dual pair (P) and (D). The set of all $\mu$-center ($\mu >0$) is the central path of (P) and (D). The limit of the central path (as $\mu$ goes to zero) exists, and since the limit point satisfies (2), it naturally yields optimal solutions for both (P) and (D) [12].

Now we describe how classical primal-dual IPMs work. We start with a current iterate (x, y, s) that satisfies the IPC. Without loss of generality (Roos et al. [12]), we may assume this for $\mu =1$, with $x(1)=s(1)=e.$ We then decrease parameter $\mu$ to $\mu : =(1-\theta )\mu$, for some $\theta \in (0, 1)$, and we solve the following Newton system

$$\begin{aligned} A\Delta x= & {} 0, \nonumber \\ A^T\Delta y+\Delta s= & {} 0, \nonumber \\ s\Delta x+ x\Delta s= & {} \mu e-xs. \end{aligned}$$

(4)

to obtain the search direction. Since matrix A has a full row rank, the Newton system (4) has a unique solution for all $\mu > 0$. Then we take a step along the search direction with a step size $\alpha \in (0, 1]$ which is defined by some line search rule. The search direction and line search rule ensure that the new triple $(x+\alpha \Delta x, y+\alpha \Delta y, s+\alpha \Delta s)$ is closer to the $\mu$-center $(x(\mu ), y(\mu ), s(\mu ))$. This step is repeated as long as the actual iterate is sufficiently close to the $\mu$-center. Then $\mu$ is reduced again by the factor $(1-\theta )$ and the process is repeated until an approximate solution to the problem is obtained, e.g., until $n\mu$ is smaller than some prescribed accuracy $\varepsilon$.

To describe the ideas underlying this paper, we introduce a scaled version of the system (4). Let

$$\begin{aligned} v := \sqrt{\frac{xs}{\mu }},~~~ d_x:= \frac{v\Delta x}{x},~~~ d_s:= \frac{v\Delta s}{s}. \end{aligned}$$

(5)

Using the above notation, we can rewrite the Newton system (4) as

$$\begin{aligned} \bar{A}d_x= & {} 0, \nonumber \\ \bar{A}^Td_y+d_s= & {} 0, \nonumber \\ d_x+d_s= & {} v^{-1}-v, \end{aligned}$$

(6)

where $\bar{A}=\frac{1}{\mu }AV^{-1}X, V=\textrm{diag}\,(v), X=\textrm{diag}\,(x), S=\textrm{diag}\,(s)$.

When analyzing the algorithm, we need to measure the closeness of a primal-dual pair (x, s) to the $\mu$-center $(x(\mu ), s(\mu ))$. The most popular tool for measuring this closeness is the so-called primal-dual logarithmic barrier function [12], which is given by

$$\begin{aligned} \Phi _{c}(x,s;\mu )=\frac{x^Ts}{\mu }-\sum _{i=1}^{n}\log \frac{x_is_i}{\mu }-n. \end{aligned}$$

(7)

The logarithmic kernel function is defined as

$$\begin{aligned} \psi _{c}(t)=\frac{t^2-1}{2}-\log t,~~~ t>0, \end{aligned}$$

(8)

which is a strictly convex function on $\Re ^n_{++}$ with $\psi _{c}(1)= \psi '_{c}(t)=0$, and attains its minimal at $t=1$. Substituting (8) in (7) we obtain

$$\begin{aligned} \Phi _{c}(x,s;\mu )=2\Psi _c(v)=2\sum _{i=1}^{n}\psi _c(v_i). \end{aligned}$$

(9)

Note that the right side of the third equation in (6) equals the negative gradient of the logarithmic barrier function $\Psi _c(v)$, i.e.

$$\begin{aligned} d_x+d_s=-\nabla \Psi _c(v). \end{aligned}$$

(10)

This shows that the negative gradient of the logarithmic barrier function determines the classical Newton search direction for primal-dual IPMs. Hence, a point on the central path can be characterized by the property of $v_i=1,$ for any i. In IPMs the iterates usually are not on the central path, but in some neighborhood of it. A natural way to measure the deviation of the i-th coordinate $v_i$ from 1 is to use the value at $v_i$ of a smooth strictly convex function $\psi (t):\Re _{++}\rightarrow \Re _{+}$ that is nonnegative, assumes its minimal value (zero) at 1 and that goes to infinity when the argument goes to zero or infinity. These requirements can be formalized as follows:

$$\begin{aligned}{} & {} \psi '(1)=\psi (1)=0, \nonumber \\{} & {} \quad \psi ''(v_i)>0, v_i>0,\nonumber \\{} & {} \quad \lim _{v_i\rightarrow 0^+}\psi (v_i)=\lim _{v_i\rightarrow \infty }\psi (v_i)=\infty . \end{aligned}$$

(11)

As these conditions already include, a proper measure need to be strictly convex and at least twice differentiable. Then a barrier function $\Psi (v)$, based on the kernel function $\psi (v_i)$, in the scaled space can be defined as the sum of the componentwise deviations:

$$\begin{aligned} \Psi (v):=\sum _{i=1}^{n}\psi (v_i). \end{aligned}$$

(12)

Replacing the barrier function $\Psi _c(v)$ by the above function, we obtain the following modified Newton system

$$\begin{aligned} \bar{A}d_x= & {} 0, \nonumber \\ \bar{A}^T\Delta y+d_s= & {} 0, \nonumber \\ d_x+d_s= & {} -\nabla \Psi (v). \end{aligned}$$

(13)

The last equality in system (13) can be expressed as

$$\begin{aligned} s\Delta x+ x\Delta s=-\mu \nu \nabla \Psi (v). \end{aligned}$$

(14)

   The generic interior-point algorithm for LO is shown in Fig. 1. It is clear from this description that the closeness of (x, y, s) to $(x(\mu ), y(\mu ), s(\mu ))$ is measured by the value of $\Psi (v)$, with $\tau$ as a threshold value: if $\Psi (v)\le \tau$, then we start a new outer iteration by performing a $\mu$-update; otherwise we enter an inner iteration by computing the search directions at the current iterate with respect to the current value of $\mu$ and apply the update $x:=x+\alpha \Delta x, y:=y+\alpha \Delta y, s:=s+\alpha \Delta s)$ to get a new iterate.

Fig. 1

Generic algorithm

   The choice of the step size $\alpha$ ($0< \alpha \le 1$) is a crucial issue in the analysis of the algorithm. It needs to ensure that the resulting iterate is feasible and stays within a certain neighborhood of the current $\mu$-center. In the theoretical analysis, the step size $\alpha$ is usually given a value that depends on the closeness of the current iterates to the $\mu$-center.

The choice of the barrier update parameter $\theta$ plays an important role in both theory and practice of IPM. If $\theta$ depends on the dimension of the problem, e.g., $\theta =\frac{1}{\sqrt{n}}$, then we call the algorithm a small-step (or small-update) method. It uses full Newton steps and the iterates stay in a small neighborhood of the central path. If $\theta$ is the constant independent of the dimension n of the problem, e.g., $\theta =\frac{1}{2}$, then we call the algorithm a large-step (or large-update) method. In large-update method the iterates are allowed to move in a wide neighborhood of the central path.

3 Properties of the new kernel and barrier functions

In this section, we discuss some properties of the new kernel function $\psi (t)$ defined in (1) and the corresponding barrier function that will be used in the complexity analysis of the algorithm. According to (1), the scaled barrier function $\Psi (v)$ is given by

$$\begin{aligned} \Psi (v)=\sum _{i=1}^{n}\psi (v_i)=\sum _{i=1}^{n}\frac{v_i^2-1}{2}+2\ln (1+\frac{1}{v_i})-2\ln 2,\ \ v_i>0, \end{aligned}$$

(15)

where $v\in R^n_{++}$. In the analysis of the algorithm, we also use the norm-based proximity measure $\delta (v)$ defined by

$$\begin{aligned} \delta (v):=\frac{1}{2}\Vert \nabla \Psi (v)\Vert =\frac{1}{2}\Vert d_x+d_s\Vert . \end{aligned}$$

(16)

Since $\Psi (v)$ is strictly convex and attains its minimum value of zero at $v = e$, we have

$$\begin{aligned} \Psi (e)=0\Leftrightarrow \delta (v)=0 \Leftrightarrow v=e. \end{aligned}$$

Obviously, the new kernel function (1) satisfies the properties

$$\begin{aligned}{} & {} \lim _{t\rightarrow 0^+}\psi (t)=\lim _{t\rightarrow \infty }\psi (t)=\infty ,\\{} & {} \quad \psi '(1)=\psi (1)=0. \end{aligned}$$

We write down the first three derivatives of $\psi (t)$ as follows

$$\begin{aligned} \psi ^{'}(t)= & {} t-\frac{2}{t+t^2}, \nonumber \\ \psi ^{''}(t)= & {} 1+2\frac{1+2t}{(t+t^2)^2}, \nonumber \\ \psi ^{'''}(t)= & {} -4\frac{3t^2+3t+1}{(t+t^2)^3}. \end{aligned}$$

(17)

Obviously, $\psi ''(t)$ is monotonically decreasing for all $t>0,$ and

$$\begin{aligned} \psi ^{''}(t)>1. \end{aligned}$$

(18)

In [6], the authors introduced a class of eligible kernel function, satisfied the following conditions

$$\begin{aligned} t\psi ''(t)+\psi '(t)> & {} 0, \ \ \ \ t>0, \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (a) \nonumber \\ t\psi ''(t)-\psi '(t)> & {} 0, \ \ \ \ t>0, \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (b)\nonumber \\ \psi ^{'''}(t)< & {} 0, \ \ \ \ t>0, \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (c) \nonumber \\ 2\psi ''(t)^2-\psi '(t)\psi ^{'''}(t)> & {} 0, \ \ \ \ 0<t<1, \ \ \ \ \ \ \ \ \ \ \ (d) \nonumber \\ \psi ''(t)\psi '(\beta t)-\beta \psi '(t)\psi ''(\beta t)> & {} 0, \ \ \ \ t>1,\beta >1. \ \ \ \ \ \ \ \ (e) \end{aligned}$$

(19)

In order to analyze the new algorithm, we would give the proof that the new kernel function is eligible in the following Lemma.

Lemma 3.1

The new kernel function (1) is eligible kernel function that satisfies conditions (19).

Proof

For any $t>0$, according to (17), we have

$$\begin{aligned}{} & {} t\psi ''(t)+\psi '(t)=2t+\frac{2t(1+2t)}{(t+t^2)^2}-\frac{2}{t+t^2}=2t+\frac{2}{(1+t)^2}>0,\\{} & {} t\psi ''(t)-\psi '(t)=2t\frac{1+2t}{(t+t^2)^2}+\frac{2}{t+t^2}=\frac{2(2+3t)}{t(1+t)^2}>0,\\{} & {} \psi ^{'''}(t)=-4\frac{3t^2+3t+1}{(t+t^2)^3}<0, \end{aligned}$$

and

$$\begin{aligned} 2\psi ''(t)^2-\psi '(t)\psi ^{'''}(t)=\frac{2(t^7+4t^6+6t^5+18t^4+33t^3+24t^2+10t+4)}{t^3(1+t)^4}, \end{aligned}$$

the right-hand side of the above equality is positive for $0<t<1$, which proves (19-d). It was shown in [6] that condition (e) is implied by (b) and (c). This completes the proof. $\square$

Lemma 3.2

For $\psi (t)$ we have

$$\begin{aligned}{} & {} \frac{1}{2}(t-1)^2\le \psi (t)\le \frac{1}{2}\psi ^{'}(t)^2, t > 0, \end{aligned}$$

(20)

$$\begin{aligned}{} & {} \psi (t)\le \frac{5}{4}(t-1)^2, t>1. \end{aligned}$$

(21)

Proof

Proof of (20): using (17) and (18), we have

$$\begin{aligned} \psi (t)=\int _1^t\int _1^\xi \psi ''(\zeta )d\zeta d\xi \ge \int _1^t\int _1^\xi d\zeta d\xi =\frac{1}{2}(t-1)^2, \end{aligned}$$

and

$$\begin{aligned} \psi (t)=\int _1^t\int _1^\xi \psi ''(\zeta )d\zeta d\xi \le \int _1^t\int _1^\xi \psi ''(\xi )\psi ''(\zeta )d\zeta d\xi =\frac{1}{2}\psi '(t)^2. \end{aligned}$$

$\square$

Proof of (21):

since $\psi (1)=\psi '(1)=0, \psi '''(t)<0, \psi ''(1)=\frac{5}{2},$ and by using Taylor’s Theorem at the right neighborhood of $t=1$, we have

$$\begin{aligned} \psi (t)=\psi (1)+\psi '(1)(t-1)+\frac{1}{2}\psi ''(1)(t-1)^2+\frac{1}{6}\psi '''(\xi )(\xi -1)^3 \le \frac{5}{4}(t-1)^2, \end{aligned}$$

for some $\xi , 1\le \xi \le t.$ This completes the proof. $\square$

Lemma 3.3

Let $\varrho :[0,+\infty )\rightarrow [1,+\infty )$ be the inverse function of $\psi (t)$ for $t\ge 1$ and $\rho :[0,+\infty )\rightarrow (0,1]$ be the inverse function of $-\frac{1}{2}\psi '(t)$ for all $t\in (0,1].$ Then we have

$$\begin{aligned} \sqrt{2s+1}\le & {} \varrho (s)\le 1+\sqrt{2s}, s \ge 0, \end{aligned}$$

(22)

$$\begin{aligned} \rho (z)\ge & {} \sqrt{\frac{\frac{2}{\lambda }}{2z+1}}, z \ge 0. \end{aligned}$$

(23)

Proof

Proof of (22): let $s=\psi (t), t\ge 1,$ i.e. $\varrho (s)=t, t\ge 1.$ By the definition of $\psi (t)$, we have

$$\begin{aligned} \frac{t^2-1}{2}=s-2\ln \left( 1+\frac{1}{t}\right) +2\ln 2. \end{aligned}$$

Because $-2\ln (1+\frac{1}{t})+2\ln 2$ is monotonically increasing with respect to $t\ge 1,$ we have

$$\begin{aligned} \frac{t^2-1}{2}\ge s, \end{aligned}$$

which implies that

$$\begin{aligned} \varrho (s)=t\ge \sqrt{2s+1}. \end{aligned}$$

By (20), we have $s=\psi (t)\ge \frac{1}{2}(t-1)^2$, so

$$\begin{aligned} \varrho (s)=t\le {1+\sqrt{2s}}. \end{aligned}$$

$\square$

Proof of (23):

let $z=-\frac{1}{2}\psi '(t), t\in (0,1].$ Using the definition of $\rho :\rho (z)=t, t\in (0,1]$, we have

$$\begin{aligned} \frac{2}{t+t^2}=2z+t, t\in (0,1]. \end{aligned}$$

On one hand, for $t\in (0,1],$ we have

$$\begin{aligned} {2z+t}\le {2z+1}. \end{aligned}$$

On the other hand, for any number $t_0\in (0,1]$, there exists a real number $\lambda =1+\frac{1}{t_0}$, such that

$$\begin{aligned} \frac{2}{t+t^2}\ge \frac{2}{t(\lambda t)}=\frac{2}{\lambda t^2},~~t_0\le t\le 1. \end{aligned}$$

The above two inequations imply that

$$\begin{aligned} \rho (z)=t\ge \sqrt{\frac{\frac{2}{\lambda }}{2z+1}}. \end{aligned}$$

This completes the proof. $\square$

The lemma below provides a bound for $\delta (v)$ in terms of $\Psi (v)$ which will play an important role in the analysis of the algorithm.

Lemma 3.4

Let $\delta (v)$ be as defined in (16). Then we have

$$\begin{aligned} \delta (v)\ge \sqrt{\frac{1}{2}\Psi (v)}. \end{aligned}$$

Proof

Using (20), we have

$$\begin{aligned} \Psi (v)= & {} \sum _{i=1}^n\psi (v_i)\le \sum _{i=1}^n\frac{1}{2}\psi '(v_i)^2\\= & {} \frac{1}{2}\Vert \nabla \Psi \Vert ^2=2\delta (v)^2, \end{aligned}$$

so

$$\begin{aligned} \delta (v)\ge \sqrt{\frac{1}{2}\Psi (v)}. \end{aligned}$$

This completes the proof. $\square$

Remark 3.5

Throughout the paper we assume that $\tau \ge 1.$ Using Lemma 3.4 and the assumption $\Psi (v)\ge \tau ,$ we have

$$\begin{aligned} \delta (v)\ge \sqrt{\frac{1}{2}}. \end{aligned}$$

4 Analysis of the algorithm

4.1 Growth behavior of the barrier function at the start of outer iteration

The following theorem yields an upper bound for $\Psi (v)$ after the $\mu$-update in terms of the inverse function of $\psi (t)$ for $t>0$.

From Theorem 3.2 in [6], we have the following Lemma 4.1.

Lemma 4.1

Let $\varrho :[0,+\infty )\rightarrow [1,+\infty )$ be defined as in Lemma 3.3. Then we have

$$\begin{aligned} \Psi (\beta v)\le n\psi \left( \beta \varrho \left( \frac{\Psi (v)}{n}\right) \right) , v\in R_{++},\beta \ge 1. \end{aligned}$$

Lemma 4.2

Let $0\le \theta <1,$ $v_+=\frac{v}{\sqrt{1-\theta }}$. If $\Psi (v)\le \tau$. Then we have

$$\begin{aligned} \Psi (v_+)\le \frac{5}{4(1-\theta )}\left( \sqrt{n}\theta +\sqrt{2\tau }\right) ^2. \end{aligned}$$

Proof

Since $\frac{1}{\sqrt{1-\theta }}\ge 1$ and $\varrho (\frac{\Psi (v)}{n})\ge 1$, we have $\frac{\varrho (\frac{\Psi (v)}{n})}{\sqrt{1-\theta }}\ge 1.$ Using Lemma 4.1 with $\beta =\frac{1}{\sqrt{1-\theta }}$, (21), (22), and $\Psi (v)\le \tau$, we have

$$\begin{aligned} \Psi (v_+)\le & {} n\psi \left( \frac{1}{\sqrt{1-\theta }}\varrho \left( \frac{\Psi (v)}{n}\right) \right) \\\le & {} n\frac{5}{4}\left( \frac{1}{\sqrt{1-\theta }}\varrho \left( \frac{\Psi (v)}{n}\right) -1\right) ^2 \\ {}= & {} \frac{5n}{4(1-\theta )}\left( \varrho \left( \frac{\Psi (v)}{n}\right) -\sqrt{1-\theta }\right) ^2 \\ {}\le & {} \frac{5n}{4(1-\theta )}\left( 1+\sqrt{\frac{2\Psi (v)}{n}}-\sqrt{1-\theta }\right) ^2 \\ {}\le & {} \frac{5}{4(1-\theta )}\left( \sqrt{n}\theta +\sqrt{2\tau }\right) ^2, \end{aligned}$$

where the last inequality holds from $1-\sqrt{1-\theta }=\frac{\theta }{1+\sqrt{1-\theta }}\le \theta , 0\le \theta <1.$ This completes the proof. $\square$

Denote

$$\begin{aligned} \Psi _0=\frac{5}{4(1-\theta )}\left( \sqrt{n}\theta +\sqrt{2\tau }\right) ^2= L(n,\theta ,\tau ), \end{aligned}$$

(24)

then $\Psi _0$ is an upper bound for $\Psi (v)$ during the process of the algorithm.

Remark 4.3

For large-update method we take $\tau =O(n), \theta =\Theta (1), {\Psi }_0=O(n)$. For small-update method we take $\tau =O(1), \theta =\Theta (\frac{1}{\sqrt{n}}), {\Psi }_0=O(1)$.

4.2 Determining the stepsize

In this section, we determine a default stepsize which not only keeps the iterations feasible but also gives rise to a sufficiently large decrease of $\Psi (t)$, as defined in (15), in each inner iteration. In each inner iteration we first compute the search direction $(\Delta x, \Delta y, \Delta s)$ from the system (14). After a stepsize $\alpha$, we have the new iterates

$$\begin{aligned} x_+:=x+\alpha \triangle x,~~~y_+:=y+\alpha \triangle y,~~~ s_+:=s+\alpha \triangle s. \end{aligned}$$

Using (5), we have

$$\begin{aligned}{} & {} x_+=x\left( e+\alpha \frac{\Delta x}{x}\right) =x\left( e+\alpha \frac{d_x}{v}\right) =\frac{x}{v}(v+\alpha d_x), \\{} & {} \quad s_+=x\left( e+\alpha \frac{\Delta s}{s}\right) =s\left( e+\alpha \frac{d_s}{v}\right) =\frac{s}{v}(v+\alpha d_s). \end{aligned}$$

So we have

$$\begin{aligned} v_+=\sqrt{\frac{x_+s_+}{\mu }}=\sqrt{(v+\alpha d_x)(v+\alpha d_s)}. \end{aligned}$$

For $\alpha > 0,$ we define

$$\begin{aligned} f(\alpha )=\Psi (v_+)-\Psi (v). \end{aligned}$$

Then $f(\alpha )$ is the difference of proximities between a new iterate and a current iterate for fixed $\mu .$ By (25), we have

$$\begin{aligned} \Psi (v_+)=\Psi (\sqrt{(v+\alpha d_x)(v+\alpha d_s)})\le \frac{1}{2}(\Psi (v+\alpha d_x)+\Psi (v+\alpha d_s)). \end{aligned}$$

Therefore we have $f(\alpha )\le f_1(\alpha )$, where

$$\begin{aligned} f_1(\alpha )=\frac{1}{2}(\Psi (v+\alpha d_x)+\Psi (v+\alpha d_s))-\Psi (v). \end{aligned}$$

(25)

Obviously $f(0)=f_1(0)=0.$ Taking the first two derivative of $f_1(\alpha )$ with respect to $\alpha$ we have

$$\begin{aligned}{} & {} f_1'(\alpha )=\frac{1}{2}\sum _{i=1}^n(\psi '(v_i+\alpha d_{xi})d_{xi}+\psi '(v_i+\alpha d_{si})d_{si}),\nonumber \\{} & {} \quad f_1''(\alpha )=\frac{1}{2}\sum _{i=1}^n(\psi ''(v_i+\alpha d_{xi})d_{xi}^2+\psi ''(v_i+\alpha d_{si})d_{si}^2). \end{aligned}$$

(26)

Using (10) and (16), we have

$$\begin{aligned} f_1'(0)=\frac{1}{2}\nabla \Psi (v)^T(d_x+d_s)=-\frac{1}{2}\nabla \Psi (v)^T\nabla \Psi (v)=-2\delta (v)^2. \end{aligned}$$

(27)

From Lemmas 4.1$-$4.3 in [6], we have the following Lemmas 4.4–4.6.

Lemma 4.4

Let $f_1(\alpha )$ be as defined in (25) and $\delta (v)$ be as defined in (16). Then we have

$$\begin{aligned} f_1''(\alpha )\le 2\delta ^2\psi ''(v_{min}-2\alpha \delta ). \end{aligned}$$

Lemma 4.5

If the step size $\alpha$ satisfies the inequality

$$\begin{aligned} -\psi '(v_{min}-2\alpha \delta )+\psi '(v_{min})\le 2\delta , \end{aligned}$$

(28)

we have

$$\begin{aligned} f_1'(\alpha )\le 0. \end{aligned}$$

Lemma 4.6

Let $\rho :[0,+\infty )\rightarrow (0,1]$ be defined as in Lemma 3.3. Then the largest step size $\bar{\alpha }$ satisfying (28) is given by

$$\begin{aligned} \bar{\alpha }=\frac{1}{2\delta }(\rho (\delta )-\rho (2\delta )). \end{aligned}$$

(29)

Lemma 4.7

Let $\rho$ be defined as in Lemma 3.3 and $\bar{\alpha }$ be defined as in Lemma 4.6. If $\Psi (v)\ge \tau \ge 1,$ then we have

$$\begin{aligned} \bar{\alpha }\ge \frac{1}{(12\lambda +2)\delta }. \end{aligned}$$

Proof

By the definition of $\rho$, we have

$$\begin{aligned} -\psi '(\rho (\delta ))=2\delta . \end{aligned}$$

Taking the derivative with respective to $\delta$, we find

$$\begin{aligned} -\psi ''(\rho (\delta ))\rho '(\delta )=2, \end{aligned}$$

which gives

$$\begin{aligned} \rho '(\delta )=-\frac{2}{\psi ''(\rho (\delta ))}<0. \end{aligned}$$

Since $\rho$ is monotonically decreasing, (29) can be written as

$$\begin{aligned} \bar{\alpha }=\frac{1}{2\delta }\int ^\delta _{2\delta }\rho '(\sigma )d\sigma =\frac{1}{\delta }\int ^\delta _{2\delta }\frac{d\sigma }{\psi ''(\rho (\sigma ))}. \end{aligned}$$

Due to (17), $\psi ''$ is monotonically decreasing. So $\psi ''(\rho (\sigma ))$ is maximal for $\sigma \in [\delta , 2\delta ]$ when $\rho (\sigma )$ is minimal. Since $\rho$ is monotonically decreasing, this occurs when $\sigma =2\delta$. Therefore

$$\begin{aligned} \bar{\alpha }=\frac{1}{\delta }\int ^\delta _{2\delta }\frac{d\sigma }{\psi ''(\rho (\sigma ))} \ge \frac{1}{\delta }\frac{\delta }{\psi ''(\rho (2\delta ))} =\frac{1}{\psi ''(\rho (2\delta ))}. \end{aligned}$$

Since $t\in (0,1],$ we have $\frac{1}{t+1}<1$ and

$$\begin{aligned} \psi ^{''}(t)\le 1+\frac{4}{t^2}. \end{aligned}$$

Using the above two inequalities, Remark 2.5 and (23), we have

$$\begin{aligned} \bar{\alpha }\ge \frac{1}{\psi ^{''}(\rho (2\delta ))} >\frac{1}{1+\frac{4}{[\rho (2\delta )]^2}} \ge \frac{1}{(12\lambda +2)\delta }. \end{aligned}$$

This completes the proof. $\square$

If we denote

$$\begin{aligned} \tilde{\alpha }=\frac{1}{(12\lambda +2)\delta }, \end{aligned}$$

(30)

then $\tilde{\alpha }$ is the default step size and $\bar{\alpha }\ge \tilde{\alpha }.$

4.3 Decrease of the barrier function during an inner iteration

Lemma 4.8

Let $\tilde{\alpha }$ be the default step size as defined in (30) and $\Psi (v)\ge 1$. Then

$$\begin{aligned} f(\bar{\alpha }) \le -\frac{1}{12\lambda +2}\sqrt{\frac{1}{2}}\Psi (v)^{\frac{1}{2}}. \end{aligned}$$

(31)

Proof

Let the univariate function h satisfy

$$\begin{aligned} h(0)= & {} f_1(0)=0,~~h'(0)=f_1'(0)=-2\delta ^2,\\ h''(\alpha )= & {} 2\delta ^2\psi ''(v_{min}-2\alpha \delta ). \end{aligned}$$

Due to Lemma 3.4, $f_1''(\alpha )\le h''(\alpha )$. As a consequence, $f_1'(\alpha )\le h'(\alpha )$ and $f_1(\alpha )\le h(\alpha )$. Taking $\alpha \le \bar{\alpha }$, with $\bar{\alpha }$ as defined in Lemma 3.6, we have

$$\begin{aligned} h'(\alpha )= & {} -2\delta ^2+2\delta ^2\int ^\alpha _0\psi ''(v_{min}-2\xi \delta )d\xi \\= & {} -2\delta ^2-\delta (\psi '(v_{min}-2\alpha \delta )-\psi '(v_{min}))\le 0. \end{aligned}$$

Since $h''(\alpha )$ is increasing with respect to $\alpha$, using Lemma 3.12 in [2], we have

$$\begin{aligned} f(\alpha )\le f_1(\alpha )\le h(\alpha )\le \alpha h'(0)=-\alpha \delta ^2. \end{aligned}$$

So, for $\bar{\alpha }\ge \tilde{\alpha }$, we have

$$\begin{aligned} f(\bar{\alpha }) \le -\bar{\alpha }\delta ^2 \le -\frac{1}{12\lambda +2}\sqrt{\frac{1}{2}}\Psi (v)^{\frac{1}{2}}. \end{aligned}$$

This completes the proof. $\square$

5 Complexity of the algorithm

In this section we estimate the complexity of our new IPM. We first estimate the complexity of the inner process, i.e., how many inner iterations are required to bring the iterates back to the specified neighborhood of the current $\mu$-center. We denote the value of $\Psi (v)$ after the $\mu$-update as $\Psi _0$, the subsequent values in the same outer iteration are denoted as $\Psi _k, k = 1,2,\ldots .$ If K denotes the total number of inner iterations in the outer iteration, we have

$$\begin{aligned} \Psi _0=\frac{5}{4(1-\theta )}\left( \sqrt{n}\theta +\sqrt{2\tau }\right) ^2, \Psi _{K-1}>\tau , 0\le \Psi _K\le \tau , \end{aligned}$$

by equation (24), and the decrease in each inner iteration is given

$$\begin{aligned} \Psi _{K+1}-\Psi _{K}\le -\frac{1}{12\lambda +2}\sqrt{\frac{1}{2}}\Psi (v)^{\frac{1}{2}}, k = 0,1,2,\ldots ,K-1 \end{aligned}$$

by inequality (31). We assume that

$$\begin{aligned} \frac{1}{12\lambda +2}\sqrt{\frac{1}{2}}\Psi (v)^{\frac{1}{2}}\ge \kappa \Psi (v)^{1-\gamma } \end{aligned}$$

for some positive constants $\kappa$ and $\gamma$, with $\gamma \in (0,1]$. We can find the appropriate values

$$\begin{aligned} \kappa =\frac{1}{(12\lambda +2)}\sqrt{\frac{1}{2}}, \gamma =\frac{1}{2}, \end{aligned}$$

such that

$$\begin{aligned} \Psi _{K+1}-\Psi _{K}\le -\kappa \Psi (v)^{1-\gamma }. \end{aligned}$$

Lemma 5.1

Let K be the total number of inner iterations in the outer iteration. Then we have

$$\begin{aligned} K\le 4(6\lambda +1)\sqrt{2}\Psi _0^{\frac{1}{2}}. \end{aligned}$$

Proof

Proof. By Lemma 1.3.2 in [3], we have

$$\begin{aligned} K\le \frac{\Psi _0^\gamma }{\kappa \gamma }=4(6\lambda +1)\sqrt{2}\Psi _0^{\frac{1}{2}}. \end{aligned}$$

This completes the proof. $\square$

Theorem 5.2

Consider LO problem with assumptions stated in Sect. 2. Then the upper bound on the number of iterations of the IPM in Fig. 1 with the new kernel function (1) to obtain $\varepsilon$-approximate solution of LO problem is

$$\begin{aligned} 4(6\lambda +1)\sqrt{2}\Psi _0^{\frac{1}{2}}\frac{\log \frac{n}{\epsilon }}{\theta }. \end{aligned}$$

Proof

The number of outer iterations is bounded above by $\frac{1}{\theta }\log \frac{n}{\epsilon }$ (see [12] ). Multiplying the number of outer iterations by the number of inner iterations stated in Lemma 5.1 we get an upper bound for the total number of iterations, namely,

$$\begin{aligned} 4(6\lambda +1)\sqrt{2}\Psi _0^{\frac{1}{2}}\frac{\log \frac{n}{\epsilon }}{\theta }. \end{aligned}$$

This completes the proof. $\square$

Corollary 5.3

. Considering the case of a large-update method, taking $\tau =O(n)$ and $\theta =\Theta (1),$ then we have

$$\begin{aligned} \Psi _0=O(n). \end{aligned}$$

So the iterations complexity for large-update method is

$$\begin{aligned} O(\sqrt{n}\log \frac{n}{\epsilon }). \end{aligned}$$

In case of a small-update method, taking $\tau =O(1), \theta =\Theta (\frac{1}{\sqrt{n}}),$ then we have

$$\begin{aligned} \Psi _0=O(1). \end{aligned}$$

Therefore, the iterations complexity for small-update method is

$$\begin{aligned} O(\sqrt{n}\log \frac{n}{\epsilon }), \end{aligned}$$

which as same as the iterations complexity for large-update IPM.

6 Conclusions

In this paper we introduced a new modified logarithmic barrier function (1) and studied its properties in Sect. 3. We used this kernel function to design and analyze IPM stated in Fig. 1. We show that iteration bound for the small-update version of the method matches the best known iteration bound for small-update IPM, namely $O(\sqrt{n}\log \frac{n}{\epsilon })$. We show that the iteration bound for large-update version of the method is the same, as for the small-update method. This is the best known upper bound for large-update method effectively closing the gap between iterations bounds of small- and large-update IPMs.