1 Introduction

Although Black and Scholes [5] achieved great success by proposing a simple and elegant model for the dynamic of the underlying price, which is widely adopted in real markets even today, its too simplified assumptions made to keep analytical tractability for European option prices may lead to the mis-pricing problem and are shown to be inappropriate. In particular, the returns of the underlying are actually asymmetric [21], and the volatility would never be constant due to the existence of the well-known “volatility smile” [8]. As a result, different models have been established to make modifications to the Black–Scholes (B–S) model so that the pricing bias could be relieved.

Among all these attempts, one of the most popular ways is to incorporate non-constant volatility into the B–S model, which can be mainly divided into two categories, i.e. local volatility and stochastic volatility. The former was considered by Dupire [9], where the volatility is set to be a deterministic function of underlying and time. However, many empirical studies suggest the “smile dynamics” are poorly captured by local volatility models (e.g., Hagan et al. [13]), which makes the latter much more popular among researchers and market practitioners.

It is believed that the continuous-time stochastic volatility model was first studied by Johnson [18], followed by Scott [22] and Wiggins [24], who solved the option pricing problem with numerical methods. Unfortunately, the lack of the closed-form solution would certainly make it time-consuming when the model is applied in real markets, which prompts the research in finding analytical solutions under different models. In fact, a progress was made by Hull and White [17], who managed to obtain a power series option pricing formula under their model. Although it may seem to be attractive than those models without analytical solutions, two major drawbacks of their model do exist; one is the zero correlation assumed between the underlying price and the volatility, which is inconsistent with empirical results that the underlying price and the volatility should be negatively correlated [2], and another is that the volatility process does not possess the mean-reverting property, which is at odds with the fact that the stochastic process for volatility is actually mean-reverting [4].

In 1993, a great breakthrough took place that the CIR model was adopted by Heston [16], who derived a closed-form pricing formula for European options. Two aspects could mainly account for the success of the Heston model. One is that the option pricing model itself satisfies a wide range of basic properties, such as the assumed arbitrary correlation between the underlying price and the volatility, and the non-negative and the mean-reverting properties for the volatility process. More importantly, an analytical formula exists when pricing options, which could provide some obvious advantages when the model is applied in real markets. For example, with closed-form solutions, computational accuracy could be guaranteed since systematical errors would always exist when numerical methods are made use of, and considerable amount of time and effort could be saved since parameter determination is time-intensive, which involves the calculation of option price every time we find a potential optimal set of parameters during our searching process. However, a lot of empirical evidence has shown that the Heston model is not perfect either. For example, it was suggested by Andersen et al. [1] that there could be insufficient kurtosis, while it was pointed out by Pan [20] that the square root specification is generally rejected based on the implication of the term structure of the volatility. In this sense, a number of modifications to the Heston have been recently proposed. Specifically, time-dependent Heston model was considered in [6, 12], while He and Chen [14] proposed a new stochastic volatility model with the long-term mean characterized by another stochastic process.

In this paper, we introduce the regime-switching mechanics into the He–Chen model [14] since there exists strong empirical evidence of regime switching stochastic volatility in real markets [23]. In our newly proposed model, the constant long-term mean in the Heston model is divided into two parts; one is controlled by the same stochastic process in the He–Chen model, while another is governed by the two state Markov chain, which is motivated by the substantial nonlinear mean-reverting property [3]. Our proposed model still preserves the most important feature, the closedness of the solution, by firstly deriving the characteristic function of the underlying price.

The rest of the paper is organized as follows. In Sect. 2, the new model will be introduced, followed by the closed-form pricing formula for European options, based on the newly derived forward characteristic function of the underlying price. In Sect. 3, numerical experiments are carried out to study the various properties of the new formula. Concluding remarks given in the last section.

2 New dynamics

In this section, we propose new dynamics for modeling the underlying price and option pricing. Based on the model proposed by He and Chen [14], who introduced the concept of stochastic long-term mean into the volatility process, a new model is presented by taking into consideration of the fact that many empirical studies (e.g., see [23]) show strong evidence of regime switching stochastic volatility in real markets.

We now first introduce the He–Chen model [14], which is specified as

$$\begin{aligned} \frac{dS}{S}& {}= rdt+\sqrt{v}dW_{t}^{1}, \\ dv& {}= k(\bar{v}+\theta -v)dt+\sigma _1\sqrt{v}dW_{t}^{2}, \\ d\theta& {}= \lambda dt+\sigma _2dB_t, \end{aligned}$$

with \(\{S_t, t\ge 0\}\) and \(\displaystyle \{v_t, t\ge 0\}\) denoting the underlying price and volatility respectively. \(W_{t}^{1}\) and \(W_{t}^{2}\) are two standard Brownian motions with correlation \(\rho\). \(B_t\) is another Brownian motion independent of \(W_{t}^{1}\) and \(W_{t}^{2}\). \(\theta\) is the stochastic source introduced into the constant long-term mean in the Heston model. However, their model can not capture the broader economic factors, which makes us consider a regime switching version of this model. In fact, we assume that \(\bar{v}\) be a function of a Markov chain \(X_t\) instead of being a constant so that the pricing dynamics we propose are

$$\begin{aligned} \frac{dS}{S}& {}= rdt+\sqrt{v}dW_{t}^{1}, \nonumber \\ dv& {}= k(\bar{v}_{X_t}+\theta -v)dt+\sigma _1\sqrt{v}dW_{t}^{2}, \nonumber \\ d\theta& {}= \lambda dt+\sigma _2dB_t, \end{aligned}$$
(2.1)

where the two-state Markov chain \(X_t\) is defined as

$$\begin{aligned} X_t=\left\{ \begin{array}{ll} 1, &{}\quad \text {when the economy is believed to be in State 1}, \\ 2, &{}\quad \text {when the economy is believed to be in State 2}, \end{array} \right. \end{aligned}$$

with the transition between the two states following a Poisson process as

$$\begin{aligned} \displaystyle P(t_{ij}>t)=e^{-\lambda _{ij}t}, i,j=1,2,~i\ne j. \end{aligned}$$

Here, \(\lambda _{ij}\) is the transition rate from State i to j, and \(t_{ij}\) is the time spent in State i before transferring to State j.

After our model is introduced, we now proceed to our main task of pricing European options, the results of which will be presented in the following theorem.

Theorem 1

Let \(U(S,v,\theta ,X_t,t)\) be the European call option price with \(S_t\) and \(v_t\) following the new dynamics (2.1). Then

$$\begin{aligned} \displaystyle U(S,v,\theta ,X_t,t)=SP_1-Ke^{-r(T-t)}P_2, \end{aligned}$$
(2.2)

where

$$\begin{aligned} \displaystyle&P_1=\frac{1}{2}+\frac{1}{\pi }\int _{0}^{\infty }Re\left[ \frac{e^{-i\phi ln(K)}f(\phi -j;\tau ,y,v,\theta ,X_t)}{i\phi f(-j;\tau ,y,v,\theta ,X_t)}\right] d\phi ,\\&P_2=\frac{1}{2}+\frac{1}{\pi }\int _{0}^{\infty }Re\left[ \frac{e^{-i\phi ln(K)}f(\phi ;\tau ,y,v,\theta ,X_t)}{i\phi }\right] d\phi ,\\&f(\phi ;\tau ,y,v,\theta ,X_t)=e^{\bar{C}(\tau ;\phi )+D(\tau ;\phi )v+E(\tau ;\phi )\theta +i\phi y}{\langle e^MX_t,I\rangle },\\&D(\tau ;\phi )=\frac{d-(i\phi \rho \sigma _1)}{\sigma _1^2}\left( \frac{1-e^{d\tau }}{1-ge^{d\tau }}\right) , \\&E(\tau ;\phi )=\frac{k}{\sigma _{1}^{2}}\left\{ [d-(i\phi \rho \sigma _1-k)]\tau -2\ln \left( \frac{1-ge^{d\tau }}{1-g}\right) \right\} ,\\&C(\tau ;\phi )=ir\phi \tau +\frac{1}{2}\int _{0}^{\tau }\sigma _{2}^{2}E^2(s;\phi )ds+\int _{0}^{\tau }\lambda E(s;\phi )ds,\\&d=\sqrt{(i\phi \rho \sigma _1-k)^2+\sigma _{1}^{2}(i\phi +\phi ^2)},~~g=\frac{(i\phi \rho \sigma _1-k)-d}{(i\phi \rho \sigma _1-k)+d},\\&M=\left( \begin{array}{ccc} \bar{v}_1E(\tau ;\phi )-\lambda _{12}\tau &{} \lambda _{21}\tau \\ \lambda _{12}\tau &{} \bar{v}_2E(\tau ;\phi )-\lambda _{21}\tau \end{array}\right) ,\\&X_t={e_1,e_2},~~e_1=(1,0)',~~e_2=(0,1)', I=(1,1)', \end{aligned}$$

with \(\tau =T-t\), \(j=\sqrt{-1}\), \(y=\ln (S)\), and \({\langle \cdot ,\cdot \rangle }\) represents the inner product of two vectors.

Proof

To find the solution of European option prices, we first derive the characteristic function of the underlying price defined as

$$\begin{aligned} \displaystyle f(\phi ;\tau ,y,v,\theta ,X_t)=E\left( e^{j\phi y_T}|y_t,v_t,\theta _t,X_t\right) , \end{aligned}$$
(2.3)

which can be further expressed as

$$\begin{aligned} \displaystyle f(\phi ;\tau ,y,v,\theta ,X_t)=E\left[ E\left( e^{j\phi y_T}|y_t,v_t,\theta _t,X_T\right) |y_t,v_t,\theta _t,X_t\right] , \end{aligned}$$
(2.4)

according to the tower rule of expectation. It is obvious that we have to work out the two expectations before we could find the characteristic function, and thus we will figure out the inner expectation

$$\begin{aligned} \displaystyle h(\phi ;\tau ,y,v,\theta ,X_t|X_T)=E\left( e^{j\phi y_T}|y_t,v_t,\theta _t,X_T\right) . \end{aligned}$$
(2.5)

Given the information of the Markov chain \(X_s\) for all \(s\in [t,T]\), \(\bar{v}_{X_t}\) becomes a deterministic function of the time t instead of being a random parameter. As a result, according to the Feynman–Kac theorem, it is not difficult to find that \(h(\phi ;\tau ,y,v,\theta ,X_t|X_T)\) should satisfy the following PDE system

$$\begin{aligned} \displaystyle \frac{\partial h}{\partial \tau }& {}= \frac{1}{2}v\frac{\partial ^{2}h}{\partial y^2}+\frac{1}{2}\sigma _{1}^{2}v\frac{\partial ^2h}{\partial v^2}+\frac{1}{2}\sigma _{2}^{2}\frac{\partial ^2g}{\partial \theta ^2}+\rho \sigma _1vS\frac{\partial ^{2}h}{\partial v\partial y}\nonumber \\&\quad +\,\left( r-\frac{1}{2}v\right) \frac{\partial h}{\partial y}+k(\bar{v}_t+\theta -v)\frac{\partial h}{\partial v}+\lambda \frac{\partial h}{\partial \theta }, \end{aligned}$$
(2.6)

with the initial condition

$$\begin{aligned} \displaystyle h(\phi ;0,y,v,\theta ,X_t|X_T)=e^{j\phi y_T}. \end{aligned}$$
(2.7)

Following [14], we assume that h take the form of

$$\begin{aligned} \displaystyle h(\phi ;\tau ,y,v,\theta ,X_t|X_T)=e^{C(\tau ;\phi )+D(\tau ;\phi )v+E(\tau ;\phi )\theta +i\phi y}, \end{aligned}$$
(2.8)

and substitute it into PDE (2.6), we could obtain the following three ODEs (ordinary differential equations)

$$\begin{aligned} \displaystyle \frac{\partial D}{\partial \tau }& {}= \frac{1}{2}\sigma _1^2D^2+(j\phi \rho \sigma _1-k)D-\frac{1}{2}(j\phi +\phi ^2),\\ \frac{\partial E}{\partial \tau }& {}= kD,\\ \frac{\partial C}{\partial \tau }& {}= \frac{1}{2}\sigma _2^2E^2+\lambda E+k\bar{v}_tD+jr\phi , \end{aligned}$$

with the initial condition being

$$\begin{aligned} \displaystyle C(0;\phi )=D(0;\phi )=E(0;\phi )=0. \end{aligned}$$

Similar to [14, 16], the three ODEs could be solved and we could obtain the analytical expression of \(C(\tau ;\phi )\), \(D(\tau ;\phi )\) and \(E(\tau ;\phi )\). In particular, \(C(\tau ;\phi )\) can be derived as

$$\begin{aligned} \displaystyle C(\tau ;\phi )=\int _{0}^{\tau }\frac{1}{2}\sigma _2^2E^2(s;\phi )+\lambda E(s;\phi )ds+jr\phi \tau +\int _{t}^{T}{\langle k\bar{v}_{X_s}D(s;\phi ),X_s\rangle }ds. \end{aligned}$$
(2.9)

As a result, the inner expectation \(h(\phi ;\tau ,y,v,\theta ,X_t|X_T)\) has been worked out, and the left work is the outer expectation

$$\begin{aligned} \displaystyle f(\phi ;\tau ,y,v,\theta ,X_t)=E\left[ h(\phi ;\tau ,y,v,\theta ,X_t|X_T)|y_t,v_t,\theta _t,X_t\right] , \end{aligned}$$
(2.10)

which can be further calculated as

$$\begin{aligned} \displaystyle f(\phi ;\tau ,y,v,\theta ,X_t)=e^{\bar{C}(\tau ;\phi )+D(\tau ;\phi )v+E(\tau ;\phi )\theta +i\phi y}E\left[ e^{\int _{t}^{T}{\langle k\bar{v}_{X_s}D(s;\phi ),X_s\rangle }ds}|X_t\right] . \end{aligned}$$
(2.11)

This means that once we figure out the value of the expectation \(E\left[ e^{\int _{t}^{T}{\langle k\bar{v}_{X_s}D(s;\phi ),X_s\rangle }ds}|X_t\right]\), we could finally reach the solution of the characteristic function. In fact, it should be noticed that the following equality

$$\begin{aligned} \displaystyle E\left( e^{\int _{t}^{T}{\langle u_{X_s},X_s\rangle }ds}|X_t\right) ={\langle e^{\int _{t}^{T}Bds}X_t,I\rangle }, \end{aligned}$$
(2.12)

has already been derived in [10] with the matrix B defined as

$$\begin{aligned} \displaystyle B=A'+diag[u_{X_s}]. \end{aligned}$$

Here, \(A'\) is the transposition of the transition rate matrix A for the two-state Markov chain \(X_t\), and diag[Q] denotes the matrix with the each element of the vector Q being on the main diagonal of the matrix. In this case, we could easily obtain

$$\begin{aligned} \displaystyle E\left[ e^{\int _{t}^{T}{\langle k\bar{v}_{X_s}D(s;\phi ),X_s\rangle }ds}|X_t\right] ={\langle e^MX_t,I\rangle }, \end{aligned}$$
(2.13)

where M can be obtained as

$$\begin{aligned} \displaystyle M=\left( \begin{array}{lll} \int _{0}^{\tau }k\bar{v}_1D(s;\phi )ds-\lambda _{12}\tau &{}\quad \lambda _{21}\tau \\ \lambda _{12}\tau &{}\quad \int _{0}^{\tau }k\bar{v}_2D(s;\phi )ds-\lambda _{21}\tau \\ \end{array}\right) . \end{aligned}$$

Therefore, we have finally derived the characteristic function \(f(\phi ;\tau ,y,v,\theta ,X_t)\).

According to the risk-neutral pricing rule, if we assume that the strike price be K, the price of a European call option can be expressed as

$$\begin{aligned} \displaystyle U(S,v,\theta ,X_t,t)& {}= e^{-r(T-t)}E\left[ \max \left( S_T-K,0\right) |S_t,v_t,\theta _t,X_t\right] ,\\& {}= e^{-r(T-t)}E\left[ \max \left( e^{y_T}-K,0\right) |y_t,v_t,\theta _t,X_t\right] ,\\& {}= e^{-r(T-t)}\int _{\ln K}^{+\infty }e^yp(y)dy-Ke^{-r(T-t)}\int _{\ln K}^{+\infty }p(y)dy, \end{aligned}$$

with p(y) defined to be the conditional probability density function of y. Clearly, pricing European options is now reduced to calculate the two integration in the above equation. Considering the fact that the characteristic function is the density function after Fourier transformation, the second integration can be formulated as

$$\begin{aligned} \displaystyle P_2\triangleq \int _{\ln K}^{+\infty }p(y)dy=\frac{1}{2}+\frac{1}{\pi }\int _{0}^{\infty }Re\left[ \frac{e^{-i\phi ln(K)}f(\phi ;\tau ,y,v,\theta ,X_t)}{i\phi }\right] d\phi , \end{aligned}$$

according to the relationship between the characteristic function and the distribution function. Moreover, we could also find that

$$\begin{aligned} \displaystyle \int _{-\infty }^{+\infty }e^yp(y)dy=f(-j;\tau ,y,v,\theta ,X_t)=Se^{r(T-t)}, \end{aligned}$$
(2.14)

with the definition of the Fourier transform. This implies that \(\displaystyle \frac{e^yp(y)}{f(-j;\tau ,y,v,\theta ,X_t)}\) is a density function of another random variable, the characteristic function of which \(\bar{f}(\phi ;\tau ,y,v,\theta ,X_t)\) could also be obtained with the definition

$$\begin{aligned} \displaystyle \bar{f}(\phi ;\tau ,y,v,\theta ,X_t)=F\left[ \frac{e^yp(y)}{f(-j;\tau ,y,v,\theta ,X_t)}\right] =\frac{f(\phi -j;\tau ,y,v,\theta ,X_t)}{f(-j;\tau ,y,v,\theta ,X_t)}. \end{aligned}$$
(2.15)

Again, the relationship between the characteristic function and the distribution function shows that

$$\begin{aligned} \displaystyle \int _{\ln K}^{+\infty }e^yp(y)dy& {}= f(-j;\tau ,y,v,\theta ,X_t)\left\{ \frac{1}{2}+\frac{1}{\pi }\int _{0}^{\infty }Re\left[ \frac{e^{-i\phi ln(K)}f(\phi ;\tau ,y,v,\theta ,X_t)}{i\phi }\right] d\phi \right\} ,\\& {}= Se^{r(T-t)}\left\{ \frac{1}{2}+\frac{1}{\pi }\int _{0}^{\infty }Re\left[ \frac{e^{-i\phi ln(K)}f(\phi ;\tau ,y,v,\theta ,X_t)}{i\phi }\right] d\phi \right\} ,\\ & {}\triangleq Se^{r(T-t)}P_1. \end{aligned}$$

This has completed the proof. \(\square\)

We have now successfully derived the closed form solution for European options under our newly proposed model. To make sure our formula could be directly applied in real markets and there are no algebraic errors, numerical comparison of the prices calculated with our formula and those obtained through directly simulating the dynamics (2.1) with Monte Carlo simulation is conducted. Furthermore, one may be also interested in whether the introduction of the mechanics of regime switching into the volatility process will make any difference. Therefore, with the confidence our formula, we will also compare the prices calculated with our formula and those from He and Chen’s formula [14]. Both of the two issues will be discussed in the next section.

3 Numerical experiments and examples

In this section, numerical experiments will be carried out to demonstrate the correctness of our formula by comparing the results calculated from our formula and those obtained through Monte Carlo simulation. Once we are confident of our formula, European option price under our model will be compared with those under the He–Chen model [14] to show the difference caused by the introduction of the regime switching mechanics. In the following, we assume that the current state is 1, i.e. \(X_0=(1,0)'\). The risk-free interest rate r and the correlation \(\rho\) are set to be 0.05 and − 0.5 respectively, the volatility of volatility \(\sigma _1\) is 0.1, the speed for mean-reversion k is 10, and the strike price K will be 100. The the initial value of \(\theta\) and v is 0.03. The two parameters associated with stochastic long-term mean, i.e., \(\sigma _2\) and \(\lambda\), both take the value of 0.01.

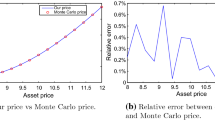
The numerical comparison of our price with Monte Carlo price under the chosen set of parameters has already been presented in Fig. 1. To be more specific, it is obvious that the two prices are quite close to each other shown in Fig. 1a. It should also be noticed that the European call option price is a monotonic increasing function of the underlying price, which is as expected. As for the relative difference, Fig. 1b further shows that our formula is accurate with only less than 0.5% relative error between our prices and Monte Carlo ones.

Fig. 1
figure 1

Our price versus Monte Carlo price with different underlying prices. Parameters are \(T=1;\,\bar{v}_1=0.1;\,\bar{v}_2=0.2;\,\lambda _{12}=10;\,\lambda _{21}=20\)

Full size image

With the confidence of our formula, the influence of introducing regime switching into the He–Chen model [14] is ready to be shown. In order to compare the two prices, we keep all the corresponding parameters same in two models, and \(\bar{v}\) in the He–Chen model will take the value of \(\bar{v}_1\) since the current state is assumed to be 1. Then, in Fig. 2, we introduce a scale parameter z such that the parameters in the transition rate matrix of the Markov chain will change with the newly introduced parameter. It is clear that when the transition rate equals to zero, our price is exactly same as that obtained with He and Chen’s formula. This is reasonable since this case can be view as removing the regime switching mechanics in our model, which would certainly lead to the degeneration of our model. Another phenomenon that should be mentioned is that our prices keeps decreasing when the transition rate parameters become larger.

Fig. 2
figure 2

Our price versus He and Chen’s price with respect to a scale parameter. Model parameters are \(T=1;\,\bar{v}_1=0.2;\,\bar{v}_2=0.1;\,\lambda _{12}=10z;\,\lambda _{21}=20z\)

Full size image
Fig. 3
figure 3

Our price versus He and Chen’s price with respect to the time to expiry. Model parameters are \(T=1;\,\bar{v}_1=0.1;\,\bar{v}_2=0.2;\,\lambda _{12}=10;\,\lambda _{21}=20\)

Full size image

Depicted in Fig. 3 is the comparison of our prices with He and Chen’s price, and what we could see first is that both prices are monotonic functions of the time to expiry, which is consistent with financial intuitions. It should also be remarked that under the current parameter settings, where the long-term mean for State 1 \(\bar{v}_1\) is less than that for State 2 \(\bar{v}_2\), the European call option prices from our model are always higher than those obtained through He and Chen’s formula, and the gap between the two prices become even larger when the time to expiry increases.

Fig. 4
figure 4

Our price versus He and Chen’s price with respect to the time to expiry. Model parameters are \(T=1;\,\bar{v}_1=0.2;\,\bar{v}_2=0.1;\,\lambda _{12}=10;\,\lambda _{21}=20\)

Full size image

However, this is not always the case for the whole parameter space. When we reverse the value of the long-term mean so that \(\bar{v}_1\) is larger than \(\bar{v}_2\), another pattern appears that our prices are always lower than those from the He–Chen model shown in Fig. 4. A similar phenomenon does exist that the larger the time to expiry is, the difference between the two prices will also become wider.

We would like to point out here that the calibration of regime switching models in practice with real market data is quite similar to that of classical models without the involvement of regime switching [7, 19]. The only difference is that regime switching models can produce different option prices corresponding to different initial states, and one needs to figure out which price should be regarded as the model price. One popular way is to introduce an additional parameter p as the probability of the underlying asset price being in State 1 at the current time when calibrating a two-state regime switching model (the probability of the underlying asset price being in State 2 is naturally \(1-p\)). In this case, the price of each option produced by the model is measured as the weighted average of the two option prices corresponding to both states [11, 15]. With this in mind, all one needs to do is to determine the regime switching related parameters, i.e., \(p, \bar{v}_1, \bar{v}_2, \lambda _{12}\) and \(\lambda _{21}\), together with other model parameters through minimizing the distance between option prices listed on the market and those produced by the model using some optimization algorithms.

4 Conclusion

In this paper, a closed-form pricing formula is successfully obtained under a newly proposed model, in which the long-term mean of the volatility process is divided into two parts with one being described by a particular stochastic process and another being modeled by a Markov chain. After the derivation of the analytical solution, numerical experiments are carried out to study the various properties of the newly derived formula, and the influence of introducing regime switching into option pricing models is demonstrated to be quite significant.