1 Introduction

Nowadays, managing risk is becoming increasingly important for market practitioners. To cope with such an increasing demand, option derivatives are developed, which are very useful in measuring and managing financial risks, especially the volatility risk. With the sharp increase in the trading volume being observed, how to accurately and efficiently determine option prices is a widely pursued topic in quantitative finance and risk management.

A breakthrough was made in 1973 by Black and Scholes [7] and Merton [33], who proposed a simple and elegant model for the pricing of options. However, this model results in some biases in option prices, because some strong assumptions made to achieve analytical simplicity and tractability are not consistent with the real behavior of financial markets. In particular, the assumption of “constant volatility” is generally thought to be unsuitable because the implied volatility extracted from real market data usually exhibits a non-constant curve across different strike prices, i.e., the well-known “volatility smile” or “volatility smirk” [17]. In addition, the implied volatility also differs for similar options with different times to maturity, which is called the “term structure of volatility”. As a result, non-constant volatility processes are adopted to overcome this particular shortcoming of the Black–Scholes (B–S) model. Among them, stochastic volatility (SV) models have received the greatest attention.

The first SV model was proposed by Johnson [29]. The price of options was then solved by Scott [41] with Monte Carlo simulations and Wiggins [44] with the finite difference method. However, one of the main disadvantages of the very first SV model is the lack of closed-form solutions for European option prices, which would certainly depress its potential application to real financial markets because the slow speed in the calculation of option prices could extremely slow down the parameter determination process. Therefore, further research interests focus on finding appropriate SV models with analytical achievability. For instance, Hull and White [25] proposed the so-called Hull-White model, and solved the price of European options with a power series approximation method. Although their model was equipped with a semi-closed form pricing formula, it is unsatisfactory due to the zero correlation assumption, which violates the so-called “leverage effect”, i.e., the underlying price and the volatility being negatively correlated [3]. Several years later, Stein and Stein [43] assumed that the volatility follows an Ornstein-Uhlenbeck process [21] and also derived a closed-form pricing formula. However, this model still suffers from two main disadvantages. On one hand, this model could not prevent the volatility from going negative. On the other hand, the assumption of no correlation between the underlying price and volatility is certainly not realistic.

A nice and elegant model was proposed by Heston [24] with the assumption that the volatility follows the Feller square-root process [14, 19]. This model enjoys a great popularity even today among market practitioners because of its two main advantages. One is that the volatility process itself has a wide range of basic properties, including non-negativity and mean reversion, and the other is that a closed-form analytical solution for European options can be derived without much effort. With such a solution, the computational accuracy can be guaranteed when pricing European options because systematical errors would always exist when numerical methods are adopted. In addition, considerable amount of time and effort in parameter estimation can be saved, a great advantage that can never be overlooked when the model is calibrated with real market data [15]. However, it should be pointed out that the Heston model is not perfect either (there may not even exist a perfect model!), and it also has some drawbacks. For example, the square root specification is generally rejected when modeling the returns of the stock index [2, 37]. Moreover, it has been pointed out that the volatility process usually has a non-linear mean-reverting property [4].

In fact, introducing time-dependent parameters or even additional stochastic factors into SV models has recently attracted lots of attention from researchers and market practitioners. For example, with the utilization of a small volatility of volatility expansion and Malliavin calculus techniques, Benhamou et al. [5] derived an analytical approximation for European option prices under the time-dependent Heston model. Under this particular model, approximated European option prices are also derived by Mikhailov and Nögel [34] with asymptotic expansions. Moreover, the time-dependent 3/2 SV models have also been considered by a few authors, including Drimus [16] and Goard [22]. On the other hand, adding stochastic factors into SV models is another main strand, a typical example of which is to include a stochastic interest rate [39, 40]. Furthermore, modeling SV with multiple stochastic factors are also very popular, and this can be achieved through two main approaches. The first approach introduces additional volatility factors into the dynamics of the underlying price [9, 11, 35, 36]. Being different from the first approach, the underlying price in the second approach remains a single-factor process, while additional stochastic factors are incorporated into the volatility process. Belonging to the second category, Elliott and Lian [18] and He and Zhu [23] introduced the regime-switching factor into the Heston model to provide better market data fitness.

Motivated by the fact that a time-dependent mean-reversion level for the variance of the Heston volatility model could provide a better fit into the term structure of implied volatility and variance swap curve [8, 20], in this paper, we propose a new SV model with the constant long-term mean in the Heston model being replaced by another stochastic process. One of the main advantages of such a modification is that our model still preserves the analytical tractability, which could substantially reduce the computational effort in terms of parameter estimation when this model is applied to real financial markets. It should be remarked here that the derived characteristic function of our newly proposed model has a similar form as the one under the Heston model, and one can follow Albrecher et al. [1] to show that our characteristic function also possesses the property of numerical continuity. It is also possible to design fast calibration algorithms for our model using the approach developed in [15], and this is left for future research, as the main focus of this paper is to propose a new multi-factor SV model. In the following, the closed-form pricing formula for European options will be derived and verified. In order to show the advantages of our newly proposed model over the Heston model, at least in certain cases, we also conduct a preliminary empirical study by comparing the pricing performance of our model and that of the Heston model.

The rest of the paper is organized as follows. In Sect. 2, a brief introduction of our new model is provided, followed by the derivation of the closed-form pricing formula for European options under this model. In Sect. 3, numerical experiments and examples are provided. In Sect. 4, empirical studies are carried out to show the meaning of introducing the stochastic long-term mean. Concluding remarks are given in the last section.

2 The newly proposed model

In this section, a new SV model will be introduced in detail. A closed-form analytical solution will then be derived for European call options under this model.

Let \(\{S_t, t\ge 0\}\) and \(\displaystyle \{v_t, t\ge 0\}\) be the underlying price and volatility at the current time t, respectively. It is known that the Heston SV model under the risk-neutral measure can be characterized as

$$\begin{aligned} \begin{aligned} \frac{dS_t}{S_t}&=rdt+\sqrt{v_t}dW_{t}^{1}, \\ dv_t&=k({\bar{v}}-v_t)dt+\sigma \sqrt{v_t}dW_{t}^{2}, \end{aligned} \end{aligned}$$
(2.1)

where \(W_{t}^{1}\) and \(W_{t}^{2}\) are two standard Brownian motions with correlation \(\rho \). r denotes the risk-free interest rate, and \(\sigma \) is the so-called volatility of volatility. k and \({\bar{v}}\) represent the speed of mean-reversion and the long-term mean, respectively. However, due to the fact that a constant long-term mean could not fully capture the term structure of implied volatility, we introduce a stochastic long-term mean \(\theta _t\) into the Heston model as

$$\begin{aligned} \begin{aligned} \frac{dS_t}{S_t}&=rdt+\sqrt{v_t}dW_{t}^{1}, \\ dv_t&=k(\theta _t-v_t)dt+\sigma _1\sqrt{v_t}dW_{t}^{2}, \\ d\theta _t&=\lambda dt+\sigma _2dB_t. \end{aligned} \end{aligned}$$
(2.2)

In specific, we assume that \(B_t\) is independent of \(W_{t}^{1}\) and \(W_{t}^{2}\), while the correlation between \(W_{t}^{1}\) and \(W_{t}^{2}\) is still \(\rho \). Note that the values of \(\lambda \) and \(\sigma _2\) are expected to be small, in which case \(\theta _t\) can be viewed as a small perturbation in \(\theta _0\), and when \(\lambda \) and \(\sigma _2\) take the value of zero, our model will degenerate to the Heston model because in this case \(\theta _t\) becomes constant.

It should also be remarked that the new pricing dynamics become much more complicated than the original Heston model after the introduction of the stochastic long-term mean. Very fortunately, the analytical tractability of the Heston model is still preserved after such a complicated modification. In particular, an analytical pricing formula for European options under our newly proposed model can be derived, which can greatly facilitate the application of this model to real financial markets because the process of model calibration can be very time-consuming without such kind of analytical solutions. In the following theorem, the pricing of European call options is formally formulated, from which, the analytical expression of the option price is derived.

Theorem 1

Let \(U(S,v,\theta ,t)\) be the European call option price with \(S_t\), \(v_t\) and \(\theta _t\) following (2.2). Then

$$\begin{aligned} \displaystyle U(S,v,\theta ,t)=SP_1-Ke^{-r(T-t)}P_2, \end{aligned}$$
(2.3)

where K is the strike price, and

$$\begin{aligned} \displaystyle&P_j=\frac{1}{2}+\frac{1}{\pi }\int _{0}^{\infty }\mathrm {RE} \left[ \frac{e^{-i\phi {\ln }(K)}f_j}{i\phi }\right] d\phi , ~~\displaystyle f_j=e^{C(\tau ;\phi )+D(\tau ;\phi )v+E(\tau ;\phi )\theta +i\phi x}, ~~j={1,2},\\&\displaystyle D(\tau ;\phi )=\frac{d-(i\phi \rho \sigma _1-k+b_j\rho \sigma _1)}{\sigma _1^2} \left( \frac{1-e^{d\tau }}{1-ge^{d\tau }}\right) , \\&\displaystyle E(\tau ;\phi )=\frac{k}{\sigma _{1}^{2}}\left\{ \left[ d-(i\phi \rho \sigma _1-k +b_j\rho \sigma _1)\right] \tau -2\ln \left( \frac{1-ge^{d\tau }}{1-g}\right) \right\} ,\\&C(\tau ;\phi )=ir\phi \tau +\frac{1}{2}\int _{0}^{\tau }\sigma _{2}^{2}E^2(s;\phi )ds +\int _{0}^{\tau }\lambda E(s;\phi )ds,\\&d=\sqrt{(i\phi \rho \sigma _1-k+b_j\rho \sigma _1)^2-2\sigma _{1}^{2}\left( i\phi u_j -\frac{1}{2}\phi ^2\right) },~~g=\frac{(i\phi \rho \sigma _1 -k+b_j\rho \sigma _1)-d}{(i\phi \rho \sigma _1-k+b_j\rho \sigma _1)+d},\\&u_1=\frac{1}{2}, u_2=-\frac{1}{2}, b_1=1, b_2=0, \tau =T-t. \end{aligned}$$

Proof

Since the martingale pricing theory requires that the discounted asset price be a martingale, implying that \(e^{-rt}U_t\) is a martingale, we obtain the following partial differential equation (PDE) governing the price of a European call option \(U(S,v,\theta ,t)\)

$$\begin{aligned}&\displaystyle \frac{1}{2}vS^2\frac{\partial ^{2}U}{\partial S^2}+\frac{1}{2}\sigma _{1}^{2}v\frac{\partial ^{2}U}{\partial v^2}+\frac{1}{2}\sigma _{2}^{2}\frac{\partial ^{2}U}{\partial \theta ^2} +\rho \sigma _1vS\frac{\partial ^{2}U}{\partial v\partial S}\nonumber \\&\quad +\, rS\frac{\partial U}{\partial S}+k(\theta -v)\frac{\partial U}{\partial v}+\lambda \frac{\partial U}{\partial \theta }+\frac{\partial U}{\partial t}-rU=0, \end{aligned}$$
(2.4)

with the terminal condition as \(U(S,v,\theta ,T)=\max (S-K,0)\). We remark that the boundary conditions along the S and v directions are the same as those under the Heston model. For the boundary conditions along the \(\theta \) direction, when \(\theta \) approaches infinity, the option price is nothing but the underlying price, because in this case, v approaches infinity as well. On the other hand, when \(\theta \) is very close to zero, the option price is constant with respect to this parameter, as suggested by the empirical evidence.

According to the risk-neutral pricing rule, we have

$$\begin{aligned} \displaystyle U(S,v,\theta ,t)= & {} e^{-r(T-t)}E[(S_T-K)^{+}|S_t]=e^{-r(T-t)} \int _{K}^{+\infty }(S_T-K)p_{S_T|S_t}dS_T\nonumber \\= & {} S_t\left[ e^{-r(T-t)}\int _{K}^{+\infty }\frac{S_T}{S_t}p_{S_T|S_t} dS_T\right] -Ke^{-r(T-t)}\int _{K}^{+\infty }p_{S_T|S_t}dS_T, \end{aligned}$$
(2.5)

where \(p_{S_T|S_t}\) denotes the probability density function of \(S_T\) conditional upon \(S_t\). Now, we assume that the solution to PDE (2.4) is in the form of

$$\begin{aligned} \displaystyle U=SP_1(S,v,\theta ,t)-Ke^{-r(T-t)}P_2(S,v,\theta ,t). \end{aligned}$$
(2.6)

Substituting (2.6) into (2.4) and applying the transforms \(x=\ln S\) and \(\tau =T-t\), we find that \(P_j\) satisfies

$$\begin{aligned} \displaystyle&\frac{1}{2}v\frac{\partial ^{2}P_j}{\partial x^2}+\frac{1}{2} \sigma _{1}^{2}v\frac{\partial ^{2}P_j}{\partial v^2}+\frac{1}{2} \sigma _{2}^{2}\frac{\partial ^{2}P_j}{\partial \theta ^2}+\rho \sigma _1v\frac{\partial ^{2}P_j}{\partial x\partial v}\nonumber \\&\quad +\, (r+u_jv)\frac{\partial P_j}{\partial x}+\left[ k(\theta -v)+b_j\rho \sigma _1v\right] \frac{\partial P_j}{\partial v}+\lambda \frac{\partial P_j}{\partial \theta }-\frac{\partial P_j}{\partial \tau }=0, ~~j={1,2}\nonumber \\ \end{aligned}$$
(2.7)

with the initial condition

$$\begin{aligned} \displaystyle P_j(x,v,\theta ,t)=E\left[ I_{(x_{j,T}>\ln K)}|x_t=x\right] =P(x_{j,T}>\ln K|x_t=x), \end{aligned}$$
(2.8)

where \(I_{(\cdot )}\) is the identity function, \(P(\cdot )\) represents the probability and \(x_{j,T}, j=1,2\) follows

$$\begin{aligned} \begin{aligned} dx_j&=(r+u_jv)dt+\sqrt{v}dW_{t}^{1}, \\ dv&=\left[ k(\theta -v)+b_j\rho \sigma _1v\right] dt+\sigma _1\sqrt{v}dW_{t}^{2}, \\ d\theta&=\lambda dt+\sigma _2dB_t. \end{aligned} \end{aligned}$$
(2.9)

Now, define \(\displaystyle f_j(x,v,\theta ,\tau ;\phi )\) as the conditional characteristic function of the underlying log-price, \(x_T\). According to the Gil-Pelaez theorem, the relationship between \(P_j\) and \(f_j\) can be found as

$$\begin{aligned} \displaystyle P_j=\frac{1}{2}+\frac{1}{\pi }\int _{0}^{\infty }\mathrm {RE} \left[ \frac{e^{-i\phi {\ln }(K)}f_j}{i\phi }\right] d\phi ,~~j={1,2}. \end{aligned}$$
(2.10)

Therefore, if we are able to derive the analytical expression of \(f_j\), we can finally obtain the desired solution \(P_j\). In the following, we shall concentrate on deriving \(f_j\) first.

According to the relationship between \(P_j\) and \(f_j\), it is not difficult to show that \(\displaystyle f_j(x,v,\theta ,\tau ;\phi )\) satisfies the same PDE as \(\displaystyle P_j(x,v,\theta ,t;\ln [K])\) does, but with a different initial condition \(\displaystyle f_j(x,v,\theta ,0;\phi )=e^{i\phi x}\). Now we assume that \(\displaystyle f_j(x,v,\theta ,\tau ;\phi )\) is in the form of

$$\begin{aligned} \displaystyle f_j=e^{C(\tau ;\phi )+D(\tau ;\phi )v+E(\tau ;\phi )\theta +i\phi x}, \end{aligned}$$
(2.11)

with \(\displaystyle C(0;\phi )=D(0;\phi )=E(0;\phi )=0\) and i being the imaginary unit. Through the substitution of (2.11) into (2.7) together with some algebraic manipulations, the equation containing C, D and E can be found as

$$\begin{aligned} \displaystyle&\left( -\frac{\partial D}{\partial \tau }\right. +\left. \frac{1}{2} \sigma _1^2D^2+(i\phi \rho \sigma _1-k+b_j\rho \sigma _1)D+i\phi u_j-\frac{1}{2}\phi ^2\right) v \nonumber \\&\quad +\, \left( -\frac{\partial C}{\partial \tau }+\frac{1}{2}\sigma _2^2E^2 +\lambda E+ir\phi \right) \nonumber \\&\quad +\, \left( -\frac{\partial E}{\partial \tau }+kD\right) \theta =0. \end{aligned}$$
(2.12)

According to the arbitrariness of the variables \(\theta \) and v, it is not difficult to derive the following three coupled ordinary differential equations (ODEs)

$$\begin{aligned} \displaystyle \begin{aligned} \frac{\partial D}{\partial \tau }&=\frac{1}{2}\sigma _1^2D^2+(i\phi \rho \sigma -k+b_j\rho \sigma _1)D+i\phi u_j-\frac{1}{2}\phi ^2,\\ \frac{\partial E}{\partial \tau }&=kD,\\ \frac{\partial C}{\partial \tau }&=\frac{1}{2}\sigma _2^2E^2+\lambda E+ir\phi .\\ \end{aligned} \end{aligned}$$
(2.13)

Consequently, once \(D(\tau ;\phi )\) is determined, \(C(\tau ;\phi )\) and \(E(\tau ;\phi )\) can be worked out straightforwardly with direct integration. In fact, the ODE governing \(D(\tau ;\phi )\) is a Riccati equation, which can be transformed into a second-order linear ODE as

$$\begin{aligned} \displaystyle \frac{d^2 y}{d \tau ^2}-B\frac{dy}{d\tau }+AMy=0, \end{aligned}$$
(2.14)

with the initial condition \(\displaystyle \frac{dy}{d\tau }\big |_{\tau =0}=0\) if we make the transformation of

$$\begin{aligned} \displaystyle D=-\frac{1}{Ay}\frac{dy}{d\tau }. \end{aligned}$$
(2.15)

Here, \(\displaystyle A=\frac{1}{2}\sigma _1^2, B=i\phi \rho \sigma _1-k+b_j\rho \sigma _1, M=i\phi u_j-\frac{1}{2}\phi ^2\). Obviously, (2.14) is a second-order linear ODE with constant coefficients, the general solution to which can be written as

$$\begin{aligned} \displaystyle y=C_1e^{d^{+}\tau }+C_2e^{d^{-}\tau }, \end{aligned}$$
(2.16)

with \(d^{+}\) and \(d^{-}\) being two real roots of

$$\begin{aligned} \displaystyle d^2-Bd+AM=0. \end{aligned}$$
(2.17)

With the initial condition presented above, we also obtain \(\displaystyle \frac{C_1}{C_2}=-\frac{d^{+}}{d^{-}}\). Substituting (2.16) into (2.15) yields

$$\begin{aligned} \displaystyle D= & {} -\frac{1}{A}\frac{C_1d^{+}e^{d^{+}\tau }+C_2d^{-}e^{d^{-}\tau }}{C_1e^{d^{+}\tau }+C_2e^{d^{-}\tau }},\nonumber \\= & {} \frac{d-(i\phi \rho \sigma _1-k+b_j\rho \sigma _1)}{\sigma _1^2} \left( \frac{1-e^{d\tau }}{1-ge^{d\tau }}\right) . \end{aligned}$$
(2.18)

With \(D(\tau ;\phi )\) available, simply integrating on both sides of the ODE governing \(E(\tau ;\phi )\) yields the final representation of \(E(\tau ;\phi )\), through which the expression of \(C(\tau ;\phi )\) can also be obtained. This has completed the proof. \(\square \)

It should be remarked that if the newly added parameters \(\sigma _2\) and \(\lambda \) are deterministic functions of t instead of being constant, the pricing formula would not be changed except \(\sigma _2\) and \(\lambda \) being replaced by time-dependent functions \(\sigma _2(T-s)\) and \(\lambda (T-s)\), respectively. This time homogeneous property has of course added flexibility to our formula.

On the other hand, once a formula has been derived, it is natural for us to check its validity. A common approach is to compare the calculated option prices with some benchmark solutions. Moreover, one may also be interested in the difference between the current model and the Heston model. These issues are discussed in the next section.

3 Numerical experiments and examples

In this section, the comparison of European call option prices calculated from our formula will be made with those obtained directly through the Monte Carlo simulation to verify the correctness of our formula. Our results are then compared with those of the Heston model to show their difference. In the following work, unless otherwise stated, values of parameters used are listed as follows. The long-term mean \({\bar{v}}\) under the Heston model and the initial value of the long-term mean under our model \(\theta _0\) are both set to 0.2 for comparison purposes. The default values for \(\lambda \) and \(\sigma _2\) in our model are set to 0.1 and 0.01, respectively. The rest of the parameters under the two models are set to the same. In specific, the risk-free interest rate r is 0.01, the mean-reversion speed k is chosen to be 5, the correlation \(\rho \) takes the value of \(-0.5\), the volatility of volatility \(\sigma _1\) is 0.1, and the initial value of the volatility is 0.1. The underlying price \(S_0\) and the strike price K are both equal to 100, while the time to expiry \(\tau \) is 0.5. Note that the current time is 0.

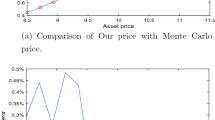
Depicted in Fig. 1 is the comparison of our price with the Monte Carlo price, i.e., the option price calculated with the Monte Carlo simulation. From Fig. 1a, it is clear that the European call option price calculated from our model is a monotonic increasing function of the underlying price, which is consistent with financial intuition. Moreover, our price agrees well with the Monte Carlo price, with the on-dot maximum relative error being less than 0.8%, as shown in Fig. 1b. All of these have already demonstrated the validity of our newly derived formula.

As pointed out previously, our model is identical to the Heston model when both \(\lambda \) and \(\sigma _2\) are zero. In order to investigate such a degeneration, we introduce a scale parameter z, such that \(\lambda =\sigma _2=0.2*z\) with z varying within [0,1]. The results are shown in Fig. 2. As expected, our price is exactly the same as the Heston price when z is set to zero. Moreover, when z is enlarged, which is equivalent to increasing both \(\lambda \) and \(\sigma _2\), one can observe that our price keeps increasing and is always higher than that of the Heston model. At this stage, two natural questions may be raised. The first one is whether there are some times when our price is lower than the Heston price, while the second one is how our price changes with respect to \(\lambda \) and \(\sigma _2\) when all the other parameters are kept unchanged. The answers to these two questions will be mentioned in the following discussions.

Fig. 1
figure 1

Our price versus Monte Carlo price with different underlying prices

Full size image
Fig. 2
figure 2

Our price versus Heston price with respect to the scale parameter

Full size image

In Fig. 3, the influence of the parameter \(\lambda \) is investigated. One can clearly observe from this figure that our price is always higher than the Heston price for positive \(\lambda \), but lower when \(\lambda \) is negative. This is mainly because when \(\lambda \) is positive (negative), the chance for the long term-mean to increase (decrease) will be higher, resulting in a higher (lower) option price. In addition, this figure also suggests that our price is quite close to the corresponding Heston price for small time to expiry, and the difference between the two becomes larger as the time to expiry increases. This is indeed reasonable because when the time to expiry of the option becomes larger, there will be more chances for the long-term mean to change, resulting in the option price of the two models being “more different”.

It is also interesting to investigate the sensitivity of the option price with respect to \(\lambda \), and the results are displayed in Fig. 4. From this figure, it is clear that the option price under our model is an increasing function of \(\lambda \). Financially, a larger \(\lambda \) can lead to a larger level of the long-term mean, resulting in a larger average value of the volatility of the underlying. In this situation, a higher risk is expected and thus the premium of buying the option to against the risk would certainly become larger as well. With the same reason, one can also understand the fact that our price is positively correlated with the initial value of the long-term mean \(\theta _0\). Interestingly, the option price as a function of \(\lambda \) becomes flatter when \(\theta _0\) becomes larger.

Fig. 3
figure 3

Our price versus Heston price with different times to expiry

Full size image
Fig. 4
figure 4

Our price against different \(\lambda \)

Full size image
Fig. 5
figure 5

Our price against different \(\sigma _2\)

Full size image

In Fig. 5, the influence of \(\sigma _2\) on the option price is investigated. From this figure, it is clear that our price is a monotonic decreasing function of \(\sigma _2\), implying that the more volatile the long-term mean is, the lower the option price will be. A possible explanation for this is that an increase in the volatility of the stochastic long-term mean makes it possible for the volatility of the underlying to attain a lower level, leading to a lower option price. It should also be noticed from this figure that our price is an increasing function of the initial level of the volatility \(v_0\). This can be understood by the fact that a higher volatility implies higher risk in investing money, resulting in a higher premium to compensate the risk. At this stage, some people may argue that the addition of \(\sigma _2\) will not cause much difference to option prices, as shown in Fig. 5. However, one should not forget that while all the other parameters are set to the same in this example for comparison purposes, the parameters need to be extracted form market data when both models are applied to real financial markets. In this situation, the corresponding parameters under both models will not necessarily be the same, which may cause a large pricing difference.

It should be remarked that the difference between our newly proposed model and the Heston model can never guarantee a better performance of our model. Whether it is meaningful to introduce a stochastic long-term mean and whether its form makes sense need to be further investigated with real market data. We have thus conducted empirical studies by calibrating our model and the Heston model to the same set of real market data, the results of which are presented in the next section.

4 Empirical studies

In this section, empirical studies are carried out with the Heston model taken as a benchmark to show the influence of the stochastic long-term mean, and to assess the performance of the newly proposed model applied to real financial data. We shall first describe the data and several important filters used for model calibration, and then introduce the method for parameter estimation in detail. The empirical results are provided at last, with which, the performance of these two models applied to real financial data is clear.

4.1 Data description

A data set of the S&P 500 Index and European call options written on it from Jan 2012 to June 2012 is chosen as an example to conduct the empirical study. As usual, mid-prices, which are equal to the average value of bid and ask prices, are used as option prices in our study. However, it should be noted that those raw data could not be adopted directly in parameter estimation as sample noise should be eliminated. Therefore, some appropriate filters are applied to the raw data before they can be safely used.

First of all, only Wednesday and Thursday option prices are adopted with Wednesday option data used in parameter estimation and Thursday data served as market prices to be compared with the theoretical option prices calculated with the estimated parameters. This is indeed a common practice in model calibration [3, 13], and is reasonable in two main aspects. One one hand, using one-day option data a week in parameter estimation enables us to study a relatively longer time series so that the obtained results are more reliable due to the time-intensiveness of model calibration processes. On the other hand, the chosen two days are least likely to be holidays in a week and less likely to be affected by the “day-of-the-week” effect than Monday and Friday. Secondly, we also need to remove options with the time to expiry being less than 30 days and more than 120 days because the former ones have small time values and their prices could be very volatile, and the latter ones usually have liquidity problems due to their high premiums [31]. Thirdly, options with the absolute moneyness being higher than 10% are excluded as well. In this way, very deep in-the-money and very deep out-of-money options are not considered because they also have liquidity problems [42]. Note that the absolute moneyness here is defined as the relative difference between the S&P 500 Index value and the corresponding strike price, i.e., \(\displaystyle \text {moneyness}=\frac{S-K}{K}\).

In addition to the careful choice of the option data, the risk-free interest rate also needs to be determined in advance. Here, we choose the three-month daily U.S. Treasury Bill Rate as a proxy of the risk-free interest rate [6, 42]. The length of this rate is enough because the time to expiry of the selected options is less than 120 days. With all the data needed available, some optimization methods for parameter estimation can be applied, the details of which are illustrated in the next subsection.

4.2 Parameter estimation

In this section, we shall first review the parameters of both models that need to be determined, and then a particular global optimization method is introduced, with which all model parameters are finally obtained.

Recall the dynamics of the Heston model given in (2.1). It is clear that five parameters need to be estimated, i.e., the mean-reversion speed k, the constant long-term mean \({\bar{v}}\), the volatility of volatility \(\sigma \), the correlation factor \(\rho \) and the initial value of volatility \(v_0\). On the other hand, the dynamics of our newly proposed model, (2.2), clearly show that seven parameters should be determined before model assessment takes place. Four are the same as those in the Heston model, including \(k, \sigma , \rho , v_0\), while the other three are the initial value of the long-term mean \(\theta _0\) and the two parameters, i.e., \(\lambda \) and \(\sigma _2\), controlling the stochastic process governing the long-term mean \(\theta _t\).

Having known all the needed parameters, we can now proceed to the estimation part. One of the most popular methods in determining model parameters is to find a set of “optimal” parameters that minimizes the “distance” between market and model prices. Therefore, we need to choose an appropriate definition for such a distance. In fact, a common approach is to take the relative mean squared error (RMSE)

$$\begin{aligned} \displaystyle \text {RMSE}=\frac{1}{N}\sum _{i=1}^{N}\left( \frac{C_i^{\text {Market}} -C_i^{\text {Model}}}{C_i^{\text {Model}}}\right) ^2, \end{aligned}$$
(4.1)

as the objective function to measure the distance, with \(C^{\text {Market}}\) and \(C^{\text {Model}}\) being the market price of an option and the price of the same option calculated from our pricing formula with a particular set of parameters, respectively. N is the total number of observations selected in a single estimation. However, the RMSE is not adopted in the current study due to one of its main drawbacks that a cheap option (i.e., low \(C^{\text {Market}}\)) would bring in an abnormally high amount of weight, resulting in the inaccuracy of the estimated parameters. Instead, following Christoffersen and Jacobs [12] and Lim and Zhi [32], the dollar mean squared error (MSE) is used, i.e.,

$$\begin{aligned} \displaystyle \text {MSE}=\frac{1}{N}\sum _{i=1}^{N}\left( C_i^{\text {Market}} -C_i^{\text {Model}}\right) ^2, \end{aligned}$$
(4.2)

as the objective function.

Another issue is to choose an appropriate method to minimize the selected objective function, which is a minimization problem. In the literature, local minimization is a first choice as it is easy to implement and fast to produce a result. Unfortunately, the objective function (4.2) is not necessarily convex and thus there exist several local minima. An appropriate initial guess of the solution is usually very crucial for the local minimization method to be safely used as it would otherwise be easily stuck in a local minimum and produce unreliable results. Therefore, in this case, global optimization is much favored because a properly designed global optimization algorithm is able to skip local minima and correctly identifies the global minimum in an efficient way.

Simulated annealing (SA) [30] is actually one of the best known global optimization approaches, which possesses striking positive features. For example, it is very easy to program and the algorithm typically has few parameters that require tuning. Moreover, its statistical guarantee of convergence makes SA very appealing. However, its main drawback is the slow speed in implementation, which makes this method unsuitable for practical purposes. Therefore, in the current work, adaptive simulated annealing (ASA) is adopted. This method is actually a variant of SA and was firstly proposed by Ingber [26]. The aim of ASA is to statistically find the best global fit of a non-linear constrained non-convex cost function over a D-dimensional space [28]. This improved version makes the algorithm more efficient and less sensitive to user defined parameters than standard SA does, while it still maintains all the advantages that SA possesses. In fact, this specific algorithm has already been applied to different areas [10, 45], and has already been adopted by a number of authors in the calibration of option pricing models, such as Poklewski-Koziell [38], and Mikhailov and Nögel [34].

It should be pointed out that the adopted ASA is realized through the open-source code provided in [27]. The feedback from many users regularly assesses the source code to ensure its soundness, which makes this method become even more flexible and powerful. In Table 1, the estimated daily-averaged parameters extracted from the selected market data for the two models under consideration are presented.

Table 1 Estimated parameters
Full size table

With all the estimated parameters available, we are now able to assess the performance of our newly proposed model. This will be the main issue of the next subsection.

4.3 Empirical results

In this subsection, the empirical results of our newly proposed model and the Heston model are provided based on the same set of option data. In particular, Table 2 exhibits the in- and out-of-sample errors of the two models.

Table 2 In- and out-of-sample errors for the two models
Full size table

From Table 2, it is not difficult to find that our newly proposed model greatly outperforms the Heston model in terms of both in- and out-of-sample errors. In specific, from the perspective of those in-sample errors, the daily averaged MSE for our model is 0.0758, only around 66% of that displayed by the Heston model. On the other hand, when the out-of-sample errors are taken into consideration, it is interesting to notice that such errors under both models are larger than their in-sample counterparts. This can be understood by the fact that in-sample errors are actually the minimized distance between market prices of a certain data set and model prices calculated with the “optimal” set of parameters for the same date set, while out-of-sample errors are measured by the distance between market prices of another data set and model prices calculated with parameters derived with the previous date set, which implies that such a distance is probably not the minimized one. Moreover, the difference between out-of-sample errors of the two models is even widened, with the MSE under our model being approximately 50% of that under the Heston model, which also suggests that our model performs better than the Heston model does. Due to the fact that a model can certainly be regarded as a better one if both of its in- and out-of-sample errors are lower than those of the other model, one can reach a conclusion that our newly proposed model serves as a better choice than the Heston model, at least for the chosen data set.

Another issue with common interest is the behavior of both models across different moneyness. Thus, we also present the out-of-sample errors sorted by moneyness, as shown in Table 3. While the range of moneyness is indicated on the top row of the table, the abbreviations “O”, “A” and “I” in the parentheses indicate “out of money”, “at the money” and “in the money”, respectively.

Table 3 Out-of-sample errors according to moneyness
Full size table

From this table, it is again clear that our newly proposed model is a better choice than the Heston model, at least for the adopted data set. In particular, it can be easily observed that out-of-sample errors associated with out-of-money options are much larger than those of in-the-money and at-the-money options. Our model works much better than the Heston model for this category, with the MSE of our model in this case being less than half of that under the Heston model. The improvement for the other two categories is also significant. Compared with the Heston model, our model shows 10% and 5% less errors for at-the-money options and in-the-money options, respectively. Therefore, we can confidently conclude that our model can of course act as a good competitor to the Heston model in real markets.

5 Conclusion

In this paper, with the long-term mean in the Heston model modeled by another stochastic process, a new SV model is proposed in order to provide a better fit to real financial data. After successfully deriving a closed-form pricing formula for European options under the newly established model, we show numerically the validity of the formula by comparing our results with those obtained from the Monte Carlo simulation. Moreover, we also make a comparison of the option prices calculated from the Heston model and and those under our model to show the difference of the two models from a numerical point of view. Finally, empirical studies are carried out based on the options written on S&P 500 Index. The results show that our newly proposed model generally outperforms the Heston model, implying that our model can be adopted as a better alternative to the Heston model in real financial markets.