Multiscale density decorrelation by Cauchy–Navier wavelets

Abstract

In this paper, we investigate a multiscale post-processing method in exploration. Based on a physically relevant mollification technique involving the Cauchy–Navier equation, we mathematically describe the extractable information within 3D density data sets. More explicitly, the developed multiscale approach extracts and visualizes geological features inherently available in signature bands of certain geological formations such as aquifers, salt domes etc. by specifying suitable wavelet bands. We compare the presented approach with already existing methods such as Newton multiscale decorrelation.

1 Introduction

In exploration, the success or failure of a project is determined by the quality of the available exploration data. Here for example, an essential difficulty lies in the analysis and interpretability of data provided by potential methods such as gravimetry and magnetometry.

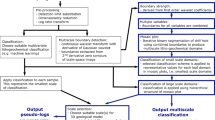
In Freeden and Blick (2013), a novel method for post-processing and inversion of exploration data was proposed. In the case of gravimetry, this method has been worked out theoretically by Freeden and Nashed (2018) (see also the references therein). Numerically, the method was realized by Blick (2015) and Blick et al. (2018) (cf. the cited literature therein). The method was also extended to reflection seismics and to acoustic tomography in the PhD thesis (Blick 2015). The essential ingredients of this method are illustrated for 2D cuts of a 3D version of the Marmousi density model in case of gravimetric data by the scheme depicted in Fig. 1.

Figure 1 shows that the gravimetric potential is very smooth, so that only rough structures can be deduced from the potential for exploration purposes (Fig. 1, top left). However, if we go over to the multiscale decomposition in terms of bandpass filtered data $V_{\tau _j}-V_{\tau _{j-1}}$ of the potential V at scale $\tau _j$, structural information of the Marmousi model become visible (Fig. 1, bottom left). The reason is that the multiscale decomposition acts similarly as a finite difference approximation of $\varDelta$ and hence, simulates V via the Poisson equation $\varDelta V(x)=\rho (x)$ in discrete way, so that the relation between potential and density function can already be detected for higher scales in the bandpass filtered potential level. The key idea of the method (Freeden and Blick 2013) is that the potential wavelets generating the potential decomposition (Fig. 1, left) can be correlated via the application of the Laplace operator to Haar-type wavelets in the density level (right). In fact, the density distribution as well as its decorrelation in density bands (Fig. 1, bottom right) sharply show the density transitions from one geological formation to the other.

The aforementioned wavelet construction is particularly powerful because of its “geophysical relevance” i.e., it forms a compromise reflecting the underlying physics (in accordance with the underlying differential equation) while still delivering an adequate multiscale decorrelation of geological signatures. However, the wavelets employed for establishing the scheme constitute radial basis functions, so that they are only dependent on the mutual distance of two points of the area under investigation. This means that no specific directionally-reflected information can be verified by the model described above.

In what follows, a method is developed which enables us to investigate also particular directional characteristics of the density field. In order to establish such a decorrelation technique, we mathematically make the transition from the Laplace equation to the Cauchy–Navier equation of elasticity. In doing so, on the one hand side, we leave the classically motivated Newton approach, on the other hand side, we are able to detect specific directional features by the elastic integral due to the tensorial nature of the fundamental solution.

Fig. 1

Schematic visualization of the multiscale decorrelation mechanism (see Blick et al. 2017)

It should be noted that the elastic potential as discussed here is not used for inversion purposes, instead, we apply the methodological framework only for post-processing. Thus, the deficit of physical interpretability in gravimetric exploration by use of an integral of none-Newtonian theory does not matter. However, physical interpretability is given in other types of application which are directly based on the Cauchy–Navier equation such as elastography, detection of material inclusions, etc.

2 Signature decorrelation based on the Cauchy–Navier equation

In what follows, we summarize relevant results without their proofs given by Blick et al. (2018) (see also Freeden and Gerhards 2013) in order to present the original idea of physically relevant wavelet construction using Newton wavelets. The start of the wavelet development is the Newton integral equation relating a given density model $\rho$ by convolution against a fundamental solution G to the Newton potential V. By mollification of G, we obtain a “potential scaling function” $G_\tau$ with scale parameter $\tau$, which after Laplace differentiation results in the “source scaling function” $\varPhi _\tau =\varDelta G_\tau$. Hence, even if our main focus lies on the application of the source scaling function, their theoretical construction always starts on the potential level.

We assume that the geometry of the exploration area is a regular region, i.e., $\mathcal {B}\subset {\mathbb {R}}^3$ is a bounded region $\mathcal {B}\subset {\mathbb {R}}^3$ which uniquely divides ${\mathbb {R}}^3$ in the inner space $\mathcal {B}$ and the outer space $\mathcal {B}^c ={\mathbb {R}}^3 \backslash \overline{\mathcal {B}}, \ \overline{\mathcal {B}} = \mathcal {B}\cup \partial \mathcal {B}$, such that the boundary $\partial \mathcal {B}$ is an orientable smooth Lipschitzian manifold of dimension two. In addition, it should be noted that for the discussion of the multiscale decomposition based on the Cauchy–Navier equation later on, we use small Latin letters to indicate vectorial functions, whereas capital Latin letters denote scalar functions.

The gravitational potential V of a body $\mathcal {B}$ in its exterior ${\mathbb {R}}^3\backslash {\overline{\mathcal {B}}}$ is given by the Newton integral

$$\begin{aligned} V(x) = \gamma \int _{\mathcal {B}} G(\varDelta ;\Vert x-y\Vert ) \rho (y)\ dy, \qquad x \in {\mathbb {R}}^3 \backslash {\overline{\mathcal {B}}}, \end{aligned}$$

(1)

where $G(\varDelta ;\cdot )$ given by

$$\begin{aligned} G(\varDelta ;\Vert x-y\Vert ) =-\frac{1}{4 \pi } \frac{1}{\Vert x-y\Vert }, \end{aligned}$$

(2)

is the fundamental solution w.r.t. the Laplace operator and $\gamma$ is the gravitational constant. The function $\rho$ is the density function. Since $\gamma$ is only a constant, we neglect to mention the gravitational constant $\gamma$ in all equations from now on.

Theorem 1

(Poisson Differential Equation) If $\rho$ is of class $\mathrm{C}^{(0,\mu )}(\overline{\mathcal {B}}),$ $\mu \in (0,1],$ then the Poisson differential equation

$$\begin{aligned} \varDelta _x \int _{\mathcal {B}} G(\varDelta ; \Vert x-y\Vert )\rho (y) \ dy = \rho (x) \end{aligned}$$

(3)

holds true for all $x \in \mathcal {B}$.

Next, we adopt the mollification of $G(\varDelta ;\cdot )$ via the function $r \mapsto G_{\tau }^n(\varDelta ;r),$ $r \in [0,\infty )$, with

$$\begin{aligned} G_\tau ^n(\varDelta ;r)=\left\{ \begin{array}{lcr}-\frac{1}{4\pi r} ,&{} \tau \le r\\ &{} &{}\\ -\frac{1}{4\pi r}+\frac{(\tau -r)^{n+2}((n+1)r+2\tau )}{8\pi r\tau ^{n+3}} ,&{} 0< r<\tau \\ &{} &{}\\ -\frac{n+3}{8\pi \tau },&{} r=0\end{array}\right. \end{aligned}$$

(4)

from Blick et al. (2018) so that by taking the Laplace derivative of $G_\tau ^n(\varDelta ;\cdot )$, we obtain with $r=\Vert x\Vert$

$$\begin{aligned} \varPhi _\tau ^n(r)=\varDelta _x G_\tau ^n(\varDelta ;r)=\left\{ \begin{array}{lr}0,&{} \tau \le r\\ &{}\\ \frac{(n+1)(n+2)(n+3)}{8\pi }\frac{(\tau -r)^n}{\tau ^{n+3}},&{}\quad 0\le r<\tau \end{array}\right. . \end{aligned}$$

(5)

Note that $r \mapsto G_\tau ^n(\varDelta ;r), r \in [0,\infty ),$ is $(n+1)$-times continuously differentiable and $r \mapsto \varPhi _\tau ^n(r), r \in [0,\infty ),$ is $(n-1)$-times continuously differentiable (where by convention in case of $n=0$, $(-1)$-times continuously differentiable means piecewise continuous). For a graphical illustration of $G(\varDelta ;\cdot )$ and its Laplace derivative $\varPhi$, see Fig. 2.

Fig. 2

Sectional profile of the scaling functions $G_\tau ^n(\varDelta ;\cdot )$ (left) and $\varPhi _\tau ^n$ (right) for $n=0,1,2$ and $\tau =1.5$. The dotted black line in the left picture indicates the fundamental solution $G(\varDelta ;\cdot )$

Summarizing our considerations, we are led to a result, which builds the theoretical basis for our approach to geological feature extraction.

Theorem 2

For $n \in {{\mathbb {N}}}_0$, the “$\tau$-Newton potential functions of order n”

$$\begin{aligned} V_\tau ^n (x)= \int _\mathcal {B}G_\tau ^n (\varDelta ;\Vert x-y\Vert )\rho (y) \ dy \end{aligned}$$

(6)

and the “$\tau$-Newton contrast functions of order n”

$$\begin{aligned} \rho _\tau ^n (x)= \int _\mathcal {B}\varPhi _\tau ^n (\Vert x-y\Vert )\rho (y) \ dy \end{aligned}$$

(7)

satisfy the limit relations

$$\begin{aligned} \lim _{\tau \rightarrow 0} \left| V (x) - V_\tau ^n (x)\right| = 0, \quad x \in \mathcal {B}\end{aligned}$$

(8)

and

$$\begin{aligned} \lim _{\tau \rightarrow 0} \left| \rho (x) -\rho _\tau ^n (x)\right| = 0, \quad x \in \mathcal {B}, \end{aligned}$$

(9)

provided that $\rho$ is $\mathrm{C}^{(0,\mu )}$-Hölder continuous in the neighborhood of $x \in \mathcal {B}$.

The kernels $G_\tau ^n (\varDelta ; \cdot )$ and $\varPhi _\tau ^n$ are called “potential scaling function of order n”and “source scaling function of order n”, respectively. It should be remarked that $G_\tau ^n (\varDelta ; \cdot )$ is constructed in such a way that the normalization condition

$$\begin{aligned} \int _{{\mathbb {R}}^3}\varDelta _x G_\tau ^n(\Vert x\Vert )\ dx= \int _{{\mathbb {R}}^3} \varPhi _\tau ^n(\Vert x\Vert ) \ dx = 1 \end{aligned}$$

(10)

holds true for all $\tau >0$ and all $n\in {{\mathbb {N}}}_0$ (note that this is a helpful feature used in the theory of singular integrals, see e.g., Louis 1989; Engl et al. 1996).

In other words, $\rho _\tau ^n (x)$ is defined via a singular integral, where the integral kernel is the Dirac sequence $\varPhi _\tau ^n$ (for more information, see e.g., Stein 1971; Hörmander 1998; Wienholtz et al. 2009).

Our task now is to adopt the Newton scheme for the Cauchy–Navier equation. We again start with the potential equation, and more specifically, its solution via fundamental solutions. By doing so, we follow the setup introduced by Kupradze (1979) and present the classical theory of elasticity for homogeneous and isotropic media. A (homogeneous and isotropic) elastic medium is a regular region $\mathcal {B}$ of the three-dimensional Euclidean space and a set of the quantities $\rho$, $\lambda$, and $\mu$ satisfying the conditions

$$\begin{aligned} \rho>0, \qquad \mu>0, \qquad 3\lambda +2\mu >0, \end{aligned}$$

(11)

where $\rho$ is the (constant) density of the medium and $\lambda$, $\mu$ are the Lamé parameters.

Definition 1

An elasto-static state of the medium $\mathcal {B}(\rho ,\lambda ,\mu )$ corresponding to the mass force f is a pair $[u,\sigma ]$ satisfying the conditions

$$\begin{aligned}&\text {i)}&\sigma \in c^{(1)}(\mathcal {B}),\qquad u\in c^{(2)}(\mathcal {B})\cap c^{(1)}(\overline{\mathcal {B}}),&\end{aligned}$$

(12)

$$\begin{aligned}&\text {ii)}&\sum _{j=1}^3\frac{\partial }{\partial {x_j}}\sigma _{ij}-\rho f_i=0,&\end{aligned}$$

(13)

$$\begin{aligned}&\text {iii)}&\sigma _{ij}=\lambda \delta _{ij}{\text {div}}u+\mu \left( \frac{\partial }{\partial x_j} u_i+\frac{\partial }{\partial x_i}u_j\right) ,&\end{aligned}$$

(14)

where $f,u\in {\mathbb {R}}^3$ and $\sigma =\{\sigma _{ij}\}\in {\mathbb {R}}^{3\times 3}$. The vector $u=(u_1,u_2,u_3)^T$ is called the displacement vector, $u_i$ a displacement component and $\sigma$ the stress tensor with components $\sigma _{ij}$. Relation (13) is called the equation of the elasto-static state and relation (14) Hooke’s law.

Substituting (14) in (13) leads to the relation

$$\begin{aligned} \mu \varDelta u_i+(\lambda +\mu )\frac{\partial }{\partial x_i}{\text {div}}u-\rho f_i=0, \end{aligned}$$

(15)

which is called the static equation (of classical elasticity) or, more precisely, the (static) Cauchy–Navier equation of the medium $\mathcal {B}(\rho ,\lambda ,\mu )$ corresponding to the mass force f in terms of the displacement. Written in vector nomenclature, we have

$$\begin{aligned} \mu \varDelta u+(\lambda +\mu )\nabla {\text {div}}u-\rho f=0, \end{aligned}$$

(16)

where

$$\begin{aligned} \varDelta u=(\varDelta u_1,\varDelta u_2,\varDelta u_3)^T. \end{aligned}$$

(17)

Definition 1 indicates that we deal with the situation that the external forces as well as the displacements and stresses are not changed in the considered time interval.

By use of the matrix differential operator

$$\begin{aligned} {{\mathbf {A}}}(\partial _x)&=\{{{\mathbf {A}}}_{ij}(\partial _x)\} \end{aligned}$$

(18)

with

$$\begin{aligned} {{\mathbf {A}}}_{ij}(\partial _x)&=\delta _{ij} \mu \varDelta +(\lambda +\mu )\frac{\partial ^2}{\partial x_i\partial x_j}, \end{aligned}$$

(19)

we can reformulate Eq. (15) as

$$\begin{aligned} {{\mathbf {A}}}(\partial _x)u-\rho f&=0. \end{aligned}$$

(20)

Kupradze (1979) showed that a (tensor) fundamental solution of the static Cauchy–Navier Eq. (20) is given by

$$\begin{aligned} \mathbf{{G}}({{\mathbf {A}}}(\partial );x)&=\frac{1}{\Vert x\Vert }\left( \frac{\mu '}{2}-\frac{1}{4\pi \mu }\right) {\mathbb {I}}-\frac{\mu '}{2}\frac{1}{\Vert x\Vert ^3}x\otimes x, \end{aligned}$$

(21)

where

$$\begin{aligned} \mu '=\frac{\lambda +\mu }{4\pi \mu (\lambda +2\mu )}, \end{aligned}$$

(22)

,$\otimes$ is the Kroneker product and ${\mathbb {I}}$ denotes the $3\times 3$ identity tensor.

It is easy to see that

$$\begin{aligned} {{\mathbf {A}}}(\partial _x)\mathbf{{G}}({{\mathbf {A}}}(\partial );x)&=0,\qquad x\ne 0. \end{aligned}$$

(23)

Like the gravitational constant in the Newton case, we set the constant density $\rho$ equal to one from now on. All in all, we are confronted with a potential

$$\begin{aligned} u&=\int _\mathcal {B}\mathbf{{G}}({{\mathbf {A}}}(\partial );x-y) f(y)\ dy, \end{aligned}$$

(24)

that represents a solution of the Cauchy–Navier Eq. (20).

Remark 1

The Cauchy–Navier equation and the mollification of its fundamental solution can be applied in a number of other applications such as wave inversion (e.g., seismic imaging, Aki and Richards 2002) and specialized wave propagation (e.g., coupling of interior/exterior wave propagation problems, Eberle 2018).

Contrary to the construction of scaling functions for the scalar fundamental solutions discussed so far, we are faced with the problem, that we cannot simply obtain a mollification in a ball by application of the Taylor expansion. Given the Taylor expansion $T_a^n$ in Einstein convention for tensorial functions $\mathbf{{G}}$ in an expansion point a by

$$\begin{aligned} T_a^n\mathbf{{G}}({\mathbf {A}}(\partial );x)&=\sum _{l=0}^{n+1}\frac{1}{l!}\mathbf{{G}}_{ij,k_1\ldots k_l}({\mathbf {A}}(\partial );a)(x-a)_{k_1\ldots k_l}, \end{aligned}$$

(25)

this would imply, that in order to get a mollification, we replace each function value $\mathbf{{G}}({\mathbf {A}}(\partial );x)$ inside a ball of radius $\tau$ around the origin with its Taylor expansion at the expansion point $\tau \frac{x}{\Vert x\Vert }$ evaluated in x. By doing so, we still obtain a $(n+1)$-times continuous potential scaling function in ${\mathbb {R}}^3\backslash \{0\}$, however, the source scaling function will be discontinuous in general for all $\Vert x\Vert =\tau$ and the limit $\lim \nolimits _{x\rightarrow 0}T_\tau ^n\mathbf{{G}}({{\mathbf {A}}}(\partial );x)$ depends on the direction from which the limit is taken and hence, is not unique. Nevertheless, there exists another way of constructing potential and source scaling functions in accordance to the previous section.

We rewrite the Cauchy–Navier fundamental solution in terms of $G(\varDelta ;\cdot )$ and then substituting $G(\varDelta ;\cdot )$ by $G_\tau ^{n+2}(\varDelta ;\cdot )$. Here, $n+2$ is chosen so that after the application of the Hessian matrix, $\mathbf{{G}}_\tau ^n({{\mathbf {A}}}(\partial );\cdot )$ is $(n+1)$-times continuously differentiable as is $G_\tau ^n(\varDelta ;\cdot )$. Hence,

$$\begin{aligned} \mathbf{{G}}({{\mathbf {A}}}(\partial );x)&=\frac{1}{\Vert x\Vert }\left( \frac{\mu '}{2}-\frac{1}{4\pi \mu }\right) {\mathbb {I}}-\frac{\mu '}{2}\frac{1}{\Vert x\Vert ^3}x\otimes x \end{aligned}$$

(26)

$$\begin{aligned}&=\left( \frac{2\pi \mu '\Vert x\Vert ^2}{3}\nabla \otimes \nabla -\frac{4\pi \mu \mu '-3}{3\mu }{\mathbb {I}}\right) G(\varDelta ;\Vert x\Vert ), \end{aligned}$$

(27)

where $\nabla \otimes \nabla$ denotes the Hessian matrix.

This enables us to define the mollification $\mathbf{{G}}_\tau ^n({{\mathbf {A}}}(\partial );\cdot ):{\mathbb {R}}^3\rightarrow {\mathbb {R}}^3\times {\mathbb {R}}^3$ for $n\in {{\mathbb {N}}}$ as

$$\begin{aligned} \mathbf{{G}}_\tau ^n({{\mathbf {A}}}(\partial );x)=\left( \frac{2\pi \mu '\Vert x\Vert ^2}{3}\nabla \otimes \nabla -\frac{4\pi \mu \mu '-3}{3\mu }{\mathbb {I}}\right) G_\tau ^{n+2}(\varDelta ;\Vert x\Vert ){,} \end{aligned}$$

(28)

which leads to

$$\begin{aligned} \mathbf{{G}}_\tau ^n({{\mathbf {A}}}(\partial );x)=\left\{ \begin{array}{lcr}\frac{1}{\Vert x\Vert }\left( \frac{\mu '}{2}-\frac{1}{4\pi \mu }\right) {\mathbb {I}}-\frac{\mu '}{2}\frac{1}{\Vert x\Vert ^3}x\otimes x ,&{} \tau \le \Vert x\Vert \\ &{} &{}\\ \mathbf{{T}}_1+\mathbf{{T}}_2 ,&{} 0< \Vert x\Vert <\tau \\ &{} &{}\\ \left( \frac{n+5}{8\pi \tau }\frac{4\pi \mu \mu '-3}{3\mu }\right) {\mathbb {I}},&{} \Vert x\Vert =0\end{array}\right. , \end{aligned}$$

(29)

with

$$\begin{aligned} \mathbf{{T}}_1&=x\otimes x\frac{2\mu '}{3r\tau ^{n+5}}\nonumber \\&\quad \times \left[ \frac{2\tau +(n+3)r}{8}\left( \frac{3(\tau -r)^{n+4}}{r^2}\right. \right. \nonumber \\&\quad \left. +\frac{3(\tau -r)^{n+3}(n+4)}{r}+(\tau -r)^{n+2}(n+3)(n+4)\right) \nonumber \\&\quad -\left. \frac{(n+3)}{4}\left( \frac{3(\tau -r)^{n+4}}{2r}+(\tau -r)^{n+3}(n+4)\right) -\frac{3\tau ^{n+5}}{4r^2}\right] ,\qquad r=\Vert x\Vert \end{aligned}$$

(30)

$$\begin{aligned} \mathbf{{T}}_2&=\left[ -\frac{\mu '}{12\tau ^{n+5}r}\left( (\tau -r)^{n+3}(2\tau ^2+r^2(n+3)(n+4)+2(n+3)\tau r)-2\tau ^{n+5}\right) \right. \nonumber \\&\quad \left. +\frac{4\pi \mu \mu '-3}{3\mu }\left( \frac{1}{4\pi r}-\frac{(\tau -r)^{n+4}((n+3)r+2\tau )}{8\pi r\tau ^{n+5}}\right) \right] {\mathbb {I}},\qquad r=\Vert x\Vert . \end{aligned}$$

(31)

We call $\mathbf{{G}}_\tau ^n({{\mathbf {A}}}(\partial );\cdot )$ the Cauchy–Navier potential scaling function with scale parameter $\tau$ and, in accordance with the construction of $\mathbf{{G}}_\tau ^n({{\mathbf {A}}}(\partial );x)$, the mollification is equal to $\mathbf{{G}}({{\mathbf {A}}}(\partial );x)$ for all $\Vert x\Vert \ge \tau$.

Remark 2

Here, we forfeit the radial symmetric property of $G(\varDelta ;\cdot )$ due to the application of the Hessian matrix $\nabla \otimes \nabla$, however this is advantageous for decorrelation purposes, since we are now able to better highlight the spreading direction of the layers contained in the data.

Lemma 1

The function $\mathbf{{G}}_\tau ^n({{\mathbf {A}}}(\partial );\cdot )$ is $(n+1)$-times continuously differentiable in ${\mathbb {R}}^3\backslash \{0\}$.

As in the Newton case, the “$\tau$-Cauchy–Navier potential functions of order n”

$$\begin{aligned} u_\tau ^n(x)=\int _{\ \mathcal {B}}\mathbf{{G}}_\tau ^n({{\mathbf {A}}}(\partial );x-y) f(y)\ dy \end{aligned}$$

(32)

converges to the Cauchy–Navier potential u independent of the order of the mollification.

Theorem 3

Suppose that $\mathcal {B}$ is a regular region in ${\mathbb {R}}^3$ and u is continuous in $\overline{\mathcal {B}}$. Further on, let $x\in \overline{\mathcal {B}}$ be arbitrary and let $f:\mathcal {B}\rightarrow {\mathbb {R}}^3$ be continuous. Then,

$$\begin{aligned} \left\| u(x)-u_\tau ^n(x)\right\|&=\left\| \int _{\ \mathcal {B}}\left( \mathbf{{G}}({{\mathbf {A}}}(\partial );x-y)-\mathbf{{G}}_\tau ^n({{\mathbf {A}}}(\partial );x-y)\right) f(y)\ dy\right\| \nonumber \\&={\mathcal {O}}(\tau ^2) \end{aligned}$$

(33)

as $\tau$ tends to zero.

Proof

First, we observe that $\mathbf{{G}}({{\mathbf {A}}}(\partial );x)=\mathbf{{G}}_\tau ^n({{\mathbf {A}}}(\partial );x)$ for all $x\in {\mathbb {R}}^3$, $\Vert x\Vert \ge \tau$. Hence, the integrand only differs from zero in the ball $\mathbb {B}_\tau (x)$ around x and radius $\tau$, so that

$$\begin{aligned}&\left\| \int _{\ \mathcal {B}}\left( \mathbf{{G}}({{\mathbf {A}}}(\partial );x-y)-\mathbf{{G}}_\tau ^n({{\mathbf {A}}}(\partial );x-y)\right) f(y)\ dy\right\| \end{aligned}$$

(34)

$$\begin{aligned}&\qquad =\left\| \int _{\ \mathbb {B}_\tau (x)}\left( \mathbf{{G}}({{\mathbf {A}}}(\partial );x-y)-\mathbf{{G}}_\tau ^n({{\mathbf {A}}}(\partial );x-y)\right) f_0(y)\ dy\right\| \nonumber \\&\qquad =\left\| \int _{\ \mathbb {B}_\tau (x)}\left( \mathbf{{G}}({{\mathbf {A}}}(\partial );x-y)-(\mathbf{{T}}_1+\mathbf{{T}}_2)\right) f_0(y)\ dy\right\| \end{aligned}$$

(35)

$$\begin{aligned}&\qquad \le \max _{y\in \mathbb {B}_\tau (x)}\left\| f_0(y)\right\| \int _{\ \mathbb {B}_\tau (0)}\left\| \mathbf{{G}}({{\mathbf {A}}}(\partial );y)-(\mathbf{{T}}_1+\mathbf{{T}}_2)\right\| \ dy \end{aligned}$$

(36)

with $\mathbf{{T}}_1$ and $\mathbf{{T}}_2$ as in Eqs. (30) and (31) and

$$\begin{aligned} f_0(x)=\left\{ \begin{array}{ccc} f(x),&{}x\in \overline{\mathcal {B}}\\ &{}&{}\\ 0,&{}x\in {\mathbb {R}}^3\backslash \overline{\mathcal {B}}\end{array}\right. . \end{aligned}$$

(37)

Explicit calculation by use of polar coordinates leads to

$$\begin{aligned}&\max _{y\in \mathbb {B}_\tau (x)}\left\| f_0(y)\right\| \int _{\ \mathbb {B}_\tau (0)}\left\| \mathbf{{G}}({{\mathbf {A}}}(\partial );y)-(\mathbf{{T}}_1+\mathbf{{T}}_2)\right\| \ dy\nonumber \\&\quad \le \max _{y\in \mathbb {B}_\tau (x)}C\Vert f_0(y)\Vert \Bigg (\int _0^{2\pi }\int _0^\pi \left| \frac{2\mu '\tau ^2\sin (\theta )(4(n+2) + 9)}{(n+2)^3 + 12(n+2)^2 + 47(n+2) + 60}\right| d\theta d\phi \nonumber \\&\qquad +\int _0^{2\pi }\int _0^\pi \left| \frac{\tau ^2\sin (\theta )(10\pi \mu \mu ' + 3)}{6\mu \pi ((n+2)^2 + 9(n+2) + 20)}\right| d\theta d\phi \Bigg )\nonumber \\&\quad =\max _{y\in \mathbb {B}_\tau (x)}C\Vert f_0(y)\Vert \Bigg (\frac{8\pi \mu '\tau ^2(4(n+2) + 9)}{(n+2)^3 + 12(n+2)^2 + 47(n+2) + 60}\nonumber \\&\qquad + \frac{2\tau ^2(10\pi \mu \mu ' + 3)}{3\mu ((n+2)^2 + 9(n+2) + 20)}\Bigg )\nonumber \\&\quad ={\mathcal {O}}(\tau ^2), \end{aligned}$$

(38)

where C is a constant. $\square$

Now, we take a look at deriving the Cauchy–Navier source scaling function corresponding to the potential scaling function $\left\{ \mathbf{{G}}_\tau ^n({{\mathbf {A}}}(\partial );\cdot )\right\} _{\tau >0}$ by applying the operator ${{\mathbf {A}}}(\partial _x)$ to $\mathbf{{G}}_\tau ^n({{\mathbf {A}}}(\partial );\cdot )$. To do that, we rewrite the expressions $\mathbf{{T}}_1$ and $\mathbf{{T}}_2$ as given in Eqs. (30) and (31) by using the auxiliary functions

$$\begin{aligned} {\mathbf {S}}^1_{n,m}(x,\tau )&=x\otimes x(\tau -r)^nr^m, \end{aligned}$$

(39)

$$\begin{aligned} {\mathbf {S}}^2_{n,m}(r,\tau )&={\mathbb {I}}(\tau -r)^nr^m \end{aligned}$$

(40)

and obtain

$$\begin{aligned} \mathbf{{T}}_1&=\frac{2\mu '}{3\tau ^{n+5}} \left[ \frac{2\tau }{8}\left( 3{\mathbf {S}}^1_{n+4,-3}(x,\tau )+3(n+4){\mathbf {S}}^1_{n+3,-2}(x,\tau )+{\mathbf {S}}^1_{n+2,-1}(x,\tau )(n+3)(n+4)\right) \right. \nonumber \\&\quad -\left. \frac{(n+3)}{4}\left( \frac{3}{2}{\mathbf {S}}^1_{n+4,-2}(x,\tau )+{\mathbf {S}}^1_{n+3,-1}(x,\tau )(n+4)\right) -\frac{3\tau ^{n+5}}{4}{\mathbf {S}}^1_{0,-3}(x,\tau )\right. \nonumber \\&\quad +\left. \frac{(n+3)}{8}\left( 3{\mathbf {S}}^1_{n+4,-2}(x,\tau )+3(n+4){\mathbf {S}}^1_{n+3,-1}(x,\tau )+{\mathbf {S}}^1_{n+2,0}(x,\tau )(n+3)(n+4)\right) \right] ,\end{aligned}$$

(41)

$$\begin{aligned} \mathbf{{T}}_2&=\left[ -\frac{\mu '}{12\tau ^{n+5}}\right. \left( (2\tau ^2{\mathbf {S}}^2_{n+3,-1}(r,\tau )+(n+3)(n+4){\mathbf {S}}^2_{n+3,1}(r,\tau )\right. \nonumber \\&\qquad \left. +2(n+3)\tau {\mathbf {S}}^2_{n+3,0}(r,\tau ))-2\tau ^{n+5}{\mathbf {S}}^2_{n+3,-1}(r,\tau )\right) \nonumber \\&\quad \left. +\frac{4\pi \mu \mu '-3}{3\mu }\left( \frac{1}{4\pi }{\mathbf {S}}^2_{0,-1}(r,\tau )-\frac{(n+3){\mathbf {S}}^2_{n+4,0}(r,\tau )+2\tau {\mathbf {S}}^2_{n+4,-1}(r,\tau )}{8\pi \tau ^{n+5}}\right) \right] . \end{aligned}$$

(42)

Lemma 2

For ${\mathbf {F}}^1_{n,m}(x,\tau )={{\mathbf {A}}}(\partial _x){\mathbf {S}}^1_{n,m}(x,\tau )$ and ${\mathbf {F}}^2_{n,m}(x,\tau )={{\mathbf {A}}}(\partial _x){\mathbf {S}}^2_{n,m}(r,\tau )$, we have

$$\begin{aligned}&{\mathbf {F}}^1_{n,m}(x,\tau )={{\mathbf {A}}}(\partial _x){\mathbf {S}}^1_{n,m}(x,\tau )\nonumber \\&\quad =(\lambda +\mu )\left[ x\otimes x \frac{(\tau - r)^{n-2}}{r^{4-m}}\biggl (((m+n)^2+4(m+n))r^4 \right. \nonumber \\&\qquad - (2m^2+2mn+8m+5n)r^3\tau + (m^2+4m)r^2\tau ^2\biggr )\nonumber \\&\qquad -\left. {\mathbb {I}}\left( \frac{(\tau - r)^{n-1}}{r^{-m}}((4+m)(r - \tau ) + nr )\right) \right] \nonumber \\&\qquad +\mu \left[ x\otimes x\frac{(\tau - r)^{n-2}}{r^{4-m}}\biggl (((m+n)^2 + 5(m+n))r^4\right. \nonumber \\&\qquad - (2m^2+2mn+10m+6n)r^3\tau + (m^2+ 5m)r^2\tau ^2 \biggr )\nonumber \\&\qquad +\left. {\mathbb {I}}\frac{(\tau - r)^{n-2}}{r^{4-m}}( 2r^6 - 4r^5\tau + 2r^4\tau ^2)\right] , \end{aligned}$$

(43)

$$\begin{aligned}&{\mathbf {F}}^2_{n,m}(x,\tau )={{\mathbf {A}}}(\partial _x){\mathbf {S}}^2_{n,m}(r,\tau )\nonumber \\&\quad =(\lambda +\mu )\left[ x\otimes x\frac{(\tau - r)^{n-2}}{r^{4-m}}\biggl (((m + n)^2\right. \nonumber \\&\qquad - 2(m+n))r^2- (2m^2+2mn-4m-n)r\tau + (m^2- 2m)\tau ^2\biggr )\nonumber \\&\qquad -\left. {\mathbb {I}}\frac{(\tau - r)^{n-1}}{r^{2-m}}((m+n)r - m\tau )\right] \nonumber \\&\qquad +\mu {\mathbb {I}}\frac{(\tau - r)^{n-2}}{r^{4-m}}\biggl (((m+n)^2 + m+ n)r^4\nonumber \\&\qquad - (2m^2 + 2mn + 2(m + n))r^3\tau + (m^2+ m)r^2\tau ^2\biggr ). \end{aligned}$$

(44)

Theorem 4

For $x,y\in {\mathbb {R}}^3$ and $n\in {{\mathbb {N}}}$, we find

$$\begin{aligned} {{\mathbf {A}}}(\partial _x) \mathbf{{G}}_\tau ^n({{\mathbf {A}}}(\partial );x-y)=\varvec{\varPhi }_\tau ^n(x-y)={{\mathbf {A}}}(\partial _y) \mathbf{{G}}_\tau ^n({{\mathbf {A}}}(\partial );x-y), \end{aligned}$$

(45)

where the Cauchy–Navier source scaling function $\varvec{\varPhi }_\tau ^n:{\mathbb {R}}^3\rightarrow {\mathbb {R}}^3\times {\mathbb {R}}^3$, $n\in {{\mathbb {N}}}$ is given by

$$\begin{aligned} \varvec{\varPhi }_\tau ^n(x)=\left\{ \begin{array}{lcr}\mathbb {O},&{} \tau \le r\\ &{} &{}\\ {{\mathbf {A}}}(\partial _x)(\mathbf{{T}}_1+\mathbf{{T}}_2) ,&{} 0<r<\tau \\ &{} &{}\\ \frac{(8\pi \mu \mu '-3)(n+3)(n+4)(n+5)}{24\tau ^3\pi (4\pi \mu \mu '-1)}{\mathbb {I}},&{} r=0\end{array}\right. \end{aligned}$$

(46)

Fig. 3

Profile of the scaling functions $\mathbf{{G}}_\tau ^n({{\mathbf {A}}}(\partial );\cdot )$ (top) and $\varvec{\varPhi }_\tau ^n$ (bottom) in $x_3=0$ for $n=1$ and their respective cuts along the $x_1/x_2$ direction (right)

with $\mathbf{{T}}_1$ and $\mathbf{{T}}_2$ as in (30) and (31), respectively and $\mathbb {O}$ denotes the zero tensor. In addition, the ${{\mathbf {A}}}(\partial _x)$-derivatives of $\mathbf{{T}}_1$ and $\mathbf{{T}}_2$ are given by

$$\begin{aligned}&{{\mathbf {A}}}(\partial _x)\mathbf{{T}}_1 =x\otimes x\frac{2\mu '}{3\tau ^{n+5}}\nonumber \\&\qquad \times \left[ \frac{2\tau }{8}\left( 3{\mathbf {F}}^1_{n+4,-3}(x,\tau ){+}3(n{+}4){\mathbf {F}}^1_{n+3,-2}(x,\tau ){+}{\mathbf {F}}^1_{n+2,-1}(x,\tau )(n{+}3)(n{+}4)\right) \right. \nonumber \\&\qquad -\left. \frac{(n+3)}{4}\left( \frac{3}{2}{\mathbf {F}}^1_{n+4,-2}(x,\tau )+{\mathbf {F}}^1_{n+3,-1}(x,\tau )(n+4)\right) -\frac{3\tau ^{n+5}}{4}{\mathbf {F}}^1_{0,-3}(x,\tau )\right. \nonumber \\&\qquad +\frac{(n+3)}{8}\left( 3{\mathbf {F}}^1_{n+4,-2}(x,\tau )+3(n+4){\mathbf {F}}^1_{n+3,-1}(x,\tau )\right. \nonumber \\&\qquad \left. \left. +{\mathbf {F}}^1_{n+2,0}(x,\tau )(n+3)(n+4)\right) \right] , \end{aligned}$$

(47)

$$\begin{aligned}&{{\mathbf {A}}}(\partial _x)\mathbf{{T}}_2\nonumber \\&\quad =\left[ -\frac{\mu '}{12\tau ^{n+5}}\right. \Bigl ((2\tau ^2{\mathbf {F}}^2_{n+3,-1}(x,\tau )+(n+3)(n+4){\mathbf {F}}^2_{n+3,1}(x,\tau )\nonumber \\&\qquad +2(n+3)\tau {\mathbf {F}}^2_{n+3,0}(x,\tau ))-2\tau ^{n+5}{\mathbf {F}}^2_{0,-1}(x,\tau )\Bigr )\nonumber \\&\qquad \left. +\frac{4\pi \mu \mu '-3}{3\mu }\left( \frac{1}{4\pi }{\mathbf {F}}^2_{0,-1}(x,\tau )-\frac{(n+3){\mathbf {F}}^2_{n+4,0}(x,\tau )+2\tau {\mathbf {F}}^2_{n+4,-1}(x,\tau )}{8\pi \tau ^{n+5}}\right) \right] {\mathbb {I}}\end{aligned}$$

(48)

with ${\mathbf {F}}^1_{n,m}$ and ${\mathbf {F}}^2_{n,m}$ as provided in Lemma 2.

Figure 3 depicts the scaling functions $\mathbf{{G}}_\tau ^n({{\mathbf {A}}}(\partial );\cdot )$ and $\varvec{\varPhi }_\tau ^n$ for the case $n=1$.

Lemma 3

The so-called volume integral of the scaling function $\varvec{\varPhi }_\tau ^n$ given by

$$\begin{aligned} V_{\varvec{\varPhi }_\tau ^n}&=\int _{{\mathbb {R}}^3}\varvec{\varPhi }_\tau ^n(y)\ dy \end{aligned}$$

(49)

satisfies

$$\begin{aligned} V_{\varvec{\varPhi }_\tau ^{n}}={\mathbb {I}}\end{aligned}$$

(50)

for all $n\in {{\mathbb {N}}}$ and all $\tau >0$.

Proof

For the proof of the lemma, we have to take a look at the integrals $\int _{\mathbb {B}_\tau (0)}{\mathbf {F}}^1_{n,m}\ dy$ and $\int _{\mathbb {B}_\tau (0)}{\mathbf {F}}^2_{n,m}\ dy$. Summing them up according to the definition of $\varvec{\varPhi }_\tau ^n$ leads to the desired result. Tables 1 and 2 summarize the respective values of those integrals. It should be noted, that only convergent integrals are involved in the calculation of $V_{\varvec{\varPhi }_\tau ^{n}}$.

Table 1 Integral values of ${\mathbf {F}}^1_{n,m}$. Here, $T=(\lambda (4+m)+\mu (6+2m))$

Table 2 Integral values of ${\mathbf {F}}^2_{n,m}$

Altogether, we have

$$\begin{aligned} V_{\varvec{\varPhi }_\tau ^n}&=\int _{{\mathbb {R}}^3}\varvec{\varPhi }_\tau ^n(y)\ dy=\int _{\mathbb {B}_\tau (0)}{{\mathbf {A}}}(\partial _x)(\mathbf{{T}}_1+\mathbf{{T}}_2)\ dy \end{aligned}$$

(51)

with ${{\mathbf {A}}}(\partial _x)\mathbf{{T}}_1$ and ${{\mathbf {A}}}(\partial _x)\mathbf{{T}}_2$ as given in Eqs. (47) and (48), respectively. At last, observing the results denoted in Tables 1 and 2, it turns out that

$$\begin{aligned} \int _{\mathbb {B}_\tau (0)}{{\mathbf {A}}}(\partial _x)\mathbf{{T}}_1\ dx&=\frac{2\mu '}{3\tau ^{n+5}}\left[ \frac{2\tau }{8}\left( -\frac{12\pi \tau ^{n+4}\lambda }{3}{\mathbb {I}}+\mathbb {O}+\mathbb {O}\right) \right. \nonumber \\&\qquad -\left. \frac{(n+3)}{4}\left( \mathbb {O}+\mathbb {O}\right) -\mathbb {O}+\frac{(n+3)}{8}\left( \mathbb {O}+\mathbb {O}+\mathbb {O}\right) \right] \end{aligned}$$

(52)

$$\begin{aligned}&=-\frac{2\mu '\lambda \pi }{3}{\mathbb {I}}, \end{aligned}$$

(53)

$$\begin{aligned} \int _{\mathbb {B}_\tau (0)}{{\mathbf {A}}}(\partial _x)\mathbf{{T}}_2\ dx&=\left[ -\frac{\mu '}{12\tau ^{n+5}}\right. \times \left( \left( \frac{8\tau ^{n+5}\pi (\lambda +4\mu )}{3}{\mathbb {I}}+\mathbb {O}+\mathbb {O}\right) -\mathbb {O}\right) \nonumber \\&\qquad \left. +\frac{4\pi \mu \mu '-3}{3\mu }\left( \frac{1}{4\pi }\mathbb {O}-\frac{(n+3)\mathbb {O}+2\tau \frac{4\tau ^{n+4}\pi (\lambda +4\mu )}{3}{\mathbb {I}}}{8\pi \tau ^{n+5}}\right) \right] \end{aligned}$$

(54)

$$\begin{aligned}&=-\frac{(\lambda + 4\mu )(2\pi \mu \mu ' - 1)}{3\mu }{\mathbb {I}}. \end{aligned}$$

(55)

With $\mu '=\frac{\lambda +\mu }{4\pi \mu (\lambda +2\mu )}$, we get

$$\begin{aligned} V_{\varvec{\varPhi }_\tau ^n}&=\int _{{\mathbb {R}}^3}\varvec{\varPhi }_\tau ^n(y)\ dy \end{aligned}$$

(56)

$$\begin{aligned}&=\int _{\mathbb {B}_\tau (0)}{{\mathbf {A}}}(\partial _x)(\mathbf{{T}}_1+\mathbf{{T}}_2)\ dy \end{aligned}$$

(57)

$$\begin{aligned}&=\left( -\frac{2\mu '\lambda \pi }{3}-\frac{(\lambda + 4\mu )(2\pi \mu \mu ' - 1)}{3\mu }\right) {\mathbb {I}}\end{aligned}$$

(58)

$$\begin{aligned}&=\frac{\lambda + 4\mu - 8\pi \mu ^2\mu ' - 4\pi \lambda \mu \mu '}{3\mu }{\mathbb {I}}\end{aligned}$$

(59)

$$\begin{aligned}&={\mathbb {I}}. \end{aligned}$$

(60)

$\square$

The scaling function $\varvec{\varPhi }_\tau ^n$ allows us to define the “$\tau$-Cauchy–Navier contrast functions of order n”$f_\tau ^n$ given by

$$\begin{aligned} f_\tau ^n(x)=\int _\mathcal {B}\varvec{\varPhi }_\tau ^n(x-y) f(y)\ dy. \end{aligned}$$

(61)

Theorem 5

The function $\varvec{\varPhi }_\tau ^n$ is $(n-1)$-times continuously differentiable in ${\mathbb {R}}\backslash \{0\}$. In addition, assume that $\mathcal {B}$ is a regular region in ${\mathbb {R}}^3$ and that $f:\overline{\mathcal {B}}\rightarrow {\mathbb {R}}^3$ is continuous. Then,

$$\begin{aligned} \lim _{{\mathop {\tau >0}\limits ^{\tau \rightarrow 0}}}\Vert f(x)-f_\tau ^n(x)\Vert =0 \end{aligned}$$

(62)

holds true for all $n\ge 0$ and all $x\in \mathcal {B}$.

Proof

Since $x\in \mathcal {B}$ and $\mathcal {B}$ is open, there exists a $\tau _0$ such that $\mathcal {B}\cap \mathbb {B}_\tau (x)=\mathbb {B}_\tau (x)$ for all $0<\tau \le \tau _0$. Hence, we have with $\varvec{\varPhi }_\tau ^n=\left( \left( \varvec{\varPhi }_\tau ^n\right) _{ij}\right) _{i,j=1,\ldots ,3}$

$$\begin{aligned} \int _\mathcal {B}\varvec{\varPhi }_\tau ^n(x-y)f(y)\ dy&= \int _{\mathbb {B}_\tau (x)}\varvec{\varPhi }_\tau ^n(x-y)f(y)\ dy \end{aligned}$$

(63)

$$\begin{aligned}&=\left( \sum _{j=1}^3\int _{\mathbb {B}_\tau (x)}\left( \varvec{\varPhi }_\tau ^n\right) _{ij}(x-y)f_j(y)\ dy\right) _{i=1,2,3}. \end{aligned}$$

(64)

We can split $\left( \varvec{\varPhi }_\tau ^n\right) _{ij}(x)$ into its positive and negative parts, so that

$$\begin{aligned}&\int _{\mathbb {B}_\tau (x)}\left( \varvec{\varPhi }_\tau ^n\right) _{ij}(x-y)f_j(y)\ dy\nonumber \\&\qquad =\int _{\mathbb {B}_\tau (x)}\left( \varvec{\varPhi }_\tau ^n\right) _{ij}^+(x-y)f_j(y)\ dy + \int _{\mathbb {B}_\tau (x)}\left( \varvec{\varPhi }_\tau ^n\right) _{ij}^-(x-y)f_j(y)\ dy, \end{aligned}$$

(65)

where

$$\begin{aligned} \left( \varvec{\varPhi }_\tau ^n\right) _{ij}^+(x)&=\left\{ \begin{array}{l@{\quad }l}\left( \varvec{\varPhi }_\tau ^n\right) _{ij}(x),&{}\qquad \left( \varvec{\varPhi }_\tau ^n\right) _{ij}(x)\ge 0\\ 0,&{}\qquad \left( \varvec{\varPhi }_\tau ^n\right) _{ij}(x)<0\end{array}\right. , \end{aligned}$$

(66)

$$\begin{aligned} \left( \varvec{\varPhi }_\tau ^n\right) _{ij}^-(x)&=\left\{ \begin{array}{ll}\left( \varvec{\varPhi }_\tau ^n\right) _{ij}(x),&{}\qquad \left( \varvec{\varPhi }_\tau ^n\right) _{ij}(x)\le 0\\ 0,&{}\qquad \left( \varvec{\varPhi }_\tau ^n\right) _{ij}(x)>0\end{array}\right. . \end{aligned}$$

(67)

Since f is continuous and $\left( \varvec{\varPhi }_\tau ^n\right) _{ij}^+$ as well as $\left( \varvec{\varPhi }_\tau ^n\right) _{ij}^-$ are integrable and do not change sign in $\mathbb {B}_\tau (x)$, the mean value theorem of integration guarantees the existence of $\xi _1,\xi _2\in \mathbb {B}_\tau (x)$, so that

$$\begin{aligned}&\int _{\mathbb {B}_\tau (x)}\left( \varvec{\varPhi }_\tau ^n\right) _{ij}(x-y)f_j(y)\ dy\nonumber \\&\qquad =f_j(\xi _1)\int _{\mathbb {B}_\tau (x)}\left( \varvec{\varPhi }_\tau ^n\right) _{ij}^+(x-y)\ dy + f_j(\xi _2)\int _{\mathbb {B}_\tau (x)}\left( \varvec{\varPhi }_\tau ^n\right) _{ij}^-(x-y)\ dy. \end{aligned}$$

(68)

According to Eq. (50), we have

$$\begin{aligned} \int _{\mathbb {B}_\tau (x)}\left( \varvec{\varPhi }_\tau ^n\right) _{ij}^+(x-y)\ dy + \int _{\mathbb {B}_\tau (x)}\left( \varvec{\varPhi }_\tau ^n\right) _{ij}^-(x-y)\ dy =\delta _{ij} \end{aligned}$$

(69)

and hence,

$$\begin{aligned} \int _{\mathbb {B}_\tau (x)}\left( \varvec{\varPhi }_\tau ^n\right) _{ij}^-(x-y)\ dy =\delta _{ij}-\int _{\mathbb {B}_\tau (x)}\left( \varvec{\varPhi }_\tau ^n\right) _{ij}^+(x-y)\ dy. \end{aligned}$$

(70)

Substituting the last equation into Eq. (68), we get

$$\begin{aligned}&\int _{\mathbb {B}_\tau (x)}\left( \varvec{\varPhi }_\tau ^n\right) _{ij}(x-y)f_j(y)\ dy \nonumber \\&\qquad = f_j(\xi _2)\delta _{ij}+\left( f_j(\xi _1)-f_j(\xi _2)\right) \int _{\mathbb {B}_\tau (x)}\left( \varvec{\varPhi }_\tau ^n\right) _{ij}^+(x-y)\ dy. \end{aligned}$$

(71)

Now with

$$\begin{aligned} \int _{\mathbb {B}_\tau (x)}\left( \varvec{\varPhi }_\tau ^n\right) _{ij}^+(x-y)\ dy\le \underbrace{\max _{y\in \mathbb {B}_\tau (x)}|\left( \varvec{\varPhi }_\tau ^n\right) _{ij}^+(x-y)|}_{={\mathcal {O}}\left( \tau ^{-3}\right) }\underbrace{\int _{\mathbb {B}_\tau (x)}\ dy}_{=\frac{4}{3}\pi \tau ^3}\le C \end{aligned}$$

(72)

for a positive constant C, we get

$$\begin{aligned} \lim _{{\mathop {\tau >0}\limits ^{\tau \rightarrow 0}}}\int _{\mathbb {B}_\tau (x)}\left( \varvec{\varPhi }_\tau ^n\right) _{ij}(x-y)f_j(y)\ dy=\delta _{ij} f_j(x), \end{aligned}$$

(73)

since $\xi _1,\xi _2\in \mathbb {B}_\tau (x)$. In connection with Eq. (64), this leads us to

$$\begin{aligned} \lim _{{\mathop {\tau >0}\limits ^{\tau \rightarrow 0}}}\int _\mathcal {B}\varvec{\varPhi }_\tau ^n(x-y)f(y)\ dy=f(x) \end{aligned}$$

(74)

and hence,

$$\begin{aligned} \lim _{{\mathop {\tau >0}\limits ^{\tau \rightarrow 0}}}\Vert f(x)-f_\tau ^n(x)\Vert =0. \end{aligned}$$

(75)

$\square$

Next, we deal with the mathematical mechanisms for interpretation and understanding of available density information inside a regular region $\mathcal {B}$. In order to do that, we again take a look at the Newton case in order to to make the reader more familiar with the idea of density decomposition and introduce the associated notation. Our purpose is to thereby exemplary demonstrate, how the multiscale procedure for the potential canonically transfers to the density by use of “Laplace derivatives” as shown in Blick et al. (2018).

Suppose that $\{\tau _j\}_{j \in {{\mathbb {N}}}_0}$ is a positive, monotonically decreasing sequence with $\lim _{j \rightarrow \infty } \tau _j =0$. For $j \in {{\mathbb {N}}}_0,$ we consider the differences

$$\begin{aligned} \mathcal {W}_{\tau _j}^n(\varDelta ;\Vert x-y\Vert )=G_{\tau _j}^n (\varDelta ;\Vert x-y\Vert )-G_{\tau _{j-1}}^n (\varDelta ;\Vert x-y\Vert ) \end{aligned}$$

(76)

and

$$\begin{aligned} \varPsi _{\tau _j}^n (\Vert x-y\Vert )=\varPhi _{\tau _j}^n (\Vert x-y\Vert )-\varPhi _{\tau _{j-1}}^n (\Vert x-y\Vert ). \end{aligned}$$

(77)

$\mathcal {W}_\tau ^n(\varDelta ;\cdot )$ and $\varPsi _\tau ^n$ are called “Newton potential wavelet function of order n”and “Newton source wavelet function of order n”.

The associated “$\tau _j$-potential wavelet functions of order n”and the “$\tau _j$-contrast wavelet functions of order n”  are given by

$$\begin{aligned} (WV)_{\tau _j}^n (x)= \int _\mathcal {B}\mathcal {W}_{\tau _j}^n (\varDelta ; \Vert x-y \Vert )\rho (y) \ dy \end{aligned}$$

(78)

and

$$\begin{aligned} (W\rho )_{\tau _j}^n (x)= \int _\mathcal {B}\varPsi _{\tau _j}^n (\Vert x-y\Vert )\rho (y) \ dy. \end{aligned}$$

(79)

The $\tau _j$-potential wavelet functions of order n and the $\tau _j$-contrast wavelet functions of order n, respectively, characterize the successive detail information contained in $V_{\tau _j}^n (x)-V_{\tau _{j-1}}^n$ and $\rho _{\tau _j}^n -\rho _{\tau _{j-1}}^n, \ j \in {{\mathbb {N}}}_0$. In other words, we are able to recover the potential V and the contrast function, i.e., the “density signature”$\rho$, respectively, in form of “band structures”

$$\begin{aligned} (WV)_{\tau _j}^n =V_{\tau _j}^n -V_{\tau _{j-1}}^n \end{aligned}$$

(80)

and

$$\begin{aligned} (W\rho )_{\tau _j}^n =\rho _{\tau _j}^n -\rho _{\tau _{j-1}}^n. \end{aligned}$$

(81)

As a consequence, the essential problem to be solved in multiscale extraction of geological features is to identify those detail information, i.e., band structures in (80), which specifically contain desired density characteristics in (81), for example, aquifers, salt domes.

Seen from a numerical point of view, it is remarkable that both wavelet functions $y \mapsto \mathcal {W}(\varDelta ;\Vert x-y\Vert )$ and $y \mapsto \varPsi (\Vert x-y\Vert )$ vanish outside a ball around the center x due to their construction, i.e., these functions are spacelimited showing a ball as local support. Furthermore, the ball becomes smaller and smaller with increasing scale parameter j,  so that more and more high frequency phenomena can be highlighted without changing the features outside the balls. Explicitly written out in our nomenclature, we obtain for $x\in \mathcal {B}$

$$\begin{aligned} (WV)_{\tau _j}^n (x)= \int _{\mathbb {B}_{\tau _j} (x)\cap \mathcal {B}}\mathcal {W}(\varDelta ;\Vert x-y\Vert )\rho (y) \ dy \end{aligned}$$

(82)

and

$$\begin{aligned} (W\rho )_{\tau _j}^n (x)= \int _{\mathbb {B}_{\tau _j} (x)\cap \mathcal {B}}\varPsi (\Vert x-y\Vert )\rho (y) \ dy. \end{aligned}$$

(83)

Thus for $x\in \mathcal {B}$, we finally end up with the following multiscale reconstruction

$$\begin{aligned} V(x)=\lim _{J\rightarrow \infty }V_{\tau _J}^n (x)=V_{\tau _0}^n (x)+\sum _{j=1}^\infty (WV)_{\tau _j}^n (x) \end{aligned}$$

(84)

and

$$\begin{aligned} \rho (x)&=\lim _{J\rightarrow \infty }\rho _{\tau _J}^n (x)=\rho _{\tau _0}^n (x)+\sum _{j=1}^\infty (W\rho )_{\tau _j}^n (x) =\lim _{J\rightarrow \infty }\varDelta _x V_{\tau _J}^n (x). \end{aligned}$$

(85)

In addition, if $\rho$ is Hölder continuous, we have

$$\begin{aligned} \rho (x) =\varDelta _x V_{\tau _0}^n (x)+\sum _{j=1}^\infty \varDelta _x (WV)_{\tau _j}^n (x). \end{aligned}$$

(86)

All in all, the potential V as well as the contrast function, i.e., the “density signature” $\rho$ can be expressed in an additive way as a low-pass filtered signal $V_{\tau _0}^n$ and $\rho _{\tau _0}^n$ and successive band-pass filtered signals $(WV)_{\tau _j}^n$ and $(W\rho )_{\tau _j}^n$, $j=1,2,\ldots ,$ respectively.

It should be mentioned that this multiscale approach is constructed such that, within the spectrum of all wavebands (cf. Eq. (80) and (81)), certain rock formations may be associated to a specific band characterizing typical features within the multiscale reconstruction. Each scale parameter in the decorrelation is assigned to a data distribution which corresponds to the associated waveband and, thus, leads to a low-pass approximation of the data at a particular resolution. The wavelet contributions are obtained as part within a multiscale approximation by calculating the difference between two consecutive scaling functions. In other words, the wavelet transformation (filtering) of a signal constitutes the difference of two low-pass filters, thus it may be regarded as a band-pass filter. Due to our construction, the wavelets show an increasing space localization as the scale increases. In this way, the characteristic signatures of a signal can be detected in certain frequency bands.

In the same way as for the Newton equation, we obtain a multiscale procedure for the potential u as well as the contrast function f. Again suppose that $\{\tau _j\}_{j \in {{\mathbb {N}}}_0}$ is a positive, monotonically decreasing sequence with $\lim _{j \rightarrow \infty } \tau _j =0$. For $j \in {{\mathbb {N}}}_0,$ we consider the differences

$$\begin{aligned} \varvec{\mathcal {W}}_{\tau _j}^n({{\mathbf {A}}}(\partial );x-y)=\mathbf{{G}}_{\tau _j}^n ({{\mathbf {A}}}(\partial );x-y)-\mathbf{{G}}_{\tau _{j-1}}^n ({{\mathbf {A}}}(\partial );x-y) \end{aligned}$$

(87)

and

$$\begin{aligned} \varvec{\varPsi }_{\tau _j}^n (x-y)=\varvec{\varPhi }_{\tau _j}^n (x-y)-\varvec{\varPhi }_{\tau _{j-1}}^n (x-y). \end{aligned}$$

(88)

$\varvec{\mathcal {W}}_\tau ^n({{\mathbf {A}}}(\partial );\cdot )$ and $\varvec{\varPsi }_\tau ^n$ are called “Cauchy–Navier potential wavelet function of order n”and “Cauchy–Navier source wavelet function of order n”. The associated “$\tau _j$-Cauchy–Navier potential wavelet functions of order n”and the “$\tau _j$-Cauchy–Navier contrast wavelet functions of order n”are given by

$$\begin{aligned} ({\mathbf {W}}u)_{\tau _j}^n (x)= \int _\mathcal {B}\varvec{\mathcal {W}}_{\tau _j}^n ({{\mathbf {A}}}(\partial ); x-y ) f(y) \ dy \end{aligned}$$

(89)

and

$$\begin{aligned} ({\mathbf {W}}f)_{\tau _j}^n (x)= \int _\mathcal {B}\varvec{\varPsi }_{\tau _j}^n (x-y) f(y) \ dy. \end{aligned}$$

(90)

As in the Newton case, the $\tau _j$-Cauchy–Navier potential wavelet functions of order n and the $\tau _j$-Cauchy–Navier contrast wavelet functions of order n, respectively, characterize the successive detail information contained in $u_{\tau _j}^n (x)-u_{\tau _{j-1}}^n$ and $f_{\tau _j}^n -f_{\tau _{j-1}}^n, \ j \in {{\mathbb {N}}}_0$. In other words, we are able to recover the potential u and the contrast function, i.e., the “signature”f, respectively, in form of “band structures”

$$\begin{aligned} ({\mathbf {W}}u)_{\tau _j}^n =u_{\tau _j}^n -u_{\tau _{j-1}}^n, \end{aligned}$$

(91)

and

$$\begin{aligned} ({\mathbf {W}}f)_{\tau _j}^n =f_{\tau _j}^n -f_{\tau _{j-1}}^n. \end{aligned}$$

(92)

Again, both wavelet functions $y \mapsto \varvec{\mathcal {W}}({{\mathbf {A}}}(\partial );x-y)$ and $y \mapsto \varvec{\varPsi }(x-y)$ vanish outside a ball around the center x due to their construction, which is of numerical advantage for the convolution. Furthermore, the ball becomes smaller and smaller with increasing scale parameter j,  so that more and more high frequency phenomena can be highlighted without changing the features outside the balls. Thus for $x\in \mathcal {B}$, we obtain the multiscale relations

$$\begin{aligned} u(x)=\lim _{J\rightarrow \infty }u_{\tau _J}^n (x)=u_{\tau _0}^n (x)+\sum _{j=1}^\infty ({\mathbf {W}}u)_{\tau _j}^n (x) \end{aligned}$$

(93)

and

$$\begin{aligned} f(x)&=\lim _{J\rightarrow \infty }f_{\tau _J}^n (x)=f_{\tau _0}^n (x)+\sum _{j=1}^\infty ({\mathbf {W}}f)_{\tau _j}^n (x) =\lim _{J\rightarrow \infty }{{\mathbf {A}}}(\partial _x) u_{\tau _J}^n (x). \end{aligned}$$

(94)

In addition, if f is Hölder continuous, we have

$$\begin{aligned} f(x) ={{\mathbf {A}}}(\partial _x) u_{\tau _0}^n (x)+\sum _{j=1}^\infty {{\mathbf {A}}}(\partial _x) ({\mathbf {W}}u)_{\tau _j}^n (x). \end{aligned}$$

(95)

Hence, the potential u as well as the contrast function f can be reconstructed as a low-pass filtered signal $u_{\tau _0}^n$ and $f_{\tau _0}^n$ and successive band-pass filtered signals $({\mathbf {W}}u)_{\tau _j}^n$ and $({\mathbf {W}}f)_{\tau _j}^n$, $j=1,2,\ldots ,$ respectively.

3 Comparison of the Newton and Cauchy–Navier decomposition based on the Marmousi density model

As point of departure, we construct a synthetic 3D density model by putting copies of the the smooth 2D Marmousi data set (Martin et al. 2006; Irons 2015) behind each other in order to test the decomposition ability of the wavelets. We specifically accept the downside of the model that it is constant in the y-direction in favor of the fact that we have a complete interpretation of the model as depicted in Fig. 4.

Fig. 4

The Marmousi model in $\left[ \frac{\hbox {kg}}{\hbox {m}^3}\right]$ (top, Symes 2014) and its interpretation (bottom, Martin et al. 2006)

3.1 Decomposition using Newton wavelets

Even if we are more interested in the decomposition of density data, our mathematical setup allows us to also decompose the potential. Hence, we borrow the results of the Newton case from Blick (2015) and present them here as a foundation for the comparison to the Cauchy–Navier decomposition scheme. As the base model, we choose a 3D variant of the Marmousi density data set depicted in Fig. 4 and present its decomposition based on the Newton potential scaling function and wavelet for the case $n=0$. Afterward, we follow with the decorrelation of the density using the Newton source scaling function and wavelet. It should be noted that we obtain a similar decomposition, if we select $n\ge 1$. In fact, selecting a larger $n\in {{\mathbb {N}}}$ while simultaneously choosing a lower scale parameter j results in a structurally alike decomposition, as shown in Blick (2015).

Remark 3

The depicted figures in this section denote 2D-cuts of the complete 3D convolution result of the 3D Marmousi density model as used in Blick (2015). Further, for the convolution with the Newton source scaling function and wavelet, a border of size $\tau _{j-1}$ is cut off in order to ignore border phenomena of the convolution due to the discontinuity of the input data.

We clearly see in Fig. 5 that the low-pass filtered potential is extremely stiff regarding the scale parameter, i.e., there is almost no change in the structure of the low-pass filtered versions of the density potential. This is due to the fact that the magnitude of the potential is of order $10^9$, whereas the detail information is only of order $10^7$ for $j=4$ and falls drastically to $10^5$ for $j=9$. That means, if we are only interested in the potential of the density data, a lower scale parameter and hence, a coarse approximation may be enough. In addition, the method provides trend information of the input data by way of the detail information.

For the decomposition of the density, Fig. 6 indicates that we obtain the original input data at scale $j=8$. For lower scales, we can calculate a rough trend of the input data (depicted in the scale-space). Furthermore, the detail-space shows coarse information of the data for lower scales, which get consecutively finer as j increases. If we study the detail information of scale $j=8$ of the Marmousi density model (Fig. 4), we recognize that we are able to highlight density information. In fact, we can clearly identify the separating layers in the density model. Here, the limit of the refinement is only determined by the denseness of the data.

Fig. 5

Multiscale approximation of the 3D Marmousi density potential by convolution of the density with the Newton potential scaling function (scale-space) and the Newton potential wavelet (detail-space) for $n=0$ and $\tau _j=9200\cdot 2^{-j}m$ in $\left[ \frac{\hbox {kg}}{\hbox {m}}\right]$. It should be noted that the gravitational constant is not included in the calculations above

Fig. 6

Multiscale approximation of the 3D Marmousi density by convolution of the density with the Newton source scaling function (scale-space) and the Newton source wavelet (detail-space) for $n=0$ and $\tau _j=9200\cdot 2^{-j}m$ in $\left[ \frac{\hbox {kg}}{\hbox {m}^3}\right]$

3.2 Decomposition using Cauchy–Navier wavelets

For the Cauchy–Navier wavelet decomposition, we have to prepare the data set beforehand. The reason is, that the wavelets are based on the Cauchy–Navier equation, which models a homogeneous medium with constant Lamé parameters $\lambda$ and $\mu$, as well as a constant density $\rho$. Hence, we choose a reference medium, in this case sandstone, with the parameters $\rho _S=2066.38 \frac{\hbox {kg}}{\hbox {m}^3}$, $\lambda =1.9\cdot 10^9\,\hbox {Pa}$ and $\mu =6.3\cdot 10^9\,\hbox {Pa}$ (Gopalakrishnan 2016) and decompose the density variation $\rho _D=\rho -\rho _S$. Further, we need vectorial input data f with unit $[\frac{\hbox {N}}{\hbox {m}^3}]$, i.e., density times acceleration. Convolution of the input data with the Cauchy–Navier potential scaling function and wavelet then results in a decomposition of the elastic potential u, i.e., the displacement vector in [m], while convolution with the Cauchy–Navier source scaling function and wavelet results in a decomposition of f itself. Here, we are only interested in the last case. Taking $f=\rho _De_i$, $i=1,2,3$, where $e_i$ is given in $\left[ \frac{\hbox {m}}{\hbox {s}^2}\right]$ and denotes the i-th Cartesian unit normal vector, the decomposition will be concentrated along the $x_i$ direction in the i-th component of the resulting vector. Moreover the remaining two components of the solution vector contain the decomposition in the diagonal direction of $x_i$ and $x_j$, $j\ne i$. Hence, for a complete decomposition, we choose

$$\begin{aligned} f=(1,1,1)^T\frac{\hbox {m}}{\hbox {s}^2}\rho _D=(e_1 + e_2+e_3)\frac{\hbox {m}}{\hbox {s}^2}\rho _D \end{aligned}$$

(96)

and present as depicted in Fig. 7 the resulting decomposition in the form of convolutions $*$ by

$$\begin{aligned} \left( \varvec{\varPhi }_{\tau _j}*( e_1\rho _D)\quad +\quad \varvec{\varPhi }_{\tau _j}*( e_2\rho _D)\quad +\quad \varvec{\varPhi }_{\tau _j}*( e_3\rho _D)\right) =\varvec{\varPhi }_{\tau _j}*f. \end{aligned}$$

(97)

Fig. 7

Cut of the input data for the decomposition via the Cauchy–Navier source scaling functions and wavelets

Fig. 8

Multiscale approximation of the potential u of f (cf. Fig. 7) by convolution with the Cauchy–Navier potential scaling function $\left\{ {\mathbf{{G}}}_{\tau _j}^0({{\mathbf {A}}}(\partial );\cdot )\right\} _{j\in {{\mathbb {N}}}}$ (top) and the Cauchy–Navier potential wavelet $\left\{ {\varvec{\mathcal {W}}}_{\tau _j}^0({{\mathbf {A}}}(\partial );\cdot )\right\} _{j\in {{\mathbb {N}}}}$ (bottom) for $n=0$, $\tau _j=9200\cdot 2^{-j}m$, and $j=4$ in $\left[ m\right]$

Fig. 9

Multiscale approximation of the potential u of f (cf. Fig. 7) by convolution with the Cauchy–Navier potential scaling function $\left\{ {\mathbf{{G}}}_{\tau _j}^0({{\mathbf {A}}}(\partial );\cdot )\right\} _{j\in {{\mathbb {N}}}}$ (top) and the Cauchy–Navier potential wavelet $\left\{ {\varvec{\mathcal {W}}}_{\tau _j}^0({{\mathbf {A}}}(\partial );\cdot )\right\} _{j\in {{\mathbb {N}}}}$ (bottom) for $n=0$, $\tau _j=9200\cdot 2^{-j}m$, and $j=8$ in $\left[ m\right]$

Fig. 10

Multiscale approximation of the data f (cf. Fig. 7) by convolution with the Cauchy–Navier source scaling function $\left\{ {\varvec{\varPhi }}_{\tau _j}^0\right\} _{j\in {{\mathbb {N}}}}$ (top) and the Cauchy–Navier source wavelet $\left\{ {\varvec{\varPsi }}_{\tau _j}^0\right\} _{j\in {{\mathbb {N}}}}$ (bottom) for $n=0$, $\tau _j=9200\cdot 2^{-j}m$, and $j=2$ in $\left[ \frac{\hbox {N}}{\hbox {m}^3}\right]$

Fig. 11

Multiscale approximation of the data f (cf. Fig. 7) by convolution with the Cauchy–Navier source scaling function $\left\{ {\varvec{\varPhi }}_{\tau _j}^0\right\} _{j\in {{\mathbb {N}}}}$ (top) and the Cauchy–Navier source wavelet $\left\{ {\varvec{\varPsi }}_{\tau _j}^0\right\} _{j\in {{\mathbb {N}}}}$ (bottom) for $n=0$, $\tau _j=9200\cdot 2^{-j}m$, and $j=8$ in $\left[ \frac{\hbox {N}}{\hbox {m}^3}\right]$

For the decomposition by use of Cauchy–Navier potential wavelets, we only depicted selected low-pass and band-pass filtered versions of u due to the larger amount of pictures. In general, the decomposition of u behaves similar to the Newton potential, that is, the potential is extremely stiff regarding the scale parameter as illustrated in Figs. 8 and 9. Again, there is almost no change in the structure of the low-pass filtered versions of the Cauchy–Navier potential. The trend information of the input data in the detail information can also be recognized on the diagonal of the band-pass filtered potential. The huge advantage however, is that the off-diagonal entries of the band-pass filtered potential already show a decorrelation of the input density, which in the Newton-case can only be detected by use of source wavelets. Specifically, the off-diagonal entries in Fig. 8 highlight the major density transitions in the Cauchy–Navier potential, however for the Newton case, the same transition can only be perceived by using source wavelets (cf. Fig. 6 at scale $j=6$). Even the finest density variations emphasized by the Newton source wavelet at scale $j=8$ (cf. Fig. 5) can already be spotted in the decomposition of the Cauchy–Navier potential on the off-diagonal at scale $j=8$ as depicted in Fig. 9. Now we concern ourselves with the decomposition via the Cauchy–Navier source wavelet exemplary for the scales $j=2$ and $j=8$. On the right hand side of Figs. 10 and 11, we see that at the final stage of the decomposition, we get the input data from Fig. 7 back. In addition at higher scales, the decomposition result is very similar to the decomposition using Newton wavelets in both the low-pass and band-pass filtered parts. The main difference can be found in the lower scales $j=2,\ldots ,6$. Exemplary taking a look at the detail information at scale $j=2$, we recognize that the structures expanding in the $x_1$ and $x_2$ direction are highlighted in the first and second component of the decomposition vector, respectively. In the $x_3$ direction, the model is constant, so that we get similar results to the decomposition using Newton wavelets here. Now, we observe the breakdown of f into the vectors $e_i\rho _D$ on the left hand side of the decomposition. The decomposition of the density variation in the $x_i$ direction can be identified on the diagonal in addition to the mixed directions in the non-diagonal pictures. It is clear that the mixed directions involving the direction $x_3$ are close to zero with an amplitude of $10^{-15}$. This is due to the corresponding entries of $\varvec{\varPhi }_{\tau _j}$ being zero in $x_3=0$. The major improvement compared to the decomposition using Newton wavelets is, that due to the radial symmetry of the Newton wavelet and scaling functions, every direction of the density model is weighted equally. This is not the case for the Cauchy–Navier wavelet and scaling functions (cf. Fig. 3). Hence, we can further decompose the model so that we can precisely highlight structures stretching in the $x_i$ direction, as well as diagonally in the data set. Therefore, an interpretation of a given density model using Cauchy–Navier wavelets will be more precise then by applying Newton wavelets. This behavior is clearly demonstrated in Fig. 10 for the band-pass filtered data f at scale $j=2$. Here, we find that the first diagonal entry of the band-pass filtered density variation f clearly highlights the structures stretching in the $x_1$ direction, while the second diagonal entry emphasizes the structures spreading in the $x_2$ direction. Due to the fact that the model is constant in the $x_3$ direction and that the profile of the figures is taken at $x_3=0$, the third diagonal entry is similar as in the case for the decomposition via the Newton source wavelet. In addition, the density signatures stretching in the $x_i-x_j$ direction, $i\ne j$ are highlighted on the off-diagonal, so that every main spreading direction can be emphasized. The same behavior is also true at higher scales however, the effect is less noticeable due to the shrinking compact support of the wavelets.

4 Conclusion

We compared the scalar wavelet decomposition using Newton wavelets and presented an approach for the directional interpretability by tensorial Cauchy–Navier wavelet and scaling functions. Decomposition results were presented and compared for both types of wavelets. The Newton wavelets lead to a good decomposition of the data, which aids the interpretation effort in exploration. The Cauchy–Navier wavelets however, allow a more precise decomposition since the data set is even further disassembled so that structures stretching in either of the three Cartesian directions as well as all diagonal directions can be highlighted. In fact, the density signatures emphasized by both the Newton potential and source wavelets can already be seen by decorrelation via the Cauchy–Navier potential wavelets due to the tensorial setup. In addition, the decomposition via the Cauchy–Navier source wavelet yields further information on the density signatures by highlighting signatures spreading in the three Cartesian coordinate directions on the diagonal and the mixed directions on the off-diagonal of the decomposition.