Global structure-guided neighborhood preserving embedding for dimensionality reduction

Abstract

Graph embedding is one of the most efficient dimensionality reduction methods in machine learning and pattern recognition. Many local or global graph embedding methods have been proposed and impressive results have been achieved. However, little attention has been paid to the methods that integrate both local and global structural information without constructing complex graphs. In this paper, we propose a simple and effective global structure guided neighborhood preserving embedding method for dimensionality reduction called GSGNPE. Specifically, instead of constructing global graph, principal component analysis (PCA) projection matrix is first introduced to extract the global structural information of the original data, and then the induced global information is integrated with local neighborhood preserving structure to generate a discriminant projection. Moreover, the $L_{2,1}$-norm regularization is employed in our method to enhance the robustness to occlusion. Finally, we propose an iterative optimization algorithm to solve the proposed problem, and its convergence is also theoretically analyzed. Extensive experiments on four face and six non-face benchmark data sets demonstrate the competitive performance of our proposed method in comparison with the state-of-the-art methods.

1 Introduction

In the era of big data, the tasks to deal with, such as image classification, text analysis and gene selection, contain hundred and thousand of features, pose some substantial challenges for effective and efficient computing and analysis [1,2,3,4,5,6,7]. Dimensionality reduction can be considered as the process of removing irrelevant or redundant information from high-dimensional data [8, 9]. Since reducing the learning process, improving interpretability, and alleviating the problem of over-fitting, dimensionality reduction has become an important pre-processing step in machine learning, pattern recognition, and computer vision [10,11,12].

In recent decades, many linear dimensionality reduction methods [13,14,15,16] have been proposed. Among these methods, principal component analysis (PCA) [13] and linear discriminant analysis (LDA) [14] are the classic ones and widely used. PCA is an unsupervised dimensionality reduction method, which aims to find a projection that maximizes the overall variance [17]. Unlike PCA, LDA is a supervised method, which tries to find a projection that not only makes the samples within the same classes compact and also keeps the samples from different classes away from each other. In practical applications, however, the data does not always have an ideal linear structure [18, 19]. In these cases, PCA and LDA may not achieve the expected performance since they do not take into account the underlying nonlinear structure of the original data. To tackle this problem, many kernelized extensions of these linear dimensionality reduction methods [20,21,22] have been proposed. Nevertheless, due to the difficulty in determining kernel function, these methods are limited in practical applications.

The high-dimensional data is always in a low-dimensional manifold embedded in the original high-dimensional space [23]. Thus, to introduce the low-dimensional manifold of high-dimensional data into the low-dimensional space, many nonlinear manifold learning methods have been proposed, including locally linear embedding (LLE) [24], isometric mapping (ISOMAP) [23], and Laplacian eigenmap (LE) [25]. Though these manifold learning methods can well preserve the inherent geometric structure of the original data in the low-dimensional space [26], they directly obtain the low-dimensional embedding without the explicit mapping functions resulting in the “out-of-sample” problem. This inconvenience limits the applications of these methods in practice. The key to solving this problem is to obtain an explicit mapping function, which can easily obtain the low-dimensional embeddings of new samples. In the past few decades, many linear manifold learning methods have emerged, including locality preserving projections (LPP) [27], neighborhood preserving embedding (NPE) [28], neighborhood preserving projections (NPP) [29], sparsity preserving projections (SPP) [30]. Many of these methods are extensions of the existing nonlinear manifold learning methods. For example, LPP is a linear extension of LE and uses an affinity graph to make the projection data retain neighborhood structure; NPE is a linear extension of LLE and uses weighted graph to minimize the reconstruction error for keeping local structure of the original data. These linear manifold learning methods can not only retain the local manifold structure of the original data but also solve the “out-of-sample” problem.

However, there are still some potential drawbacks in nonlinear and linear manifold learning methods mentioned above. First, most of these methods neglect the global structure of the original data which is also useful to identify the underlying structural information of the data [31]. Second, the local structure graph depends on the pair-wise Euclidean distances between samples, which is easily contaminated by noise and outlier [32]. To address these problems, many graph embedding based methods [33,34,35,36] have been proposed, which can hold the global and local structure of the original data in low-dimensional space. These methods preserve the structural information by constructing the complex structure graphs. For example, Shen et al. [35] constructed a global structure graph by calculating the distance between all samples, which is combined with the local graph embedding based method to get the low-dimensional embedding. In [36], Gou et al. assumed that the samples within the same classes will hold the similar sparse reconstructions. By constructing the global and local structure graphs, they gave the definition of sparsity and geometry preserved scattering and employed maximum margin criterion (MMC) [22] to obtain the low-dimensional embedding.

Although keeping the global and local structure simultaneously in the low-dimensional space can effectively improve the performance of dimensionality reduction, the construction of structure graphs in the existing methods are very complicated. Also, it is difficult to find an appropriate method to efficiently and easily combine the global and local structural information in practical applications. To deal with this problem, we propose a simple and effective dimensionality reduction method named GSGNPE (global structure guided neighborhood preserving embedding), which can simultaneously retain the global and local structure of the original data in low-dimensional space. In detail, we use a concise and efficient least-square term to obtain the global structure information from the PCA projection matrix which can retain the global Euclidean structure of the original data. On this basis, we modify the NPE loss function so that it can hold the global and local structure of the original data concurrently. In addition, the $L_{2,1}$-norm regularization is utilized in GSGNPE model to make the final projection matrix have the sparse structure, promote effective learning of global structure information, and reduce the interference of global structure information on local structure information, which helps to retain essential structural information and makes GSGNPE robustness to occlusion and noise. Hence, the performance of GSGNPE can be further improved. The main contributions of this work are summarized as follows:

• 1) A novel unsupervised graph embedding based dimensionality reduction method named GSGNPE is proposed. Instead of constructing the global structure graph, GSGNPE introduces the global structural information in the projection matrix obtained by PCA into the NPE to guide the retention of structural information, which provides a simple and effective way to extract the features with global and local structural information.

• 2) Consider the negative effect of noise and occlusion, GSGNPE integrates $L_{2,1}$-norm regularization into its objective function, which could effectively promote the retention of essential structural information and enhance the robustness to occlusion and noise. The experiments on the face data sets show that GSGNPE achieves better results under different sizes and positions of occlusion.

• 3) An iterative algorithm is elaborately designed for solving the resulting optimization problem of the proposed GSGNPE, and the corresponding convergence is analyzed and proved theoretically. Extensive experimental results demonstrate the superior performance and fast convergence of the proposed GSGNPE.

The rest of this paper is organized as follows. Section 2 presents some notations and definitions, and gives a brief review of the related works. Section 3 describes the proposed GSGNPE method and the corresponding optimization algorithm, and gives the convergence analysis. A series of experimental results and analysis are given in Sect. 4. Finally, the conclusions are drawn in Sect. 5.

2 Related works

In this section, we first give some notation and definitions, and then briefly review some related methods, including PCA, LPP, and NPE.

2.1 Notation and definitions

Suppose that $\mathbf {X}=[\mathbf {x}_1,\mathbf {x}_2,\ldots , \mathbf {x}_n]\in \mathfrak {R}^{d\times n}$ is the centralized data matrix, and $\mathbf {x}_i \in \mathfrak {R}^{d}$ is the ith sample of $\mathbf {X}$. Let $x_{ij}$ be the element in the ith row and jth column of the matrix $\mathbf {X}$, and $\mathbf {x}^{i}$ is the ith row vector of data matrix $\mathbf {X}$. Then, the $L_{2,1}$-norm of data matrix $\mathbf {X}$ is defined as follows:

$$\begin{aligned} ||\mathbf {X}||_{2,1} =\sum _{i=1}^d\sqrt{\sum _{j=1}^n x_{ij}^2} =\sum _{i=1}^d||\mathbf {x}^i||_2, \end{aligned}$$

(1)

The goal of the linear dimensionality reduction methods is to learn a projection matrix $\mathbf {P} \in \mathfrak {R}^{d\times c}$ that can project a high-dimensional sample $\mathbf {x}_i$ to a low-dimensional one with $\mathbf {y}_i=\mathbf {P}^T\mathbf {x}_i$, where $c \ll d$.

2.2 PCA

PCA is one of the most commonly used dimensionality reduction methods in pattern recognition and machine learning. The basic idea of PCA is to maximize the overall variance of the samples, and the projection data preserves the global Euclidean structure of the original data [37]. The objective function of PCA is defined as:

$$\begin{aligned} \max _{\varvec{\Theta }}\sum _{i=1}^n||\varvec{\Theta }^T \mathbf {x}_i||_2^2=tr(\varvec{\Theta }^T \varvec{\Sigma } \varvec{\Theta }),\quad \mathrm {s.t.}\ \ \varvec{\Theta }^T \varvec{\Theta }=I, \end{aligned}$$

(2)

where $\varvec{\Theta }\in \mathfrak {R}^{d\times c}$ is the projection matrix, and $\varvec{\Sigma }=\mathbf {X}\mathbf {X}^T$ is the covariance matrix of the samples. The optimal solution $\varvec{\Theta }$ consists of the eigenvectors corresponding to the first c largest eigenvalues of the covariance matrix $\varvec{\Sigma }$.

2.3 LPP

Unlike PCA, LPP is a local graph embedding-based method which aims to find a low-dimensional space retaining the local structure of the original data. The objective function is defined as follows:

$$\begin{aligned} \min _\mathbf {P}\sum _{ij}||\mathbf {P}^T\mathbf {x}_i -\mathbf {P}^T\mathbf {x}_j||_{2}^2 w_{ij}, \end{aligned}$$

(3)

where $\mathbf {P}\in \mathfrak {R}^{d\times c}$ is the projection matrix, and $w_{ij}$ is an entry of $\mathbf {W} \in \mathfrak {R}^{n\times n}$ that describes the similarity between $\mathbf {x}_i$ and $\mathbf {x}_j$, defined as:

$$\begin{aligned} w_{ij}={\left\{ \begin{array}{ll} { exp}(-||\mathbf {x}_i-\mathbf {x}_j||^2/t), &{} \text {if nodes}\ i\ \text {and}\ j\ \text {are adjacent}, \\ 0, &{}\text {otherwise}. \end{array}\right. } \end{aligned}$$

(4)

With the constraint of $\mathbf {P}^T\mathbf {X} \mathbf {D} \mathbf {X}^T \mathbf {P}=\mathbf {I}_{c}$, where $\mathbf {I}_{c}$ is a $c\times c$ identity matrix, the objective function (3) can be written as:

$$\begin{aligned} \min _{\mathbf {P}} tr(\mathbf {P}^T\mathbf {X} \mathbf {L} \mathbf {X}^T \mathbf {P}), \quad \mathrm {s.t.} \ \ \mathbf {P}^T\mathbf {X} \mathbf {D} \mathbf {X}^T \mathbf {P}=\mathbf {I}_{c} \end{aligned}$$

(5)

where $\mathbf {D} \in \mathfrak {R}^{n\times n}$ is a diagonal matrix with $\mathbf {D}_{ii}=\varvec{\Sigma }_j w_{ij}$, and $\mathbf {L}=\mathbf {D}-\mathbf {W}$ is the graph Laplacian matrix. The objective function (5) can be converted to the following eigenvalue problem:

$$\begin{aligned} \mathbf {X} \mathbf {L} \mathbf {X}^T\mathbf {P}= \mathbf {X} \mathbf {D} \mathbf {X}^T\mathbf {P} \mathbf { E}, \end{aligned}$$

(6)

where $\mathbf {E}$ is the eigenvalue matrix. LPP could keep the neighboring high-dimensional samples adjacent to each other in the low-dimensional space.

2.4 NPE

NPE is a linear approximation extension of LLE. Unlike LPP, NPE finds a low-dimensional embedding by minimizing the local reconstruction error between the samples and their neighbors [30]. The calculation process of the weight matrix $\mathbf {W}$ in NPE is similar to that of LLE, which is defined as:

$$\begin{aligned} \min _{\mathbf {W}}\sum _{i}^n\left\| \mathbf {x}_i-\sum _{j} w_{ij}\mathbf {x}_j\right\| _2^2,\ \ \mathrm {s.t.}\ \ \sum _j w_{ij} = 1, \end{aligned}$$

(7)

where $\mathbf {x}_j$ is one of the k neighbors of $\mathbf {x}_i$, and the KNN algorithm is often used to determine the neighbors of $\mathbf {x}_i$. The objective function of NPE is defined as follows:

$$\begin{aligned} \min _{\mathbf {P}}\sum _{i}^n\left\| \mathbf {P}^T \mathbf {x}_i -\sum _{j}^k w_{ij}\mathbf {P}^T \mathbf {x}_j\right\| _{2}^2, \quad \mathrm {s.t.}\ \quad \mathbf {P}^T \mathbf {X} \mathbf {X}^T\mathbf {P} = \mathbf {I}_{c}, \end{aligned}$$

(8)

where $\mathbf {P}\in \mathfrak {R}^{d\times c}$ is the projection matrix, and $\mathbf {I}_{c}$ is a $c\times c$ identity matrix. The objective function (8) can be written as:

$$\begin{aligned} \min _\mathbf {P}tr(\mathbf {P}^T \mathbf {X} \mathbf {M} \mathbf {X}^T\mathbf {P}), \quad \mathrm {s.t.} \ \quad \mathbf {P}^T \mathbf {X} \mathbf {X}^T \mathbf {P} = \mathbf {I}_{c}, \end{aligned}$$

(9)

where $\mathbf {M}$ is a symmetric matrix and $\mathbf {M}=(\mathbf {I}-\mathbf {W})^T(\mathbf {I}-\mathbf {W})$. The minimization problem (9) can be converted to the following eigenvalue problem:

$$\begin{aligned} \mathbf {X} \mathbf {M} \mathbf {X}^T\mathbf {P}= \mathbf {X} \mathbf {X}^T\mathbf {P} \mathbf {E}, \end{aligned}$$

(10)

where $\mathbf {E}$ is the eigenvalue matrix.

3 The proposed method

In this section, we propose a simple and effective unsupervised graph embedding based method for dimensionality reduction, which can maintain the global and local structural information of the original data in low-dimensional space. We first introduce the motivation of our proposed method. After that we will detailedly describe the proposed method and optimization algorithm. Finally, the convergence analysis is given.

3.1 Motivation

Many graph embedding based subspace learning methods are implemented by finding the low-dimensional embedding that preserves the local structure of the original data. Among these methods, LLE and its extension methods get the low-dimensional manifold embedding by reconstructing the linear relationship between the samples and their neighborhoods in the low-dimensional space. Neighborhood relations in these methods represent the similarity of samples, which can gather together similar samples [38]. Most of these graph embedding based methods can be expressed by [35]:

$$\begin{aligned} \min _{\mathbf {p}_i} \mathbf {p}_i^T\mathbf {X}\mathbf {G} \mathbf {X}^T\mathbf {p}_i, \quad \mathrm {s.t.} \ \quad \mathbf {p}_i^T\mathbf {X} \mathbf {D} \mathbf {X}^T \mathbf {p}_i = 1, \end{aligned}$$

(11)

where $\mathbf {p}_i$ is the column vector of projection matrix $\mathbf {P}=\{\mathbf {p}_1,\mathbf {p}_2,\ldots ,\mathbf {p}_c\}\in \mathfrak {R}^{d\times c}$, $\mathbf {G}\in \mathfrak {R}^{n\times n}$ is an affinity graph which represents the local neighborhood structure of samples, and $\mathbf {D}$ is the discriminate matrix. The difference between these graph embedding based methods lies in the way of the construction of affinity graph $\mathbf {G}$. However, these methods do not take into account the global structure of the original data, the obtained projection matrix $\mathbf {P}$ cannot retain the global structure in the low-dimensional space. When the overall structure of the data is relatively scattered, the local graph embedding based methods may not achieve good performance. Therefore, it is worthwhile to investigate the dimensionality reduction method preserving both the global and local structure of the original data in the low-dimensional space, simultaneously. By constructing a global graph, the global structural information of the original data could be captured. However, it is not easy to construct a suitable global structure graph for dimensionality reduction, and the effectiveness of the constructed graph may not be guaranteed. While some classic linear dimensionality reduction methods, such as PCA, can hold the global structure of the original data, and the effectiveness of these methods has been widely confirmed [39]. Inspired by this, we propose a simple and effective method to preserve the global and local graph structural information of the original data in the low-dimensional space, which avoids the construction of global structure graph and ensures the effectiveness.

3.2 The objective function of GSGNPE

Let $\varvec{\Theta }=\{\theta _1,\theta _2,\ldots ,\theta _c\}\in \mathfrak {R}^{d\times c}$ be the projection matrix of PCA, $\theta _i\in \mathfrak {R}^{d}$ is the column vector of $\varvec{\Theta }$, and $\mathbf {A} \in \mathfrak {R}^{d\times d}$ is an orthogonal square matrix with $\mathbf {A}^T\mathbf {A} = \mathbf {A}\mathbf {A}^T = \mathbf {I}$. Consider the following optimization problem:

$$\begin{aligned} \min _{\mathbf {P},\mathbf {A}}\sum _{i=1}^c\left\| \theta _i -\mathbf {A}^T \mathbf {p}_i \right\| _2^2, \quad \mathrm {s.t.} \quad \mathbf {A}^T\mathbf {A} = \mathbf {I}, \end{aligned}$$

(12)

where $\mathbf {P}=\{\mathbf {p}_1,\mathbf {p}_2,\ldots ,\mathbf {p}_c\}\in \mathfrak {R}^{d\times c}$, $\mathbf {p}_i\in \mathfrak {R}^{d}$ is the column vector of $\mathbf {P}$. When $\mathbf {A}$ is fixed, we have:

$$\begin{aligned} \mathbf {p}_i=(\mathbf {A} \mathbf {A}^T)^{-1} \mathbf {A} \theta _i = \mathbf {A} \theta _i. \end{aligned}$$

(13)

Optimization problem (12) aims to project $\mathbf {p}_i$ into $\theta _i$, which passes the information of $\theta _i$ to $\mathbf {p}_i$. And this conclusion can also be drawn from (13). The projection matrix $\varvec{\Theta }$ obtained by PCA maximizes the overall variance, which also keeps the global Euclidean structure of the original data [37]. Naturally, in the process of dynamically fitting $\theta _i$, $\mathbf {p}_i$ efficiently gains the global Euclidean structural information in $\theta _i$. Inspired by (12), we modify the model of NPE so that it can retain the global and local structural information of the original data in the low-dimensional space. Take the following optimization problem into consideration:

$$\begin{aligned}&\min _{\mathbf {P},\mathbf {A}}\sum _{i}^n\left\| \mathbf {P}^T \mathbf {x}_i -\sum _{j} w_{ij}\mathbf {P}^T \mathbf {x}_j\right\| _F^2 +\alpha \sum _{i=1}^c||\theta _i - \mathbf {A}^T\mathbf {p}_i ||_2^2,\nonumber \\&\quad \mathrm {s.t.}\quad \mathbf {A}^T\mathbf {A} = \mathbf {I}, \end{aligned}$$

(14)

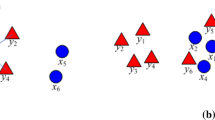
where $\mathbf {P}$ is the projection matrix, $w_{ij}$ is an entry of $\mathbf {W} \in \mathfrak {R}^{n\times n}$ which can be computed by function (7), and $\alpha$ is a regulation parameter to control the trade-off between the global and local structural information. The first term of (14) captures the local structural information of the original data for $\mathbf {P}$ but lacks the global structural information, and the second term of (14) introduces the global Euclidean structural information to $\mathbf {P}$. Finally, the projection matrix $\mathbf {P}$ can obtain the global and local structural information of the original data. Figure 1 illustrates the main idea of the proposed method.

However, the projection matrix $\mathbf {P}$ obtained by (14) is dense and has poor interpretability. To overcome this problem, we employ the $L_{2,1}$-norm penalty. The main reason is that $L_{2,1}$-norm has the property of structured sparsity which helps select the important features of the high-dimensional data. Hence, the $L_{2,1}$-norm penalty can effectively promote the retention of essential structural information and improve the robustness of our model. Finally, the objective function of GSGNPE is defined as follows:

$$\begin{aligned}&\min _{\mathbf {P},\mathbf {A}}\sum _{i}^n\left\| \mathbf {P}^T \mathbf {x}_i - \sum _{j} w_{ij}\mathbf {P}^T \mathbf {x}_j\right\| _F^2\nonumber \\&\quad + \alpha \sum _{i=1}^c||\theta _i - \mathbf {A}^T\mathbf {p}_i ||_2^2 + \lambda ||\mathbf {P}||_{2,1},\quad \mathrm {s.t.} \quad \mathbf {A}^T\mathbf {A} = \mathbf {I}, \end{aligned}$$

(15)

where $\lambda$ is the parameter used to adjust the penalty. Compared with other dimensionality reduction methods [33,34,35,36] that combine the global and local structure graphs, we adopt a simpler and more effective way to combine global and local structural information instead of constructing complex structure graphs. Our method can also avoid the “out-of-sample” problem. A new sample $\tilde{\mathbf {x}}$ can be explicitly mapped to the low-dimensional space through the projection matrix $\mathbf {P}$ to obtain the low-dimensional representation $\mathbf {P}^T\tilde{\mathbf {x}}$, then using the nearest neighbor classifier to determine the nearest neighbor, and finally we can get the label result based on the nearest neighbor’s label. More importantly, the objective function of GSGNPE is concise and easy to optimize.

Fig. 1

The illustration of the idea of GSGNPE

3.3 Optimization

There are two variables $\mathbf {P}$ and $\mathbf {A}$ in the objective function of GSGNPE, which are difficult to solve directly. We adopt an iterative algorithm to obtain $\mathbf {P}$ and $\mathbf {A}$.

• Update $\mathbf {P}$ by keeping $\mathbf {A}$ fixed

When $\mathbf {A}$ is fixed, the loss function (15) can be written as:

$$\begin{aligned}&\min _{\mathbf {P}}\sum _{i}^n\left\| \mathbf {P}^T \mathbf {x}_i - \sum _{j}^k \mathbf {W}_{ij}\mathbf {P}^T \mathbf {x}_j\right\| _F^2 + \alpha ||\varvec{\Theta } - \mathbf {A}^T\mathbf {P} ||_F^2 + \lambda ||\mathbf {P}||_{2,1} \nonumber \\&\quad =\min _{\mathbf {P}}tr(\mathbf {P}^T\mathbf {X}(\mathbf {I} -\mathbf {W})^T(\mathbf {I}-\mathbf {W})\mathbf {X}^T \mathbf {P}) \nonumber \\&\qquad + \alpha ||\varvec{\Theta } - \mathbf {A}^T \mathbf {P}||_F^2 + \lambda ||\mathbf {P}||_{2,1} \nonumber \\&\quad = \min _{\mathbf {P}}tr(\mathbf {P}^T \mathbf {H}\mathbf {P}) +\alpha ||\varvec{\Theta } - \mathbf {A}^T \mathbf {P} ||_F^2 + \lambda ||\mathbf {P}||_{2,1}, \end{aligned}$$

(16)

where $\mathbf {H}=\mathbf {X}(\mathbf {I}-\mathbf {W})^T (\mathbf {I}-\mathbf {W})\mathbf {X}^T$. Take the derivative of (16) with respect to $\mathbf {P}$ and set it to zero, we have:

$$\begin{aligned} (\mathbf {H}+\mathbf {H}^T)\mathbf {P}+\alpha (-2\mathbf {A} \varvec{\Theta }+2\mathbf {A}\mathbf {A}^T\mathbf {P}) +\lambda \mathbf {Q} \mathbf {P}=0, \end{aligned}$$

(17)

where $\mathbf {Q}$ is a diagonal matrix with $\mathbf {Q}_{ii}=\frac{1}{||\mathbf {P}^i||_2}$ and $\mathbf {P}^i$ is the ith row vector of $\mathbf {P}$. Denote $(\mathbf {H}+\mathbf {H}^T)$ by $\mathbf {M}$ and we have:

$$\begin{aligned} \mathbf {P}=2\alpha (\mathbf {M}+2\alpha \mathbf {A}\mathbf {A}^T +\lambda \mathbf {Q})^{-1} \mathbf {A}\varvec{\Theta } \end{aligned}$$

(18)

• Update $\mathbf {A}$ by keeping $\mathbf {P}$ fixed

The objective function (15) can be written as:

$$\begin{aligned} \min _{\mathbf {A}}\sum _{i=1}^c||\theta _i - \mathbf {A}^T \mathbf {p}_i ||_2^2=\min _{\mathbf {A}}||\varvec{\Theta }^T -\mathbf {P}^T \mathbf {A} ||_F^2, \quad \mathrm {s.t.} \quad \mathbf {A}^T\mathbf {A} = \mathbf {I}. \end{aligned}$$

(19)

If $\mathbf {A}$ is an orthogonal square matrix with $\mathbf {A}^T\mathbf {A} = \mathbf {A}\mathbf {A}^T = \mathbf {I}$, the above equation can be converted to:

$$\begin{aligned}&\min _{\mathbf {A}}||\varvec{\Theta }^T - \mathbf {P}^T \mathbf {A} ||_F^2 \nonumber \\&\quad = \min _{\mathbf {A}} tr(\varvec{\Theta }^T\varvec{\Theta } - 2\mathbf {A}^T\mathbf {P}\varvec{\Theta }^T + \mathbf {P}^T \mathbf {A}\mathbf {A}^T\mathbf {P}^T) \nonumber \\&\quad = \min _{\mathbf {A}} ||\varvec{\Theta }^T||_F^2 +||\mathbf {P}^T \mathbf {A}||_F^2 -2tr(\mathbf {A}^T\mathbf {P}\varvec{\Theta }^T) \nonumber \\&\quad = \min _{\mathbf {A}} ||\varvec{\Theta }^T||_F^2 + ||\mathbf {P}^T||_F^2 - 2tr(\mathbf {A}^T\mathbf {P}\varvec{\Theta }^T). \end{aligned}$$

(20)

Thus, (19) is equivalent to the following problem:

$$\begin{aligned} \max _{\mathbf {A}^T\mathbf {A} = \mathbf {I}}tr(\mathbf {A}^T \mathbf {P}\varvec{\Theta }^T). \end{aligned}$$

(21)

Therefore, (19) can be converted into an orthogonal Procrustes problem, by using the conclusion in [40], we perform the singular value decomposition of $\mathbf {P} \varvec{\Theta }^T$, that is, $\mathbf {P} \varvec{\Theta }^T=\mathbf {U} \varvec{\Lambda } \mathbf {V}^T$. Then we have:

$$\begin{aligned} \mathbf {A}=\mathbf {UV}^T. \end{aligned}$$

(22)

The detailed optimization procedure of GSGNPE is shown in Table 1.

Table 1 The optimization procedure of GSGNPE

3.4 Convergence analysis

In this section we will give the convergence analysis of the iterative algorithm in Table 1. Formally, the $L_{2,1}$ norm of the projection matrix $\mathbf {P}$ can be rewritten as:

$$\begin{aligned} ||\mathbf {P}||_{2,1}=2tr(\mathbf {P}^T \mathbf {S} \mathbf {P}), \end{aligned}$$

(23)

where $\mathbf {S}$ is a diagonal matrix and the ith diagonal element is denoted as:

$$\begin{aligned} \mathbf {S}_{ii}=\frac{1}{2||\mathbf {p}^i||_2}, \end{aligned}$$

(24)

where $\mathbf {p}^i$ is the ith row vector of matrix $\mathbf {P}$. The objective function of GSGNPE can be rewritten as

$$\begin{aligned} \min _{\mathbf {P,A}}tr(\mathbf {P}^T\mathbf {HP})+\alpha || \varvec{\Theta } - \mathbf {A}^T \mathbf {P} ||_F^2 +\lambda ^{'} tr(\mathbf {P}^T \mathbf {S P}), \quad \mathrm {s.t.} \quad \mathbf {A}^T \mathbf {A} = \mathbf {I}, \end{aligned}$$

(25)

where $\lambda ^{'}=2\lambda$. In order to prove the convergence of the iterative algorithm, we use the following Lemma.

Lemma 1

[41] For any nonzero vector a and b, the following inequality holds:

$$\begin{aligned} ||a||_2-\frac{||a||_{2}^2}{2||b||_2}\le ||b||_2 -\frac{||b||_{2}^2}{2||b||_2}. \end{aligned}$$

(26)

Let $\mathbf {P}_{k+1}$ and $\mathbf {P}_{k}$ denote the projection matrices in the $(k+1)$th and kth iteration, respectively. By using Lemma 1, we can get the following inequality:

$$\begin{aligned} ||\mathbf {p}_{k+1}^i||_2-\frac{||\mathbf {p}_{k+1}^i ||_{2}^2}{2||\mathbf {p}_{k}^i||_2}\le || \mathbf {p}_{k}^i||_2-\frac{||\mathbf {p}_{k}^i ||_{2}^2}{2||\mathbf {p}_{k}^i||_2}, \end{aligned}$$

(27)

where $\mathbf {p}_{k+1}^i$ and $\mathbf {p}_{k}^i$ are the ith row vectors of $\mathbf {P}_{k+1}$ and $\mathbf {P}_{k}$, respectively.

Proposition 1

The iterative algorithm in Table 1 decreases the value of the objective function of GSGNPE in each iteration.

Proof

For simplicity, we denote the value of the objective function in the kth iteration as $J(\mathbf {P}_k,\mathbf {S}_k,\mathbf {A}_k)$. Now suppose that $\mathbf {P}_k$, $\mathbf {S}_k$, and $\mathbf {A}_k$ are given. Since $\mathbf {P}_{k+1}$ is updated by (18), the following inequality holds:

$$\begin{aligned} J(\mathbf {P}_{k+1},\mathbf {S}_k,\mathbf {A}_k)\le J(\mathbf {P}_{k}, \mathbf {S}_k,\mathbf {A}_k), \end{aligned}$$

(28)

According to (25), we can rewrite (28) as:

$$\begin{aligned}&tr(\mathbf {P}_{k+1}^T \mathbf {H} \mathbf {P}_{k+1}) +\alpha ||\varvec{\Theta } - \mathbf {A}_{k}^T \mathbf {P}_{k+1} ||_F^2 + \lambda ^{'} tr(\mathbf {P}_{k+1}^T \mathbf {S}_{k} \mathbf {P}_{k+1}) \nonumber \\&\quad \le tr(\mathbf {P}_{k}^T \mathbf {H} \mathbf {P}_{k}) +\alpha ||\varvec{\Theta } - \mathbf {A}_{k}^T \mathbf {P}_{k} ||_F^2 + \lambda ^{'} tr(\mathbf {P}_{k}^T \mathbf {S}_{k} \mathbf {P}_{k}). \end{aligned}$$

(29)

Based on the definition of $L_{2,1}$-norm, we can get the following inequality:

$$\begin{aligned}&tr(\mathbf {P}_{k+1}^T \mathbf {H} \mathbf {P}_{k+1}) +\alpha ||\varvec{\Theta } - \mathbf {A}_{k}^T \mathbf {P}_{k+1} ||_F^2 + \lambda ^{'} \sum _{i=1}^d \frac{||\mathbf {p}_{k+1}^i||_{2}^2}{2||\mathbf {p}_{k}^i||_2}\nonumber \\&\quad \le tr(\mathbf {P}_{k}^T \mathbf {H} \mathbf {P}_{k}) +\alpha ||\varvec{\Theta } - \mathbf {A}_{k}^T \mathbf {P}_{k} ||_F^2 + \lambda ^{'} \sum _{i=1}^d \frac{||\mathbf {p}_{k}^i||_{2}^2}{2||\mathbf {p}_{k}^i||_2} \end{aligned}$$

(30)

The above inequality can be further transformed into the following inequality:

$$\begin{aligned}&tr(\mathbf {P}_{k+1}^T \mathbf {H} \mathbf {P}_{k+1}) +\alpha ||\varvec{\Theta } - \mathbf {A}_{k}^T \mathbf {P}_{k+1} ||_F^2 \nonumber \\&\qquad +\lambda ^{'} \sum _{i=1}^d|| \mathbf {p}_{k+1}^i||_2 -\left( \lambda ^{'} \sum _{i=1}^d|| \mathbf {p}_{k+1}^i||_2 - \lambda ^{'} \sum _{i=1}^d \frac{||\mathbf {p}_{k+1}^i||_{2}^2}{2||\mathbf {p}_{k}^i||_2}\right) \nonumber \\&\quad \le tr(\mathbf {P}_{k}^T \mathbf {H} \mathbf {P}_{k}) +\alpha ||\varvec{\Theta } - \mathbf {A}_{k}^T \mathbf {P}_{k} ||_F^2\nonumber \\&\qquad + \lambda ^{'} \sum _{i=1}^d||\mathbf {p}_{k}^i||_2 -\left( \lambda ^{'} \sum _{i=1}^d||\mathbf {p}_{k}^i||_2 - \lambda ^{'} \sum _{i=1}^d \frac{||\mathbf {p}_{k}^i||_{2}^2}{2||\mathbf {p}_{k}^i||_2}\right) . \end{aligned}$$

(31)

It is equivalent to the following inequality:

$$\begin{aligned}&tr(\mathbf {P}_{k+1}^T \mathbf {H} \mathbf {P}_{k+1}) +\alpha ||\varvec{\Theta } - \mathbf {A}_{k}^T \mathbf {P}_{k+1} ||_F^2 +\lambda ^{'} \sum _{i=1}^d|| \mathbf {p}_{k+1}^i||_2 \nonumber \\&\quad \le tr(\mathbf {P}_{k}^T \mathbf {H} \mathbf {P}_{k}) +\alpha ||\varvec{\Theta } - \mathbf {A}_{k}^T \mathbf {P}_{k} ||_F^2 + \lambda ^{'} \sum _{i=1}^d|| \mathbf {p}_{k}^i||_2 \nonumber \\&\qquad -\left( \left( \lambda ^{'} \sum _{i=1}^d||\mathbf {p}_{k}^i||_2 -\lambda ^{'} \sum _{i=1}^d\frac{||\mathbf {p}_{k}^i||_{2}^2}{2||\mathbf {p}_{k}^i||_2}\right) \right. \nonumber \\&\qquad \left. -\left( \lambda ^{'} \sum _{i=1}^d|| \mathbf {p}_{k+1}^i||_2 - \lambda ^{'} \sum _{i=1}^d \frac{||\mathbf {p}_{k+1}^i||_{2}^2}{2||\mathbf {p}_{k}^i||_2}\right) \right) . \end{aligned}$$

(32)

By using (27), the following inequality holds:

$$\begin{aligned}&tr(\mathbf {P}_{k+1}^T \mathbf {H} \mathbf {P}_{k+1}) +\alpha ||\varvec{\Theta } - \mathbf {A}_{k}^T \mathbf {P}_{k+1} ||_F^2 +\lambda ^{'} \sum _{i=1}^d|| \mathbf {p}_{k+1}^i||_2 \nonumber \\&\quad \le tr(\mathbf {P}_{k}^T \mathbf {H} \mathbf {P}_{k}) +\alpha ||\varvec{\Theta } - \mathbf {A}_{k}^T \mathbf {P}_{k} ||_F^2 + \lambda ^{'} \sum _{i=1}^d|| \mathbf {p}_{k}^i||_2. \end{aligned}$$

(33)

According to the definition of $L_{2,1}$-norm and (23), we have the following inequality:

$$\begin{aligned}&tr(\mathbf {P}_{k+1}^T \mathbf {H} \mathbf {P}_{k+1}) +\alpha ||\varvec{\Theta } - \mathbf {A}_{k}^T \mathbf {P}_{k+1} ||_F^2 +\lambda ^{'} tr(\mathbf {P}_{k+1}^T \mathbf {S}_{k+1} \mathbf {P}_{k+1}) \nonumber \\&\quad \le tr(\mathbf {P}_{k}^T \mathbf {H} \mathbf {P}_{k}) +\alpha ||\varvec{\Theta } - \mathbf {A}_{k}^T \mathbf {P}_{k} ||_F^2 + \lambda ^{'} tr(\mathbf {P}_{k}^T \mathbf {S}_{k} \mathbf {P}_{k}). \end{aligned}$$

(34)

The above inequality is equivalent to

$$\begin{aligned} J(\mathbf {P}_{k+1},\mathbf {S}_{k+1},\mathbf {A}_k) \le J(\mathbf {P}_{k},\mathbf {S}_k,\mathbf {A}_k). \end{aligned}$$

(35)

Since the optimization of $\mathbf {A}_k$ is an orthogonal Procrustes problem, the following inequality holds:

$$\begin{aligned} J(\mathbf {P}_{k+1},\mathbf {S}_{k+1},\mathbf {A}_{k+1}) \le J(\mathbf {P}_{k},\mathbf {S}_k,\mathbf {A}_k). \end{aligned}$$

(36)

$\square$

Proposition 1 shows that the objective function of GSGNPE monotonically decreases in each iteration, and the convergence of our proposed algorithm is thus guaranteed.

4 Experiments

In this section, to demonstrate the effectiveness of our proposed method, GSGNPE is compared with the state-of-the-art methods including PCA, LPP, NPE, UDFS [42], RDR [43], LRPPGRR [44], SOGFS [45], and GLSRGE [35]. The comparison experiments are conducted on ten well-known data sets that are FERET [46], AR [47], CMU PIE [48], extended YaleB [49], The PolyU FKP,¹ binary,² and four real benchmark data sets of UCI.³ For all experiments, we use MATLAB R2020a to run the codes on the machine with an Intel(R) Core(TM)i5-6500 CPU 3.20 GHz and 16 GB RAM.

4.1 Data sets

Table 2 The divisions of all databases

FERET data set contains 13,539 face images of 1565 individuals, and there is only one individual in each image. Each individual in the images has different illumination, facial expressions, and face orientations. We select a subset from FERET data set, which contains 1400 images of 200 individuals, and each individual has 7 images. All images in the subset are resized to $40\times 40$ pixels.

AR data set consists of 4000 face images of 126 individuals. We selected a subset of 2400 images of 120 individuals from the original data set. The images in selected subset are under different illumination, facial expressions and occlusions. These images are resized to $50\times 40$ pixels.

CMU PIE data set contains 41,368 face images consisting of 68 individuals under different lighting conditions and facial expressions. Our experiments usea selected subset contains 1632 images of 68 individuals, and each individual has 24 images. All images used in our experiments are resized to $32\times 32$ pixels.

Extended YaleB data set used in the experiment contains 2414 frontal cropped facial images of 38 individuals under different illumination and facial expressions. All images of the data set are resized to $32\times 32$ pixels.

The PolyU FKP contains 7920 pictures of fingers of 165 volunteers (125 males and 40 females). We select a subset from PolyU FKP data set, which contains 1980 images of 165 individuals, and each individual has 12 images. All PolyU FKP images used in our experiments are resized to $28\times 55$ pixels.

Binary alpha character data set contains 1404 handwriting images of 26 letters (A–Z) and 10 numbers (0–9). Each subject has 39 images with different handwriting. All images in our experiments are resized to $46\times 46$ pixels.

Four real benchmark data sets of UCI including synthetic control chart time series (SCCTS), image segmentation (IS), a subset of ISOLET (Isolet), and dermatology data sets. The detailed information of the data sets is described in Table 2.

Figure 2 shows some images from the data sets used in the experiments. Note that we added the occlusion blocks with different sizes to the four face data sets.

Fig. 2

Some images from the selected data sets. a FERET (from top to bottom, occlusion block size: $0\times 0$, $5\times 5$, $10\times 10$, $15\times 15$, $20\times 20$), b AR (from top to bottom, occlusion block size: $0\times 0$, $5\times 5$, $10\times 10$, $15\times 15$, $20\times 20$), c PIE (from top to bottom, occlusion block size: $0\times 0$, $5\times 5$, $10\times 10$, $15\times 15$, $20\times 20$), d extended YaleB (from top to bottom, occlusion block size: $0\times 0$, $5\times 5$, $10\times 10$, $15\times 15$), e FKP, f binary

4.2 Experimental settings

Table 3 Best recognition accuracy (%), standard deviation, and dimensions of the comparison methods on FERET

Table 4 Best recognition accuracy (%), standard deviation, and dimensions of the selected methods on AR

All data sets used in the experiments are divided into two parts: training set and test set. For each data set, we randomly selected l images from each class to form the training sets, and the rest r images in each class form the test sets. The detailed settings of all data sets are shown in Table 2. To verify the robustness of GSGNPE, we randomly added some black occlusion blocks with different sizes to each image of the four face data sets including FERET, AR, CMU PIE, and extended YaleB, as shown in Fig. 2a–d. In order to reduce the consumption of computing resources and avoid the problem of small samples caused by high dimensional features, PCA is employed to reduce the dimensions of the original data. More specifically, we selected the first 200 principal components for FERET, AR, CMU PIE, extended YaleB, PolyU FKP, and Isolet. For binary, we only picked the first 50 principal components which could retain most of its information. We do not perform dimensionality reduction on SCCTS, IS, and Dermatology data sets because of their low dimensionality. The GSGNPE method uses the function (7) to generate the weight matrix W. In order to maintain the consistency of the experiments, the manifold graph matrix in GLSRGE is also constructed by function (7). GSGNPE uses k-nearest neighbor to construct the adjacent graphs, and the effect of the different values of k on the performance of GSGNPE is given in Sect. 4.6. In our experiments, k is set to the number of samples in each class. On each data set, we conducted 10 independent experiments using the nearest neighbor classifier, and their results are averaged.

Table 5 Best classification accuracy (%), standard deviation, and dimensions of the selected methods on CMU PIE

Table 6 Best classification accuracy (%), standard deviation, and dimensions of the selected methods on extended YaleB

4.3 Experimental results and analysis

Table 7 Best classification accuracy (%), standard deviation, and dimensions of the selected methods on FKP, binary, and four UCI data sets

Fig. 3

Average classification accuracy on FERET a no occlusion, b 5 $\times$ 5 occlusion block, and c 20 $\times$ 20 occlusion block

Fig. 4

Average classification accuracy on AR a no occlusion, b 5 $\times$ 5 occlusion block, and c 15 $\times$ 15 occlusion block

Table 8 Average classification accuracy (%) and standard deviation among different dimensions of the selected methods on FERET

Table 9 Average classification accuracy (%) and standard deviation among different dimensions of the selected methods on AR

Fig. 5

Average classification accuracy on CMU PIE a 5 $\times$ 5 occlusion block, b 10 $\times$ 10 occlusion block, and c 20 $\times$ 20 occlusion block

Table 10 Average classification accuracy (%) and standard deviation among different dimensions of the selected methods on CMU PIE

Fig. 6

Average classification accuracy on a extended YaleB (5 $\times$ 5 occlusion block), b extended YaleB (10 $\times$ 10 occlusion block), and c FKP

Table 11 Average classification accuracy (%) and standard deviation among different dimensions of the selected methods on extended YaleB

Table 12 Average classification accuracy (%) and standard deviation among different dimensions of the selected methods on FKP, binary and four UCI data sets

We first conducted the experiments on four face data sets including FERET, AR, CMU PIE, and extended YaleB. Tables 3, 4, 5 and 6 give the average classification accuracy, standard deviation, and corresponding dimensions under the occlusion blocks with different sizes in first 100 dimensions. After that, the experiments were performed on 6 non-face data sets including PolyU FKP, binary, and four UCI data sets, and the results are reported in Table 7. We performed the selected methods on different number of dimensions and repeated the independent experiment 10 times, and the average value of these 10 experiment results was used as the verification result with respect to each dimension. The highest average result of different dimensions in 10 independent repeated experiments was selected as the final evaluation result. The average classification accuracy reported in Tables 3, 4, 5, 6 and 7 is the highest average result over different dimensions. All data sets will be reduced to different dimensions by selected methods. Specifically, the dimensions of four face data sets, FKP and ISO are reduced to 100 dimensions, and the dimension of binary is reduced to 50. Due to the low dimension, SCCTC, IS and Dermatology are respectively projected into the new spaces whose dimensions are the same as the original dimensions. In order to further explore the overall performance of GSGNPE among different dimensions, Tables 8, 9, 10, 11 and 12 report the average performance of all selected methods among different reduced dimensions. The best results among the selected methods are boldfaced in each table. Note that all standard deviations in the tables are calculated for ten classification accuracy under the dimensions corresponding to best average classification accuracy. The standard deviation in Table 3 is relatively large, the possible cause comes from the fact that each class of FERET has a small number of samples but with different characteristics. Each randomly divided training set has different characteristics of samples, hence the standard deviation for the classification accuracy of 10 repeated experiments is relatively large. Figures 3, 4, 5, 6 and 7 show the performance of different methods in different dimensions. Based on the above experimental results, we can draw the following conclusions.

First, in the case of no occlusion, our method achieves the best results on face and non-face data sets, and could obtain stable performance in the subspace with higher dimensions. The potential reason is that preserving the global and local structure of the original data in the low-dimensional space is necessary for dimensionality reduction. The way of combining global and local structure in GSGNPE is more efficient than that in the selected comparison methods.

Second, as the size of occlusion blocks increases, the classification accuracy of all methods decreases gradually, GSGNPE still performs better than comparison methods. GSGNPE integrates global information and $L_{2,1}$-norm, which could alleviate the impact of occlusion blocks.

Third, compared with GSGNPE, GLSRGE has the next-best performance on the four face data sets under the occlusion blocks with different sizes, yet it cannot maintain the stable performances in higher dimensions. The possible explanation is that the information of the global structure retained by GSGNPE is more effective than that of GLSRGE, yet the latter constructs a complex global structure graph. In addition, the structured sparsity of $L_{21}$-norm makes GSGNPE more robust than GLSRGE under the occlusion situations, and also reduces the impact of irrelevant features on retaining global structural information of the original data.

Fourth, the average performance of GSGNPE among different dimensions on all face data sets and most non-face data sets is still better than selected methods. Although the average performance obtained by GSGNPE on AR (with 10 $\times$ 10 and 15 $\times$ 15 occlusion blocks), SCCTS, and IS are not the best, the corresponding results are still competitive, which are almost the second best on these data sets. The overall performance of GSGNPE among different dimensions is better than the selected methods, which further shows the superiority and effectiveness of GSGNPE in keeping the global and local structures in the low-dimensional space.

From the above experimental results, we can conclude that GSGNPE performs better than the comparison methods on both face and non-face data sets. Although GSGNPE retains both global and local structural information in a simple way, it is very efficient. Compared to other selected methods, GSGNPE shows better robustness in the case of occlusion blocks with different sizes and yields better performance under different numbers of dimensions.

To validate the convergence of the proposed iterative algorithm, we recorded the values of the objective function of GSGNPE during the training iterations on three data sets including PIE(with 20 $\times$ 20 occlusion block), SCCTS, and IS. Figure 8 shows the trends of the values of the objective function on three data sets, which indicates that GSGNPE can converge quickly within 10 iterations and verifies our previous conclusion in Proposition 1.

4.4 Statistical significance test

Based on the experimental results obtained, statistical significance tests are conducted for GSGNPE against the comparison methods. We first calculate the average rank of the classification accuracy of each method on the unoccluded and occluded data sets, and then Friedman tests [50] followed by Nemenyi tests [51] are employed. The statistic value $F_F$ in Friedman tests is obtained by the following equation:

$$\begin{aligned} F_F=\frac{(N-1)\tau _{\chi ^2}}{N(K-1)-\tau _{\chi ^2}}, \end{aligned}$$

(37)

where N and K are the numbers of data sets and methods, respectively, and $\tau _{\chi ^2}$ is defined as:

$$\begin{aligned} \tau _{\chi ^2}=\frac{12N}{K(K+1)}\left( \sum _{i=1}^{K} r_i^2 -\frac{K(K+1)^2}{4}\right) , \end{aligned}$$

(38)

where $r_i$ is the average rank of the classification accuracy of the ith method on N data sets. Generally Nemenyi test is adopted to post-hoc tests for Friedman tests. The critical value of Nemenyi test is defined as:

$$\begin{aligned} Nv=q_{\alpha }\sqrt{\frac{K(K+1)}{6N}}, \end{aligned}$$

(39)

where $q_{\alpha }$ is the critical value of the Turkey distribution. There are 15 occluded data sets with different sizes of occlusion blocks and 10 unoccluded data sets. The number of comparison methods in our experiment is 9. We respectively calculate the $F_F$ values on the unoccluded and occluded data sets, which are 5.54 and 20.37. The critical values of F(10, 9) and F(15, 9) in Friedman test for the significance level $\alpha =0.05$ are 2.07 and 2.02, which are smaller than 5.54 and 20.37, respectively. This means that the performance differences between these methods are statistically significant. The critical value of the Turkey distribution $q_{\alpha }=3.10$ when the significance level $\alpha =0.05$ and $K=9$. Then we can obtain the critical values of Nemenyi tests for the unoccluded and occluded data sets, which are 3.80 and 3.10, respectively.

Fig. 7

Average classification accuracy on a IS, b isolet, and c dermatology

Fig. 8

The trend of the value of the objective function with the different numbers of iterations on a PIE (with 20 $\times$ 20 occlusion block), b SCCTS and c IS

The average rank value of all methods and the critical values of Nemenyi tests are reported in Table 13. Figure 9 is drawn according to Table 13 to show the significant differences between all compared methods. As shown in Fig. 9a, on the unoccluded data sets, there are statistically significant between GSGNPE and the selected methods LRPPGRR, UDFS, NPE, and LPP. However, there is no statistically significant between GSGNPE and the selected methods GLSRGE, SOGFS, RDR, and PCA. When there are occlusion blocks in the data sets, as shown in Fig. 9b, there are statistically significant between GSGNPE and the selected methods LRPPGRR, SOGFS, RDR, NPE, LPP, and PCA, yet, not between GSGNPE and the methods GLSRGE and UDFS. A possible explanation is that the comparison methods in our experiment can retain the structure information when there is no occlusion blocks in data sets, hence they have the similar performance on some cases, resulting in the overlap between their line segments in Friedman test. Nevertheless, compared with other comparison methods, GSGNPE can effectively preserve the structure information of the data sets with occlusion blocks, which makes it have better performance.

4.5 Image visualization

Table 13 The average order value and Nv on unoccluded and occluded data sets

Fig. 9

The significant differences between all compared methods on a unoccluded data sets and b occluded data sets

Fig. 10

The t-SNE visualization of distributions of samples. a The original samples in CMU PIE, b the projected samples by SOGFS in CMU PIE, c the projected samples by GSGNPE in CMU PIE, d the original samples in extended YaleB, e the projected samples by SOGFS in extended YaleB, and f the projected samples by GSGNPE in extended YaleB

Fig. 11

Classification accuracy with different parameters $\alpha$ and $\lambda$ on a AR (no occlusion block), b AR (with 5 $\times$ 5 occlusion block), c AR (with 10 $\times$ 10 occlusion block), and d FKP

Fig. 12

Classification accuracy with different numbers of neighbors k on a FERET, b FKP, and c dermatology

Table 14 Ablation experiments classification accuracy (%), standard deviation, and dimensions

To further explore the ability of GSGNPE to preserve the global and local graph structure information of the original data, we use t-SNE [52] to visualize the distribution of CMU PIE and extended YaleB. SOGFS is a graph embedding based method and also adopts the $L_{2,1}$-norm. Therefore, We employ SOGFS for comparison to prove the effectiveness of our method. Figure 10 indicates the distribution of CMU PIE and extended YaleB before and after projection. We find that compared with SOGFS, GSGNPE can better gather samples with similarities together, which shows that GSGNPE can well retain the local structure of the original data. Furthermore, GSGNPE better keeps different data clusters away from each other in projection space, which proves the effectiveness of GSGNPE in combining global and local structures.

4.6 Parameter selection

In this section, we investigate the impacts of the parameters related to GSGNPE including the regulation parameter $\alpha$ and $\lambda$, and the number of neighbors k. For all data sets, $\alpha$ and $\lambda$ are selected from $\{10^{-9},10^{-8}, \ldots ,10^8,10^9\}$. Figure 11 shows the classification accuracy with different $\alpha$ and $\lambda$ on AR (no occlusion block), AR (with 5 $\times$ 5 occlusion block), AR (with 10 $\times$ 10 occlusion block), and FKP. As shown in Fig. 11a, in the case of face data set with no occlusion block, when the values of $\lambda$ and $\alpha$ are in the range of ${(}10^7,10^8]$ and $[10^{-9},10^7]$ or $[10^{-9},10^7]$ and ${(}10^7,10^8]$, respectively, GSGNPE will perform better. Nevertheless, when there are occlusion blocks on the face data sets, as shown in Fig. 11b and c, $\alpha$ in the range of $[10^7,10^8]$ and $\lambda$ smaller than $\alpha$ will usually enable GSGNPE to have the better performance. Moreover, as shown in Fig. 11d, we find that on FKP, the optimal values of $\lambda$ and $\alpha$ are around $10^7$ and $[10^{-9},10^7{)}$ or ${(}10^{6},10^{-9}]$ and $[10^{6},10^7]$, respectively. Figure 11a–d indicate that the model generally performs better when $\alpha$ is smaller than $\lambda$. However, when the value of $\alpha$ is in the range of $[10^7,10^8]$, $\lambda$ smaller than $\alpha$ usually makes the model perform well. Based on the above analysis, both $\lambda$ and $\alpha$ tend to take the large values to make GSGNPE the better performance.

Figure 12 indicates the classification accuracy with different numbers of k on FERET, FKP, and Dermatology. The values of neighbor k in each data set range from 1 to 1.5 times the sample size in each class. We can find that the effectiveness of GSGNPE is not sensitive to k. The possible reason is that the global structural information in GSGNPE is independent of k, which reduces the influence of k in the process of combining local information.

4.7 Ablation experiments

We conducted ablation experiments on FERET, AR, PIE, YaleB, FKP, and binary, and the results are shown in Table 14. It can be seen from the experimental results that although the local structure preserving module (LSPM) enables the model to retain the local structure of the original data in the low-dimensional space, only LSPM cannot make the model achieve good performance. However, when the global structure information learning module (GSILM) is added to the model, the performance of the model on the experimental data sets has been improved, which indicates that the model can effectively learn the global structure information of the original data from the existing projection matrix and effectively retain the global and local structure in the low-dimensional space. By adding the $L_{2,1}$-norm to the model, the performance of the model on the experimental data sets has been further improved, which shows that the $L_{2,1}$-norm can effectively promote the model to obtain the essential structural information of the data, learn effectively global structure information, and enhance the robustness of the model. In summary, each part of the final model can effectively enhance the performance of the model and promote the model to retain the essential structural information of the original data in the low-dimensional space.

5 Conclusions

In this paper, we propose a novel graph embedding based method called GSGNPE for unsupervised dimensionality reduction, which is simple and effective. In GSGNPE, the global and local structure of the original high-dimensional data can be effectively retained in the low-dimensional space in a novel way. The projection matrix of PCA rather than the complex global structure graph is employed as the global structural information since PCA could keep the global Euclidean structure in low-dimensional space. A concise yet efficient least-square term is adopted to minimizes the difference between rotated projection matrix and the PCA projection matrix, so as to obtain the global structural information. By combining the objective function of NPE, the global and local structure information of original data can be efficiently combined. The $L_{2,1}$-term regularization is introduced into GSGNPE to enhance the robustness and improve the interpretability of the obtained projection matrix. Moreover, an iterative optimization algorithm is developed, which could effectively address the optimization problem of GSGNPE and converge fast. Experimental results on face and non-face data sets demonstrate that GSGNPE outperforms the state-of-the-art graph embedding based methods. In the future, it could be worth to construct different local structure graphs and analyze their effect on the performance of GSGNPE. Also, the extended kernel version of GSGNPE for nonlinear complex data is worthy of further research.