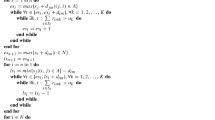Resource-constrained project scheduling problem with uncertain durations and renewable resources

Abstract

Resource-constrained project scheduling problem is to make a schedule for minimization of the makespan subject to precedence and resource constraints. In this paper, we consider an uncertain resource-constrained project scheduling problem (URCPSP) in which the activity durations, with no historical data generally, are estimated by experts. In order to deal with these estimations, an uncertainty-theory-based project scheduling model is proposed. Furthermore, a genetic algorithm integrating a 99-method based uncertain simulation is designed to search the quasi-optimal schedule. Numerical examples are also provided to illustrate the effectiveness of the model and the algorithm.

1 Introduction

The resource-constrained project scheduling problem (RCPSP) has been a widely studied optimization problem since it was initiated. The problem considers the minimization of the makespan while schedules the project subject to precedence and resource constraints [1]. As a job-shop generalization, RCPSP is NP-hard which was proved by Blazewicz et al. [2]. Most literature about RCPSP has based on the deterministic assumption that complete information of resource usage and deterministic activity duration are given in advance in which a feasible baseline schedule, i.e., a list of activity starting times and a definite makespan, can be determined as a result. During project execution, however, this simplification may lead to poor performance since project activities are usually subject to considerable disruptions such as unavailable resources, delayed delivery of materials, absent workers etc. [3]. Stochastic resource-constrained project scheduling problem (SRCPSP) has been developed to deal with the variability in activity durations [4–10]. In these researches, the execution of a project is viewed as a dynamic decision process in which activity durations are represented as random variables. Aiming at the minimization of the expected makespan, different scheduling policies are proposed to schedule the activities with random durations; these policies define which activities to start at each decision point (the start of project and the completion times of activities).

Considering the uniqueness of each project in real world, it is not uncommon that its activities are seldom or even never have been executed before. As a result, the activity durations cannot be depicted by probability distributions for the lack of historical data. In this case, belief degrees given by experienced project managers or experts can be employed to estimate distributions of the durations. Surveys have shown that these human beings’ estimations generally possessed much wider range of values than the real ones [11]. Therefore, these indeterminacies cannot be treated as fuzziness [12, 13], probability [14, 15], roughness [16], ambiguity [17] or entropy [18]. Instead, uncertainty theory, initiated by Liu [19, 20], can be a useful tool to deal with these belief degrees. So far, the new theory has been successfully applied in various problems: option pricing problem [21, 22], production control problem [23], inventory problem [24], assignment problem [25], supply chain pricing problem [26] etc. In project scheduling field, Zhang and Chen [27] built an uncertain model to minimize the expected project makespan under chance constraint of the total cost. Ji and Yao [28] considered an uncertain project scheduling problem to make a schedule for allocating the loans so that the total cost and the completion time of project are balanced. Ding and Zhu [29] considered two types of models for uncertain project scheduling problems to satisfy different management requirements. Based on genetic algorithm, Ke [30] proposed a hybrid approach to solve a project time-cost trade-off problem with uncertain measure, and also further studied this trade-off problem in uncertainty and randomness coexisting environment [23, 31].

However, no research deal with the RCPSP with uncertain durations and renewable resource constraints, this paper will fill the gap and explore this uncertain resource-constrained project scheduling problem. Specially, the activity durations whose distributions are estimated by professional managers or experts are characterized as uncertain variables. Furthermore, an uncertain serial project generation scheme (US-SGS) is introduced to produce a schedule from an activity list. An uncertain simulation based on 99-method is employed to approximate the uncertain functions, since the calculated makespan based on the expected value or medium number of each activity duration is usually less than the real one [6]. Afterwards, we design a GA-based algorithm to search for the quasi-optimal schedule.

The reminder of this paper organized as follows: In Sect. 2, formulations of the URCPSP are detailed. An uncertain expected value model is established and transformed into a crisp form in some special cases in Sect. 3. Furthermore, Sect. 4 proposes a hybrid algorithm integrating 99-method and genetic algorithm. Section 5 presents numerical examples to illustrate the effectiveness of the model and the algorithm. Relevant conclusions and some prospective extensions are discussed in Sect. 6. Specially, some basic concepts in uncertainty theory are introduced in appendix.

2 Problem description

The URCPSP considered in this paper is described as an activity-on-the-node network G(N, A), where N is the set of activities and A is the set of pairs of activities between which a zero-lag finish-start precedence relationship exists. Dummy activities $i =1$ and $i=N+2$ respectively mark the beginning and the end of the project. The duration of each activity $\tilde{d}_{i}$ is assumed to be an uncertain variable whose distribution is given by experts’ or managers’ belief degrees, and the resource requirement of resource k is indicated by $r_{ik}$. For renewable resource k, the availability $R_{k}$ is a constant, which is constrained throughout the project. Each activity is executed in exclusive one mode and preemption is not allowed in this paper.

The execution of a project in uncertain context can be regarded as a dynamic decision process. At each decision time (the start of the project and the completion times of activities), the manager makes decisions about which activities to start subject to the precedences and resource constraints. Therefore, the solution of URCPSP is an activity order list which depicts the priority of each activity. Due to the uncertainty, the actual activity duration can only be attained after its entire processes completed, and meanwhile, the decision maker can merely apply partial information which is available before or at the time he makes the decision. So the schedule generation scheme (SGS) used in deterministic condition may not always be feasible. In this paper, we develop a new procedure denoted as US-SGS to decode the activity list $\lambda$, which works as the Serial SGS, but adds the side constraint

$$\begin{aligned}&s_{i}(\lambda )\le \max \limits _{\lambda ^{j}<\lambda ^{i}} \Big (s_{j}(\lambda ) \Big ) \end{aligned}$$

(1)

where $\lambda ^{i}$ is the position of activity i in activity list $\lambda$ and $s_{i}$ is the starting time of activity i.

The US-SGS works as follows:

0: Given a network G(N, A). $\lambda$:= activity list; $\lambda _{i}$:=activity in position i; ${\varvec{d}}$:= duration; A:= underway activity set; U:= unexecuted activity set; S:= starting time; F:= finish time; T:= Time point; num: number of the activities; K:=the number of renewable resources; $r_{ik}$: demand of activity i for resource type k; $R_{k}$:= available amount of resource i.

1: $A=\varnothing , \ U=[1,2,\ldots ,num], \ F=[inf, inf,\ldots ,inf],\ S=[0, 0,\ldots ,0]$

2: $im=1$, $T=0$

3:    While is empty $(U)=0$

4:       $S_{\lambda _{im}}=\max \limits _{i<im} S_{\lambda _{i}}\vee \max \limits _{(j,\lambda _{im})\in A}F_{j}$

5:          if $\sum \limits _{i\in A}(r_{ik})+r_{imk}\le R_{k},\ k=1,2\ldots \,K \&\,S_{\lambda _{im}}\le T$

6:             $F(\lambda _{im})=T+d(\lambda _{im})$

7:             Put $\lambda _{im}$ into A

8:             $im=im+1$

9:          else

10:          $T=\min \limits _{i\in A} (F(i))$

11:          Take out i from A and U if: $F(i)_{i\in A}\le T$

12:       end

13:    end

14: Return S and F

3 The expected value model

The URCPSP aims at minimizing the expected total project duration (makespan), equivalent to the start time of activity $N+2$, denoted as $s_{n+2}$, since it is a dummy end. Therefore the makespan $F_{t}$ is:

$$\begin{aligned} F_{t}=s_{n+2} \end{aligned}$$

The mathematical model of the URCPSP can be established as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} \min \ \text {E}[F_{t}] \\ \text {subject\, to}{:}\\ s_{i}+ d_{i}\le s_{j},\ \forall (i,j)\in A\\ \sum \limits _{i\in P_{t}}r_{ik}\le R_{k},\ k=1,2\ldots \,K, \ \ P_{t}=\{i\mid s_{i}\le t < s_{i}+d_{i}\} \end{array}\right. } \end{aligned}$$

In the above model, the objective function is to minimize expected makespan. The first constraint ensures that the earliest start time of activity j is forbidden to be smaller than the finish time of its predecessor activity i. The second constraint guarantees, for each time point t and resource type k, the resource demand should be below the resource limitation. Note that $P_{t}$ represents the set of underway activities at time t, $r_{ik}$ is the demand of activity i for resource type k, and $R_{k}$ is the given available amount of resource k.

Because of the uncertain durations, the finish time of each activity is changeable and the makespan is an uncertain variable as well. Given the activity list $\lambda$, the finish time of each activity can be attained as follows:

$$\begin{aligned} \tilde{f_{i}}(\lambda )=s_{i}+\tilde{d}_{i} \end{aligned}$$

The critical problem is to determine the starting time of activity i. If resource constraint is eliminated, the $s_{i}$, which is an uncertain variable as well, can be computed by

$$\begin{aligned}&s_{i}(\lambda )=\max \limits _{(j,i)\in A} \Big (s_{j}(\lambda )+\widetilde{d_{j}} \Big ) \end{aligned}$$

(2)

where $\lambda$ is an activity list depicting the priority of each activity.

When resource constraint is considered, however, this formula is no longer valid. Since activity may be feasible in terms of precedence relation when all of its predecessors have been finished, while simultaneously infeasible for the lack of resource. In other words, one activity has predecessors in both precedence relation logic and resource logic. Besides, a side constraint is added to decode the activity list. To address this problem, similar with Artigues and Roubellat [32], we define an extended precedence relation set as $G(N, A^{*})$ by adding extra resource flow network into the original activity-on-the-node network G(N, A). The resource flow network exists if there is a resource flow between two activities without precedence relations. Then the starting time of activity i, the function of activity list $\lambda$ and uncertain durations, can be attained by

$$\begin{aligned}&s_{i}(\lambda )=\max \limits _{\lambda ^{j}<\lambda ^{i}} \Big (s_{j}(\lambda ) \Big ) \vee \max \limits _{(j,i)\in A^*} \Big (s_{j}(\lambda )+\widetilde{d_{j}} \Big ). \end{aligned}$$

(3)

where $\lambda ^{i}$ is the position of activity i in activity list $\lambda$.

Given an activity list $\lambda$, one can attain that $s_{i}(\lambda )$is monotone increasing function of $\widetilde{d_{j}}$ where $\lambda ^{j}<\lambda ^{i}$ or $(j,i)\in A^*$. Therefore, referring to Lemma 3, we have

Theorem 1

Suppose that the duration of activity i has regular distribution $\Phi _{i}$ and inverse uncertainty distribution $\Phi ^{-1}_{i}(\alpha )$. Given the activity list $\lambda$, $s_{i}(\lambda )$ has an inverse uncertainty distribution $\Psi _{i}^{-1}(\lambda ,\alpha )$ $\alpha \in (0,1]$, we can get

$$\begin{aligned}\Psi _{i}^{-1}(\lambda ,\alpha )= \max \limits _{\lambda ^{j}<\lambda ^{i}} \Big (\Psi _{j}^{-1}(\lambda ,\alpha ) \Big ) \vee \max \limits _{(j,i)\in A^*} \Big (\Psi _{j}^{-1}(\lambda ,\alpha )+\Phi _{j}^{-1}(\alpha ) \Big )\end{aligned}$$

With Theorem 1, we can attain that the $\alpha$-value of the makespan can be calculated by $\varvec{d} = (\Phi _{d_{1}}^{-1}(\alpha ), \Phi _{d_{2}}^{-1}(\alpha ), \ldots , \Phi _{d_{n+2}}^{-1}(\alpha ))$. Therefore, referring to Lemma 4, we have

Theorem 2

The expected makespan, depicting by the starting time of dummy end activity, can be attained as follows:

$$\begin{aligned} E[F_{t}]= \int _{0}^{1} \Psi _{n+2}^{-1}(\lambda ,\alpha )\mathrm{d}\alpha \end{aligned}$$

The equivalent form of the uncertain model can be transformed as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} \min \quad \int _{0}^{1} \Psi _{n+2}^{-1}(\lambda ,\alpha )\mathrm{d}\alpha \\ \text {subject\, to}{:}\\ s_{i}+ d_{i}\le s_{j},\ \forall (i,j)\in A\\ \sum \limits _{i\in P_{t}}r_{ik}\le R_{k},\ k=1,2\ldots \,K, \ \ P_{t}=\{i\mid s_{i}\le t < s_{i}+d_{i}\} \end{array}\right. } \end{aligned}$$

With the crisp-form of the expected model, 99-method can be applied to make approximation of the expected makespan.

$$\begin{aligned} {\left\{ \begin{array}{ll} \min \ \sum \limits _{m=1}^{99} \Psi _{n+2}^{-1}(\lambda ,m/100)/99 \\ \text {subject\, to}{:}\\ s_{i}+ d_{i}\le s_{j},\ \forall (i,j)\in A\\ \sum \limits _{i\in P_{t}}r_{ik}\le R_{k},\ k=1,2\ldots \,K, \ \ P_{t}=\{i\mid s_{i}\le t < s_{i}+d_{i}\} \end{array}\right. } \end{aligned}$$

4 GA-based algorithms

In RCPSP with uncertain durations, the expected duration or medium number is usually employed to replace the random or uncertain numbers and then the deterministic model is applied. However, the optimal solution attained from the deterministic model may perform very poor in real context. Meanwhile, the expected value of calculated makespan, based on the expected value of each activity duration, is often less than the real one. Stork [6] presented that the expected makespan is more than 4 % larger than the deterministic makespan with instances containing 20 activities. Moreover, coherently, Ballestin [7] revealed that this variation may extend to more than 10 % when the number of activities increases to 120.

Even just for precedence constrained jobs without any resource restrictions, the computation of the expected length of a critical path is NP-complete, if each activity processing time distribution has two (discrete) values. Similar to the researches in stochastic cases, uncertain simulation is essential for approximation of the expected makespan.

In order to solve URCPSP, a heuristic algorithm integrated by 99-method and GA is introduced in this section. The chromosome is denoted by the activity list $\lambda$ in which activities are arranged in different orders on the premise that the precedence relationship is satisfied. Then, with a specific schedule generation scheme, a feasible solution can be gained. Besides, the most essential part of the algorithm is the process of decoding in accordance with different schedule generation schemes, which will be highlighted in this part.

The structure of the hybrid algorithm is as follows:

Step 1: Initialization

The first step is to randomly generate initial population with size Popsize as parent population. Individual creations rely on a list of chromosome representation: an activity order list ($\lambda$) in which activities are arranged randomly on the premise that the precedence relationship is satisfied.

Step 2: Crossover

Crossover is the main operation to produce the new chromosomes, simultaneously expanding the population. In this paper, we implement one point crossover. The crossover points are randomly generated as well as the randomly chosen mother and father chromosomes. Taking the position denoted by crossover point as divide, the left positions inherit exactly the same activity order from the mother. Subsequently, the remaining right positions are filled according to the father by left-to-right scan on the premise that the precedence relationship is satisfied, skipping the activities already taken from the mother.

Step 3: Mutation

Mutation is significant for the purpose of population diversity. For the activity order list, mutation begins with randomly selecting the activity which will be mutated. Mutation applied to the activity order list is built to keep list precedence feasible. It determines the predecessor and successor of the selected activity first, taking their positions as bound, and then randomly chooses and inserts in a position in the range to generate a feasible child chromosome.

Step 4: Decoding

In this step, we employ the US-SGS to decode the activity list $\lambda$ and approximate the fitness of each chromosome by uncertain simulation based on 99-method, initiated by [20] and successfully applied in project scheduling by [27].

The uncertain simulation based on 99-method for $E[F_{t}]$ is presented in Algorithm 1.

Algorithm 1 (Uncertain simulation for $E[F_{t}]$)

1: Given an activity list $\lambda$;

2: Generate $d_{1}^m, d_{2}^m, \ldots , d_{n}^m$ according to the inverse uncertainty distributions of activities’ durations $\Phi _{d_{1}}^{-1}, \Phi _{d_{2}}^{-1}, \ldots , \Phi _{d_{n}}^{-1} ,$ and denote   $\varvec{d^m} = (\Phi _{d_{1}}^{-1}(m/100), \Phi _{d_{2}}^{-1}(m/100), \ldots , \Phi _{d_{n}}^{-1}(m/100))$, $m = 1,2,\ldots ,99$, respectively;

3: Decode the activity list $\lambda$ by using US-GSG for each $\varvec{d^m}$, $m = 1,2,\ldots ,99$. Then the start time $\varvec{s^{m}}$ and finish time $\varvec{f^{m}}$ can be attained;

4: $f_{t}^{m}=s_{n}^{m}$, $m = 1,2,\ldots ,99$;

5: $E[F_{t}]$=$\sum \limits _{m = 1}^{99}f_{t}^{m}/99.$

Step 5: Selection

With the purpose of keeping the population size consistent, new parent population requires to be selected from the combined population. This paper employs the genetic roulette wheel selection, in which individuals with better fitness value are awarded with larger probability to be selected in the roulette wheel. Additionally, the top-5 best-to-now chromosomes are specifically preserved in the population. As a consequence, selection process guarantees the high quality of population, and meanwhile avoids the local optimum.

The framework of the algorithm is presented in Fig. 1.

Fig. 1

Outline of the hybrid GA algorithm

5 Numerical examples

In this section, we consider a project scheduling problem containing 30 activities (J30) and 4 renewable resources. Specially, the durations are estimated by experts and characterized as uncertain variables. Interested readers can consult [11] for more details about how to use experts’ belief degrees to estimate uncertain distributions. Information of the numerical instance including durations, resource utilizations and successor activities is presented in Table 1, and correspondingly, the structure of the project is provided in Fig. 2.

Fig. 2

The activity-on-the-node network of the project

Table 1 The information of the test instances

To minimize the expected makespan, the following model can be applied.

$$\begin{aligned} {\left\{ \begin{array}{ll} \min \ \text {E}[F_{32}] \\ \text {subject\, to}{:}\\ s_{i}+ d_{i}\le s_{j},\ \forall (i,j)\in A\\ \sum \limits _{i\in P_{t}}r_{ik}\le R_{k},\ k=1,2\ldots \,4, \ \ P_{t}=\{i\mid s_{i}\le t < s_{i}+d_{i}\} \end{array}\right. } \end{aligned}$$

The algorithm is coded by MATLAB and runs on a PC with core i3 with 2.3GHz clock speed and 2G RAM. The quasi-optimal schedules attained from experiments are presented in Table 2, resulting from 10 times’ run of the hybrid intelligent algorithm with 1000 cycles for the expected models under different parameter settings.

Table 2 The top 10 quasi-optimal schedules

Similar to [33, 34], the quality of solution can be obtained via the deviation of the worst solution from the optimal solution attained in the 10 times’ run and the results are presented in Table 3. The results reveal that the deviation denoted by percent error does not exceed $5~\%$, which implies the effectiveness of the algorithm integrating uncertain simulations.

Table 3 The effectiveness of the GA

Additionally, some other computational experiments are presented. Our test instances are all come from the benchmark library PSPLIB http://www.om-db.wi.tum.de/psplib/data.html initiated by [35] in which different characteristics of the deterministic RCPSP are presented. Since the uncertain simulation is the time-consuming task, this paper only considers four instances with 30, 60, 90 and 120 activities under 4 renewable resource constraints. The uncertain distributions of the activity processing times are generated by $\fancyscript{Z}(d_{i}-\sqrt{d_{i}},d_{i}, d_{i}+\sqrt{d_{i}})$ with the deterministic $d_{i}$ as expectation. After running each instance 10 times, the results are presented in Table 4. Referring to Table 4, we can find that the deviation denoted by percent error does not exceed $10~\%$.

Table 4 The results of the computational experiments

6 Conclusion

In this paper, an uncertain model was proposed to deal with uncertain resource constrained project scheduling problem (URCPSP), in which the durations, with no historical data generally, were described as uncertain variables. Furthermore, an uncertain serial schedule generation scheme (US-SGS) was introduced to process the activities with uncertain durations. Besides, a GA-based hybrid algorithm integrating uncertain simulation was designed to search the quasi-optimal schedule. Numerical examples were provided to illustrate the effectiveness of model and the algorithm as well.

Meanwhile, there are some limitations in this paper. First of all, this paper involves merely one type of indeterminacy, while the real world project might be complicated that randomness (activity duration estimated by historical data) and uncertainty (activity duration estimated by experts’ experienced data) might co-exist. Future research can extend the RCPSP to twofold indeterminacy and correspondingly uncertain random variable can be applied. Secondly, this paper assumed that each activity was executed with one mode, multi-mode RCPSP in uncertain environment can be taken into consideration in further development.

Appendix

In this section, some concepts and theorems of uncertainty theory are introduced to lay the foundation for the URCPSP modeling. Uncertainty theory is a branch of axiomatic mathematics for subjective uncertainty modeling, which has been well developed and applied in a wide variety of real problems.

Let $\Gamma$ be a nonempty set, $\fancyscript{ L }$ a $\sigma$-algebra over $\Gamma$, and each element $\Lambda$ in $\fancyscript{L}$ is called an event. Uncertain measure is defined as a function from $\fancyscript{L}$ to [0, 1]. In detail, the concept of uncertain measure is pioneered by [19] and redefined by [20]. Uncertain measure $\fancyscript{M}$ is a set function defined over the following four axioms.

Axiom 1

(Normality Axiom) $\fancyscript{M}\{\Gamma \}=1$.

Axiom 2

(Duality Axiom) $\fancyscript{M}\{\Lambda \}+\fancyscript{M}\{\Lambda ^{c}\}=1$ for any event $\Lambda$.

Axiom 3

(Subadditivity Axiom) For every countable sequence of events $\{\Lambda _{i}\}$, we have:

$${\fancyscript{M}}\left\{{\bigcup\limits_{{i = 1}}^{\infty } {\Lambda _{i} }}\right\} \le \sum\limits_{{i = 1}}^{\infty } M \{ \Lambda _{i} \} .$$

Axiom 4

(Product Measure Axiom) Let $(\Gamma _k, \fancyscript{L}_{k}, \fancyscript{M}_{k})$ be uncertainty spaces for $k=1,2,\ldots$, the product uncertain measure $\fancyscript{M}$ is an uncertain measure satisfying

$$\begin{aligned} \fancyscript{M}\left\{ \prod \limits _{k=1}^\infty A_{k}\right\} =\bigwedge _{k=1}^\infty \fancyscript{M}_{k}\{A_{k}\} \end{aligned}$$

where $A_{k}$ are arbitrarily chosen events from $\fancyscript{ L }_{k}$ for $k=1,2,\ldots$, respectively.

Definition 1

[19] An uncertain variable is a measurable function $\xi$ from an uncertainty space $(\Gamma , \fancyscript{ L }, \fancyscript{M})$ to the set of real numbers, i.e., for any Borel set B of real numbers, the set

$$\begin{aligned} \{\xi \in B\}=\{\gamma \in \Gamma \ \big |\ \xi (\gamma )\in B\} \end{aligned}$$

is an event.

The uncertainty distribution is indispensable to establish the practical uncertain optimization problems model.

Definition 2

[19] The uncertainty distribution $\Phi$ of an uncertain variable $\xi$ is defined by

$$\begin{aligned} \Phi (x)=\fancyscript{M}\{\xi \le x\} \end{aligned}$$

for any real number x.

An uncertainty distribution $\Phi$ is confirmed to be regular if its inverse function $\Phi ^{-1}(\alpha )$ exists uniquely for each $\alpha \in [0,1]$.

Definition 3

[19] Let $\xi$ be an uncertain variable. The expected value of $\xi$ is defined by

$$\begin{aligned} E[\xi ]=\int _0^{+\infty }\fancyscript{M}\{\xi \ge r\}\mathrm{d}r-\int _{-\infty }^{0}\fancyscript{M}\{\xi \le r\}\mathrm{d}r \end{aligned}$$

provided that at least one of the above two integrals is finite.

Lemma 1

[20] Let $\xi$ be an uncertain variable with uncertainty distribution $\Phi$. If the expected value exists, then

$$\begin{aligned} E[\xi ]=\int _{0}^{+\infty } (1-\Phi (x))\mathrm{d}x-\int _{-\infty }^{0} \Phi (x)\mathrm{d}x. \end{aligned}$$

Lemma 2

([20]) Let $\xi$ be an uncertain variable with regular uncertainty distribution $\Phi$. If the expected value exists, then

$$\begin{aligned} E[\xi ]=\int _0^1 \Phi ^{-1}(\alpha )d \alpha . \end{aligned}$$

Example 1

The expected value of the zigzag uncertain variable $\xi =\fancyscript{ Z }(a,b,c)$ is:

$$\begin{aligned} E[\xi ]=&\int _{0}^{0.5}((1-2\alpha )a + 2\alpha b)\mathrm {d}\alpha +\int _{0.5}^{1}((2-2\alpha )b + (1-2\alpha ) c)\mathrm{d}\alpha \\ =&\frac{a+2b+c}{4}.\nonumber \end{aligned}$$

(4)

Lemma 3

[20] Let $\xi _{1}, \xi _{2}, \ldots ,\xi _{n}$ be independent uncertain variables with regular uncertainty distributions $\Phi _{1},\Phi _{2},\ldots ,\Phi _{n}$, respectively. A function $f(x_{1},x_{2},\ldots ,x_{n})$ which is strictly increasing with respect to $x_{1},x_{2},\ldots ,x_{m}$ and strictly decreasing with respect to $x_{m+1},x_{m+2},\ldots ,x_{n}$. Then the $\xi =f(\xi _{1},\xi _{2},\ldots , \xi _{n})$ is an uncertain variable with inverse uncertainty distribution

$$\begin{aligned} \Psi ^{-1}(\alpha )= f(\Phi _{1}^{-1}(\alpha ),\ldots ,\Phi _{m}^{-1}(\alpha ),\Phi _{m+1}^{-1}(1-\alpha ),\ldots ,\Phi _{n}^{-1}(1-\alpha )). \end{aligned}$$

(5)

Lemma 4

[36] Let $\xi _{i}(i = 1, 2, . . . , n)$ be independent uncertain variables with regular uncertainty distributions $\Phi _{1},\Phi _{2},\ldots ,\Phi _{n}$ respectively. If a function $f(x_{1},x_{2},\ldots ,x_{n})$ is strictly increasing with respect to $x_{1},x_{2},\ldots ,x_{m}$ and strictly decreasing with respect to $x_{m+1},x_{m+2},\ldots ,x_{n}$ , respectively, then the expected value of uncertain variables $\xi =f(\xi _{1},\xi _{2},\ldots , \xi _{n})$ has an expected value as follows:

$$\begin{aligned} E [\xi ]&=\int _{0}^{1}f(\Phi _{1}^{-1}(\alpha ),\ldots ,\Phi _{m}^{-1}(\alpha ),\Phi _{m+1}^{-1}(1-\alpha ),\Phi _{n}^{-1}(1-\alpha ))\mathrm{d}\alpha \end{aligned}$$

(6)

provided that the expected value $E[\xi ]$ exists.