Introduction

Horizontal wells with massive hydraulic fracturing have been proved as an efficient technology for enhancing fluid recovery from low permeability reservoirs in the USA. Recently, this technology has been utilized aggressively across the world. It is obvious that the transient pressure analysis is a powerful tool to recognize fluid flow characteristics underground, where the conditions are difficult to be predicted. Also, the modeling studies are mainly based on the solution of a three-dimensional diffusivity equation coupled with related definite solution conditions for fluid flow in porous media. The choice of the mathematical method to solve these models usually depends on the complexity of the problems and the constraints of the application. Generally, analytical and semi-analytical methods are two most commonly used methods to obtain the transient pressure response and production performance since the spring up of the percolation mechanism theory. Even for complex structural wells, such as horizontal, slanted, and fractured wells, these methods are still widely applied. On the other hand, numerical methods, such as finite element method (FEM), finite difference method (FDM), and boundary element method (BEM), were invented later and widely applied along with the development of computers, which are more suitable to obtain the pressure response and fluid saturation in heterogeneous porous media with irregular shaped boundary reservoirs (Medeiros 2007).

Many analytical and semi-analytical models have been proposed to analyze the pressure response of wells in oil/gas reservoirs (Gringarten and Ramey 1973; Odeh and Babu 1989; Ozkan and Raghavan 1991; Escobar et al. 2013). Most of these models presented the solution for a regular shaped (such as infinite, circular, or rectangular outer boundary) reservoir or simple composite models. Based on the review of previous studies related to the transient pressure response for MFHW, the Green’s and source function method as well as the integral transformation method are the most popular used techniques for solving the model.

The Green’s and source function method can incorporate all fractures into the mathematical model simultaneously, which could be used to analyze the interface effects between the fractures. In addition, this method can deal with the situation of the fractures distributed along the well with arbitrary space, angle, and length, which is often the case in the field. Therefore, many individuals adopted this method to analyze the pressure response of MFHW in conventional or unconventional reservoirs with infinite, circular, and box-shaped outer boundaries (Guo et al. 1994; Horne and Temeng 1995; Chen and Raghavan 1996; Wan and Aziz 1999, 2002; Zerzar et al. 2004; Medeiros 2007; Xu et al. 2013; Zhao et al. 2013, 2014). In this method, it is always necessary to derive the solution under specified boundary condition, which usually corresponds to a point/linear solution. The detailed discussion for a continuous source function in a circular and rectangular-shaped boundary oil and gas reservoir could be found in Ozkan and Raghavan (1991) and Zhao et al. (2015, 2016), respectively. As the widely application of a fractured horizontal well in a low permeability reservoirs, the fluid flow period in such a reservoir is mainly concentrated on the linear flow period, so scholars have established many linear flow models to describe this main flow period in order to overcome the computational complexity of source functions (Brown 2009; Al-Ahmadi et al. 2010; Bello and Watenbargen 2010; Cai 2014; Ozkan et al. 2011; Nobakht et al. 2012; Stalgorova and Mattar 2012, 2013; Nobakht and Clarkson 2012; Xu et al. 2013).

Although analytical and semi-analytical methods can solve many well models to analyze the transient pressure response of fractured horizontal wells in various reservoirs, it is not difficult to find that most of the papers mentioned above are concentrated on wells located in a regular shape boundary reservoir. For a MFHW, the drainage area not only depends on the well location and well pattern type, but also has an intimate connection with the fracture length and distribution, which would result in the drainage boundary being irregular. For the pressure and production performance of a well in such a reservoir, most analytical and semi-analytical methods are helpless. Even if some of them could treat these problems, the solving process would be very complicated.

Due to the limitations existing in analytical and semi-analytical methods, the use of numerical simulation methods, such as FDM, FEM, and BEM, was introduced into the petroleum engineering. Although the FDM and the FEM could be used to analyze the pressure of a fractured horizontal well in an arbitrary shaped gas reservoir, both of them discrete the full reservoir area into small grids (“domain type” method). On the contrary, the BEM resorts the solution based on the Green’s function in free space called the fundamental solution, which satisfies the governing partial differential equation at a point source without satisfying any of the prescribed boundary condition. Meanwhile, since the total grid number of BEM is much less than FDM and FEM, BEM can efficiently and accurately solves various boundary value problems. Compared to FDM and FEM, BEM has a great advantage in handling problems with complex boundary geometries since there is no interior of the domain under consideration and it is practically free of grid orientation effects (Jongkittinarukorn et al. 1998). A schematic of the grid system for three methods are shown in Fig. 1. The BEM is also superior to the Green’s function method in that it features the flexibility of being applicable to any reservoir boundary condition and to arbitrary shapes in a reservoir (Chen 2003).

Fig. 1
figure 1

Schemes of discretization for various numerical methods

Full size image

In the review of the petroleum literature, many papers were concentrated on the vertical wells or fractured vertical wells in 2D domain flow problems (Kikani and Horne 1989; Sato and Horne 1993; Pecher and Stanislav 1997; Jongkittinarukorn and Tiab 1998; Kryuchkov and Sanger 2004; Yin et al. 2005; Gao et al. 2007; Wang and Zhang 2009). With the BEM, reservoirs with arbitrary shaped boundaries can be easily handled. As for the complex well, such as fractured horizontal well, the related reports are rare. Therefore, in this paper, the transient pressure behaviors of MFHW in arbitrary shape tight gas reservoir were analyzed by the BEM. The solution was developed in the Laplace domain, and the Stehfest’s algorithm was applied to obtain the corresponding solution in real space domain.

Governing differential equations

In order to make the problem more tractable and formulate the problem easily, the following assumptions were made: A single-phase compressible fluid flowed in the homogeneous porous medium, which obeyed Darcy’s law; rock compressibility could be negligible since the deformation amount was limited comparing to gas under the same pressure difference; and the effect of gravity and capillary force was ignored.

According to the seepage mechanism theory, the governing diffusivity equation incorporating the point source terms can be derived from the mass conservation principle and Darcy’s law. For homogeneous and anisotropic porous media, the diffusivity equation for the flow of single-phase compressible fluid is given by:

$$- \nabla \cdot \left( {\rho v} \right) - \rho_{\text{sc}} q_{\text{v}} \delta \left( {R,R^{\prime } } \right) = \frac{{\partial \left( {\rho \phi } \right)}}{\partial t}$$
(1)

where q v is the flow rate per unit volume withdrawn from the point source (m3/s); ϕ is the porosity of the medium, fraction; ρ and ρ sc are the gas density at the reservoir and standard conditions, respectively (kg/m3); R presents an arbitrary point in the field; R′ represents the source point location in the field; and t is the production time, s.

In Eq. (1), ∇··· is the divergence operator, which has the following relationship in Cartesian coordinates:

$$\nabla \cdot = \frac{\partial }{\partial x} + \frac{\partial }{\partial y} + \frac{\partial }{\partial z}$$
(2)

δ() is the Dirac delta function satisfying the following fundamental properties:

$$\delta \left( {R,R^{\prime } } \right) = \left\{ {\begin{array}{ll} {0,} \hfill & {R \ne R^{\prime } } \hfill \\ { + \infty ,} \hfill & {R = R^{\prime } } \hfill \\ \end{array} } \right.$$
(3)

which is also constrained to satisfy the following identity,

$$\int\limits_{\varOmega } {f(R)\delta \left( {R,R^{\prime } } \right)} {\text{d}}\alpha = f(R^{\prime } )$$
(4)

Substituting the equations of Darcy’s law and gas state equation into Eq. (1), the following expressions can be obtained,

$$\nabla \cdot \left( {\frac{{\overline{\overline{{\mathbf{K}}}} }}{\mu }\frac{p}{Z}\nabla p} \right) - \frac{{Tp_{{{\text{sc}}}} }}{{T_{{{\text{sc}}}} }}q_{{\text{v}}} \delta \left( {R,R^{\prime } } \right) = \frac{\partial }{{\partial t}}\left( {\frac{p}{Z}\phi } \right)$$
(5)

where μ is the gas viscosity, Pa s; p is the reservoir pressure, Pa; P sc is the standard pressure, which equals 0.101325 × 106 Pa; and Z is the gas deviation factor, sm3/m3.

In Eq. (5), \({{\overline{\overline{{\mathbf{K}}}} }}\) is the permeability tensor. For three-dimensional gas flow in porous media, the permeability tensor can be expressed as a diagonal tensor, where the diagonal elements present the principle permeability of the anisotropic porous medium.

$${{\overline{\overline{{\mathbf{K}}}} }} = \left[ {\begin{array}{*{20}c} {k_{x} } & 0 & 0 \\ 0 & {k_{y} } & 0 \\ 0 & 0 & {k_{z} } \\ \end{array} } \right]$$
(6)

In reservoir engineering, the following assumption that the reservoir is at uniform pressure p i before production is always established. Therefore, the initial condition can be expressed as:

$$p(R,t) = p_{\text{i}},\quad \text{ }\left( {R \in \varOmega ,\text{ }t = 0} \right)$$
(7)

The unique solution of Eq. (5) combined with Eq. (7) must be ensured by supplying well-posed boundary conditions. For the outer boundary condition, the following three types can be classified.

  1. 1.

    The Dirichlet boundary condition (constant pressure boundary)

    $$\left. p \right|_{{R \in \varGamma ,\text{ }t > 0}} = p_{\text{i}}$$
    (8)
  2. 2.

    The Neumann boundary condition (no-flow outer boundary)

    $$\left. {\frac{\partial p}{\partial n}} \right|_{{R \in \varGamma ,\text{ }t > 0}} = 0$$
    (9)
  3. 3.

    The mixed boundary condition

    $$\left. p \right|_{{R \in \varGamma_{1} ,\text{ }t > 0}} = p_{\text{i}} \quad {\text{and}}\quad \, \left. {\frac{\partial p}{\partial n}} \right|_{{R \in \varGamma_{2} ,\text{ }t > 0}} = 0 \;\left( {\varGamma = \varGamma_{1} + \varGamma_{2} } \right)$$
    (10)

where Γ is the domain boundary; Γ 1 and Γ 2 are the subdomain boundary; n is the outward normal (vector) to the boundary Γ; and p i is the initial pressure of the reservoir (Pa).

Unlike the slightly compressible fluids flowing in the multi-porous media, the gas viscosity, μ, the deviation factor, Z, and the gas compressibility, c g, are strongly dependent on pressure. Therefore, it is not possible to derive closed form expressions directly like that of liquids because the partial differential equation governing the flow of gas is strongly nonlinear. In order to overcome this problem, Al-Hussainy et al. (1966) proposed the concept of real gas pseudo-pressure, which incorporated the gas deviation factor and viscosity to linearize the diffusivity equation for gas flow in porous media. The function of pseudo-pressure is defined as:

$$m\left( p \right) = \int\limits_{{p_{\text{ref}} }}^{p} {\frac{{2p^{\prime } }}{\mu Z}} {\text{d}}p^{\prime }$$
(11)

where p ref is the reference pressure (Pa).

For an anisotropic porous media, Eq. (5) can be transformed into an equivalent isotropic system by using the following coordinate transformation,

$$\overline{\xi } = \xi \sqrt {\frac{k}{{k_{\xi } }}} \quad {\text{for}}\quad \xi = x,y,\text{ }z$$
(12)

In Eq. (12), the permeability, k, corresponds to the equivalent isotropic system permeability and is defined as:

$$k = \sqrt[ 3]{{k_{x} k_{y} k_{z} }}$$
(13)

where k x, k y, and k z are the permeability in the x, y, and z directions, respectively, m2.

Taking the transformation of Eqs. (12)–(5) and then combining Eq. (11) with it, we have

$$\nabla^{2} m - \frac{{2Tp_{\text{sc}} }}{{kT_{\text{sc}} }}q_{\text{v}} \delta \left( {R,R^{\prime } } \right) = \frac{{\phi \mu c_{\text{g}} }}{k}\frac{\partial m}{\partial t}$$
(14)

Similarly, the corresponding initial and boundary conditions can be expressed in the form of pseudo-pressure.

In order to solve the governing equation more conveniently, the dimensionless process for the model is often imposed by introducing the corresponding dimensionless variables. Hence, the following dimensionless variables are defined according to the problems we analyzed:

$$\begin{aligned} & x_{\text{D}} = \frac{x}{{L_{\text{ref}} }},\quad y_{\text{D}} = \frac{y}{{L_{\text{ref}} }},\quad z_{\text{D}} = \frac{z}{{L_{\text{ref}} }},\quad R_{\text{D}} = \sqrt {x_{\text{D}}^{2} + y_{\text{D}}^{2} + z_{\text{D}}^{2} } = \frac{R}{{L_{\text{ref}} }}, \\ & t_{\text{D}} = \frac{kt}{{\phi \mu_{\text{gi}} c_{\text{gi}} L_{\text{ref}}^{2} }},\quad m_{\text{D}} = \frac{{\pi khT_{\text{sc}} }}{{q_{\text{sct}} p_{\text{sc}} T}}\left( {m_{\text{i}} - m} \right) \\ \end{aligned}$$

where L ref is the reference length, m; q sct is the total production rate of the well, m3/s; and m i is the pseudo-pressure under the initial condition, Pa/s.

$$\nabla^{2} m_{\text{D}} + \frac{2\pi }{{q_{\text{sct}} }}L_{\text{ref}}^{2} q_{\text{v}} \delta \left( {R,R^{\prime } } \right) = \frac{{\partial m_{\text{D}} }}{{\partial t_{\text{D}} }}$$
(15)

If all the fractures are fully penetrated, which manifests that the fracture height is equal to the formation thickness, the fluid flow in gas reservoir can be simplified into two-dimensional problem. Thus, Eq. (15) can be rewritten into the following form:

$$\frac{{\partial^{2} m_{\text{D}} }}{{\partial x_{\text{D}}^{2} }} + \frac{{\partial^{2} m_{\text{D}} }}{{\partial y_{\text{D}}^{2} }} + \frac{2\pi }{{q_{\text{sct}} }}q_{L} \delta \left( {r_{\text{D}} ,r_{\text{D}}^{\prime } } \right) = \frac{{\partial m_{\text{D}} }}{{\partial t_{\text{D}} }}$$
(16)

Taking the Laplace transform with respect to t D, Eq. (16) can be changed into the following form:

$$\frac{{\partial^{2} \bar{m}_{\text{D}} }}{{\partial x_{\text{D}}^{2} }} + \frac{{\partial^{2} \bar{m}_{\text{D}} }}{{\partial y_{\text{D}}^{2} }} + \frac{2\pi }{s}\frac{{q_{L} }}{{q_{\text{sct}} }}\delta \left( {r_{\text{D}} ,r_{\text{D}}^{\prime } } \right) = s\bar{m}_{\text{D}}$$
(17)

where s is the Laplace variable; and r D and \(r_{\text{D}}^{\prime }\) are the arbitrary and source point location in 2D domain field.

Boundary element method (BEM)

To derive the solution of Eq. (17), the fundamental solution, G, must be imposed, which satisfies the following equation:

$$\nabla^{2} G - sG + 2\pi \delta \left( {P,Q} \right) = 0$$
(18)

The fundamental solution can be expressed as Eq. (19) by solving Eq. (18), which is:

$$G\left( {P,Q,s} \right) = K_{0} \left[ {r_{\text{D}} \left( {P,Q} \right)\sqrt s } \right]$$
(19)

where r D (P,Q) is the distance between points P and Q. Due to the diffusivity equation being satisfied at any point of the study region,

$$\nabla^{2} \bar{m}_{\text{D}} \left( {P,s} \right) + \frac{2\pi }{s}\frac{{q_{L} }}{{q_{\text{sct}} }}\delta \left( {P,Q} \right) = s\bar{m}_{\text{D}} \left( {P,s} \right)$$
(20)

Multiply Eq. (18) by \(\bar{m}_{\text{D}} (P,s)\), and we have

$$\nabla^{2} G\left( {P,Q,s} \right)\bar{m}_{\text{D}} (P,s) - sG\left( {P,Q,s} \right)\bar{m}_{\text{D}} (P,s) + 2\pi \bar{m}_{\text{D}} (P,s)\delta \left( {P,Q} \right) = 0$$
(21)

Multiply Eq. (21) by G(P, Q, s), and we have

$$G\left( {P,Q,s} \right)\nabla^{2} \bar{m}_{\text{D}} (P,s) - s\bar{m}_{\text{D}} \left( {P,s} \right)G\left( {P,Q,s} \right) + \frac{2\pi }{s}G\left( {P,Q,s} \right)\frac{{q_{L} }}{{q_{\text{sct}} }}\delta \left( {P,Q} \right) = 0$$
(22)

Subtracting Eq. (21) from Eq. (22) and then integrating the solution with respect to P over space domain yields;

$$\begin{aligned} & \int\limits_{\varOmega } {\left[ {\bar{m}_{\text{D}} (P,s)\nabla^{2} G\left( {P,Q,s} \right) - G\left( {P,Q,s} \right)\nabla^{2} \bar{m}_{\text{D}} (P,s)} \right.} \\ & \quad + \left. {2\pi \bar{m}_{\text{D}} (P,s)\delta \left( {P,Q} \right) - \frac{2\pi }{s}G\left( {P,Q,s} \right)\frac{{q_{L} }}{{q_{\text{sct}} }}\delta \left( {P,Q} \right)} \right]{\text{d}}\varOmega = 0 \\ \end{aligned}$$
(23)

According to the following Green’s second identity,

$$\int\limits_{\varOmega } {\left( {u\nabla^{2} v - v\nabla^{2} u} \right)} {\text{d}}\varOmega = \int\limits_{\varGamma } {\left( {u\nabla v - v\nabla u} \right)} \cdot \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{{\bar{\mathbf{n}}}}} {\text{d}}\varGamma$$
(24)

The first time, the left side of Eq. (23) can be reduced into:

$$\begin{aligned} & \int\limits_{\varOmega } {\left[ {\bar{m}_{\text{D}} (P,s)\nabla^{2} G\left( {P,Q,s} \right) - G\left( {P,Q,s} \right)\nabla^{2} \bar{m}_{\text{D}} (P,s)} \right]} {\text{d}}\varOmega \\ & \quad = \int\limits_{\varGamma } {\left[ {\bar{m}_{\text{D}} (P,s)\frac{{\partial G\left( {P,Q,s} \right)}}{\partial n} - G\left( {P,Q,s} \right)\frac{{\partial \bar{m}_{\text{D}} (P,s)}}{\partial n}} \right]} {\text{d}}\varGamma \end{aligned}$$
(25)

where n is the normal vector of the outer boundary; and \(\varGamma (\varGamma = \sum _{\text{i}} \varGamma_{\text{i}} )\) comprises the boundary surfaces of the domain Ω.

Combining Eq. (25) with Eq. (23) and according to the properties of delta function, the boundary integral equation of the diffusivity equation can be transformed as:

$$\begin{aligned} \bar{m}_{\text{D}} (Q,s) & = \frac{1}{2\pi }\int\limits_{\varGamma } {\left[ {G\left( {P,Q,s} \right)\frac{{\partial \bar{m}_{\text{D}} (P,s)}}{\partial n} - \bar{m}_{\text{D}} (P,s)\frac{{\partial G\left( {P,Q,s} \right)}}{\partial n}} \right]} {\text{d}}\varGamma \\ & \quad + \frac{1}{s}\int\limits_{\varOmega } {\frac{{q_{L} }}{{q_{\text{sct}} }}G\left( {P,Q,s} \right)\delta \left( {P,Q} \right){\text{d}}\varOmega } \end{aligned}$$
(26)

When point Q is located in an arbitrary point of the space domain, including the boundary, the general expression of Eq. (26) can be written as:

$$\begin{aligned} \beta \bar{m}_{\text{D}} (Q,s) & = \frac{1}{2\pi }\int\limits_{\varGamma } {\left[ {G\left( {P,Q,s} \right)\frac{{\partial \bar{m}_{\text{D}} (P,s)}}{\partial n} - \bar{m}_{\text{D}} (P,s)\frac{{\partial G\left( {P,Q,s} \right)}}{\partial n}} \right]} {\text{d}}\varGamma \\ & \quad + \frac{1}{s}\int\limits_{\varOmega } {\frac{{q_{L} }}{{q_{\text{sct}} }}G\left( {P,Q,s} \right)\delta \left( {P,Q} \right){\text{d}}\varOmega }\end{aligned}$$
(27)

where β is a parameter related to the geometrical factor of the point Q, which is

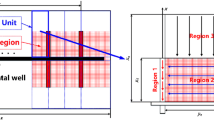
$$\beta = \left\{ {\begin{array}{*{20}l} {1/2\text{ }} \hfill & {{\text{for points on smooth parts of the boundary }}\varGamma \, } \hfill \\ {\alpha /2\pi \text{ }} \hfill & {{\text{for points on non - smooth parts of the boundary }}\varGamma } \hfill \\ 1 \hfill & {{\text{for points inside the domain }}\varOmega } \hfill \\ \end{array} } \right.$$
(28)

Right now, the boundary integral equation of a well located in an arbitrary shaped tight gas reservoir is derived. Next, in order to evaluate the contour integral involved in the boundary integral equation, the boundary should be discretized into some elements (the element numbering and its orientation are shown in Fig. 2). In this paper, the linear elements on both the inner and outer boundaries are utilized, and the detailed description of the solving process is found in previous studies (Wang and Zhang 2009).

Fig. 2
figure 2

Boundary discretized into several elements (counterclockwise node numbering for outer boundary and clockwise node numbering for inner boundary)

Full size image

Pressure response analysis and results

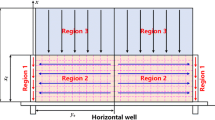
In the above sections, the theory of the BEM application in tight gas reservoir is described. Now, we will use this method to analyze the pressure response of a fractured horizontal well in arbitrary shaped tight gas reservoir. As shown in Fig. 3, there is a MFHW drilled in an arbitrary shaped gas reservoir. The following assumptions are made to make the problem easy to be dealt with: M fractures distributed along the horizontal well with random distribution; all of the fractures are infinite conductivity, symmetrical, and transverse along the well; the width of the fractures is neglected; the half length of the fractures are x fi (i = 1, 2, …, M); the reservoir is homogeneous with the initial pressure p i; the fractures fully penetrate the formation with the height of h; fluid can only enter the wellbore through the fractures at the perforation position and we neglect the contribution of the fluid flow from the formation into horizontal well; and the outer boundary of the reservoir is closed.

Fig. 3
figure 3

Conceptual model of a multiple fractured well in an arbitrary boundary reservoir

Full size image

Model validation

As we have mentioned in Introduction part of this paper, there are mainly two types of methods to analyze the transient pressure response of a fractured horizontal well. Right now, the semi-analytical method based on source functions is wildly applied in hydraulics and petroleum field, but it can only be used to handle the problems of regular outer boundary. The other method is the numerical method. From the point of our review, the reports related to this method are rare and there are few papers based on the numerical software or BEM. In this section, we will validate our models by comparing them to the results derived from the semi-analytical method.

Case 1: Infinite outer boundary

This case is a multiple fractured horizontal well (MFHW) drilled in an infinite outer boundary gas reservoir. The schematic of the physical model is shown in Fig. 4.

Fig. 4
figure 4

Schematic of a MFHW in an infinite outer boundary reservoir

Full size image

Since the Green’s and source function was introduced into the application of petroleum engineering for a relatively long time, this method has become the main technology to analyze the pressure response of complex structure wells. As mentioned in instruction section, if one wants to utilize this method to analyze the well performance, the corresponding source function must be derived, and different boundaries correspond to different functions. In this case, due to the well located in an infinite outer boundary reservoir, we can easily find the continuous line source function in the following references: Ozkan and Raghavan (1991) and Zhao et al. (2015). After that, the transient pressure solution can be obtained by discretizing the hydraulic fractures into small elements and coupling them together.

From the previous research, a continuous line source for a well located in an infinite outer boundary gas reservoir can be expressed as shown in Eq. (29) (Ozkan and Raghavan 1991):

$$\bar{m}_{\text{fLD}} = \frac{{q_{\text{scLD}} }}{s}\left[ {K_{0} \left( {r_{\text{D}} \sqrt s } \right) + 2\sum\limits_{n = 1}^{\infty } {\cos \left( {n\pi \frac{{z_{\text{D}} }}{{h_{\text{D}} }}} \right)\cos \left( {n\pi \frac{{z_{\text{wD}} }}{{h_{\text{D}} }}} \right){\text{K}}_{0} \left( {r_{\text{D}} \sqrt {s + \frac{{n^{2} \pi^{2} }}{{h_{\text{D}}^{2} }}} } \right)} } \right]$$
(29)

where r D is the dimensionless radial in the 2D space, \(r_{\text{D}} = \sqrt {x_{\text{D}}^{2} + y_{\text{D}}^{2} }\); h D is the dimensionless formation thickness, \(h_{\text{D}} = {h \mathord{\left/ {\vphantom {h {L_{\text{ref}} }}} \right. \kern-0pt} {L_{\text{ref}} }}\); z wD is the dimensionless midpoint of the line source; and q sclD is the dimensionless linear source rate.

In Eq. (29), the definition of dimensionless pseudo-pressure is

$$m_{\text{fD}} = \frac{{\pi khT_{\text{sc}} }}{{p_{\text{sc}} Tq_{\text{sc}} }}\Delta m_{\text{f}}$$
(30)

According to the source function of Eq. (29), the dimensionless pressure and pressure derivative curves versus dimensionless time on log–log curves can be obtained, which is shown by the circular markers listed in Fig. 5. Taking the same parameters (C D = 10−5, S kin = 0.1, L = 800 m, L f = 50 m, M = 3) into the model proposed in this paper, the type curves are also plotted as shown by the dark lines in Fig. 5. By comparing the semi-analytical method to the BEM, it is evident that the agreement between them is excellent.

Fig. 5
figure 5

Comparison of the classical semi-analytical solution to our model with the BEM

Full size image

Case 2: Rectangular outer boundary

This case is a MFHW located in a rectangular closed outer boundary reservoir, and the schematic model is shown in Fig. 6. In such a reservoir, the continuous linear source function is also used to analyze the transient pressure response. According to previous research results, the source function corresponds to the continuous linear source solution in the Laplace domain for a rectangular parallelepiped, as is presented in Eq. (31) (Ozkan and Raghavan 1991; Zhao 2015).

$$\begin{aligned} \bar{m}_{\text{fLD}} & = \frac{{q_{\text{scLD}} }}{s}\frac{\pi }{{x_{\text{eD}} }}\left\{ {\frac{{\cos h\left( {\sqrt s y_{\text{D1}} } \right) + \cos h\left( {\sqrt s y_{\text{D2}} } \right)}}{{\sqrt s \sin h\left( {\sqrt s y_{\text{eD}} } \right)}}} \right. \\ & \quad + \text{ }2\sum\limits_{k = 1}^{ + \infty } {\cos \left( {k\pi \frac{{x_{\text{D}} }}{{x_{\text{eD}} }}} \right)\cos \left( {k\pi \frac{{x_{\text{wD}} }}{{x_{\text{eD}} }}} \right)\left. {\frac{{\cos h\left( {\sqrt {\varepsilon_{k} } y_{{{\text{D}}1}} } \right) + \cos h\left( {\sqrt {\varepsilon_{k} } y_{{{\text{D}}2}} } \right)}}{{\sqrt {\varepsilon_{k} } \sin h\left( {\sqrt {\varepsilon_{k} } y_{\text{eD}} } \right)}}} \right\}} \\ \end{aligned}$$
(31)

In Eq. (31),

$$y_{{{\text{D}}1}} = y_{\text{eD}} - \left| {y_{\text{D}} - y_{\text{wD}} } \right|$$
(32)
$$y_{{{\text{D}}2}} = y_{\text{eD}} - \left| {y_{\text{D}} + y_{\text{wD}} } \right|$$
(33)

and

$$\varepsilon_{n} = u + \frac{{n^{2} \pi^{2} }}{{h_{\text{D}}^{2} }}$$
(34)

When we neglect the wellbore storage and skin effects and take the following values of C D = 0, S kin = 0, L = 800 m, L f = 50 m, M = 4, x e = 4000 m, and y e = 800 m into the BEM as well as the semi-analytical models, then the corresponding dimensionless pressure and pressure derivative curves will be drawn, as shown in Fig. 7. Comparing the circular markers from the semi-analytical method with the dark linear curves from the BEM, it can be clearly seen that the accuracy of our method is also excellent. Therefore, we can use the BEM to analyze the pressure response in a more complex boundary structure.

Fig. 6
figure 6

Schematic of a MFHW in a rectangular closed outer boundary reservoir

Full size image
Fig. 7
figure 7

Comparison of the semi-analytical solutions to our model with the BEM for a rectangular reservoir

Full size image

Case 3: Fractured well in arbitrary shaped reservoir—validated by commercial software

In the above two cases, the BEM are used to analyzed the transient pressure response of fractured horizontal well in infinite and rectangular outer boundary conditions. And also, the results’ correctness is validated by comparing it with conventional semi-analytical solutions. In this case, we use our method to study the pressure response for a MFHW in an arbitrary shaped outer boundary tight gas reservoir. For this model, the conventional analytical and semi-analytical methods are helpless. Just like the description in Introduction part, the numerical methods, such as FDM and FEM, are very powerful tools to analyze the transient fluid flow of complex structure wells in complex boundary drainage area. In order to prove the correctness of our results, the commercial software is used.

Figure 8 shows the schematic of a fractured horizontal well in an arbitrary shaped outer boundary tight gas reservoir. The horizontal well length is 1000 m, and there are six equal-spaced hydraulic transverse fractures distributed along the wells. The formation permeability is 0.001 mD, and the formation thickness is 10 m. The half length of the fractures is 100 m and the gas flow from the formation to horizontal wellbore obeys Darcy’s law. Due to the formation permeability for tight gas reservoir is very low (<0.1 mD) and the permeability of hydraulic fractures are always range from 1D to 1000D, the hydraulic fractures can be treated as infinite conductivity. For the BEM, the outer boundary is discretized into 26 elements, and the node number is shown in Fig. 8. Also, each hydraulic fracture is discretized into four elements. After we obtained the coordinate of each outer boundary and fracture elements, the corresponding well bottomhole pressure can be calculated by substituting them and formation parameters into the BEM model. Thereafter, the dimensionless pressure and its derivative with time on log–log curves are shown in Fig. 11 with the solid line.

Fig. 8
figure 8

Schematic of the boundary discrete grid with BEM

Full size image

Well testing software is useful and effective tool to analyze the transient pressure response of different kind of wells, which has been widely used in oil companies and high schools around the world. It is based on the analysis of the derivative of the pressure transient data and provides ease of use and good graphical representations of results. The numerical simulation analysis in well testing software is a very powerful part, which utilizes the unstructured grid (hexagonal grid) to discrete the study area. Through inputting the essential parameters as well as the well model into the software, the grid can be automatically created by it, which is shown in Fig. 9. Once the simulation is started, pressure value on each grid will be recorded and the corresponding pressure field will be also showed dynamically. Figure 10 shows the pressure field distribution for time at 0 h, 5.9 × 105, 4.4 × 106 and 6.2 × 106 h, and the dimensionless bottomhole pseudo-pressure as well as its derivative curves are shown in Fig. 11 with circle marks. It can be clearly seen from Fig. 11 that the agreement of the results derived by BEM and a commercial software is perfect, which can prove the correctness of our method.

Fig. 9
figure 9

Unstructured grid with commercial software

Full size image
Fig. 10
figure 10

Pressure field distribution for different production time

Full size image
Fig. 11
figure 11

Comparison of commercial software to our BEM for arbitrary shaped outer boundary

Full size image

Discussion of results and analysis

Here, we investigate a case of a MFHW drilled in an elliptical closed boundary reservoir. As mentioned in Introduction section, the conventional semi-analytical method is unavailable for this problem. So, in this section, we will use the BEM to analyze the pressure response of the MFHW. The schematic of a MFHW in an elliptical gas reservoir is shown in Fig. 12.

Fig. 12
figure 12

Schematic of a MFHW in an elliptical boundary reservoir

Full size image

Figure 13 shows the effects of the reservoir size on the type curves. Firstly, the following variables of C D = 10−5, S kin = 0.1, L = 800 m, L f = 50 m, and M = 3, as well as the major and minor axis distances of the outer boundary, are taken into the BEM model. Then, the corresponding coefficient matrix including the production rate, dimensionless pressure, and the well bottomhole pressure on all the boundaries are assembled. Finally, all the variables are obtained simultaneously by Gaussian elimination. The pressure derivative response in Fig. 13 indicates that there are no significant differences between the three cases (a = 1500 m, b = 200 m/500 m/1000 m) in the early flow period. But, with the increase in b, the upward time during the later flow period is advanced. This is mainly because a small b means that the space between the well and the boundary is small, which causes the pressure wave to reach the boundary early.

Fig. 13
figure 13

Pressure and pressure derivative curves with different reservoir sizes

Full size image

Figure 14 indicates the effects of fracture number on the MFHW pressure response. In this situation, the assumption of an identical half fracture length and equal spacing are made, and we adjust the fracture number along the horizontal well. As a larger number of fractures represent a larger volume of drainage area during the early flow period, it will need a small pressure drop during this period when the well produces at a constant rate. A smaller M means a larger drainage volume for a single fracture, so an early fracture radial flow period can be clearly seen on the pressure derivative curves when M equals 3. However, when the pressure wave propagates into the outer region of the fractures, all the curves will coincide, and then the boundary dominated flow period will occur.

Fig. 14
figure 14

Effects of fracture number (M) on the pressure response

Full size image

Figures 15 and 16 present the effects of reservoir shape on the pressure response with the same control volume. When the product of the major axis and minor axis is 7.5 × 105, the control volume of the model is a constant. The value of the minor axis will be changed along with the variation of the major axis. For this case, because the reservoir size is much larger than the size of the well, the effect of the reservoir shape on the pressure response is very weak. From the pressure derivative curves in Fig. 15, it can be clearly seen that the boundary shape has little influence on the boundary reflective flow after the elliptical flow period. This case also manifests that, for a large control volume, the effect of boundary shape on the pressure response curves can be negligible. But for a small control volume, the pressure wave will reach the closer boundary sooner right after the early linear flow period finishes. Also, the smaller a is, the closer the well is to the boundary. Therefore, the earlier the boundary reflection time will arrive, which can be observed in Fig. 16.

Fig. 15
figure 15

Effects of reservoir shape on the pressure response with the same control volume (a × b = 7.5 × 105 m2)

Full size image
Fig. 16
figure 16

Effects of reservoir shape on the pressure response with the same control volume (a × b = 8 × 104 m2)

Full size image

Conclusion

In this paper, BEM was adopted to analyze the transient pressure response of a MHFW in an arbitrary shaped boundary tight gas reservoir, which was not reported before. Through the research, the following conclusions could be reached:

  1. 1.

    The BEM was extended to analyze the transient pressure response of a MFHW in tight gas reservoir with an arbitrary shape, which cannot be solved by conventional integral transformation or Green’s and source function method.

  2. 2.

    Various methods and models (semi-analytical method and Saphir commercial software) are utilized to validate the correctness of our method, and the comparing results show that the BEM can be successfully solved the problems of MFHW with arbitrary shaped outer boundary.

  3. 3.

    For a well located in an elliptical reservoir, the smaller the minor axis is, the earlier the boundary reflection period will occur and the shorter the duration of the elliptical flow period will be.

  4. 4.

    As the fracture number increases, the pressure derivative curves will be lower due to the larger drainage volume of the well during the early flow period. For a larger drainage volume, the effects of reservoir shape on the pressure curves are negligible, but for a smaller drainage volume, the situation is adverse.

  5. 5.

    According to our study, the effect of boundary shape on the pressure type curves only displays on the middle or later flow periods, which maybe need a long time to reach in real situation. So, the regular outer boundary models can be used to analyze the well testing data for tight or low permeability reservoirs.