Introduction

Pumping test is one of the most important investigation ways to estimate aquifer parameters in the hydrogeology (Barker and Herbert 1982; Wang et al. 2013; Li et al. 2014). Because of the large storage capacity, large-diameter pumping wells have been commonly used all over the world especially in developing countries such as China and India (Wang et al. 2005; Sushil 2006). The hydraulics of groundwater flow to a larger-diameter well might be somewhat different from that of flow to an infinitesimal well because the pumping rate mainly comes from the storage of the well at early times for a large-diameter pumping well. In the past few decades, groundwater flow to an infinitesimal well has been extensively investigated (Theis 1935; Hantush and Jacob 1955; Hantush 1959; Neuman and Witherspoon 1969). The first mathematical model for unsteady groundwater flow to an infinitesimal pumping well was the well-known Theis model (Theis 1935). Later, numerous models had been established for different aquifer systems (Hantush and Jacob 1955; Hantush 1959; Neuman and Witherspoon 1969; Salcedo et al. 2013; Yeh and Chang 2013). For instance, Hantush and Jacob (1955) investigated the groundwater flow to an infinitesimal well in a leaky aquifer. Boulton (1954) developed a mathematical model for groundwater flow to a pumping well in an unconfined aquifer. Meanwhile, research on flow to a finite-diameter pumping well had also been reported (Papadopulos and Cooper 1967; Lai and Su 1974; Fenske 1977; Sen 1982; Patel and Mishra 1983; Cimen 2001).

All the above-mentioned studies were based on the assumption that the flow was Darcian. However, flow could be non-Darcian under certain circumstances when the pumping rate is relatively large (Sen 1990; Wen et al. 2008a, 2009), meaning that the relationship between the specific discharge and hydraulic gradient was no longer linear. Non-Darcian flow can be classified into two general types, i.e., pre-linear flow and post-linear flow. When the specific discharge (or the hydraulic gradient) is less than a critical value and the linear relationship between the specific discharge and the hydraulic gradient becomes invalid, the flow can be regarded as pre-linear. On the other hand, if the specific discharge (or the hydraulic gradient) is larger than a critical value and such a linear relationship is also invalid, the flow can be regarded as post-linear. The pre-linear flow often happens in petroleum engineering or groundwater flow in silt–clay aquitards because of the low flow velocities, while the post-linear flow often happens in fractured media (Kolditz 2001) or near the pumping well because of the high velocities of flow (Sen 1987, 1989).

During the past few decades, non-Darcian flow to a pumping well has caught the attention of many investigators. However, progress on non-Darcian flow is still very limited because of the nonlinearity nature of the problem. Sen (1987, 1989, 1990) might be one of the first hydrologists to investigate non-Darcian flow to a pumping well. The methodology used by him was one type of the similarity methods, called the Boltzmann transform. The basic idea of the Boltzmann transform was to convert the partial differential equation of unsteady groundwater flow to an ordinary differential equation by combining the spatial and the temporal coordinates into a single Boltzmann variable (Özisik 1989). For example, Sen (1987) used the Boltzmann transform to solve non-Darcian flow to a pumping well in a confined aquifer based on the assumption that the non-Darcian flow can be described by the Izbash equation. Sen (1990) also used the Boltzmann transform to solve non-Darcian flow to a large-diameter well on the basis of the Forchheimer equation. Although Sen used Boltzmann transform to solve non-Darcian flow to a pumping well under different conditions and a series of papers had been published, the Boltzmann transform had been proven to be problematic for some problems (Mathias et al. 2008; Wen et al. 2008a). In a rigorous sense, the Boltzmann transform was only applicable for an infinitesimal pumping well. It may bring in errors when the pumping well radius was not infinitesimal. Especially, when the wellbore storage was considerable, the errors associated with such a transform might be unacceptable. Recently, Wen et al. (2008a, b) developed a linearization procedure which can deal with the nonlinear term in the governing equation for non-Darcian flow successfully. The linearization procedure worked generally well when the pumping time was relatively large meaning that the flow approaches a quasi-steady state, while it would underestimate the drawdown at early times (Wen et al. 2009). As mentioned before, the solutions obtained by the Boltzmann transform and the linearization procedure were approximate analytical solutions. It is very difficult, if not impossible, to obtain closed-form analytical solutions for non-Darcian flow problems because of the nonlinear nature of the problem. Meanwhile, numerical approaches had also been used to solve non-Darcian flow problems (Ewing et al. 1999; Mathias et al. 2008; Wen et al. 2009).

After a careful check on the literature, one can find that most of the studies on non-Darcian flow to a pumping well focus on the fully penetrating wells. Research on non-Darcian flow to a partially penetrating well was limited. In fact, partially penetrating wells were commonly used in the real-field applications, especially in the site where the thickness of the aquifer was large (Shu et al. 2013). Wen et al. (2013) firstly investigated non-Darcian flow toward a partially penetrating well in a confined aquifer, and some approximate analytical solutions were obtained. In addition, the wellbore storage should also be considered when the radius of the well is relatively large. Therefore, it was necessary and interesting to investigate the non-Darcian flow to a larger-diameter partially penetrating well. This study was an extension of a previous study (Wen et al. 2013), which did not consider the wellbore storage. The main purpose of this study was to analyze the impact of the wellbore storage under non-Darcian flow and partially penetrating condition.

In this study, non-Darcian flow to a partially penetrating well was investigated taking into account the wellbore storage. Both the Izbash equation and the Forchheimer equation describing the non-Darcian flow were used widely. The Izbash equation was used in this study, and the Forchheimer equation will be investigated separately elsewhere. The Izbash equation had been proven to describe non-Darcian flow very well in coarse porous media (Bordier and Zimmer 2000; Moutsopoulos et al. 2009). The linearization procedure associated with the Laplace transform and the finite cosine Fourier transform were used to solve the mathematical model. The drawdowns inside the well and in the aquifer had been thoroughly analyzed for different possible field cases.

Problem statement and semi-analytical solutions

Problem statement

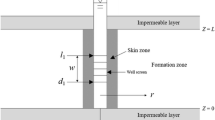
The schematic diagram of the problem investigated here is shown in Fig. 1. In order to simplify the flow system and make the problem mathematically tractable, the following assumptions have been used in this study: (1) the aquifer is homogenous, horizontally isotropic, and laterally infinite with a constant thickness; (2) the well partially penetrates the aquifer, and the radius of the well is relatively large and equal to r w , meaning that the wellbore storage cannot be ignored; (3) the pumping rate is constant and equal to Q (positive for pumping); (4) the whole system is hydrostatic before the pumping starts; (5) the horizontal flow is assumed to be non-Darcian, while the flow in the vertical direction is assumed to be Darcian (the dominating flow component is generally along the horizontal direction, supplemented by a secondary vertical flow component close to the well. The vertical flow component drops quickly when moving away from the well). Based on these assumptions, the flow mathematical model can be established:

$$\frac{{\partial q_{\text{r}} }}{\partial r} + \frac{{q_{\text{r}} }}{r} + \frac{{\partial q_{\text{z}} }}{\partial z} = S_{\text{s}} \frac{\partial s(r,z,t)}{\partial t},$$
(1)
$$s(r,z,0) = 0,$$
(2)
$$s(\infty ,z,t) = 0,$$
(3)
$$\frac{\partial s(r,0,t)}{\partial z} = 0,$$
(4)
$$\frac{\partial s(r,B,t)}{\partial z} = 0,$$
(5)
$$\mathop {\lim }\limits_{{r \to r_{\text{w}} }} 2\pi r(l - d)q_{\text{r}} - \pi r_{\text{w}}^{2} \frac{{{\text{d}}s_{\text{w}} (t)}}{{{\text{d}}t}} = - Q[U(z - d) - U(z - l)],\quad 0 \le z \le B,$$
(6)

where q r is the radial specific discharge [m/h]; q z is the vertical specific discharge [m/hr]; r is the radial coordinate [m]; z is the vertical coordinate [m]; s(r, z, t) is the drawdown [m]; S s is the specific storage coefficient [m−1]; Q is the pumping rate [m3/h]; B is the thickness of the aquifer [m]; r w is the radius of the pumping well [m]; s w(t) is the drawdown inside the well [m]; l is the distance from the top of the well screen to the bottom of the aquifer [m]; d is the distance from the bottom of the well screen to the bottom of the aquifer [m]; U(.) is the Heaviside step function, U(z − d) is zero when z is less than d, otherwise U(z − d) equals one. The origin of coordinates is located at the intercept of the vertical axis through the center of the well and the bottom of the aquifer.

Fig. 1
figure 1

Schematic diagram of the flow system

Full size image

The flow in the radial direction is assumed to be non-Darcian and can be described by the Izbash equation, that is,

$$q_{\text{r}} |q_{\text{r}} |^{n - 1} = K_{\text{r}} \frac{\partial s(r,z,t)}{\partial r},$$
(7)

where n is a power index, K r is an empirical coefficient [mn/hn], and it can be regarded as an apparent radial hydraulic conductivity when n is 1. As q r is negative, which is the case for a pumping scenario, the above equation can be rewritten as:

$$- |q_{\text{r}} |^{n} = - ( - q_{\text{r}} )^{n} = K_{\text{r}} \frac{\partial s(r,z,t)}{\partial r}$$
(8)

The flow in the vertical direction is assumed to be Darcian described as:

$$q_{\text{z}} = K_{\text{z}} \frac{\partial s(r,z,t)}{\partial z},$$
(9)

where K z is the vertical hydraulic conductivity [m/h].

Approximate analytical solutions in Laplace–Fourier domain

Substituting Eqs. (8) and (9) to Eq. (1), one can obtain

$$\frac{{K_{\text{r}} }}{{n( - q_{\text{r}} )^{n - 1} }}\frac{{\partial^{2} s(r,z,t)}}{{\partial r^{2} }} + \frac{{K_{\text{r}} }}{{r( - q_{\text{r}} )^{n - 1} }}\frac{\partial s(r,z,t)}{\partial r} + K_{\text{z}} \frac{{\partial^{2} s(r,z,t)}}{{\partial z^{2} }} = S_{s} \frac{\partial s(r,z,t)}{\partial t} \,$$
(10)

The above equation has a nonlinear term (−q r)n−1, which is very difficult to handle analytically. Fortunately, Wen et al. (2008a) proposed a linearization procedure which can be used to solve such nonlinear equation successfully. In this study, the linearization procedure was also used to deal with the nonlinear term in the above equation. According to Wen et al. (2008a), one has the following approximation:

$$( - q_{\text{r}} )^{n - 1} \approx \left( {\frac{Q}{2\pi rB}} \right)^{n - 1} .$$
(11)

Then, Eq. (10) can be transformed as:

$$\frac{{\partial^{2} s(r,z,t)}}{{\partial r^{2} }} + \frac{n}{r}\frac{\partial s(r,z,t)}{\partial r} + \frac{{K_{\text{z}} n}}{{K_{\text{r}} }}\left( {\frac{Q}{2\pi rB}} \right)^{n - 1} \frac{{\partial^{2} s(r,z,t)}}{{\partial z^{2} }} \approx \frac{n}{{K_{\text{r}} }}\left( {\frac{Q}{2\pi rB}} \right)^{n - 1} S_{\text{s}} \frac{\partial s(r,z,t)}{\partial t} \, .$$
(12)

Eq. (12) indicates that the flow rate at any cylindrical cross section is equal to the pumping rate Q. It should be pointed out that this is exactly true only at the center of the pumping well (the inner boundary). Obviously, for the area far away from the pumping well, the flow rate at the cylindrical cross section is less than the pumping rate Q. It has been proven that such a linearization procedure will underestimate the drawdown at early times and it works generally well at late times (Wen et al. 2009).

Eq. (12) can be solved by the Laplace transform associated with the finite cosine Fourier transform along the z-direction. When considering the initial and boundary conditions, the final solution for Eq. (12) in Laplace domain can be expressed as:

$$\begin{aligned} \bar{s}(r,z,p) = & \frac{{Q(l - d)r^{{\frac{1 - n}{2}}} K_{{\frac{1 - n}{3 - n}}} \left( {\frac{2}{3 - n}r^{{\frac{3 - n}{2}}} \sqrt {\delta^{\prime}} } \right)}}{{Bp\left\{ {\frac{{[2\pi r_{\text{w}} (l - d)]^{n} }}{{Q^{n - 1} }}K_{\text{r}} r_{\text{w}}^{1 - n} \sqrt {\delta^{\prime}} K_{{\frac{2}{3 - n}}} \left( {\frac{2}{3 - n}r_{\text{w}}^{{\frac{3 - n}{2}}} \sqrt {\delta^{\prime}} } \right) + \pi r_{\text{w}}^{{\frac{5 - n}{2}}} pK_{{\frac{1 - n}{3 - n}}} \left( {\frac{2}{3 - n}r_{\text{w}}^{{\frac{3 - n}{2}}} \sqrt {\delta^{\prime}} } \right)} \right\}}} \\ & \; + \frac{2Q}{p\pi }\sum\limits_{N = 1}^{\infty } {\frac{{\left[ {\sin \left( {\frac{N\pi l}{B}} \right) - \sin \left( {\frac{N\pi d}{B}} \right)} \right]r^{{\frac{1 - n}{2}}} K_{{\frac{1 - n}{3 - n}}} \left( {\frac{2}{3 - n}r^{{\frac{3 - n}{2}}} \sqrt \delta } \right)\cos \left( {\frac{N\pi z}{B}} \right)}}{{N\left\{ {\frac{{[2\pi r_{\text{w}} (l - d)]^{n} }}{{Q^{n - 1} }}K_{\text{r}} r_{\text{w}}^{1 - n} \sqrt \delta K_{{\frac{2}{3 - n}}} \left( {\frac{2}{3 - n}r_{\text{w}}^{{\frac{3 - n}{2}}} \sqrt \delta } \right) + \pi r_{\text{w}}^{{\frac{5 - n}{2}}} pK_{{\frac{1 - n}{3 - n}}} \left( {\frac{2}{3 - n}r_{\text{w}}^{{\frac{3 - n}{2}}} \sqrt \delta } \right)} \right\}}}} \\ \end{aligned}$$
(13)

in which, \(\delta^{\prime} = \frac{{S_{\text{s}} pn}}{{K_{\text{r}} }}\left( {\frac{Q}{2\pi B}} \right)^{n - 1} ,\delta = \frac{{B^{2} S_{\text{s}} pn + K_{\text{z}} nN^{2} \pi^{2} }}{{K_{\text{r}} B^{2} }}\left( {\frac{Q}{2\pi B}} \right)^{n - 1}\). N is the finite cosine Fourier transform variable. p is Laplace transform variable, \(K_{{\frac{{1 - {\text{n}}}}{3 - n}}} \left( {\frac{1 - n}{3 - n}} \right)\) and \(K_{{\frac{2}{3 - n}}} \left( {\frac{2}{3 - n}} \right)\) are the second kind of Bessel functions with order \(\frac{{1 - {\text{n}}}}{3 - n}\) and \(\frac{2}{3 - n}\), respectively. The details for the derivation of the solution can be found in the “Appendix.”

Simplified solutions

If the power index n in the Izbash equation happens to be 1, the Izbash equation then becomes Darcy’s law. For such a special case, the solution of Eq. (12) becomes

$$\begin{aligned} \bar{s}(r,z,p) & \quad = \frac{{Q(l - d)K_{0} \left( {r\sqrt {\frac{{S_{\text{s}} p}}{{K_{\text{r}} }}} } \right)}}{{\pi pBr_{\text{w}} \left[ {2(l - d)K_{\text{r}} \sqrt {\frac{{S_{\text{s}} p}}{{K_{\text{r}} }}} K_{1} \left( {r_{\text{w}} \sqrt {\frac{{S_{\text{s}} p}}{{K_{\text{r}} }}} } \right) + pr_{\text{w}} K_{0} \left( {r_{\text{w}} \sqrt {\frac{{S_{\text{s}} p}}{{K_{\text{r}} }}} } \right)} \right]}} \\ & \qquad + \frac{2Q}{{p\pi^{2} r_{\text{w}} }}\sum\limits_{N = 1}^{\infty } {\frac{{\left[ {\sin \left( {\frac{N\pi l}{B}} \right) - \sin \left( {\frac{N\pi d}{B}} \right)} \right]K_{0} (r\sqrt {\delta^{\prime\prime}} )\cos \left( {\frac{N\pi z}{B}} \right)}}{{N[2(l - d)K_{\text{r}} \sqrt {\delta^{\prime\prime}} K_{1} (r_{\text{w}} \sqrt {\delta^{\prime\prime}} ) + pr_{\text{w}} K_{0} (r_{\text{w}} \sqrt {\delta^{\prime\prime}} )]}}} , \\ \end{aligned}$$
(14)

where \(\delta^{\prime\prime} = \frac{{B^{2} S_{\text{s}} p + K_{\text{z}} N^{2} \pi^{2} }}{{K_{\text{r}} B^{2} }}\). Equation (14) is the same as the solution obtained by Mishra et al. (2012) who investigated Darcian flow to a partially penetrating well with storage in an anisotropic confined aquifer.

If l = B and d = 0, then the partially penetrating well becomes a fully penetrating well, and the solution of Eq. (12) becomes

$$\bar{s}(r,p) = \frac{{Qr^{{\frac{1 - n}{2}}} K_{{\frac{1 - n}{3 - n}}} \left( {\frac{2}{3 - n}r^{{\frac{3 - n}{2}}} \sqrt {\delta^{\prime}} } \right)}}{{\frac{{(2\pi r_{\text{w}} B)^{n} }}{{Q^{n - 1} }}K_{\text{r}} pr_{\text{w}}^{1 - n} \sqrt {\delta^{\prime}} K_{{\frac{2}{3 - n}}} \left( {\frac{2}{3 - n}r_{\text{w}}^{{\frac{3 - n}{2}}} \sqrt {\delta^{\prime}} } \right) + \pi p^{2} r_{\text{w}}^{{\frac{5 - n}{2}}} K_{{\frac{1 - n}{3 - n}}} \left( {\frac{2}{3 - n}r_{\text{w}}^{{\frac{3 - n}{2}}} \sqrt {\delta^{\prime}} } \right)}}$$
(15)

Equation (15) is the same as the solution obtained by Wen et al. (2009) who investigated non-Darcian flow to a fully penetrating well with considering wellbore storage.

If l = B, d = 0, and n = 1, the problem investigated here is the same as that of Papadopulos and Cooper (1967). Then, Eq. (13) can be simplified as:

$$\bar{s}(r,z,p) = \frac{{QK_{0} \left( {r\sqrt {\frac{{S_{\text{s}} p}}{{K_{\text{r}} }}} } \right)}}{{\pi pr_{\text{w}} \left[ {2BK_{\text{r}} \sqrt {\frac{{S_{\text{s}} p}}{{K_{\text{r}} }}} K_{1} \left( {r_{\text{w}} \sqrt {\frac{{S_{\text{s}} p}}{{K_{\text{r}} }}} } \right) + pr_{\text{w}} K_{0} \left( {r_{\text{w}} \sqrt {\frac{{S_{\text{s}} p}}{{K_{\text{r}} }}} } \right)} \right]}} \, ,$$
(16)

which is the solution obtained by Papadopulos and Cooper (1967).

Results and discussions

Drawdowns inside the well

For a large-diameter well, it is very interesting to analyze the drawdown inside the well because the pumping rate is mainly from the wellbore storage at early times.

Firstly, this solution was compared with some benchmark analytical solutions, i.e., the solution of Papadopulos and Cooper (1967) for Darcian flow to a fully penetrating well with wellbore storage, the solution of Wen et al. (2008a, b) for non-Darcian flow to a fully penetrating well with wellbore storage, and the solution of Mishra et al. (2012) for Darcian flow to a partially penetrating well with wellbore storage. The default values of parameters are given in Table 1. As shown in Fig. 2, it can be seen that all the curves for different cases converge to the same asymptotic value at early times, meaning that all the pumping rate comes from the water stored inside the well. At late times, the drawdown for Darcian flow case is larger than that for non-Darcian flow case, and the drawdown for the partially penetrating case is larger than that for the fully penetrating case, if the other conditions are the same. The impacts of different parameters on the drawdown inside the well have also been analyzed and one found that the early-time behavior was the same as that reflected in Fig. 2, while the late-time behavior is the same as those of the drawdown in the aquifer, which will be explained in more detail below.

Table 1 Default value of parameters used in this study
Full size table
Fig. 2
figure 2

Comparison between the solution for the drawdown inside the well of this study and those of the previous studies

Full size image

Drawdowns in the aquifer

Figure 3 shows the comparison between the drawdown calculated at a radial distance of 5 m from the well, using the model developed in this study and model that have been analyzed in Fig. 2. The default values of parameters are given in Table 1. The late-time behavior shown in this figure is the same as that in Fig. 2. However, at early times, the drawdown for the non-Darcian flow case is larger than that of the Darcian flow case. It is also found that the drawdown for a partially penetrating well is the same as that of a fully penetrating well at early times.

Fig. 3
figure 3

Comparison between the solution for the drawdown in the aquifer of this study and those of the previous studies

Full size image

Figure 4 shows the impact of n value on the drawdown in the aquifer with n = 1.0, 1.2, 1.5, or 1.8. Other default values of parameters are given in Table 1. From this figure, it is found that a larger value of n leads to a larger drawdown at early times, while a larger value of n will lead to a smaller drawdown at late times. A larger n means greater deviation from Darcian flow. For early times, a larger n implies greater resistance to flow; therefore, a larger drawdown was found. For the late times, the flow approaches a quasi-steady state. The elastic release of the aquifer is nearly completed, and the pumping rate is mainly from the recharge from the area where it is relatively far away from the pumping well. It can also be found that the flow approach the quasi-steady state earlier when n is larger in this figure. The impact of n value on the drawdown inside the well has also been analyzed, as shown in Fig. 5. It is evident to see that the wellbore storage effect at early times, as shown in this figure, different n values led to the same drawdowns at early times. The late-time behavior is the same as that of Fig. 4, which has been explained before.

Fig. 4
figure 4

Impact of n value on the drawdown in the aquifer with n = 1.0, 1.2, 1.5, or 1.8

Full size image
Fig. 5
figure 5

Impact of n value on the drawdown in the well with n = 1.0, 1.2, 1.5, or 1.8

Full size image

In order to analyze the impact of non-Darcian flow on the wellbore storage effect, one can draw the curves for different r w values with different n values at the same figure. As shown in Fig. 6, one can also see the wellbore storage effect at early times, and a larger n led to a smaller drawdown at late times. Interesting enough, if comparing the curves for different n values, one can see that the wellbore storage effect disappears earlier when n is larger (the disappearing time is 32.5 h for n = 1, 5.0 h for n = 1.5, and 2.1 h for n = 1.8).

Fig. 6
figure 6

Impact of different r w values with different n values on the drawdown in the aquifer

Full size image

Figure 7 is the comparison between the fully penetrating case and the partially penetrating case with different r w values. As shown in this figure, the drawdowns for the fully penetrating case are larger than those of the partially penetrating case. This is because a longer well screen can transmit water more easily, which is somewhat like the aquifer has a larger hydraulic conductivity. Thus, a smaller drawdown will be found at late times.

Fig. 7
figure 7

Impact of different r w values under partially penetrating pumping well and fully penetrating pumping well on the drawdown in the aquifer

Full size image

The impact of S s, K r, and the length of the well screen l − d on the drawdowns in the aquifer was investigated, and the features were similar to those without considering the wellbore storage (Wen et al. 2013), which will not be repeated here.

Conclusions

In this study, non-Darcian flow to a large-diameter partially penetrating well in a confined aquifer was investigated. The wellbore storage was considered. The horizontal non-Darcian flow was assumed to follow the Izbash equation, while the vertical flow was still assumed to be Darcian. The Laplace transform associated with the finite cosine Fourier transform was used to solve such non-Darcian flow model. Both the drawdowns inside the well and in the aquifer were analyzed under different conditions. The main findings can be concluded as follows:

  1. 1.

    The drawdowns inside the well are generally the same at early times under different aquifer conditions, indicating the wellbore storage effect. The features of the drawdowns inside the well at late times are the same as those of the drawdowns in the aquifer.

  2. 2.

    The drawdown in the aquifer for the non-Darcian flow case is larger than that of the Darcian flow case at early times, while the drawdown in the aquifer for the non-Darcian flow case is smaller than that of the Darcian flow at late times.

  3. 3.

    The drawdowns for a partially penetrating well are the same as those of a fully penetrating well at early times, while the drawdowns for the partially penetrating case are larger than those for the fully penetrating case at late times, and a longer well screen results in a smaller drawdown in the aquifer at late times, if the other conditions are the same.

  4. 4.

    From the curves for different r w values with different n values, one can see that a larger n led to a smaller drawdown at late times, and the wellbore storage effect disappears earlier when n is larger.