Abstract
Distributed generation units (DGUs) as auxiliary sources of power generation can play an effective role in meeting the load consumption of the distribution network, also have positive effects such as reducing loss and improving voltage. Moreover, capacitors by reactive power compensation produce positive effects similar to DGUs in the distribution networks. The idea of joint operation of DGUs and shunt capacitors (SCs) in the presence of demand response program (DRP) to derive maximum benefits from their installation is proposed in this paper. The time of use (TOU) mechanism is used as one of the demand response programs (DRPs) to alter the consumption pattern of subscribers and improve the performance of the distribution system. Objective functions include minimization of energy loss, operational cost, and energy not supplied (ENS). In general, the problem of determining the optimal capacity of DGUs and SCs is complex due to the demand variation. Also, considering the effect of uncertainty sources complicate the optimization problem. Hence, a modified shuffled frog leaping algorithm (MSFLA) is proposed to overcome the complexities of this problem. The proposed approach is tested on two 95, and 136-node test networks, and the results are compared with other evolutionary algorithms. According to the obtained results, after using the proposed approach in determining the optimal capacity of DGUs and SCs in the first system, the amount of energy loss, operational cost and ENS dropped by 11, 25.5 and 5% compared to baseline values. After applying the TOU mechanism in allocation of DGUs and SCs simultaneously in the second system by proposed method, the values obtained for the mentioned objectives reduced by 29, 65 and 7% compared to initial values.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Distribution systems’ operation strategies have changed dramatically in recent years due to the proliferation of DGUs. Development and integration of these units in distribution systems have exerted positive effects on voltage profile of buses, line current profile, and reliability. Hence, a great number of studies have explored the effect of DGUs to optimally operation distribution systems (Azizivahed et al. 2017, 2018). In addition, shunt capacitors (SCs) are used in distribution systems to improve network performance for a variety of purposes, such as enhancing the power quality and decreasing loss by injecting reactive power (Askarzadeh 2016). Hence, some studies have explored the separate effect of DGUs and SCs on the network’s operation to augment the performance of the distribution systems.
The distribution network reconfiguration and DGUs allocation was solved using a genetic algorithm (GA) to reduce loss and harmonic distortion (Din et al. 2019). Taguchi performance analysis method was proposed for optimal DGUs allocation to diminish loss (Galgali et al. 2019). A particle swarm optimization (PSO) algorithm was proposed for optimal sizing of DGUs to decrease loss (Kumari et al. 2017). A new analytical method was presented to determine the optimal capacity and location of distributed generation units to decrease loss (Tah and Das 2016); this model obviates the need to consider the impedance matrix. A biogeography-based algorithm was presented for optimal sizing and placement of DGUs using the effective power factor model to minimize loss (Ravindran and Victoire 2018). A two-step method based on combination of sensitivity analysis and cuckoo optimization algorithm was used for optimal locating and sizing of SCs to reduce loss (Reddy and Prasad 2014). An artificial bee colony (ABC) method was proposed to allocate shunt capacitors in radial test system to enhance the voltage stability considering load variable (El-Fergany and Abdelaziz 2014). Two hybrid evolutionary methods were used for placement and sizing of SCs to minimize loss (Abdelaziz et al. 2016; Lotfi et al. 2016). A crow search optimization algorithm was introduced to determine the size and location of SCs in the network to reduce active loss and modifying the voltage profile (Askarzadeh 2016). Most of the above studies have considered the power loss and voltage profile as objective functions in solving the optimization problem in 33 and 69 bus test networks, and good results have achieved in reducing loss and improving the voltage profile. Also, they have been able to provide practical optimization algorithms to solve the considered optimization problem. But, these studies have neglected to consider the objective function of reliability in solving the optimization problem, which is very critical in the distribution network, failure to account for this point will result in frequent blackouts in the network and the distribution system instability. There is also no trace of the operational cost objective function related to the cost of grid power generation and distributed generation units. Moreover, these studies have considered the problem as a single-objective problem and have not presented a strategy for solving the multi-objective problem. In fact, the simultaneous effect of two objective functions in solving the problem is not seen. In the following, the references that have modeled the considered optimization problem in a Multi-objective framework, are examined.
A Multi-objective fire butterfly optimization was presented for optimal DGUs allocation to reduce loss, voltage deviation and pollution of DGUs (Elattar and ElSayed 2020). A hybrid PSO-incremental learning algorithm was suggested for placement and sizing of DGUs to reduce loss and improve the voltage profile (Grisales-Noreña et al. 2018). Two state-art-of methods including Non-dominated sorting genetic and ant lion optimization were proposed for locating and sizing of DGUs to reduce loss and voltage deviation (Liu et al. 2019; VC 2018). A population-based algorithm was proposed for the placement and sizing of SCs to decrease loss and enhance voltage stability (Al-Ammar et al. 2021). Honey-Bee mating (HBM) method was proposed to determine the capacity and optimal location of SCs in the distribution system to diminish loss and voltage deviation (Kavousi-Fard and Samet 2013). A two-step method that combines sensitivity analysis and ant colony optimization algorithm was suggested to determine the capacity and placement of SCs in the distribution network in an attempt to diminish loss and voltage deviation (Abou El-Ela et al. 2018). These studies have solved the multi-objective optimization problem using Pareto fronts and weighting factor methods. In addition to presenting novel and state-of-art algorithms in these studies, the presence of several new objective functions such as voltage stability and pollution is also seen in these studies. But similar to the studies examined in the previous paragraph, changes in electrical load and electricity price are not considered in solving the problem. Since the electrical load in real distribution systems is variable, dynamic planning is required for the optimal operation of the distribution network considering DGUs and capacitors. Moreover, some objective functions such as operational costs and energy loss must be calculated under the time-varying electrical load and electricity price.
Using DGUs and SCs simultaneously has additional advantages and capabilities for the distribution system than the separate presence of these units in the network. Hence, another group of studies has focused on the simultaneous effect of DGUs and SCs in the optimal operation of distribution network. An improved PSO-Simulated annealing algorithm was introduced to determine the capacity and placement of DGUs and SCs to reduce network loss and operational cost (Su 2019). The GA was proposed to determine the capacity and optimal location of DGUs and SCs with variable electrical load to diminish active loss (Das et al. 2019). An evolutionary algorithm based on decomposition was utilized for placement and sizing of DGUs and SCs in the network to reduce active and reactive loss (Biswas et al. 2017). The water cycle evolutionary algorithm was suggested for placement and sizing of DGUs and SCs to reduce network loss (Abou El-Ela et al. 2016). The PSO algorithm was presented for placement and sizing DGUs and SCs in the distribution network by considering the uncertainty of the electrical load in order to reduce active loss and strengthen voltage stability (Zeinalzadeh et al. 2015). Given the valuable work discussed above on the problem of optimal placement and sizing of capacitors and distributed generation sources, acceptable results are observed in reducing loss and operational cost in the simultaneous presence of DGUs and SCBs compared to the separate presence of these units in the distribution network. However, in most of these studies, the effect of uncertainty resources on solving the optimization problem has not been considered. As a result, the solution found for the problem could be far from the actual operating point of the system. Therefore, considering the effect of these resources on the optimal use of the network enables the network operator to have correct and accurate planning based on the real situation of the system. Another noteworthy point derived from the review of the above studies in this field is the inadequate attention allocated to the issue of demand response programs (DRPs). DRPs are usually implemented at the lowest cost and with the participation of consumers to improve the performance and reliability of the distribution network at certain times.
As far as the solution method is concerned, it should be noted that optimal placement and sizing of DGUs and SCs in distribution systems is not linear and convex. Therefore, mathematical algorithms are not suited for solving this complex optimization problem due to their limitations. Evolutionary methods are used for solving engineering optimization problems due to their features such as simple implementation and low computational volume. Most of the research examined in this study have used evolutionary methods including NSGA II (Liu et al. 2019), GA (Din et al. 2019), and PSO (Kumari et al. 2017) for solving optimal placement and sizing DGUs and SCs in the distribution network. However, due to the random nature of these methods, they may encounter initial convergence in solving some complex optimization problems. Therefore, finding a suitable and practical optimization method is of paramount importance.
The main ideas presented in the paper are as follows:
-
Providing a novel approach for optimal sizing of DGUs and SCs in the distribution network by considering the variable electrical load.
-
Presenting a TOU mechanism as one of the DRPs for optimal sizing of DGUs and SCs in the network to modify the consumption pattern of subscribers.
-
Considering the ENS index as a function of the reliability objective in this study and improving this index by allocating DGUs and SCs in the distribution system.
-
Considering sources of uncertainty, including consumption power demand and electricity purchase price, for solving the considered optimization problem.
-
Presenting a MSFLA to address the complexity of the optimization problem and to provide a new type of mutation operator in the proposed algorithm to enhance search-ability and population diversity.
-
Utilizing the Pareto optimization approach based on the domination concept in the proposed algorithm to solve the multi-objective optimization problem and introducing two various criteria, Generational Distance (GD), Diversity Metric (DM) to evaluate Pareto solutions.
The primary goal of this study is to introduce an efficient approach to obtain the optimal sizing of DGUs and SCs, considering the resources of uncertainty and DRPs. Energy loss, operational cost, and ENS index are considered as objective functions in this research. Also, to demonstrate the capability of the proposed approach, two 95 and 136-bus test networks are utilized. Given the different objective functions in this study, the proposed algorithm uses a fuzzy strategy to save the set of non-dominated solutions in an external repository. This study is organized as follows. In Sect. 2, the problem formulation, including objective functions, constraints, uncertainty modeling and time of mechanism are presented. The optimization methodology and simulation results are described in Sects. 3 and 4. The Pareto solution analysis and conclusions are presented in Sects. 5 and 6.
2 Problem formulation
The optimization problem addressed in this paper is to find the optimal size of DGs and SCs for installation in radial distribution systems taking into account variable load and uncertainty of load and electricity price. The objective functions adopted in this study are to minimize energy loss, ENS, and operational cost. Objective functions are bounded by equality and inequality constraints. In the following, uncertainty sources modeling and time of use mechanism are presented in this section.
2.1 Objective function
In this study, the objective functions include minimization of energy loss, operational cost, and ENS index.
-
Energy loss
Distribution system energy loss is obtained from Eq. (1) (Lotfi et al. 2019)
$${\mathrm{f}}_{1}(\mathrm{X})=\sum_{\mathrm{i}=1}^{{\mathrm{N}}_{brch}}{\mathrm{R}}_{i}{\left|{\mathrm{I}}_{i}\right|}^{2}$$(1)$$\mathrm{X}=\left[{\mathrm{P}}_{DG1},{\mathrm{P}}_{DG2},\dots .{\mathrm{P}}_{DG,NDG},{\mathrm{Q}}_{Cap1},{\mathrm{Q}}_{Cap2},\dots .{\mathrm{Q}}_{Cap,NCap}\right]$$(2) -
Operational cost
The operational cost in this study is derived from the following equation:
$${\mathrm{f}}_{2}\left(\mathrm{X}\right)=\sum_{\mathrm{j}=1}^{{\mathrm{N}}_{DG}}{\mathrm{Price}}_{DG,j}\,{\mathrm{P}}_{DG,j}+\sum_{\mathrm{s}=1}^{{\mathrm{N}}_{sub}}{\mathrm{Price}}_{Sub,s}{\mathrm{ P}}_{Sub,s}$$(3) -
Energy not supplied
The ENS of the reliability objective function is derived from Eq. (4):
where, \(v= \left\{0.1.\dots .(n-1)\right\}\) is the set of the nodes in the distribution network. The final equation to calculate the ENS of the network without considering the reference node is calculated from Eq. (5):
2.2 Constraints
In this section, some equality and inequality limitations for the optimization problem are provided that should be satisfied.
-
Load flow equations
$${\mathrm{P}}_{j}=\sum_{\mathrm{i}=1}^{{\mathrm{N}}_{Bus}}{\mathrm{V}}_{i}{\mathrm{V}}_{j}{\mathrm{Y}}_{ij}\mathrm{cos}\left({{\theta}}_{ij}-{\updelta }_{i}+{\updelta }_{j}\right)$$(6)$${\mathrm{Q}}_{j}=\sum_{\mathrm{i}=1}^{{\mathrm{N}}_{Bus}}{\mathrm{V}}_{i}{\mathrm{V}}_{j}{\mathrm{Y}}_{ij}\mathrm{sin}({{\theta}}_{ij}-{\updelta }_{i}+{\updelta }_{j})$$(7) -
Bus voltage range
$${\mathrm{V}}_{min}\le {\mathrm{V}}_{i}\le {\mathrm{V}}_{max}\quad i=1,2,\dots {,\mathrm{N}}_{Bus}$$(8) -
Feeder current
$$\left|{\mathrm{I}}_{f,i}\right|\le {\mathrm{I}}_{f,i}^{Max} \quad i=1,2,\dots {,\mathrm{N}}_{feeder}$$(9) -
DGs constraint
$${\mathrm{P}}_{DG}^{\mathrm{min}}\le {\mathrm{P}}_{DG,i}\le {\mathrm{P}}_{DG}^{\mathrm{max}} \quad i=1,2,\dots {,\mathrm{N}}_{DG}$$(10) -
Shunt capacitor limit
$${\mathrm{Q}}_{Cap,i}\le {\mathrm{Q}}_{d} \quad i=1,2,\dots {,N}_{Cap}$$(11)
2.3 Uncertainty sources modeling
In this study, power demand and electricity purchase price are considered as uncertainty resources in the optimization problem. Uncertainty in the projected power demand and the purchase price of electricity formulated by the normal and log-normal distribution functions are expressed as follows:
In this study, the scenario generation method is utilized to account for the uncertainty of system design parameters. In this method, using Monte Carlo simulation, a number of random modes are developed for the system variables using the probabilistic distribution function of system variables, then the occurrence probability of each mode is computed (Barani et al. 2018; Niknam et al. 2012). Equations (14, 15) reveal the samples extracted from the probabilistic distributions for power demand and the purchase price of electricity, respectively. The sum of probabilities must be equal to one, Eq. (16) shows how samples are combined to generate scenarios in which the sum of the probabilities of the generated scenarios is always equal to one (17).
It should be noted that in this paper, to reduce computational complexities and accelerate program execution, the scenario reduction is employed using the backward technique (Barani et al. 2018; Niknam et al. 2012). This method, in addition to reducing the computational complexities of the problem and improving its speed, ensures the accuracy required for problem solving. Scenario reduction is a method for optimal selection of useful scenarios from a set of generated scenarios that not only shortens the execution time of the algorithm, but also considerably reduces the computational complexity of the problem. For this purpose, the backward reduction technic is used to reduce the number of scenarios. Suppose that the initial probability distribution \(\mathrm{Q}\) is defined on the scenario set \(\Omega\). The problem of optimal reduction of set \(\Omega\) can be expressed as follows:
Define a subset of scenarios \(\Omega s \subset\Omega\) and assign a new distribution to remaining scenarios so that the reduced probability distribution \({\mathrm{Q}}^{{\prime}}\) defined on Ωs set is the nearest distribution to the main distribution \(\mathrm{Q}\) in terms of probability distance. The Kantorovich distance can be expressed as follows:
In the above equation, \(\mathrm{S}\) is a string scenario that has \(\mathrm{H}\) subsets of \({\mathrm{s}}_{i}\), \(\mathrm{d }(\mathrm{S, S}^{\prime\prime})\) is the distance between the two scenarios S and S″.
The scenario reduction algorithm is as follows:
-
Collect the generated scenarios and determine the obtained scenarios probabilities so that the sum of scenario probabilities in each step is one.
-
Calculate the vector distance matrix for each scenario pair, and compute the Kantorovich distance matrix by multiplying the probabilities of scenarios.
-
Find the scenario with the lowest Kantorovich distance and mark it in the Kantorovich matrix.
-
Choose a scenario with minimum Kantorovich distance and the scenario with the closest Kantorovich distance from that scenario.
-
Eliminate the scenario with the lowest Kantorovich distance due to its low probability and closeness to the other scenario, and add its probability to the closest scenario. By doing so, the sum of the remaining scenarios will always be one.
-
Update the probability matrix with the new matrix.
2.4 Time of use mechanism
Demand response programs (DRPs) refer to a set of measures taken to modify energy usage pattern to boost system stability and hamper price rise, particularly at peak network loads. Participants in the DRPs are subscribers who, instead of reducing consumption, are responsible for modifying their energy usage patterns to diminish their costs, which ultimately results in lower electricity usage. In general, DRPs can be split into two sections: incentive programs and price-based programs (Azizivahed et al. 2019; Jahani et al. 2019).
In this paper, one of the DRPs called time of use mechanism (TOU) is used to alter the consumers’ usage pattern to improve system performance. Mathematical modeling of the TOU mechanism is presented in (20)–(22). Based on this mechanism, the total modified energy cannot exceed a fixed value (assuming 15% of the base demand). Also, a balance must be struck between the increase and drop of overall power over a particular period.
3 Multi-objective optimization strategy
In this section, original shuffled frog leaping algorithm (SFLA), modified shuffled frog leaping algorithm (MSFLA) and fuzzy clustering strategy are briefly presented.
3.1 Shuffled frog leaping algorithm
The SFLA was first introduced in 2003 by Eusuff et al. (2006). In this algorithm, each frog possesses information about a solution to a problem. The SFLA consists of the initial population of possible solutions to the problem. These solutions are actually a set of virtual frogs that are further divided into several groups. Each group of frogs has characteristics that can be influenced by the characteristics of frogs in other groups. In each group, the worst and best frogs are shown by \({\mathrm{X}}_{w}\) and \({\mathrm{X}}_{b}\), respectively. The best frog between the groups is indicated by \({\mathrm{X}}_{G}\). The evolutionary process is performed by changing the position of the worst frog \({\mathrm{X}}_{w}\) in each group as follows:
After applying Eqs. (23, 24), if the new position of the worst frog is not improved, the evolutionary process is conducted by replacing \({\mathrm{X}}_{G}\) with \({\mathrm{X}}_{b}\) in Eq. (24). If the position of frogs cannot be enhanced, a new frog is randomly generated in the place of the worst frog in the above equations. Figures 1 and 2 show the movement of the worst frog toward the optimal position and the pseudo-code of the SFLA, respectively.
3.2 Modified shuffled frog leaping algorithm
The classic SFLA, where frogs with the worst fit adjust their position relative to the group or the best frog, deploy them along a line between \({\mathrm{X}}_{b}\) and \({\mathrm{X}}_{w}\). This may lead the algorithm towards the wrong answers. For this reason, we present a new strategy to improve the performance of the MSFLA. Equation (26) is suggested for the kth repetition due to the limited search score.
In the above equation \(\mathrm{C}\) is a search acceleration factor that prevents algorithm to stagnate at a local optimum leading to its premature convergence (Elbeltagi et al. 2007). A review of previous studies reveals that the range of acceleration values between 1.3 and 2.1 (1.3 < C < 2.1) (Elbeltagi et al. 2007) provides the MSFLA with the best opportunity to find the global optimal with a minimum number of iterations. To have more control over Eq. (26), a weight \(\mathrm{W}\) is added. It expresses the relationship between the local optimum point and the global optimum point in the frog leap process according to Eq. (27):
In the above equation, parameter \(\mathrm{W}\) has a huge effect on the convergence behavior of the algorithm. A higher value of parameter \(\mathrm{W}\) boosts the algorithm’s ability to find the global point in the search space and undermines the ability to find the local point. The effect of the previous speed on the current speed of the algorithm can be controlled by modifying \(\mathrm{W}\) according to Eq. (28).
Thus, the value of \(\mathrm{W}\) will gradually decrease from \({\mathrm{W}}_{max}\) to the minimum value \({\mathrm{W}}_{min}\) in a linear iterative process. The search capacity in an algorithm iteration process is high and the algorithm will be able to search a large solution space and new areas will be constantly explored to find the solution. From the perspective of intermittent iteration, the algorithm progressively shrinks its search range to one area, thus increasing the convergence rate. The flowchart of the MSFLA is depicted in Fig. 3.
3.3 Fuzzy clustering strategy
In this study, the problem of Multi-objective optimization where there are contradictory objective functions is performed using a fuzzy optimization tool (Lotfi et al. 2019). The membership function is applied to have the same range for all objective function as follows:
The normalized objective function (Lotfi 2020; Lotfi et al. 2019) is calculated for each individual as follows:
\({\upbeta }_{k}\) is chosen based on the degree of priority from the point of view of operator. In this study, (\({\mathrm{B}}_{1} = {\mathrm{B}}_{2} = {\mathrm{B}}_{3}\)= 0.33) for three-objective optimization and (\({\mathrm{B}}_{1} = {\mathrm{B}}_{2}\) = 0.5) for two-objective optimization.
4 Simulation result
In this section, 95 and 136-node test systems are employed to assess the ability of the MSFLA for solving the problem of determining the optimal capacity of DGUs and SCs in the distribution network. All simulations are done in MATLAB (ver. 2016a). The scenario reduction strategy with 50 scenarios is used to model the sources of uncertainty. Also, the sources of uncertainty in solving the optimization problem include consumption demand and electricity purchase price. The TOU mechanism as one of the DRPs is executed in all nodes of the two test networks, the idea of using TOU is to reduce the operational cost and improve the system performance by shifting the electrical loads from peak times to off-peak times. To compare and validate the results of the proposed method, gravitational search algorithm (GSA), Imperialist competitive algorithm (ICA), Non-dominated sort genetic algorithm II (NSGA II), and SFLA are utilized to solve the considered optimization problem. After the introduction of the first version of the Genetic Algorithm in 1993, in 2002, the proponents of this algorithm introduced an elitist mechanism based on the importance of defective queues called the NSGA II to provide diversity in Pareto-optimal solutions (Liu et al. 2019; Parvizi and Rezvani 2020). In order to shown the mechanism and ability of the proposed algorithms to solve the optimization problem, the values of the parameters related to these algorithms are depicted in Table 1. Moreover, three cases are simulated to solve the optimal sizing of DGs and SCs in each test network:
-
1-
Only installation of SCs.
-
2-
Only installation of DGs.
-
3-
Installation of both DGs and SCs simultaneously.
4.1 95-node test system
This test system is depicted in Fig. 4, and the demand characteristic of this system is depicted in Fig. 5 (Lotfi et al. 2019). Five 1000 kW DGUs (diesel generators) are installed in buses # 6, # 10, # 25, # 34 and # 45 along with four 100 kVAr capacitors in buses # 10, # 24, # 34 and # 70. The cost of purchasing electricity from DGUs is $ 0.042 per kW. The cost of energy purchased from substations at high and low demand periods is $ 0.04465 per kWh and $ 0.0401 per kWh, respectively. The energy loss, operational cost, and ENS before installing DGUs and SCs are 31,869.54 kWh, $ 140,651.91, and 345.56 kWh/ year, respectively.
In this section, the optimization problem in the presence of separate and simultaneous DGUs and SCs in the single-objective framework is solved by various algorithms. The best, worst and average results along with the standard deviation (STD) of MSFLA, SFLA, ICA, GSA, and NSGA II algorithms for optimization cases 1 and 2 in 20 different experiments are depicted in Table 2. In order to provide more details of the results of methods used in 20 different experiments, Tables 3, 4, and 5 compares the single-objective optimization results obtained by different methods in 20 experiments for cases 1 and 2, respectively.
According to Table 2, it is clear that the proposed MSFLA converges to better results than other methods. Moreover, DGUs allocation has a significant role in reducing the objective functions compared to SCs allocation in the distribution test system. For example, the values of ENS and energy loss obtained by the MSFLA for case 1 are 304.46 kWh/year and 30,075.35 kWh, respectively. In case 2, these values have reached 294.31 kWh/year and 29,889.35 kWh, respectively. Also, the values of ENS, energy loss, and operational cost obtained from the MSLA for case 2 dropped by about 17%, 6.5%, and 5.5% compared to the initial values.
To illustrate the impact of DRP on objective functions assessment, the results of different objective function optimization attained by several algorithms for case 3 without and applying the TOU mechanism are listed in Table 6. Moreover, the optimal shame of active and reactive power generation of DGUs and SCs for optimizing energy loss is depicted in Table 7. According to Tables 2, 3, 4, 5 and 6, the following points can be taken.
Firstly, the solution found by the MSFLA outperforms than other evolutionary methods. Secondly, the amount of objective functions including energy loss, ENS, and operational cost obtained from the MSLA have dropped by 11%, 25.5%, and 5% compared to the initial values, which shows the effectiveness of the simultaneous allocation of DGUs and SCs than the separate allocation of these units in the test network. Thirdly, applying the TOU program has reduced the objective functions in this study. For instance, values of energy loss, ENS, and operational cost dropped by 12.5%, 30%, and 5.5% compared to the initial values, respectively. Also, comparing the results of the objective functions between non-execution and execution of the TOU program reveals the effect of the DRP on improving the results of the objective functions. For example, the value of objective functions for energy loss, ENS, and operational cost dropped from 28,563.21 kW, 276.51 kWh/year, and $ 133,661.31 to 28,365.21 kW, 262.13 kWh/year and $ 133,586.15, respectively.
Finally, the highest and lowest total active power generation of DGUs is at 6 pm, and 11 am with 4368.72 kW and 1006.47 kW, respectively. Also, the highest and lowest active power generation of these units in 24 h belong to units 1 and 5 at 8 pm and 3 am with 979.74 kW and 103.54 kW, respectively. Moreover, the highest and lowest values of the total reactive power generation of SCs are observed at 4 pm, and 3 am with 347.94 kVAr and 67.78 kVAr, respectively. Similarly, the highest and lowest reactive power generation of SCs in 24 h are observed in units 4 and 1 at 3 pm, and 3 am with 93.79 kVAr and 10.13 kVAr, respectively.
Figures 6 depicts the convergence curve of the operational cost objective function gained by utilizing the five algorithms including MSFLA, NSGA II, SFLA, GSA, and ICA for 95-node test system. Given this figure, it is clear that the MSFLA is converged to the optimal solution earlier compared to other methods.
Comparing the values of the objective functions in Table 2 exhibits that the objective functions of this study are inconsistent with each other. In other words, not all three objective functions improved at the same time. As a result, the problem of Multi-objective optimization cannot be solved with the concept of single-objective. Therefore, we use Pareto optimization strategy to satisfy all objective functions. Figures 7 and 8 show the Pareto optimal fronts related to the optimization of two and three-objective obtained from the MSFLA. Moreover, the best compromise solution of each front is shown in red.
According to Figs. 7 and 8, it can be concluded that the difference between value of objective functions in best compromise response with their optimal values is not much different, which it shows the ability of the proposed method to solve the Multi-objective optimization problem. Besides, the value of objective functions in best compromise response related to Fig. 8, including loss, ENS, and operational cost declined by 11.5%, 24%, and 5% compared to the initial values.
Figure 9 exhibit the effects of DGUs, SCs, and DRP on the profiles of voltage in the distribution test system at 6 pm. To this end, three scenarios are defined to illustrate the effect of DGUs, SCs, and DRP on the voltage profiles of the two test systems. Scenario 1 is defined based on the initial network conditions, and scenarios 2 and 3 are based on the simultaneous presence of DGUs, SCs, and TOU mechanism, as well as the simultaneous presence of DGUs and SCs in both test networks, respectively. Voltage profile improvement in Fig. 9 indicates that the simultaneous presence of DGUs, SCs, and DRP exerts more significant effect on improving the voltage profile than the simultaneous presence of DGUs and SCs in solving the optimization problem.
4.2 136-node test system
This test system (López et al. 2016; Lotfi and Ghazi 2020) covers ten distributed units of 300 kW (diesel generator) in buses # 5, # 22, # 24, # 5, # 79, # 81, # 99, # 102, # 114 and # 126. Also, four 100 kVAr capacitors have been installed in buses # 10, # 20, # 34, # 70. Load profile and electricity price in 24 h are shown in Figs. 10 and 11. The purchase price of electricity from DGUs is $ 0.0425 per kWh. The energy loss, operational cost, and ENS before installing DGUs and SCs are 2155.64 kW, $ 14,549.91, and 43.53 kWh /year, respectively.
In this section, the problem of optimal sizing of DGUs and SCs in a single-objective form is solved by different evolution algorithms. Table 8 lists the results of objective functions optimization obtained from the MSFLA and other methods for cases 1 and 2, the optimization results are obtained from 20 separate experiments. Also, to further explain the results of the optimization methods in 20 different experiments, Tables 9, 10 and 11 compares the single-objective optimization results obtained by different methods for cases 1 and 2, respectively. Table 12 draws a comparison between the results of the different objective functions by several methods for case 3 in the absence and presence of DRPs. The optimal scheme of reactive and active power generation of SCs and DGUs for optimizing the operational cost are depicted in Tables 13 and 14.
According to Tables 8, 9, 10, 11 and 12, it is clear that the solution yielded by the MSFLA excels other algorithms. Moreover, the allocation of DGUs and SCs separately in the distribution network plays an important role in reducing the objective functions. The values of ENS, energy loss, and operational cost obtained from the MSLA for case 1 dropped by about 30%, 13%, and 5% compared to their initial values. These values obtained from the MSLA for case 2 decrease by about 38%, 15%, and 4.3% compared to their baseline values.
A comparison of the optimization results in the three cases indicates that the simultaneous allocation of DGUs and SCs has changed the value of objective functions of energy loss, operational cost, and ENS from 2155.64 kWh and $ 14,549.91 and 43.53 kWh/year to 1821.49 kWh, $ 13,958.45 and 28.46 kWh/year. Also, considering the TOU program and the effect of DGUs and SCS decreased the value of objective functions of energy loss, operational cost, and ENS by 29%, 7% and, 65% compared to the initial values. According to Tables 13 and 14, it is obvious that when optimizing the operational cost function, DGUs do not operate at their maximum power and the output power generation of these units has increased by 100 kW from 3 to 9 pm. Also, at 9 pm, the total maximum active power generation of DGUs reached its peak of 11,514.33 kW and the lowest total active power generation of DGUs belonging to 12 pm with 514.18 kW. Moreover, the highest and lowest reactive power generation of SCs have observed in units 4 and 2 at 8 pm, and 2 am with 97.62 kVAr and 26.94 kVAr, respectively. Also, the highest and lowest total reactive power of SCs have observed at 8 pm and 2 pm with 287.97 kVAr and 117.34 kVAr, respectively.
The convergence plot of MSFLA and other methods is shown in Fig. 12 for the energy loss objective function. This figure demonstrates that the proposed algorithm converges to the better results in less time with respect to other evolutionary algorithms.
To meet all the objectives of the problem simultaneously, the Pareto fronts related to the optimization of two and three-objective obtained from the MSFLA are shown in Figs. 13 and 14. According to Fig. 14, the value of objective functions of energy loss, operational cost, and ENS in best compromise response dropped by 16%, 7%, and 20% compared to the initial values. Another important point is that expanding the scale of the test network and increasing decision variables does not reduce the performance of the MSFLA.
Figure 15 displays the effect of DGUs, SCs, and DRP on voltage profiles in the 136-bus network at 6 pm. According to Fig. 15, it is clear that the improvement of the voltage profile in the simultaneous presence of DGUs, SCs, and TOU mechanism is more obvious than the simultaneous presence of DGUs and SCs in the test network.
5 Pareto solution analysis
The optimal Pareto fronts obtained should be evaluated to demonstrate the performance of the proposed method. For this purpose, two different criteria Generational Distance (GD) and Diversity Metric (D-Metric) (Lotfi et al. 2019) are presented as follows:
The ideal numerical value for GD criterion is zero, which indicates that all components are on the optimal Pareto front and are also close to each other. Moreover, a higher value for (D-Metric) criterion indicates that many of the components in the Pareto front are close together.
Table 15 tabulates the best values of \(\mathrm{GD}\) and \(\mathrm{DM}\) indicators which helps readers to learn more about the powerful performance of the proposed algorithm for managing these cases. These values are achieved from solving multi-objective optimal allocation of DG sources and capacitors for two test systems. According to Table 15, it is obvious that the proposed MSFLA algorithm are able to handle Multi-objective optimization problems. Also, as shown by Table 15, it is clear that the criterions provided by the proposed MSFLA demonstrates the MSFLA algorithm's ability in solving the multi-objective problem.
6 Conclusion
Increasing the high penetration rate of distributed generation units (DGUs) in distribution networks and also considering the simultaneous effect of these units with shunt capacitors (SCs) in order to improve the performance of the distribution system, has created challenges such as reliability and economic issues for system operator. In this study, a novel approach called MSFLA is provided to obtain the optimal sizing of DGUs and SCs, considering the sources of uncertainty and demand response program. Compared with original SFLA, it expands local exploration scope and enhances the population diversity. Reduction of energy loss, operational cost, and ENS are defined as objectives in this study. The problem limitations include buses voltage, lines current and DGUs generation boundaries. The MSFLA uses the concept of dominance to obtain the Pareto-optimal solution in solving the presented Multi-objective optimization problem. The proposed method is tested on two 95 and 136-node test systems. The results which are achieved from the proposed method in comparison with the results of other evolutionary and state-of-art methods including SFLA, ICA, NSGA II, and GSA prove the claim that the proposed method has high accuracy and efficiency to solve single and Multi-objective problems regardless of the complexities and dimensions of the problem.
Simultaneous allocation of DGUs and SCs in the distribution network reduces energy loss, ENS, and operational cost. For example, the values energy loss, ENS, and operational cost obtained by MSFLA in the first system are dropped by 11%, 25.5%, and 5% compared to initial values. Considering the TOU program as one of the DRPs in allocation of DGUs and SCs simultaneously in the distribution network, while changing the consumption pattern of subscribers, improved the performance of the distribution system due to diminished energy loss and operational cost. Moreover, the values energy loss, ENS, and operational cost obtained by MSFLA in the second system are reduced by 29%, 65%, and 7% compared to the initial values. Also, the voltage profile in both test networks, considering DGUs, SCs, and DRP, has a more noticeable improvement compared to the presence of only DGUs and SCs in the distribution network.
Some suggestions for future studies of this research are as follows:
-
Simultaneous scheduling of distributed generation units or shunt capacitors and FACTS taking into account the actual model of the electric load as well as its uncertainty.
-
Integrating battery storage system with distributed generation units in the distribution network considering technical and operational constraints.
-
Stochastic optimal planning of the distribution network with the sporadic nature of distributed generation units and electrical vehicles according to the optimal location of charging stations.
-
Coordinated planning in the distribution network by simultaneously performing strategies of capacitor placement, dispatchable distributed generation units and distributed feeder reconfiguration.
Abbreviations
- \({{\varphi }}_{Pd}{{\varphi }}_{Ep}\) :
-
Occurrence probability of load demand and electricity price
- \({\mathrm{C}}_{Ep}\,\,{\mathrm{C}}_{Ep}\) :
-
Numerical values extracted from probabilistic distributions for load demand and electricity purchase price
- \({\mathrm{P}}_{t,i}^{MDF}\) :
-
Modified demand of the ith feeder at time t
- Ns :
-
Number of scenarios
- \({\mathrm{P}}_{t,i}^{\mathrm{TOU}}\,\,\) \({\mathrm{P}}_{t,i}^{\mathrm{INI}}\) :
-
Surge or drop in the demand for this mechanism and the initial demand values in ith feeder at time t without TOU mechanism
- \({\mathrm{TOU }}^{\mathrm{max}}\) :
-
Maximum speed of demand surge or drop in the TOU mechanism
- \(\upmu\) :
-
Mean value
- \(\upsigma\) :
-
Standard deviation
- \({\mathrm{X}}_{w}{\mathrm{X}}_{b}\) :
-
Worst and best frogs
- \({\mathrm{P}}_{DG,j}\) :
-
Active power of jth DG unit
- \({\mathrm{P}}_{Sub,s}\) :
-
Active power of sth sub-station
- \({\mathrm{Price}}_{DG,j}\) :
-
Purchase price of electricity from jth DG unit
- \({\mathrm{Price}}_{Sub,s}\) :
-
Purchase price of electricity from sth sub-station
- \({\mathrm{U}}_{i,j }{\mathrm{ U}}_{i,j}^{\prime}\) :
-
Repair time (hours per year) and the compensation time for the branches related to bus i
- \({\uplambda }_{i,j}{\mathrm{ d}}_{i,j}\) :
-
Failure rate and line length
- \({\mathrm{N}}_{Sub}\) :
-
Number of sub-stations
- \(\mathrm{C}\) :
-
Constant value
- \({\mathrm{Y}}_{ij}{{\theta}}_{ij}\) :
-
Magnitude and branch admittance angle between buses i and j
- \({\mathrm{KK}}_{\mathrm{max}}\) :
-
Number of current iteration and maximum iteration number
- \(\mathrm{W}\) :
-
Inertia weight
- \({\mathrm{f}}_{i}^{\mathrm{min}}{\mathrm{f}}_{i}^{\mathrm{max}}\) :
-
Lower and upper limits of ith objective function
- \({\upmu }_{i}\) :
-
Fuzzy membership function of ith objective function
- \({\upbeta }_{k}\) :
-
kTh weight of objective function
- \({\mathrm{E}}^{\mathrm{pr}}\) :
-
Distribution function parameter
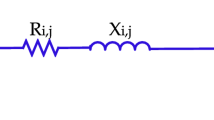
- \({\mathrm{R}}_{i}\) :
-
Resistance of the ith line
- \({\mathrm{I}}_{i}\) :
-
Current of ith line
- \({\mathrm{N}}_{\mathrm{brch}}\) :
-
Number of branches
- \(\mathrm{X}\) :
-
Vector of decision variables
- \({\mathrm{X}}_{G}\) :
-
Best frog between all memblexes
- \(\mathrm{rand}\) :
-
Random number in [0,1]
- \({\mathrm{D}}_{\mathrm{min}}\,\,{\mathrm{D}}_{\mathrm{max}}\) :
-
Minimum and Maximum displacement of ith frog
- \({\mathrm{V}}_{\min}{\mathrm{V}}_{\max}\) :
-
Minimum and maximum allowable values of ith bus voltage
- \({\mathrm{Q}}_{C,i} {\mathrm{Q}}_{d}\,\,{\mathrm{I}}_{f,i}{\mathrm{I}}_{f,i}^{\mathrm{Max}}\) :
-
Current amplitude at time t and the maximum current of ith feeder
- \({\mathrm{P}}_{DG}^{\mathrm{min}}{\mathrm{P}}_{DG}^{\mathrm{max}}\) :
-
Minimum and maximum output power of ith DG unit
- \({\mathrm{N}}_{\mathrm{Cap}}\) :
-
Number of capacitors
- \({\mathrm{t}}_{i,j} {\mathrm{t}}_{i,j}^{\prime}\) :
-
Average repair time and the average line recovery time between the ith and jth buses
- \({\mathrm{P}}_{\mathrm{j}}\,\, {\mathrm{Q}}_{\mathrm{j}}\) :
-
Active and reactive power injected by the network in the ith bus
- \({\mathrm{N}}_{\text{Bus}}\) :
-
Number of buses
- \({\mathrm{V}}_{i}{\updelta }_{i}\) :
-
Voltage magnitude and Voltage angel of the ith bus
- \(\mathrm{m}\,\,\mathrm{n}\) :
-
Number of non-dominated solution and objective functions
- \({\mathrm{W}}_{\mathrm{min}}{\mathrm{W}}_{\mathrm{max}}\) :
-
Boundaries of inertia weight
- \({\mathrm{N}}_{DG}\) :
-
Number of DG units
- \({\mathrm{N}}_{\mu j}\) :
-
Normalized membership function of each for each member
References
Abdelaziz A, Ali E, Abd Elazim S (2016) Optimal sizing and locations of capacitors in radial distribution systems via flower pollination optimization algorithm and power loss index. Eng Sci Technol Int J 19(1):610–618
Abou El-Ela AA, El-Sehiemy RA, Kinawy A-M, Mouwafi MT (2016) Optimal capacitor placement in distribution systems for power loss reduction and voltage profile improvement. IET Gener Transm Distrib 10(5):1209–1221
Abou El-Ela AA, El-Sehiemy RA, Abbas AS (2018) Optimal placement and sizing of distributed generation and capacitor banks in distribution systems using water cycle algorithm. IEEE Syst J 12(4):3629–3636
Al-Ammar EA, Ghazi GA, Ko W, Khan Y, Beroual A, Hong J, Song S-H (2021) Comprehensive impact analysis of ambient temperature on multi-objective capacitor placements in a radial distribution system. Ain Shams Eng J 12(1):717–727
Askarzadeh A (2016) Capacitor placement in distribution systems for power loss reduction and voltage improvement: a new methodology. IET Gener Transm Distrib 10(14):3631–3638
Azizivahed A, Naderi E, Narimani H, Fathi M, Narimani MR (2017) A new bi-objective approach to energy management in distribution networks with energy storage systems. IEEE Trans Sustain Energy 9(1):56–64
Azizivahed A, Barani M, Razavi S-E, Ghavidel S, Li L, Zhang J (2018) Energy storage management strategy in distribution networks utilised by photovoltaic resources. IET Gener Transm Distrib 12(21):5627–5638
Azizivahed A, Lotfi H, Ghadi MJ, Ghavidel S, Li L, Zhang J (2019) Dynamic feeder reconfiguration in automated distribution network integrated with renewable energy sources with respect to the economic aspect. In: Paper presented at the 2019 IEEE Innovative Smart Grid Technologies-Asia (ISGT Asia)
Barani M, Aghaei J, Akbari MA, Niknam T, Farahmand H, Korpås M (2018) Optimal partitioning of smart distribution systems into supply-sufficient microgrids. IEEE Trans Smart Grid 10(3):2523–2533
Biswas PP, Mallipeddi R, Suganthan PN, Amaratunga GA (2017) A multiobjective approach for optimal placement and sizing of distributed generators and capacitors in distribution network. Appl Soft Comput 60:268–280
Das S, Das D, Patra A (2019) Operation of distribution network with optimal placement and sizing of dispatchable DGs and shunt capacitors. Renew Sustain Energy Rev 113:109219
Din FU, Ahmad A, Ullah H, Khan A, Umer T, Wan S (2019) Efficient sizing and placement of distributed generators in cyber-Physical power systems. J Syst Archit 97:197–207
Elattar EE, ElSayed SK (2020) Optimal location and sizing of distributed generators based on renewable energy sources using modified moth flame optimization technique. IEEE Access 8:109625–109638
Elbeltagi E, Hegazy T, Grierson D (2007) A modified shuffled frog-leaping optimization algorithm: applications to project management. Struct Infrastruct Eng 3(1):53–60
El-Fergany AA, Abdelaziz AY (2014) Artificial bee colony algorithm to allocate fixed and switched static shunt capacitors in radial distribution networks. Electr Power Compon Syst 42(5):427–438
Eusuff M, Lansey K, Pasha F (2006) Shuffled frog-leaping algorithm: a memetic meta-heuristic for discrete optimization. Eng Optimiz 38(2):129–154
Galgali VS, Ramachandran M, Vaidya G (2019) Multi-objective optimal sizing of distributed generation by application of Taguchi desirability function analysis. SN Appl Sci 1(7):742
Grisales-Noreña LF, Gonzalez Montoya D, Ramos-Paja CA (2018) Optimal sizing and location of distributed generators based on PBIL and PSO techniques. Energies 11(4):1018
Jahani MTG, Nazarian P, Safari A, Haghifam M (2019) Multi-objective optimization model for optimal reconfiguration of distribution networks with demand response services. Sustain Cities Soc 47:101514
Kavousi-Fard A, Samet H (2013) Multi-objective performance management of the capacitor allocation problem in distributed system based on adaptive modified honey bee mating optimization evolutionary algorithm. Electr Power Compon Syst 41(13):1223–1247
Kumari RL, Kumar GN, Nagaraju SS, Jain MB (2017) Optimal sizing of distributed generation using particle swarm optimization. Paper presented at the 2017 International Conference on Intelligent Computing, Instrumentation and Control Technologies (ICICICT)
Liu W, Luo F, Liu Y, Ding W (2019) Optimal siting and sizing of distributed generation based on improved nondominated sorting genetic algorithm II. Processes 7(12):955
López JC, Lavorato M, Rider MJ (2016) Optimal reconfiguration of electrical distribution systems considering reliability indices improvement. Int J Electr Power Energy Syst 78:837–845
Lotfi H (2020) Multi-objective energy management approach in distribution grid integrated with energy storage units considering the demand response program. Int J Energy Res 44(13):10662–10681
Lotfi H, Ghazi R (2020) Optimal participation of demand response aggregators in reconfigurable distribution system considering photovoltaic and storage units. J Ambient Intell Humaniz Comput 12:2233–2255
Lotfi H, Samadi M, Dadpour A (2016) Optimal capacitor placement and sizing in radial distribution system using an improved Particle Swarm Optimization algorithm. Paper presented at the 2016 21st Conference on Electrical Power Distribution Networks Conference (EPDC)
Lotfi H, Ghazi R, Sistani MBN (2019) Providing an optimal energy management strategy in distribution network considering distributed generators and energy storage units. Paper presented at the 2019 International Power System Conference (PSC)
Lotfi H, Ghazi R, bagher Naghibi-Sistani M (2020) Multi-objective dynamic distribution feeder reconfiguration along with capacitor allocation using a new hybrid evolutionary algorithm. Energy Syst 11:779–809
Niknam T, Kavousifard A, Aghaei J (2012) Scenario-based multiobjective distribution feeder reconfiguration considering wind power using adaptive modified particle swarm optimisation. IET Renew Power Gener 6(4):236–247
Parvizi E, Rezvani MH (2020) Utilization-aware energy-efficient virtual machine placement in cloud networks using NSGA-III meta-heuristic approach. Cluster Comput 23:2945–2967
Ravindran S, Victoire TAA (2018) A bio-geography-based algorithm for optimal siting and sizing of distributed generators with an effective power factor model. Comput Electr Eng 72:482–501
Reddy P, Prasad D (2014) Sensitivity based capacitor placement using cuckoo search algorithm for maximum annual savings. IOSR J Eng 4(4):6
Su H (2019) Siting and sizing of distributed generators based on improved simulated annealing particle swarm optimization. Environ Sci Pollut Res 26(18):17927–17938
Tah A, Das D (2016) Novel analytical method for the placement and sizing of distributed generation unit on distribution networks with and without considering P and PQV buses. Int J Electr Power Energy Syst 78:401–413
Veera Reddy VC (2018) Ant Lion optimization algorithm for optimal sizing of renewable energy resources for loss reduction in distribution systems. J Electr Syst Inf Technol 5(3):663–680
Zeinalzadeh A, Mohammadi Y, Moradi MH (2015) Optimal multi objective placement and sizing of multiple DGs and shunt capacitor banks simultaneously considering load uncertainty via MOPSO approach. Int J Electr Power Energy Syst 67:336–349
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that there is no conflict of interest regarding the publication of this paper.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Lotfi, H. Optimal sizing of distributed generation units and shunt capacitors in the distribution system considering uncertainty resources by the modified evolutionary algorithm. J Ambient Intell Human Comput 13, 4739–4758 (2022). https://doi.org/10.1007/s12652-021-03194-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12652-021-03194-w