1 Introduction

As is well known, the thermal phenomena have destructive and constructive effects in the electromagnetic devices [1,2,3]. Usually, thermal effects are appeared by a factor in the permittivity of materials in the electromagnetic instruments. The transportation of electromagnetic waves in electro magneto-active materials such as the plasmas [4,5,6], the piezo semiconductors [7, 8] and the semiconductors [9] are effected from the thermal effects of their electrical carriers.

In some cases, the electromagnetic energy can be transported from electromagnetic waves to the warm charged particles and it causes to increase the kinetic energy of the system. In the opposite case, the kinetic energy of warm charged particles is transferred to increase of amplitude of electromagnetic waves as electromagnetic energy and the waves will be amplified [10,11,12]. The process of electromagnetic energy transportation from the waves to the warm charged particles is called as particle acceleration and the energy transportation from the warm charged particles to electromagnetic waves is known as wave amplification [13, 14].

On the other hand, as we know, passing the waves from a region to the other region will be caused the reflection phenomenon and transmission phenomenon of the waves. The transmission and reflection of the waves from a region to another region are strongly depend on electromagnetic properties of two regions. This effect can be shown by a parameter which it will be presented in permittivity function of material [15].

One of the electromagnetic instruments in which the electromagnetic waves are controlled and guided is the waveguides. Recently, the presence of electro magneto-active materials in the waveguides have been widely used in the particle acceleration, wave amplification and material heating [16,17,18,19,20]. One of the main problems in transportation of energy from a waveguide to the other waveguide is obtaining of the transmission and reflection coefficients of the waves in this process [21].

The passing of electromagnetic waves from a semi-bounded loss free waveguide to another semi-bounded waveguide with a plasma rod can be a suitable structure for plasma heating. Also, the simulation of wave transportation from the waveguide to a semi-bounded plasma waveguide can provide a suitable tool for amplification of the electromagnetic fields in the plasma region, which is widely used in the particles acceleration in the plasma waveguides [22].

As is well known, the charged carriers of a plasma have a considerable kinetic energy. Therefore, calculation of the transmission and reflection coefficients in the prose of the transportation waves will be closer to reality if the thermal effects are considered.

Recently, the passing of the electromagnetic waves from a semi-bounded dielectric waveguide to a semi-bounded plasma waveguide have been studied [23]. In the mentioned paper, the role of the incident wave frequency on reflected and transmitted waves was investigated and the plasma rod was thermodynamically considered in cold approximation. In this paper, it is assumed that the thermal velocity of the electric charged carriers is considerable. Therefore, the comparison of the phase velocity and the thermal velocity will be inevitable. This issue is caused that the adiabatic and non-adiabatic states are considered. As result, the role of the plasma temperature on reflected and transmitted waves for adiabatic and non-adiabatic states are investigated.

This paper consists of five sections, that the introduction presented as Sect. 1. In Sect. 2, the configuration of the waveguide is presented and the governed equations of the reflection and transmission coefficients are obtained.

In Sect. 3, the graphs of transmission coefficients in terms of the ratio of thermal velocity to phase velocity will be investigated.

Section 4 will be presented to the simulation of reflection coefficients.

Also, the diagram of the phase difference in terms of the ratio of thermal velocity to phase velocity will be studied for both transmitted and reflected waves. In both Sects. 3 and 6, the simulations have been done for Vph > Vth (adiabatic phenomenon) and Vph < Vth (non-adiabatic phenomenon). Here Vph is the phase velocity of transmitted wave and Vth is the thermal velocity of plasma charges carriers. In Sect. 5, a summary and conclusion are presented.

2 Configuration and governing equations

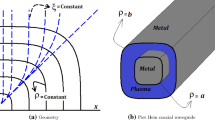
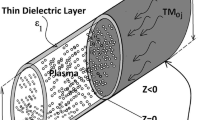
The studied waveguide is shown in Fig. 1. As shown in Fig. 1, it is a cylindrical waveguide with circular cross-section, loss-free metallic wall and infinite length which is consisted of two semi-bounded waveguides. An incident wave with axially symmetrical TM0j mode and harmonic time variations e−iωt is propagating in the mentioned waveguides from the first waveguide toward the second waveguide. The transversal boundary of these waveguides is placed in z = 0.

Fig. 1
figure 1

Geometrical configuration of the waveguide

Full size image

The first waveguide is filled with a loss-free dielectric material with real permittivity εd1 and real permeability μ0 in the region z < 0 and the second waveguide is filled with a loss-free dielectric material with real permittivity εd2 and real permeability μ0, in the region z > 0 [24, 25]. A warm plasma column is placed on the waveguide axis in z > 0.

The radii of the waveguide and the plasma column are Rm and Rp, respectively. The radius of the plasma column is considered to be much smaller than the radius of the waveguide (Rp <  < Rm).

The plasma is assumed to warm and collision less approximation for the high frequency region.

Since, the propagation of the transmitted waves in the plasma region in this waveguide is longitudinal, therefore, the appropriated permittivity coefficient for the plasma region is as follows [26]:

$$\varepsilon_{p} = \varepsilon_{0} \left( {1 - \frac{{\frac{{\omega_{p}^{2} }}{{\omega^{2} }}}}{{1 - \frac{{(k_{zn}^{t} )^{2} }}{{\omega^{2} }}\frac{{\gamma k_{B} T}}{{m_{e} }}}}} \right)$$
(1)

where ω is wave frequency, ktzn is the wavenumber of the transmitted waves in the plasma in z > 0 region and ωp is electron plasma frequency

$$\omega_{p} = \sqrt {\frac{{n_{0} e^{2} }}{{{\upvarepsilon }_{0} m_{e} }}}$$

Here e and me are the electric charge and mass of electron, respectively. Also, in Eq. (1) KB is Boltzmann constant, T is the temperature of the electrons in the plasma and γ is atomicity coefficient which is γ = 3 for one-dimensional adiabatic and γ = 1 for isothermal processes [27, 28].

The phase velocity and thermal velocity are defined as

$$\begin{aligned} V_{ph} &= \frac{\omega }{{{\text{k}}_{zn}^{t} }} \hfill \\ V_{th} &= \sqrt {\frac{{{\text{k}}_{{\text{B}}} {\text{T}}}}{{m_{e} }}} \hfill \\ \end{aligned}$$

Introducing the ratio of thermal velocity to the phase velocity as U(T) and the ratio plasma frequency to the wave frequency as ωr, we have

$$\begin{aligned} {\text{U}}\left( {\text{T}} \right) &= \frac{{\sqrt \gamma V_{th} }}{{V_{ph} }} \hfill \\ \omega_{r} &= \frac{{{\upomega }_{p} }}{\omega } \hfill \\ \end{aligned}$$

Therefore, the permittivity of the warm plasma for the longitudinal propagation of the waves which is presented in Eq. (1) can be written as follows:

$${\upvarepsilon }_{{\text{p}}} = {\upvarepsilon }_{0} \left( {1 - \frac{{\omega_{r}^{2} }}{{1 - \left( {U\left( T \right)} \right)^{2} }}} \right)$$
(2)

With taking in to account the relation (2), it is obvious that U(T) variation is coincident with the temperature variations for a fixed wave phase velocity.

By writing the wave equation in terms of the vector potential and solving it for the incident wave, the z-component of the vector potential A of the incident wave in j-th mode is obtained as follows [21, 23]:

$$A_{zj}^{i} = J_{0} \left( {\frac{{\eta_{j} }}{{R_{m} }}r} \right)e^{{ik_{zj}^{i} Z}}$$
(3)

where J0 is the Bessel function of the zero order, ηj is the jth zero of the Bessel function of the zero order and \(k_{zj}^{i}\) is the propagation constant of the incident wave,

$$\left( {k_{zj}^{i} } \right)^{2} = \Gamma_{d1}^{2} - \left( {\frac{{\eta_{j} }}{{R_{m} }}} \right)^{2}$$
(4)
$$\Gamma_{d1} = \omega \sqrt {\varepsilon_{d1} \mu_{0} }$$
(5)

The reflected waves and transmitted waves are consisted of the new modes [23]. Therefore, these waves can be written as a series of new modes that each mode is reflected and transmitted with coefficients rm and tn, respectively.

On the other hand, by solving the mentioned wave equation for the reflected and transmitted waves, the z-component of the vector potential A of these waves in mth mode and nth are obtained as follows, respectively [23, 29]:

$$A_{z}^{r} = \mathop \sum \limits_{m = 1}^{\infty } A_{zm}^{r}= \mathop \sum \limits_{m = 1}^{\infty } r_{m} J_{0} \left( {\frac{{\eta_{m} }}{{R_{m} }}r} \right)e^{{ - ik_{zm}^{r} Z}}$$
(6)
$$\begin{gathered} A_{z}^{t} = \mathop \sum \limits_{n = 1}^{\infty } A_{zn}^{t} = \mathop \sum \limits_{n = 0}^{\infty } t_{n} \left\{ {\begin{array}{ll} {J_{0} \left( {\frac{{\chi_{pn} }}{{R_{m} }}r} \right) \times e^{{ik_{zn}^{t} Z}} } & { 0 < r < R_{p} } \\ {\left( {x_{1} \left( n \right)H_{0}^{1} \left( {\frac{{\chi_{dn} }}{{R_{m} }}r} \right) + x_{2} \left( n \right)J_{0} \left( {\frac{{\chi_{dn} }}{{R_{m} }}r} \right) } \right) \times e^{{ik_{zn}^{t} Z}} } & {R_{p} < r < R_{m} } \\ \end{array} } \right. \hfill \\ \hfill \\ \end{gathered}$$
(7)

where krzm is the propagation constant of the reflected wave for mth mode,

$$\left( {k_{zm}^{r} } \right)^{2} = \Gamma_{d1}^{2} - \left( {\frac{{\eta_{m} }}{{R_{m} }}} \right)^{2}$$
(8)

and ktzn is the propagation constant of the transmitted wave for nth mode,

$$\left( {k_{zn}^{t} } \right)^{2} = \Gamma_{d2}^{2} - \left( {\frac{{\chi_{dn} }}{{R_{m} }}} \right)^{2} = \Gamma_{p}^{2} - \left( {\frac{{\chi_{pn} }}{{R_{m} }}} \right)^{2}$$
(9)

Here, \(H_{0}^{\left( 1 \right)}\) is the Hankel function of first kind of the zero order, χdn, χpn, x1(n) and x2(n) are constant coefficients and the indexes pn and dn referred to the coefficient value of the χ for the nth mode of the transmitted waves in the plasma and dielectric, respectively.

Also, Eq. (9) shows that the wave number of the transmitted waves in the dielectric and plasma must be equal with each other in the region z > 0.

In continue, the constant coefficients χdn, χ_pn, x1(n) and x2(n) in Eqs. (7) will be obtained by using the boundary conditions in the second part of the waveguide.

Now, by taking into account the continuity of the components Ez and Hϕ on the boundary between the plasma and dielectric (r = Rp) in z > 0, the coefficients x1(n) and x2(n) in Eqs. (7) can be obtained as

$$x_{1} \left( n \right) = \frac{{\chi_{pn} }}{{\chi_{d n} }}\frac{{J_{1} \left( {\frac{{\chi_{pn} }}{{R_{m} }}R_{p} } \right)J_{0} \left( {\chi_{dn} } \right)}}{{H_{1}^{\left( 1 \right)} \left( {\frac{{\chi_{dn} }}{{R_{m} }}R_{p} } \right)J_{0} \left( {\chi_{dn} } \right) - H_{0}^{\left( 1 \right)} \left( {\chi_{dn} } \right)J_{1} \left( {\frac{{\chi_{dn} }}{{R_{m} }}R_{p} } \right)}}$$
(10)
$$x_{2} \left( n \right) = - x_{1} \left( n \right)\frac{{H_{0}^{\left( 1 \right)} \left( {\chi_{dn} } \right)}}{{J_{0} \left( {\chi_{dn} } \right)}}$$
(11)
$$\frac{{\varepsilon_{d2} }}{{\varepsilon_{p} }}\frac{{J_{0} \left( {\frac{{\chi_{pn} }}{{R_{m} }}R_{p} } \right)}}{{H_{0}^{\left( 1 \right)} \left( {\frac{{\chi_{dn} }}{{R_{m} }}R_{p} } \right)J_{0} \left( {\chi_{dn} } \right) - H_{0}^{\left( 1 \right)} \left( {\chi_{dn} } \right)J_{0} \left( {\frac{{\chi_{dn} }}{{R_{m} }}R_{p} } \right)}} = \frac{{\chi_{dn} }}{{\chi_{pn} }}\frac{{J_{1} \left( {\frac{{\chi_{pn} }}{{R_{m} }}R_{p} } \right)}}{{H_{1}^{\left( 1 \right)} \left( {\frac{{\chi_{\ln } }}{{R_{m} }}R_{p} } \right)J_{0} \left( {\chi_{dn} } \right) - H_{0}^{\left( 1 \right)} \left( {\chi_{dn} } \right)J_{1} \left( {\frac{{\chi_{dn} }}{{R_{m} }}R_{p} } \right)}}$$
(12)

where H1(1) and J1 are the Hankel function of first kind of the first order and Bessel function of the first order, respectively [21, 23].

Based on Fig. 1 and the considered assumption Rp <  < Rm, since, the exact determination of the χdn and χpn in Eq. (7) are very difficult, these coefficients are extended in powers of \(\frac{{R_{p} }}{{R_{m} }}\).

The expansion coefficients are obtained by substituting extended coefficients in Eqs. (9) and (12),

$$\chi_{dn} = \eta_{n} + \left[ {\frac{\pi }{4}\frac{{N_{0} \left( {\eta_{n} } \right)}}{{J_{1} \left( {\eta_{n} } \right)}}\frac{{\varepsilon_{d2} - \varepsilon_{p} }}{{\varepsilon_{d2} }}\eta_{n}^{2} } \right]\left( {\frac{{R_{p} }}{{R_{m} }}} \right)^{2}$$
$$\begin{aligned} \chi_{pn} & = \sqrt {R_{m}^{2} \Gamma_{p}^{2} - R_{m}^{2} \Gamma_{d2}^{2} + \eta_{n}^{2} } \\ & \quad + \left[ {\frac{\pi }{4}\frac{{N_{0} \left( {\eta_{n} } \right)}}{{J_{1} \left( {\eta_{n} } \right)}}\frac{{\varepsilon_{d2} - \varepsilon_{p} }}{{\varepsilon_{d2} }}\frac{{\eta_{n}^{3} }}{{\sqrt {R_{m}^{2} \Gamma_{p}^{2} - R_{m}^{2} \Gamma_{d2}^{2} + \eta_{n}^{2} } }}} \right]\left( {\frac{{R_{p} }}{{R_{m} }}} \right)^{2} \\ \end{aligned}$$

where N0 is the Bessel function of the second kind of zero order [23].

At the end, by using the continuity of the components Er and Hϕ on the boundary z = 0 and using the orthogonality of the Bessel functions, the transmission and reflection coefficients of the transmitted and reflected waves can be calculated as the following form [21, 23, 30–32]

$$\begin{aligned} r_{m} &= \frac{2}{{\left( {J_{1} \left( {\eta_{m} } \right)} \right)^{2} \eta_{j} }}\left( {\mathop \sum \limits_{n = 1}^{\infty } \left[ {\frac{{\chi_{pn} }}{{R_{m} }}\mathop \int \limits_{0}^{{R_{p} }} J_{1} \left( {\frac{{\chi_{pn} }}{{R_{m} }}r} \right)J_{1} \left( {\eta_{m} \frac{r}{{R_{m} }}} \right)rdr} \right]t_{n} } \right. \\ & \quad \left. + \mathop \sum \limits_{n = 1}^{\infty } \left[ {\frac{{\chi_{dn} }}{{R_{m} }}\mathop \int \limits_{{R_{p} }}^{{R_{m} }} \left( {x_{1} \left( n \right)H_{1}^{\left(1 \right)} \left( {\frac{{\chi_{dn} }}{{R_{m} }}r} \right) + x_{2} \left( n \right)J_{1} \left( {\frac{{\chi_{dn} }}{{R_{m} }}r} \right) } \right) \times J_{1} \left( {\eta_{m} \frac{r}{{R_{m} }}} \right)rdr} \right]t_{n} \right) \\ & \quad - \frac{{\eta_{j} }}{{\eta_{m} }}\delta_{jm} \\ \end{aligned}$$
(13)
$$\begin{aligned} & \frac{{\left( {J_{1} \left( {\eta_{m} } \right)} \right)^{2} \eta_{j} }}{2}\left( {k_{zj}^{i} + k_{zm}^{r} } \right)\delta_{jm} \\ & \; = \mathop \sum \limits_{n = 1}^{\infty } \left( {k_{zm}^{r} + \frac{{\varepsilon_{d1} }}{{\varepsilon_{p} }}k_{zn}^{t} } \right)\left[ {\frac{{\chi_{pn} }}{{R_{m} }}\mathop \int \limits_{0}^{{R_{p} }} J_{1} \left( {\frac{{\chi_{pn} }}{{R_{m} }}r} \right)J_{1} \left( {\eta_{m} \frac{r}{{R_{m} }}} \right)rdr} \right]t_{n} \\ & \quad + \mathop \sum \limits_{n = 1}^{\infty } \left( {(k_{zm}^{r} + \frac{{\varepsilon_{d1} }}{{\varepsilon_{d2} }}k_{zn} } \right) \\ & \quad \left[ {\frac{{\chi_{dn} }}{{R_{m} }}\mathop \int \limits_{{R_{p} }}^{{R_{m} }} ( x_{1} \left( n \right)H_{1}^{\left( 1 \right)} \left( {\frac{{\chi_{dn} }}{{R_{m} }}r} \right) + x_{2} \left( n \right)J_{1} \left( {\frac{{\chi_{dn} }}{{R_{m} }}r} \right) ) \times J_{1} \left( {\eta_{m} \frac{r}{{R_{m} }}} \right)rdr} \right]t_{n} \\ \end{aligned}$$
(14)

As it can be seen that, the reflection and transmission coefficients of each mode depend on the incident wave frequency and the plasma temperature, because of the presence of the plasma column in the waveguide. Also, these equations show that the transmission and reflection coefficients are complex number with real and imaginary parts.

Therefore, the reflected and the transmitted waves have phase difference respect to the incident wave where are obtained from the ratio of imaginary part to real part of the transmission and reflection coefficients, respectively.

In the next sections, the role of plasma in the transmission and reflection coefficients as well as in the phase difference of the transmitted and reflected waves will be discussed.

3 The simulation of the transmission coefficients

In this section, the numerical simulation results are presented.

and discussed. We will investigate the effects of the plasma temperature on the transmission coefficients by solving the set of the coupled Eqs. (13) and (14).

In present work, the numerical calculations are done by Maple software of version10.

we choose Rm = 10−2 m for the radius of the waveguide, \(\frac{{R_{p} }}{{R_{m} }} = 0.004\) for the plasma rod radius, εd1 = 2.4ε0 for the dielectric permittivity in z < 0, εd1 = 9ε0 for the dielectric permittivity in z > 0, ωp = \(\sqrt {30}\) × 1010 Hz for the plasma frequency and ω = 3 × 1010 Hz for the incident wave frequency.

Also, the numbers of the incident mode are assumed j = 1, 2, 3.

It must be mentioned that in all presented graphs in this manuscript, the phase velocity of the waves is fixed. This assumption is caused that we chose a fixed wave propagation constant kz from several branches of the dispersion relations (12).

Figures 2 and 3 illustrate the variations of the transmission coefficients of the transmitted waves in term of the ratio of the thermal velocity to the phase velocity (U(T)) for the first three incident modes for adiabatic case (Vph > Vth) and non-adiabatic case (Vph < Vth), respectively. As shown, Figs. 2(a) and 3(a) have been presented for incident number j = 1, Figs. 2(b) and 3(b) for incident number j = 2 and Figs. 2(c) and 3(c) for incident number j = 3, respectively. In the all mentioned figures, the graphs of the transmission coefficients have been presented for n = 1, n = 2 and n = 3. Here, we introduced the transmitted mode number n = j as the dominant mode and the transmitted mode number n ≠ j as the new produced mode of the transmitted waves.

Fig. 2
figure 2

The effects of the plasma temperature on the transmission coefficients for the adiabatic case. (a) for incident number j = 1, (b) for incident number j = 2 and figure (c) for incident number j = 3

Full size image
Fig. 3
figure 3

The effects of the plasma temperature on the transmission coefficients, for the non-adiabatic case. (a) for incident number j = 1, (b) for incident number j = 2 and (c) for incident number j = 3

Full size image

As seen in Figs. 2 and 3, the magnitude of the transmission coefficient of the all modes of the transmitted waves have a peak. So that, for the incident wave with mode j = 1, the domain mode of the transmitted wave (n = j) has a peak in the non-adiabatic case (Fig. 3(a)) and for the incident wave with modes j = 2 and j = 3, the peak of the domain mode of the transmitted wave is appeared in the adiabatic case as is shown in Figs. 2(b) and (c).

Also, the peak magnitude of the transmission coefficient of produced modes (n ≠ j) is smaller than the peak magnitude of the transmission coefficient of domain modes (n = j).

In high temperature, the magnitude of the transmission coefficient of all modes is fixed and it is independent from the plasma temperature (in non- adiabatic case).

On the other hands by considering the diagrams in Figs. 2 and 3, one can find that the magnitude of the transmission coefficient of the produced modes (n ≠ j) has a maximum when the phase velocity is almost equal with the thermal velocity or 0.9 < U(T) < 1.1. The reason is that when the phase velocity and the thermal velocity will be equal, the Cherenkov absorption is occurred and the wave is damped. The wave damping will be caused production of the new modes. On the other words, since the Cherenkov absorption is occurred in the amplitude of the waves, from the Fourier transform of the amplitude of the waves, the new radial space harmonics are produced. Therefore, the new the quantization in the transmitted and reflected waves will be appeared.

Figures 4 and 5 illustrate the variations of the phase angle of the transmitted waves versus the ratio of the thermal velocity to the phase velocity (U(T)) for adiabatic case and non-adiabatic case, respectively. Here, the arrangement of Fig. 4(a)–(c), Fig. 5(a)–(c) are based on the details presented previously for j = 1, 2, 3, respectively.

Fig. 4
figure 4

The dependence of the phase angle of the transmitted waves on the plasma temperature for the adiabatic case. (a) for incident number j = 1, (b) for incident number j = 2 and (c) for incident number j = 3

Full size image
Fig. 5
figure 5

The dependence of the phase angle of the transmitted waves on the plasma temperature for the non-adiabatic case. (a) for incident number j = 1, (b) for incident number j = 2 and (c) for incident number j = 3

Full size image

It can be seen that for adiabatic case and non-adiabatic case, each mode (domain mode and produced modes) of the transmitted waves has a phase difference respect to the incident wave which is fixed and is independent of the plasma temperature.

It means that, by changing the plasma temperature or changing the mode number of the incident wave, the phase difference of these modes respect to the incident wave aren't changed in adiabatic case and non-adiabatic case.

4 The simulation of the reflection coefficients

In this section, we will show the effects of the plasma temperate on the reflection coefficients of the reflected waves. For this reason, we used the presented data in the previous section.

Figures 6 and 7 show the variations of the reflection coefficients in terms of U(T) for adiabatic case and non-adiabatic case, respectively. The serial Figs. 6 and 7 are the same as the serial Figs. 2 and 3 but for the reflection coefficients.

Fig. 6
figure 6

The effects of the plasma temperature on the reflection coefficients for the adiabatic case. (a) for incident number j = 1, (b) for incident number j = 2 and (c) for incident number j = 3

Full size image
Fig. 7
figure 7

The effects of the plasma temperature on the reflection coefficients for the non-adiabatic case. (a) for incident number j = 1, (b) for incident number j = 2 and (c) for incident number j = 3

Full size image

Here, the quantization number m = 1, m = 2 and m = 3 have been used for the reflected modes of the reflected waves.

For adiabatic case non-adiabatic case, as it can be seen that, the magnitude of the reflection coefficient of the dominant mode of the reflected waves (m = j) will be almost constant and is about 1.

On the other hands, the magnitude of the reflection coefficient of the produced modes of the reflected waves (m ≠ j) similar to the magnitude of the transmission coefficients of the produced modes of the transmitted waves, has a maximum point in the region that the phase velocity is equal with the thermal velocity. Therefore, the Cherenkov absorption is caused that the magnitude of the reflection coefficient of the produced mode of the reflected waves to be maximum in 0.9 < U(T) < 1.1.

Also, there is a critical behavior in the graph of the reflection coefficient (Fig. 6(b)). It must be mentioned that the exact graph of variations of.

\(\left| {r_{3} } \right|\) In Fig. 6(b) around the value 0.741 < U(T) < 0.743 shows that, the critical behavior of the curve is only a rapid variation of this graph around U(T) = 0.742. This phenomenon refers to the Cherenkov absorption of the waves with phase velocity greater than thermal velocity (Vph > Vth).

Therefore, in this situation the magnitude of the reflection coefficient is decreased due to the Cherenkov absorption phenomenon.

It is obvious that in this situation the magnitude of the transmission coefficient must be changed, too. Since the order of the transmission coefficient variations is about 10−3 in Fig. 2(b), therefore, these variations can't be observed in comparison with the order of the reflection coefficient variations (10−7).

So, the exact numerical investigations show that the rapid variations for the transmission coefficient in this situation exist.

Figures 8 and 9 show the variations of the phase angle of the reflected waves in term of U(T) for adiabatic case and non-adiabatic case, respectively. The serials Figs. 8 and 9 are the same as the serials Figs. 4 and 5.

Fig. 8
figure 8

The dependence of the phase angle of the reflected waves on the plasma temperature for the adiabatic case. (a) for incident number j = 1, (b) for incident number j = 2 and (c) for incident number j = 3

Full size image
Fig. 9
figure 9

The dependence of the phase angle of the reflected waves on the plasma temperature, for the non-adiabatic case. (a) for incident number j = 1, (b) for incident number j = 2 and (c) for incident number j = 3

Full size image

As it can be seen, the dominant mode of the reflected waves (m = j) is reflected without the phase difference respect to the incident wave in adiabatic and non-adiabatic cases.

In opposite case, the produced modes of reflected waves (m ≠ j) have phase difference respect to the incident wave. In the temperature that the phase velocity is almost equal with thermal velocity, the phase difference of these modes is changed. In the other temperatures, this phase difference is independence of the plasma temperature. In fact, the Cherenkov absorption caused to the phase angle variation in the reflected waves.

5 Conclusions

In this paper, we have studied the reflected and transmitted waves in a circular waveguide with a transverse boundary between plasma and dielectric. This waveguide had two parts. The first part of the waveguide was a semi-bounded waveguide which was filled by loss free dielectric material. A semi-bounded dielectric waveguide with a warm plasma column as the second part.

It was assumed that a single mode was falling on the transverse boundary from first part toward to second part, so that it was reflected and transmitted in the boundary.

The boundary conditions were used to derive the transmission and reflection coefficients in each mode.

It was proved that the reflected and transmitted waves had a phase difference respect to the incident wave because the reflection and transmission coefficients have been obtained as a complex number.

The variations of the transmission and reflection coefficients for each reflected and transmitted waves, versus the ratio of the thermal velocity to the phase velocity (\({\text{U}}\left( {\text{T}} \right) = \frac{{\sqrt \gamma V_{th} }}{{V_{ph} }}\)), have been have been studied for the adiabatic case (Vph > Vth) and non-adiabatic case (Vph < Vth).

It was proved that the Cherenkov absorption was accrued when the thermal velocity was equal to phase velocity and it was caused the magnitude of transmission coefficient of the produced modes of the transmitted waves and the magnitude of reflection coefficient of the produced modes of the reflected waves to be maximum.

Also, the variations of the phase angle of the reflected and transmitted waves in term of U(T) have been shown for adiabatic case and non-adiabatic case.

It was observed that the phase difference of all modes of the transmitted waves respect to the incident wave was same for adiabatic case and non-adiabatic case.

On the other hands, for adiabatic case and non-adiabatic case, the dominant mode of the reflected waves not have any phase difference respect to the incident wave.