1 Introduction

The solitary waves (SW) and double layers (DL) of ion-acoustic waves (IAW) have been studied by various authors considering different types of plasma (negative ion plasma, positron plasma, quantum plasma, dusty plasma, etc.) having different parameters (ion temperature, nonisothermal electrons, two-temperature electrons, nonthermal electrons, superthermal electrons, Tsallis distributed electrons, etc.) to fit their results in various physical situations in the laboratory and astrophysical plasma. However, two-temperature electrons in the plasma have special kind of effects in exciting the SW and DL of IAW. It has been found that a small percentage of the cooler component of electrons leads to effect qualitatively different from those obtained for a plasma having only one-temperature electron species. Goswami and Buti [1] and some other authors [2,3,4,5,6,7,8] have investigated the SWs and DLs and other aspects of ion-acoustic waves in plasma having two-temperature electrons.

However, from the experimental observations of various authors [9,10,11], it is found that theoretically predicted values of the amplitude, width and velocity of SW do not obey the experimental results. To remove the discrepancy between the theoretical and experimental results, a large number of authors have studied and analyzed the inclusion of higher-order perturbation corrections into the Korteweg–deVries (KdV) solitons, and the resulting solution has been termed as dressed solitons (DS). Initially, Ichikawa et al. [12] have first examined such higher-order effects by the reductive perturbation method (RPM) for SW in a plasma consisting of cold ions. Later, the temperature of ions in the plasma has been considered by Lai [13] and has investigated the higher-order effect on the SW of IAW. Subsequently, Kodama and Taniuti [14] have reconsidered this problem and have shown by the method of renormalization how to eliminate the secular terms appearing in higher-order terms of the expansion. Later, several authors have considered the effect of higher-order nonlinearity for investigating the DS of IAW in nondegenerate plasma and obtained interesting results [15,16,17,18,19,20].

Considering quantum (degenerate) plasma, Chatterjee et al. [21] have used the RPM for the study of DS of IAW in a dense quantum plasma whose constituents are electrons, positrons and positive ions. Later, Roy and Chatterjee [22] have investigated the DSs in an unmagnetized two-species electron–ion quantum plasma by using the RPM. They have derived a higher-order inhomogeneous (KdV-type) differential equation for the second-order correction and have obtained the nonsecular solution by the use of renormalization procedure. Moreover, they have applied a new technique to obtain the particular solution of the higher-order inhomogeneous equation which is found to be simpler compared to the technique used by previous investigators. Subsequently, Wang et al. [23] have presented a theory for the DS of quantum ion-acoustic waves (QIAW) in unmagnetized plasmas composed of positive and negative ions and weakly relativistic beams of electron considering higher-order corrections. They have investigated the properties of the QIAW using a quantum hydrodynamic (QHD) model from which a KdV equation has been derived using the RPM. They have also derived an equation including higher-order dispersion and nonlinearity corrections, and the effect of the physical parameter has been discussed for the importance of these corrections.

On the other hand, propagation of waves in relativistically degenerate (RD) and ultra-relativistic dense (URD) plasma has been studied by various authors following the works of Chandrasekhar [24, 25]. Using Sagdeev potential approach, Esfandyari-Kalejahi et al. [26] have investigated arbitrary amplitude SWs in electron–positron-ion plasma having ultra-relativistic or nonrelativistic degenerate electrons and positrons and have numerically investigated the matching criteria of existence of such solitary waves. Later, Shah et al. [27] have investigated the effect of trapping for the formation of solitary structures in RD plasma. Masood and Eliasson [28] have studied electrostatic solitary waves in quantum plasma having RD electrons and cold ions. Subsequently, Roy et al. [29] have investigated the DSs in a dense plasma composed of URD electrons and positrons, and inertial cold mobile ions, and negatively charged static dust particles by using the RPM. Later, using the QHD model and degenerate electron pressure Chandra et al. [30] have studied electro-acoustic solitary waves in RD quantum plasma with two-temperature electrons. It has been shown that the degeneracy parameter significantly influences the conditions of formation and properties of solitary structures. However, in a dense plasma consisting of URD electrons and positrons, cold and mobile inertial ions, and negatively charged static dust particles, Paul et al. [31] have investigated the modulation instability, envelope solitons and rogue waves of ion-acoustic waves using Fried and Ichikawa method [32].

From the discussions, it is seen that two-temperature electrons have important roles on the excitation of K-dV solitons, DL and DS of IAW in the plasma. Moreover, URD electrons have a significant effect on the nonlinear propagation of waves in plasma. But, no investigation has yet been reported on the DS in a dense dusty plasma with URD two-temperature electrons obeying the equation of state. So, in this paper, we are interested to study the DS and the DL of IAW in a dense dusty plasma with cold ions and URD two-temperature electrons with static negatively charged dust particles. To solve the problem we have used the integral form of governing equations in terms of pseudopotential. The effects of higher-order nonlinear and dispersive effects have been considered for obtaining the DS in URD two-temperature-electron plasma. It is to be mentioned that our mathematical technique has been used by several authors to investigate the effects of higher-order nonlinear and dispersive terms on the propagation of ion-acoustic solitary waves in nondegenerate plasma [33,34,35].

2 Formulation

We consider four-component plasma consisting of inertialess URD two-temperature electrons, cold inertial ion fluid and negatively charged static dust particles. The degenerate pressure of electrons has been expressed in terms of density by using the ultra-relativistic limit of Chandrasekhar [24, 25]. The nonlinear dynamics of the electrostatic wave in such URD dense plasma is described by the following equations:

$$ \frac{{\partial n_{s} }}{\partial t} + \frac{\partial }{\partial x}(n_{s} u_{s} ) = 0 $$
(1)
$$ \frac{{\partial u_{i} }}{\partial t} + u_{i} \frac{{\partial u_{i} }}{\partial x} = - \frac{\partial \varphi }{{\partial x}} $$
(2)
$$ n_{ec} \frac{\partial \varphi }{{\partial x}} - \frac{3}{4}\beta_{ec} \frac{{\partial n_{ec}^{4/3} }}{\partial x} = 0 $$
(3)
$$ n_{eh} \frac{\partial \varphi }{{\partial x}} - \frac{3}{4}\beta_{eh} \frac{{\partial n_{eh}^{4/3} }}{\partial x} = 0 $$
(4)
$$ \frac{{\partial^{2} \varphi }}{{\partial x^{2} }} = \alpha_{ec} n_{ec} + \alpha_{eh} n_{eh} - n_{i} + \alpha_{d} $$
(5)

where the subscript ‘s’ (= e, i, p) denotes for electron, ion and positron; velocity us is normalized by ion-acoustic speed \(C_{i} = (m_{e} c^{2} /e)^{1/2}\), density ns is normalized by the equilibrium ion density, the electrostatic potential ϕ is normalized by mec2/e, space variable x and time variable t are normalized by (mec2/4πni0e2)1/2 and ion plasma period (\(\omega_{pi}\))−1; \(\omega_{pi} = (4\pi n_{i0} e^{2} /m_{i} )^{1/2}\);

$$ \begin{gathered} \alpha _{{ec}} = \lambda _{c} n_{{ec0}}^{{1/3}} ,\alpha _{{eh}} = \lambda _{c} n_{{eh0}}^{{1/3}} ,\lambda _{c} = h/m_{e} c, \hfill \\ \beta _{{ec}} = K_{0} \alpha _{{ec}} ,\beta _{{eh}} = K_{0} \alpha _{{eh}} ,K_{0} = (\rlap{-} h/m_{e} c), \hfill \\ \alpha _{{ec}} = (n_{{ec0}} /n_{{i0}} ),\alpha _{{eh}} = (n_{{eh0}} /n_{{i0}} ),\alpha _{d} = (Z_{d} n_{{d0}} /n_{{i0}} ) \hfill \\ \end{gathered} $$
(6)

\(n_{ec0} ,n_{eh0}\) are the equilibrium densities of electrons at low and high temperature; \(n_{i0}\) is the equilibrium density of positive ions; \(Z_{d}\) is the number of negative charges of dust particles. Other parameters have their usual meanings.

The charge neutrality condition is

$$ \alpha_{ec} + \alpha_{ec} + \alpha_{d} = 1,\,{{i}}{{.e}}{.}\,\alpha_{ec} + \alpha_{eh} = 1 - \alpha_{d} $$
(7)

In absence of dust particles, \(\alpha_{d}\) = 0, i.e.,\(\alpha_{ec} + \alpha_{eh} = 1\).

For a solitary wave solution, we assume that the dependent variables depend on a single independent variable \(\xi = x - Vt\), where \(V\) is the phase velocity of a solitary wave. Then from Eqs. (1)–(3), we obtain after using the boundary conditions \(n_{i} \to 1,\varphi \to 0\) as \(\xi \to \pm \infty\)

$$ n_{i} = \frac{1}{{\sqrt {1 - \frac{2\varphi }{{V^{2} }}} }},\,n_{ec} = \left( {1 + \frac{\varphi }{{3\beta_{ec} }}} \right)^{3} ,\,n_{eh} = \left( {1 + \frac{\varphi }{{3\beta_{eh} }}} \right)^{3} $$
(8)

where \(\beta_{ec}\) and \(\beta_{eh}\) are the temperature of degenerate electrons at low and high temperatures.

Now using (8) in (4) we get

$$ \frac{{\partial^{2} \varphi }}{{\partial \xi^{2} }} = \Delta_{1} \varphi + \Delta_{2} \varphi^{2} + \Delta_{3} \varphi^{3} $$
(9)

where

$$ \Delta_{1} = \left[\frac{{\alpha_{ec} }}{{\beta_{ec} }} + \frac{{\alpha_{eh} }}{{\beta_{eh} }} - \frac{1}{{V^{2} }}\right] $$
(10a)
$$ \Delta_{2} = \left[\frac{{\alpha_{ec} }}{{3\beta_{ec}^{2} }} + \frac{{\alpha_{eh} }}{{3\beta_{eh}^{2} }} - \frac{3}{{2V^{4} }}\right] $$
(10b)
$$ \Delta_{3} = \left[\frac{{\alpha_{ec} }}{{27\beta_{ec}^{3} }} + \frac{{\alpha_{eh} }}{{27\beta_{eh}^{3} }} - \frac{5}{{2V^{6} }}\right] $$
(10c)

An integral of (9) satisfying the conditions \({{d\varphi } \mathord{\left/ {\vphantom {{d\varphi } {{\rm d}X \to 0,\,\,\varphi \to 0{\text{ as }}\xi \to \pm \,\infty {\text{ is }}}}} \right. \kern-\nulldelimiterspace} {{\rm d}X \to 0,\,\,\varphi \to 0{\text{ as }}\xi \to \pm \,\infty {\text{ is }}}}\)

$$ \frac{\varepsilon }{2}\left( {\frac{{\rm d}\varphi }{{{\rm d}X}}} \right)^{2} = \frac{1}{2}\Delta_{1} \,\varphi^{2} + \frac{1}{3}\Delta_{2} \varphi^{3} + \frac{1}{4}\Delta_{3} \varphi^{4} $$
(11)

where we have stretched the \(\xi\)-coordinate according to the relation

$$ X = \varepsilon^{1/2} \xi . $$
(12)

In (11) and (12), \(\varepsilon\) is a smallness parameter. ε is positive and ε < 1 (i.e., \(0 < \varepsilon < 1\)).

For obtaining the solutions of higher-order nonlinear equations, we now follow the works of Refs. [33,34,35] and make the following perturbation expansions for electrostatic potential \(\phi \, \). and phase velocity V of the wave as

$$ \varphi = \varepsilon \varphi^{\left( 1 \right)} + \varepsilon^{2} \varphi^{(2)} + \,\varepsilon^{3} \varphi^{(3)} + \cdot \cdot \cdot \cdot \cdot \,, $$
(13a)
$$ V = V_{0} + \varepsilon V^{(1)} + \varepsilon^{2} V^{(2)} + \,\varepsilon^{3} V^{(3)} + \cdot \cdot \cdot \cdot \cdot $$
(13b)

where \(V_{0}\) is the linear phase velocity of ion-acoustic wave.

In (13a) and (13b), the terms with \(\varepsilon ,\varepsilon^{2} ,\varepsilon^{3}\), etc., represent the perturbed values of respective parameters.

Moreover, using the expansion of V given by (13b), we have expanded \(\Delta_{1} ,\Delta_{2}\) and \(\Delta_{3}\) of Eq. (9) in power series of \(\varepsilon\) and get the following equations:

$$ \begin{aligned} \Delta_{1} & = \delta_{1}^{(0)} + \varepsilon \delta_{1}^{\left( 1 \right)} + \varepsilon^{2} \delta_{1}^{\left( 2 \right)} + \varepsilon^{3} \delta_{1}^{\left( 3 \right)} + \, \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \\ \Delta_{2} & = \delta_{2}^{\left( 0 \right)} + \varepsilon \delta_{2}^{\left( 1 \right)} + \varepsilon^{2} \delta_{2}^{\left( 2 \right)} + \, \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \\ \Delta_{3} & = \delta_{3}^{\left( 0 \right)} + \varepsilon \delta_{3}^{\left( 1 \right)} + \, \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \\ \end{aligned} $$
(14)

where

$$ \begin{gathered} \delta_{1}^{(0)} = 0, \hfill \\ \delta_{1}^{\left( 1 \right)} = 2\gamma_{1}^{2} V_{0} V^{\left( 1 \right)} , \hfill \\ \delta_{1}^{\left( 2 \right)} = 2\gamma_{1}^{2} V_{0} V^{\left( 2 \right)} + \gamma_{1}^{2} (1 - 4\gamma_{1} \,V_{0}^{2} )(V^{\left( 1 \right)} )^{2} , \hfill \\ \delta_{1}^{\left( 3 \right)} = 2\gamma_{1}^{2} V_{0} V^{\left( 3 \right)} + 2\gamma_{1}^{3} (1 - 4\gamma_{1} V_{0}^{2} )V^{(1)} V^{(2)} + 4\gamma_{1}^{3} V_{0} (2\gamma_{1}^{2} V_{0}^{2} - 1)(V^{(1)} )^{3} , \hfill \\ \delta_{2}^{\left( 0 \right)} = \gamma_{2} - \frac{3}{2}\gamma_{1}^{2} , \hfill \\ \delta_{2}^{\left( 1 \right)} = 6\,\gamma_{1}^{3} V_{0} V^{\left( 1 \right)} , \hfill \\ \delta_{2}^{\left( 2 \right)} = 6\,\,\gamma_{1}^{3} V_{0} V^{\left( 2 \right)} + 3\gamma_{1}^{3} (1 - 6\gamma_{1} V_{0}^{2} )(V^{(1)} )^{2} , \hfill \\ \delta_{3}^{\left( 0 \right)} = \gamma_{3} - \frac{5}{2}\gamma_{1}^{3} ,\, \hfill \\ \delta_{3}^{\left( 1 \right)} = 15\,\gamma_{1}^{4} \,V_{0} (V^{\left( 1 \right)} )^{2} , \hfill \\ \gamma_{1} = \frac{{\alpha_{ec} }}{{\beta_{ec} }} + \frac{{\alpha_{eh} }}{{\beta_{eh} }},\,\gamma_{2} = \frac{{\alpha_{ec} }}{{3\beta_{ec}^{2} }} + \frac{{\alpha_{eh} }}{{3\beta_{eh}^{2} }},\,\gamma_{3} = \frac{{\alpha_{ec} }}{{27\beta_{ec}^{3} }} + \frac{{\alpha_{eh} }}{{27\beta_{eh}^{3} }}. \hfill \\ \end{gathered} $$
(15)

Substituting expansions (15) in (11), we get the sequence of equations for the \(\varphi^{\left( i \right)} {{^{\prime}s}}\) and the equation for \(\varphi^{\left( i \right)}\) at each order becomes a first-order inhomogeneous differential equation for \(i > 1.\)

For linear dispersion relation, \((\Delta_{1} )_{0} = \partial_{1}^{(0)} = 0\). Therefore,

$$ \frac{{\alpha_{ec} }}{{\beta_{ec} }} + \frac{{\alpha_{eh} }}{{\beta_{eh} }} = \frac{1}{{V_{0}^{2} }} = \gamma_{1} , $$
(16a)
$$ {{i}}{{.e}}{.}\,V_{0} = = \sqrt {\frac{{\beta_{ec} \beta_{eh} }}{{(\alpha_{ec} \beta_{eh} + \alpha_{eh} \beta_{ec} )}}} ,\,\gamma_{1} = V_{0}^{ - 2} $$
(16b)

3 Solitary wave solutions

3.1 First-order equation and its solution

In the first order, i.e., in the lowest order which is at the order of ε3, we obtain the following equation for \(\varphi^{\left( 1 \right)} .\)

$$ \frac{1}{2}\left( {\frac{{{\rm d}\varphi^{(1)} }}{{\rm d}X}} \right)^{2} = \frac{1}{2}\delta_{1}^{(1)} \varphi^{{(1)^{2} }} + \frac{1}{3}\delta_{2}^{(0)} \varphi^{{(1)^{3} }} $$
(17)

The solution can be written as

$$ \frac{{{\rm d}\varphi ^{{(1)}} }}{{{\rm d}X}} = \pm \sqrt {\frac{2}{3}} \varphi ^{{(1)}} [3V_{0} - \varphi ^{{(1)}} ]^{{\frac{1}{2}}} $$
(18)

The solution of which is the first-order KdV solitons

$$ \varphi^{\left( 1 \right)} = f_{1} \sec \,h^{2} \eta $$
(19)

where

$$ f_{1} = - \frac{{6V_{0}^{ - 5} }}{{(2\gamma_{2} - 3V_{0}^{ - 4} )}}V^{(1)} , $$
(20a)
$$ \eta = \left( {\frac{{V_{0}^{ - 3} V^{(1)} }}{2}} \right)^{\frac{1}{2}} X, $$
(20b)

\(f_{1}\) is the first-order amplitude. \(\varphi^{(1)}\) vanishes at infinity, and it attains a maximum value at η = 0 giving the amplitude of first-order solitary wave \(f_{1}\), \(f_{1} = \alpha_{01} (say)\).

$$ V^{(1)} = \frac{{(2\gamma_{2} - 3V_{0}^{ - 4} )V_{0}^{5} f_{1} }}{6} $$
(21)

The first-order width \(D_{1}\) of the solitary wave is

$$ D_{1} = \left( {\frac{2}{{V_{0}^{ - 3} V^{(1)} }}} \right)^{\frac{1}{2}} \eta_{1} $$
(22)

where \(\eta_{1}\) is the positive root of the equation \(\tanh^{2} \eta_{1} = 0.58\).

The Mach number correct up to first order is given by

$$ M_{1} = 1 + \frac{{V^{(1)} }}{{V_{0} }} = 1 + \frac{{(2\gamma_{2} - 3V_{0}^{ - 4} )V_{0}^{4} f_{1} }}{6} $$
(23)

It is important to note that the perturbed part \(V^{(1)}\) of the expansion for \(V\) in (13b) remains unspecified and hence the amplitude of the solitons, \(f_{1}\), can be changed by varying \(V^{(1)}\).

3.2 Second-order equation and its solution

At the second order, we get the following equation for \(\varphi^{\left( 2 \right)}\) using (16) and (22)

$$ \frac{{{\rm d}\varphi^{\left( 1 \right)} }}{{\rm d}X}\frac{{{\rm d}\varphi^{(2)} }}{{\rm d}X} - \left[ {\partial_{1}^{(1)} \varphi^{(1)} + \partial_{2}^{(1)} \varphi^{{(1)^{2} }} } \right]\varphi^{(2)} = \frac{1}{2}\delta_{1}^{\left( 2 \right)} \varphi^{{\left( 1 \right)^{2} }} + \frac{1}{3}\delta_{2}^{\left( 1 \right)} \varphi^{{\left( 1 \right)^{3} }} + \frac{1}{4}\delta_{3}^{\left( 0 \right)} \varphi^{{\left( 1 \right)^{4} }} $$
(24)

Differentiating (24) with respect to \(\varphi^{(1)}\) we get

$$ \frac{{d^{2} \varphi^{(1)} }}{{{\rm d}X^{2} }} = \delta_{1}^{(1)} \varphi^{(1)} + \delta_{2}^{(0)} \varphi^{{(1)^{2} }} $$
(25)

By the use of this relation and by introducing the independent variables given by (22) Eq. (23) can be written as

$$ \frac{{{\rm d}\varphi^{(2)} }}{d\eta }\frac{{\varphi_{\eta \eta }^{(1)} }}{{\varphi_{\eta }^{(1)} }}\varphi^{(2)} = \frac{{\partial_{1}^{(2)} }}{{V_{0} V^{(1)} }}\frac{{\varphi_{1}^{{(1)^{2} }} }}{{\varphi_{\eta }^{(1)} }} + \frac{{2\delta_{2}^{(1)} }}{{3V_{0} V^{(1)} }}\frac{{\varphi_{1}^{{(1)^{3} }} }}{{\varphi_{\eta }^{(1)} }} + \frac{{\delta_{3}^{(0)} }}{{2V_{0} V^{(1)} }}\frac{{\varphi_{1}^{{(1)^{4} }} }}{{\varphi_{\eta }^{(1)} }} $$
(26)

Multiplying both sides of (26) by the integrating factor \({1 \mathord{\left/ {\vphantom {1 {\varphi_{\eta }^{\left( 1 \right)} }}} \right. \kern-\nulldelimiterspace} {\varphi_{\eta }^{\left( 1 \right)} }}\) and then integrating we obtain the following solution \(\varphi^{\left( 2 \right)}\) that vanishes at infinity and that attains a maximum at \(\eta = 0.\)

$$ \varphi^{\left( 2 \right)} = \frac{{6V_{0} V^{\left( 1 \right)} \,\delta_{1}^{\left( 2 \right)} }}{{4V_{0} \,\,V^{\left( 1 \right)} }}\,\eta \,{\text{sec}}\,h^{2} \eta \,{\text{tan}}\,h\eta + 6V_{0} V^{\left( 1 \right)} \left( {\frac{{\delta_{1}^{\left( 2 \right)} }}{{4V_{0} V^{\left( 1 \right)} }} + \frac{{\delta_{2}^{\left( 1 \right)} }}{2\,} + \frac{{9\delta_{3}^{\left( 0 \right)} \,V_{0} V^{\left( 1 \right)} }}{4\,}} \right)\,{\text{sec }}h^{2} \eta - \frac{{27\delta_{3}^{\left( 0 \right)} \,V_{0}^{2} V^{{\left( 1 \right)^{2} }} }}{4\,}\,{\text{sec}}\,h^{4} \eta $$
(27)

Owing to the presence of the first term in the above expression, the \({{\varphi^{\left( 2 \right)} } \mathord{\left/ {\vphantom {{\varphi^{\left( 2 \right)} } {\varphi^{\left( 1 \right)} }}} \right. \kern-\nulldelimiterspace} {\varphi^{\left( 1 \right)} }}\) does not remain finite at \(\eta \to \pm \infty .\). So for a uniformly valid expansion of \(\varphi^{(2)}\) the coefficient of this term must be equal to zero. Therefore we get \(\delta_{1}^{\left( 2 \right)} = 0\) which gives

$$ V^{\left( 2 \right)} = - \frac{{3V_{0} V^{{\left( 1 \right)^{2} }} }}{2} $$
(28)

Removing the secular term, the solution of (27) is obtained as

$$ \varphi^{\left( 2 \right)} = \left[ {f_{2} + f_{3} \,\tan h^{2} \eta } \right]\,{\text{sec}}\,h^{2} \eta $$
(29)

where

$$ \begin{aligned} f_{1} & = - \frac{3}{2}\frac{{\delta_{1}^{(1)} }}{{\delta_{2}^{(0)} }} = - \frac{{6V_{0}^{ - 5} }}{{(2\gamma_{2} - 3V_{0}^{ - 4} )}}V^{(1)} \\ f_{2} & = \frac{{2f_{1}^{2} }}{{\delta_{1}^{(1)} }}\left[ {\frac{1}{3}\delta_{2}^{(1)} + \frac{1}{2}f_{1} \delta_{3}^{(0)} } \right] = \frac{36}{{V_{0}^{6} (2\gamma_{2} - 3V_{0}^{ - 4} )^{2} }}\left[ {2\, + \frac{3}{{2(2\gamma_{2} - 3V_{0}^{ - 4} )}}(2\gamma_{3} - 5V_{0}^{ - 6} } \right]V_{0}^{2} (V^{(1)} )^{2} \\ f_{3} & = - \frac{{f_{1}^{3} }}{2}\frac{{\delta_{3}^{(0)} }}{{\delta_{1}^{(1)} }} = - \frac{{f_{1}^{3} }}{2} \frac{{(\gamma_{3} - \frac{5}{2}V_{0}^{ - 6} )}}{{2V_{0}^{ - 3} V^{\left( 1 \right)} }} = - \frac{{f_{1}^{3} }}{8}\frac{{V_{0}^{3} (2\gamma_{3} - 5V_{0}^{ - 6} )}}{{V^{\left( 1 \right)} }} \\ \end{aligned} $$
(30)

The amplitude of second-order correction term of (29) is

$$ f_{2} = \frac{36}{{V_{0}^{6} (2\gamma_{2} - 3V_{0}^{ - 4} )^{2} }}\left[ {2\, + \frac{3}{{2(2\gamma_{2} - 3V_{0}^{ - 4} )}}(2\gamma_{3} - 5V_{0}^{ - 6} } \right]V_{0}^{2} (V^{(1)} )^{2} $$
(30a)

The second-order width D2 of the SW is

$$ D_{2} = \left( {\sqrt {\frac{{2V_{0}^{3} }}{{V^{(1)} }}} } \right)\eta_{2} $$
(31)

where \(\eta_{2}\) is the positive root of the following equation,

$$ (f_{3} /f_{2} )\tanh^{4} \eta_{2} - [1 + 2(f_{3} /f_{2} )]\tanh^{2} \eta_{2} + [(f_{3} /f_{2} ) + 0.58] = 0 $$
(32)

3.3 Corrected higher-order solution up to second order (dressed solitons)

Using (19) and (29) the solitary waves correct up to second order become

$$ \varphi_{2} = \varphi^{(1)} + \varphi^{(2)} = f_{4} (1 + f_{5} \tanh^{2} \eta )\sec h^{2} \eta $$
$$ {\text{where}},\,f_{4} = f_{\begin{subarray}{l} 1 \\ + \end{subarray} } + f_{2} ,f_{5} = f_{3} /f_{4} $$

The amplitude of corrected second-order SW (or DS) is \(f_{4} ,\)

$$ f_{4} = \frac{{6V^{(1)} }}{{V_{0}^{7} (2\gamma_{2} - 3V_{0}^{ - 4} )}}\left[ {1 + \frac{{6V_{0}^{ - 2} }}{{(2\gamma_{2} - 3V_{0}^{ - 4} )}}\left\{ {2\, + \frac{3}{{(2\gamma_{2} - 3V_{0}^{ - 4} )}}(\gamma_{3} - \frac{5}{2}V_{0}^{ - 6} )} \right\}V_{0} V^{(1)} } \right] $$
(34b)

The Mach number of second-order correction term is

$$ M_{2} = \frac{{V^{{(1)^{2} }} }}{{2V_{0}^{2} }} $$
(35)

The Mach number of DS is

$$ M = 1 + \frac{{V^{(1)} }}{{V_{0} }} + \frac{{V^{{(1)^{2} }} }}{{2V_{0}^{2} }}, $$
(36)

where \(V^{(1)}\) is given by ( 21).

4 Special case: dressed solitons near-critical state

In the critical state, the nonlinear coefficient vanishes, i.e., \(\delta_{2}^{(0)}\) = 0. Under this condition, the SW will not be excited in plasma. But, the near- critical value of phase velocity V0 (i.e., when \(\delta_{2}^{(0)} \approx 0\)), the SW will be excited with sechη profile instead of usual sech2η profile. To study the SW near-critical state when \(\delta_{2}^{(0)} \approx 0\), the following perturbation expansion for ϕ should be used,

$$ \varphi = \varepsilon^{1/2} \varphi^{\left( 1 \right)} + \varepsilon \varphi^{(2)} + \,\varepsilon^{3/2} \varphi^{(3)} + \cdot \cdot \cdot \cdot \cdot \cdot $$
(37)

where ε is a smallness parameter, \(0 < \varepsilon < 1\).

Substituting (12), (13b) and (37) in (9) and equating the coefficients of ε2 from l.h.s. and r.h.s. we get

$$ \frac{1}{2}\left( {\frac{{{\rm d}\varphi^{(1)} }}{{\rm d}X}} \right)^{2} = \frac{1}{2}\delta_{1}^{(1)} \varphi^{{(1)^{2} }} + \delta_{2}^{(0)} \varphi^{{(1)^{2} }} \varphi^{(2)} + \frac{1}{4}\delta_{3}^{(0)} \varphi^{{(1)^{4} }} $$
(38)

Near-critical state when \(\delta_{2}^{(0)} \approx 0\), Eq. (38) is reduced to

$$ \left( {\frac{{{\rm d}\varphi^{(1)} }}{{\rm d}X}} \right)^{2} = \delta_{1}^{(1)} \varphi^{{(1)^{2} }} + \frac{1}{2}\delta_{3}^{(0)} \varphi^{{(1)^{4} }} $$
(39)

Equation (39) has the solution for SW in the form

$$ \varphi_{c}^{(1)} = A_{1} \sec h\eta $$
(40)

where \(A_{1}\) is amplitude of first-order SW near-critical state,

$$ A_{1}^{2} = - \frac{{2\delta_{1}^{(1)} }}{{\delta_{3}^{(0)} }} = - \frac{{4V_{0}^{ - 3} }}{{(\gamma_{3} - 2.5V_{0}^{ - 6} )}}V^{(1)} $$
(41)
$$ \eta = \frac{1}{2}\left( {\sqrt {\delta_{1}^{(1)} } } \right)X,\,\delta_{1}^{\left( 1 \right)} = 2V_{0}^{ - 3} V^{(1)} $$

In near-critical state, \(\delta_{2}^{(0)} \approx 0\); so, from (15) we obtain

$$ \gamma_{2} - \frac{3}{2}\gamma_{1}^{2} = 0 $$
(42)

where

$$ \gamma_{1} = \frac{{\alpha_{ec} }}{{\beta_{ec} }} + \frac{{\alpha_{eh} }}{{\beta_{eh} }},\,\gamma_{2} = \frac{{\alpha_{ec} }}{{3\beta_{ec}^{2} }} + \frac{{\alpha_{eh} }}{{3\beta_{eh}^{2} }} $$

Using the values of \(\gamma_{1}\) and \(\gamma_{2}\) in (42), we obtain the following quadratic equation for the near-critical value of density of URD electrons at \(\delta_{2}^{(0)} \approx 0,\)

$$ \alpha_{ec}^{2} - \left[ {\frac{{(\beta_{eh} + 9\alpha_{eh} \beta_{ec} )}}{{3\beta_{eh} }}} \right]\alpha_{ec} - \left[ {\frac{{(2 - 3\alpha_{eh} )\alpha_{eh} \beta_{ec}^{2} }}{{2\beta_{eh}^{2} }}} \right] = 0 $$
(43)

From (43) we obtain two values of the density of URD electrons at the low temperature given by

$$ \alpha_{ec1} = B + (B^{2} + 4C)^{1/2} $$
(44a)
$$ \alpha_{ec2} = B - (B^{2} + 4C)^{1/2} $$
(44b)

where

$$ B = \left[ {\frac{{(\beta_{eh} + 9\alpha_{eh} \beta_{ec} )}}{{3\beta_{eh} }}} \right],\,C = \frac{{(2 - 3\alpha_{eh} )\alpha_{eh} \beta_{ec}^{2} }}{{2\beta_{eh}^{2} }} $$

From (44a) and (44b) the critical values of density \(\alpha_{ec1}\) and \(\alpha_{ec2}\) of electrons at the low temperature may be obtained, if other plasma parameters, e.g., \(\alpha_{eh} ,\beta_{ec} ,\beta_{eh}\), are known.

Similarly, at near-critical state, values of the temperatures \(\beta_{ec}\) of URD electrons at low temperature for the excitation of SW of IAW may be obtained from the quadratic equation of \(\beta_{ec}\) using Eq. (42).

Now, to find the higher-order correction in solitons at near-critical state of second-order Eq. (24) we equate the coefficient €5/2 and obtain the following equation,

$$ \frac{{{\rm d}\varphi^{\left( 1 \right)} }}{{\rm d}X}\frac{{{\rm d}\varphi^{(2)} }}{{\rm d}X} = \partial_{1}^{(1)} \varphi^{(1)} \varphi^{(2)} + \partial_{2}^{(0)} \varphi^{(1)} \varphi^{{(2)^{2} }} + \partial_{2}^{(0)} \varphi^{{(1)^{2} }} \varphi^{(3)} + \frac{1}{3}\delta_{2}^{\left( 1 \right)} \varphi^{{\left( 1 \right)^{3} }} + \delta_{3}^{\left( 0 \right)} \varphi^{{(1)^{3} }} \varphi^{(2)} $$
(45)

Assuming \(\delta_{2}^{(0)} \approx 0\) for near-critical state, we solve Eq. (45) for obtaining the second-order correction term \(\varphi^{(2)}\) given by

$$ \varphi_{c}^{(2)} = [A_{2} \sec h\eta + \tanh \eta ]\sec h\eta $$
(46)

where \(A_{2}\) is the amplitude of second-order correction term at near-critical state,

$$ A_{2} = - \frac{2}{3}\frac{{\delta_{2}^{(1)} }}{{\delta_{3}^{(0)} }} = - \frac{{4\,\gamma_{1}^{3} V_{0} V^{\left( 1 \right)} }}{{(\gamma_{3} - 5\gamma_{1}^{3} /2)}} = - \frac{{4\,V_{0}^{ - 5} V^{\left( 1 \right)} }}{{(\gamma_{3} - 2.5V_{0}^{ - 6} )}} $$
(47)

Using (40) and (46) the corrected solution of DS of IAW at near-critical state is obtained as

$$ \varphi_{2C} = \varphi_{c}^{(1)} + \varphi_{c}^{(2} = [A_{1} + A_{2} \sec h\eta + \tanh \eta ]\sec h\eta $$

5 Double layers

The solution of DL of IAW in URD two-temperature-electron plasma can also be obtained from Eq. (9). To obtain the solution of DL, we make an approximation taking the coefficients of \(\varphi^{3}\) of Eq. (9) as \(\varepsilon \Delta_{3}\) where ε is smallness parameter, \(0 < \varepsilon < 1\).

Moreover, we substitute a new scaling with different perturbation expansions for V and \(\xi\) given by

$$ V = V_{0} + \varepsilon^{2} V^{(1)} + \varepsilon^{3} V^{(2)} $$
(49a)

and

$$ X = \varepsilon \xi $$
(49b)

where ε is a smallness parameter, \(0 < \varepsilon < 1\).

Using (49a) and (49b) in Eq. (9), we get after integration

$$ \frac{{\varepsilon^{2} }}{2}\left( {\frac{{\rm d}\varphi }{{{\rm d}X}}} \right)^{2} = \frac{1}{2}\Delta_{1} \,\varphi^{2} + \frac{1}{3}\Delta_{2} \varphi^{3} + \frac{1}{4}\varepsilon \Delta_{3} \varphi^{4} $$
(50)

Now using \(\Delta_{1}\), \(\Delta_{2}\) and \(\Delta_{3}\) of (9) in (50) and equating the coefficient of \(\varepsilon^{4}\) on both l.h.s. and r.h.s. we obtain

$$ \frac{1}{2}\left( {\frac{{{\rm d}\varphi^{(1)} }}{{\rm d}X}} \right)^{2} = \frac{1}{2}\partial_{1}^{(1)} \,(\varphi^{(1)} )^{2} + \frac{1}{3}\partial_{2}^{(0)} (\varphi^{(1)} )^{3} + \frac{1}{4}\partial_{3}^{(0)} (\varphi^{(1)} )^{4} $$
(51)

Now, Eq. (51) is written in the form

$$ \frac{1}{2}\left( {\frac{{{\rm d}\varphi^{(1)} }}{{\rm d}X}} \right)^{2} + \psi (\varphi^{(1)} ) = 0 $$
(52)

where

$$ \psi (\varphi^{(1)} ) = - \frac{1}{2}\partial_{1}^{(1)} \,(\varphi^{(1)} )^{2} - \frac{1}{3}\partial_{2}^{(0)} (\varphi^{(1)} )^{3} - \frac{1}{4}\partial_{3}^{(0)} (\varphi^{(1)} )^{4} $$
(53)

Equation (52) describes the motion of a pseudoparticle of unit mass with velocity \({\rm d}\varphi^{(1)} /{\rm d}X\) and position \(\varphi^{(1)}\) in a potential well \(\psi (\varphi^{(1)} )\). The first term of Eq. (53 ) can be regarded as the kinetic energy of the pseudoparticle, whereas the second term is the potential energy of the same particle at that instant.

For the solutions of DL, \(\psi (\varphi^{(1)} )\) must satisfy the following boundary conditions:

$$ ({\text{i}})\,\psi (\varphi^{(1)} ) = 0,d\psi /{\rm d}\varphi^{(1)} = 0\,{\text{and}}\,d^{2} \psi /{\rm d}\varphi^{2} < 0\,{\text{at}}\,\varphi = 0, $$
(54a)
$$ ({\text{ii}})\,\psi (\varphi^{(1)} ) = 0,d\psi /{\rm d}\varphi^{(1)} = 0\,{\text{and}}\,d^{2} \psi /{\rm d}\varphi^{{(1)^{2} }} < 0\,{\text{at}}\,\varphi^{(1)} = \varphi_{m}^{(1)} ( \ne 0), $$
(54b)
$$ ({\text{iii}})\,{\text{for}}\,0 < \left| {\varphi^{(1)} } \right| < \left| {\varphi_{m}^{(1)} } \right| $$
(54c)

When the above conditions are satisfied, \(\varphi^{(1)} = 0\) is an unstable equilibrium position. The pseudoparticle is not reflected at \(\varphi^{(1)} = \varphi_{m}^{(1)}\) because the pseudoforce and the pseudovelocity have vanished. Instead, it goes to another state producing an asymmetrical DL with a net potential drop \(\varphi_{m}^{(1)}\).

Applying boundary conditions (54a) and (54b) in (53) we obtain

$$ \varphi_{m} = - \frac{2}{3}\frac{{\partial_{2}^{(0)} }}{{\partial_{3}^{(0)} }} = - \frac{2}{3}\frac{{(\gamma_{2} - 1.5V_{0}^{ - 4} )}}{{(\gamma_{3} - 2.5V_{0}^{ - 6} )}} $$
(55)

and

$$ \psi (\varphi^{(1)} ) = - \frac{{\partial_{3}^{(0)} }}{4}\varphi^{{(1)^{2} }} (\varphi_{m}^{(1)} - \varphi^{(1)} )^{2} $$
(56a)
$$ {\text{i.e.}} \,\psi (\varphi^{(1)} ) = - \frac{{(\gamma_{3} - 2.5V_{0}^{ - 6} )}}{4}\varphi^{{(1)^{2} }} (\varphi_{m}^{(1)} - \varphi^{(1)} )^{2} $$
(56b)

The solution of (52) for DL satisfying (55) is obtained as

$$ \varphi_{D} = \frac{{\varphi_{m}^{(1)} }}{2}\left( {1 - \tanh [\sqrt {(\partial_{3}^{(0)} /8\varphi_{m}^{(1)} } )X]} \right) $$
(57a)
$$ {\text{i.e.}}\, \varphi_{D} = - \frac{1}{3}\frac{{(\gamma_{2} - 1.5V_{0}^{ - 4} )}}{{(\gamma_{3} - 2.5V_{0}^{ - 6} )}}\left( {1 - \tanh [\sqrt {\left\{ {(\gamma_{3} - 2.5V_{0}^{ - 6} )} \right./} \left. {8\varphi_{m}^{(1)} } \right\}X]} \right) $$
(57b)

The width of DL is given by

$$ W_{DL} = 2\left( {\frac{{\partial_{3}^{(0)} }}{{8\left| {\varphi_{m}^{(1)} } \right|}}} \right)^{1/2} $$
(58a)
$$ {\text{i.e.}}\,W_{DL} = 2\left( {\frac{{[\gamma_{3} - 2.5V_{0}^{ - 6} ]}}{{8\left| {\varphi_{m}^{(1)} } \right|}}} \right)^{1/2} $$
(58b)

It is seen that the width of DL depends on the parameters of URD two-temperature-electron plasma. It is important to note that the DL in plasma can only exist for positive value of \(\delta_{3}^{(0)}\), i.e., \(\partial_{3}^{(0)} > 0\). To satisfy this condition, the plasma parameters should have some critical values. Using (15) we get the critical value of the density of URD electrons at low temperature,

$$ \alpha_{ec} > [27\beta_{ec}^{3} (2.5V_{0}^{ - 6} - \frac{{\alpha_{eh} }}{{27\beta_{eh}^{3} }})] $$
(59)

From Eqs. (55) and (57b) it is observed that the nature of DL (compressive or rarefactive) depends on the sign of the coefficient of the quadratic nonlinear term. Moreover, from (55) it is evident that for positive values of \(\delta_{2}^{(0)}\) the rarefactive DL is formed since \(\delta_{3}^{(0)}\) is positive. On the other hand, if \(\delta_{2}^{(0)}\) is negative, the compressive DL will be excited. The nature, amplitude and width of the DL depend on the plasma parameters such as the density and temperature of electrons of URD two-temperature-electron plasma.

6 Results and discussion

We have studied the DS and the DL of IAW in dense dusty plasma having URD two-temperature electrons considering higher-order nonlinear and dispersive effects by carrying out calculations up to second order. The secularity conditions at each order give corrections to the velocity of the SW at the corresponding higher order. It is shown that higher-order nonlinear and dispersion terms have significant contributions to the formation of DS in the plasma under consideration. To find the DS we have first obtained the first-order SW (KdV solitons), then second-order correction to the KdV solitons and finally the corrected second-order SW ( i.e., the DS). From (19), (29) and (33) it is seen that the density and the temperature of URD two-temperature electrons have significant contribution to excite the DS. Considering a model URD plasma, we have numerically estimated the respective amplitudes and have drawn the profiles of KdV solitons, second-order correction to the KdV soliton and finally the DS in the plasma. The effects of plasma parameters on the DS are graphically shown in Figs.(1)–(4).

To understand the nature of DS in URD two-temperature-electron plasma, the profiles are drawn taking different values of density and temperature of degenerate electrons. In Fig. 1 to Fig. 4 the structures of KdV solitons and DS are shown with the variation of density and temperature of ultra-relativistic degenerate two-temperature electrons (dimensionless) for fixed values of other plasma parameters.

  1. i)

    Effect of \(\alpha_{ec.}\)

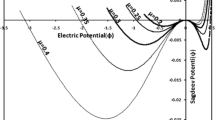
    In Fig. 1(a), the profile of KdV solitons (\(\varphi^{(1)}\)) is shown for different values of degenerate electron density (\(\alpha_{ec}\)) at low temperature for fixed values of the plasma parameters \(\beta_{ec}\) = 0.1, \(\beta_{eh}\) = 0.5, \(\alpha_{d}\) = 0.01. It is observed that rarefactive KdV solitons would be excited in the plasma and the amplitude will increase with the increase of \(\alpha_{ec}\). In Fig. 1(b), the structure of second-order correction to KdV solitons (\(\varphi^{(2)}\)) is shown for the same plasma. It is observed that second-order correction term \(\varphi^{(2)}\) is compressive in nature and the amplitude is large for the large values of density of degenerate electrons at low temperature. Figure 1(c) shows the profiles of the DS (dressed solitons) (\(\varphi_{2}\)) for degenerate electron density \(\alpha_{ec}\) = 0.1, for fixed values of the plasma parameters \(\beta_{ec}\) = 0.1, \(\beta_{eh}\) = 0.5, \(\alpha_{d}\) = 0.01. It is seen that the DS is compressive in nature and the amplitude of DS is much larger than that of the KdV solitons. The variation of amplitude of the KdV solitons and the DS in URD two-temperature electrons are shown in Fig. 1(d) and Fig. 1(e). It is observed that for the increase of \(\alpha_{ec}\) the amplitudes of rarefactive KdV solitons and the compressive DS are decreasing. Figure 1(f) shows the variation of Mach numbers of the KdV solitons (\(M_{1}\)), second-order correction to KdV solitons (\(M_{2}\)) and DS ( \(M = M_{1} + M_{2}\)) is described for different values of \(\alpha_{ec}\) in URD plasma for fixed values of the plasma parameters \(\beta_{ec}\) = 0.1, \(\beta_{eh}\) = 0.5, \(\alpha_{d}\) = 0.01. It is observed that the Mach number of dressed solitons (M) is greater than that of KdV solitons (\(M_{1}\)).

  2. ii)

    Effect of \(\beta_{ec}\)

Fig. 1
figure 1

(a) (colour online) The profiles of KdV solitons (\(\varphi^{(1)}\)) for different values of density (\(\alpha_{ec}\)) of degenerate electrons for fixed values of the plasma parameters \(\beta_{ec}\) = 0.1, \(\beta_{eh}\) = 0.5, \(\alpha_{d}\) = 0.01; the graphs a and c correspond to \(\alpha_{ec}\) = 0.1, 0.2 and 0.3; (b) (colour online) the profiles of second-order correction (\(\varphi^{(2)}\)) to the KdV solitons for different values of density (\(\alpha_{ec}\)) of degenerate electrons for fixed values of the plasma parameters \(\beta_{ec}\) = 0.1, \(\beta_{eh}\) = 0.5, \(\alpha_{d}\) = 0.01; the graphs a, b and c correspond to \(\alpha_{ec}\) = 0.1, 0.2 and 0. (c) (colour online) The profiles of the dressed solitons (\(\varphi_{2}\)) for density \(\alpha_{ec}\) = 0.1 of degenerate electrons for fixed values of the plasma parameters \(\beta_{ec}\) = 0.1, \(\beta_{eh}\) = 0.5, \(\alpha_{d}\) = 0.01; the graphs a, b and c represent the KdV solitons (\(\varphi^{(1)}\)), second-order correction (\(\varphi^{(2)}\)) and dressed solitons (\(\varphi_{2} = \varphi^{(1)} + \varphi^{(2)}\)(d) (colour online) Variation of the amplitude of KdV solitons for different values of density (\(\alpha_{ec}\)) of degenerate electron for fixed values of \(\beta_{ec}\) = 0.1, \(\beta_{eh}\) = 0.5, \(\alpha_{d}\) = 0.01. (e) (colour online) Variation of the amplitude of dressed solitons for different values of density (\(\alpha_{ec}\)) of degenerate electrons for fixed values of \(\beta_{ec}\) = 0.1, \(\beta_{eh}\) = 0.5, \(\alpha_{d}\) = 0.01. (f) (colour online) Variation of the Mach number with density (\(\alpha_{ec}\)) of degenerate electrons for fixed values of \(\beta_{ec}\) = 0.1, \(\beta_{eh}\) = 0.5, \(\alpha_{d}\) = 0.0; curves (a), (b) and (c) represent the Mach number of the KdV solitons (\(M_{1}\)), second-order correction of solitons (\(M_{2}\)) and dressed solitons (\(M = M_{1} + M_{2}\)), respectively

Full size image

Similarly, the effect of temperature (\(\beta_{ec}\)) of URD electrons at low temperature on the KdV solitons is shown in Fig. 2a in the plasma for fixed values of other parameters \(\alpha_{ec}\) = 0.1, \(\beta_{eh}\) = 0.6, \(\alpha_{d}\) = 0.01. It is observed that both compressive and rarefactive SW may be excited in the plasma depending upon the values of \(\beta_{ec}\). For \(\beta_{ec}\) = 0.01 and 0.02, the SW will be compressive and the amplitude is large for the large value of \(\beta_{ec}\), but when \(\beta_{ec}\) = 0.1 and 0.2 the rarefactive SW will be excited and amplitude is increased with the increase of \(\beta_{ec}\). The profiles of second-order correction \(\varphi^{(2)}\) are shown in Fig. 2b for different values temperature of degenerate electrons \(\beta_{ec}\) for fixed values of the plasma parameters \(\alpha_{ec}\) = 0.1, \(\beta_{eh}\) = 0.6 are \(\alpha_{d}\) = 0.01. It is observed that second-order corrections \(\varphi^{(2)}\) to KdV solitons are compressive in nature and amplitude is large for the large values of \(\beta_{ec.}\). At low value of \(\beta_{ec} ,\) it is compressive with wave-like behavior.

Fig. 2
figure 2

(a) (colour online) The profiles of KdV solitons (\(\varphi^{(1)}\)) for different values of temperature (\(\beta_{ec}\)) of degenerate electron for fixed values of the plasma parameters \(\alpha_{ec}\) = 0.1, \(\beta_{eh}\) = 0.6, \(\alpha_{d}\) = 0.01; the red, blue, green and magenta graphs represent \(\beta_{ec}\) = 0.01, 0.02, 0.1 and 0.2. (b) (colour online) The profiles of the second-order correction (\(\varphi^{(2)}\)) to the KdV solitons for different values of temperature (\(\beta_{ec}\)) of degenerate electrons for fixed values of the plasma parameters \(\alpha_{ec}\) = 0.1, \(\beta_{eh}\) = 0.6, \(\alpha_{d}\) = 0.01. The graphs a, b, c and d represent \(\beta_{ec}\) = 0.01, 0.1, 0.15 and 0.2; (c) (colour online) the profiles of dressed solitons (\(\varphi_{2}\)) for the temperature \(\beta_{ec}\) = 0.01 of degenerate electrons for fixed values of the plasma parameters \(\alpha_{ec}\) = 0.1, \(\beta_{eh}\) = 0.6, \(\alpha_{d}\) = 0.01; the graphs a, b and c represent the KdV solitons (\(\varphi^{(1)}\)), second-order correction (\(\varphi^{(2)}\)) and dressed solitons (\(\varphi_{2} = \varphi^{(1)} + \varphi^{(2)}\)); (d) (colour online) the profiles of dressed solitons for the temperature \(\beta_{ec}\) = 0.5 of degenerate electron with fixed values of \(\alpha_{ec}\) = 0.1, \(\beta_{eh}\) = 0.6, \(\alpha_{d}\) = 0.01; curves (a), (b) and (c) represent KdV solitons (\(\varphi^{(1)}\)), second-order correction (\(\varphi^{(2)}\)) and dressed solitons (\(\varphi_{2}\) = \(\varphi^{(1)}\) + \(\varphi^{(2)}\)); (e) (colour online) variation of the amplitude of KdV solitons for different values of temperature (\(\beta_{ec}\)) of degenerate electrons with fixed values of \(\alpha_{ec}\) = 0.1, \(\beta_{eh}\) = 0.6, \(\alpha_{d}\) = 0.01. (f) (colour online) Variation of amplitude of dressed solitons for different values of temperature (\(\beta_{ec}\)) of degenerate electrons with fixed values of \(\alpha_{ec}\) = 0.1, \(\beta_{eh}\) = 0.6, \(\alpha_{d}\) = 0.01. g (colour online) Variation of the Mach number with temperature (\(\beta_{ec}\)) of degenerate electrons for fixed values of \(\alpha_{ec}\) = 0.1, \(\beta_{eh}\) = 0.6, \(\alpha_{d}\) = 0.01; curves (a), (b) and (c) represent the Mach number of the KdV solitons (\(M_{1}\)), second-order correction of solitons (\(M_{2}\)) and dressed solitons (\(M = M_{1} + M_{2}\)), respectively

Full size image

The profiles of DS are shown in Fig. 2c, d in URD two-temperature-electron plasma for the values of \(\beta_{ec}\) = 0.01 and \(\beta_{ec}\) = 0.5 for fixed values of \(\alpha_{ec}\) = 0.1, \(\beta_{eh}\) = 0.5 and \(\alpha_{d}\) = 0.01. It is observed that structure of DS is more interesting for low values of \((\beta_{ec} = 0.01)\)

than large values of βec = 0.5.

The variation of the amplitude of the KdV solitons and the DS in URD plasma having two-temperature electrons is shown in Fig. 2e, f. It is observed that for the increase of \(\beta_{ec}\) the amplitudes of compressive DS are increasing for the low value \(\beta_{ec}\) and the amplitudes are decreasing for the large values \(\beta_{ec}\). Figure 2g shows the variation of Mach numbers of the KdV solitons (\(M_{1}\)), the second-order correction to KdV solitons (\(M_{2}\)) and the DS (\(M = M_{1} + M_{2}\)) with the temperature of degenerate electrons (\(\beta_{ec}\)) for fixed values of \(\alpha_{ec}\) = 0.1, \(\beta_{eh}\) = 0.6, \(\alpha_{d}\) = 0.01. It is observed that the Mach number (M) of DS is greater than that of the KdV solitons (\(M_{1}\)).

Special Cases:

Dressed solitons near-critical state

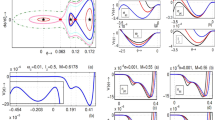
Effect of \(\alpha_{ec}\) In near-critical state, the nonlinear coefficient vanishes, i.e., \(\delta_{2}^{(0)} \approx 0\), the profiles of KdV solitons (\(\varphi_{1C}\)) are shown in Fig. 3a for different values of \(\alpha_{ec}\) in URD two-temperature electrons for fixed values of \(\beta_{ec}\) = 0.1, \(\beta_{eh}\) = 0.5, \(\alpha_{d}\) = 0.01. It is observed that in near-critical state the KdV solitons are compressive and the amplitude increases with the increase of \(\alpha_{ec}\). The second-order correction to the KdV solitons \(\varphi^{(2)}\) is shown in Fig. 3b for different values of \(\alpha_{ec}\) for fixed values of the parameters of same plasma. It is observed that the nature of second-order corrections to the KdV solitons (\(\varphi^{(2)}\)) may be compressive and rarefactive and the amplitude is large for the large values of \(\alpha_{ec} .\) At near- critical state, the DS in URD two-temperature electrons is shown in Fig. 3c for the electron density \(\alpha_{ec}\) = 0.1 with fixed values of \(\beta_{ec}\) = 0.1, \(\beta_{eh}\) = 0.5 and \(\alpha_{d}\) = 0.01. It is seen from Fig. 3d that amplitude of the DS is lower than the KdV solitons.

Fig. 3
figure 3

(a) (colour online) The profiles of first-order KdV solitons (\(\varphi_{1C}\)) near-critical state for different values of density (\(\alpha_{ec}\)) of degenerate electron with fixed values of \(\beta_{ec}\) = 0.1, \(\beta_{eh}\) = 0.5, \(\alpha_{d}\) = 0.01; curves (a), (b) and (c) represent three values of \(\alpha_{ec}\) = 0.1, 0.2 and 0.5, respectively. (b). (colour online) The profiles of second-order correction to KdV solitons (\(\varphi_{2C}\)) near-critical state of degenerate electron density (\(\alpha_{ec}\)) for fixed values of \(\beta_{ec}\) = 0.1, \(\beta_{eh}\) = 0.5, \(\alpha_{d}\) = 0.01; curves (a), (b) and (c) represent three different values of \(\alpha_{ec}\) = 0.1, 0.2 and 0.5, respectively. (c) (colour online) The profiles of the dressed solitons near-critical state for degenerate electron density \(\alpha_{ec} = 0.1\) with fixed values of \(\beta_{ec}\) = 0.1, \(\beta_{eh}\) = 0.6, \(\alpha_{d}\) = 0.01; curves (a), (b) and (c) represent the KdV solitons (\(\varphi_{1C}\)), second-order correction (\(\varphi_{2C}\)) and dressed solitons (\(\varphi_{2C}\) = \(\varphi_{1C}\) + \(\varphi_{2C}\)). (d) (colour online) Variation of amplitude of first-order KdV solitons and dressed solitons near-critical state for different values of degenerate electron density (\(\alpha_{ec1}\)) for fixed values of \(\beta_{ec}\) = 0.1, \(\beta_{eh}\) = 0.5, \(\alpha_{d}\) = 0.01. Curves a and b represent \(\varphi {}_{01c}\) and \(\varphi_{02c}\), respectively

Full size image

Effect of \(\beta_{ec}\) The temperatures of URD two-temperature electrons also have important roles of the nature of DS at near-critical state. Let us first see the effect of \(\beta_{ec}\) on the KdV solitons. In Fig. 4a, the structures of KdV solitons are shown for different values of \(\beta_{ec}\) in plasma for fixed values of \(\alpha_{ec}\) = 0.1, \(\beta_{eh}\) = 0.5 and \(\alpha_{d}\) = 0.01. It is seen that the KdV solitons are compressive in nature and the amplitude of it decreases with the increase of \(\beta_{ec} .\) At near-critical state, the higher-order corrections (\(\varphi_{2C}\)) to the KdV solitons for different values of \(\beta_{ec}\) are shown in Fig. 4b in same plasma. It is observed that the correction term \(\varphi_{2C}\) may be compressive and rarefactive in nature. Moreover, the amplitude of \(\varphi_{2C}\) is small for the large values of \(\beta_{ec}\). The DS at near-critical state in URD two-temperature electrons is shown in Fig. 4c for \(\beta_{ec}\) = 0.1 with fixed values of \(\alpha_{ec}\) = 0.1, \(\beta_{eh}\) = 0.6 and \(\alpha_{d}\) = 0.01. It is seen that the amplitude of DS is lower than the first-order SW. In this regard, it is necessary to state that the DS will be excited in the URD plasma at near-critical state (\(\delta_{2}^{(0)} \approx 0\)), when the density \(\alpha_{ec}\) will have two critical values \(\alpha_{ec1}\) and \(\alpha_{ec2}\) given by (48a) and (48b). The variations of \(\alpha_{ec1}\) and \(\alpha_{ec2}\) with \(\beta_{ec}\) for fixed values of \(\beta_{eh}\) = 0.6 and \(\alpha_{d}\) = 0.01 are shown in Fig. 4(d)-1,-2. It is seen that with the increase of \(\beta_{ec}\) both \(\alpha_{ec1}\) and \(\alpha_{ec2}\) are increased.

Fig. 4
figure 4

(a) (colour online) The profiles of first-order KdV solitons (\(\varphi_{1C}\)) near-critical state for different values of temperature (\(\beta_{ec}\)) of degenerate electrons with fixed values of \(\alpha_{ec}\) = 0.1, \(\beta_{eh}\) = 0.5, \(\alpha_{d}\) = 0.01; curves (a), (b) and (c) represent three different values of \(\beta_{ec}\) = 0.1, 0.2 and 0.5, respectively. (b) (colour online) The profiles of second- order of solitons (\(\varphi_{2C}\)) near-critical state for different values of temperature (\(\beta_{ec}\)) of degenerate electrons with fixed values of \(\alpha_{ec}\) = 0.1, \(\beta_{eh}\) = 0.5, \(\alpha_{d}\) = 0.01; curves (a), (b) and (c) represent three different values of \(\beta_{ec}\) = 0.1, 0.2 and 0.5, respectively. (c) (colour online) The profiles of dressed solitons near-critical state for the temperature \(\beta_{ec} = 0.1\) of degenerate electrons with fixed values of \(\alpha_{ec}\) = 0.1, \(\beta_{eh}\) = 0.6, \(\alpha_{d}\) = 0.01; curves a, b and c represent the KdV solitons (\(\varphi_{1C}\)), second-order correction (\(\varphi_{2C}\)) and dressed solitons (\(\varphi_{2C}\) = \(\varphi_{1C}\) + \(\varphi_{2C}\)), respectively. (d) (colour online) Variation of critical value of electron density \(\alpha_{ec1}\) with electron temperature \(\beta_{ec}\) in ultra-relativistic degenerate plasma for fixed values of \(\beta_{eh}\) = 0.6, \(\alpha_{d}\) = 0.01. (e) (colour online) Variation of critical value of electron density \(\alpha_{ec2}\) with electron temperature \(\beta_{ec}\) in ultra-relativistic degenerate plasma for fixed values of \(\beta_{eh}\) = 0.6, \(\alpha_{d}\) = 0.01

Full size image

Double Layers in URD plasma

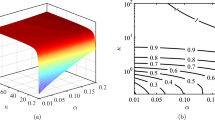
The solution of DL of IAW in URD two-temperature-electron plasma is obtained from Eq. (9) which is given by (57b), and the amplitude and width are given by (55) and (58b), respectively. It is to be noted that there are some critical values of \(\alpha_{ec}\) and \(\beta_{ec}\) for the excitation of the DL in URD plasma. The variation of critical value of \(\alpha_{ec}\) with \(\beta_{ec}\) is shown in Fig. 5a for excitation of DL for the fixed values of \(\beta_{eh}\) = 0.6, \(\alpha_{d}\) = 0.01 in URD plasma.

Fig. 5
figure 5

(a) (colour online) Variation of critical value of degenerate electrons density (\(\alpha_{ec}\)) with degenerate electron temperature ( \(\beta_{ec}\)) for fixed values of \(\beta_{eh}\) = 0.6, \(\alpha_{d}\) = 0.01 for excitation of double layers. (b) (colour online) The profiles of double layers for different values of degenerate electron density (\(\alpha_{ec}\)) with fixed values of \(\beta_{ec}\) = 0.01, \(\beta_{eh}\) = 0.5, \(\alpha_{d}\) = 0.01; curves a, b, c and d represent four different values of \(\alpha_{ec}\) = 0.0011, 0.0022, 0.0033 and 0.0044, respectively. (c) (colour online) Variation of the width (\(W_{DL}\)) of double layers with \(\alpha_{ec}\) for different \(\beta_{ec}\) of degenerate electrons with fixed values of \(\beta_{eh}\) = 0.5, \(\alpha_{d}\) = 0.001; curves (a), (b) and (c) represent three different values of \(\beta_{ec}\) = 0.010, 0.011 and 0.012, respectively

Full size image

Effect of \(\alpha_{ec}\) Using the limiting values of critical \(\alpha_{ec}\) and \(\beta_{ec}\) the profiles of DL in URD two-temperature-electron plasma are drawn for different values of \(\alpha_{ec}\) and \(\beta_{ec}\). In Fig. 5b it is shown that the formation of both compressive and rarefactive types of DL is possible to be excited in the URD plasma understudy for different values of \(\alpha_{ec}\) with the fixed values of \(\beta_{ec}\) = 0.01, \(\beta_{eh}\) = 0.5, \(\alpha_{d}\) = 0.01. It is found that the amplitude of rarefactive DL is increasing with the increase of \(\alpha_{ec} .\) The variation of width of DL with \(\alpha_{ec}\) for different values of \(\beta_{ec}\) of URD electrons for the fixed values of \(\beta_{eh}\) = 0.5 and \(\alpha_{d}\) = 0.01 is depicted in Fig. 5c. It is seen that the width of DL increases with the increase of \(\alpha_{ec}\), but it decreases with the increase of \(\beta_{ec} .\)

Effect of \(\beta_{ec}\) In Fig. 6a the profiles of DL of IAW are shown for different values of \(\beta_{ec}\) with the fixed values of \(\alpha_{ec}\) = 0.1, \(\beta_{eh}\) = 0.5 and \(\alpha_{d}\) = 0.01 in URD two-temperature-electron plasma. Figure 6a shows that only rarefactive DL is excited in the plasma and the amplitude of rarefactive DL is increased with the increase of \(\beta_{ec} .\) The variation of width of DL with \(\beta_{ec}\) is shown in Fig. 6b for different values of \(\alpha_{ec}\) with the fixed values of \(\beta_{eh}\) = 0.8, \(\alpha_{d}\) = 0.1. It is observed that width of DL decreases with the increase of \(\beta_{ec}\), but it increases with the increase of \(\alpha_{ec}\).

Fig. 6
figure 6

(a) (colour online) The profiles of double layers for different degenerate electron temperature (\(\beta_{ec}\)) for fixed values of \(\alpha_{ec}\) = 0.1, \(\beta_{eh}\) = 0.5, \(\alpha_{d}\) = 0.01; curves (a), (b) and (c) represent three different values of \(\beta_{ec}\) = 0.1, 0.2 and 0.3, respectively. (b) (colour online) Variation of the width (\(W_{DL}\)) of double layer with \(\beta_{ec}\) for different \(\alpha_{ec}\) of degenerate electrons with fixed values of \(\beta_{eh}\) = 0.8, \(\alpha_{d}\) = 0.1; curves (a), (b) and (c) represent three different values of \(\alpha_{ec}\) = 0.01, 0.03 and 0.06, respectively

Full size image

7 Conclusions

In this paper, we have theoretically studied the DS and the DL of IAW in a dusty plasma composed of URD two-temperature electrons, cold ions and negatively charged dust particles. Starting from an integrated form of the system of governing equations in terms of the pseudopotential considering higher-order nonlinear and dispersive effects, the DS and the DL have been theoretically studied using the approach based on the expansion of the Sagdeev potential up to second order and the RPM. Most important and significant results in this paper on the DS and the DL in cold ion and dense dusty plasma having URD two-temperature electrons are:

  • The rarefactive first-order SW (KdV solitons) would be excited for different values of \(\alpha_{ec}\) in URD two-temperature-electron plasma, and the amplitude of KdV solitons will increase with the increase of \(\alpha_{ec}\).

    In URD two-temperature-electron plasma, the second-order correction to the KdV solitons is compressive in nature for different values of \(\alpha_{ec}\) and the amplitude of KdV solitons is large for the large values of \(\alpha_{ec}\).

    The DS is compressive in URD two-temperature-electron plasma for different values of \(\alpha_{ec}\). The amplitude of DS is much larger than that of the KdV solitons.

  • Both compressive and rarefactive KdV solitons would be excited in URD two-temperature-electron plasma depending upon the values of \(\beta_{ec}\). For the values of \(\beta_{ec}\) = 0.01 and 0.02, the KdV solitons will be compressive and the amplitude is large for the large value of \(\beta_{ec}\), but for \(\beta_{ec}\) = 0.1 and 0.2 the rarefactive KdV solitons will be excited and the amplitude is increased with increase of \(\beta_{ec}\).

    The structures of DS are found interesting with the increase of temperature of electrons. The DS is compressive with wave-like structure, and its amplitude is lower than that of the KdV solitons.

    The second-order corrections to KdV solitons are compressive having wave-like structure for low value of \(\beta_{ec} .\)

  • In near-critical state, the KdV solitons are compressive and the amplitude increases with the increase of \(\alpha_{ec}\). The DS is also compressive, and its amplitude is lower than that of the KdV solitons.

    In near-critical state, the temperatures of URD electrons have important roles on the nature of the SW. It is seen that the KdV solitons are compressive and its amplitude decreases with the increase of \(\beta_{ec} .\) The DS is also compressive, and the amplitude of DS is lower than that of the KdV solitons.

  • It is possible to excite both compressive and rarefactive DL of IAW in URD two-temperature-electron plasma for different values of \(\alpha_{ec} .\) The amplitude of the rarefactive DL will be increased with the increase of \(\alpha_{ec}\). Moreover, the width of DL increases with the increase of \(\alpha_{ec}\), but it decreases with the increase of \(\beta_{ec}\).

Only rarefactive DL would be excited in URD two- temperature-electron plasma for different values of \(\beta_{ec}\), and the amplitude of DL will be increased with the increase of \(\beta_{ec} .\) The width of DL decreases with the increases of \(\beta_{ec}\), but it increases with the increase of \(\alpha_{ec}\).

It is important to be mentioned that most of the authors have studied the DS by the use of renormalization procedure in RPM. But, in the present paper, we have used the integral form of governing equations in terms of pseudopotential. The advantage of this method over the RPM is that instead of solving a second-order inhomogeneous differential equation at each order one has to solve a first-order inhomogeneous equation at each order except at the first. This technique has been successfully used by some authors [33,34,35] for investigating the effects of higher-order nonlinear and dispersive terms on the propagation of ion-acoustic SW in nondegenerate plasma systems. In this paper, we have also investigated the DS in URD two-temperature electrons near-critical state. It is necessary to be mentioned that using the renormalization procedure in RPM previous authors have studied the DS in plasma but not considered the situation in near-critical state. In our present investigation, we have considered the density of dust particles is low and is much smaller than the density of URD electrons. In dense dusty plasma, the dust particles would play significant roles on the nature of KdV solitons and the DS. The space plasmas are known to have multispecies composition with two-temperature electrons. So, our results on the DS and the DL may be useful for the study of nonlinear propagation of waves in understanding many phenomena in space plasma environments where the effects of URD electrons are important.