Upgraded NLMS algorithm for speech enhancement with sparse and dispersive impulse responses

Abstract

To have the effective speech communication, the information should be clearly passed in a noise-free environment. However, in real-world environment, the existence of background noise degrades the performance of the system. Based on the blind source separation strategy, various adaptive algorithms are designed and implemented using both dispersive impulse response and sparse impulse response. Even though the existing dual fast normalized least mean square algorithm works well under different noisy situations and gives a good performance, the problem is that it involves large number of processing steps. To overcome the complexity in finding the signal prediction parameter and to improve the performance of speech enhancement, we propose three adaptive filtering algorithms namely revised twofold rapid normalized least mean square algorithm, diminished twofold normalized least mean square algorithm and upgraded balanced twofold normalized least mean square algorithm (UBTNLMS). Taking the performance objective criteria into account, these algorithms have been tested for segmental signal-to-noise ratio, segmental mean square error, signal-to-noise ratio, mean square error and cepstral distance. On comparing the performance of the existing and proposed algorithms, UBTNLMS performs better than the other algorithms.

1 Introduction

Human being naturally possesses variety of ways to get back the information from the exterior world and much aware how to communicate with each other. Speech, images and text are the three most essential sources of information. For most of the cases, speech stands as the most resourceful and comfortable one. Speech not only delivers the content of linguistic information, but also delivers the extra valuable information like the mood of the speaker. Once the speaker and listener are close to each other in a calm situation, communication is normally easy and accurate. On the other hand, when the listener and speaker are at a long distance or in a noisy background situation, the listener’s ability to understand the particular information may get diminished. So, in most of the speech communication systems, the quality and intelligibility of speech play a major role. To reduce the noise and to improve the speech quality, several enhancement algorithms have been developed over past decades [1, 2]. Adaptive filters [3] are very important in telecommunication systems such as hand-free telephony [4], teleconferencing systems [5], hearing aids [6] with acoustic noise cancellation [7] and speech quality enhancement.

The most accepted single channel speech enhancement algorithms include minimum mean square error estimation (MMSE) [8], spectral subtraction [9] and log minimum mean square error (logMMSE) [10]. Some of these techniques have limitations in speech enhancement applications [11]. The alternate approach to speech enhancement is the signal subspace method [12]; the signal subspace method is based on the singular value decomposition [13]. In time domain and frequency domain, several algorithms have been developed [14,15,16], the double affine projection algorithm [17], double fast Newton transversal filter [18] and double pseudo double affine projection algorithm [19], partial update double affine projection algorithm [20], and sub-band algorithm [7]. In a moving car environment, a recent technique named blind source separation is used [21]. In the literature, we find two widely used structures of blind source separation, the forward blind source separation [22] and the backward blind source separation [23]. Forward blind source algorithm is used to update the cross-filters using recursive least square algorithm [24]. The symmetric adaptive de correlation (SAD) algorithms of forward and backward types [25,26,27] are essential keys to detach the speech signal from noisy observations. A dual fast normalized least mean square algorithm is used to improve the intelligibility of the speech enhancement systems [18, 28]. In most of the cases, blind source separation algorithms are used to find the dispersive impulse response. But this paper concentrates on dispersive and sparse impulse responses of convolution mixture. In this paper, we have revised and discussed three different types of dual channel adaptive algorithms for speech enhancement. This paper is organized as follows: in Sect. 2, we discuss about the convolution mixture model of the adaptive filters. In Sect. 3, we discuss about the mathematical formulation for the existing DFNLMS algorithm. In Sect. 4, we discuss about the proposed methods. In Sect. 5, the comparison results of the various developed algorithms are given, and finally, the conclusion is given in Sect. 6.

2 Convolution mixture model

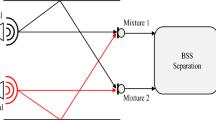
Convolution is a mathematical operation on two functions to produce a third function that expresses how the shape of one is modified by the other. Convolution is used here to mix speech and noise signals. The convolution mixture model consists of two components: an original speech signal and a noise signal. The original speech signal $a\left( n \right)$ and noise signal $b\left( n \right)$ are convolutedly mixed with two impulse responses, i.e. dispersive and sparse impulse responses of mixture contain (h₁₁(n), h₂₂(n), h₁₂(n) and h₂₁(n)) as shown in Fig. 1. The output signal of the convoluted mixture model is given as below

$$s_{1} \left( n \right) = a\left( n \right)*h_{11} \left( n \right) + b\left( n \right)*h_{21} \left( n \right)$$

(1)

$$s_{2} \left( n \right) = b\left( n \right)*h_{22} \left( n \right) + b\left( n \right)*h_{12} \left( n \right)$$

(2)

where (*) represents the convolution operation. Consider the two direct acoustic paths through h₁₁(n) and h₂₂(n) are assumed to be identity, i.e. h₁₁ (n) = h₂₂(n) = δ(n). Hence, here we consider the dispersive and sparse impulse responses between the cross-coupling effects of the channels h₁₂(n) and h₂₁(n). The two acoustic paths are found to be unity, and hence, the model is further simplified and is given by the following expression

$$k_{1} \left( n \right) = a\left( n \right) + b\left( n \right)*h_{21} \left( n \right)$$

(3)

$$k_{2} \left( n \right) = b\left( n \right) + a\left( n \right)*h_{12} \left( n \right).$$

(4)

Fig. 1

Convolution mixture model

Sparse impulse response is nothing but an impulse response that consists only a small percentage of its components with a significant magnitude, while others are zeros which is shown in Fig. 2(a) for the adaptive filter length L = 64. The vice versa is the dispersive impulse response, i.e. large number of components having its significant magnitude and small portions are containing zeros which is shown in Fig. 2(b).

Fig. 2

Impulse response with L = 64. (a) Sparse impulse response (b) dispersive impulse response

3 Existing method

In this section, we discuss about the mathematical formulation of the dual fast normalized least mean square method [20]. This algorithm is used to update the two cross-filters. To estimate the original speech signal, the adaptive filters p₂₁(n) and p₁₂(n) are used. From the mixing model, the enhanced speech output is given below:

$$s_{1} \left( n \right) = a\left( n \right) - p_{1}^{T} \left( n \right)K_{2} \left( n \right)$$

(5)

$$s_{2} \left( n \right) = b\left( n \right) - p_{2}^{T} \left( n \right)K_{1} \left( n \right)$$

(6)

where K₁(n) = [k₁(n), k₁(n − 1) …., k₁(n − L+1)]^T and K₂(n) = [k₂(n), k₂(n − 1)…..,k₂(n − L+1)]^T.

The adaptive filter is used for updating the relation which is given as:

$$p_{1} \left( {n + 1} \right) = p_{1} \left( n \right) - \mu_{1} \left( {s_{1} \left( n \right)d_{1} \left( n \right)} \right)$$

(7)

$$p_{2} \left( {n + 1} \right) = p_{2} \left( n \right) - \mu_{2} \left( {s_{2} \left( n \right)d_{2} \left( n \right)} \right)$$

(8)

where 0 < μ₁, μ₂ < 2 are the two step sizes which control the convergence behaviour of the adaptive filters. The adaptation gains d₁(n) and d₂(n) are given by the following relation:

$$d_{1} \left( n \right) = \gamma_{1} \left( n \right)N_{1} \left( n \right)$$

(9)

$$d_{2} \left( n \right) = \gamma_{2} \left( n \right)N_{2} \left( n \right)$$

(10)

where γ₁(n), γ₂(n) and N₁(n), N₂(n) are the likelihood variables and dual Kalman gain, respectively. The likelihood variables γ₁(n) and γ₂(n) and Kalman variables N₁(n), N₂(n) can be calculated as follows:

$$\gamma_{1} \left( n \right) = \frac{1}{{1 - N_{1}^{T} K_{2} \left( n \right)}}$$

(11)

$$\gamma_{2} \left( n \right) = \frac{1}{{1 - N_{2}^{T} K_{1} \left( n \right)}}$$

(12)

$$\left[ {\begin{array}{*{20}c} {N_{1} \left( n \right)} \\ * \\ \end{array} } \right] = \frac{{c_{1} \left( n \right)}}{{\lambda Z_{1} \left( {n - 1} \right) + c_{0} }}\left[ {\begin{array}{*{20}c} { - 1} \\ {N_{1} \left( {n - 1} \right)\frac{{\lambda Z_{1} \left( {n - 1} \right) + c_{0} }}{{c_{1} \left( n \right)}}} \\ \end{array} } \right]$$

(13)

$$\left[ {\begin{array}{*{20}c} {N_{2} \left( n \right)} \\ * \\ \end{array} } \right] = \frac{{c_{2} \left( n \right)}}{{\lambda Z_{2} \left( {n - 1} \right) + c_{0} }}\left[ {\begin{array}{*{20}c} { - 1} \\ {N_{2} \left( {n - 1} \right)\frac{{\lambda Z_{2} \left( {n - 1} \right) + c_{0} }}{{c_{2} \left( n \right)}}} \\ \end{array} } \right]$$

(14)

where $\left( * \right)$ represents the last element of the Kalman variable, c₀ is a small positive constant, λ (0 < λ < 1) is an exponential forgetting factor, and $\lambda_{a}$ is a small positive constant.

The parameters Z₁(n) and Z₂(n) are the forward prediction errors variances, and c₁(n) and c₂(n) are given below:

$$Z_{1} \left( n \right) = \lambda_{a} Z_{1} \left( {n - 1} \right) + c_{1}^{2} \left( n \right)$$

(15)

$$Z_{2} \left( n \right) = \lambda_{a} Z_{2} \left( {n - 1} \right) + c_{2}^{2} \left( n \right)$$

(16)

$$c_{1} \left( n \right) = k_{2} \left( n \right) - g_{1} k_{2} \left( {n - 1} \right)$$

(17)

$$c_{2} \left( n \right) = k_{1} \left( n \right) - g_{2} k_{1} \left( {n - 1} \right).$$

(18)

The variables g₁(n) and g₂(n) can be calculated as

$$g_{1} \left( n \right) = \frac{{f_{1} \left( n \right)}}{{f_{2} \left( n \right) + c_{a} }}$$

(19)

$$g_{2} \left( n \right) = \frac{{f_{3} \left( n \right)}}{{f_{4} \left( n \right) + c_{a} }}$$

(20)

where f₁(n) and f₂(n) represent the first autocorrelation mixture of k₂(n), and f₃(n) and f₄(n) represent the first autocorrelation mixture of k₂(n). The following relations f₁(n), f₂(n), f₃(n) and f₄(n) are estimated recursively by

$$f_{1} \left( n \right) = \lambda_{a} f_{1} \left( {n - 1} \right) + k_{2} \left( n \right)k_{2} \left( {n - 1} \right)$$

(21)

$$f_{2} \left( n \right) = \lambda_{a} f_{2} \left( {n - 1} \right) + k_{2}^{2} \left( n \right)$$

(22)

$$f_{3} \left( n \right) = \lambda_{a} f_{3} \left( {n - 1} \right) + k_{1} \left( n \right)k_{2} \left( {n - 1} \right)$$

(23)

$$f_{4} \left( n \right) = \lambda_{a} f_{4} \left( {n - 1} \right) + k_{1}^{2} \left( n \right).$$

(24)

4 Proposed algorithms

Under different noisy circumstances, the existing DFNLMS algorithm works well and offers good performance. But the challenge lies in estimating the parameters of the signal prediction using vast computation. In order to eliminate the problem of signal prediction parameter and to improve speech enhancement performance, we proposed three algorithms derived as follows:

4.1 Revised twofold rapid normalized least mean square (RTRNLMS) algorithm

The main objective of this RTRNLMS algorithm is to reduce the steps of derivation in the existing DFNLMS algorithm and to overcome the complexity of signal prediction problem. In the RTRNLMS method, we neglect the parameters, g₁(n) and g₂(n) from Eqs. (17) and (18), respectively, because the signal prediction parameter has little significance and offered no such greater improvement in performance of the speech. In RTRNLMS, we get a better performance by subtracting the previous values directly. The mathematical expression for the RTRNLMS is given below:

The parameter error variances are as in (15) and (16). The c₁(n) and c₂(n) are given as:

$$c_{1} \left( n \right) = k_{2} \left( n \right) - k_{2} \left( {n - 1} \right)$$

(25)

$$c_{2} \left( n \right) = k_{1} \left( n \right) - k_{1} \left( {n - 1} \right).$$

(26)

In (25), by subtracting the previous value of mixture k₂ from the present value of mixture k₂, we get a better improvement in the speech quality. The mixture k₁ is obtained by convolving the impulse response with noise signal and then added with the speech signal, and mixture k₂ is obtained by convolving the impulse response with speech signal and then added with noise signal. The likelihood variables γ₁(n) and γ₂(n) are given in (11) and (12).The Kalman variables N₁(n), N₂(n) can be calculated as follows:

$$\left[ {\begin{array}{*{20}c} {N_{1} \left( n \right)} \\ * \\ \end{array} } \right] = - \frac{{c_{1} \left( n \right)}}{{\lambda Z_{1} \left( {n - 1} \right) + c_{0} }} + N_{1} \left( {n - 1} \right)$$

(27)

$$\left[ {\begin{array}{*{20}c} {N_{2} \left( n \right)} \\ * \\ \end{array} } \right] = - \frac{{c_{1} \left( n \right)}}{{\lambda Z_{2} \left( {n - 1} \right) + c_{0} }} + N_{2} \left( {n - 1} \right).$$

(28)

The adaptation gains d₁(n) and d₂(n) are given in (9) and (10), the updating is as per (7) and (8), and the enhanced speech $s_{1} \left( n \right)$ and $s_{2} \left( n \right)$ are as given in (5) and (6).

4.2 Diminished twofold normalized least mean square (DTNLMS) algorithm

In diminished twofold normalized least mean square method, the derivation steps are minimized to few steps. The filter weight update equation used in DTNLMS is different from the existing and the RTRNLMS algorithms. In DTNLMS, we used the enhanced speech convolved with the segments of enhanced speech, instead of mixtures of noise that we used in DFNLMS and RTRNLMS. By using the weight adaptation method, we get a better improvement in the enhanced speech. The controlled parameter used here is with the step size $\mu_{1} = \mu_{2} = 0.1,$ and β = 10⁻²

The estimated speech signal is given by,

$$s_{1} \left( n \right) = a\left( n \right) - u_{1}^{T} \left( n \right)K_{2} \left( n \right)$$

(29)

$$s_{2} \left( n \right) = b\left( n \right) - u_{2}^{T} \left( n \right)K_{1} \left( n \right).$$

(30)

For updating the adaptive filter, the expression is given by,

$$p_{1} \left( {n + 1} \right) = p_{1} \left( n \right) - (\mu_{1} \left( {s_{1} \left( n \right)\varvec{s}_{2} \left( n \right)/\varepsilon } \right)$$

(31)

$$p_{2} \left( {n + 1} \right) = p_{2} \left( n \right) - (\mu_{2} \left( {s_{2} \left( n \right)\varvec{s}_{1} \left( n \right)/\varepsilon } \right)$$

(32)

where s₁(n) = [s₁(n), s₁(n − 1),….,s₁(n − L+1)]^T, and s₂(n) = [s₂(n), s₂(n − 1),….,s₂(n − L+1)]^T, $\varepsilon$ is a small positive constant. The K₁(n) and K₂(n) are defined in Sect. 3. The filter weight adaptation is obtained by convolving the enhanced speech signal with the segments of enhanced speech signal and also with the step size and then divided by the controlled parameter and then it is subtracted from the value of the weight in adaptive filter. The enhanced speech signal depends on the $\beta$ value. By properly selecting the step sizes and $\beta$, we get the better enhanced speech quality.

4.3 Upgraded balanced twofold normalized least mean square (UBTNLMS) algorithm

DTNLMS gives a better result when compared to DFNLMS and RTRNLMS. There exist few issues to enhance the speech signal, because it is controlled by a single variable β. We cannot rely on adjusting that single value to obtain the enhanced speech signal. So, we go for the UBTNLMS method. In UBTNLMS method, we used many parameters to obtain the enhanced speech. The controlled parameter used here is with step size $\mu_{1} = \mu_{2} = 0.1,\;{\text{and}}\; \xi$ = 1 and $\alpha$ is − 0.5. In UBTNLMS, we used a different updating expression for the adaptive filter and the adaptive filter is designed with diagonal weight elements. Diagonal matrix contains the value only in the diagonals, remaining are zeros. This algorithm possesses the stability of the outcomes with the best performance by the balanced control parameters. So this algorithm is named as upgraded balanced twofold normalized least mean square algorithm. The two diagonal step size control matrixes w₁₂(n) and w₂₁(n) are given by,

$$\begin{aligned} w_{12} \left( n \right) & = {\text{diag}}\{ w_{12,0} \left( n \right),w_{12,1} \left( n \right) \ldots .w_{12,L - 1} \left( {n - 1} \right) \\ & = \left[ {\begin{array}{*{20}c} {w_{12,0} \left( n \right)} & 0 & \cdots & 0 \\ 0 & {w_{12,1} \left( n \right)} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & {w_{12,L - 1} \left( n \right)} \\ \end{array} } \right] \\ w_{21} \left( n \right) & = {\text{diag}}\{ w_{21,0} \left( n \right),w_{21,1} \left( n \right) \ldots .w_{21,L - 1} \left( {n - 1} \right) \\ & = \left[ {\begin{array}{*{20}c} {w_{21,0} \left( n \right)} & 0 & \cdots & 0 \\ 0 & {w_{21,1} \left( n \right)} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & {w_{21,L - 1} \left( n \right)} \\ \end{array} } \right] \\ \end{aligned}$$

$$w_{12,l} \left( n \right) = \frac{1 - \alpha }{2L} + \left( {1 + \alpha } \right)\frac{1}{{2 \times \left( {\mathop \sum \nolimits_{i = 0}^{L - 1} w_{12,i} \left( n \right)} \right) + \varphi }}$$

(33)

$$w_{21,l} \left( n \right) = \frac{1 - \alpha }{2L} + \left( {1 + \alpha } \right)\frac{1}{{2 \times \left( {\mathop \sum \nolimits_{i = 0}^{L - 1} w_{21,i} \left( n \right)} \right) + \varphi }} .$$

(34)

The $\alpha$ is a small value takes between − 1 and 1, and $\varphi$ is a small positive constant. In UBTNLMS, we have used a different updating formulas for the adaptive filter. We have used diagonal weight elements of the diagonal step size control matrixes w₁₂(n) and w₂₁(n) in the adaptive filter Eqs. (33) and (34). By using this step in UBTNLMS algorithm, it possesses stability of the outcomes and better performance with the support of balanced control parameters.

The tap weight adaptation is given by,

$$p_{12} \left( n \right) = p_{12} \left( {n - 1} \right) + \mu_{1} \frac{{w_{12} \left( {n - 1} \right)\varvec{s}_{1} \left( n \right)s_{2} \left( n \right)}}{{K_{1}^{T} \left( n \right)K_{1} \left( n \right) + \xi }}$$

(35)

$$p_{21} \left( n \right) = p\left( {n - 1} \right) + \mu_{2} \frac{{w_{21} \left( {n - 1} \right)s_{1} \left( n \right)\varvec{s}_{2} \left( n \right)}}{{K_{2}^{T} \left( n \right)K_{2} \left( n \right) + \xi }}.$$

(36)

The weight adaptation is obtained by multiplying the previous values of diagonal elements with the enhanced speech signal along with segments of enhanced speech signal and then divided with the sum of mixtures of k₁ and $\xi$. The value of $\xi$ is 1, and the value of $\alpha$ is − 0.5. By substituting the tap weight adaptation in the output, we get the enhanced speech as per (5) and (6). Based on the update equations of the two adaptive filters (35) and (36) and the diagonal elements presented in $w_{21} \left( n \right)$ and $w_{12} \left( n \right)$, enhanced speech signal is obtained.

5 Evaluation of simulation result

In this section, evaluation results of the proposed algorithms are discussed. From Sect. 2, we take the convolution mixture model for mixing the noise and the speech. Figure 3 shows a clean speech and its spectrogram, while Fig. 4 represents a noise signal and its spectrogram.

Fig. 3

(a) Clean speech signal and (b) spectrogram of clean speech signal

Fig. 4

(a) Noise signal and (b) spectrogram of noise signal

The original speech signal and noise signal are subjected to convolution operation with two impulse responses, i.e. dispersive and sparse impulse responses. An impulse response is sparse, if a large fraction of its energy is concentrated in a small fraction of its duration. According to [18], sparse and dispersive impulse response sequences are generated by using the expression $h\left( n \right) = Ae^{ - Bn}$, where A represents a scalar factor that is equal to one and B is a damping factor which is related to the reverberation time $tr$. The damping factor for dispersive impulse response is $B = 3log \left( {10} \right)/tr$. Therefore, the decay factor is 10⁻³. For the sparse impulse response, the damping factor is $B = 20log \left( {10} \right)/tr$. Therefore, the decay factor is 10⁻²⁰ which is a very less compared to 10⁻³. Hence, in dispersive impulse response, the damping decays very slowly and has more damping than sparse. Sparse impulse response decays fast and has more zero values. The impulse response is generated when the length of the adaptive filter is taken as L = 64

The database used here is NOIZEOUS database with the sampling rate = 8 kHz. It consists of 30 speakers that contain different noises like car, train, airport, street, station, restaurant noise at input with SNR of 0, 5, 10 and 15 dB.

Figure 5 represents the mixing samples of mixture 1 and 2. Figure 6 represents the enhanced speech signal. In this section, we compare the performance of the existing algorithm with the proposed algorithms. The first proposed algorithm is revised twofold normalized least mean square (RTRNLMS) algorithm. This algorithm improves the performance by avoiding the problem of prediction parameters. The second proposed algorithm is the diminished twofold normalized least mean square (DTNLMS) algorithm. This algorithm reduces the level of noise to a maximum level. The third proposed algorithm is upgraded balanced twofold normalized least mean square algorithm (UBTNLMS). This algorithm used a diagonal matrix in the weight update equation to improve the performance of enhanced speech signal. The parameters of the existing and proposed algorithm are summarized in Table 1.

Fig. 5

(a) Mixing samples of mixture 1 and (b) mixing samples of mixture 2

Fig. 6

Enhanced speech signal

Table 1 Simulation parameter values of the existing and proposed algorithm with L = 64

In the case of DFNLMS algorithm, we have selected the optimum step size as $\mu_{1} = \mu_{2} = 0.1$, forgetting factor λ = 0.09, $\lambda_{a}$ = 0.1 and constant $c_{0}$ = 0.0009, $c_{a}$ = 1. However, in RTRNLMS algorithm, we have fixed the step size as $\mu_{1} = \mu_{2} = 0.1$, forgetting factor λ = 0.09, $\lambda_{a}$ = 0.1 and constant $c_{0}$ = 0.0009. Similarly, for DTNLMS and UBTNLMS, we fixed the step size as $\mu_{1}$ = $\mu_{2}$ = 0.1, ε = 1, α = − 0.5 and φ = 10⁻². The values for the parameters are selected by referring the parameter ranges from the literature [21], and then by iteratively fixing the parameter values, it gives the best result by implementing the algorithm. In RTRNLMS algorithm, λ varies between 0 < λ<1 and similarly step size μ also changes from 0 to 1. So the values are randomly selected between 0 to 1 for both μ and λ. For different values of μ₁ = μ₂ such as 0.8, 0.6, 0.4, 0.2, 0.1, the corresponding readings are taken for λ = 0.09, 0.06, 0.04, 0.01. From this, we infer that for 0 dB, 5 dB, 10 dB and 15 dB inputs, the parameters $\mu_{1} = \mu_{2} = 0.1$ and λ = 0.09 gave a comparatively good improvement and these parameter values are used for the enhancement in RTRNLMS algorithm. Similarly, in DTNLMS and UBTNLAM algorithms, the same iterative procedure is used for fixing the parameter values.

The size of the adaptive filter used in this work is 64. For simulation results, we have taken the filter size as 64,128 and 256. The filter weights are adjusted according to the filter weight update equation of the respective algorithm, until it gives the best result. In UBTNLMS, we used a different updating formulas for the adaptive filter. The balanced control parameters in this algorithm ensure performance stability. When compared to other algorithms, UBTNLMS performs best in enhancing the speech. To analyse the quality of the speech signal, in the next section, we present the comparative results of the existing and proposed algorithms in terms of the objective measures (1) the segmental signal-to-noise ratio, (2) the segmental mean square error, (3) signal-to-noise ratio, (4) cepstral distance and (5) mean square error.

5.1 Segmental signal-to-noise ratio (segSNR)

It is defined as the ratio of the enhanced speech signal to that of the background noise. The segmental signal-to-noise ratio is calculated by the following relation:

$$({\text{segsnr}})_{\text{dB}} = 10\log_{10} \left( {\frac{{\mathop \sum \nolimits_{i = 0}^{R} \left| {a\left( i \right)} \right|^{2} }}{{\mathop \sum \nolimits_{i = 0}^{R} \left| {a\left( i \right) - S_{1} \left( i \right)} \right|^{2} }}} \right)$$

(37)

where R is the number of frames and s₁ represents the enhanced speech signal, and a is the clean speech signal. The VAD is the voice activity detector which detects the presence and absence of speech and noise components. The segmental signal-to-noise ratio is calculated only in presence of speech only presence periods. In segmental SNR, the block size represents the total number of frame segments which has voice activity. After VAD detection, if the length of the speech only presence region has 9000 samples for the given input speech signal, we split the region into 100 × 90 frames. The total frame is now 100, and each frame consists of 90 samples. The 100 frames represent the block size. The block size depends on frame size. First, we divide the presence of speech regions into frames, where each frame consists of segments of particular length. In this paper, we have split the speech only presence regions into 45 frames and each frame consists of 75 samples.

Figures 7. 8, 9 and 10 portray the measure segmental SNR for both dispersive impulse and sparse responses for L = 64 and 128. The impulse responses at 0 dB and 5 dB are analysed for the bloc of 45 samples. Among the existing and proposed algorithms, the UBTNLMS algorithm responded with the better response. The SegSNR is about 98 dB at 0 dB and 100 dB at 5 dB. The sparse responses are also analysed at 0 dB and 5 for a bloc of 45 samples which give the performance better than the dispersive impulse response. At 0 dB, the SegSNR is about 100 dB which is higher than the dispersive impulse responses. By increasing the adaptive length of the filter, sparse impulse response performs better when compared to dispersive impulse response.

Fig. 7

SegSNR for the proposed and existing algorithm having the input SNR 0 dB (left) and 5 dB (right) and by using the dispersive impulse response. The adaptive filter length is taken as L = 64

Fig. 8

SegSNR for the proposed and existing algorithm having the input SNR 0 dB (left) and 5 dB (Right) by using the sparse impulse response. The adaptive filter length is taken as L = 64

Fig. 9

SegSNR for the proposed and existing algorithm having the input SNR 0 dB (left) and 5 dB (right) by using the dispersive impulse response. The adaptive filter length is taken as L = 128

Fig. 10

SegSNR for the proposed and existing algorithm having the input SNR 0 dB (left) and 5 dB (right) by using the sparse impulse response. The adaptive filter length is taken as L = 128

5.2 Segmental mean square error (SegMSE)

It is defined as the difference between the square of the true values and the estimated value. The segmental mean square error is given by the following relation

$$({\text{segmse}})_{\text{dB}} = \left( {10\log_{10} \mathop \sum \limits_{i = 0}^{R} |a\left( i \right) - S_{1} \left( i \right)|^{2} } \right)$$

(38)

where R is the number of frames and s₁ represents the enhanced speech signal, and a is the clean speech signal. The segmental mean square error ratio is calculated only in the absence of speech only presence periods, i.e. only in noise presence periods. First, we divide the noise only presence regions into frames and each frame consists of segments of particular length. In this paper, we have split the speech signal into 55 frames and each frame with of 75 samples.

Figures 7, 8, 9, 10, 11, 12, 13 and 14 portray the performance measure with segmental SNR and segmental MSE for both dispersive impulse and sparse impulse for length L = 64 and 128. The impulse responses at 0 dB and 5 dB are analysed for the bloc of 45 samples for segmental SNR, and the bloc of 75 samples is analysed for segmental MSE. Among the discussed algorithms, the UBTNLMS algorithm responded with the better response in both dispersive and spare impulse responses. From Figs. 5, 6, 7 and 8, it is clear that the sparse impulse response performs better than the dispersive impulse response. By increasing the adaptive filter length, sparse impulse response performs better than dispersive impulse response.

Fig. 11

SegMSE for the proposed and existing algorithm having the input SNR 0 dB (left) and 5 dB (right) by using the dispersive impulse response. The adaptive filter length is taken as L = 64

Fig. 12

SegMSE for the proposed and existing algorithm having the input SNR 0 dB (left) and 5 dB (right) by using the dispersive impulse response. The adaptive filter length is taken as L = 64

Fig. 13

SegMSE for the proposed and existing algorithm having the input SNR 0 dB (left) and 5 dB (right) by using the dispersive impulse response. The adaptive filter length is taken as L = 128

Fig. 14

SegMSE for the proposed and existing algorithm having the input SNR 0 dB (left) and 5 dB (right) by using the sparse impulse response. The adaptive filter length is taken as L = 128

5.3 Signal-to-noise ratio (SNR)

It is defined as the ratio of the speech signal to that of noise signal. The signal-to-noise ratio is given in (37). Here, SNR is calculated for total length of the samples.

5.4 Cepstral distance (CD)

It is used to measure the distortion present in the signal. The cepstral distance is given by the relation,

$${\text{CD}}_{\text{dB}} = \mathop \sum \limits_{i = 1}^{R} {\text{ISFT}}[{ \log }\left( {\left| {a\left( {\omega ,i} \right)} \right| - { \log }\left( {\left| {s_{1} \left( {\omega ,i} \right)} \right|} \right)} \right]^{2}$$

(39)

where ISFT denotes the inverse short-time Fourier transform. The STFT of the original speech signal and enhanced speech signal is $a\left( {\omega ,i} \right),\; {\text{and}}\; s_{1} \left( {\omega ,i} \right)$, respectively.

5.5 Mean square error (MSE)

Mean square error is calculated for the difference between the true values and the estimated value. The mean square error equation is given in (38). Here, MSE is calculated for total length of the samples. Table 4 shows the performance of MSE for the existing and proposed algorithms for dispersive and sparse impulse responses. From Table 4, we infer that, at 0 dB input SNR for dispersive impulse response for DFNLMS, the MSE is − 65.90 dB, RTRNLMS has − 73.17 dB, DTNLMS has − 98.34 dB, UBTNLMS has − 98.55 dB and for sparse impulse response the existing DFNLMS has the MSE of − 73.58 dB, RTRNLMS has − 80.94 dB, DTNLMS has − 106.24 dB, and UBTNLMS has − 116.99 dB. On comparing, sparse impulse response shows better performance for all the proposed algorithms when compared to the dispersive impulse response.

Table 2 shows the SNR performance for the existing and proposed algorithms for dispersive and sparse impulse responses. From Table 2, we infer that, at 0 dB input SNR for dispersive impulse response for DFNLMS, the SNR is 19.57 dB, RTRNLMS has 28.23 dB, DTNLMS has 42.85 dB, UBTNLMS has 63.74 dB and for sparse impulse response the existing DFNLMS has the SNR of 27.58 dB, RTRNLMS has 35.33 dB, DTNLMS has 42.66 dB, and UBTNLMS has 71.79 dB. On comparing with dispersive and sparse impulse responses, sparse impulse response shows better performance for all the algorithms. Table 3 shows the performance of CD for the existing and proposed algorithms for dispersive and sparse impulse responses. From Table 3, we infer that, at 0 dB for dispersive impulse response for DFNLMS, the cepstral distance is − 2.49 dB, RTRNLMS has − 3.52 dB, DTNLMS has − 6.77 dB, UBTNLMS has − 7.96 dB and for sparse impulse response the existing DFNLMS has the cepstral distance of − 3.40 dB, RTRNLMS has − 4.41 dB, DTNLMS has − 6.46 dB, and UBTNLMS has − 8.97 dB. Sparse impulse response performs better for all the algorithms.

Table 2 Performance of SNR for the existing and proposed algorithms in terms of dispersive and sparse impulse responses

Table 3 Performance of CD for the existing and proposed algorithms in terms of dispersive and sparse impulse responses

From the measures shown in Tables 2, 3 and 4, while analysing the performances in dispersive impulse response and sparse impulse response, UBTNLMS outperforms all other algorithms for sparse impulse response. Taking all the performance measure into account, while comparing the overall algorithms in both dispersive and sparse impulse responses, Sparse impulse response performance in UBTNLMS has improved much better than the dispersive impulse response in all the noise types because it automatically determines the locations of the nonzero impulse response coefficients for their adaptation and eliminates the unnecessary adaptation for zero coefficients.

Table 4 Performance of MSE for the existing and proposed algorithms in terms of dispersive and sparse impulse responses

6 Conclusion

In this work, we show that the proposed algorithms RTRNLMS, DTNLMS and UBTNLMS perform better than the existing DFNLMS algorithm. The existing algorithm has large number of processing steps for enhancing the speech signal. To overcome this problem, proposed algorithms are designed to improve the performance with reduced computational steps. Out of the three proposed algorithms, the UBTNLMS algorithm shows good behaviour of superiority for both dispersive impulse response and sparse impulse response. In specific, the UBTNLMS shows better performance for sparse impulse response. The algorithms are tested under the objective criteria like SNR, MSE, SegMSE and CD. For all the objective criteria, UBTNLMS performs better in both sparse and dispersive impulse response.