1 Introduction

In recent years, considerable attention has been directed towards time-delayed feedback stochastic systems due to its potential applications in various fields, such as neural networks [1, 2], biological control, economic market etc. The time delay is ubiquitous in nature owing to the transport of the key quantities (such as energy, matter, information) within finite propagation time. Studies have confirmed that time delay plays an important role in the dynamic systems [3, 4]. In particular, many studies have been devoted to the effects of time delay on stochastic resonance (SR) [5–7].

Noise usually plays a disruptive role in nature. However, the influence of noise on nonlinear systems has proven to be of considerable interest in recent years. Many experimental facts have clearly shown that noise can play a constructive role in nonlinear systems, such as noise enhanced stability [8–11] and noise induced stochastic resonance [12–34]. SR is a cooperative phenomenon that an external forcing signal may be enhanced by presence of an optimal amount of noise. It is originally proposed by Benzi in order to explain the periodic recurrences of the Earth’s ice ages [12]. Later, SR has attracted considerable attention and has been developed to be applied in a variety of fields, such as biophysics [13–16], neural networks [17, 18], complex networks [19], plasma physics [20], social sciences [21], soft matter systems [22], colloidal systems [23], magnetic systems [24]. There have been many theoretical and experimental developments of stochastic dynamic properties in conventional bistable systems [25, 26]. Since bistable system is an important system in real applications. SR in this system has been widely investigated in the fields of physics, chemistry, the other natural and social sciences [27–30]. In particular, SR in bistable systems with time delay driven by a variety of noises has been studied, such as Gaussian white noise [31, 32], colored noise [33], non-Gaussian noise [34].

Most of the previous studies for SR phenomenon are subject to Gaussian noise, but an experimental research shows that a lot of noises in the neural, biological and physical systems are not Gaussian. Trichotomous noise is a kind of three-level Markovian noise that is characterized by three parameters: amplitude, correlation time and flatness [35]. Due to its flexibility to model natural colored fluctuation, trichotomous noise is useful in practical applications. Recently, the SR phenomenon in dynamic systems driven by trichotomous noise has been investigated [36–40]. It is noteworthy that these literatures are for the non-delayed systems. Therefore, it is worth considering the effects caused by time delay of SR in bistable system subjected to trichotomous noise. The combination of trichotomous noise and the time delay greatly increases the statistical complexity of the system, thus many interesting dynamics phenomenon have been found.

2 Generation of trichotomous noise

In this section, the trichotomous noise is introduced in detail [35]. The noise is a random stationary Markovian process that consists of jumps between three values a, b and c. The jumps follow in time according to a Poisson process, while the values occur with the stationary probabilities:

$$P_{s} (a) = P_{s} (c) = q,\quad P_{s} (b) = 1 - 2q.$$
(1)

The transition probabilities between the three states can be obtained as follows:

$$\begin{aligned} P(a,t + \tau \left| {a,t} \right.) & = q - (q - 1)e^{ - v\tau } ,\quad \quad P(a,t + \tau \left| {b,t} \right.) = q(1 - e^{ - v\tau } ),\quad \quad P(a,t + \tau \left| {c,t} \right.) = q(1 - e^{ - v\tau } ) \\ P(b,t + \tau \left| {a,t} \right.) & = (1 - 2q)(1 - e^{ - v\tau } ),\quad \quad P(b,t + \tau \left| {b,t} \right.) = 1 - 2q(1 - e^{ - v\tau } ),\quad \quad P(b,t + \tau \left| {c,t} \right.) = (1 - 2q)(1 - e^{ - v\tau } ) \\ P(c,t + \tau \left| {a,t} \right.) & = q(1 - e^{ - v\tau } ),\quad \quad P(c,t + \tau \left| {b,t} \right.) = q(1 - e^{ - v\tau } ),\quad \quad {\kern 1pt} P(c,t + \tau \left| {c,t} \right.) = q - (q - 1)e^{ - v\tau } \\ \end{aligned}$$
(2)

Here τ > 0, 0 < q < 1/2, v > 0. P(b, t + τ|a, t) is the conditional probability that the variable ξ(t) will assume the value b at some time t + τ given that it is a at the earlier time t, denoted by P ab . Others can be defined similarly. The law of total probability at each value demands

$$P(a,t + \tau \left| {x,t} \right.) + P(b,t + \tau \left| {x,t} \right.) + P(c,t + \tau \left| {x,t} \right.) = 1,\quad x = a,b,c$$
(3)

The process is completely determined by Eqs. (1) and (2). Thus, the mean value 〈ξ(t)〉 and correlation function 〈ξ(t + τ)ξ(t)〉 of the trichotomous noise in the steady state can be calculated as:

$$\left\langle {\xi (t)} \right\rangle = aq + b(1 - 2q) + cq$$
(4)
$$\left\langle {\xi (t + \tau )\xi (t)} \right\rangle = [aq + b(1 - 2q) + cq]^{2} + \{ a^{2} q + b^{2} (1 - 2q) + c^{2} q - [aq + b(1 - 2q) + cq]^{2} \} e^{ - v\tau }$$
(5)

We can easily find that v is the reciprocal of the noise correlation time τ cor , namely v = 1/τ cor . The noise intensity D is defined as

$$\begin{aligned} D & = 2\int_{0}^{\infty } {\left( {\left\langle {\xi (\tau )\xi (0)} \right\rangle_{s} - \left\langle {\xi (\tau )} \right\rangle_{s}^{2} } \right)d\tau } \\ & = 2\frac{{a^{2} q + b^{2} (1 - 2q) + c^{2} q - [aq + b(1 - 2q) + cq]^{2} }}{v} \\ & = 2\tau_{cor} \left\{ {a^{2} q + b^{2} (1 - 2q) + c^{2} q - [aq + b(1 - 2q) + cq]^{2} } \right\} \\ \end{aligned}$$
(6)

From the above, we are now in a position to generate realizations of a stochastic process for a trichotomous noise. The numerical algorithm of the sequence generation of ξ(t) is similar to that of dichotomous noise [41, 42]. First of all, let the particle be located initially at x n  = a. To determine whether the particle moves at time t + Δt to other two sites x n+1 = b, x n+1 = c or remains at the same site x n+1 = a, we consider the transition probabilities P aa , P ab , P ac given by Eq. (2). A random number R n from a uniform distribution on [0, 1] is generated using Matlab, which is used to compare with the transition probabilities. If R n  < P aa , we accept the value of the noise a, i.e., x n+1 = a; otherwise, if P aa  < R n  < P aa  + P ab , we accept the value x n+1 = b; otherwise x n+1 = c.

If the value of the noise is x n+1 = s(s = b, c), then we compare the transition probabilities P sa , P sb , P sc with another uniformly distributed random number R n+1 between 0 and 1. If R n+1 < P sa , the value of the noise at t + 2Δt is x n+2 = a; otherwise, if P sa  < R n+1 < P sa  + P sb , we accept the value x n+2 = b; otherwise x n+2 = c. By repeating the procedure we obtain a sequence of random numbers ξ(t) switching among three values a, b and c.

Figures 1(a) and 1(b) show the profiles of the asymmetric trichotomous noise for the states a = 3, b = 0, c = −1. Figs. 1(c) and 1(d) show the profiles of the symmetric trichotomous noise for the states a = 1, b = 0, c = −1. One can observe clearly that the residence time extends with the increase of noise intensity under the same states and q. When q = 1/2, the trichotomous noise reduces to dichotomous noise, as shown in Fig. 1(d).

Fig. 1
figure 1

(a, b) are the profiles of asymmetric trichotomous noise for the states a = 3, b = 0, c = −1. (a) D = 1, q = 0.3, (b) D = 5, q = 0.3, (c, d) are the profiles of symmetric trichotomous noise for the states a = 1, b = 0, c = −1. (c) D = 0.2, q = 0.3, (d) D = 1, q = 0.5

Full size image

In order to check the accuracy of the numerical method for generating the trichotomous noise ξ(t), Fig. 2 shows the plots of the normalized correlation function 〈ξ(t + t′)ξ(t)〉/〈ξ(t)2〉 versus t′ of the noise for a = 1, b = 0, c = −1, q = 0.3 for several values of τ cor . In this condition, we can calculate the noise intensity D according to τ cor from Eq. (6) that is, when τ cor  = 0.5, 2, 5, D = 0.6, 2.4, 6. The analytical results have a good agreement with the numerical simulation results when the noise correlation time τ cor is relatively small, i.e., τ cor  ≤ 2. In the following section, all the values of the noise intensity D are found to be satisfactory (D ≤ 1).

Fig. 2
figure 2

Plots of the normalized correlation function versus t′ for a = 1, b = 0, c = −1, q = 0.3, for three different noise profiles with given correlation times τ cor  = 0.5, 2 and 5. The red lines refer to analytical results from Eq. (5), and the blue filled circles, rhombuses and triangles represent numerical simulation results

Full size image

3 Model system

Delay plays very important role in dynamics systems. Refs. [43–46] concern the time delay inserted in the linear term of the different models. Refs. [47, 48] study the nonlinear case. Here we consider a typical time-delayed bistable system [49] driven by trichotomous noise and a periodic cosinoidal signal. Our prototypical model is the overdamped particle motion in the double-well quartic potential, which can be described by the following Langevin equation:

$$\begin{aligned} \frac{dx(t)}{dt} & = - \frac{\partial U(x(t),x(t - \tau ))}{\partial x} + \xi (t) + A_{0} \cos (\omega_{0} t) \\ & = x(t) - x(t)^{3} + \varepsilon x(t - \tau ) + \xi (t) + A_{0} \cos (\omega_{0} t) \\ \end{aligned}$$
(7)

where τ is the time delay in the linear term and ɛ is the feedback strength, A 0 and ω 0 are the amplitude and the frequency of the signal, respectively. ξ(t) is symmetric trichotomous noise with a = −c, b = 0 as defined in Sect. 2. According to Eq. (7), we can calculate and obtain two stable points \(x_{1} = - \sqrt {1 + \varepsilon }\), \(x_{2} = \sqrt {1 + \varepsilon }\) and the unstable point x 0 = 0 in the absence of the external periodic force. It means that the locations of unstable point and stable points are not affected by the time delay. The potential function of Eq. (7) can be obtained by means of small delay approximation method as Ref. [31].

$$U(x) = - (1 + \varepsilon \tau )\left( {\frac{1}{2}x^{2} - \frac{1}{4}x^{4} } \right) - \frac{1}{2}\varepsilon (1 + \varepsilon \tau )x^{2} + (1 + \varepsilon \tau )\,A_{0} \cos (\omega t)x$$
(8)

Notice that the depth and width of potential wells is related to the time delay τ and feedback strength ɛ.

Figure 3(a) shows the potential profile of the bistable system in the average and limiting positions due to amplitude of the periodical driving. It is clearly shown that the depth in left well extends while in right well reduces with the increase in signal amplitude A 0. Moreover, Fig. 3(b) shows the potential profile in the limiting positions due to the three values of the trichotomous noise: a = 1, b = 0, c = −1 in the presence and in the absence of the periodical driving signal. All these profiles of the potential will give more insight in understanding the physics and therefore to obtain good explanation of results obtained in the SNR behavior and system responses in the following section.

Fig. 3
figure 3

(a) The potential profile U(x) without the trichotomous noise for different values of signal amplitude A 0. Other parameters are ɛ = −0.3, τ = 0.2, ω 0 = 0.05. (b) The potential profile U(x) with the trichotomous noise in the presence and in the absence of the periodic driving signal. Other parameters are a = 1, b = 0, c = −1, D = 0.1, q = 0.3, ɛ = −0.3, τ = 0.2, ω 0 = 0.05

Full size image

4 Numerical results

Due to the existence of time delay and trichotomous noise, the random response is not essentially Markovian. Thus, it is difficult to derive the analytic expression of SNR. In this paper, we use SNR metric to quantify the SR by means of numerical simulation. The definition of SNR is given as follows [50]:

$$SNR = 10\log \frac{S}{N}dB = 10\log \frac{{S(\omega_{0} )}}{{N(\omega_{0} )}}dB$$
(9)

The signal power S = |Y(ω 0)|2 is the magnitude of output power spectrum Y(ω) at input frequency ω 0. The background noise spectrum N(ω 0) at input frequency ω 0 is some average of |Y(ω)|2 at nearby frequencies.

Figure 4 shows the system responses for different values of feedback strength ɛ with fixed noise strength. It is clearly shown that the switching between the two wells decreases with increase in feedback strength. Thus, the larger feedback strength may suppress the occurrence of SR. In order to further study the influence of the feedback strength on SR behavior, the SNR, as a function of the noise intensity for different values of the feedback strength ɛ, are displayed in Fig. 5. We observe a maximum SNR for small ɛ with increased noise intensity D, indicating the existence of SR. In addition, with increasing ɛ, the maximum of SNR decreases and the position of the maximum shifts towards the larger value of noise intensity, which show that the SR is weakened. The reason for this phenomenon is that the depth and width of the potential wells increase with the increase of ɛ under fixed τ, since the particles need larger noise D to cross the barrier. Figs. 4 and 5 are in good agreement with each other. In conclusion, the increase of the feedback strength ɛ leads to the weakening of SR phenomenon.

Fig. 4
figure 4

The system responses for different values of the feedback strength ɛ with fixed noise strength τ = 0.2 and the other parameters D = 0.1, a = 1, q = 0.3, A 0 = 0.15, ω 0 = 0.05 (a) ɛ = −0.3, (b) ɛ = −0.1, (c) ɛ = 0, (d) ɛ = 0.4

Full size image
Fig. 5
figure 5

SNR as a function of noise intensity D for different values of the feedback strength ɛ. Other parameters are same as Fig. 4

Full size image

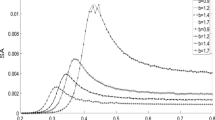
The plots of SNR under noise intensity D and time delay τ with negative feedback strength ɛ = −0.3 are presented in Fig. 6. It can be seen from Fig. 6(a) that the curves of SNR always have a peak as increasing the noise intensity which indicates the occurrence of SR phenomenon. The height of the peaks increases slightly with increasing time delay τ. To see it more clearly, the SNR as a function of the noise intensity D for different time delay τ = 0.1, 0.3, 0.8 are given in Fig. 6(b). These two figures demonstrate that larger time delay has a positive effect on enhancing the SNR in the case of negative feedback strength.

Fig. 6
figure 6

(a) SNR as a function of noise intensity D and time delay τ. (b) SNR as a function of noise intensity D for different values of time delay τ. Other parameters are ɛ = −0.3, A 0 = 0.15, ω 0 = 0.05, a = 1, q = 0.3

Full size image

Similarly, the influence of the time delay τ on SNR is presented with positive feedback strength ɛ = 0.2 in Fig. 7. The SNR as a function of noise intensity D and time delay τ is presented in Fig. 7(a). Note that each curve has a peak and the value of the peak decreases with increase in time delay. Thus, in the case of positive feedback strength, the larger time delay suppresses the SR phenomenon. In particular, the curves of SNR for different time delay τ = 0.1, 0.3, 0.8 are shown in Fig. 7(b). Comparing Figs. 6 and 7, all the peaks in Fig. 6 have larger values than that in Fig. 7, and the peak’s positions shift to larger noise intensity, which have a good agreement with the above-mentioned results in Figs. 4 and 5.

Fig. 7
figure 7

(a) SNR as a function of noise intensity D and time delay τ. (b) SNR as a function of noise intensity D for different values of time delay τ. Other parameters are ɛ = 0.2, A 0 = 0.15, ω 0 = 0.05, a = 1, q = 0.3

Full size image

In Figs. 8 and 9, the influence of signal amplitude and frequency on SNR is studied. The SNR as a function of noise intensity D and signal amplitude A 0 are investigated in Fig. 8(a). It can be seen that, for any value of A 0, the curves of SNR always have a peak with increasing noise intensity D, which is characteristic of the SR phenomenon. Also, the height of the peaks increases gradually while the position on the x-axis almost remains unchanged with increase of A 0. In Fig. 8(b), the SNRs are plotted as a function of the noise intensity D with signal amplitude A 0 = 0.05, 0.08, 0.12, 0, 16, respectively. Therefore it is concluded that larger amplitude A 0 leads to the promotion of SR phenomenon.

Fig. 8
figure 8

(a) SNR as a function of noise intensity D and signal amplitude A 0. (b) SNR as a function of noise intensity D for different values of signal amplitude A 0. Other parameters are ω 0 = 0.05, ɛ = −0.3, τ = 0.5, a = 1, q = 0.3

Full size image
Fig. 9
figure 9

(a) SNR as a function of noise intensity D and signal frequency ω 0. (b) SNR as a function of noise intensity D for different values of signal frequency ω 0. Other parameters are A 0 = 0.15, ɛ = −0.3, τ = 0.5, a = 1, q = 0.3

Full size image

Compared to Fig. 8, the phenomenon observed from Fig. 9 is opposite. Figure 9 shows the effect of signal frequency ω 0 on SNR. It can be seen that, for ω 0 ≥ 0.06, the SNR first decreases rapidly and reaches a minimum, then it increases monotonically until it reaches a maximum, and then it decreases with increasing the value of D. The maximum of SNR decreases with the increase in frequency ω 0 i.e., the larger frequency suppresses the occurrence of SR. Concerning the behavior shown in the Fig. 9, it is worthwhile to note that for small noise intensity D, the presence of the minimum in the SNR versus the noise intensity is a typical behavior observed experimentally and predicted theoretical [51, 52].

Further the influence of trichotomous noise parameters on SNR to be considered. In Fig. 10(a), SNR is a function of noise intensity D for different amplitudes a. Within a certain range of a, the non-monotonic structure of SNR affirms the occurrence of SR. The SNR curve changes slightly with the increase of a. Note that when the amplitude a is too large, the SR phenomenon disappears. Figure 10(b) shows SNR as a function of the noise intensity D with different stationary probability q. For any values of q, there exists a peak in each curve of SNR, which denotes the existence of SR. With increasing q, the height of peaks gradually increases and the position of the peak shifts towards larger noise intensity, which indicates that the SR can be enhanced by increasing q. In conclusion, SR can be enhanced by adjusting noise parameters.

Fig. 10
figure 10

SNR as a function of noise intensity D for different values of (a) the noise amplitude a and (b) the noise stationary probability q with ɛ = −0.3, τ = 0.5, A 0 = 0.15, ω 0 = 0.05. (a) q = 0.3, (b) a = 1

Full size image

5 Conclusion

In this paper, we have focused on the SR phenomenon in a time-delayed bistable system subjected to trichotomous noise by using numerical simulation.

First, an algorithm for numerically generating a trichotomous noise is created and its accuracy is checked using normalized autocorrelation function. The agreement between analytical results and numerical results is found to be satisfactory. Second, the effects of the feedback strength and time delay on the system responses and SNR are discussed in detail. The results indicate that an increase in the feedback strength leads to the weakening of SR phenomenon i.e., the negative feedback strength is more beneficial to promote SR than positive feedback. Also, the effect of time delay on SNR with negative feedback strength is opposite to the positive one. Third, the influence of signal amplitude and frequency on SNR is observed. It is found that larger amplitude signal lead to the promotion of SR phenomenon and larger signal frequency suppressed the occurrence of SR. Finally, the influence of trichotomous noise parameters on SR phenomenon is focused. The results show that SR occurs only with a certain range of noise amplitude and it is more beneficial for occurrence of SR phenomenon with large stationary probability.